Domain movements in human fatty acid synthase by quantized elastic deformational model

Abstract

This paper reports the results of applying a computational method called the quantized elastic deformational model, to the determination of conformational flexibility of the supermolecular complex of human fatty acid synthase. The essence of this method is the ability to model large-scale conformational changes such as domain movements by treating the protein as an elastic object without the knowledge of protein primary sequence and atomic coordinates. The calculation was based on the electron density maps of the synthase at 19 Å. The results suggest that the synthase is a very flexible molecule. Two types of flexible hinges in the structure were identified. One is an intersubunit hinge formed by the intersubunit connection and the other is an intrasubunit hinge located between domains I and II. Despite the fact that the dimeric synthase has a chemically symmetric structure, large domain movements around the hinge region occur in various directions and allow the molecule to adopt a wide range of conformations. These domain movements are likely to be important in facilitating and regulating the entire palmitate synthesis by coordinating the communication between components of the molecule, for instance, adjusting the distance between various active sites inside the catalytic reaction center. Finally, the ability to describe protein motions of a supermolecular complex, without the information of protein sequence and atomic coordinates, is a major advance in computational modeling of protein dynamics. The method provides an unprecedented ability to model protein motions at such a low resolution of structure.

The synthesis of long-chain saturated fatty acids—palmitate, from acetyl-CoA, malonyl-CoA, and NADPH—is catalyzed by the fatty acid synthase (FAS; EC 2.3.1.85; ref. 1). In this reaction, acetyl-CoA is the primer, malonyl-CoA is the two-carbon donor, and NADPH is the source of reduction of various intermediate products. In animal tissues, including human's, the entire synthesis is carried out by FAS that contains seven catalytic activities and an acyl-carrier protein (ACP). The seven catalytic sites of FAS and ACP are covalently connected together in a single polypeptide chain encoded by a single gene (1–4). The native enzyme is a dimer of two identical subunits (1, 3), each of which has a molecular weight of 272,000. The homodimer, whose formation is essential to FAS function (5–8), is arranged in a head-to-tail fashion, forming two active catalytic centers (6). On each subunit, from the N terminus to the C terminus, the catalytic sites along the multifunctional polypeptide chain are arranged in the order of β-ketoacyl synthase (KS), acetyl/malonyl transcylase (AT/MT), β-hydroxyacyl dehydratase (DH), enoyl reductase (ER), β-ketoacyl reductase (KR), ACP, and thioesterase (TE). Biochemical studies showed that these active sites are grouped into three structural domains (9–13). Domain I (residues 1 to 980) contains KS, AT/MT, and DH. Domain II (residues 1,631 to 2,208) contains ER, KR, and ACP. Domain III (residues 2,209 to 2,504) contains TE. In addition, there is an interdomain region of 649 aa (residues 981 to 1,630) between domains I and II with no catalytic activity. It has been shown that this interdomain region plays a role in the dimer formation (14). Because of the antiparallel arrangement of the subunits (6), each active catalytic center is formed by domain I of one subunit and domains II and III of the second subunit. Both centers have been shown to be simultaneously active (3). Abolishing the formation of the dimer results only in loss of palmitate synthesis and the β-ketoacyl synthase activity but not the other six partial activities.

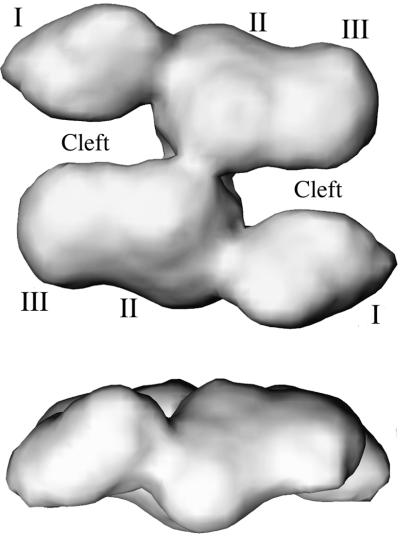
Recently, the three-dimensional (3D) structure of FAS was determined by the cryo-electron microscopy (cryo-EM) technique to about 19 Å resolution (15). The results (Fig. 1) confirmed previous biochemical studies that the two subunits in the dimer are arranged in an antiparallel fashion. There is also clear electron density located between the two subunits, presumably corresponding to the interdomain region. In addition, two distinct clefts with a stride of 20 to 25 Å wide between domain I of one subunit and domains II and III of the second subunit were observed, which have been proposed to be the locations of the catalytic reaction centers (15).

Figure 1.

The electron density maps of FAS determined by cryo-EM at 19 Å resolution (15). Only the one with a 2-fold symmetry imposed in the reconstruction is shown. The Upper one is a top view and the Lower one is a side view. Domains I, II, III, and clefts are labeled. The figures are made by using software vmd (41).

One of the central issues in the function of FAS is the structural flexibility. FAS is a multidomain complex with a very unique nonglobular quaternary arrangement. Much like many other multidomain supermolecular complexes (16, 17, 42), the dynamics of the structure likely play a very important role in the functions (18), especially in the enzyme regulatory mechanisms. In particular, domain movements of FAS are likely to be essential for facilitating the multistep catalytic reaction of the synthesis of palmitate. The flexibility of FAS has been suggested from the conformational heterogeneity of the dimer in the cryo-EM reconstruction (15), despite the apparent symmetry in its chemical structure.

To study structural dynamics of a protein such as FAS, computer simulations (19, 20) can play an important role. To date, however, all of the methods for describing the motions of a protein require the knowledge of protein sequence and atomic coordinates. In the case of FAS, the only available structural information is a fuzzy image of the molecule at 19 Å resolution, which is not much more than the rough shape of the molecule. This situation is also true for many other supermolecular complexes and membrane-bound proteins. Therefore, a fundamental challenge is to describe the motions of these proteins, at least the gross features, based on their fuzzy images. The success of such an attempt would elevate one's ability to model protein motions to a completely new level. It could also influence broader fields such as bioinformatics, structural genomics, and proteomics, in which one's ability to extract motional information from less well-defined structural models is critically important.

To meet such a challenge, we have recently developed a computational method, the quantized elastic deformational model (QEDM; ref. 43), which is able to extract the gross motional information of a protein solely based on its rough shape and mass distribution. The fundamental assumption of this method is that the structure of a folded protein can be treated as an elastic object. The mass density distribution of the object is equivalent to the electron density distribution of the protein. The thermal motions of the structure are then treated as elastic deformations. This assumption is especially valid for supermolecular complexes such as FAS, in which the functionally important conformational changes, such as domain movements (18), are mediated by collective global deformations of the structure. As shown in numerous cases of standard normal mode analysis (NMA; refs. 16, 17, 21–25, and 44), the motional patterns of the functionally important conformational changes can be matched by the intrinsic low-frequency deformational modes. Moreover, these collective global motions are not sensitive to the local connectivity of the protein structure. They are predominantly influenced by the global shape and mass distribution of the molecule (26).

In this paper, we applied QEDM to the 19-Å electron density maps of FAS to study the conformational flexibility. Significant insights into the functionally important motions of FAS have been obtained.

Methods

The domain movements of FAS were determined by the quantized elastic deformational model (QEDM) based on cryo-EM electron density maps at 19 Å resolution. QEDM is a computational method that combines and enhances the vector quantization method and elastic network models for computing intrinsic deformational motions of protein structures by using low-resolution electron density maps. In this section, we outline the essential features of QEDM.

Vector Quantization Method.

Vector quantization is a method initially designed for image processing or digital signal compression (27, 28). It has recently been introduced to the docking of a flexible protein structure into a cryo-EM density map (29). The method discretizes an irregularly shaped three-dimensional electron density map of a biological molecule into a set of finite Voronoi cells. The centroids of these cells are represented by a set of vectors vⁱ ∈ ℜ³, i = 1, … , N, whose positions are determined by minimizing the error function E of the discrete data representation:

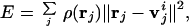1

where r_j ∈ ℜ³ is the data point with the grid index j, ρ(r_j) is the corresponding electron density on the grid point, and v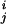 is the centroid vector closest to r_j. Here, E is the mean-square deviation of the centroid vectors of Voronoi cells from the encoded 3D electron density map. To locate an optimal set of centroid positions, the topology-representing neural network (30, 31) is used to find the global minimum of E. Therefore, the resulting set of Voronoi cells can best characterize the shape and density of the 3D object. In handling a protein electron density map, the number of Voronoi cells N can be either the same as the number of amino acids in the protein, or not.

Elastic Network Models.

In recent years, there have been methods that operate under a fundamental assumption that the dynamics of a folded globular protein can be approximately described as an elastic network. It has been shown that these methods can reproduce the amplitudes and directionality of thermal fluctuations of a protein structure remarkably well. Two relevant ones are the Gaussian network model (GNM; refs. 32, 33) and the anisotropic network model (ANM; refs. 34 and 35). GNM was developed to compute the amplitudes of isotropic thermal fluctuations of amino acid residues based on C_α positions. Its improved version, ANM, can deliver the directionality of the fluctuations, which is often more important. Mathematically, ANM is essentially an NMA (36) on the harmonic potential (35),

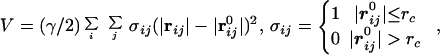2

where |r_ij| and |r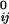| are the instantaneous and equilibrium values (or initial values from the coordinates) of pairwise distance between the ith and the jth C_α atoms, respectively. The value of σ_ij is that of the Heaviside step function, which describes the cutoff effect of the interaction. The functional form of Eq. 2 resembles that of the molecular mechanics potential function commonly used for chemical bond (37), i.e., the potential is proportional to the square of the difference of the instantaneous and the equilibrium values of the pair distance. A very important advantage of ANM is that it regards the initial coordinates as the equilibrium coordinates. This feature allows one to avoid the initial energy minimization required in standard NMA (36) that often significantly distorts structures.

Similar to standard NMA (36), the direction of motion in each deformational mode is given by a 3N-dimensional eigenvector calculated from diagonalization of the second derivative matrix, H, of the total potential function (Eq. 2; ref. 36) by a matrix transformation,

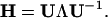3

Here, U is a matrix whose columns are the eigenvectors of H, and Λ is a diagonal matrix that contains the eigenvalues of H (force constants of the harmonic modes). For a nonlinear 3D system, there are totally 3N − 6 deformational modes.

The Quantized Elastic Deformational Model.

In the original GNM (32, 33) and ANM (34, 35), the flexibility of a protein structure is determined based on the positions of C_α atoms, or a subset of them (38). Therefore, they still require the knowledge of atomic coordinates. QEDM combines and enhances the vector quantization method and ANM (or GNM) to determine protein dynamics from the low-resolution electron density map of a protein without the atomic coordinates. In QEDM, vector quantization is used to numerically discretize the 3D continuous electron density map of a biological molecule into a set of Voronoi cells that rationally approximate the shape and density distribution of the original map. The number of cells can be chosen at will for a desired level of accuracy in characterizing the density map. Then, the deformational modes can be determined by ANM. QEDM has been tested on proteins with known atomic structures, and the results were compared with those from more vigorous methods. It was shown that the new method is capable of delivering reliable patterns of thermal deformational motions of proteins (43). In following sections, QEDM is applied to computing the patterns of thermal deformational motions of FAS from 19-Å electron density maps obtained from cryo-EM reconstruction (15).

Results and Discussion

Application of QEDM to the 19-Å Electron Density Maps of FAS.

The new method QEDM is applied to the 19-Å electron density maps of FAS to compute the patterns of thermal deformational motions. There are two types of structural models available from cryo-EM reconstruction (15). One has a 2-fold symmetry imposed during the reconstruction and the other one does not. In this study, the one with 2-fold symmetry imposed was used for calculation. As will be shown later, the heterogeneity of conformational distribution will come out naturally in the patterns of the deformational modes.

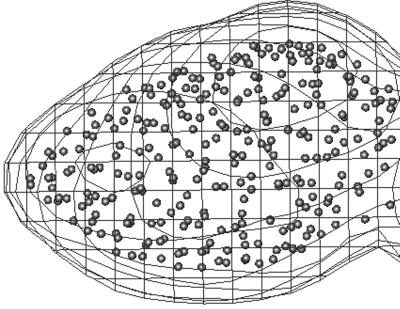
In discretizing the electron density maps of FAS, the number of Voronoi cells was chosen to be 2,300, which is about half of the number of amino acid residues in the homodimer of FAS. Our previous studies have shown that the patterns of the lowest-frequency modes are not sensitive to the number of the cells (43), especially for very large complex systems. Fig. 2 shows the positions of a portion of Voronoi centroids superimposed with corresponding cryo-EM electron density map. The density threshold used in discretizing the electron-density map was 0.2 (39). A modified topology-representing neural network (30, 31) was used for determining and optimizing the positions of the Voronoi centroids. The cutoff distance for potential energy function in Eq. 2 was 13 Å. This distance was sufficient to result in six zero-frequency modes before the lowest frequency vibrational mode (mode 7; Fig. 3a). The force constant, γ, in Eq. 2 was set to 1.0. It has been shown that the patterns of deformational modes, or the directionality of the eigenvectors, do not depend on the value of this constant (43). With high-resolution structures, the value of γ can be determined by normalizing the B-factors against the experimental data (33, 43), which, however, is not possible in FAS. That is also why the absolute values of the eigenvalues of the deformational modes are irrelevant in this case.

Figure 2.

The positions of the Voronoi centroids used in QEDM. For clarity, only a portion of density for the domain I is shown. The electron density is depicted by the contour lines and the small spheres are used to indicate the positions of the Voronoi centroids.

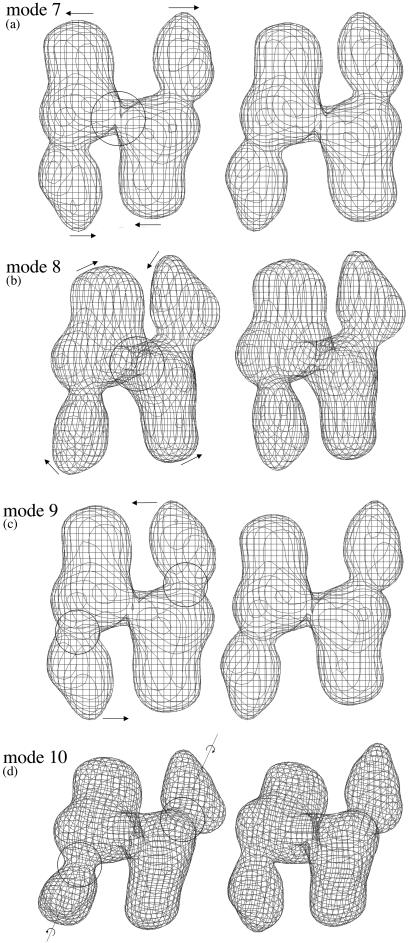
Figure 3.

The motional patterns of the first four lowest-frequency deformational modes: mode 7 (a), 8 (b), 9 (c), and 10 (d). Note that the first six modes are zero modes corresponding to global translation and rotation of the entire molecule. For each mode, two opposite conformations (left and right) during harmonic vibration are shown to illustrate the direction of the motion. The amplitude of the motion was arbitrarily chosen for visual clarity. The arrows are used to indicate the directions of the motions. The larger circles in a and b indicate the intersubunit hinge, and the smaller circles in c and d indicate the intrasubunit hinges. The dotted lines in d indicate the longest axes of the subunits.

Domain Movements of FAS Revealed by QEDM.

The most significant results from the simulation are that there exist two types of major flexible hinges in the dimeric structure of FAS. One is an intersubunit hinge located at the small intersubunit connection (Fig. 3 a and b), and the other is an intrasubunit hinge located at the relatively thin neck region between domains I and II (Fig. 3 c and d). A FAS dimer has one intersubunit hinge between two subunits and two intrasubunit hinges from two subunits.

The features of the low-frequency deformational modes clearly reveal the nature of rigid-body domain movements of FAS around these hinges. In the very lowest-frequency mode (mode 7), the motion is primarily around the intersubunit hinge (Fig. 3a). Each subunit moves as a rigid body, and the dimer undergoes a see-saw-like bending around the 2-fold symmetry axis in the pseudoplane of the dimer. Such a motion can transiently alter the width of the cleft by, for example, bringing domain I closer toward domains II and III in the opposite subunit, which would be advantageous in facilitating the elongation of fatty acyl chain between the cysteine sulfhydryl group of condensing enzyme and the phosphopantetheine sulfhydryl group of ACP. Early biochemical study (1) showed that the two sulfhydryl groups from two opposite sides of the catalytic reaction center can be cross-linked by a disulfide bond very quickly, indicating that the two sides are in direct proximity—an event that can presumably take place via large domain movements similar to what is described here. It should also be noted that the traditional textbook view of the mechanism is that the enzyme subunits do not have to move too much; rather, it is the long and flexible (20-Å maximal length) phosphopantetheinyl moiety of ACP that carries the substrate from one active site to the another. Although our work here does not directly rule out such a possibility, there are growing lines of biochemical evidence showing that the flexibility of the enzyme plays a dominating role in shuffling the substrates. One of those is the fact that the termination of fatty acid synthesis, catalyzed by thioesterase TE2 expressed in lactating mammary gland in the same reaction center, does not occur until the length of the chain reaches 14 carbons or longer. But a free TE introduced externally can terminate the synthesis for a shorter chain (1). A reasonable explanation for this fact is that the motion of fatty acid chain is restricted during synthesis by, for example, remaining bound to the enzyme. Then, it would be the enzyme that carries out the transporting between various active sites.

In addition to the very lowest-frequency mode, other neighboring low-frequency modes also reveal important domain movements. The second lowest-frequency mode (mode 8) describes an out-of-plane twisting, nearly perpendicular to mode 7, between two rigid subunits around the intersubunit hinge (Fig. 3b). This type of motion could effectively bring the subunits in two opposite catalytic reaction centers closer. The combination of mode 7 and 8 would allow the two subunits to make large-scale motions around the intersubunit hinge, as those described by the Lissajous figure in classical mechanics (40). The third (mode 9; Fig. 3c) and fourth (mode 10; Fig. 3d) lowest-frequency modes reveal the motions around the two intrasubunit hinges. In the third one, domains II and III from both subunits act like a single connected rigid body, whereas the two domain I swing in the opposite direction more or less in the plane of the dimer. In the fourth mode, the motions of the two domain I are primarily a twisting motion around the longest axis of their own subunit. Similar to the third mode, no significant relative movements are involved between domains II and III in the fourth mode. The modes immediately after these four lowest-frequency ones have mixed motional features around different hinges (not shown).

Taken together, the conformational fluctuation of FAS can be viewed as the combination of these fundamental deformational modes. Despite the fact that the dimeric FAS molecule has a chemically symmetric structure and our calculation was based on the structure with a 2-fold symmetry imposed, the results of QEDM clearly demonstrate that the structure of FAS is highly flexible and heterogeneous. Large-scale domain movements can occur in various directions, which allow the FAS molecule to adopt a wide range of conformations. Those domain movements are likely to be important to facilitating and regulating the entire synthesis by coordinating the communication between components of the structure, for instance, altering the distance between various active sites inside the catalytic reaction center. It should also be noted that another usage of the heterogeneous conformational distribution revealed in QEDM is to improve the refinement in the cryo-EM reconstruction. Moreover, despite the high flexibility of FAS domains, this study suggests that the two ends of FAS have an equal probability for adopting different conformations. Therefore, the results justify our choice of performing the computation based on the symmetric electron density map (15).

In conclusion, this paper reports the results of application of a computational method called the quantized elastic deformational model (QEDM), to the determination of conformational flexibility of the supermolecular complex FAS based on the low-resolution electron density maps at 19 Å. The concept of QEDM lies in the realization that, in modeling large conformational changes such as domain movements, it is feasible to abandon the traditional concepts of protein structure (bonds, angles, and dihedrals, etc.) and to regard the structure as an elastic object. The shape and mass distribution of the elastic object are provided by the electron density maps of the proteins, at various resolutions, from methods such as x-ray diffraction or cryo-EM. The amplitudes and directionality of the elastic deformational modes of the structure can then be determined solely based on the low-resolution electron density map. Numerous previous studies have demonstrated that the patterns of those modes match the biologically relevant conformational changes of proteins.

It should be cautioned that, although the rigid-body domain movements of FAS are unequivocally revealed in this study and those movements are almost as accurate as what one can get from atomic coordinates (43), our ability to decipher the roles of these motions in the synthesis turnover of FAS is still limited by the resolution of the structure. Issues regarding more detailed catalytic mechanisms for each individual reaction step still await the atomic-resolution structure of FAS.

Abbreviations

QEDM

quantized elastic deformational model

GNM

Gaussian network model

ANM

anisotropic network model

NMA

normal mode analysis

cryo-EM

cryo-electron microscopy

FAS

fatty acid synthase

ACP

acyl-carrier protein

TE

thioesterase

3D

three-dimensional

Note Added in Proof.

We learned in the proof stage that another team of scientists at The Scripps Research Institute is also working on similar approaches (Charles L. Brooks III, personal communication).