Simulations of β-hairpin folding confined to spherical pores using distributed computing

Abstract

We report the thermodynamics and kinetics of an off-lattice Go model β-hairpin from Ig-binding protein confined to an inert spherical pore. Confinement enhances the stability of the hairpin due to the decrease in the entropy of the unfolded state. Compared with their values in the bulk, the rates of hairpin formation increase in the spherical pore. Surprisingly, the dependence of the rates on the pore radius, R_s, is nonmonotonic. The rates reach a maximum at R_s/R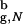 ≃ 1.5, where R 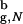is the radius of gyration of the folded β-hairpin in the bulk. The denatured state ensemble of the encapsulated β-hairpin is highly structured even at substantially elevated temperatures. Remarkably, a profound effect of confinement is evident even when the β-hairpin occupies less than a 10th of the sphere volume. Our calculations show that the emergence of substantial structure in the denatured state of proteins in inert pores is a consequence of confinement. In contrast, the structure of the bulk denatured state ensemble depends dramatically on the extent of denaturation.

Folding in cells occurs in the presence of lipids, carbohydrates, and other biological molecules, i.e., in a crowded environment (1, 2). Therefore, many proteins spontaneously fold to their native states in the environment, which geometrically restricts their conformational space (3). There are many reasons for considering folding in confined spaces. The recognition and encapsulation of a substrate protein by the GroEL molecule places it in a cylindrical cavity. Much of the annealing action takes place in a dynamic cage that is built by the interactions of GroEL with GroES (4). In the course of protein synthesis the nascent polypeptide chain is confined to a narrow “tube” (5). Such a narrow space subjects the protein to a tensile force (f ∼ k_BT/D, where D is the diameter of the pore), which may play a role in mechanically squeezing the newly synthesized protein out of the ribosome. These considerations and other studies (6–9) probing the effect of confinement on protein stability have motivated the present work.

Recently, Eggers and Valentine examined the structure of four proteins encapsulated in a silica matrix (8). They showed that, in general, confinement leads to enhanced stability of the folded protein. For example, they surmised that the encapsulation of α-lactalbumin results in the increase in the melting temperature, T_m, by ≈30°C. However, the relationship between confinement and enhanced stability of a folded state is not simple, because changes in the water structure in pores could alter the interactions stabilizing the native state (9). Nevertheless, it seems that confinement generally increases the stability of the native structure.

Folding in a crowded cellular environment may be modeled by confining a polypeptide chain to narrow pores. The enhanced stability in pores was explained recently by Zhou and Dill using polymer physics concepts (6). If the denatured state of a polymer chain is assumed to be a random coil, then the free energy cost to localize it in a region of size D (e.g., sphere, slit, or tube) is ΔF_U ≈ RTN(a/D)^1/ν (10), provided that D < N^νa, where a may be taken to be the average distance between the C_α atoms (≈3.8 Å), and N is the number of residues. (This estimate is accurate up to a logarithmic factor in D.) The Flory exponent ν relates the radius of gyration of a chain R_g at D → ∞ (the size of a chain in bulk solution) to N according to R_g ≃ aN^ν. If the chain is ideal, then ν = 0.5 and ΔF_U = RTN(a/D)². Because of the reduction in the translational entropy, confinement also increases the free energy of the native state, i.e., ΔF_N > 0. If ΔF_N/ΔF_U ≪ 1, then localization of a protein in a confined space stabilizes the native state compared with the bulk. It also follows that there is a range of D values over which stability is maximized. These arguments and the explicit calculations of polymers confined to slits (11) suggest that excluded volume effects should not qualitatively alter the conclusions reached by Zhou and Dill (6). Because confining an unfolded chain with excluded volume leads to higher entropy costs (provided a < D < N^νa), the change in stability estimated by assuming that the denatured state is ideal should be a lower bound.

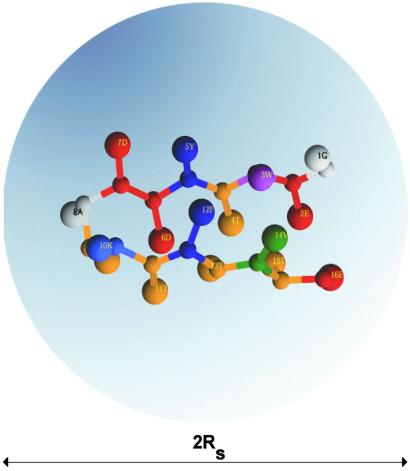
In this article we examine the effects of confinement on the nature of the denatured state ensemble (DSE), folding rates, and stability by studying β-hairpin formation in spherical pores of different radii R_s (Fig. 1). We find that confinement, which may be considered as a model for the hydrophilic cavity in GroEL (12), leads to enhancement in the folding rates and stability compared with their values at R_s → ∞. Throughout the paper we refer to the bulk hairpin when R_s → ∞ and the terms “confined” and “encapsulated” hairpins are used interchangeably. Superscripts b and c refer to bulk and confined cases, respectively.

Figure 1.

Encapsulation of 16-mer C-terminal β-hairpin from the protein G in a spherical pore of the radius R_s is sketched. The surprising outcome of this work is that even confinement to relatively large pores (R_s/R ≳ 2.0) has a profound effect on the hairpin stability and folding rates. The amino acids in the β-hairpin are color-coded and annotated with a one-letter code.

Methods

Model.

To study confinement effects we use a 16-residue C-terminal β-hairpin from protein G (Fig. 1), for which experimental (13, 14) and theoretical (15) studies have been reported. We provide a brief overview of the model and simulation technique (see ref. 15 for details) focusing on the relevant changes caused by confinement.

The off-lattice coarse-grained protein model explicitly includes the backbone C_α carbons and side chains, which are represented as spheres of appropriate van der Walls radii positioned at the centers of mass of amino acids. The model includes backbone hydrogen bonds (HBs) between NH and CO groups, which are treated as virtual moieties between adjacent C_α atoms (15). The potential energy of a bulk conformation of polypeptide chain V_b is given by the sum of bond-length potential, side chain–backbone connectivity potential, bond-angle potential, dihedral angle potential, HB and nonbonded long-range potentials (15).

Because our goal is to study the effect of confinement on the β-hairpin formation, the Go model, which includes only native interactions, should suffice. Previous studies have shown that the Go models provide a qualitative description of two-state folding sequences (16–18). Therefore, we consider amino acid-dependent interactions only for the side chains that are in contact in the wild-type native structure of C-terminal hairpin from protein G. Side chains are in contact if their centers of mass are less than 7.6 Å apart. We also consider only native HBs.

Confining Potential.

To study the effects of confinement, a polypeptide chain is encapsulated into a sphere of radius R_s. Confinement is achieved by assigning short-range repulsive interactions between hairpin atoms and the sphere's inner walls. The interaction between a unit surface element of the sphere located at R⃗_s and the hairpin atom (C_α carbon or side chain) located at R⃗ is taken to be

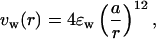1

where r = |R⃗_s − R⃗| and ɛ_w = ɛ_h = 1.25 kcal/mol (ɛ_h is the energy unit in the model), and a = 3.8 Å is the average distance between successive C_α carbon atoms. The total interaction energy of a hairpin atom with the confining sphere is

2

where ρ is the sphere surface density (ρa² ≡ 1) and the integral is taken over the entire inner surface of the sphere S. By integrating ν_w over S, we obtain the confining potential for a hairpin atom located at R⃗

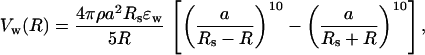3

where R = |R⃗|. A similar approach has been used to describe monomer–wall interactions in the simulations of grafted polymeric brushes in polymer melts (19). The form of the confining potential in Eq. 3 was chosen because it is well defined (no singularities) for all values of R < R_s. The precise functional form of V_w(R) is not important for the conclusions of this study as long as V_w(R) is a short-ranged repulsive potential. For example, we tested the case in which Eq. 3 is replaced with Eq. 1 with r = R_s − R and found that the conclusions of the study do not change qualitatively. Furthermore, it has been shown (11) that the size of a homopolymer confined to slits is the same irrespective of the interaction potential (soft or hard) with the wall. In general, a soft wall can always be replaced by a hard wall with a slightly larger range of interactions (20). However, the physics of folding would be altered if the confining potential is long-ranged or contains attractive terms.

The potential energy of the confined hairpin is the sum of V_b and the energies V_w for all hairpin atoms. In this study we consider R_s ≥ R_s,0 = 4.475a = 1.40R, where R is the radius of gyration of the bulk native conformation. The value of R_s,0 is the smallest radius of the confining sphere, which minimally perturbs the bulk native structure.

Numerical Simulations.

Langevin simulations based on the velocity form of the Verlet algorithm and the multiple histogram technique were used to compute the equilibrium properties of confined hairpins (15). Folding kinetics in a sphere was obtained by using Langevin dynamics at approximately water viscosity. Hundreds of folding trajectories were generated at each value of R_s to calculate the folding rate k_F = 1/M ∑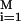 τ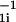, where M is the total number of trajectories and τ_1i is the first passage time to the native state. To assess the heterogeneity of the folding pathways we computed the fraction of unfolded molecules at time t P_u(t) = 1 − ∫ P_fp(s)ds, where P_fp = 1/M ∑ δ(s − τ_1i) is the distribution of first passage times (21).

Characterization of DSE.

To characterize changes in the DSE caused by confinement, we sample the conformational space in long equilibrium simulations at T_s = 1.2T, where T is the folding transition temperature in the bulk. To assess how the DSE changes with the degree of denaturation, which is determined by the temperature in this work, the equilibrium states also were analyzed at T_s = 1.6T. The heterogeneity of the DSE was determined by applying a pattern-recognition algorithm to the DSE structures (15). This method allows us to assign DSE conformations to structural clusters based on their similarity to the native conformation. The resulting clusters represent structurally distinct denatured states. Our focus is to distinguish between the DSEs of bulk and confined hairpins.

Distributed Computing.

To calculate folding trajectories for a β-hairpin, we used distributed computing. This computational approach capitalizes on the recent explosive growth in the number of internet-connected computers. Traditional computer simulations are performed on clusters of workstations or by using supercomputers. In both cases, the number of available CPUs is limited. In dramatic contrast, distributed computing harnesses scattered world-wide heterogeneous resources for concerted work. FRONTIER, the system developed by Parabon Computation on which we ran some of our simulations, is capable of distributing hundreds of thousands of individual tasks to run independently. It also is useful in handling all the scheduling, distribution, checkpointing, resumption, and collation aspects of computations. The number of individual tasks sent to the FRONTIER server for simultaneous execution is limited by the number of PCs connected to the server. This number is on the order of 10⁵. Since the number of individual folding trajectories (i.e., elementary individual tasks) used for computing k_F at a given R_s is ∼10³, virtually all trajectories were executed in parallel. In practice, it requires ∼200 h to complete 1,000 individual folding trajectories on the workstation with a single 600-MHz alpha processor. For comparison, the FRONTIER server allowed us to perform the same computations in ∼2–4 h, which results in a dramatic speedup of otherwise extremely long and intensive simulations. Distributed computing is a powerful and general computational tool suitable for a wide variety of computationally intensive applications (including those targeting biomolecules).

Results

Equilibrium Folding in Confined Space.

We describe the folding thermodynamics of the β-hairpin confined to a sphere with R_s = 4.6a. For the bulk hairpin the largest distance between its center of mass and any of the backbone or side chain atoms is 3.3a (the native radius of gyration in the bulk R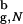 = 3.2a). Thus, the sphere with R_s = 4.6a = 1.43R 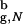can accommodate the polypeptide with relatively small perturbations of the structure. (The value V_w for the atom closest to the sphere wall is 0.3 kcal/mol). The size of the native structure of the confined hairpin is R 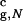= 3.1a. Confinement introduces an additional native contact, thus increasing Q, the number of native contacts, to 22. All native contacts of the bulk hairpin are present also in the confined native conformation. 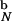The energy of interactions with the wall is merely 1.0 kcal/mol, and it makes minor contribution to the total energy of the native conformation (E = −24.4 kcal/mol and E = −25.9 kcal/mol). The overlap, χ (22), of the confined native conformation with the bulk exceeds 0.9 (χ = 1 implies identical conformations). Thus, encapsulating the hairpin to a sphere with R_s = 4.6a only marginally affects the hairpin native conformation.

In Fig. 2a we show several thermodynamic functions that probe the formation of the native state for the confined and bulk β-hairpins. The temperature scale (horizontal axis) is given in the units of the folding temperature T = 308 K (15). The thermal fractions of native contacts f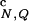 and HBs f (solid thick black and gray lines) reveal a broad weakly cooperative folding transition. Both quantities change most rapidly (i.e., df_N/dT reaches maximum) at 1.1T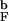, which is identified with T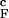, the folding transition temperature for the confined hairpin. Remarkably, <R> (solid thin black curve) changes with temperature by merely 3%. The collapse transition may be associated with the peaks in d <R>/dT or, alternatively, specific heat C_v. Both quantities indicate that the collapse temperature is T ≃ T = 1.1T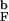. Confinement to a sphere severely limits the available conformation space and almost eliminates any variation in <R>(T) (Fig. 2a). In effect, nearly all hairpin structures accessible in a spherical cavity are now compact collapsed species.

Figure 2.

(a) Thermal refolding of the β-hairpin in a spherical pore with the radius R_s = 4.6a. The black and gray thick solid lines represent the fractions of the native contacts f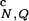 and the HBs f, respectively. The black thin solid line refers to the radius of gyration <R>. Dashed curves correspond to the quantities of the bulk hairpin. Comparison of the curves for the encapsulated and bulk β-hairpins shows that confinement eliminates expanded conformations and stabilizes the folded state (see text for details). (b) Dependence of the folding rates k_F (●) and the fraction of fast trajectories Φ (○) on R_s. Encapsulation generally accelerates folding rates. A nonmonotonic dependence of k_F on R_s reflects changes in the mechanisms of β-hairpin formation in small pores. The solid line is drawn as a guide to the eye. The arrows mark the bulk values k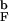 = 47 μs⁻¹ and Φ^b = 0.89.

Comparison of f_N for the confined and bulk hairpins (solid and dashed lines in Fig. 2a) shows that confinement stabilizes the hairpin. The folding transition temperature T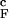 increases by ∼10%. The increase in the stability of the native state due to confinement is reflected in the free energy of stability ΔG = −T_sln[P_NBA/(1 − P_NBA)], where P_NBA is the thermal probability of occupancy of the native basin of attraction (NBA). The NBA is the set of conformations, for which χ ≥ < χ >(T_F). At T_s = 0.82T, ΔG for the bulk hairpin is −0.9 kcal/mol, whereas for the confined hairpin it decreases by a factor of 2.3 to −2.1 kcal/mol. The large increase in |ΔG| is remarkable given the finite size of the model system! A qualitatively similar effect of stabilization of the native state is observed at other values of R_s. However, as expected the gain in stability decreases as the sphere radius increases (at R_s = 4.85a and 5.1a ΔG = −1.9 and −1.6 kcal/mol, respectively). Nevertheless, even when R_s/R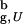 > 1.2 [R 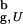is the radius of gyration of the bulk hairpin at T > 2T 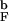(Fig. 2a)] there is substantial gain in the stability.

Confinement Effect on the Kinetics of β-Hairpin Formation.

We have computed the folding rates k_F at T_s = 0.82T for 4.475a ≤ R_s ≤ 7.1a and R_s → ∞. Initial conformations were equilibrated at T_h = 2.4T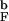. By using the distribution of first passage times P_fp, the fraction of unfolded molecules as a function of time, P_u(t), is calculated (see Methods). Both k_F and P_u(t) are useful probes of folding kinetics.

At the smallest value of R_s the ratio (R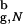/R_s)³ ≈ 1/3, which would suggest that the confining sphere should not alter the β-hairpin formation significantly. Thus, for the range of R_s considered here, k_F(R_s) is expected to increase compared with k_F(R_s → ∞), because the search for the native state takes place among the restricted set of compact structures. Surprisingly, we find that the dependence of folding rate k_F on R_s is not monotonic (Fig. 2b, closed circles). As R_s is decreased from its bulk value, the folding rates increase compared with k_F(R_s → ∞) ≡ k = 47 μs⁻¹. At R_s = 5.1a, k_F reaches a maximum of 103 μs⁻¹, which is more than twice the bulk value. Strikingly, the folding rate decreases when R_s < 4.85a. The value of k_F at the smallest R_s = 4.475a is marginally higher than k. Hence, encapsulation in a sphere generally accelerates β-hairpin formation over a broad range of R_s values.

Although encapsulation leads to rate acceleration, the mechanism of β-hairpin formation changes, especially for R_s/R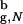 ≲ 1.5. In this range of R_s folding trajectories partition into slow and fast kinetic phases, such that P_u(t) ≃ Φexp(−k_fastt) + (1 − Φ) exp(−k_slowt). The overall folding rate k_F(R_s) = Φk_fast + (1 − Φ)k_slow. For large cavities the fast phase amplitude Φ is comparable to the bulk value Φ^b = 0.89 (Fig. 2b). However, Φ decreases for R_s ≲ 6.0a. The opposing behavior of k_fast(R_s) and Φ(R_s) leads to an optimal value of R_s, for which the overall rate k_F is maximum. For R_s ≲ 4.8a a certain fraction of trajectories becomes transiently trapped. The transition to the native state requires partial unfolding, which becomes difficult in a tight, confining space.

Effect of Confinement on DSE.

Encapsulation has a profound effect on the kinetics and thermodynamics of β-hairpin formation. At most values of R_s the energy of the native state (and conformations belonging to the NBA) is changed only moderately. In contrast, encapsulation severely restricts the conformational space of the DSE. It follows that the enhanced stability of the β-hairpin at finite R_s is due to the decrease in the entropy of the DSE compared with its bulk value. To investigate changes in DSE upon confinement we analyzed the unfolded conformations for the bulk and confined hairpins by using the pattern-recognition method (see Methods and ref. 15). The ensemble of unfolded conformations was generated in long equilibrium simulations at T = 1.2T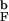. We choose R_s = 4.85a, at which k_F ≈ k. In all, for each hairpin we collected 10,000 distinct conformations.

The DSE of the bulk hairpin consists of three distinct clusters, DS1–DS3 (Fig. 3a). The bulk DS1 is compact (its radius of gyration exceeds that of the native state by 10%), and on average one-third of interstrand contacts and half of HBs are formed. The turn region is structured, and the HC is partially formed. DS2 and DS3 are unstructured and expanded (R_g/R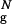 is 1.2 and 1.4, respectively). In both DS2 and DS3 only a few interstrand contacts and HBs are formed in the turn region, while the HC is not formed. Overall, the DSE of the bulk hairpin consists of two nearly equally populated types of conformations: the structured compact conformations with significant native content and open unstructured ones, which do not contain native interactions.

Figure 3.

(a) The distribution of DSE structures for the bulk and confined β-hairpins at 1.2T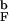 (mild denaturation). The percentage numbers indicate the distribution of DSE conformations over the structural clusters. Bulk DS1 has significant probability (0.43) of hydrophobic cluster (HC) formation, whereas other bulk DSs are unstructured. The DSE of the encapsulated hairpin has two distinct structural clusters, DS1 and DS2, in which HC is formed. More than 80% of all confined DSE conformations belong to these clusters. The third cluster, DS3, is unstructured. Thus, confinement to a sphere induces native interactions in the DSE. A DSE structural cluster is represented as an averaged conformation computed over a given cluster. The HC side chains are color-coded and labeled. The sizes of the amino acids correspond to their actual van der Waals radii. (b) Comparison of DSE clusters for the bulk and encapsulated hairpins at 1.6T (strong denaturation). The clusters shown have the largest fraction of native interactions, yet the difference between them is dramatic. Under strong denaturation the bulk DSE loses almost all native interactions, whereas the encapsulated DSE still retains significant native content (see text for details).

The DSE of the confined hairpin can be partitioned into three distinct conformational clusters (Fig. 3a), all of which are compact (R_g/R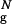 ranges from 1.03 to 1.07). Similar to the bulk DSE, DS1 has substantial native content and is well structured. About half of native interstrand contacts and HBs are present. More significantly, the HC is formed. Although DS2 is overall less structured, we find that the HC is formed with the probability of 0.5. As in the bulk DS2 and DS3 clusters, the confined DS3 has a significantly lower fraction of native interactions, which are localized near the turn region. HC is not formed in DS3.

The DSEs for the bulk and confined hairpins have common characteristics. Both partition (in terms of their native content) into two types of clusters. One has a significant amount of native interactions and is composed of structured conformations, in which the HC is formed or partially formed (as in the bulk DS1). The other constitutes unstructured conformations with low native content. These observations are highly significant, because they suggest that elements of the native structure are present even in the denatured states of the bulk and encapsulated hairpins.

There are also crucial differences between both DSEs. All conformations in the confined DSE are compact, whereas in the bulk only half are compact. More importantly, confinement strongly induces the formation of native interactions. In the bulk DSE only 45% of all conformations have high probability for the HC formation, but in the confined DSE their fraction almost doubles and reaches 83%! The fraction of open unstructured species in which HC is not present drops from 55% in the bulk case to a mere 17% for the confined hairpin. Thus, confinement of a hairpin to a sphere significantly alters the distribution of states in the DSE by forcing the formation of the HC. We surmise that confining a hairpin biases the DSE toward the native state.

To determine how the DSE changes with temperature (i.e., extent of denaturation) we generated unfolded structures for the bulk and confined hairpins at T = 1.6T (Fig. 3b). The bulk DSE falls into two clusters that differ only in their size. Strikingly, almost no native interactions are present in either of these, and the probability of forming HC is negligible. On the other hand, confined DSE resembles that at lower T = 1.2T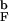 and consists of three clusters. In two (72% of all DSE structures) the probability of HC formation is significant (≳0.3), while the third has no traces of HC. All three DSE clusters are compact. These computations shows that the nature of DSE of the encapsulated hairpin weakly depends on the degree of denaturation, whereas the bulk DSE shows very strong dependence on the temperature.

Conclusions

Substantial reduction in the entropy of the DSE leads to enhanced stability of proteins encapsulated in inert cavities. It is remarkable that even modest confinement (R_s/R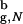 ≳ 2.2) leads to rate enhancement and increased stability of the native conformation. Confinement makes the open unstructured conformations inaccessible. Thus, the increase in k_F(R_s) is due to the restricted search for the native state among a subset of compact structures. Our calculations also show that for R_s/R 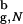≲ 1.5 the mechanism of β-hairpin formation changes. A large fraction of folding β-hairpins becomes transiently trapped in compact misfolded conformations. The transition from such states can occur only through partial unfolding, which becomes less probable in restricted spaces.

There are several implications of this study:

1.

Chan and Dill argued that the internal architecture of proteins can arise by chain compaction alone (23–25). The steric constraints that arise in the collapsed states of polypeptide chains force them to adopt elements of regular structure. The present work shows that confinement leads to compact structures (Fig. 2a). A detailed analysis of the equilibrium structures obtained even at elevated temperatures shows that the peptide is forced to adopt substantial elements of native structure (Fig. 3), which is in accord with the studies by Chan and Dill.

2.

The structural characterization of the denatured states of proteins is receiving increasing attention in recent years (26). In this context, few lessons from the present work are pertinent. (i) There are only few structural clusters in the bulk DSE at temperatures slightly above T_F, which would correspond to mild denaturation. In the dominant structural cluster there is significant residual native structure. However, at more elevated temperatures, corresponding to strong denaturation, the residual native structure is present only marginally. Hence, the amount of native content in the bulk DSE depends on the degree of denaturation. (ii) The situation is dramatically different when the polypeptide chain is encapsulated in a pore. In this case, substantial native structure in the DSE is retained both at mild and strong denaturation and is determined mostly by the pore's size. Thus, confinement alone confers significant residual native structure that only weakly depends on the extent of denaturation.Shortle and Ackerman (26) recently examined dipolar couplings of certain residues in Δ131Δ fragment of the α + β staphylococcal nuclease. A remarkable finding of that work is that long-ranged order persists in Δ131Δ even in 8 M urea. Their experiments also suggest that the presence of such ordering is more or less independent of the urea concentration. The experiments were performed in a polyacrylamide gels, in which Δ131Δ is oriented slightly. In an inert gel the protein should be localized in the largest pores. In the bulk denatured state Δ131Δ is expanded by a factor of 1.3–1.5 (26). The approximate size of Δ131Δ in the native state may be estimated by using the Flory formula R_g ≈ aN^1/3 ≈ 19 Å (for comparison R_g for the 149-mer wild-type staphylococcal nuclease is 20 Å, which is 25% larger than the measured value of 16 Å). Although the gel confines Δ131Δ to pores, some of the properties of a protein may not change due to confinement. For example, we expect small changes in the rotational relaxation time τ_R ∼ R as long as the protein is in large enough voids. Hence, encapsulation in a cavity that can accommodate Δ131Δ should produce little change in τ_R compared with the bulk (26).In contrast to the properties that only depend on the overall chain dimensions, others can be altered dramatically by confinement. Theoretical (27, 28) and experimental (29) studies have shown that homopolymers in inert gels are collapsed. The present work shows that such confinement-induced collapse states can have substantial residual structure even at high temperatures for the pores, for which R_s/R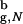 ≳ 2.2! Thus, moderate confinement, which would not alter τ_R, could induce long-range order in Δ131Δ. If long-ranged order is purely due to the confinement, it implies that the structure would be insensitive to the extent of denaturation, i.e., the concentration of urea, which would be consistent with our finding that the structures of the DSE for the encapsulated β-hairpin at T = 1.2T and 1.6T are similar. The agreement between the simulation and experimental findings (26) allows us to speculate that the presence of significant native interactions in Δ131Δ even at strongly denaturing conditions is caused by the conformational restrictions introduced by the surrounding gel.

3.

The argument that confinement stabilizes proteins is based on the assumption that the entropy of the DSE is reduced so greatly that ΔF_N/ΔF_U ≪ 1 (see the Introduction). If ΔF_N ≳ ΔF_U, then encapsulation can destabilize the protein. If the residual entropy of the NBA is negligible, then ΔF_N ≳ ΔF_U only if the entropy of the native interactions increases in restricted space, which would imply that the interactions that stabilize the native state (e.g., hydrophobic effect) become less favorable upon confinement. This reasoning might explain the observed destabilization of apomyoglobin in the silica matrix (8). Our arguments also lead to a testable prediction that if the experiments were performed in 2,2,2-trifluoroethanol solution, that is known to render stability to helical proteins, then the extent of destabilization of apomyoglobin in pores can be reversed or minimized.

Abbreviations

DSE

denatured state ensemble

HB

hydrogen bond

HC

hydrophobic cluster