Quantitative prediction of NF-κB DNA– protein interactions

Abstract

We describe a general method based on principal coordinates analysis to predict the effects of single-nucleotide polymorphisms within regulatory sequences on DNA–protein interactions. We use binding data for the transcription factor NF-κB as a test system. The method incorporates the effects of interactions between base pair positions in the binding site, and we demonstrate that such interactions are present for NF-κB. Prediction accuracy is higher than with profile models, confirmed by crossvalidation and by the experimental verification of our predictions for additional sequences. The binding affinities of all potential NF-κB sites on human chromosome 22, together with the effects of known single-nucleotide polymorphisms, are calculated to determine likely functional variants. We propose that this approach may be valuable, either on its own or in combination with other methods, when standard profile models are disadvantaged by complex internucleotide interactions.

The genetic basis of complex disease may stem partly from diversity in gene regulation. Eukaryotic genes are regulated largely through the interactions of transcription factors and their assembly into multicomponent enhancer complexes (1). Each gene is regulated by a unique combination of activators that produce activation and transcription specific to it. The arrangement of transcription factor-binding sites and their bound activators generates protein–DNA and protein–protein interactions unique to an enhancer (2). DNA variation in the enhancer is known to affect transcription factor binding, for example in the NF-κB and Oct-1 sites in the tumor necrosis factor promoter (3, 4), the SP-1 site in the Matrix metalloproteinase-2 promoter (5), and the AP-1-binding site in the Matrix γ-carboxyglutamic acid protein promoter (6).

There is a clear need for a quantitative model of how variations at the binding site affect binding affinity. The simplest nonquantitative representation of a binding site is as a consensus sequence and is best suited to highly conserved sites. The profile or position–weight matrix (7–9), in which variation is modeled at each position in the binding site, independently of the neighboring base pairs, is more widely applicable. Usually profiles predict the likelihood that a sequence is a binding site rather than binding affinity. This subtle distinction arose historically because profiles were constructed from a multiple alignment of sequences that bind in vivo, although in fact binding affinity and binding probability are interchangeable (9).

Profiles are very useful, but they cannot model interactions between positions within the binding site (9, 10). They normally describe only fixed-length motifs, whereas some DNA-binding proteins can bind to variable length sites (11). Finally, it is not always possible to construct a multiple alignment of binding sites, because there may be no consistent choice for the sequences' orientations such that every pair of sequences is optimally aligned. This is a serious problem in microarray (12, 13) and selex (14, 15) studies, where all binding sites are tested. selex uses a pool of random sequences to assay binding but tends to provide little information about low-affinity sites, which are important in multifactor complexes.

Here we introduce a quantitative model that predicts the effects of nucleotide variations within the binding motif on binding affinity. It is applicable to any DNA-binding protein, and requires only binding data from a subset of sites, chosen to span the space of the binding sites. Interactions between positions within the binding site are incorporated by using principal coordinate (PC) analysis to map the DNA-binding sites into a Euclidean space, such that the distance between any two sites' spatial coordinates approximates the dissimilarity between their DNA sequences. A site's binding affinity is modeled as a function of its coordinates.

We illustrate the model with an analysis of binding affinity in the NF-κB/Rel family of transcription factors. NF-κB, which binds with DNA through the Rel homology domain (RHD) (16, 17), coregulates many genes and has a critical role in immunity, inflammation, and apoptosis (18). Crossvalidation and experimental verification of predicted NF-κB binding affinities confirm the model's accuracy, and comparisons are made with profile (P) models to demonstrate the presence of base pair interactions. Finally, we analyze two finished human genome regions for potential NF-κB-binding sites containing single-nucleotide polymorphisms (SNPs) likely to affect binding significantly.

Methods

PC Model.

Many observations are required to fit a statistical model that systematically tests the significance of each position in the DNA motif and the interactions between positions, etc. Instead, we made the assumption that similar DNA motifs will tend to have similar binding affinities, although certain consensus positions, or combinations of positions, will be more influential than others.

For two oligonucleotides i, j of the same length, with sequences S_i, S_j, let h(S_i, S_j) be the Hamming distance between S_i, S_j, defined as the number of corresponding positions that differ, and let S_j be the reverse complement of S_j. Define a dissimilarity measure between S_i, S_j as

1

i.e., the minimum of the distance between S_i and S_j or its reverse complement. For example, GGGATGGCCC and GGAATTGCCC differ at positions 3 and 6 thus have Hamming distance 2, and the second sequence's reverse complement GGGCAATTCC has Hamming distance 5, so d is 2.

Metric scaling (19, 20) projects sequence i to a point x_i in n-1-dimensional space (where n is the number of sequences) such that

2

Although d_ij is not a metric, and hence the embedding into Euclidean space is only approximate, it is sufficient for our purposes.

The logarithm of binding affinity y_i is modeled by linear regression on the m largest principal coordinates containing most of the variance between the sequences:

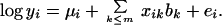3

The mean μ_i includes the experiment batch effect, b is a vector of coefficients estimated by least squares, and e_i is the residual error. The columns (principle coordinates) of the matrix x_ik are orthogonal, so the least-squares estimates of the b_k are uncorrelated.

The predicted relative log-binding affinity for sites r, s is z_rs = (x_r − x_s)b, a linear function of the vector displacement between their coordinates. Nonsignificant coefficients in b are set to zero for prediction. Prediction variance is

4

where s_k is the SE of the coefficient b_k. Predicted affinities are either expressed relative to the affinity of sequence GGGGTTCCCC (used as an experimental control on each gel) or ranked from 0 (weakest) to 1 (strongest). Any sequence r not in the training set is embedded into the sequence space by kernel density mapping with coordinate

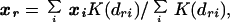5

where K(d) = 10^−d is a kernel density. The relative binding affinity is then calculated as before.

Profile (P) and Symmetric Additive Profile (SAP) Models.

We fitted two quantitative P models to test whether the PC model improved the fit and whether interactions were present. The inner 6-bp variable core of the NF-κB site comprises three pairs of nucleotides, in which position n on one strand is identified with position 11-n on the reverse strand. For instance, the pairs AG (3,8), AG (4,7), and TT (5,6) represent 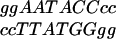. The log-binding affinity is modeled as the sum of effects of the three pairs, i.e., log y = μ + p₃₈ + p₄₇ + p₅₆ + e. In the P model, there are 10 df, 2 each for p₃₈ and p₄₇, and 5 for p₅₆. In the simpler SAP model, the effects of the nucleotides within each pair are additive and symmetric; e.g., the effect of an A at position 1 is the same as an A at position 6; there are 5 df, one each for p₃₈ and p₄₇, and 3 for p₅₆. Analyses used software written in perl and the nag c library (http://www.nag.co.uk) (available on request) and the SPLUS 2000 statistical analysis package.

Binding Assay.

p50_RHRs/p65_RHRs heterodimer expressing construct (containing amino acids 39–350 of p50 and 19–291 of p65) (21) was kindly provided by G. Ghosh (Department of Chemistry and Biochemistry, University of California, San Diego). p50 expressing construct was previously described (22). Both constructs were used to transform BL21(DE3) bacterial strain, and the cultures were grown in LB media at 37°C to A₆₀₀ = 0.4–0.6, induced with 0.2 mM isopropyl β-D-thiogalactoside, and shaken overnight at 30°C. Protein extraction and purification were performed as described in ref. 22.

Standardized oligonucleotide probes (e.g., F: 5′-agctGGGGTTCCCC-3′, R: 5′-agctGGGGAACCCC-3′) were radiolabeled with [α-³²P]-dCTP (Amersham Pharmacia Biotech). Labeled probe (0.2–0.5 ng) (1–5 × 10⁴ cpm) was used in the binding reaction that contained 12 mM Hepes, pH 7.8, 80–100 mM KCl, 1 mM EDTA, 1 mM EGTA, 12% glycerol, 0.2 μg of BSA, 0.5 μg of poly dI-dC (Amersham Pharmacia Biotech), and 10–50 ng of recombinant protein. The reaction was analyzed by nondenaturing 5% PAGE at 4°C. Binding was quantified by PhosphorImager (Molecular Dynamics) normalized against the control sequence GGGGTTCCCC, included on each gel, which was given the value 227.

Results

Wide Variation in NF-κB p50p50 and p50p65 Binding Affinities.

We assayed by electrophoretic mobility-shift assay (EMSA) 52 of a possible 256 variants of the GGRRNNYYCC NF-κB motif for binding affinity to recombinant p50p50 homodimer and p50p65 heterodimer complexes (Fig. 1A). The consensus used generalizes the original NF-κB motif GGGRNNYYCC by introducing variation at position 3. The 52 sites were chosen to span the consensus sequence space (see Methods). The data are plotted in Fig. 1B. With both dimers, we observed up to a 1,000-fold reproducible variation in binding among the sites (published as supporting information on the PNAS web site, www.pnas.org). Although the original version of the consensus is too restrictive (e.g., GGAAATTTCC has relatively high p50p65 affinity), neither discriminates well between high- and low-affinity sites. A single-nucleotide change between two sequences, depending on context, can have little effect on binding affinity (e.g., GGGATACCCC, GGGATATCCC, p50p50 ratio 1.5) or can cause a significant change (e.g., GGGGCTTCCC, GGGGCTCCCC, p50p50 ratio 5.7) (Fig. 1B).

Figure 1.

Wide range of affinities for sites matching the generalized NF-κB consensus GGGRNNYYCC. (A) Recombinant purified p50 and p50_RHDs/p65_RHDs proteins were used in EMSA with radiolabeled probes corresponding to different variants of NF-κB consensus sequence. (B) p50p50- and p50p65-binding data for 50 NF-κB-like sequences. The sequences are sorted along the x axis by their binding affinity to p50p50. Each point represents the geometric mean of two independent measurements. The data are from eight gels quantified by PhosphorImager and normalized against the control sequence GGGGTTCCCC, which is given a value of 227. See text for explanation of labeled sequences.

PC Model Fitting.

We used metric scaling (19) to embed the DNA sequences in a Euclidean space, such that the distance between the points representing any pair of sequences approximated their sequence dissimilarity, taking into account that reverse complement sequences have the same binding as forward ones (Eq. 1). Each sequence was initially mapped to a vector in a high-dimensional space, but most of the variance in the coordinates that correlates with binding affinity maps to a 12-dimensional subspace.

The logarithm of a sequence's binding affinity y was modeled by least-squares linear regression on its principal coordinates, plus a term for the experimental inter-gel effect (Eq. 3). Models were fitted to the raw data, not to the grand means, and hence incorporate the variation between duplicated observations. Regression coefficients were estimated for each dimer. The regressions explained over 90% of the variance (Table 1). Only eight (p50p50) and nine (p50p65) coefficients of 12 in the regression were significant (P-value <0.05). The significant coefficients identify principal coordinates that influence binding affinity (Table 5, which is published as supporting information on the PNAS web site), whereas nonsignificant coefficients indicate where the consensus can vary without affecting binding.

Table 1.

Comparison of the fits of the PC model and the profile models P and SAP (see Methods)

Model*	df†	R‡	P-value§	X-val R¶
		p50p50
SAP	5	0.85		0.74
P	10	0.90		0.80
PC	12	0.92		0.88
SAP + PC	5 + 12	0.93	8.8 × 10−8
P + PC	10 + 12	0.96	4.2 × 10−8
PC + SAP	12 + 5	0.93	0.04
PC + P	12 + 10	0.96	1.8 × 10−7
PC opt‖	8	0.91		0.90
		p65p50
SAP	5	0.85		0.71
P	10	0.87		0.66
PC	12	0.93		0.78
SAP + PC	5 + 12	0.93	1.7 × 10−8
P + PC	10 + 12	0.94	1.5 × 10−9
PC + SAP	12 + 5	0.93	ns
PC + P	12 + 10	0.94	0.03
PC opt‖	9	0.90		0.82

^*Model fitted: e.g., SAP + PC means fitting SAP followed by PC, to test whether PC explains significant extra variance over that explained by SAP. 

^† The model's degrees of freedom, e.g., SAP + PC has 17 = 5 + 12 df. 

^‡ Correlation between observed and fitted log affinities, after subtracting gel effects. 

^§ P-value of the analysis of variance partial F-statistic for fitting one model after the other. 

^¶ Crossvalidated correlation between the predicted and observed mean log affinities. 

^‖ Optimized PC models, with nonsignificant (P > 0.05) terms removed. 

The 52 oligonucleotides assayed span the sequence space, in that each of the putative 256 NF-κB-binding sites differs from at least one of the 52 (or its reverse) by no more than one nucleotide. Consequently, the PC model should predict binding affinity across all 256 potential binding sites and will be more accurate than a single observation as it reduces the effect of experimental variability.

Comparison of PC and P Models.

(i) matinspector (7) (www.genomatix.de) predicts binding affinity by using the transfac database (23, 24). It predicts affinity by comparing the sequence to a profile of the binding site. All sites scoring below a threshold are treated as nonbinding and set to 0. We used the lowest allowed threshold (0.70). Of the 52 sequences assayed, 71% had nonzero matinspector scores with p50p50 and 84% with p50p65. These values were compared with our experimental data, which were ranked on a scale of 0–1 after averaging duplicated observations and correcting for gel effects. The correlations of experimental data with matinspector predictions were 0.69 (p50p50) and 0.51 (p50p65), compared with correlations of 0.90 (p50p50) and 0.89 (p50p65) for experimental data versus PC predictions.

(ii) We fitted our NF-κB-binding data to two quantitative P models, one a simple P and the other a SAP (see Methods). The SAP model performs significantly worse than both P and PC (Table 1). For p50p50, the PC and P models have similar goodness-of-fit, but interestingly they explain different aspects of the data, because the result of fitting one model after the other is highly significant. In contrast, for p50p65, PC fits much better than P; fitting the PC after P is highly significant (P < 10⁻⁸), but fitting the profile after the PC model is only marginally significant (P < 0.05). For the purposes of fair comparison, no attempt was made to optimize the models by removing nonsignificant terms; however, the fits of the optimal PC models are also reported. Thus, the PC model fitted the data marginally (p50p50) or significantly (p50p65) better than the P models.

Crossvalidation.

After correcting for variability between experiments and averaging the affinities for each duplicated sequence, each of the 52 sequences of the training set was excluded in turn, and the linear regression repeated on the remaining 51. The binding affinity of the excluded sequence was predicted and compared with the observed value. The crossvalidated predictions, as assessed by the correlation coefficient between the observed and prediction affinities, were only slightly less accurate than the predictions when the observation was included in the regression (Table 1, 10-val correlation coefficients). As an affinity predictor, the PC model outperformed the P models for both p50p50 and p50p65. Fig. 2 compares the crossvalidated PC predictions and observed data for p50p50 and p50p65. The predictions are accurate, and the errors are stable over the wide range of binding affinities.

Figure 2.

Crossvalidated predicted binding affinities (y axis) plotted against observed values (x axis). The error bars give the 95% confidence intervals.

Prediction of New Sites.

We assayed the affinities of nine additional oligonucleotides (three each with low, moderate, and high predicted affinities). The comparison of ranked experimental binding data with the PC prediction is shown in Table 2. In all cases, the differences were within 10 percentile points. Predictions for all 256 sites are published as supporting information on the PNAS web site (Table 6). Overall, the PC model predicts quantitative binding affinity in the NF-κB motif accurately and is an improvement over profiles.

Table 2.

Comparison of experimental binding data with predicted binding affinity

	p50p50		p50p65
	Predicted	Observed	Predicted	Observed
GGAGCCCTCC	0.043	0.016	0.020	0.016
GGAAGATTCC	0.070	0.059	0.066	0.117
GGAAACCTCC	0.102	0.125	0.074	0.109
GGAAGATCCC	0.414	0.481	0.379	0.422
GGAGTTCCCC	0.656	0.613	0.703	0.660
GGAGAGCCCC	0.570	0.594	0.555	0.613
GGGATGCCCC	0.871	0.863	0.820	0.789
GGGAGTCCCC	0.883	0.895	0.887	0.828
GGGGATCCCC	0.988	0.988	0.938	0.953

Nine consensus sequence variants were tested by EMSA with recombinant p50 and p50_RHDs/p65_RHDs. Predicted values are represented by rank, on a scale of 0–1, within the 256 sequences examined by the PC model. Observed values are represented by rank within the total set of sequences tested experimentally. 

Interaction Between Nucleotide Positions.

Fitting the PC model after fitting P models significantly improved the fit (Table 1), indicating there are interactions between positions in the binding sites for both p50p50 and p50p65. The PC model shows how positions in the binding site interact with each other. For p50p65, interactions occur between the outer core positions 3, 4 and 7, 8, and within the inner core positions 5,6 for both complexes.

We looked for sequence characteristics that correlated with each principle coordinate, k: first the training set sequences i were sorted by their coordinates x_ik, and then at each consensus position the average sequence composition was computed within the top and bottom 25% of the sorted sequences. Large differences in composition between the high and low groups indicated variation along that direction of sequence space. Fig. 3 shows the result of subtracting the bottom-quartile frequencies from the top quartile for four major significant principal coordinates, at each position within the variable central 6-bp core of the binding site. For example, PC1 involves the outer core positions 3, 4, 7, 8, in a contrast between GGGG**CCCC (high affinity) and GGAA**TTCC (low affinity). In contrast, PC3 involves the inner core positions 5, 6 GGA*AA**CC vs. GGG*GC**CC.

Figure 3.

Sequence characteristics of four major principal coordinates. PC1, PC2, and PC4 are significant for both p50p50 and p50p65 complexes, PC3 is significant for p50p65 only (as indicated in brackets). For each statistically significant principal coordinate, sequences were sorted along the coordinate. Mean base frequencies were computed for the Upper and Lower 25% of sites at each position within the 6-bp core of the NF-κB site, e.g., for principal coordinate 1, 12/13 upper-quartile sequences had a G at position 3 and one had an A, whereas 10/13 lower-quartile sequences had an A and 3 had a G. The result of subtracting the sequence composition from the Upper and Lower quartiles is plotted (PC1, position 3: 9 for G and −9 for A). Thus PC1 represents a contrast between GGGG**CCCC (high affinity) and GGAA**TTCC (low affinity).

Differences Between p50p50 and p50p65.

The corresponding regression coefficients for p50p50 and p50p65 were broadly similar in sign and magnitude, and the correlation between p50p50 and p50p65 raw data was about 80% after correcting for gel effects. Nevertheless, there are systematic differences in binding affinity between the dimers. One dimer was regressed on the other to remove common features, and the residuals regressed on the principle coordinates (data not shown); significant coefficients indicate binding affinity differences. PC3 and PC10, which mainly involve the inner core positions 5 and 6, were the main distinguishing factors.

Genomic Analysis of NF-κB-Binding Motifs.

We analyzed two completed and annotated regions of the human genome: chromosome 22 (35 Mbp, 832 genes/pseudogenes) and MHC on chromosome 6 (4 Mbp, 229 genes/pseudogenes). The locations and affinities of all 256 variants of NF-κB were predicted. Motifs (11,198) were identified on chromosome 22 and 1,161 motifs in the MHC. On chromosome 22, the frequencies of the individual motifs ranged widely from 5 to 133 occurrences. In contrast, on a randomized version of the chromosome, which preserved local sequence composition in each 10-kb window of the original, the frequencies ranged from 15 to 42 (Fig. 5, which is published as supporting information on the PNAS web site). There was a significant correlation (R = 0.61, P < 0.01) between the frequencies of the sites on chromosome 22 and the MHC.

NF-κB motifs were classified as (i) within 1 kbp upstream of a gene, (ii) within exons or introns, (iii) within 1 kbp downstream of a gene, or (iv) elsewhere. About 10% of the motifs occurred significantly more often (5–30 times more than expected) in upstream or downstream regions (P < 0.01). There was a slight but significant under-representation of high-affinity p50p65 sites across chromosome 22 overall (P < 0.01), and an over-representation of high-affinity p50p50 sites in upstream regions (P < 0.01). Similar results hold for the MHC region. Consequently, selection for higher-affinity NF-κB-binding sites may have occurred near genes and may have been inhibited elsewhere, although it is also possible this phenomenon is due to variation in sequence composition.

Of 20,000 SNPs reported for chromosome 22, 89 are within NF-κB-like-binding motifs. In 53 cases, the variant no longer matches the NF-κB consensus and is expected to have low affinity. This was partially confirmed when five of these SNPs, selected at random, were assayed by EMSA. Four showed significant loss of affinity (Fig. 4, compare lanes 1 and 2, etc.). The exception was the high-affinity site GGGGATTCCC, in which the mutation C₁₀/T₁₀ had almost no effect on its p50p65-binding affinity (1.3-fold reduction), although p50p50 affinity was significantly reduced (5.5-fold). In the 36 cases where the variant still matches the NF-κB consensus, we predicted the binding affinity of both wild type and variant. In nine of these cases, the predicted affinity is strongly affected by the polymorphism, defined as a change in rank of greater than 25 percentiles for either dimer (Table 3).

Figure 4.

Effect of nucleotide variation in the flanking G₁, G₂, C₉, and C₁₀ positions on the binding affinities of p50p50 and p50p65. Recombinant purified p50 and p50_RHDs/p65_RHDs proteins were used in EMSA with radiolabeled probes corresponding to five random NF-κB consensus sequences (lanes 1, 3, 5, 7, 9) and their polymorphic variants found on chromosome 22 (lanes 2, 4, 6, 8, 10).

Table 3.

SNPs within the consensus NF-κB sites on chromosome 22 that strongly affect binding affinity

	Position	Wild-type site	Variant site	p50p50		p50p65
				Wild	Variant	Wild	Variant
G/C	11377920	GGGAAGCTCC	GGGAACCTCC	0.523	0.309	0.531	0.277
T/C	19233627	GGGATCTTCC	GGGATCCTCC	0.418	0.156	0.383	0.086
A/G	22583878	GGAACACTCC	GGGACACTCC	0.215	0.348	0.176	0.422
T/G	23290863	GGAGTTTTCC	GGAGGTTTCC	0.445	0.106	0.391	0.078
C/T	27669037	GGAACTCCCC	GGAACTCTCC	0.719	0.109	0.871	0.215
G/A	28028256	GGGACATTCC	GGAACATTCC	0.508	0.063	0.727	0.102
C/T	28583158	GGGATGCTCC	GGGATGTTCC	0.336	0.453	0.262	0.520
T/C	30437898	GGAGCTCCCC	GGAGCCCCCC	0.598	0.395	0.527	0.238
G/A	34313170	GGGGCCTCCC	GGAGCCTCCC	0.754	0.262	0.625	0.231

The predicted rank for either NF-κB dimer changed by more than 0.25 by the SNP. 

Discussion

We have described a method to predict the quantitative effect of sequence variation on binding affinity, applicable to the analysis of any DNA-binding protein. It requires experimental binding data from only a selection of potential binding sites chosen so that all other sites are within a single base change of this training set. For NF-κB, binding data from only 52 of 256 decamers were used to predict the remainder. The least number of sequences spanning the consensus sequence space is 23. However, it is desirable that the number of data points should be large enough to reduce prediction error because of experimental variation. With microarrays, it is possible to assay the training set in a single experiment (12, 13). In theory, data could also be acquired from crystallographic or NMR studies generated for a single site (25), but data from many structures would be needed to match the predictive power of the model presented here.

The PC analysis projects the set of binding sites into a space that reflects accurately the differences between the sequences. Directions in sequence space along which the binding sites do not vary are implicitly ignored, so parameters that could not contribute to the model are never included. We confirmed its accuracy by crossvalidation and by experimentally verifying our predictions for nine additional motifs not included in the training set. For NF-κB, binding affinity was modeled as a linear function of the sequences' coordinates. Nonlinear models did not improve the fit significantly (data not shown) but might be appropriate in other contexts. The PC model is accurate at prediction within the space of sequences matching the binding consensus but not necessarily outside of that space.

The PC approach compares favorably with profile-based methods. For instance, matinspector (7) predictions show much lower correlation with observed binding than does our PC model. However, because the profile database used by matinspector lacks our empirical data, as a fairer test we compared the PC model with two P models created from those data. The PC model performs significantly better than both P models for p50p65 and marginally better for p50p50. The crossvalidated correlation between predictions and observations is higher with the PC model in all cases, and moreover the fit improves significantly when the PC model is combined with either P model. Because the only additional information encoded by the PC model relates to the covariation of nucleotide positions in the binding site, these interactions must have a role in NF-κB binding. The extent to which such interactions occur in general remains to be seen, and a comprehensive study is desirable. The PC model is therefore valuable, either on its own or in combination with other methods, when empirical data are limited, and where internucleotide interactions occur. Profiles will continue to be useful, but we have shown they have limitations, and that one can do better.

Although the binding affinities for p50p50 and p50p65 are strongly correlated, we identified two directions in sequence space where the dimers had significantly different regression coefficients. The main distinguishing factors between the two complexes predominantly involve the inner core positions 5 and 6, defined as NN in the original consensus. We can therefore predict those sequences that are likely to bind differently to the two complexes. Kunsch et al. (14) came to a similar conclusion based on the selex-type assay with homodimeric NF-κB complexes, in which the preferential binding motif for p50p50 was GGGGATYCCC, whereas p65p65 preferred GGGRNTTTCC. Our results extend this observation. We find a number of motifs that have a higher predicted preference for one of the dimers (e.g., GGAAAGTTCC, 5 times higher for p50p65 that for p50p50). This is of particular biological relevance, as p50p65 is a potent transcriptional activator, and p50p50 is believed to act as a repressor (26, 27).

Those sequences that define the original NF-κB consensus and that rank high in our model were discovered by their roles in the transcriptional regulation of Igκ, IFN-β, IL-6, E-selectin, tumor necrosis factor (TNF), etc. As it excludes some sequences that bind strongly, e.g., the human TNF promoter (22), we broadened the consensus slightly. Fig. 4 suggests the consensus may need to be widened still further—for instance, a pair of flanking guanidines is not always necessary.

Our analysis of chromosome 22 and the MHC region indicates we can predict which NF-κB sites are likely to bind. These predictions should be tested in vivo (28, 29) to determine whether other factors such as chromatin are involved. For example, the binding site for yeast Repressor-activated protein 1 is found throughout the yeast genome, but binding occurs preferentially to potential promotors in intergenic regions (30). It will also be interesting to examine the regions of extended cross-species homology, as it is believed that long-range regulatory sequences tend to be conserved among mammals (31).

We can readily predict those SNPs occurring within binding sites that are likely to have functional effects. Previously (3), we demonstrated that a SNP within the NF-κB motif of the tumor necrosis factor promoter dramatically decreased the binding of p50p50, yet left the binding of p50p65 practically unchanged and resulted in a higher level of gene transcription. We identified about 50 SNPs located within NF-κB-like motifs on chromosome 22 that would alter NF-κB binding to DNA. These SNPs may be good candidates for disease association studies.

Finally, NF-κB is only one among a few scores of common transcription factors that regulate a majority of genes. It should therefore be feasible to construct quantitative models for all these factors by performing a relatively small number of binding assays. Armed with these data, one would be well placed to predict the binding affinities at the complex of transcription sites that regulate each gene (32, 33) and then begin to model how gene expression varies as a function of polymorphisms within the binding sites.

Abbreviations

PC

principal coordinate

SNP

single-nucleotide polymorphism

P

profile

SAP

symmetric additive profile

EMSA

electrophoretic mobility-shift assay