Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2025 Jul 28;15:27466. doi: 10.1038/s41598-025-11863-5

Topological modeling and QSPR based prediction of physicochemical properties of bioactive polyphenols

Abdul Hakeem 1, Asad Ullah 2,✉, Shahid Zaman 3,✉, Emad E Mahmoud 4, Hijaz Ahmad 5,6,7,11, Parvez Ali 8, Melaku Berhe Belay 9,10,✉
PMCID: PMC12304092  PMID: 40721442

Abstract

Molecular graph theory provides a powerful mathematical framework for representing chemical structures, where atoms and bonds are modeled as vertices and edges of a graph. Topological indices, derived from these graphs, serve as numerical descriptors capturing the structural features of molecules. These indices are widely applied in Quantitative Structure–Property Relationship (QSPR) analysis to predict the physicochemical behavior of chemical compounds. In this study, we investigate a novel class of bioactive polyphenols—namely ferulic acid, syringic acid, p-hydroxybenzoic acid, benzoic acid, vanillic acid, and sinapic acid—well known for their antioxidant, anti-inflammatory, antibacterial, anticancer, and antiviral properties. Using several widely recognized degree-based topological indices, we construct molecular graph models of these polyphenols and establish linear regression models correlating the computed indices with essential physicochemical properties. Our QSPR analysis demonstrates strong predictive correlations, highlighting the potential of graph-theoretical descriptors in rational drug design and bioactivity prediction. The results validate the utility of topological indices as efficient computational tools in cheminformatics, offering valuable insights for future applications in pharmaceutical chemistry and material sciences.

Keywords: Polyphenols, Molecular graph, Topological index, QSPR analysis, Cheminformatics

Subject terms: Theoretical chemistry, Computational chemistry, Structure prediction, Cheminformatics, Applied mathematics

Introduction

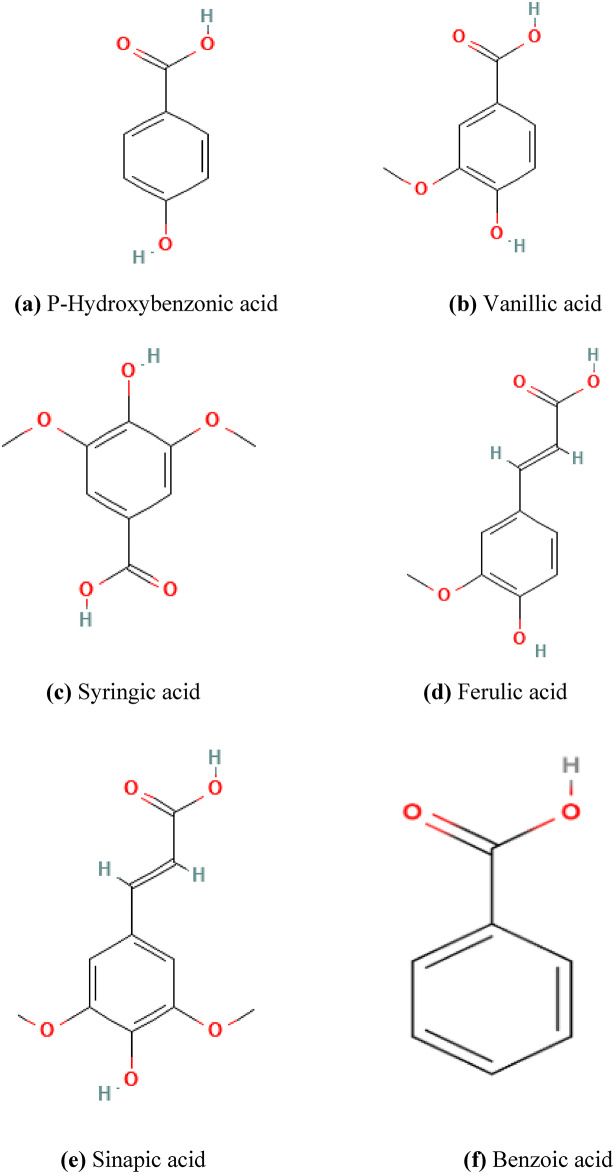
Polyphenols are a diverse group of natural compounds found in plants. They are well-known for having antioxidant qualities that help shield the body from damaging free radicals. Fruits, vegetables, tea, coffee, cocoa, and certain spices are some of the known sources of polyphenols. However, it is important to note that the specific health effects of polyphenols depend on its type and concentration present in different foods. Research suggests that polyphenols have several health benefits. They can reduce the risk of various chronic diseases like heart disease, certain cancers, and neurodegenerative disorders. Polyphenols are secondary bioactive naturally occurring chemicals produced by plants. They have a broad spectrum of bioactivities that support health promotion1,2. Polyphenols can be described as phenolic rings connected to various functional groups. These compounds have gained significant attention and interest due to their multiple applications, ranging from food processing and preservation, to the pharmaceutical industry3–5. The past investigations revealed that, numerous phenols have been used for preparing traditional medicines6. Many deaths worldwide have been attributed to factors like oxidative stress, hypertension, weak immune system, microbial infections, and the development of resistance to antibiotics7. It enables them to assist in treating various illnesses and other medical conditions8. Dietary polyphenols are a diverse class of naturally occurring compounds with two phenyl rings and one or more hydroxyl (O H) groups which belongs to the kingdom Plantae9. Around 4000–8000 currently known polyphenolic substances exclusively includes flavonoids10. A heterogeneous group of phenolic chemicals are called polyphenols11. Flavonoids and phenolic acids are the two main groups of polyphenols. Hydroxycinnamic and Hydroxybenzonic acids are the two subcategories of Phenolic acids12. They are either non-conjugated (as an aglycone) or conjugated with substances, such as glucose, amines, lipids, organic acids, and carboxylic acids1. The structures of some notable polyphenols are shown in the Fig. 1. Polyphenols are also known as secondary metabolites, which are mostly found in the kingdom of plants. Due to the anti-bacterial, anti-oxidant, anti-cancer, anti-hypertensive, immunomodulatory, and anti-inflammatory properties, polyphenols have considerable health-promoting benefits. Therefore, it is the prime objective of this paper to model the molecular topology of these important polyphenols and perform a QSPR analysis to predict the physicochemical properties.

Fig. 1.

Fig. 1

Open in a new tab

Molecular structures of considered Polyphenols.

Chemical graph theory is the branch of graph theory that applies to the mathematical modelling of chemical substances. A molecular graph/ chemical graph is a graph representation of structural interrelation of atoms and chemical bonds among them in a molecule. Chemical graph theory applies mathematical methods to predictions of the properties of chemicals. This approach relates molecular chemical structure to its chemical reactivity, physical behavior, and physicochemical properties. Chemical graph theory is widely applicable to chemical reaction analysis, material design, drug design etc1,13–25. A molecular graph G represents the unsaturated hydrocarbon skeletons of molecules/compounds. The vertex set denoted by V (G) correspond to non-hydrogen atoms. The edge set E(G) of a molecular graph represent covalent bonds between atoms26–30. Omar et al. developed eight derivatives based on the main structure of hydroxychloroquine to treat COVID-19 and used QSAR investigation to calculate the biological activity of the designed compounds. These compounds were evaluated for their biological activity using a method called QSAR investigation31. Havare generated curvilinear regression models for the boiling point of prospective medicines against COVID-19 using multiple topological criteria32.

Gutman, in 197233, defined and formulated The first and second Zagreb indices as

graphic file with name d33e419.gif
graphic file with name d33e424.gif

Shirdel et al.34 formulated The Hyper Zagreb index as

graphic file with name d33e435.gif

The second and third Zagreb index was redefined by Ranjini et al.35 as

graphic file with name d33e446.gif
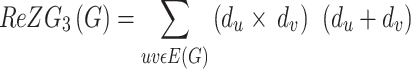graphic file with name d33e451.gif

Vukičević et al.36 suggested the Symmetric division degree index as

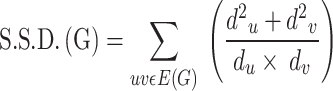graphic file with name d33e462.gif

Similarly, many other indices can be used in QSPR/QSAR analysis14,26,37–52. Recently, many scientists have shown an increased interest in mathematical chemistry. Since 1988, numerous academic articles on mathematical chemistry are being released annually. Chemical graph theory connects graph theory with chemistry, and produces useful results that chemists can use. The chemical applications of graph theory have been thoroughly discussed in a wide range of works53–68.

Materials and methods

Simple polyphenol graphs are considered for molecular topological modeling. Edge partitioning, Vertex partitioning, and computational techniques of graph theory are applied to compute the topological indices of the six structures under consideration. Regression models are then formulated to compare the computed topological indices with the properties of the considered molecules. The regression analysis was performed using MS Excel software.

Results and discussion

Regression model

Four physical properties (Complexity, Boiling Point (BP), Molecular Weight (MW), and Polar Surface Area (PSA)) are studied for each of the six Polyphenols. Regression analysis is performed for the six polyphenols based on the below model

graphic file with name d33e499.gif 1

where , → constants, → Physical property of the drug, → topological descriptor.

The regression model for the topological indices in question is defined using this linear regression equation. Six polyphenols’ molecular networks’ topological indices are regarded as independent variables. On the other hand, the physical attributes are considered as dependent variables. Models for linear regression are created in MS Excel package. The constants A and B in the regression Eq. (1) can be found by the data in Tables 1 and 2.

Table 1.

Experimental properties.

Polyphenols Complexity Molecular weight (g/mol) Polar surface area (Ų) Boling point °C
p-Hydroxybenzonic acid 125 138.12 57.5 335
Vanillic acid 168 168.15 66.8 353.43
Syringic acid 191 198.17 76 440
Serulic acid 224 194.18 68.8 373
Sinapic acid 249 224.21 76 403.41
Benzoic acid 104 122.12 37.3 249.2
Open in a new tab

Table 2.

Topological indices values.

Polyphenols M1 M2 HM ReZG2 ReZG3 SSD
p-Hydroxybenzonic acid 46 50 216 10.55 242 24.6667
Vanillic acid 56 63 270 12.91667 316 29.3333
Syringic acid 66 76 324 15.28333 390 34
Serulic acid 64 70 300 14.81667 338 33.6667
Sinapic acid 74 83 354 17.18333 412 38.3333
Benzoic acid 40 43 182 9.4 202 21
Open in a new tab

For first Zagreb index M1 (G)

graphic file with name d33e537.gif

For second Zagreb index M2 (G)

graphic file with name d33e551.gif

For hyper Zagreb index HM (G)

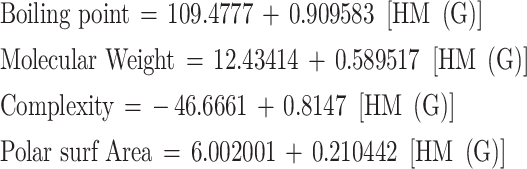graphic file with name d33e561.gif

For Redefined second Zagreb index ReZG2 (G)

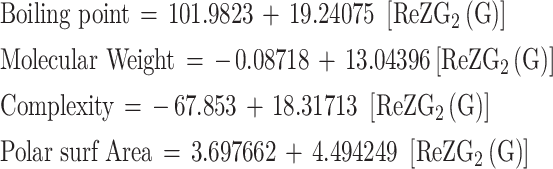graphic file with name d33e576.gif

For Redefined third Zagreb index RezG3 (G)

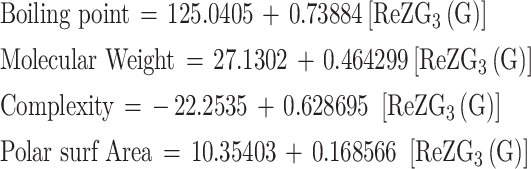graphic file with name d33e590.gif

For symmetric division degree index SSD(G)

graphic file with name d33e600.gif

The correlation coefficients

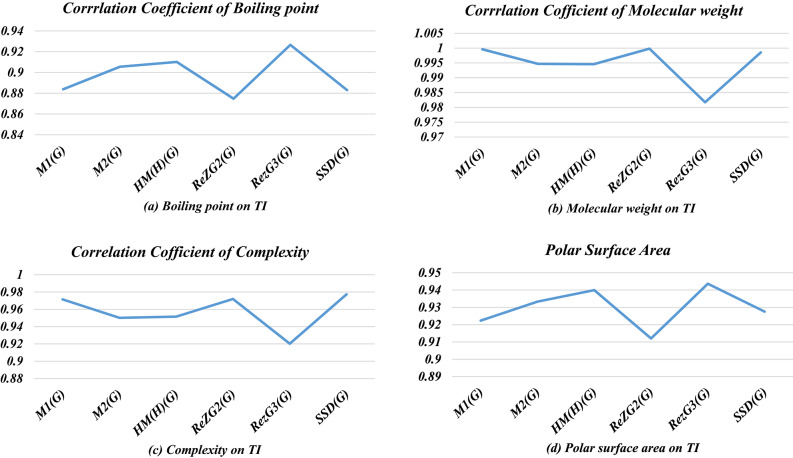
Table 1 lists the four physical parameters of the Polyphenols used in this study, these properties have been taken from Pubchem database. Table 2 shows the six topological indices values, which have been obtained via edge partitioning, vertex partitioning, and computational techniques of graph theory. Table 3 shows the correlation coefficients of six physical attributes and topological indices. From Table 3, it can be observed that, the first Zagreb index shows a strong correlation value (r = 0.992706) for molecular weight. Figure 2 is a graphic depiction of the correlation coefficients of TIs and physical properties. Tables 4, 5, 6, 7, 8 and 9 depict the statistical parameters. The parameter N shows sample size, b is slope, A is a constant and r shows the correlation coefficient. The null hypothesis is tested when each term’s coefficient is equal to zero; the greater the p-value, the more probable it is that changes in the predictor have nothing to do with changes in the responder. In this case, the null hypothesis’s regression coefficients are all zero, yet the test yields a F value. This kind of scenario cannot be predicted by the model. This test can be used to assess whether the coefficients in a model are superior to those without predictor variables. Table 10 gives the standard error of estimation for physical properties of polyphenols under study. Tables 11, 12, 13 and 14 is a comparison of computed and actual values of all physical attributes of polyphenols.

Table 3.

Correlation Coefficients.

Topological indices Complexity Molecular weight Polar Surface Area Boiling point
M1(G) 0.971506 0.999604 0.922344 0.883799
M2(G) 0.950196 0.994674 0.933317 0.905492
HM(H)(G) 0.951506 0.994565 0.939974 0.910158
ReZG2(G) 0.971951 0.999813 0.912038 0.87472
RezG3(G) 0.920267 0.981735 0.943655 0.926583
SSD(G) 0.977303 0.99853 0.927559 0.882992
Open in a new tab

Fig. 2.

Fig. 2

Open in a new tab

Physical properties on T1.

Table 4.

The statistical parameters for M1.

Properties N A B r r 2 F P Indicator
BP 6 99.84728 4.494093 0.883799 0.781101 14.27324 0.01947 Significant
MW 6 0.306809 3.014766 0.999604 0.999207 5041.65 2.36E-07 Significant
Complexity 6 -67.2393 4.232474 0.971506 0.943824 67.20491 0.001206 Significant
PSA 6 3.143836 1.050685 0.922344 0.850718 22.79496 0.008812 Significant
Open in a new tab

Table 5.

The statistical parameters for M2.

Properties N A B r r 2 F P Indicator
BP 6 111.4944 3.857334 0.905492 0.819915 18.21178 0.012976 Significant
MW 6 12.89697 2.513164 0.994674 0.989377 372.5453 4.25E-05 Significant
Complexity 6 -45.6952 3.467977 0.950196 0.902873 37.18327 0.003659 Significant
PSA 6 6.581182 0.890683 0.933317 0.871082 27.02736 0.006522 Significant
Open in a new tab

Table 6.

The statistical parameters for HM.

Properties N A B r r 2 F P Indicator
BP 6 109.4777 0.909583 0.910158 0.828387 19.30822 0.011745 Significant
MW 6 12.43414 0.589517 0.994565 0.98916 365.0007 4.42E-05 Significant
Complexity 6 -46.6661 0.8147 0.951506 0.905365 38.26746 0.00347 Significant
PSA 6 6.002001 0.210442 0.939974 0.883552 30.35011 0.005296 Significant
Open in a new tab

Table 7.

The statistical parameters for ReZG2.

Properties N A B r r 2 F P Indicator
BP 6 101.9823 19.24075 0.87472 0.765135 13.03106 0.02256 Significant
MW 6 -0.08718 13.04396 0.999813 0.999627 10719.48 5.22E-08 Significant
Complexity 6 -67.853 18.31713 0.971951 0.944688 68.31685 0.001169 Significant
PSA 6 3.697662 4.494249 0.912038 0.831813 19.78312 0.011266 Significant
Open in a new tab

Table 8.

The statistical parameters for ReZG3.

Properties N A B r r 2 F P Indicator
BP 6 125.0405 0.73884 0.926583 0.858556 24.27966 0.007887 Significant
MW 6 27.1302 0.464299 0.981735 0.963804 106.5096 0.000497 Significant
Complexity 6 -22.2535 0.628695 0.920267 0.846891 22.12514 0.009283 Significant
PSA 6 10.35403 0.168566 0.943655 0.890484 32.52435 0.004673 Significant
Open in a new tab

Table 9.

The statistical parameters for SSD.

Properties N A B r r 2 F P Indicator
BP 6 89.26778 8.941635 0.882992 0.779675 14.15496 0.019735 Significant
MW 6 -6.76119 5.997342 0.99853 0.997063 1357.899 3.24E-06 Significant
Complexity 6 -78.9525 8.479101 0.977303 0.955122 85.13038 0.000767 Significant
PSA 6 0.255878 2.104229 0.927559 0.860366 24.6463 0.007681 Significant
Open in a new tab

Table 10.

Standard error of estimate.

Topological indices Complexity Molecular weight Polar Surface Area Boiling point
M1(G) 14.85026 1.221258 6.329849 34.21536
M2(G) 19.52669 4.470514 5.882304 31.03396
HM(G) 19.27463 4.515985 5.590567 30.29524
ReZG2(G) 14.73565 0.837719 6.718704 35.44117
RezG3(G) 24.51657 8.252133 5.421615 27.50374
SSD(G) 13.27322 2.350681 6.121892 34.32663
Open in a new tab

Table 11.

Comparison of the computed values generated by regression model of T1 with actual values of boiling points.

Name BP M1 M2 HM ReZG2 ReZG3 SSD
p- Hydr .acid 335 306.575558 304.3611 119.0738007 304.9722125 303.83978 309.8284081
Vanillic acid 353.43 351.516488 354.506442 121.2264834 350.5087183 358.51394 351.5527595
Syringic acid 440 396.457418 404.651784 123.3791572 396.0450317 413.1881 393.28337
Ferulic acid 373 387.469232 381.50778 122.9546911 387.0661433 374.76842 390.3031231
Sinapic acid 403.41 432.410162 431.653122 125.1073649 432.6024567 429.44258 432.0301569
Benzoic acid 249.2 279.611 277.359762 118.0277802 282.84535 274.28618 277.042115
Open in a new tab

Table 12.

Comparison of the computed values generated by regression model of T1 with actual values of molecular weight.

Name MW M1 M2 HM ReZG2 ReZG3 SSD
p- Hydr .acid 138.12 138.986045 138.55517 18.65354435 137.526598 139.490558 141.1734459
Vanillic acid 168.15 169.133705 171.226302 20.04873655 168.3973468 173.848684 169.1588429
Syringic acid 198.17 199.281365 203.897434 21.44392285 199.2679652 208.20681 197.148438
Ferulic acid 194.18 193.251833 188.81845 21.16881885 193.1808708 184.063262 195.1495239
Sinapic acid 224.21 223.399493 221.489582 22.56400515 224.0514892 218.421388 223.1367201
Benzoic acid 122.12 120.897449 120.963022 17.9755998 122.526044 120.918598 119.182992
Open in a new tab

Table 13.

Comparison of the computed values generated by regression model of T1 with actual values of complexity.

Name Complexity M1 M2 HM ReZG2 ReZG3 SSD
p- Hydr .acid 125 127.454504 127.70365 129.3091 125.3927215 129.89069 130.1989406
Vanillic acid 168 169.779244 172.787351 173.3029 168.7433236 176.41412 169.7649696
Syringic acid 191 212.103984 217.871052 217.2967 212.0937424 222.93755 209.336934
Ferulic acid 224 203.639036 197.06319 197.7439 203.5458706 190.24541 206.5108496
Sinapic acid 249 245.963776 242.146891 241.7377 246.8962894 236.76884 246.0794224
Benzoic acid 104 102.05966 103.427811 101.6093 104.328022 104.74289 99.108621
Open in a new tab

Table 14.

Comparison of the computed values generated by regression model of T1 with actual values of Polar surface area.

Name PSA M1 M2 HM ReZG2 ReZG3 SSD
p-Hydro acid 57.5 51.475346 51.115332 51.457473 51.11198895 51.147002 52.16026347
Vanillic acid 66.8 61.982196 62.694211 62.821341 61.74839323 63.620886 61.97922726
Syringic acid 76 72.489046 74.27309 74.185209 72.38475257 76.09477 71.799664
Ferulic acid 68.8 70.387676 68.928992 69.134601 70.28746633 67.329338 71.09832447
Sinapic acid 76 80.894526 80.507871 80.498469 80.92382567 79.803222 80.91791953
Benzoic acid 37.3 45.171236 44.880551 44.302445 45.9436026 44.404362 44.444687
Open in a new tab

Table 3; Fig. 2 demonstrate that all the topological indices show a good correlation with the appropriate physical characteristic. By examining correlation coefficients, we see that M1(G) index gives the highest correlation value (r = 0.992706) for molecular weight. The second Zagreb index has a high correlation (r = 0.999204) with Complexity, the atom bond connectivity index has a high correlation (r = 0.99985) with polar surface area, the geometric arithmetic index has the highest correlation coefficient (r = 0.999883) for molecular weight, the symmetric division degree gives the best correlated value (r = 0.999484) for polar surface area, and the harmonic index shows good correlation (r = 0.999483) with molecular weight. These results indicate that, the considered topological indices have the potential to predict the properties efficiently and can replace the laborious laboratory experimentations as alternative theoretical tools.

Conclusions

Degree-based topological indices can be used to quantify and analyze the structural features of polyphenolic compounds. By incorporating these indices into QSPR models, we can establish relationships between the structural characteristics of polyphenols and their physical properties. The results demonstrate that all the topological indices show a good correlation with the appropriate physical characteristic. By examining correlation coefficients, we see that M1(G) index gives the highest correlation value (r = 0.992706) for molecular weight. The second Zagreb index has a high correlation (r = 0.999204) with Complexity, the atom bond connectivity index has a high correlation (r = 0.99985) with polar surface area, the geometric arithmetic index has the highest correlation coefficient (r = 0.999883) for molecular weight, the symmetric division degree gives the best correlation value (r = 0.999484) for polar surface area, and the harmonic index shows good correlation (r = 0.999483) with molecular weight. Degree-based topological indices also provide insights into the number of bonds, connectivity patterns, and branching characteristics in polyphenolic compounds. QSPR analysis utilizes these indices and corresponding experimental data on the physical characteristics of polyphenols to develop predictive models.

In future work, the integration of machine learning techniques, such as random forests, support vector machines, and gradient boosting regressors, can enhance the predictive power of QSPR models by capturing complex, non-linear relationships between topological indices and physicochemical properties. Ensemble learning methods, in particular, offer robustness against overfitting and can aggregate predictions from multiple base models to improve generalization. These data-driven approaches can complement traditional linear regression by identifying subtle structural patterns and interactions that may be overlooked in linear models. As more polyphenolic data becomes available, combining degree-based descriptors with advanced regression frameworks could lead to more accurate, scalable, and interpretable models for screening and evaluating polyphenolic compounds in drug discovery, nutraceuticals, and materials chemistry.

Acknowledgements

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-94).

Author contributions

All the authors Abdul Hakeem, Asad Ullah, Shahid Zaman, Emad E. Mahmoud, Hijaz Ahmad, Parvez Ali and Melaku Berhe Belay have equally contributed to this manuscript in all stages, from conceptualization to the write-up of final draft.

Funding

This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-94).

Data availability

All data generated or analyzed during this study are included within this article.

Declarations

Competing interests

The authors declare no competing interests.

Declaration of Generative AI and AI-assisted technologies in the writing process

During the preparation of this work the authors used ChatGPT 3.5 in order to improve readability and language of the manuscript. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Contributor Information

Asad Ullah, Email: dr.asadullah@kiu.edu.pk.

Shahid Zaman, Email: zaman.ravian@gmail.com.

Melaku Berhe Belay, Email: melaku.berhe@aastu.edu.et.

References

  • 1.Abbas, M. et al. Natural polyphenols: an overview. Int. J. Food Prop.20, 1689–1699 (2017). [Google Scholar]
  • 2.Rathod, N. B. et al. Recent developments of natural antimicrobials and antioxidants on fish and fishery food products. Compr. Rev. Food Sci. Food Saf.20, 4182–4210 (2021). [DOI] [PubMed] [Google Scholar]
  • 3.Kammerer, D. R., Kammerer, J., Valet, R. & Carle, R. Recovery of polyphenols from the by-products of plant food processing and application as valuable food ingredients. Food Res. Int.65, 2–12 (2014). [Google Scholar]
  • 4.Sajadimajd, S. et al. Advances on natural polyphenols as anticancer agents for skin cancer. Pharmacol. Res.151, 104584 (2020). [DOI] [PubMed] [Google Scholar]
  • 5.Inanli, A. G., Tümerkan, E. T. A., Abed, N. E., Regenstein, J. M. & Özogul, F. The impact of Chitosan on seafood quality and human health: A review. Trends Food Sci. Technol.97, 404–416 (2020). [Google Scholar]
  • 6.Liu, J. & Henkel, T. Traditional Chinese medicine (TCM): are polyphenols and saponins the key ingredients triggering biological activities? Curr. Med. Chem.9, 1483–1485 (2002). [DOI] [PubMed] [Google Scholar]
  • 7.Gupta, S. C. et al. Downregulation of tumor necrosis factor and other Proinflammatory biomarkers by polyphenols. Arch. Biochem. Biophys.559, 91–99 (2014). [DOI] [PubMed] [Google Scholar]
  • 8.Kim, Y. H. et al. Green tea Catechin metabolites exert immunoregulatory effects on CD4 + T cell and natural killer cell activities. J. Agric. Food Chem.64, 3591–3597 (2016). [DOI] [PubMed] [Google Scholar]
  • 9.Hanhineva, K. et al. Impact of dietary polyphenols on carbohydrate metabolism. Int. J. Mol. Sci.11, 1365–1402 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Cheynier, V. Polyphenols in foods are more complex than often thought. Am. J. Clin. Nutr.81, 223S–229S (2005). [DOI] [PubMed] [Google Scholar]
  • 11.Pandey, K. B. & Rizvi, S. I. Plant polyphenols as dietary antioxidants in human health and disease. Oxid. Med. Cell. Longev.2, 270–278 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Dias, R., Pereira, C. B., Pérez-Gregorio, R., Mateus, N. & Freitas, V. Recent advances on dietary polyphenol’s potential roles in Celiac disease. Trends Food Sci. Technol.107, 213–225 (2021). [Google Scholar]
  • 13.Havare, Ö. Ç. Topological indices and QSPR modeling of some novel drugs used in the cancer treatment. Int. J. Quantum Chem.121, e26813 (2021). [Google Scholar]
  • 14.Zaman, S., Jalani, M., Ullah, A., Ali, M. & Shahzadi, T. On the topological descriptors and structural analysis of cerium oxide nanostructures. Chem. Pap.77, 2917–2922 (2023). [Google Scholar]
  • 15.Mondal, S. & Das, K. C. Zagreb connection indices in structure property modelling. J. Appl. Math. Comput. 69, 3005–3020 (2023).
  • 16.Mondal, S., Dey, A., De, N. & Pal, A. QSPR analysis of some novel neighbourhood degree-based topological descriptors. Complex. Intell. Syst.7, 977–996 (2021). [Google Scholar]
  • 17.Mondal, S., De, N. & Pal, A. On neighborhood Zagreb index of product graphs. J. Mol. Struct.1223, 129210 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Khan, A. R. et al. Computation of differential and integral operators using M-polynomials of gold crystal. Heliyon 10, e34419 (2024). [DOI] [PMC free article] [PubMed]
  • 19.Sharma, K., Bhat, V. K. & Liu, J. B. Second leap hyper-Zagreb coindex of certain benzenoid structures and their polynomials. Comput. Theor. Chem.1223, 114088 (2023). [Google Scholar]
  • 20.Sharma, K., Bhat, V. K. & Sharma, S. K. On Degree-Based Topological Indices of Carbon Nanocones, ACS Omegapp. 45562–45573 (American Chemical Society, 2022). [DOI] [PMC free article] [PubMed]
  • 21.Radhakrishnan, M., Prabhu, S., Arockiaraj, M. & Arulperumjothi, M. Molecular structural characterization of superphenalene and supertriphenylene. Int. J. Quantum Chem.122, e26818 (2022). [Google Scholar]
  • 22.Zhang, Q. et al. Mathematical study of silicate and oxide networks through Revan topological descriptors for exploring molecular complexity and connectivity. Sci. Rep.15, 8116 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Zhang, Q., Zaman, S., Ullah, A., Ali, P. & Mahmoud, E. E. The Sharp lower bound of tricyclic graphs with respect to the ISI index: applications in octane isomers and benzenoid hydrocarbons. Eur. Phys. J. E. 48, 10 (2025). [DOI] [PubMed] [Google Scholar]
  • 24.Tang, J. H. et al. Chemical applicability and predictive potential of certain graphical indices for determining structure-property relationships in polycrystalline acid magenta (C20H17N3Na2O9S3). Sci. Rep.15, 13886 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Kara, Y., Özkan, Y. S., Ullah, A., Hamed, Y. S. & Belay, M. B. QSPR modeling of some COVID-19 drugs using neighborhood eccentricity-based topological indices: A comparative analysis. PLoS ONE. 20, e0321359 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Ullah, A., Qasim, M., Zaman, S. & Khan, A. Computational and comparative aspects of two carbon nanosheets with respect to some novel topological indices. Ain Shams Eng. J.13, 101672 (2022). [Google Scholar]
  • 27.Ö & Çolakoğlu QSPR modeling with topological indices of some potential drug candidates against COVID-19, Journal of Mathematics, (2022) 1–9. (2022).
  • 28.Prabhu, S. et al. Computational Analysis of Some More Rectangular Tessellations of Kekulenes and Their Molecular Characterizations, Molecules, (2023). [DOI] [PMC free article] [PubMed]
  • 29.Arulperumjothi, M., Prabhu, S., Liu, J. B., Rajasankar, P. Y. & Gayathri, V. On counting polynomials of certain classes of polycyclic aromatic hydrocarbons. Polycycl. Aromat. Compd.43, 4768–4786 (2023). [Google Scholar]
  • 30.Prabhu, S., Arulperumjothi, M., Manimozhi, V. & Balasubramanian, K. Topological characterizations on hexagonal and rectangular tessellations of Antikekulenes and its computed spectral, nuclear magnetic resonance and electron spin resonance characterizations. Int. J. Quantum Chem.124, e27365 (2024). [Google Scholar]
  • 31.Wazzan, S. & Ozalan, N. U. Exploring the symmetry of curvilinear regression models for enhancing the analysis of fibrates drug activity through molecular descriptors. Symmetry15, 1160 (2023). [Google Scholar]
  • 32.Omar, R. M. K., Najar, A. M., Bobtaina, E. & Elsheikh, A. F. Pryazolylpyridine and Triazolylpyridine Derivative of Hydroxychloroquine as Potential Therapeutic against COVID-19 (Theoretical Evaluation, 2020).
  • 33.Gutman, I. & Trinajstić, N. Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett.17, 535–538 (1972). [Google Scholar]
  • 34.Shirdel, G., Rezapour, H. & Sayadi, A. The hyper-Zagreb index of graph operations, DOI (2013).
  • 35.Ranjini, P., Lokesha, V. & Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory. 1, 116–121 (2013). [Google Scholar]
  • 36.Vukicevic, D. & Gasperov, M. Bond additive modeling 1. Adriatic indices. Croat Chem. Acta. 83, 243 (2010). [Google Scholar]
  • 37.Iqbal, Z., Aslam, A., Ishaq, M. & Gao, W. The edge versions of degree-based topological descriptors of dendrimers. J. Cluster Sci.31, 445–452 (2020). [Google Scholar]
  • 38.Aslam, A., Ahmad, S., Binyamin, M. A. & Gao, W. Calculating topological indices of certain OTIS interconnection networks. Open. Chem.17, 220–228 (2019). [Google Scholar]
  • 39.Khabyah, A. A., Zaman, S., Koam, A. N., Ahmad, A. & Ullah, A. Minimum Zagreb eccentricity indices of two-mode network with applications in boiling point and benzenoid hydrocarbons. Mathematics10, 1393 (2022). [Google Scholar]
  • 40.Zaman, S., Yaqoob, H. S. A., Ullah, A. & Sheikh, M. QSPR analysis of some novel drugs used in blood Cancer treatment via degree based topological indices and regression models, polycyclic aromatic compounds, (2023). 10.1080/10406638.2023.2217990 1–17 .
  • 41.Zaman, S. et al. Three-Dimensional Structural Modelling and Characterization of Sodalite Material Network concerning the Irregularity Topological Indices, Journal of Mathematics, (2023) 1–9. (2023).
  • 42.Zaman, S., Jalani, M., Ullah, A., Saeedi, G. & Guardo, E. Structural Analysis and Topological Characterization of Sudoku Nanosheet, Journal of Mathematics, (2022) 1–10. (2022).
  • 43.Zaman, S., Jalani, M., Ullah, A., Ahmad, W. & Saeedi, G. Mathematical analysis and molecular descriptors of two novel metal–organic models with chemical applications. Sci. Rep.13, 5314 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Ullah, A., Zaman, S., Hussain, A., Jabeen, A. & Belay, M. B. Derivation of mathematical closed form expressions for certain irregular topological indices of 2D nanotubes. Sci. Rep.13, 11187 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Ullah, A., Zaman, S., Hamraz, A. & Muzammal, M. On the construction of some bioconjugate networks and their structural modeling via irregularity topological indices. Eur. Phys. J. E. 46, 72 (2023). [DOI] [PubMed] [Google Scholar]
  • 46.Ullah, A. et al. Network-Based Modeling of the Molecular Topology of Fuchsine Acid Dye with Respect to Some Irregular Molecular Descriptors, Journal of Chemistry, (2022) 1–8. (2022).
  • 47.Ullah, A., Shamsudin, S., Zaman, A. & Hamraz Zagreb connection topological descriptors and structural property of the triangular chain structures. Phys. Scr.98, 025009 (2023). [Google Scholar]
  • 48.Ullah, A., Bano, Z. & Zaman, S. Computational aspects of two important biochemical networks with respect to some novel molecular descriptors. J. Biomol. Struct. Dynamics. 1–15. 10.1080/07391102.2023.2195944 (2023). [DOI] [PubMed]
  • 49.Hayat, S. & Asmat, F. Sharp Bounds on the Generalized Multiplicative First Zagreb Index of Graphs with Application to QSPR Modeling, Mathematics, (2023).
  • 50.Khan, A. et al. Computational and topological properties of neural networks by means of graph-theoretic parameters. Alexandria Eng. J.66, 957–977 (2023). [Google Scholar]
  • 51.Hayat, S., Mahadi, H., Alanazi, S. J. F. & Wang, S. Predictive potential of eigenvalues-based graphical indices for determining thermodynamic properties of polycyclic aromatic hydrocarbons with applications to polyacenes. Comput. Mater. Sci.238, 112944 (2024). [Google Scholar]
  • 52.Saravanan, B., Prabhu, S., Arulperumjothi, M., Julietraja, K. & Siddiqui, M. K. Molecular structural characterization of supercorenene and Triangle-Shaped discotic graphene. Polycycl. Aromat. Compd.43, 2080–2103 (2023). [Google Scholar]
  • 53.Golbraikh, A., Bonchev, D. & Tropsha, A. Novel ZE-isomerism descriptors derived from molecular topology and their application to QSAR analysis. J. Chem. Inf. Comput. Sci.42, 769–787 (2002). [DOI] [PubMed] [Google Scholar]
  • 54.Das, K. C., Gutman, I. & Furtula, B. On atom-bond connectivity index. Chem. Phys. Lett.511, 452–454 (2011). [Google Scholar]
  • 55.Hakeem, A., Ullah, A. & Zaman, S. Computation of some important degree-based topological indices for γ-graphyne and zigzag Graphyne nanoribbon. Mol. Phys. 121, e2211403 (2023).
  • 56.Liu, J. B., Zheng, Y. Q. & Peng, X. B. The statistical analysis for Sombor indices in a random polygonal chain networks. Discrete Appl Math.338, 218–233 (2023). [Google Scholar]
  • 57.Liu, J. B., Zheng, Q., Cai, Z. Q. & Hayat, S. On the laplacians and normalized laplacians for graph transformation with respect to the Dicyclobutadieno derivative of [n]Phenylenes. Polycycl. Aromat. Compd.42, 1413–1434 (2022). [Google Scholar]
  • 58.Liu, J. B., Xie, Q., Gu, J. J. & Wu, S. Statistical Analyses of a Class of Random Pentagonal Chain Networks with respect to Several Topological Properties, Journal of Function Spaces, (2023) 1–17. (2023).
  • 59.Das, K. C., Mondal, S. & Raza, Z. On Zagreb connection indices. Eur. Phys. J. Plus. 137, 1242 (2022). [Google Scholar]
  • 60.Balasubramaniyan, D. & Chidambaram, N. On some neighbourhood degree-based topological indices with QSPR analysis of asthma drugs. Eur. Phys. J. Plus. 138, 823 (2023). [Google Scholar]
  • 61.Zhao, D. et al. Topological analysis of entropy measure using regression models for silver iodide. Eur. Phys. J. Plus. 138, 805 (2023). [Google Scholar]
  • 62.Arockiaraj, M. et al. QSPR analysis of distance-based structural indices for drug compounds in tuberculosis treatment. Heliyon10, e23981 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 63.Raza, Z., Arockiaraj, M., Maaran, A., Kavitha, S. R. J. & Balasubramanian, K. Topological entropy characterization, NMR and ESR spectral patterns of Coronene-Based transition metal organic frameworks. ACS Omega. 8, 13371–13383 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 64.Arockiaraj, M., Paul, D., Ghani, M. U., Tigga, S. & Chu, Y. M. Entropy structural characterization of zeolites BCT and DFT with bond-wise scaled comparison. Sci. Rep.13, 10874 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 65.Shanmukha, M. C., Gowtham, K. J., Usha, A. & Julietraja, K. Expected values of Sombor indices and their entropy measures for graphene. Mol. Phys.122, e2276905 (2024). [Google Scholar]
  • 66.Kirana, B., Shanmukha, M. C. & Usha, A. Comparative study of Sombor index and its various versions using regression models for top priority polycyclic aromatic hydrocarbons. Sci. Rep.14, 19841 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 67.Shanmukha, M. C. et al. Chemical applicability and computation of K-Banhatti indices for benzenoid hydrocarbons and triazine-based covalent organic frameworks. Sci. Rep.13, 17743 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 68.Govardhan, S., Roy, S., Prabhu, S. & Arulperumjothi, M. Topological characterization of cove-edged graphene nanoribbons with applications to NMR spectroscopies. J. Mol. Struct.1303, 137492 (2024). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

All data generated or analyzed during this study are included within this article.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES