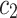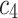Abstract
This study explores some geometric properties of the class of symmetric starlike functions associated with a Crescent-shaped domain denoted by 
. Initially, we establish key coefficient inequalities and investigate upper bounds for the 2nd and 3rd order Hankel determinants. All the obtained results are sharp. These bounds provide deeper insights into the structural behavior of this class and contribute to a broader understanding of Geometric Function Theory. In addition to the theoretical findings, the practical implications of the results obtained are demonstrated in the domain of image processing. We used our estimated sharp Hankel determinants to develop a novel algorithm for image enhancement. The performance of the algorithm is evaluated on different image datasets of varying dimensions, with key quality metrics such as PSNR, SSIM, PCC, and MAE. Our experimental results indicate a significant improvement over conventional image enhancement techniques, particularly in retaining structural integrity and reducing distortions. In addition, a comparative study highlights the effectiveness of the proposed algorithm compared to existing methods reported in the literature, demonstrating its potential to enhance image quality in practical applications.
Subject terms: Health care, Mathematics and computing
Introduction
The theory of analytic and univalent functions has long been a central topic in Geometric Function Theory. Functions that are analytic and univalent not only offer rich geometric insights, but also arise in practical problems involving conformal mappings, fluid flow, and dynamic systems1. A fundamental aspect of this theory is the study of various subclasses of univalent functions, such as classes of starlike and convex functions. These subclasses have been extensively investigated due to their geometric characterizations and ease of analyzing their coefficient bounds2 .
Hankel determinants have significant importance in studying the behavior of coefficients of analytic functions in the field of geometric function theory. Pommerenke3 was the one who introduced the concept of Hankel determinants, that was later explored further by Noonan and Thomas4. Janteng5 continued the line of investigation, especially for subclasses such as starlike and convex functions.
In this study, we focus on estimating second- and third-order Hankel determinants for subclasses of analytic functions involving symmetric points. These classes, inspired by the work of Sakaguchi6 and generalized by Ravichandran7, are characterized by symmetry related subordination conditions and are of current interest in complex analysis. We now provide the necessary definitions and background that will serve as the foundation for our main results.
Let 
be the class of analytic functions f in an open unit disc 
, normalized by 
, and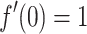 
. Then if 
, then it has the Taylor’s series form
 |
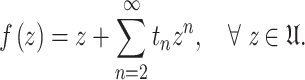1 |
Let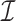 
be the subclass of 
8 consisting of functions that are also univalent in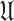 
. Goodman9 introduced two important subclasses 
and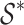 
of convex and starlike functions respectively. These subclasses possess significant and interesting geometric properties. A function 
is said to be starlike in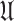 
iff
 |
2 |
and a function 
is said to be convex in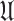 
iff
 |
3 |
The idea of subordination between analytic functions was given by Lindelof10. Furthermore, Littlewood11 and Rogosinski12 introduced fundamental results involving subordination. Let g(z) and h(z) are two analytic functions in 
. Then g(z) is subordinated to h(z), denoted as 
h(z), if there exists a Schwarz function w(z) in 
, with 
, such that 
. The class 
represents the class of Caratheodory functions13, which satisfies 
and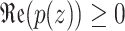 
. The function 
has following series representation
 |
4 |
Hankel determinants14 of analytic functions are of considerable interest to current researchers working in the field of Geometric Function Theory. In 1966 Pommerenke3 examined Hankel determinants for univalent functions, which were further explored by Noonan and Thomas4. For 
, the 
th Hankel determinant denoted by 
is defined as,
 |
5 |
where 
,
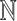such that 
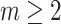and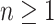 
. Different Hankel determinants can be obtained by taking different values of 
and 
. For 
and 
, the determinant is
 |
6 |
where 
and its modified form is 
where 
is real. This is the particular case of the Fekete Szego functional. The maximum value of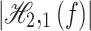 
for various subclasses was studied by many researchers15 . The second Hankel determinant was given by Janteng5 of the form:
 |
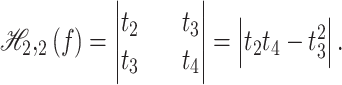7 |
Furthermore, for 
and 
, the Hankel determinant of order 3rd is given below:
 |
8 |
In 1992, Maand Minda16 defined the unified form of the family of star-like functions as
 |
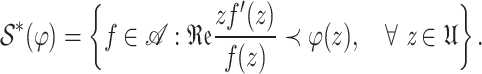where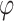 
indicates the analytic function with 
and 
. In addition, the region 
is star-shaped with 
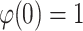and is symmetric along the real axis. The star-like functions was generalized by Sakaguchi6 in 1959 by introducing the class 
of star-like functions with respect to symmetric points. In6, the author provided the analytical formulations of this class as follow,
 |
Ravichandran7 introduce the class 
of star-like function w.r.t symmetric point, defined as follow,
 |
9 |
For specific choices of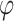 
we obtain
Definition 1.1
If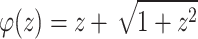 
was introduced by Raina and Sokol17, 
maps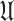 
to the crescent-shaped region 
, we will define 
, is the class of symmetric star-like functions linked with Cresent-shaped domain.
Literature review
Recent developments in geometric function theory seem to have a special focus on the exploration of Hankel determinants, particularly within various subclasses of analytic and starlike functions.These determinants play a crucial role in determining the behavior of coefficient bounds, with applications in both mathematics and computational techniques. For example, Joshi and Kumar18 investigated the third Hankel determinant in a class of starlike functions associated with the exponential function. This offers important generalizations of the classical results. Likewise, Allu and Shaji19 obtained the sharp bounds of the second Hankel determinant of inverse logarithmic coefficients for both starlike and convex functions.
Furthermore, Kumar, Kumar and Das20 explored Hermitian–Toeplitz determinants, which are related to Hankel, for starlike functions with real coefficients, including the determinant on the fourth-order. Al-Shbeil et al.21 and Banga and Kumar22 considered the use of q-calculus to obtain bounds on determinants for q-starlike functions. These advancements highlight the analytical depth and capacity for utilizing such function-theoretic findings in computational domains.
Moreover, scholars have also extended the scope of starlike and convex functions mapping to cover specialized and non-traditional domains. For example, Kumar and Giri23 presented a class of starlike functions associated with the non-convex domain. The results included growth and sharp third-order Hankel and Hermitian–Toeplitz determinants. These findings enrich new perspectives in Geometric Function Theory. Meanwhile, Marımuthu et al.24 proposed cosine-based starlike and convex subclasses, deriving initial coefficient bounds and sharp estimates for third and fourth-order Hankel determinants. They successfully computed sharp determinant estimates for higher-order cases.
To the best of our knowledge, little research has utilised these mathematical findings for real-world issues, especially in image processing. We found that Nithiyanandham and Keerthi25 presented an algorithm to enhance image edge detection. The algorithm is based on coefficient estimates from Sakaguchi-type functions, and the results show improvements in images with detail retention. However, the use of Hankel determinants in image enhancement remains unexplored. Therefore, this study fills the gap by linking Geometric Function Theory with practical image enhancement.
Various approaches have been developed to address image quality improvement through different computational methods. Traditional spatial domain techniques focus on direct pixel manipulation, with histogram equalization being particularly prevalent due to its computational efficiency and broad applicability26. However, such methods can produce unnatural contrast when normalizing image intensities, prompting the development of Joint Histogram Equalization (JHE) to incorporate neighborhood pixel information for more balanced enhancement.
Specialized applications have seen tailored solutions, like Chen et al.’s27 fuzzy-based contrast enhancement for infrared vein imaging. Mathematical approaches have also contributed, including Ibrahim et al.’s28 fractional order heat equations and Priya’s29 texture analysis using coefficient bounds.
This study introduces a novel enhancement algorithm based on the convolution of Hankel determinants from Symmetric starlike functions associated with Crescent-shaped domain with image pixels through a 3
3 mask window. Our method builds upon these existing techniques while addressing their limitations in preserving structural integrity during enhancement.
Preliminaries
Lemma 3.1
30
Let
, is given in (4). Then,
 |
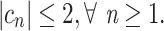10 |
Lemma 3.2
30
Let
, is given in (4). Then,
 |
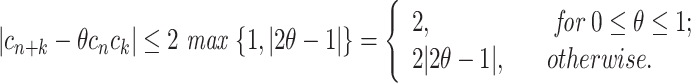11 |
Lemma 3.3
31,32
Let
, is given in (4). Then, if
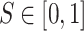with
, we have
 |
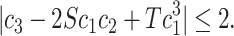12 |
Lemma 3.4
Let
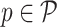, is in the form (4). Then, for
, we have
 |
13 |
 |
14 |
 |
15 |
Lemma 3.5
35
Let
and
u
satisfy
and
 |
16 |
If
, is given in (4). Then,
 |
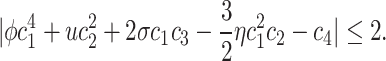17 |
Main results
Theorem 4.1
Let
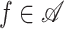be given by (1). If
, then
 |
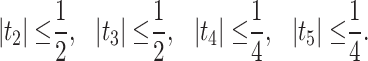18 |
These bounds are the best possible.
Proof
Let 
. Then utilizing Schwarz function, (9) can be written as
 |
If 
, and can written in the form of Schwarz function as follows
 |
a simple computation yield
 |
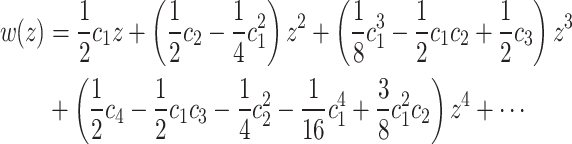19 |
Utilizing (1), we get
 |
20 |
By using (19) and after some simplification, we get
 |
21 |
Now, comparing (20) and (21), we get
 |
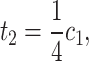22 |
 |
23 |
 |
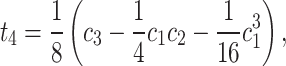24 |
 |
25 |
Implementing (10) in (22), we obtain
 |
 |
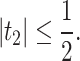Rearranging (24) gives
 |
Let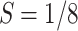 
and 
. Using Lemma 3.3 leads us to
 |
Rearranging (25) gives
 |
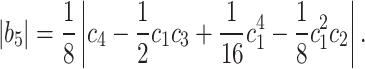By utilizing (13), (14) and (15) we express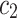 
, 
and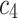 
in terms of 
and take 
, also let 
in Lemma (3.4), we obtain
 |
By utilizing 
and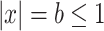 
and applying triangular inequality, if 
, we get
 |
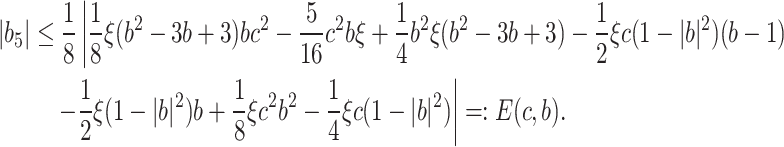It is not difficult to observe that 
for [0, 1], then we have 
. Replacing 
gives
 |
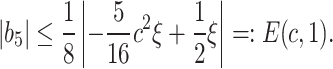It is obvious that 
, so E(c, 1) is a decreasing function and attains its maximum value at 
. Then, we get
 |
Theorem 4.2
Let
and is given in (1). If
, then
 |
26 |
This result is sharp.
Proof
 |
after some steps
 |
Using Lemma(3.2)
 |
Theorem 4.3
Let
and is given in (1). If
, then
 |
27 |
This inequality is the best possible.
Proof
From (22), (23) and (24), we get
 |
after simplification
 |
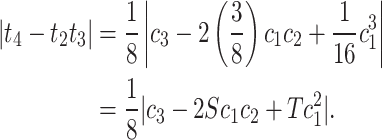Let 
and 
. Using Lemma (3.3) leads us to
 |
Theorem 4.4
Let
and is given in (1). If
, then
 |
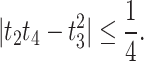28 |
This inequality is the best possible.
Proof
From (22), (23) and (24), we get
 |
after simplification
 |
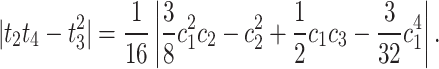Now, by using (13) and (14) in order to express 
and 
in terms of 
and also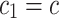 
, also let 
in Lemma (3.4), we obtain
 |
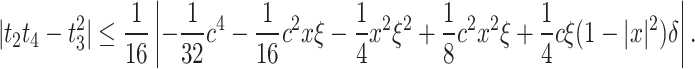By utilizing 
and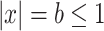 
and applying triangular inequality, if 
, we get
 |
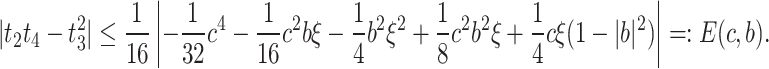It is not difficult to observe that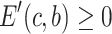 
for [0, 1], so we have 
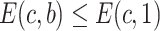. Replacing 
gives
 |
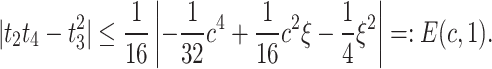It is obvious that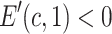 
, so E(c, 1) is a decreasing function and attains its maximum value at 
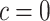. Then,
 |
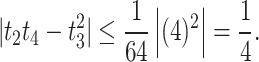Theorem 4.5
Let
and is given in (1). If
, then
 |
29 |
This inequality is the best possible.
Proof
Using triangular inequality in
 |
By using (23), (24), (25), (26), (27), and (28), we have
 |
after some simplifications, the required result is obtained. 
Application of Hankel determinant in image enhancement
Digital images are subject to several types of alterations during the capture, restoration, enhancement, compression, and transmission processes. For further image processing or analysis, it is crucial to remove such degradations. In image compression and transmission, the least amount of change is preferred, and quantitative measurements like PSNR, MSE, and others are frequently used to evaluate the level of distortion relative to the original image.
Image enhancement essentially deals with improving the image quality for better vision. The three basic parameters that control the quality of an image are contrast, brightness, and sharpness. The images are altered to make them more suitable for particular uses than the originals. Techniques for image enhancement highlight particular aspects of a picture or highlight hidden details. As an illustration of enhancement, we occasionally raise an image’s contrast to make it look better. A graphic presentation highlights visual components such as boundaries, limitations, or contrast to increase effectiveness for study and exhibition. The enhancement increases the specified characteristics, making simpler to recognize even though it does not increase the data’s fundamental information richness.
An essential part of digital image processing, image enhancement aims to improve a picture’s quality by altering its components to make it easier to understand or more aesthetically pleasing. The following arguments support the importance of image enhancement: Improve details, visual quality, eliminate noise, adjust contrast and brightness.
Image Quality Assessment (IQA) techniques36 can be classified into subjective and objective assessment, which automatically measures image quality. The quality of the images can be analyzed using a variety of techniques and metrics. The quality metrics that are commonly used in the image quality evaluation are Peak Signal to Noise Ratio (PSNR)37, Mean Squared Error (MSE)37, Structural Similarity Index Measure (SSIM)38, Pearson Correlation Coefficient (PCC)26, Root Mean Squared Error (RMSE)39 and Mean Absolute Error (MAE)39.
In this section, we will utilize the proposed coefficients and Hankel determinants for the enhancement of medical images. We will compare the effectiveness of image enhancement by estimating different quality metrics and providing graphical illustration.
Proposed Algorithm
In the following section, we define a novel algorithm established on Hankel determinants for the class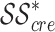 
. We represent the Hankel determinants 
, 
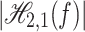and 
for the class that are calculated above, as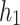 
, 
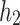and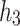 
respectively. The Hankel determinants 
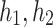, and 
are obtained in Theorems 3.2, 3.4, and 3.5. By using convolution, the processed image can be represented as 
,
 |
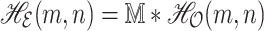where 
is the input image,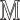 
denotes a 
mask window, and 
represents convolution production. The first three Hankel determinant values are denoted by 
and 
and the corresponding mask windows at different angles are as follows:
Step 1: Transform original images to gray-scale.
Step 2: Set introduced mask over
pixel size.Step 3: Apply convolution of mask window over the original image in 4 directions.
Step 4: For enhanced image, compute the quality metrics.
Earlier studies40–43 have explored algorithms derived from coefficients of specific subclasses of analytic functions for image processing. In this study, we propose a novel algorithm that utilizes the convolution of an image with a diagonal matrix. The entries of this matrix are Hankel determinants associated with the class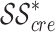 
. Our method demonstrates significant improvements in image quality. The results show that the proposed Hankel determinant-based algorithm outperforms existing coefficient-based methods26,44 in image enhancement. This function-theoretic approach has not been applied in previous image enhancement methods and demonstrates a notable improvement in PSNR and SSIM scores across diverse datasets, as shown in Tables 3 and 4.
Table 3.
Comparison of DOG, ARGYLE, and X-RAY with average PSNR and SSIM value.
Table 4.
Comparison of MESSIDOR dataset with average PSNR and SSIM value.
The aforementioned algorithm is first tested on a variety of image formats with varying pixel values to ensure that they are functioning properly. We used JPG images DOG, ARGYLE, X-RAY and MESSIDOR dataset that are transformed to gray-scale images shown in Figs. 1, 2, 3, 4, 5, 6 and 7.
Fig. 1.
Enhancement of DOG at different angles.
Fig. 2.
Enhancement of ARGYLE at different angles.
Fig. 3.
Enhancement of X-RAY at different angles.
Fig. 4.
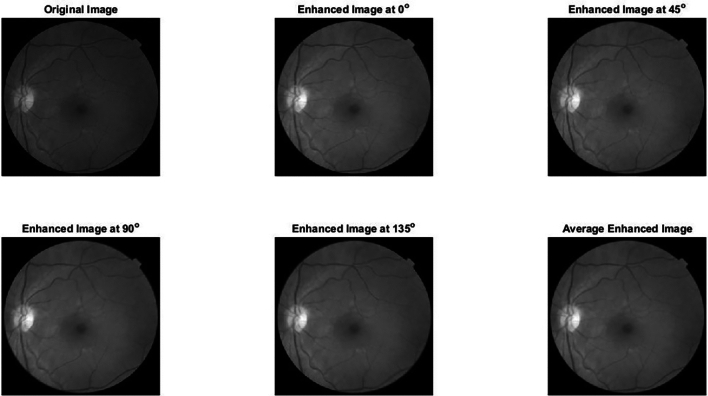
Enhancement of MESSIDOR 1 at different angles.
Fig. 5.
Enhancement of MESSIDOR 2 at different angles.
Fig. 6.
Enhancement of MESSIDOR 3 at different angles.
Fig. 7.
Enhancement of MESSIDOR 4 at different angles.
Figures 1, 2, 3, 4, 5, 6 and 7 show the enhancement of DOG, ARGYLE, X-RAY and MESSIDOR dataset for various angles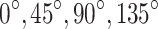 
and the average of all angles. The average enhanced image is obtained by applying the average mask window to the image. The average mask window is the average of four mask windows 
,
, 
and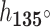 
.
The enhanced images are comparatively different in pixel from the original images. Visually, the details on the enhanced images are clearly shown. Better results are achieved at average of all angles with respect to the constraints of PSNR, SSIM.
By comparing enhanced images using the proposed algorithm and the algorithm defined in26,44, we observed that the best enhancement is given by the proposed algorithm. Initially the pictures are dark making them difficult to examine, but after applying the proposed algorithm on the DOG, ARGYLE, X-RAY and MESSIDOR dataset, the brightness level slightly improved so that small details are bit easier to see. Most importantly, the details on the enhanced images using the proposed algorithm are much more visible and bright. The quality metrics values for enhanced images using the algorithm are calculated in Tables 1 and 2.
Table 1.
Quality metrics for DOG, ARGYLE, and X-RAY.
| Quality metrics | DOG | ARGYLE | X-RAY |
|---|---|---|---|
| PSNR | 27.37 | 35.68 | 33.86 |
| SSIM | 0.9368 | 0.9749 | 0.9328 |
| RMSE | 10.9179 | 0.0419 | 5.1715 |
| PCC | 0.9833 | 0.9943 | 0.9988 |
| MAE | 0.0302 | 0.0001 | 0.0080 |
Table 2.
Quality metrics for MESSIDOR dataset.
| Quality metrics | Messidor 1 | Messidor 2 | Messidor 3 | Messidor 4 |
|---|---|---|---|---|
| PSNR | 36.30 | 35.01 | 34.26 | 33.43 |
| SSIM | 0.9972 | 0.9506 | 0.9771 | 0.9714 |
| RMSE | 3.9039 | 4.5275 | 4.9383 | 5.4315 |
| PCC | 0.9992 | 0.9992 | 0.9998 | 0.9981 |
| MAE | 0.0105 | 0.0121 | 0.0138 | 0.0149 |
Comparative analysis
The proposed image enhancement algorithm can be used in different real-world applications. For example, enhancing image quality in medical imaging is crucial for accurate diagnosis and treatment planning. Such techniques can improve contrast, reduce noise, and help doctors better visualize anatomical structures and detect abnormalities as Dinh and Giang45 proposed a novel algorithm to solve noise, blur, and low contrast problems on images simultaneously. Furthermore, image enhancement can play a vital role in the field of security and surveillance, particularly in improving facial recognition and object detection. A lot of research has been applied to many different techniques to improve low-light images46. Similarly, high-resolution images are essential for satellite images for environmental monitoring, resolving low-resolution signals and enhancing earth observation data. Many techniques have been employed to enhance satellite images, allowing for more detailed and accurate data analysis47. By integrating the proposed algorithm into these domains, it has the potential to significantly improve image quality and contribute to advancements in healthcare, security, and geospatial analysis. The novel algorithm gives satisfactory enhancements for the images compared to the enhanced images obtained in26,44. The performance of our algorithm is assessed using metrics such as PSNR and SSIM. In particular, more accurate enhancements are obtained using higher PSNR while preserving image details.
As we see in Table 3, we achieved higher PSNR and SSIM value compared to Aarthy in26. In Table 4, we use the average PSNR and SSIM values of the “MESSIDOR” dataset for a novel algorithm.
As we see in Table 4, we achieved higher PSNR and SSIM value compared to all PSNR and SSIM values obtained in previous researches. If we use the proposed Hankel algorithm compared to the coefficient algorithm defined in26,44, we get stronger results. The quality metrics obtained for the class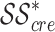 
demonstrate a high level of satisfaction.
Now we verify our results using different graphical illustrations. For the assessment of the proposed cryptosystem and the graphical results from Figs. 8, 9, 10, 11, 12, 13 and 14, we use MATLAB R2022a. We used a mesh representation for our obtained images and then compared the results. A collection of vertices and polygons forms a mesh representation which is a three-dimensional image representation. We analyze our enhanced images using mesh representations. Mesh representation is very useful, since it reveals some minor details that are not visible by the 2D image. A mesh representation model gives the structure as 3D geometric meshes. We provide a mesh representation of original images, images enhanced by the proposed algorithm for better understanding and comparison.
Fig. 8.
Mesh representation of pixel values of “DOG”.
Fig. 9.
Mesh representation of pixel values of “ARGYLE”.
Fig. 10.
Mesh representation of pixel values of “X-RAY”.
Fig. 11.
Mesh representation of pixel values of “MESSIDOR 1”.
Fig. 12.
Mesh representation of pixel values of “MESSIDOR 2”.
Fig. 13.
Mesh representation of pixel values of “MESSIDOR 3”.
Fig. 14.
Mesh representation of pixel values of “MESSIDOR 4”.
Figure 8 illustrates the transformation from an original image with uneven pixel intensity and low contrast to an enhanced version with pronounced peaks and valleys. The enhanced mesh representation shows clearer edges and smoother transitions, indicating both noise reduction and contrast improvement.
Figure 9 demonstrates the algorithm’s proficiency in handling repetitive patterns. The original mesh representation displays moderate intensity variations, while the enhanced version exhibits sharper peaks that correspond to the fabric’s geometric design.
Figure 10 illustrates the algorithm’s impact on medical imaging. The original mesh representation contains low-intensity valleys that obscure anatomical details, while the enhanced version elevates these valleys, uncovering hidden bone structures and soft tissues.
Figures 11, 12, 13 and 14 (MESSIDOR Retinal Images) highlight the algorithm’s performance in enhancing retinal scans. The original mesh representations exhibit hazy textures with poorly defined vasculature, common challenges in ophthalmology. Post-enhancement, the mesh representations show sharper peaks along blood vessels and smoother backgrounds, indicating noise suppression and vessel delineation. Such enhancements are vital for early detection of conditions like diabetic retinopathy.
Conclusions
In this study, using the subordination technique, we have derived sharp coefficient inequalities for the class of symmetric star-like functions linked with the Cresent-shaped domain. These coefficient estimates shed light on the geometric and analytic properties of the functions, including growth, distortion, and rotation. Additionally, we calculated the 2nd and 3rd order Hankel determinants for the class 
.
We used these estimated sharp Hankel determinants to develop a novel algorithm in this article for image processing. In previous studies40–43 algorithms were based on coefficients of some subclasses of analytic functions for image processing. This study introduces a novel algorithm based on the convolution of an image with a diagonal matrix whose entries are Hankel determinants of the class 
. This approach results in substantial enhancement of the image quality.
The results demonstrate that the newly proposed algorithm based on Hankel determinants achieves better image enhancement compared to previously established coefficient-based methods in26,44. This work establishes a novel connection between Geometric Function Theory and image processing, paving the way for further interdisciplinary applications. Although the suggested algorithm performs well on the datasets, its effectiveness across different image types, such as medical scans, low-light surveillance images, and satellite imagery needs further validation. Future research should evaluate its efficiency in various domains, also the research is helpful to obtain higher-order Hankel determinants. The presented algorithm can also be refined to achieve even more precise results.
Acknowledgements
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R721), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
List of Symbols
Complex plane
Natural numbers
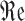
Real part of complex numbers
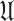
Open unit disc
- w
Schwarz function
Class of normalized analytic functions
Class of normalized univalent functions
Class of Caratheodory functions
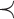
Subordination
Convolution
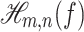
Hankel determinants of order
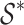
Class of starlike functions
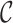
Class of convex functions
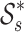
Class of star-like functions w.r.t. symmetric points
Class of
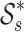linked with crescent-shaped domain- IQA
Image quality assessment
- PSNR
Peak signal to noise ratio
- MSE
Mean squared error
- SSIM
Structural similarity index measure
- PCC
Pearson correlation coefficient
- RMSE
Root mean squared error
- MAE
Mean absolute error
Processed image
Input image
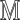
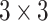Mask window
Author contributions
1. Conceptualization, Methodology, Supervision and Formal analysis: B.K. 2. Writing original draft and Formal analysis: A.I. 3. Methodology, Review and editing: S.K. 4. Experimental Results: A.K.A.
Data availability
The data sets of Dog, Argyle and Hand Xray are available in the Kaggle repository, https://www.kaggle.com/c/ultrasound-nerve-segmentation/data/?select=sample. The source file of Medissor dataset (“RETINAL IMAGE”.)
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Duren, P. L. Univalent Functions Vol. 259 (Springer Science & Business Media, 2001). [Google Scholar]
- 2.Pommerenke, C. Univalent Functions (Vandenhoeck and Ruprecht, 1975). [Google Scholar]
- 3.Pommerenke, C. On the Hankel determinants of univalent functions. Mathematika14(1), 108–112 (1967). [Google Scholar]
- 4.Noonan, J. W. & Thomas, D. K. On the second Hankel determinant of areally mean univalent functions. Trans. Am. Math. Soc.223, 337–346 (1976). [Google Scholar]
- 5.Janteng, A., Halim, S. A. & Darus, M. Hankel determinant for starlike and convex functions. Int. J. Math. Anal1(13), 619–625 (2007). [Google Scholar]
- 6.Sakaguchi, K. On a certain univalent mapping. J. Math. Soc. Japan11(1), 72–75 (1959). [Google Scholar]
- 7.Ravichandran, V. & Verma, S. Bound for the fifth coefficient of certain starlike functions. Comptes Rendus Math.353(6), 505–510 (2015). [Google Scholar]
- 8.Shi, L., Arif, M., Iqbal, J., Ullah, K. & Ghufran, S. M. Sharp bounds of Hankel determinant on logarithmic coefficients for functions starlike with exponential function. Fractal Fract.6(11), 645 (2022). [Google Scholar]
- 9.Goodman, A. W. On uniformly starlike functions. J. Math. Anal. Appl.155(2), 364–370 (1991). [Google Scholar]
- 10.Littlewood, J. E. Lectures on the Theory of Functions (Oxford University Press, 1944). [Google Scholar]
- 11.Lindelöf, E. L. Mémoire sur certaines inégalités dans la théorie des fonctions monogènes et sur quelques propriétés nouvelles de ces fonctions dans le voisinage d’un point singulier essentiel (1909).
- 12.Rogosinski, W. Uber die Abschimlte Vol potenzreihen die in ernein Kreise be schrarikt bleiben. Math. Z.28, 73–94 (1928). [Google Scholar]
- 13.Goodman, A. W. (Mariner Publishing Company, Inc., 1983).
- 14.Sunthrayuth, P., Aldawish, I., Arif, M., Abbas, M. & El-Deeb, S. Estimation of the second-order Hankel determinant of logarithmic coefficients for two subclasses of starlike functions. Symmetry14(10), 2039 (2022). [Google Scholar]
- 15.Shafiq, M. et al. An upper bound of the third Hankel determinant for a subclass of q-starlike functions associated with k-Fibonacci numbers. Symmetry12(6), 1043 (2020). [Google Scholar]
- 16.Ma, W. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis (International Press Inc., 1992).
- 17.Raina, R. K. & Sokół, J. Some properties related to a certain class of starlike functions. Comptes Rendus Math.353(11), 973–978 (2015). [Google Scholar]
- 18.Joshi, K. & Kumar, S. S. Third Hankel determinant for a class of starlike functions associated with exponential function. arXiv preprint arXiv:2206.13707 (2022).
- 19.Allu, V. & Shaji, A. Second Hankel determinant for logarithmic inverse coefficients of convex and starlike functions. Bull. Aust. Math. Soc.111(1), 128–139 (2025). [Google Scholar]
- 20.Kumar, D., Kumar, V. & Das, L. Hermitian-Toeplitz determinants and some coefficient functionals for the starlike functions. Appl. Math.68(3), 289–304 (2023). [Google Scholar]
- 21.Al-shbeil, I. et al. Hankel and symmetric Toeplitz determinants for a new subclass of q-starlike functions. Fractal Fract.6(11), 658 (2022). [Google Scholar]
- 22.Banga, S. & Kumar, S. S. Sharp bounds of third Hankel determinant for a class of starlike functions and a subclass of \$ q \$-starlike functions. arXiv preprint arXiv:2201.05808 (2022).
- 23.Kumar, S. S. & Giri, S. Starlike functions associated with a non-convex domain. arXiv preprint arXiv:2412.04819 (2024).
- 24.Marımuthu, K., Uma, J. & Bulboaca, T. Coefficient estimates for starlike and convex functions associated with cosine function. Hacet. J. Math. Stat.52(3), 596–618 (2023). [Google Scholar]
- 25.Nithiyanandham, E. K. & Keerthi, B. S. Image edge detection enhancement using coefficients of Sakaguchi type functions mapped onto petal shaped domain. Heliyon10(10), e31430 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Aarthy, B. & Keerthi, B. S. Enhancement of various images using coefficients obtained from a class of Sakaguchi type functions. Sci. Rep.13(1), 18722 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen, L., Li, Z., Li, Z., Chen, S., Yang, Q. & Du, Y. A contrast enhancement method of infrared finger vein image based on fuzzy technique. In 2019 IEEE 14th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), 307–310 (IEEE, 2019).
- 28.Ibrahim, R. W., Jalab, H. A., Karim, F. K., Alabdulkreem, E. & Ayub, M. N. A medical image enhancement based on generalized class of fractional partial differential equations. Quant. Imaging Med. Surg.12(1), 172 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Priya, H. & Sruthakeerthi, B. Texture analysis using Horadam polynomial coefficient estimate for the class of Sakaguchi kind function. Sci. Rep.13(1), 14436 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sunthrayuth, P., Jawarneh, Y., Naeem, M., Iqbal, N. & Kafle, J. Some sharp results on coefficient estimate problems for four-leaf-type bounded turning functions. J. Funct. Spaces2022(1), 8356125 (2022). [Google Scholar]
- 31.Libera, R. J. & Złotkiewicz, E. J. Coefficient bounds for the inverse of a function with derivative in P. Proc. Am. Math. Soc.87(2), 251–257 (1983). [Google Scholar]
- 32.Pommerenke, C. & Vasil’ev, A. Angular derivatives of bounded univalent functions and extremal partitions of the unit disk. Pac. J. Math.206(2), 425–450 (2002). [Google Scholar]
- 33.Kwon, O. S., Lecko, A. & Sim, Y. J. On the fourth coefficient of functions in the Carathéodory class. Comput. Methods Funct. Theory18, 307–314 (2018). [Google Scholar]
- 34.Libera, R. J. & Złotkiewicz, E. J. Early coefficients of the inverse of a regular convex function. Proc. Am. Math. Soc.85(2), 225–230 (1982). [Google Scholar]
- 35.Ravichandran, V. & Verma, S. Borne pour le cinquieme coefficient des fonctions etoilees. Comptes Rendus Math.353(6), 505–510 (2015). [Google Scholar]
- 36.Wang, Z., & Bovik, A. C. Modern Image Quality Assessment, Doctoral dissertation (Morgan & Claypool Publishers, 2006).
- 37.Girod, B. What’s wrong with mean-squared error. In Digital Images and Human Vision 207–220 (1993).
- 38.Jaya, V. L. & Gopikakumari, R. IEM: a new image enhancement metric for contrast and sharpness measurements. Int. J. Comput. Appl.79(9), 1–9 (2013). [Google Scholar]
- 39.Planitz, B. & Maeder, A. Medical image watermarking: a study on image degradation. In Proceedings of Australian Pattern Recognition Society Workshop on Digital Image Computing, WDIC (2005).
- 40.Panetta, K., Xia, J. & Agaian, S. Color image enhancement based on the discrete cosine transform coefficient histogram. J. Electron. Imaging21(2), 021117–021117 (2012). [Google Scholar]
- 41.Hossain, F. & Alsharif, M. R. Image enhancement based on logarithmic transform coefficient and adaptive histogram equalization. In 2007 International Conference on Convergence Information Technology (ICCIT 2007), 1439–1444 (IEEE, 2007).
- 42.Lu, L., Zhou, Y., Panetta, K. & Agaian, S. Comparative study of histogram equalization algorithms for image enhancement. Mob. Multimed. Image Process. Secur. Appl.2010(7708), 337–347 (2010). [Google Scholar]
- 43.Xia, J., Panetta, K., & Agaian, S. Color image enhancement algorithm based on logarithmic transform coefficient histogram. In Image Processing: Algorithms and Systems IX, Vol. 7870, 289–298 (2011).
- 44.Nithiyanandham, E. K. & Keerthi, B. S. A new proposed model for image enhancement using the coefficients obtained by a subclass of the Sakaguchi-type function. Signal Image Video Process.18(2), 1455–1462 (2024). [Google Scholar]
- 45.Dinh, P. H. & Giang, N. L. A new medical image enhancement algorithm using adaptive parameters. Int. J. Imaging Syst. Technol.32(6), 2198–2218 (2022). [Google Scholar]
- 46.Ai, S. & Kwon, J. Extreme low-light image enhancement for surveillance cameras using attention U-Net. Sensors20(2), 495 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Deudon, M., Kalaitzis, A., Goytom, I., Arefin, M. R., Lin, Z., Sankaran, K. et al. HighRes-net: recursive fusion for multi-frame super-resolution of satellite imagery. arXiv preprint arXiv:2002.06460 (2020).
- 48.Zhou, M., Jin, K., Wang, S., Ye, J. & Qian, D. Color retinal image enhancement based on luminosity and contrast adjustment. IEEE Trans. Biomed. Eng.65(3), 521–527 (2017). [DOI] [PubMed] [Google Scholar]
- 49.Gupta, B. & Tiwari, M. Color retinal image enhancement using luminosity and quantile based contrast enhancement. Multidimens. Syst. Signal Process.30(4), 1829–1837 (2019). [Google Scholar]
- 50.Priyadharsini, C. Retinal image enhancement based on color dominance of image. Sci. Rep.13, 7172 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data sets of Dog, Argyle and Hand Xray are available in the Kaggle repository, https://www.kaggle.com/c/ultrasound-nerve-segmentation/data/?select=sample. The source file of Medissor dataset (“RETINAL IMAGE”.)