Diversity and complexity of HIV-1 drug resistance: A bioinformatics approach to predicting phenotype from genotype

Abstract

Drug resistance testing has been shown to be beneficial for clinical management of HIV type 1 infected patients. Whereas phenotypic assays directly measure drug resistance, the commonly used genotypic assays provide only indirect evidence of drug resistance, the major challenge being the interpretation of the sequence information. We analyzed the significance of sequence variations in the protease and reverse transcriptase genes for drug resistance and derived models that predict phenotypic resistance from genotypes. For 14 antiretroviral drugs, both genotypic and phenotypic resistance data from 471 clinical isolates were analyzed with a machine learning approach. Information profiles were obtained that quantify the statistical significance of each sequence position for drug resistance. For the different drugs, patterns of varying complexity were observed, including between one and nine sequence positions with substantial information content. Based on these information profiles, decision tree classifiers were generated to identify genotypic patterns characteristic of resistance or susceptibility to the different drugs. We obtained concise and easily interpretable models to predict drug resistance from sequence information. The prediction quality of the models was assessed in leave-one-out experiments in terms of the prediction error. We found prediction errors of 9.6–15.5% for all drugs except for zalcitabine, didanosine, and stavudine, with prediction errors between 25.4% and 32.0%. A prediction service is freely available at http://cartan.gmd.de/geno2pheno.html.

Resistance testing significantly improves response to antiretroviral therapy in patients infected with HIV type 1 (HIV-1), as was recently demonstrated in retrospective and prospective studies (1–3). Drug resistance can either be directly assessed by phenotypic assays or can be deduced from genotypic assays, which are based on sequencing of the relevant parts of the viral genome (4). Most phenotypic assays use recombinant virus techniques directly measuring viral replication in the presence of increasing drug concentrations (5, 6). The results can be interpreted easily, but the assays are time- and labor-consuming, and are therefore restricted to specialized laboratories. In contrast, genotypic assays can provide results within a few days, are less expensive, and are now available as commercial test kits for routine virologic diagnostics. The challenge with using genotypic assays is the interpretation of sequence information. Interpretation usually relies on tables of drug-resistance-associated mutations (7). Whether a mutation is considered resistance-associated or not is either based on the emergence of this mutation in clinical samples or cell culture under continuous drug pressure, or on the determination of drug resistance, after the respective mutation has been inserted into a wild-type background. However, with increasing numbers of antiretroviral drugs and drug resistance-associated mutations, interpretation is becoming increasingly difficult. This difficulty is because the influence of a certain mutation on drug resistance cannot be considered independently of other mutations, but that different types of interactions must be taken into account (8). Furthermore, viruses may exhibit varying degrees of cross-resistance even to drugs to which the patient has not yet been exposed (9).

Although it could be shown that phenotypic resistance to protease inhibitors may be predicted by a few simple, carefully chosen rules (10), computer-based methods that can quickly analyze large sets of matched genotypic and phenotypic data are becoming more and more helpful with growing complexity of resistance patterns. Described approaches comprise database pattern search (11, 12), the application of neural networks (13), multiple correspondence analysis (14), cluster analysis, and linear discriminant analysis (15). Using the so-called mutual information, an information–theoretic correlation measure, we quantitatively evaluated the statistical significance of each sequence position for drug resistance. We generated decision trees (16–18) for the discrimination between resistant and susceptible viruses as a tool for the prediction of the resistance phenotype from genotypic data. Decision trees appear to be appropriate for this task, as they naturally handle discrete data, evaluate information context-specifically, and represent extracted knowledge intelligible to human experts. They have recently been applied successfully to protein sequence classification tasks such as discriminating between soluble and insoluble proteins (19) and the prediction of protein secondary structure (20). In particular, decision trees were used for assigning HIV-1 protease sequences to clusters of genotypically similar samples and predicting resistance to two protease inhibitors by the mean phenotype of these clusters (15). Here we show that decision tree building based on mutual information is a powerful method for the prediction of drug resistance and susceptibility from complex mutational patterns for a broad spectrum of antiretroviral drugs.

Materials and Methods

Data Set.

We analyzed 471 clinical samples from 397 patients sent in for resistance testing between January 1998 and June 2000, mostly because of therapy failure. We determined viral genotype and drug susceptibility to six nucleoside inhibitors of the reverse transcriptase (NRTIs), zidovudine (ZDV), zalcitabine (ddC), didanosine (ddI), stavudine (d4T), lamivudine (3TC), and abacavir (ABC); three nonnucleoside reverse transcriptase inhibitors (NNRTIs), nevirapine (NVP), delavirdine (DLV), and efavirenz (EFV); and five protease inhibitors (PIs), saquinavir (SQV), indinavir (IDV), ritonavir (RTV), nelfinavir (NFV), and amprenavir (APV). We obtained 443–469 genotype–phenotype pairs for each of these drugs, except for APV, for which we obtained 277 pairs.

Resistance Testing.

HIV drug resistance testing was performed as described (6, 10). For genotyping, a fragment of the pol gene containing the complete protease and the first 650–750 nt of the reverse transcriptase (RT) was analyzed by direct sequencing of PCR products. All sequences have been deposited in GenBank (accession numbers AF347117 to AF347605). The detection limit for minority species was about 30%.

Phenotyping was performed by using a recombinant virus assay (6). A PCR product containing the complete protease and the first 900 nt of the RT was obtained from patient plasma and ligated into a matched deletion mutant of pNL4–3 (GenBank accession number U26942). After titration, recombinant viruses were cultivated in the presence of increasing amounts of antiretroviral drugs. Sensitive detection of viral replication was obtained by an indicator cell line containing the secreted alkaline phosphatase gene under the control of the simian immunodeficiency virus long terminal repeat (21). The resistance factor was calculated by dividing the 50% inhibitory concentration (IC₅₀) of the respective recombinant virus by the IC₅₀ of the nonresistant reference strain (NL4–3).

Data Modeling.

After sequence alignment to the pol gene of HXB2 (GenBank accession number K03455), we found one sample with a deletion and eight samples containing insertions of two amino acids between positions 67 and 70 of the RT as described (22).

We modeled each protease sequence with one attribute for each of its 99 aa, allowing as a value either 1 of the 20 naturally occurring amino acids or “unknown” for positions for which ambiguous or no sequence information was available. For the RT, we defined one binary attribute indicating the occurrence of an insertion and 250 further attributes for each of the first 250 aa of the RT. A binary attribute for deletions was not introduced because only one sequence showed a deletion. For more than 95% of the samples, sequence information was available for the entire protease and up to position 220 or further for the RT.

For each drug, we divided the sample set into two classes by attaching to each sequence either the label “resistant” or “susceptible,” depending on whether the resistance factor of the sample exceeded a certain drug-specific cutoff value or not. We decided to use the following values based on previously published data (10, 23–25): 8.5 for ZDV, 3TC, and the NNRTIs; 2.5 for ddC, ddI, d4T, and ABC; and 3.5 for all PIs (Table 1).

Table 1.

Results from decision tree building (learning phase), leave-one-out experiments, and an example of a prediction compared with the actual phenotype

Drug	Cutoff	No. of samples	Resistant fraction, %	Learning phase			Leave-one-out experiments			Prediction example
				Minimal split*	No. of interior vertices	Training error, %	Prediction error, %	Sensitivity, %	Specificity, %	Observed resistance factor	Observed class	Predicted class	Confidence factor
ZDV	8.5	456	58.1	2	5	8.8	10.7	92.1	85.8	419	resistant	resistant	0.79
ddC	2.5	456	43.0	7	5	23.7	26.3	58.2	85.4	1	susceptible	susceptible	0.78
ddI	2.5	456	49.1	7	4	25.7	32.0	73.7	62.5	3	resistant	resistant	0.58
d4T	2.5	456	38.6	7	4	21.5	25.4	63.1	81.8	2	susceptible	susceptible	0.68
3TC	8.5	452	54.4	2	4	7.7	10.4	87.4	92.2	13	resistant	resistant	0.60
ABC	2.5	445	66.3	5	5	13.5	15.5	92.5	68.7	4	resistant	resistant	0.66
NVP	8.5	457	45.1	2	7	7.0	9.6	82.0	97.2	407	resistant	resistant	0.74
DLV	8.5	455	36.5	2	5	8.1	10.5	77.7	96.2	168	resistant	resistant	0.73
EFV	8.5	443	35.9	2	6	7.7	10.2	79.9	95.4	7	susceptible	susceptible	0.92
SQV	3.5	465	46.7	2	5	11.2	12.5	87.6	87.5	39	resistant	resistant	0.87
IDV	3.5	469	48.8	2	5	11.2	10.9	89.5	88.8	32	resistant	resistant	0.87
RTV	3.5	469	50.1	2	4	9.0	10.2	89.8	89.7	33	resistant	resistant	0.88
NFV	3.5	468	53.6	2	4	9.6	11.5	89.6	87.1	93	resistant	resistant	0.91
APV	3.5	277	32.9	2	4	10.5	12.6	82.4	89.8	3	susceptible	susceptible	0.92

Samples with a resistance factor higher than the value denoted “Cutoff” are considered resistant. The two rightmost columns show the output of the prediction system for a selected sample. This sample contained the following amino acid exchanges relative to the reference virus HXB2: Q2X, V3I, I15V, Q18X, L19X, K20I, L23R, M36I, K43T, I62V, L63P, A71T, I72V, G73S, and L90M in the protease gene, and V35T, M41L/M/V, V60I, D67N, T69D, K70R/S, L74X, V75T, R83S, F87F/L, L92F, I94S, V108I, E122K, I135V, S162C, V179I, Y181F, Q207E, L210L/F, L214F, and T215Y in the RT gene. 

^*Minimum number of samples that have to be present in at least two branches at each split. 

Mutual Information.

For a random variable X with finite alphabet (set of possible outcomes) Ω and probability distribution p the quantity,

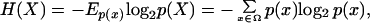where E denotes the expectation, is called the entropy of X (26). If Y is another discrete random variable and p(Y | X) denotes the conditional probability, then H(Y | X) = −E_p(x,y) log₂ p(Y | X) is known as the conditional entropy. The mutual information between X and Y is defined as I(X, Y) = H(Y) − H(Y | X). This quantity measures the amount of information that X provides about Y. It follows from these definitions that

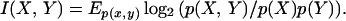Therefore, I(X, Y) is proportional to the log-likelihood ratio between the joint distribution p(X, Y) and the product distribution p(X)p(Y).

Here, the observed amino acids at specific sequence positions were considered as the outcomes of random variables X_i (i = 1, … , 99 for the protease and i = 0, … , 250 for the RT) with alphabet Ω comprising the 20 natural amino acids. Similarly, the sequence label was interpreted as the outcome of another random variable Y with possible outcomes in Ω = {resistant, susceptible}. Thus, I(X_i, Y) is the amount of information that sequence position i provides about discriminating resistant from susceptible samples.

Decision Trees.

A decision tree is an acyclic graph whose interior vertices specify tests to be carried out on a single attribute and whose leaves indicate classes. Classification of a sample is achieved by running through the tree from the root to a leaf according to the values (amino acids) of the attributes (sequence positions) of the sample that appear on this path. We used the software package C4.5 to generate decision trees (16). The classifiers were constructed by recursively splitting the sample set. Each subset gives rise to one new vertex connected with an edge to its parent. For each of the new subsets we proceed in the same way until at each leaf all samples belong to the same class.

For determining the split, the normalized mutual information, defined as I(X_i, Y)/H(X_i), is calculated from the subset to be split. This ratio expresses the information generated by the split that appears helpful for classification. We chose the attribute for which this ratio is maximal subject to the constraint that the mutual information is at least as great as the average mutual information over all attributes. The normalized mutual information is one possible measure of impurity, and other possible measures are discussed elsewhere (16, 17). Unknown attribute values are assumed to be distributed probabilistically according to the known values, and are therefore divided into fractions distributed over several vertices.

To avoid overfitting, trees are pruned following a “reduced error-pruning” strategy (27). The error estimate for the removal of subtrees also gives rise to confidence factors given with each prediction based on the tree (Table 1). At each leaf of the decision trees, the (possibly fractional) number of samples that have been classified by this leaf and the number of errors that are estimated to occur on unseen samples are given in brackets. The minimum number of samples in at least two branches at each split was optimized with respect to the estimated prediction error. Best results were obtained with seven samples for ddC, ddI, and d4T, five samples for ABC, and two samples for all other drugs.

Results

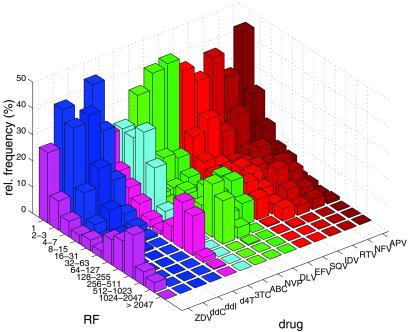
Analysis of the frequency distribution of resistance factors revealed considerable differences between drugs (Fig. 1). Whereas resistance factors of more than 100 were detected for samples resistant to ZDV, 3TC, NNRTIs, and PIs, the maximum of resistance was much lower for ddI, ddC, d4T, and ABC. Furthermore, a second peak in the frequency distribution at higher resistance factors was not observed for these drugs.

Figure 1.

Frequency distribution of resistance factors of a subset of 271 samples for which data are available for all 14 antiretroviral drugs. Resistance factors (RF) have been rounded to integers and grouped into equidistant bins on a logarithmic scale. RF values smaller than one are reported as equal to one.

Mutual Information.

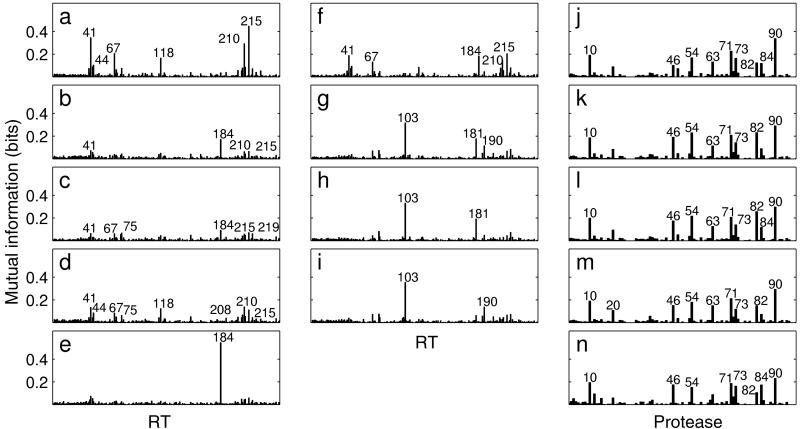
For all drugs, we calculated mutual information profiles quantifying the usefulness of each sequence position for discriminating between susceptible and resistant samples (Fig. 2 a–n). All amino acid positions showing substantial information content have already been described to be associated with HIV drug resistance and many of them appear in the profiles for several drugs. The approach was validated by calculating mutual information profiles for randomly drawn subsets of 200–300 samples (data not shown). Very little variation was observed for the different data sets indicating that the mutual information profiles do not depend critically on the sample size.

Figure 2.

Mutual information profiles for ZDV (a), ddC (b), ddI (c), d4T (d), 3TC (e), ABC (f), NVP (g), DLV (h), EFV (i), SQV (j), IDV (k), RTV (l), NFV (m), and APV (n). In a–i, position 0 denotes the insertion flag, 1–250 represent the first 250 positions of the HIV-1 reverse transcriptase; in j–n, positions 1–99 of the HIV-1 protease are displayed. Peaks above 0.06 bits are annotated for ddC, ddI, and d4T, and peaks above 0.1 bits are annotated for all other drugs.

Comparing profiles within drug classes reveals a high similarity among NNRTIs (Fig. 2 g–i) and especially among PIs (Fig. 2 j–n). For all PIs, position 90 appeared to be highly relevant, however, several other positions (10, 46, 54, 63, 71, 73, and 82) also have a substantial information content for all PIs investigated. Consistent with recent findings (28), position 84 provided more relevant information on resistance to APV than to the other PIs. Among the NRTIs, we observed substantially different, distinct profiles for ZDV and 3TC, whereas the other NRTI profiles showed much weaker signals. Profiles for ddI and ABC combine elements of ZDV and 3TC profiles, whereas those for ddC and d4T resemble 3TC and ZDV profiles, respectively, on a lower scale.

Decision Trees.

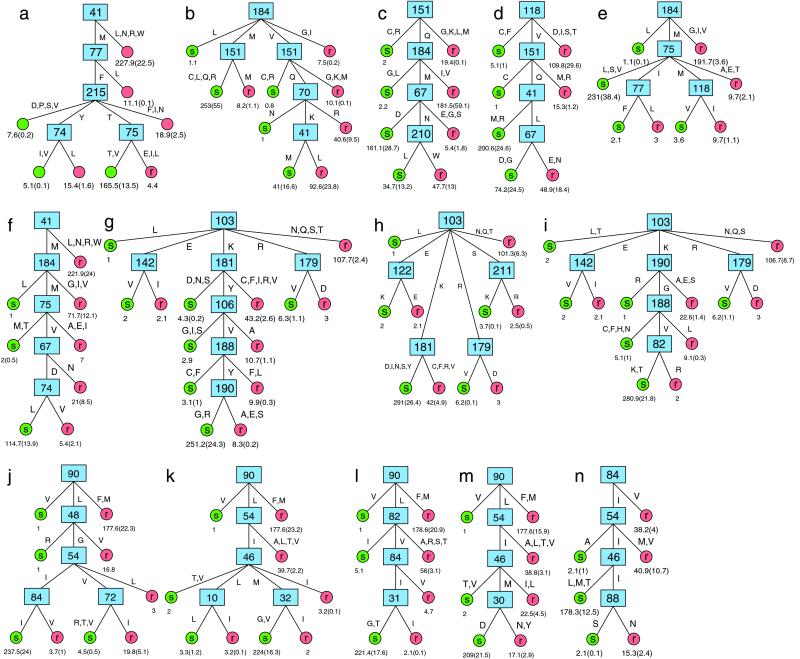
We generated decision tree models that describe phenotypic drug resistance in terms of the amino acid composition of the enzyme targeted by the drug. This learning phase resulted in one decision tree for each drug (Fig. 3 a–n). We found rather simple models for all drugs with only 4–7 interior vertices (Table 1). We observed the highest degree of heterogeneity of structures within the group of NRTIs, as was suggested by the mutual information profiles. Also, when generated with only at least two samples in each branch (instead of seven and five, respectively, see Materials and Methods), the trees for ddC, ddI, d4T, and ABC grew much larger (8–12 interior vertices, data not shown), but tended to overfit the data. Thus, the genetic basis of drug resistance appears to be more complex for these drugs. Several trees show a linear structure without major branchings, where most of the resistant samples are classified by considering two to five sequence positions one after another, whereas most of the susceptible samples are assigned to their class after considering all these positions. In contrast, decision trees for the NNRTIs (Fig. 3 g–i) exhibit a different structure with three or four branches arising from the first split.

Figure 3.

Decision trees for ZDV (a), ddC (b), ddI (c), d4T (d), 3TC (e), ABC (f), NVP (g), DLV (h), EFV (i), SQV (j), IDV (k), RTV (l), NFV (m), and APV (n). Numbers N(E) at the leaves denote the number of samples (N) and the estimated error (E). Branches leading to the same leaf are summarized. Capital letters annotating the edges denote amino acids in one-letter code.

Several amino acid positions that do not show high peaks in the mutual information profiles (positions 70, 74, 77, 82, 122, 124, 151, 179, and 211 in the RT, and 30, 31, 32, 72, and 88 in the protease) appear in the decision trees, whereas on the other hand a number of sequence positions with high peaks in the mutual information profiles do not show up in the decision trees, especially for the PI.

We examined the ability of the decision trees to model our set of training samples by calculating the training error, defined as the percentage of misclassified training samples. Training errors ranged from 7.0–13.5% except for ddC, ddI, and d4T with training errors between 21.5% and 25.7% (Table 1).

Prediction Quality.

To estimate the predictive power of the models on unseen cases we performed leave-one-out experiments. In this crossvalidation technique, for each sample, a decision tree is generated on all but this sample and the respective tree is then used for classifying this sample. The percentage of misclassified samples, the prediction error, estimates the ability of the models to generalize from the sample set (29). We found prediction errors in the range of 10.2–12.6% for the PIs, 9.6–10.5% for the NNRTIs, and 10.7, 10.4, and 15.5% for ZDV, 3TC, and ABC, respectively. Error rates for ddC, ddI, and d4T ranged from 25.4% to 32.0% (Table 1). A more detailed picture of the error rates is given in terms of the sensitivity (percentage of phenotypically resistant viruses that were correctly scored as “resistant”) and specificity (percentage of phenotypically susceptible samples that were correctly scored as “susceptible”) of the models. The decision trees achieved sensitivities ranging from 77.7% to 92.5% and specificities between 68.7% and 97.2%, except for ddC, ddI, and d4T, where sensitivities between 58.2% and 73.7% and specificities between 62.5 and 85.4% were obtained (Table 1). The prediction method described here can be used freely on the world wide web at http://cartan.gmd.de/geno2pheno.html. A confidence factor is given for all predictions.

Discussion

We applied a machine learning approach to analyze correlations between HIV-1 genotype and resistance phenotype based on more than 400 samples. No prior knowledge about drug resistance has been incorporated and all sequence positions have been considered equally. Thus, the results provide an unbiased picture of drug resistance in clinical samples.

Although our approach is therefore principally capable of identifying as yet unknown resistance-associated mutations, all sequence positions that were recovered in the mutual information profiles have been described as resistance-associated (7). Nevertheless, some results are unexpected. For example, RT positions 44 and 118 show high peaks in the profiles for ZDV and d4T, but in clinical samples and mutagenesis experiments they have been associated only with resistance to 3TC (30). On the other hand, some positions previously associated with drug resistance (e.g., protease position 30 for NFV, RT position 151 for NRTI multidrug resistance) do not show up in the mutual information profiles; this may be because they are too rare in the data set or because their appearance is associated with different resistance levels than the chosen cutoffs specify. For example, using a cutoff value of 8.5 instead of 2.5 for ABC increased substantially the mutual information of position 151 (data not shown).

One may wonder if the observed similarities between some mutual information profiles reflect true crossresistance or only statistical coincidence, e.g., because of preferred combination therapies. The lack of similarities between profiles of NRTIs and NNRTIs, which are often administered together, as well as the mutually exclusive profiles of ZDV and 3TC—also a frequent drug combination—demonstrate the general ability of the method to distinguish different profiles even within the same drug class. Thus, the observed similarities in the mutual information profiles indeed appear to indicate crossresistance.

We generated decision trees that identify patterns of several positions predictive of drug resistance or susceptibility. The decision tree method appears adequate because the classification knowledge is presented in a form that human experts can easily understand and examine, and because it is capable of representing effects of interactions between different mutations. From decision trees it is easy to derive rules, the currently dominating form of representing HIV-1 resistance knowledge. Tracing out a path from the root of the tree to a leaf yields a rule whose premise is induced by the interior vertices on the path and whose conclusion is the class represented by the leaf. For example, following the path through positions 184 and 75 for 3TC yields (among others) the rule: if RT codon 184 codes for Methionine (M) and RT codon 75 codes for Alanine (A), Glutamic acid (E), or Threonine (T), then the virus carrying this gene is resistant to 3TC (Fig. 3e). Human experts can examine such rules, and they can be used for coding resistance knowledge in expert systems designed for selecting optimal therapies (31). Derived rules either predict resistance or susceptibility to a certain drug, thus addressing the problem of identifying drugs that will most probably be active as part of a new regimen. The extracted knowledge can also be useful in investigating the structural basis for drug resistance. The findings obtained from the SQV decision tree, for example, are in concordance with insights into the molecular mechanisms of drug resistance recently obtained from the crystal structure of a mutant–inhibitor complex (32).

It has been shown that mutations often evolve in a certain order (33) and that the effect of several mutations depends on the presence or absence of other mutations (8). Decision trees represent this dependence in a natural way. Indeed, two examples show that the decision trees are able to capture resensitizing or hypersusceptibility effects. In the first case, ZDV resistance deduced from RT mutation T215Y appears to be reversed by mutations V or I at RT position 74 (Fig. 3a), an effect that has been described (7). In the second case, the APV hypersusceptibility effect of protease mutation N88S that has been recently described in vitro (34) is also represented in the APV decision tree (Fig. 3n). Interestingly, a similar pattern is observed in the SQV decision tree, where samples with the resistance-associated mutation I54V and additional mutations R, T, or V at position 72 are classified as susceptible (Fig. 3j). This finding suggests that the latter mutations at position 72 can reverse the effect of mutation I54V, though independent confirmation is needed.

The mutational patterns that appear in the decision trees do not necessarily consist of those sequence positions with the highest peaks in the corresponding mutual information profiles, because profiles generated on subsets of samples created by subsequent splits are in general different from those of the complete sample set. Even the roots of the trees do not always correspond directly to the highest peaks in the profiles, because the test criterion further requires normalization (see Materials and Methods). In particular, mutations that frequently occur simultaneously will not all appear in a decision tree because this would not provide additional information for classification. For example, of the six amino acid positions with the highest peaks in the profile for ZDV (Fig. 2a) only two (41 and 215) appear in the ZDV decision tree (Fig. 3a). A similar observation can be made for the prominent protease sequence positions (Figs. 2 j–m and 3 j–m). Thus, decision trees reduce the complexity observed in mutual information profiles.

On the other hand, a number of sequence positions without high peaks in the profiles are incorporated into the decision trees. These positions are considered useful for classification either because of a very low entropy and an only moderate amount of mutual information (e.g., RT position 151 in the ddI decision tree; Fig. 3c) or because of a specific context (e.g., position 30 in the NFV decision tree in the context of 90L, 54I, and 46M; Fig. 3m).

The predictive power of the decision trees on unseen cases is very good, with error rates ranging between 9.6% and 15.5% for most drugs. Higher error rates for ddC, ddI, and d4T may be caused by the fact that for these drugs the sample set is not divided into two parts, one being clearly susceptible, the other highly resistant (Fig. 1). Furthermore, the cutoff value of 2.5 used for these drugs overlaps with the phenotypic interassay variability (6). However, this low value has been shown to be predictive of therapy failure (23). Nevertheless, we could obtain a concise model with good prediction results for ABC, which shows a frequency distribution of resistance factors similar to ddC, ddI, and d4T (Fig. 1). All of these four NRTIs combine characteristics of ZDV and 3TC resistance. Therefore, it may be speculated that there are two principal NRTI resistance mechanisms, one responsible for ZDV resistance and the other responsible for 3TC resistance. Both mechanisms may act synergistically in the case of ABC, but antagonistically for ddC, ddI, and d4T. This hypothesis could explain the weak signals observed in the profiles for the latter drugs.

Prediction accuracy will always be limited by the uncertainty of the experimental data, e.g., because of the variability of phenotyping, sequencing errors and the quasi-species nature of HIV. Another constraint consists in the limited flexibility of describing the functional relationship between sequence information and drug resistance provided by the chosen type of model. Furthermore, because the treatment history of patients is a major driving force for the development of amino acid changes, the usefulness of our analysis may be limited for patients with substantially different therapy regimens. For example, our results for amprenavir, a PI not yet approved for clinical use in Germany during the time the samples were taken, may lack genotypic changes that develop exclusively under amprenavir-containing regimens (such as protease mutation I50V).

Certainly, a comparison of the decision tree method presented here with other approaches (rule-based or data-driven) is desirable. Toward this end, it has been shown that linear support vector machines, a highly performant machine learning technique, gives slightly (but nonsignificantly) better predictions on the same data set analyzed here (35). However, contrary to decision trees, interpretation of the support vector models and comparison with existing knowledge is not straightforward. Thus, decision trees provide suitable models for revealing the diversity and complexity of HIV-1 drug resistance. They have proven to provide concise and interpretable models that for most drugs are capable of reliable predictions.

Abbreviations

HIV-1

HIV type 1

NRTIs

nucleoside inhibitors of the reverse transcriptase

ZDV

zidovudine

ddC

zalcitabine

ddI

didanosine

d4T

stavudine

3TC

lamivudine

ABC

abacavir

NNRTI

nonnucleoside reverse transcriptase inhibitors

NVP

nevirapine

DLV

delavirdine

EFV

efavirenz

PI

protease inhibitor

SQV

saquinavir

IDV

indinavir

RTV

ritonavir

NFV

nelfinavir

APV

amprenavir

RT

reverse transcriptase