Accuracy of 7 intraocular lens power calculation formulas in primary angle-closure glaucoma eyes, according to axial length and anterior chamber depth

Abstract

Purpose

To assess the impact of Axial Length (AL) and anterior chamber depth (ACD) on the performance of the Kane, EVO 2.0, Barrett Universal II (BU II), SRK/T, Haigis, Holladay 2 and Hoffer Q formulas when calculating intraocular lens power in primary angle-closure glaucoma (PACG) patients.

Setting

Eye hospital, Wen Zhou Medical University, Zhejiang, China.

Design

Retrospective, consecutive case series.

Methods

Patients who underwent cataract surgery diagnosed with PACG or not were included. The main outcome measures comprised mean prediction error (ME), mean absolute refractive error (MAE), median absolute refractive error (MedAE). Additionally, the proportions of eyes with postoperative refractive errors within ± 0.25 diopter (D), ± 0.50 D, ± 0.75 D, and ± 1.00 D were calculated. Subgroup analyses were conducted based on AL and ACD.

Results

A total of 116 eyes were included, with 66 in the PACG group and 50 in the control group. The PACG group showed significantly larger MAEs compared to the control group. In PACG eyes, the BUII formula tends to cause negative residual refractive errors, while the Kane, EVO, and Holladay 2 formulas often lead to positive ones (P < 0.01). Notably, the SRK/T and Haigis formulas demonstrated better predictability for ME (P < 0.01). PACG patients with an AL under 22 mm or an ACD under 2.5 mm have lower IOL power calculation predictability (P < 0.05). Subgroup analysis shows that PACG eyes with both AL under 22 mm and ACD under 2.5 mm have the lowest predictability and are most prone to significant prediction errors (P < 0.05). A negative correlation was found between postoperative prediction error and AL.

Conclusions

PACG eyes showed lower prediction accuracy, especially in short ALs and shallow ACD cases. SRK/T and Haigis formulas had better ME predictability. The study stresses optimizing IOL power calculation formulas for PACG eyes, considering AL and ACD effects.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12886-025-04238-x.

Key Messages

What is known:

- Primary angle-closure glaucoma (PACG) is associated with challenges in intraocular lens (IOL) power calculation due to its impact on ocular biometrics such as axial length (AL) and anterior chamber depth (ACD).

- Traditional and new-generation IOL power calculation formulas have varying degrees of success in predicting refractive outcomes, with some showing a tendency for hyperopic shifts in eyes with shorter ALs.

What is new:

- This study provides evidence that PACG eyes, particularly those with short ALs and shallow ACDs, exhibit lower prediction accuracy compared to control eyes across multiple IOL power calculation formulas.

- SRK/T and Haigis formulas demonstrated superior predictability in eyes with shallow ACDs (≥2.50 mm), highlighting their potential as optimized formulas for such cases.

- Among PACG patients, the BUII formula is more likely to lead to a negative postoperative refractive outcome, whereas the Kane, EVO, and Holladay 2 formulas are associated with a positive one.

- The findings underscore the necessity for refined IOL power calculation formulas in PACG eyes, emphasizing the influence of both AL and ACD on prediction accuracy and the need for personalized approaches.

Synopsis

PACG eyes showed lower prediction accuracy, especially in short ALs and shallow ACDs. The BUII formula caused negative residual refractive errors, whereas Kane, EVO, and Holladay 2 formulas led to positive ones. SRK/T and Haigis had better predictability.

Introduction

Current number of people (aged 40–80 years) with glaucoma worldwide is 64.3 million and is expected to increase to 111.8 million in 2040 [1]. As for people with Primary angle-closure glaucoma (PACG), Asia will contain the greatest number with increments of 9.0 million (58.4%) [1]. It is known that in the development of primary angle-closure disease, age-related degenerative changes of the lens contributes a lot [2]. When the position of lens shifts forward or tilts, it is prone to adhesion with the iris, causing anterior displacement of the lens-iris diaphragm, leading to shallowing of the anterior chamber, iris bulging, and pupillary block, ultimately resulting in angle closure.

To date, the majority of IOL calculation formulas utilized in clinical settings are based on the principle of convergence, employing between two to seven variables to estimate the postoperative effective lens position (ELP). While these formulas yield precise refractive outcomes for patients with normal eyes, they are inclined to result in hyperopic shifts for those with shorter axial lengths (AL) [3, 4] Furthermore, according to previous study, compared with healthy individuals with short eyes, patients with PACG tended to have a decrease in anterior chamber depth (ACD) depth and a significant increase in Lens thickness (LT) which might influence the prediction precision [5]. Currently, there is a limited body of literature focused on the IOL power reservation for PACG using different formulas.

Kim et al. stratified patients with acute primary angle closure (APAC) by AL and found that in eyes with AL < 22 mm, the Haigis (0.49 D) and Hill-RBF 3.0 (0.54 D) formulas yielded the lowest median absolute refractive error (MedAE) [6]. Notably, the Hoffer Q formula demonstrated even better performance in this subgroup, with the lowest median absolute prediction error (0.292 D), followed closely by EVO 2.0 (0.298 D) and Kane (0.300 D).

Similarly, Li et al. reported that in PACG eyes undergoing cataract surgery combined with goniosynechialysis, the Kane (−0.06 D) and Barrett Universal II (BU II) (−0.07 D) formulas achieved mean prediction errors (MEs) closest to zero, outperforming the Hoffer Q and SRK/T formulas in the overall cohort [7]. These findings suggest that modern formulas (e.g., Kane, Barrett) may offer improved accuracy in angle-closure populations.

However, while prior research has established that short AL and shallow anterior chamber depth (ACD) are associated with reduced IOL power prediction accuracy in PACG [8] few studies have systematically evaluated how ACD and AL interact to influence formula performance. Importantly, although ACD and AL typically correlate positively, many PACG eyes exhibit atypical anatomical relationships (e.g., disproportionately shallow ACD relative to AL), which may further complicate IOL calculations. This anatomical variability could explain observed discrepancies in formula accuracy and warrants further investigation.

Therefore, in this study we compared the prediction errors with seven IOL power calculation formulas (SRK/T, Haigis, BUII, Kane, and EVO 2.0 formulas) in PACG on the effect of AL and ACD. It is hoped that the results can provide new evidence for the selection of IOLs in the PACG population.

Methods

Participant selection and exclusion criteria

The study cohort comprised PACG patients who underwent uneventful cataract extraction with intraocular lens IOL implantation at Wenzhou Medical University Eye Hospital (Zhejiang, China) between January 2018 and November 2023. PACG diagnosis required: (1) occludable anterior chamber angles, (2) signs of trabecular meshwork obstruction by the peripheral iris, and (3) glaucomatous optic neuropathy. Some participants received concurrent goniosynechialysis (GSL) or pupilloplasty. Exclusion criteria encompassed prior glaucoma surgeries (e.g., peripheral iridectomy or trabeculectomy). The control group consisted of individuals with cataracts but no other ocular pathologies, and they were enrolled randomly without specific AL criteria. All surgeries were performed by a single experienced glaucoma specialist (YuanBo, Liang). Additional exclusion criteria were: age < 18 years, coexisting ocular conditions (e.g., zonular weakness, uveitis, corneal astigmatism > 2.0 D), postoperative CDVA < 20/40, inability to comply with diagnostic procedures, or significant retinal disorders (e.g., clinically significant macular edema, macular hole, epiretinal membrane, proliferative diabetic retinopathy).

IOL power calculation methodology

Demographic and clinical data, including age, sex, preoperative intraocular pressure (IOP, measured via Goldmann applanation tonometry), and visual acuity (VA), were collected. Ocular biometry was performed using the IOL Master 500 (Carl Zeiss Meditec, Germany), with three repeated measurements averaged for AL, lens thicknes, ACD, and keratometry (Km). IOL power was computed using the BUII, SRK/T, Haigis, EVO 2.0, Kane formulas, Holladay 2 and Hoffer Q formulas. Formulas (SRK/T, Haigis, BUII, Holladay 2 and Hoffer Q) were provided by IOL master 500. Since the IOL Master 500 does not natively support newer-generation formulas (Kane and EVO 2.0), biometric data were manually input into their respective online calculators (Kane: iolformula.com; EVO 2.0: evoiolcalculator.com). Optimized lens constants for SA60WF, A1-UV, CT ASPHINA 509 M, and Akreos MI60 were sourced from the Users Group for Laser Interference Biometry (ULIB, ocusoft.de/ulib) or provided by the calculators.

Postoperative refractive outcomes were assessed ≥ 1 month after surgery. Spherical equivalent (SE) was derived from subjective refraction. Prediction error (PE) was computed as the difference between actual and predicted SE, with negative values indicating a myopic shift. Mean absolute error (MAE) represented the unsigned magnitude of PE. Refractive accuracy was further stratified by absolute error thresholds (< 0.25, < 0.5, < 0.75, < 1.0 D). In the comparative analysis of IOL power calculation formulas for PACG patients, subgrouping by AL (short: <22.0 mm; long: ≥22.0 mm) and ACD (shallow: <2.5 mm; deep: ≥2.5 mm) is essential. The 22.0 mm cutoff for AL is used because it effectively differentiates between short and normal/long eyes, which is crucial given that the accuracy of IOL power calculation formulas varies across these ranges [9]. For ACD, the 2.5 mm threshold is chosen to distinguish between shallow and normal/deep anterior chambers. This distinction is important because shallow anterior chambers, common in PACG, can lead to significant errors in IOL power calculations if not properly accounted for [10, 11]. Previous studies have shown that certain formulas perform better in eyes with shallow ACDs, while others are more accurate in eyes with deeper ACDs [10, 11]. By using these specific cutoffs, researchers can more accurately assess the performance of different IOL power calculation formulas in PACG patients. Accordingly, in our research, PACG patients were subgrouped by AL (short: <22.0 mm; long: ≥22.0 mm) and ACD (shallow: <2.5 mm; deep: ≥2.5 mm) for comparative analysis.

Statistical analysis

Data were analyzed using SPSS (IBM, version 27). Normality was assessed via the Shapiro–Wilk test. Normally distributed variables were reported as mean ± standard deviation (SD) and compared using independent t-tests; nonparametric data were expressed as median (interquartile range) and analyzed with Mann-Whitney U tests. Intergroup comparisons (PACG vs. control) for each formula employed Mann-Whitney U tests, while MAE differences across formulas were evaluated via one-way ANOVA with LSD post hoc testing. The chi-square test compared proportions of eyes achieving absolute errors < 0.5 D. Subgroup analyses (AL and ACD categories) used Mann-Whitney U tests and two-way ANOVA. Pearson’s correlation assessed associations between PE and biometric parameters. Statistical significance was set at P < 0.05.

Result

Demographics and biometric characteristics

This study included 116 eyes of 116 patients, among which 50 were control group (42.4%) and 66 were PACG group (57.6%). The implanted IOL types were the SA60WF (Alcon, n = 84), A1-UV (Proming, n = 18), 509 M (Zeiss, n = 11) and MI60 (Akreos, n = 3). IOP pre-surgery was significantly different between the two groups (12.71 ± 3.23 mmHg for control vs. 23.32 ± 13.24 mmHg for PACG group, independent sample t-test, P < 0.001). Median AL was significantly shorter in the PACG group than the control group (22.37 mm for PACG vs. 23.33 mm for Control, P < 0.001). Mean ACD was significantly deeper in the control group than the PACG group (2.91 ± 0.37 mm for Control vs. 2.32 ± 0.19 mm for PACG, P < 0.001). There were no significant differences between the two groups regarding age, Flat K, Steep K and Mean K values. Table 1 shows the detailed ocular biological parameters among patients in this study.

Table 1.

Demographic and preoperative and postoperative clinical measurements in participants

Parameter	Control (n = 50)	PACG (n = 66)	P value
Age (Yrs)	69.56 ± 8.78 (53 ~ 90)	69.18 ± 7.17 (50 ~ 87)	0.799
IOP pre-surg (mmHg)	12.71 ± 3.23 (5.0 ~ 20.0)	23.32 ± 13.24 (6.4 ~ 56.4)	< 0.001
SE post-surg (D)	−0.25 (0.63) (−2.37 ~ 0.63)	−0.31(0.91) (−1.75 ~ 1.50)	0.911
Axial length (mm)	23.33 (0.93) (21.37 ~ 29.67)	22.37 (0.81) (20.66 ~ 23.90)	< 0.001
Anterior chamber depth (mm)	2.91 ± 0.37 (2.07 ~ 3.69)	2.32 ± 0.19 (1.92 ~ 2.79)	< 0.001
Flat K (D)	44.18 ± 1.17 (41.21 ~ 46.62)	44.61 ± 1.29 (41.06 ~ 47.80)	0.071
Steep K (D)	44.95 ± 1.31 (42.24 ~ 47.40)	45.44 ± 1.33 (41.56 ~ 48.75)	0.051
Mean K (D)	44.56 ± 1.22 (41.73 ~ 47.01)	45.02 ± 1.29 (41.31 ~ 47.97)	0.056

Data with a normal distribution are shown as the mean ± standard deviation, an independent sample t-test was used. Data with a non-normal distribution are shown as the median and interquartile range, Mann-Whitney U-test was used.

IQR interquartile range, SD standard deviation, PACG Primary angle-closure glaucoma, AL axial length, ACD anterior chamber depth, K keratometry, IOP intraocular pressure, SE spherical equivalent

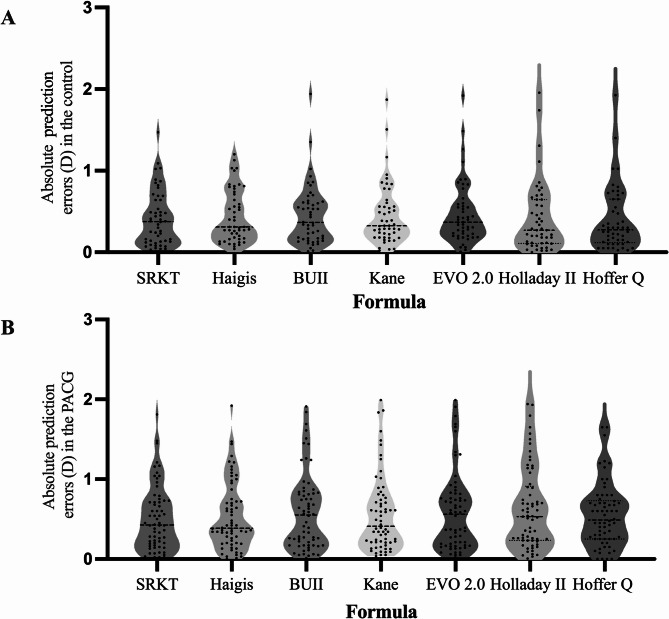
Table 2; Fig. 1 showed the refractive outcomes in the PACG and control groups. The MAE and MedAEs were larger in the PACG group compared to the control group. (for MAE, Two-way ANOVA, P < 0.01; for MedAEs, Mann-Whitney U tests, P < 0.05) In PACG eyes, the SRK/T and Haigis formulas had better predictability for ME than the Kane, EVO, and Holladay 2 formulas. (Two - way ANOVA with LSD, P < 0.01) For the BUII formula, the PACG group exhibits a negative postoperative refractive deviation, while the Kane, EVO, and Holladay 2 formulas exhibit a positive deviation. (Two-way ANOVA with LSD, P < 0.01) The PACG group showed a lower proportion of eyes within ± 0.50 D of prediction error (PE) (45.5 − 59.1%) compared to the control group (58 − 74%). Specifically, when using the Holladay 2, Hoffer Q, and EVO formulas, the control group had a significantly higher proportion of eyes within ± 0.50 D of PE (Chi-square test, P < 0.05).

Table 2.

MEs, maes, and MedAEs of the seven IOL formulas, as well as the proportions of eyes that Met the refractive thresholds for each formula

Formula	Group	MAE(D)	MedAE (D)	ME ± SD (D)	Eyes within PE (%)
					± 0.25D	± 0.50D	± 0.75D	± 1.00D
SRK/T	Control	0.42	0.38	−0.05 ± 0.54#	42%	68%	82%	92%
	PACG	0.51	0.43	0.08 ± 0.42	33.3%	56.1%	78.8%	84.8%
Haigis	Control	0.44	0.31	−0.27 ± 0.47#	34%	62%	78%	92%
	PACG	0.53	0.39	0.11 ± 0.46	27.3%	59.1%	77.3%	83.3%
BUII	Control	0.45	0.37	0.34 ± 0.47	38%	58%	86%	94%
	PACG	0.59	0.56	−0.37 ± 0.46#	33.3%	48.5%	68.2%	84.8%
Kane	Control	0.45	0.33	0.37 ± 0.21#	34%	66%	80%	94%
	PACG	0.57	0.41	0.32 ± 0.45#	36.4%	54.5%	74.2%	83.3%
EVO 2.0	Control	0.47	0.37	0.39 ± 0.22#	32%	66%*	80%	92%
	PACG	0.60	0.56	0.37 ± 0.47#	33.3%	48.5%*	69.7%	84.8%
Holladay 2	Control	0.41	0.27	0.28 ± 0.64	48%*	74%*	90%	98%
	PACG	0.63	0.53	0.39 ± 0.71#	28.8%*	45.5%*	71.2%	77.3%
Hoffer Q	Control	0.39	0.28	0.11 ± 0.54	50%*	72%*	88%	92%
	PACG	0.55	0.49	−0.07 ± 0.68	27.3%*	51.5%*	77.3%	89.4%

ACD anterior chamber depth, ME mean prediction error, MAE mean absolute error, MedAE median absolute error, SD standard deviation; EVO 2.0 = Emmetropia verifying optical 2.0 

*P < 0.05,# P < 0.01

Fig. 1.

Absolute errors of seven IOL formulas in the control group (A) and the PACG group (B) The middle line represents the median value PACG = Primary angle-closure glaucoma; EVO 2.0 = Emmetropia verifying optical 2.0

For AL-based analysis, PACG eyes were stratified into two subgroups: those with AL < 22 mm (n = 16) and those with AL ≥ 22 mm (n = 50). (Table 3; Fig. 2). The average AL were 21.53 mm ± 0.45 in the eyes with AL < 22 mm and 22.67 mm ± 0.48 in the eyes with AL ≥ 22 mm. In PACG eyes with AL < 22 mm, all formulas show reduced predictability compared to those with AL ≥ 22 mm. (Two-way ANOVA, P < 0.01) Additionally, PACG eyes with AL < 22 mm showed higher proportion of large - magnitude PE (> 1.0 D) with almost all formulas (Chi-square test, P < 0.01 of all formulas except Holladay 2), indicating short - AL eyes are more prone to such errors. When evaluating the percentage of eyes with PE within ± 0.50 D, the Haigis formula showed the highest predictability (50% in eyes with AL < 22 mm and 64% in eyes with AL ≥ 22 mm). However, none of the differences in these percentages reached statistical significance among formulas.

Table 3.

Refractive errors according to the AL in the PACG group

Formula	AL(mm)	MAE (D)	MedAE (D)	ME ± SD (D)	Eyes within PE (%)
					± 0.25D	± 0.50D	± 0.75D	± 1.00D
SRK/T	< 22	0.73	0.7	0.10 ± 0.93	25%	43.75%	56.25%#	62.5%#
	≥ 22	0.44	0.4175	0.07 ± 0.54	36%	62%	90%#	96%#
Haigis	< 22	0.67	0.535	0.22 ± 0.84	25%	50%	68.75%	81.25%
	≥ 22	0.49	0.3675	0.07 ± 0.62	28%	64%	84%	88%
BUII	< 22	0.91	0.8125	−0.82 ± 0.75	18.75%	31.25%	43.75%#	62.5%#
	≥ 22	0.49	0.40	−0.23 ± 0.59	38%	56%	78%#	96%#
Kane	< 22	0.88	0.7225	0.78 ± 0.77	25%	37.5%	62.5%	62.5%#
	≥ 22	0.46	0.355	0.18 ± 0.57	40%	62%	82%	94%#
EVO 2.0	< 22	0.93	0.7325	0.83 ± 0.78	25%	31.25%	62.5%	62.5%#
	≥ 22	0.49	0.3675	0.23 ± 0.59	36%	56%	76%	96%#
Holladay 2	< 22	0.76	0.605	0.17 ± 1.01	18.75%	43.75%	62.5%	68.75%
	≥ 22	0.59	0.5325	0.47 ± 0.59	32%	46%	74%	80%
Hoffer Q	< 22	0.74	0.525	−0.3 ± 0.89	18.75%	50%	62.5%	68.75%#
	≥ 22	0.49	0.4875	0.01 ± 0.58	30%	52%	82%	96%#

ACD anterior chamber depth, ME mean prediction error, MAE mean absolute error, MedAE median absolute error, SD standard deviation; EVO 2.0 = Emmetropia verifying optical 2.0. *P < 0.05, # P < 0.01

Fig. 2.

Comparison of median absolute errors in the eyes with AL < 22 mm (A) and AL ≥ 22 mm (B) in the PACG group The middle line represents the median value One-way ANOVA test with LSD post-hoc analysis was used to compare the mean absolute errors of each IOL formula PACG = Primary angle-closure glaucoma; EVO 2.0 = Emmetropia verifying optical 2.0

For ACD-based analysis, PACG eyes were stratified into two subgroups: shallow anterior chamber (ACD < 2.5 mm; n = 51) and deeper anterior chamber (ACD ≥ 2.5 mm; n = 15). (Table 4). All formulas had larger MAEs in eyes with ACD < 2.5 mm than eyes with ACD ≥ 2.50 mm. (Two-way ANOVA, P < 0.01) As for PACG with ACD < 2.5 mm, the BUII often results in a negative ME tendency, in contrast to the Kane, EVO, and Holladay 2, which show a positive tendency. (Two-way ANOVA with LSD, P < 0.01).

Table 4.

Mean prediction error MAE, SD, and medae of each formula (in diopters) of each formula, according to the ACD

Formula	ME ± SD	MAE ± SD (D)	MedAE (D)	± 0.50 D (%)
Group 1—ACD < 2.50 (n = 51)
SRK/T	−0.04 ± 0.87	0.56 ± 0.43	0.45	50.98%
Haigis	−0.02 ± 0.87	0.59 ± 0.45	0.42	54.90%
BUII	−0.55 ± 0.86#	0.62 ± 0.52	0.54	49.02%
Kane	0.50 ± 0.87#*	0.58 ± 0.51	0.38	56.86%
EVO 2.0	0.61 ± 0.88#	0.63 ± 0.53	0.54	49.02%
Holladay 2	0.42 ± 0.78	0.69 ± 0.55	0.535	43.14%
Hoffer Q	−0.09 ± 0.73	0.6 ± 0.43	0.6	43.14%
Group 2—ACD ≥ 2.50 (n = 15)
SRK/T	0.09 ± 0.59	0.36 ± 0.21	0.28	66.67%
Haigis	0.13 ± 0.66	0.33 ± 0.20	0.28	73.33%
BUII	−0.23 ± 0.68#*	0.51 ± 0.34	0.66	46.67%
Kane	0.27 ± 0.59	053 ± 0.32	0.60	46.67%
EVO 2.0	0.31 ± 0.61	0.50 ± 0.35	0.59	46.67%
Holladay 2	0.31 ± 0.44	0.45 ± 0.28	0.49	53.33%
Hoffer Q	0.02 ± 0.44	0.39 ± 0.18	0.45	80.00%
ACD anterior chamber depth, ME mean prediction error, MAE mean absolute error, MedAE median absolute error, SD standard deviation, EVO 2.0 Emmetropia verifying optical 2.0.*P < 0.05, # P < 0.01 ME: Barrett Universal II vs. all formulas (#) For subgroup ACD < 2.50 mm: Hoffer Q vs. Kane, EVO, Holladay 2 (#); vs. BUII (*) BU II vs. Hoffer, Kane, EVO (#) For subgroup ACD ≥ 2.50 mm: BUII vs. Kane, EVO, Holladay 2 (#); vs. SRK/T, Haigis, Hoffer Q (*)

We divided eyes of all patients into three sub-groups: Group A-shallow ACD and short AL group (ACD ≤ 2.5 mm; AL ≤ 22 mm), Group B-shallow ACD and normal AL group (ACD ≤ 2.5 mm; AL > 22 mm); Group C- normal ACD and normal AL group (ACD > 2.5 mm; AL > 22 mm). The proportions of eyes within ± 0.25 D, ± 0.50 D, and ± 1.00 D according to ACD are shown in Table 5. As is shown, Group A exhibited lower predictability than other groups at almost all portions with all the formula. For large prediction errors, Haigis, BUII, Holladay 2, and Hoffer Q formulas showed a higher proportion of eyes with PE within ± 1.00 D in Group C compared to Group A. (Chi-square test, Haigis and BUII, P < 0.05; Holladay 2 and Hoffer Q, P < 0.01). Although there were no statistically significant differences in the proportion of eyes with specific PE across the formulas, the Holladay 2 and Hoffer Q formulas showed significant differences in predictability among the three groups, with Group A having worse predictability than Group C. (Chi-square test, P < 0.05) Table 6 presents the MAE and MedAE results for the three groups. No significant differences were found in prediction outcomes across seven formulas. However, significant differences in MAE were observed among the three groups, with Group A showing the poorest prediction outcomes. (Two-way ANOVA with LSD, P < 0.01)

Table 5.

Predictive outcomes of each formula in subgroups of patients according to anterior chamber depth and axial length

Formula	ACD ≤ 2.5 mm; AL ≤ 22 mm n = 15(Group A)(%)	ACD ≤ 2.5 mm; AL > 22 mm n = 44(Group B)(%)	ACD > 2.5 mm; AL > 22 mm n = 54(Group C)(%)	P value
SRK/T
± 0.25 D	40	31.82	38.89	0.731
± 0.50 D	53.33	54.44	66.67	0.402
± 1.0 D	73.33	84.09	84.09	0.617
Haigis
± 0.25 D	26.67	25	31.48	0.769
± 0.50 D	46.67	59.09	62.96	0.524
± 1.0 D	66.67	79.55	94.44	0.013*
BUII
± 0.25 D	20	31.82	37.04	0.402
± 0.50 D	40	54.44	53.70	0.594
± 1.0 D	73.33	84.09	96.40	0.036*
Kane
± 0.25 D	33.3	31.82	33.33	0.986
± 0.50 D	46.67	52.27	59.26	0.623
± 1.0 D	73.33	81.82	92.59	0.103
EVO 2.0
± 0.25 D	20	22.73	31.48	0.513
± 0.50 D	46.67	45.45	61.11	0.263
± 1.0 D	73.33	84.09	92.59	0.121
Holladay 2
± 0.25 D	20	31.82	46.30	0.113
± 0.50 D	46.67	43.18	70.37	0.018*
± 1.0 D	66.67	72.73	96.30	0.002#
Hoffer Q
± 0.25 D	20	25	53.70	0.004#
± 0.50 D	40	47.73	74.07	0.008#
± 1.0 D	66.67	93.18	94.44	0.004#
ACD anterior chamber depth, AL aixal length, EVO 2.0 Emmetropia verifying optical The chi-squared test was used to compare the proportions of eyes within ± 0.25 D, ± 0.50 D, and ± 1.00 D in each subgroup Comparison among three Groups: * P < 0.05, # P < 0.01

Table 6.

Prediction errors of each formula in subgroups of all the patients according to axial length and anterior chamber depth

Subgroups	Groups	SRK/T	Haigis	BUII	Kane	EVO 2.0	Holladay 2	Hoffer Q
	A (ACD ≤ 2.50 mm and AL ≤ 22 mm, n = 15)
	MAE + SD	0.66 ± 0.60	0.71 ± 0.59	0.74 ± 0.61	0.74 ± 0.69	0.77 ± 0.67	0.77 ± 0.68	0.76 ± 0.55
	MedAE	0.58	0.59	0.565	0.595	0.58	0.52	0.675
	B (ACD ≤ 2.50 mm and AL > 22 mm, n = 44)
	MAE + SD	0.49 ± 0.36	0.53 ± 0.38	0.56 ± 0.5	0.61 ± 0.54	0.66 ± 0.50	0.64 ± 0.51	0.53 ± 0.34
	MedAE	0.44	0.4175	0.435	0.485	0.5975	0.5725	0.6
	C (ACD > 2.50 mm and AL > 22 mm, n = 54)
	MAE + SD	0.41 ± 0.31	0.42 ± 0.28	0.46 ± 0.32	0.47 ± 0.32	0.47 ± 0.34	0.39 ± 0.36	0.37 ± 0.35
	MedAE	0.34	0.325	0.3975	0.3825	0.395	0.28	0.25
ACD anterior chamber depth (measured from corneal epithelium to lens), AL axial length, EVO Emmetropia Verifying Optical 2.0, BUII Barrett Universal II, MAE mean absolute error, MedAE median absolute error, SD standard deviation

Through multiple linear regression analysis incorporated the variables ACD, AL, IOP and preoperative SE, we found that the postoperative ME are related to preoperative IOP. The BUII formula shows a negative correlation between AL and ME, while the Kane, EVO, Holladay 2, and Hoffer Q formulas all show positive correlations. (BUII: B = −0.365, P = 0.008; Kane: B = 0.291, P = 0.037; EVO: B = 0.319, P = 0.022; Holladay 2: B = 0.355, P = 0.010; Hoffer Q: B = 0.325, P = 0.020) These findings highlight the differing performance of IOL formulas across varying ALs in PACG patients.

Discussion

This study compared the accuracy of seven IOL calculation formulas in predicting refractive outcomes following phacoemulsification and IOL implantation in eyes with PACG. Generally, PACG eyes exhibited inferior predictability in refractive outcomes than the control eyes with all formulas. In PACG patients, the BUII formula is associated with negative residual refractive error, whereas the Kane, EVO, and Holladay 2 formulas are more likely to be associated with positive residual refractive error. The SRK/T and Haigis formulas demonstrated better predictability for ME. For the PACG group, eyes with short AL (AL < 22 mm) or shallow ACD (ACD < 2.5 mm) exhibited significantly higher MAE across all formulas compared to their control groups. These eyes were also more likely to experience large-magnitude refractive PE (percentage of eye with PE > 1.0 D). Generally, the SRK/T and Haigis formulas showed smaller postoperative ME and MAE compared to other formulas, and also demonstrated a higher percentage of PE within ± 0.50 D. However, these differences did not reach statistical significance.

We further analyzed how ACD and AL together influence the accuracy of IOL calculation formulas in PACG eyes. Eyes with both short AL (AL < 22 mm) and shallow ACD (ACD < 2.5 mm) had lower predictability than other groups with all the formula. Additionally, a significant inverse correlation was identified between postoperative prediction error and AL, with a correlation coefficient of −0.23.

AL and ACD represent well-established biometric parameters that significantly influence refractive outcome prediction accuracy. In the immediate primary phacoemulsification for PACG eyes, it is important to pay attention to the refractive prediction error caused by preoperative AL elongation due to IOP. In this study, we found that the predictability of PACG decreases as the AL shortened. Kim et al. conducted a comparative analysis of postoperative refractive outcomes between 44 APAC eyes and 60 control eyes, evaluating six new-generation IOL calculation formulas: Barrett Universal II (BUII), Hill-Radial Basis Function (RBF) 3.0, Kane, EVO 2.0, Ladas Super Formula, and Pearl-DGS [7]. In APAC eyes with AL < 22 mm, the Haigis formula (0.49 D) and the Hill-RBF 3.0 formula (0.54 D) demonstrated lower median absolute errors (MedAEs) compared to the SRK/T formula (0.82 D) (all P < 0.05). Additionally, the Haigis and Hill-RBF 3.0 formulas achieved the highest percentage (46.7%) of eyes with PE within ± 0.5 D in APAC eyes with AL < 22 mm. Hou et al. documented that in a cohort of 129 PACD eyes, the Kane formula had the highest proportion (71.3%) of eyes with PE within ± 0.50 D. The formula performance index (FPI) was ordered as follows: Kane (0.067), RBF 3.0 (0.064), Haigis (0.062), SRK/T (0.060), Barrett Universal II (BUII) (0.058), Hoffer Q (0.055), and LSF (0.049). In a study of a Chinese population, the percentage of PE of the Kane formula in the short AL eyes was 68.42% in the ± 0.5 D range, lower than the SRK/T formula of 71.05% and the Haigis of 78.95%.¹² In this study, we observed that the Haigis formula demonstrated the highest predictability in percentage of PE within ± 0.50 D across both AL groups. Notably, eyes with shorter ALs (AL < 22 mm) exhibited a larger MAE when using the BUII, Kane, and EVO 2.0 formulas. (Table 3; Fig. 2). This suggests that these new-generation formulas may not be as precise as other formulas in eyes with shorter ALs.

We also found that MAE in PACG became greater as ACD decrease for all formulas. Previous studies addressing the prediction of IOL outcomes in eyes with shallow ACD have demonstrated that new generation formulas, such as Kane and BUII, are comparable in accuracy to SRK/T. ¹¹However, these studies had not specifically targeted the PACG demographic, and the ACD in their subjects were not typically shallow as this study [12–14]. Also it should be noted that the small sample size of the shallow ACD group in this study also imposes potential constraints on our conclusions.

When considering both AL and ACD together, eyes with short AL with shallow ACD (AL < 22 mm and ACD < 2.5 mm), had lower predictability than other groups with all formula. EVO had largest MAE and MedAE in eyes with shallow ACD and normal AL (AL > 22 mm and ACD < 2.5 mm). Mo and colleagues [14] investigated the effects of ACD on the accuracies in elongated eyes. Varying depths of ACD of high myopia were included. The SRK/T and Haigis formulas are not recommended. However, the above conclusion is not applicable in PACG. In this study, traditional formulas demonstrated relatively better predictive accuracy in patients with short AL and shallow ACD, while new-generation formulas did not show outstanding performance. This may be related to the inclusion of some extreme data in our study, which affected the predictions of the new-generation formulas. Currently, there are few articles that focus on specific subgroups defined by ACD and AL for PACG, and future refined categorization of different types of PACG will lead to more precise conclusions.

The Hoffer Q formula has traditionally performed well in eyes with short AL and shallow ACD, which were typical features of PACG eyes. Joo et al. and Seo et al. both reported that Hoffer Q achieved the lowest refractive prediction errors among SRK/T and Haigis in PACG eyes, supporting its use in eyes with crowded anterior segments [3, 15]. However, the EAGLE study by Day et al. found Hoffer Q had the highest MAE (1.11 D), while Haigis performed best (0.30 D), with Hoffer Q showing a myopic shift [16]. Similarly, Lee et al. reported that in the peripheral anterior synechiae (PAS) (+) group, the MAE was significantly larger than in the PAS (–) group using all formulae. In the (PAS) (+) group, Hoffer Q had the highest MAE (0.70 ± 0.46 D), while Haigis performed best (0.61 ± 0.43D). The presence of PAS suggests that anatomical factors may affect refractive outcomes regardless of formula choice [17]. In our study, Hoffer Q showed moderate accuracy (ME: − 0.07 D, MAE: 0.55 D) in PACG eyes, consistent with its known myopic bias. However, its performance worsened in eyes with AL < 22 mm, where Haigis yielded a lower MAE (0.67 D). This trend became more pronounced in eyes with both short AL (< 22 mm) and shallow ACD (< 2.5 mm), where Hoffer Q showed further increases in MAE and reduced accuracy, indicating less reliability under these atypical biometric conditions. This result is consistent with the findings of Eom et al., which showed that the MedAE predicted by the Hoffer Q formula (0.66 D) was significantly higher than that predicted by the Haigis formula (0.40 D) in eyes with both short AL (< 22 mm) and shallow ACD (< 2.4 mm) [18]. In such cases, the Hoffer Q formula tends to overestimate the ELP in eyes with atypical biometric characteristics.

Recently, several studies have attested to the superior predictive precision of new-generation formulas. However, the present study did not substantiate the purported advantages of them over others. Studies found that in PACG eyes with shallow ACD, the actual effective lens position after cataract surgery would be more posteriorly located due to ACD deepening, thus resulting in hyperopic shift [4]. In addition to this, PACG eyes had already been shown to have thicker lens and larger capsular than normal eyes, which is more likely to cause IOLs to be tilted or eccentric [19]. Thus, it can be concluded that despite the utilization of new-generation formulas, which incorporate various parameters more than ACD and AL, prediction errors may still arise due to these anatomical variations influencing ELP determination. In the new-generation formulas, the mandatory biometric parameters, such as biological sex (BS), AL, ACD, K and optional biometric parameters LT and center corneal thickness (CCT) can be used to calculate the IOL refractive power. Take Kane formula for example, though authors suggested the convenience of using optional biometric parameters LT and CCT, when biometric instruments or ocular conditions were limited in clinical practice, only partial optional biometric parameters can be measured, which affects the calculation of IOL power. Li et al. found that the parameter LT has a great influence on the Kane formula results for the IOL power calculation in cataract patients with short AL, shallow ACD and steep K_m [13]. IOP of PACG patients might often not be well controlled, as well as corneal edema, which limit the accuracy of anterior segment parameter measurements before surgery. This explained that the Kane and EVO 2.0 formula seemed to have a higher predictive accuracy in eyes with normal ACDs and AL.

To decrease the prediction errors in PACG eyes, except for the evolution of IOL calculation formulas, there are other ways to improve the accuracy of the prediction. Enhancements in biometry techniques that allow for more precise measurements of the eye’s optical characteristic. Goto et al. reported the segmented ALs were longer in short eyes and shorter in long eyes than the composite ALs [20]. The refractive accuracy can be improved in the Hoffer Q, Holladay 1, and SRK/T formulas by changing the composite ALs to the segmented ALs. Kim et al. demonstrated that for every 1 mm Hg reduction in IOP, the AL decreases by 6 mm, resulting in a hyperopic shift of 0.015 D [21]. In this study, it was found that 53.73% (36 of 67) of PACG patients had IOP exceeding 21 mmHg, which could be a contributing factor affecting the accuracy of prediction adjustments.

Another issue that requires declaration is that our study employed the IOL Master 500 for ocular biometric measurements. The IOL Master 500, though widely used in clinical practice, does have limitations when compared to the IOL Master 700. While the IOL Master 500 provides reliable biometric measurements, it is based on partial coherence interferometry (PCI), which has a lower depth resolution than the swept-source optical coherence tomography (SS-OCT) technology used in the IOL Master 700 [22, 23]. The IOL Master 700’s ability to offer superior three-dimensional imaging allows for more precise measurements of ACD and AL, especially in challenging cases like dense cataracts [24, 25]. Nevertheless, the IOL Master 500 remains a reliable tool in settings where the latest technology is not accessible, which is still the case in many ophthalmic practices, particularly in regions where PACG is more prevalent. Existing studies have shown that, although the IOL Master 500 and IOL Master 700 yield differing results in certain measurements, such as AL and ACD, these differences are clinically negligible [23–25]. Therefore, these two devices can be used interchangeably. This view is supported by Sebastian et al., whose study involved a large cohort and demonstrated that the differences between the IOL Master 500 and IOL Master 700 were minimal and that switching between them is safe for bilateral patients [25].

Our study has some limitations. Firstly, our sample size was relatively small, especially in subgroup analyses, which may have somewhat reduced the statistical power and confidence. Secondly, the control group was not matched with the PACG group based on baseline IOP, AL, and ACD. The lack of baseline matching may introduce potential confounding effects, as these parameters are known to influence IOL power calculations and refractive outcomes. Future studies with more standardized AL-based matching between groups could help minimize potential confounding effects and strengthen the comparability of findings. Thirdly, our study included multiple IOLs in a small sample size, which made the constant optimization difficult. The optimization constants utilized in our study were drawn from the overall population data available in the ULIB database, as were used in recent studies. Future research incorporating a larger sample of eyes with a single IOL model would be more effective in assessing the accuracy of various formulas and the impact of constant optimization. Finally, glaucoma patients used anti-glaucoma drugs before surgery, some of them underwent GSL and pupilloplasty at the same time as well. The potential effect of these drugs and surgeries on anterior segment structure is not clear.

In summary, PACG eyes showed a lower prediction accuracy compared to the control eyes, especially in PACG eyes with short ALs and swallow ACDs. SRK/T and Haigis achieved satisfying performances in eyes with atypical biometric characteristics.

Authors'contributions

H.X. and RR.L. wrote the main manuscript text.H.X. and YJ.Z. prepared Figs. 1 and 2. XL.L. and LY.L. prepared Tables 1, 2, 3 and 4. R.Y. and RR.L. prepared Tables 4, 5 and 6. All authors reviewed the manuscript.

Funding

This study was supported in part by grants from Zhejiang Provincial Natural Science Foundation Exploration Project. (Project Number: MS25H120013), Zhejiang Provincial Medical and Health Project. (Project Number: 2025KY1021) and Zhejiang Province Traditional Chinese Medicine Science and Technology Plan Project (Project Number: 2025ZL404).

Data availability

All data generated or analysed during this study are included in this published article.

Declarations

Ethics approval and consent to participate

The ethics committee approved this study protocol from the leading institution, the Ethics Committee of Eye Hospital Wenzhou Medical University, in January 2021 (No. 2021-011-K-08). Written informed consent was obtained from all study participants. The research complied with the ethical principles outlined in the.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.