Abstract
The demand for faster data transfer rates rises along with the number of mobile devices, such as smartphones and IoT gadgets, which makes the radio spectrum more crowded. The forthcoming 5G wireless communication technology seeks to significantly enhance data speeds and spectrum efficiency by dynamically adjusting to fluctuating channel conditions. This research presents a new approach in the form of a hierarchical machine learning system for automation of modulation classification and adaptive parameter selection that optimizes spectral efficiency for different communication channels. A hierarchical approach is adopted in place of traditional methods that classify modulation schemes as separate entities. This method first predicts the modulation type (e.g., PSK, FSK, CPM), and subsequently determines the optimal parameters (M, h, L) corresponding to the identified channel conditions. During experimentation, seven modulation schemes were tested (2-PSK, 4-PSK, 8-PSK, 2-FSK, 4-FSK, 8-FSK, and CPM) for different modulation orders (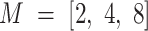 ) and spectral efficiencies
) and spectral efficiencies 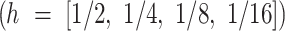 as well as for overlap factors
as well as for overlap factors 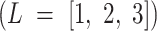 . A detailed MATLAB simulation was built and signals were transmitted over different channels (AWGN and SUI Stanford University Interin) for evaluation over different frequency ranges. Performance of our proposed hierarchical framework was examined based on the Bit Error Rate (BER) and achievable data rate in different signal-to-noise ratio (SNR) situations. The accuracy achieved by our proposed hierarchical classifier was 98.57%, proving effectiveness in adaptive modulation selection. These achievements suggest plainly how cognitive radio systems and next generation wireless networks can benefit by the real-time spectrum adaptation and improvement in data reliability in transmission.
. A detailed MATLAB simulation was built and signals were transmitted over different channels (AWGN and SUI Stanford University Interin) for evaluation over different frequency ranges. Performance of our proposed hierarchical framework was examined based on the Bit Error Rate (BER) and achievable data rate in different signal-to-noise ratio (SNR) situations. The accuracy achieved by our proposed hierarchical classifier was 98.57%, proving effectiveness in adaptive modulation selection. These achievements suggest plainly how cognitive radio systems and next generation wireless networks can benefit by the real-time spectrum adaptation and improvement in data reliability in transmission.
Subject terms: Electrical and electronic engineering, Computer science
Introduction
Meeting the demanding requirements for effective, reliable, and robust communication in a tactical setting has proven to be a difficult task. Unlike regular wireless networks, the establishment of permanent fixed infrastructure is neither feasible nor viable in tactical networks due to challenging circumstances. In such difficult environments, software-defined radios (SDRs) have been delivering efficient, reliable, robust, and secure communication solutions1. Adaptive Modulation and Coding (AMC) methodologies significantly improve the spectral efficiency of wireless communication channels while preserving quality. AMC dynamically modifies the parameters to enhance performance in real time. This adaptability facilitates the efficient use of spectrum resources under various channel conditions2. Using SDRs with AMC as “cognitive radios” or “cognition engines” is a reliable way to improve spectrum efficiency in a wide range of channel conditions, making it the best way to ensure reliable communication in complex networks.
Selecting the appropriate modulation strategy facilitates the transmission of increased information within constrained spectral resources. Conventional signal modulation classification techniques are based on various experiments and manually designed feature extraction algorithms. Although these methods demonstrate satisfactory performance, they are computationally demanding and encounter difficulties in managing complex signal environments and varied modulation patterns3. The choice of modulation methods has a significant impact on how well radio networks work. There is a critical need for a flexible and smart system that can switch between modulation schemes based on data from the real-time transmission environment4. This system should use machine learning to analyze channel conditions, customer needs, quality of service (QoS), and signal-to-noise ratio (SNR). It should then change modulation settings to improve reliability and throughput. SDRs encounter considerable obstacles due to channel impairments, poor SNR, and varied service demands. Managing operational limits and changing data rate needs is more difficult due to these conditions5.
We propose link adaption cognitive engine to automate the process of modulation parameter section for user defined requirements. In this article the focus is on narrowband waveforms such as Phase Shift Keying (PSK), Frequency Shift Keying (FSK), and Continuous Phase Modulation (CPM) which utilize parameters like modulation order (M), spectral efficiency (h) and overlap factor (L) for generating a particular type of waveform. A hierarchical machine learning classifier is proposed to identify the modulation type and then categorize the parameters M, h, and L that influence data throughput and performance. The goal here is to create an adaptive cognitive radio system to deal with the typical problems faced by SDR by using a number of advanced modulation and coding methods.
The performance of our proposed framework has been evaluated across several frequency bands for the modulated messages transmitted through the Additive White Gaussian Noise (AWGN) and Stanford University Interim (SUI) channels. The Bit Error Rate (BER) and the data rates were evaluated at various SNRs. The suggested system aims to efficiently adapt to the varying channel conditions and communication requirements by dynamically switching between several modulation schemes and coding approaches. This approach provides steady performance, efficient resource utilization, and enhanced service quality in congested and dynamic wireless settings. The improved accuracy of the classifier emphasizes its capacity to improve communication networks through adaptive modulation.
The remainder of the paper is structured as follows. “Background” provides a comprehensive analysis of modulation schemes, channel models, and modulation classification approaches, particularly those based on machine learning. “Literature review” discusses the evolution of communication technologies and the techniques used to overcome the constraints to enhance the performance of communication cognition engines. “Materials and methods” discusses the data acquisition and proposed methodology phase with a focus on the hierarchical machine learning classifier, system model, modulation and channel simulation configuration, and methodology. “Evaluation and results of the proposed methodology” breaks down the experimental configuration, bit stream generation, modulation scheme establishment, and assessment criteria. “Evaluation and results of the proposed methodology” highlights the simulation results, which encompass the BER and the data rate performance across various modulation schemes and channel conditions, in addition to the precision and resilience of the machine learning classifier. “Conclusion and future works” concludes the work by summarizing key findings, emphasizing the importance of adaptive communication systems, and proposing avenues for further research.
Background
Future generations of wireless radios (WRs) are expected to dynamically adjust their transmission parameters, such as frequency and modulation scheme, to improve spectrum utilization and increase data rates6. SDRs have addressed the dual challenge of meeting the required QoS and managing variable physical ranges, while dealing with limited bandwidth, time, and other resources in various ways. As a result, ensuring that operating frequency resources are allocated at the right time and at the right place is a key objective, which must be achieved while maintaining stable management and meeting QoS requirements7.
Digital modulation schemes play a crucial role in determining the quality, speed, and reliability of communication systems and can be classified into constant envelope schemes, such as FSK and PSK, and non-constant envelope schemes, such as ASK and QAM. Other options include M-APK (Amplitude and Phase Keying) and n-m PCM. The main criteria for selecting a modulation scheme include maximizing the data rate, minimizing transmitted power, optimizing channel bandwidth, reducing symbol errors, and improving resistance to interference8. CPM is also a type of digital modulation scheme. It modulates the phase of the carrier signal based on the input data while maintaining a continuous phase throughout the transmission. The CPM scheme is often used in transmitters that are low in complexity, cost, and power consumption. Since CPM does not require I/Q signals, transmitters using this scheme are simpler, more affordable, and consume less power9. One of the key parameters that defines a CPM signal is its modulation index, which controls the phase sensitivity with respect to the input symbols. A CPM waveform with a larger modulation index generally offers better minimum distance properties, resulting in improved performance10. Contemporary research on modulation-type classification frequently encounters constraints in its variety. In addition, the channel effects examined in prior studies often struggle to accurately reflect real-world noise conditions. In this work, a multimode, multiband, and multi-scheme adaptive cognition engine based on certain user-controlled requirements is proposed. Integrating M-PSK, M-FSK, and CPM modulation schemes as shown in Table 1, into a single SDR to allow the adaptability of various narrowband communication scenarios: M-PSK for high-throughput, high-SNR settings; M-FSK for robust communication in interference-prone environments; and CPM for optimal performance in bandwidth-limited or multipath conditions.
Table 1.
Comparison of modulation schemes for adaptive unified diverse communication scenarios.
| Aspect | M-FSK | M-PSK | CPM |
|---|---|---|---|
| Low SNR performance | Excellent: high robustness due to orthogonality, low BER for low M | Moderate: BPSK performs well; higher M suffers from noise | Good: continuous phase offers robustness |
| High SNR performance | Poor: not spectrally efficient at higher SNR | Excellent: high-order PSK (e.g., 16-PSK) achieves high data rates | Good: spectrally efficient with moderate complexity |
| Impact of M (order) | Higher M increases bandwidth usage and decreases robustness at low SNR | Higher M increases data rates but is sensitive to noise and phase errors | Higher M adds complexity but maintains robustness with efficient spectral usage |
| Overall best use | Low SNR, narrowband scenarios | Preferably BPSK/QPSK for robustness in low SNR | Moderate SNR, energy-constrained systems |
Recognition of radio signal modulation schemes is increasingly critical, particularly in addressing electromagnetic signal congestion in 5G networks through dynamic spectrum access. This knowledge enables adaptive communications, allowing intelligent, context-driven decisions to minimize interference and optimize spectrum utilization. Traditional approaches to classifying modulated signals rely on specifying hand-crafted or learned features, followed by a classifier to identify the modulation class11. However, these classical methods face significant limitations, particularly their inability to capture all high-order dependencies, either due to the constraints of manual feature design or the limited capacity of the learning machine. In contrast, machine learning, particularly deep learning, offers a transformative approach by automatically extracting meaningful features directly from the data12. This ability to learn high-order dependencies and complex relationships enhances recognition rates, even when accommodating a wide variety of modulation types.
Literature review
The rapid evolution of wireless communication technologies has led to the development of advanced techniques for efficient signal transmission and reception. Active research on Cognitive Radio Networks (CRNs) continues, since they have emerged as an essential management tool to tackle the increasing complexity of wireless communication networks. In essence, cognitive networks enhance the interdisciplinary coordination between novel communication platforms by employing efficient spectrum management techniques. In the13 article, the authors discuss how to effectively incorporate cognitive radio techniques into the design of satellite communication networks. CRNs have experienced notable progress in the use of traditional optimization techniques and machine learning technologies to improve performance. Classical algorithms, like Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Artificial Bee Colony (ABC), have been employed for problems such as spectrum allocation and resource management. These techniques utilize population-based methods to traverse intricate optimization terrains; however, each has constraints in real-time operating scenarios.
As discussed in14, efficient power distribution and dynamic modulation enhance the performance of communication systems. The transmission strength of each subcarrier must be calibrated according to the channel conditions to achieve a specified BER. Although they carry less data, lower-order modulation techniques such as BPSK and QPSK exhibit greater resistance to multipath interference. Higher-order modulation facilitates faster data transmission but is more susceptible to multipath fading. Enhancing system performance, bandwidth efficiency, SNR, and BER requires adaptive modulation. The HLD method was created by Jajo et al. and is an unsupervised hierarchical approach that finds eight modulation schemes with high accuracy and lower complexity. It was successfully tested on PXIe RF transmitters and receivers15. However, incorporating additional modulation types, enhancing performance in low-SNR environments, optimizing for real-time applications, and augmenting HLD’s durability across various hardware and channel circumstances will improve its applicability for contemporary communication systems.
Hashib et al. describe the SUI channel model as a broad structure for simulating effective wireless environments. Principal characteristics cover (a) increased path loss compared to conventional supercell topologies, (b) integration of macroscopic and microscopic fading phenomena, (c) evaluation of cochannel and adjacent channel interference, and (d) adjustment to significant multipath delay and Doppler spread. The model also integrates practical elements such as geography, antenna specifications, wind velocity, traffic range, and bandwidth16. The properties of the SUI model make it an appropriate tool for tackling real-world deployment difficulties and improving network performance analysis and optimization. Shahzad et al. identified critical parameters for selecting a modulation scheme, highlighting the requires for the modulated signal to be robust against additive noise and channel impairments while still being bandwidth efficient17. Considering these variables, they selected CPM for narrowband applications.
Ali et al. investigated the creation of a high-precision classifier for automatic modulation recognition (AMR) of PSK, QAM, and DVB-S2 APSK signals, utilizing multilayer perceptron (MLP) and radial basis function (RBF) neural network classifiers18. The authors in19 proposed a feature-based hierarchical classification method using quadratic SVM to precisely categorize higher-order modulation schemes, using a detailed vector of 45 statistical features, higher-order moments, and cumulants for improved feature extraction. Their assessment of many classifiers yielded an overall accuracy of 96% at a SNR of 5 dB. In addition studies also highlight the evolution of intelligent communication systems and the role of advanced algorithms in enhancing spectrum efficiency and modulation adaptability, Table 2 summarizes key studies addressing spectrum sensing, automatic modulation classification, and hierarchical machine learning models. These works demonstrate the impact of machine learning and deep learning in improving adaptive modulation, signal classification, and real-time spectrum optimization in dynamic communication environments.
Table 2.
Summary of recent research in cognitive radio spectrum sensing and adaptive modulation.
| Ref | Study | Method/model | Key findings |
|---|---|---|---|
| 20 | Deep learning-based multi neural network architecture for spatial cognitive radio | Multi-domain fusion deep learning architecture | Enhanced signal detection in challenging environmental conditions through multi-domain fusion, improving spectrum sensing (SS) in CR systems |
| 21 | Time-frequency cross fusion network (TFCFN) for spectrum sensing | GRU for temporal feature extraction, CNN for spatial feature fusion in non-Gaussian noise environments | Significantly improved detection performance under non-Gaussian noise, highlighting the effectiveness of combining temporal and spatial features |
| 22 | Assessment of SU mobility effect on SS performance | Real-time adaptive modulation methods and recursive estimation techniques | Demonstrated necessity for real-time adaptive modulation due to mobility-induced fluctuations in signal strength, impacting AMC accuracy |
| 23 | Feature selection in spectrum sensing techniques for 5G CR networks | Re-standardized energy detection and complex feature extraction for ML models | Highlighted the robustness and improved accuracy of complex features over conventional ones, especially at low SNR levels |
| 24 | Recursive estimation for mobile users in cluttered environments | Recursive estimation to mitigate signal strength fluctuation effects | Improved spectrum sensing reliability in dynamic environments affected by multipath fading and shadowing |
| 25 | Deep learning-based AMC with transfer learning on RadioML2016.10b dataset | CNN-based transfer learning model | Achieved improved modulation classification performance across varying SNR levels, demonstrating the promise of CNN architectures for AMC in CR networks |
| 26 | Spectrum mobility optimization in congested CR-LANs | Simple recursive estimator, Kalman and alpha-beta filters for SU tracking | Reduced total transmission time to 4.1827 s and improved end-to-end throughput to 3.67 kbps |
| 27 | Cooperative AMC using higher-order cumulant-based features | Spatially distributed sensor nodes and weight vector-based controllability factor | Improved classification accuracy by 15% at 10 dB SNR compared to traditional higher-order statistics-based methods |
| 28 | Hybrid prediction in multipath and shadowed fading (MSF) environments | Alpha-Beta filtering with Neyman–Pearson type detector | Reduced detection error probability and achieved an average relative error of  , improving primary signal prediction in MSF conditions , improving primary signal prediction in MSF conditions |
This study expands on previous findings by integrating higher-order modulation schemes into SUI channels, so offering a more precise depiction of actual noise environments. A hierarchical classifier was created that reduces complexity by organizing the classification process by modulation type and order, while also fine-tuning the other parameters based on a 15-element feature vector. The proposed hierarchical classifier will autonomously select the optimal modulation scheme from 168 options based on channel conditions and SNR, eliminating the need for manual feature extraction. Its stepwise classification improves efficiency, while its scalable design allows new waveforms to be added without retraining the entire model. Following are the contributions of our proposed schemes by presenting a more thorough method that improves classification accuracy, can adapt to real-world channel conditions, and makes real-time applications run more smoothly.
Proposed an effective hierarchical classifier that categorizes classifications by modulation type and order, enhancing accuracy and minimizing complexity with a targeted 15-feature vector.
Implemented various modulation algorithms (M-PSK, M-FSK, CPM) to improve the model’s applicability by meeting modulation needs in real-time communication.
Implemented a variation of channel effects, encompassing AWGN and SUI channels across various SNR levels (-3 dB to 15 dB in 1 dB increments), to precisely depict noise conditions and evaluate the model’s robustness, enhancing its adaptive performance in dynamic, real-world communication settings.
Materials and methods
The conventional physical layer architecture within the communication infrastructure, shown in Fig. 1, includes modulation, which controls the waveform of the output signal. Incidentally, this waveform controls the bandwidth, bit rate, and distance that the signal can travel through certain channels. The waveforms are affected tremendously based on the channel conditions, which affect the overall communication mechanism.
Fig. 1.
Key components and functions in the traditional physical layer.
The proposed scheme intends to make use of machine learning methods for adaptive cognition of SDR. In order for machine learning models to learn, relevant data is required to train the proposed cognition engine. In this section, data acquisition methodology is presented which is followed by the proposed novel framework. Figure 2 depicts the overall workflow of our proposed scheme. The input signal is modulated according to defined parameters during the signal modulation phase. Subsequently, during channel transmission, the modulated signal traverses various channel conditions, encompassing AWGN and SUI-1 to SUI-6 channels. During the signal demodulation phase, the signal is demodulated after its transmission across the channel. Metrics such as BER and data rate are then collected during the data collection phase. A Hierarchical classification/cognition Engine utilizes these measures for adaptive mode selection, enhancing signal processing according to the gathered data. Our implementation has demonstrated strong performance across various terrains, including flat areas with light to moderate tree density (SUI-1 to SUI-4) and hilly regions with heavier tree cover (SUI-5, SUI-6). Table 3 summarizes the terrains and their corresponding SUI channel models, as well as the AWGN channel used in the study.
Fig. 2.
Outline of the workflow for hierarchical classification and modulation parameter optimization.
Table 3.
Terrain types and corresponding channel models.
| Terrain type | Characteristics | Channel models |
|---|---|---|
| AWGN | Additive white Gaussian noise, idealized channel with no fading or interference | AWGN |
| Terrain C | Flat regions with light tree density, minimal obstruction effects | SUI-1, SUI-2 |
| Terrain B | Flat or moderately dense tree coverage | SUI-3, SUI-4 |
| Terrain A | Hilly areas with moderate to heavy tree density | SUI-5, SUI-6 |
The performance was tested over these varying terrain conditions, simulating complex and dynamic wireless environments to assess the adaptability of the proposed hierarchical classification model. Since these scenarios reflect real-world wireless conditions, the results indicate the model’s ability to perform well in complex and dynamic environments.
Data acquisition for multimode, multiband, and multi-scheme framework
The dataset for this study of the modulation classification and parameter optimization framework collects performance information across varied operational conditions through MATLAB simulations to improve the accuracy of the classifier. Signal samples are simulated iteratively, utilizing 2-PSK, 4-PSK, 8-PSK, 2-FSK, 4-FSK, 8-FSK, and CPM modulation schemes with different settings to represent a broad performance landscape. Each modulation technique was implemented with 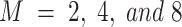 , revealing how complexity affects the accuracy of the classification mechanism. Other improvements to explore inter-symbol interference effects include adjusting spectral efficiency (h) to values of 1/2, 1/4, 1/8, and 1/16 for different bandwidth efficiencies and altering overlap factor (L) to 1, 2, and 3 values. To accurately represent noise situations, the simulations cover an SNR range of -3 dB to 15 dB, increased by 1 dB. The parameter ranges for M, h, and L were selected based on the literature to analyze their impact on SNR and bandwidth. Higher modulation orders improve data rates but are noise-sensitive, while lower CPM indices enhance efficiency with complex detection. Sensitivity analysis ensures adaptability to diverse modulation schemes and channel conditions5,17,29.
, revealing how complexity affects the accuracy of the classification mechanism. Other improvements to explore inter-symbol interference effects include adjusting spectral efficiency (h) to values of 1/2, 1/4, 1/8, and 1/16 for different bandwidth efficiencies and altering overlap factor (L) to 1, 2, and 3 values. To accurately represent noise situations, the simulations cover an SNR range of -3 dB to 15 dB, increased by 1 dB. The parameter ranges for M, h, and L were selected based on the literature to analyze their impact on SNR and bandwidth. Higher modulation orders improve data rates but are noise-sensitive, while lower CPM indices enhance efficiency with complex detection. Sensitivity analysis ensures adaptability to diverse modulation schemes and channel conditions5,17,29.
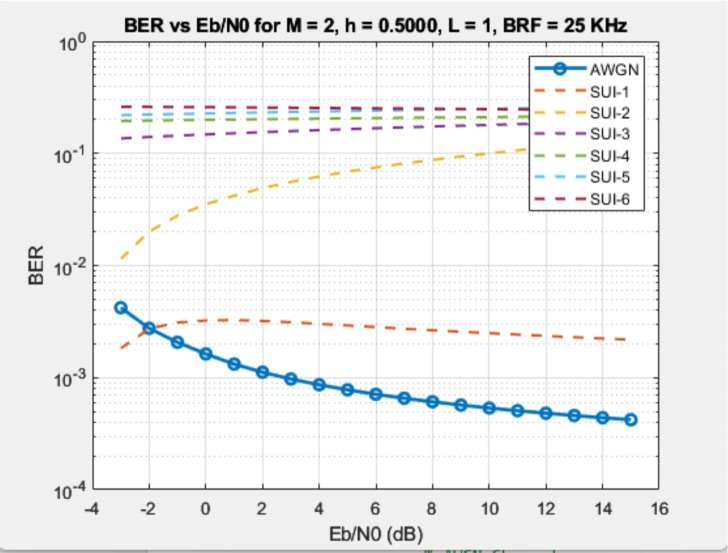
The AWGN channel and six SUI channel models representing different terrain types, including light tree density (SUI-1, SUI-2), moderate tree density (SUI-3, SUI-4), and heavy tree density (SUI-5, SUI-6), were used to simulate performance covering ideal and realistic multipath fading situations. Different bandwidth values (25, 50, 75, and 100 kHz) were used to evaluate the signals, affecting the allocation of bandwidth and the robustness of the interference of each modulation scheme. The BER curves shown in Fig. 3 were determined for each configuration across all SNR levels and SUI channel models, generating BER curves for each CPM modulation configuration mode varying all the respective parameters, including M, h, L, and BRF.
Fig. 3.
BER curves for CPM under different channel parameters.
Similarly, the M-PSK and M-FSK modulation schemes were simulated by iteratively adjusting M and the bandwidth factors (BRFs) over the SNR range and various channel conditions, as shown in Fig. 4. In M-PSK, increasing the modulation order improves throughput in high SNR scenarios; however, it also reduces BER performance, especially in SUI channels where multipath fading negatively impacts phase detection. Meanwhile, M-FSK demonstrated significant resilience in SUI channels due to its dependence on frequency diversity. However, FSK requires larger bandwidth allocations to maintain this orthogonality to perform well under interference-prone conditions.
Fig. 4.
BER curves for M-PSK and M-FSK under different parameters.
Signal parameters, and data rate computation
The signal features for the data set employ parameters such as modulation order, SNR, spectral efficiency, overlap factor, modulation type, and bandwidth. It is important to note that these parameters were identified as critical factors that affect the effectiveness of modulation schemes in different channel environments. Out of these fixed features, performance measures such as BER and the data rate for the whole dataset are calculated. These derived performance measures offer an understanding of how the modulation techniques perform at various SNRs and channel conditions, which will be used for classification purposes in the machine learning model.
In this approach, data rate computation varies by modulation scheme, utilizing specific parameters for accuracy. For CPM signals, narrowband computations are based on RF bandwidths of 25kHz, 50kHz, 75kHz, and 100kHz, although the formula also applies to higher bandwidths. The throughput 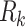 is calculated using the relationship shown in Eq. (1):
is calculated using the relationship shown in Eq. (1):
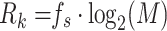 |
1 |
where
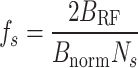 |
2 |
with 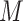 as the modulation order,
as the modulation order, 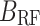 as the RF bandwidth,
as the RF bandwidth, 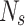 as the upsampling factor, and
as the upsampling factor, and  as the normalized bandwidth, determined by the 3dB points on the CPM signal’s power spectral density (PSD). The value of
as the normalized bandwidth, determined by the 3dB points on the CPM signal’s power spectral density (PSD). The value of 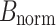 is adjusted according to the parameters
is adjusted according to the parameters 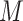 ,
,  , and
, and 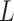 29.
29.
For 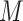 -PSK and
-PSK and 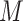 -FSK, the data rate is computed30 using Eq. (3):
-FSK, the data rate is computed30 using Eq. (3):
 |
3 |
where
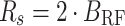 |
4 |
with 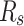 as the symbol rate.
as the symbol rate.
Based on the simulations and calculations above, an overview of the data obtained for the CPM modulation is presented in Table 4, which includes the parameters and BER values for several configurations. The parameters encompass modulation order (M), modulation index (h), length (L), bandwidth (BRF in kHz), normalized bandwidth ( ), sampling frequency (
), sampling frequency (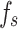 in kHz), bit rate (
in kHz), bit rate (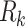 in kbps), as well as Eb/N0 in dB, channel type, and resultant BER. The configurations were evaluated under varying SNRs and channel conditions to evaluate BER-based performance, providing information on the reliability of each modulation scheme. Although the data presented in Table
4 offer a limited representation of the performance of CPM, it is however, interesting to note that every mode in the class went through a more complex simulation process that involved 134 different parametric combinations. The simulations aimed to understand the effects of several key parameters on the performance of the considered system. In particular, each mode was simulated at different
in kbps), as well as Eb/N0 in dB, channel type, and resultant BER. The configurations were evaluated under varying SNRs and channel conditions to evaluate BER-based performance, providing information on the reliability of each modulation scheme. Although the data presented in Table
4 offer a limited representation of the performance of CPM, it is however, interesting to note that every mode in the class went through a more complex simulation process that involved 134 different parametric combinations. The simulations aimed to understand the effects of several key parameters on the performance of the considered system. In particular, each mode was simulated at different 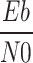 values to assess the SNR conditions with respect to the systems and to estimate the least SNR that produces an adequate proportion of bit errors. For different channel types, simulations were also carried out to see what the effect of channel variation was on BER and which modes are best suited for that channel type.
values to assess the SNR conditions with respect to the systems and to estimate the least SNR that produces an adequate proportion of bit errors. For different channel types, simulations were also carried out to see what the effect of channel variation was on BER and which modes are best suited for that channel type.
Table 4.
Data table of continuous phase modulation (CPM) parameters and corresponding bit error rate (BER) values across varying SNR levels.
| Mode | M | h | L | BRF_KHz | Bnorm | fs_KHz | Rk_Kbps | EbN0_dB | Channel | BER |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.5 | 1 | 25 | 0.9465 | 26.4143 | 26.4143 | 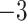 |
0 | 0.0040 |
| 2 | 2 | 0.5 | 1 | 50 | 0.9465 | 52.8286 | 52.8286 | 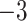 |
0 | 0.3087 |
| 3 | 2 | 0.5 | 1 | 75 | 0.9465 | 79.2430 | 79.2430 |  |
4 | 0.2193 |
| 4 | 2 | 0.5 | 1 | 100 | 0.9465 | 105.6573 | 105.6573 | 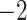 |
0 | 0.2223 |
| 5 | 2 | 0.5 | 2 | 25 | 0.6857 | 36.4610 | 36.4610 | 1 | 6 | 0.2201 |
| 6 | 2 | 0.5 | 2 | 50 | 0.6857 | 72.9220 | 72.9220 | 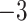 |
0 | 0.2141 |
| 7 | 2 | 0.5 | 2 | 75 | 0.6857 | 109.3830 | 109.3830 | 1 | 6 | 0.2932 |
| 8 | 2 | 0.5 | 2 | 100 | 0.6857 | 145.8440 | 145.8440 | 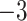 |
0 | 0.2905 |
| 9 | 2 | 0.5 | 3 | 25 | 0.5932 | 42.1450 | 42.1450 | 1 | 6 | 0.2984 |
| 10 | 2 | 0.5 | 3 | 50 | 0.5932 | 84.2900 | 84.2900 | 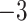 |
0 | 0.2905 |
To study the influence of M, its value was varied to determine the number of bits to transmit for each symbol, which was represented logarithmically as base 2 (M). This analysis highlights the trade-off between achieving higher data throughput and the resulting BER performance. h was adjusted to study its influence on spectral efficiency, where lower modulation indices improve bandwidth usage, while higher indices enhance signal robustness. Furthermore, the effect of the overlap factor L, which governs the length of the phase-shaping pulse, on the CPM waveform and hence on system performance and complexity was also investigated. Finally, varying the radio frequency bandwidth allowed the evaluation of system performance at different data rates, which is critical to determine the required bandwidth to achieve the desired data rate.
In total, 144 CPM modes were simulated, and each mode was subjected to these parametric variations to completely evaluate the performance of the CPM system. Such rigorous analysis helps in better understanding the compromise or trade-off between BER, spectral efficiency, and system robustness and in choosing the best configuration under various scenarios.
Table 5, similarly, presents a statistical overview of the M-PSK and M-FSK modulation schemes, encompassing various combinations of M, bandwidth (BRF in kHz) and SNR (Eb/N0 in dB). The BER and associated data rate (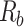 in kbps) for each mode were documented under various channel conditions to evaluate the influence of each parameter on the performance of the system. This table offers a comparative analysis of the BER and the data rates in various modulation techniques, facilitating the selection of an appropriate configuration based on the desired BER performance and the data rate.
in kbps) for each mode were documented under various channel conditions to evaluate the influence of each parameter on the performance of the system. This table offers a comparative analysis of the BER and the data rates in various modulation techniques, facilitating the selection of an appropriate configuration based on the desired BER performance and the data rate.
Table 5.
Data table for M-PSK and M-FSK modulation schemes.
| Mode | M | BRF_KHz | Eb/N0_dB | Channel | BER |
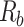 _kbps _kbps |
|---|---|---|---|---|---|---|
| 1 | 2 | 25 | 13 | 6 | 0.4455 | 25 |
| 2 | 4 | 25 | 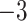 |
0 | 0.2405 | 50 |
| 3 | 8 | 25 | 13 | 6 | 0.4883 | 75 |
| 4 | 2 | 50 | 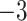 |
0 | 0.1619 | 50 |
| 5 | 4 | 50 | 13 | 6 | 0.5365 | 100 |
| 6 | 8 | 50 | 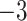 |
0 | 0.3144 | 150 |
| 7 | 2 | 75 | 9 | 2 | 0.5168 | 75 |
| 8 | 4 | 75 | 9 | 2 | 0.5260 | 150 |
| 9 | 8 | 75 | 5 | 0 | 0.1135 | 225 |
Multimode, multiband, and multi-scheme framework for adaptive communication systems
The ability to adapt is an essential element in contemporary communication systems. This capability enables the system to operate satisfactorily under a wide range of channel conditions. To this end, a multimode, multiband, and multi-scheme cognitive communication system is proposed. This implementation uses different modulation methods, works in different frequency bands, and has several transmission methods to increase the performance of the system. Our proposed framework also helps to improve throughput and reduce BER under different SNRs and different environmental conditions by automatically altering parameters such as modulation type, spectral efficiency, and bandwidth.
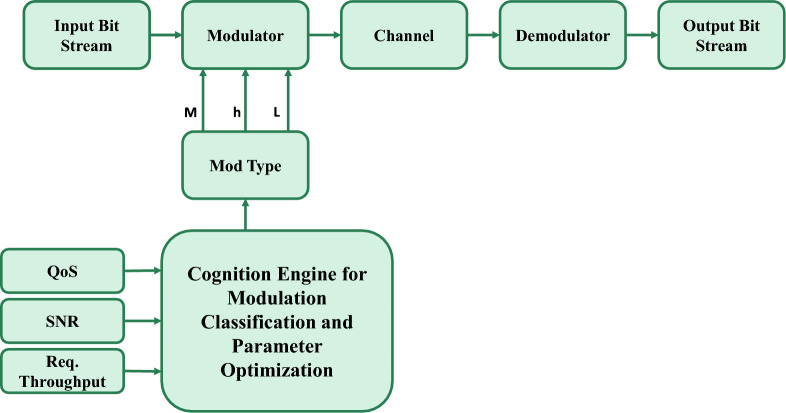
In Fig. 5, the cognition engine block diagram is shown for the modulation categorization and parameter optimization procedure, in which traditionally the modulator transforms an input bit stream into modulated signals suitable for transmission. The communication channel may impart noise and interference to these signals. The demodulator retrieves the transmitted data and produces the output bitstream to the receiver.
Fig. 5.
Proposed cognition engine module for modulation classification and parameter optimization.
The cognition engine block will be utilized to select the effective modulation scheme based on QoS, SNR, and required throughput, which will eventually allow the Mod Type block to dynamically pick modulation parameters based on the selected modulation type, such as M, h, and L for CPM, and only M as the parameter for M-PSK and M-FSK. A cognitive engine categorizes and enhances modulation factors in real-time, ascertaining this selection. The engine persistently assesses system conditions to determine suitable modulation schemes and parameter combinations to enhance performance across varying channel conditions, and selects the modulation type and parameters based on the required throughput given SNR, and the desired QoS.
Proposed hierarchical classifier
In this section, a hierarchical classification framework is presented which is designed to improve the accuracy and efficiency of modulation scheme prediction under varying channel conditions. The hierarchical classifier begins its role by identifying the most suitable modulation type from the three options: M-PSK, MFSK, and CPM. This initial multi-scheme classification phase guarantees that the modulation scheme most suited for the given channel circumstances and performance requirements is selected. Factors such as SNR, BER, and the necessary throughput drive this decision-making process. The classification commences with the entry of raw data, which is analyzed by the hierarchical classifier to determine the modulation type. The initial phase, primary classification (C-1), determines the modulation category, including CPM, FSK, or PSK.
Upon identifying the primary modulation type, subsequent classification is conducted via specialized blocks: C-2 (CPM classification), C-3 (FSK classification), and C-4 (PSK classification). Each block retrieves the parameters pertinent to its modulation type. The critical parameters for CPM are h, L, and M. The value of M is derived in the context of FSK and PSK.
The outputs from these classifiers are subsequently combined in the Mode block, which integrates the recognized modulation type and associated parameters to select a mode for the current user requirement. This hierarchical method shown in Figure 6 presents accurate modulation classification and precise parameter extraction, facilitating optimal system performance. The system adaptively updates the derived parameters, such as M, L, and h, resulting in a specific mode based on the specified modulation type and in response to channel alterations. These improvements are guided by essential performance measures, such as BER and data rate, to improve communication efficiency. Optimizing for the lowest BER and the best achievable data rate, the system provides reliable and efficient operation. This adaptive flexibility is critical for real-time cognitive radio applications, where channel conditions can change quickly and require dynamic modifications to maintain effective communication.
Fig. 6.
Hierarchical machine learning cognitive block for adaptive multimode, multiband, multi-scheme classification.
The algorithm for the classification framework is described in Algorithm 1, which takes an input data table that contains signal samples, as discussed in Section 4, and produces a prediction table with the modulation type, associated parameters and mode. The classification process begins by predicting the modulation type (Mod_Type) to identify whether the signal belongs to PSK, FSK, or CPM.
Algorithm 1.
Hierarchical modulation classification and parameter prediction.
For example, consider a dataset row with parameters such as: 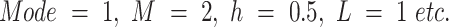 . In this case, if the algorithm predicts the modulation type as PSK, then the modulation order is established as
. In this case, if the algorithm predicts the modulation type as PSK, then the modulation order is established as 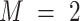 , while h and L are still unknown. Similarly, when CPM was predicted, the parameters M was equal to 2, h was equal to 0.5, and L was equal to 1, and the appropriate mode was determined. In this way, accurate classification and parameter prediction is achieved, which in turn allows reliable operation of the signal processing under different conditions. The estimates of the individual signal sample are stored one after the other, and when all the samples are finished, their results are placed in a table called the prediction table.
, while h and L are still unknown. Similarly, when CPM was predicted, the parameters M was equal to 2, h was equal to 0.5, and L was equal to 1, and the appropriate mode was determined. In this way, accurate classification and parameter prediction is achieved, which in turn allows reliable operation of the signal processing under different conditions. The estimates of the individual signal sample are stored one after the other, and when all the samples are finished, their results are placed in a table called the prediction table.
Evaluation and results of the proposed methodology
This section describes the experimental setup, evaluation parameters, and comparative results of our proposed scheme with state-of-the-art work. In particular, we are interested in the evaluation of the proposed hierarchical model which is developed to solve the classification problem in cognitive engines for communication systems. In addition, the proposed hierarchical classification model is compared with the direct model. In addition to the confusion matrix, predictions on the newly created dataset, were also analyzed based on the hierarchical classifier that was trained first. The parameters used included the cost of computation and the cost of the model in terms of its complexity. This work demonstrates that hierarchical clustering offers improved efficiency and scalability without compromising accuracy, particularly compared to conventional techniques used for similar tasks.
Experimental setup and evaluation parameters
Three modulation techniques, namely M-PSK, M-FSK, and CPM, were simulated using changeable parameters (M, h, L) and bandwidth factors (25, 50, 75, 100 kHz). The signals were tested in conditions of the AWGN and SUI(1-6) channels, establishing a synthetic database with characteristics of SNR, throughput, and BER. This data set was applied in training a hierarchical machine learning classifier to first categorize the modulation type (PSK, FSK, or CPM); the model also estimates the parameters (M, h, L) required for a given throughput at different SNR. This approach integrated signal processing and machine learning to effectively tackle the problem of modulation scheme analysis and classification.
Two methodologies, namely, the hierarchical classification approach and the direct classification approach, were evaluated and tested to incorporate cognitive perception into the physical layer. To test the effectiveness of these approaches, experiments were carried out using MATLAB. Using MATLAB’s signal processing toolbox, Communications System Toolbox, Machine Learning, and Deep Learning Toolbox, BER is stored for each channel (AWGN and SUI 1–6) in all  values, capturing the performance of CPM, M-PSK, and M-FSK in varying SNR levels initially. This computation resulted in 168 modes across the three modulation categories, which are subsequently utilized for mode selection. Approximately 22,344 samples are used in all modes, at various levels of
values, capturing the performance of CPM, M-PSK, and M-FSK in varying SNR levels initially. This computation resulted in 168 modes across the three modulation categories, which are subsequently utilized for mode selection. Approximately 22,344 samples are used in all modes, at various levels of 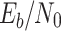 to train and evaluate the cognitive engine for mode selection that satisfies the required QoS. Table 6 summarizes the key parameters related to data analysis.
to train and evaluate the cognitive engine for mode selection that satisfies the required QoS. Table 6 summarizes the key parameters related to data analysis.
Table 6.
Summary of key parameters for modulation scheme classification and performance evaluation.
| Parameter | Value | Description |
|---|---|---|
| Total schemes | 3 | M-PSK, M-FSK, CPM |
| Channels per scheme | 7 | AWGN and SUI channels |
| Data range |
 to 15 to 15 |
15 dB with a step size of 1 dB |
| Data points per channel | 19 | Data points across the SNR range |
| Total modes | 168 | 144 for CPM and 24 for PSK and FSK |
| Total population size | 22344 | Total data points for analysis |
| Confidence level | 95% | Statistical confidence level |
| Margin of error | 5% | Acceptable margin of error |
| Calculated sample size | 378 | Data points needed for analysis for 95% confidence |
The proposed hierarchical classifier, Technique 1, solves the classification problem by dividing it into subtasks, such as an initial phase of the primary modulation type classification and other predictions of the specific parameter. This decomposition allows for the use of simpler models like decision trees and ensemble subspace KNNs, which help increase accuracy in each step while keeping the computation time and overall cost low.
The accuracy of the classifier was the determining factor of the overall performance of the classification system in relation to the correct retrieval of information, and detailed information of true positive, false positive, true negative, and false negative was analyzed for each class through the confusion matrix. In addition, the performance of the trained model on the unseen data is a measure of the generalizability of the model, and this was tested by evaluating the classifier model on the new dataset, which confirmed the robustness and reliability of the model to the task of classifying modulation schemes along with their parameters. In Fig. 7, a portion of the original dataset is displayed, showing correctly labeled data, which serves as the basis for the proposed hierarchical classifier.
Fig. 7.
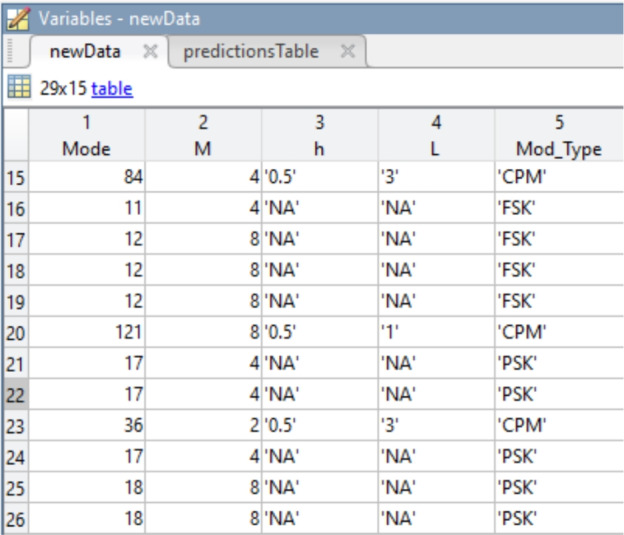
Original labeled data for predictive analysis.
Figure 8 presents the predictions generated by the hierarchical model. The displayed snippet of the predictions table intentionally includes instances of both correct classifications and misclassifications highlighting the model’s ability to accurately classify the majority of samples, along with their parameters showcasing its overall effectiveness and strong performance.
Fig. 8.
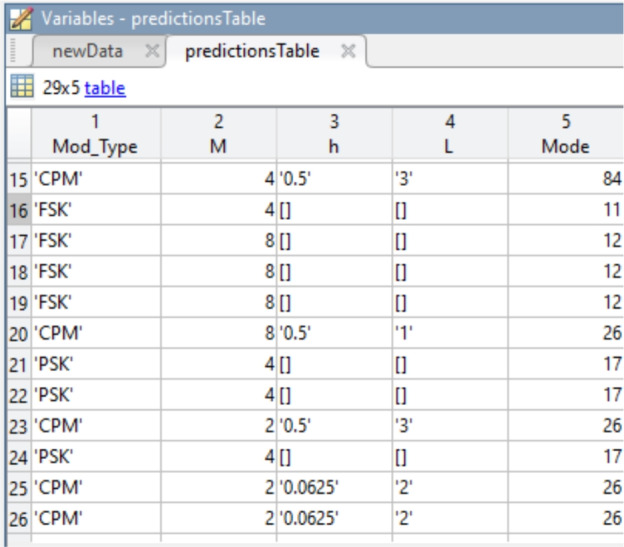
Original labeled data for predictive analysis.
Initially, the modulation type is identified as a first step in the hierarchical classifier, which can be seen in Fig. 9a. This confusion matrix demonstrated the classifier’s ability to distinguish between the primary modulation types: M-PSK, M-FSK, and CPM, with high classification accuracy. Subsequently, parameter-specific classifiers were employed to refine the classification by predicting detailed modulation properties. For the MPSK and MFSK signals, the modulation order 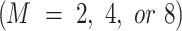 is determined using a specialized classifier, as shown in Fig. 9b.
is determined using a specialized classifier, as shown in Fig. 9b.
Fig. 9.
Confusion matrix using technique 1: hierarchical classification for (a) modulation type classification, (b) modulation index classification.
For CPM signals, additional parameters such as the modulation index 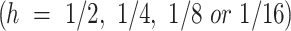 and the overlap factor
and the overlap factor 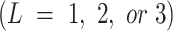 are predicted using dedicated classifiers. Figure 10a, b provide confusion matrices for the classification of L and h, respectively. These matrices reveal the precision of the model in distinguishing between closely related parameter values, demonstrating the effectiveness of the hierarchical approach in CPM-specific classification tasks. Various variants of SVMs, neural networks, and ensembles were used to train the classifier. However, decision trees and ensemble subspace KNN models produced promising results while being less computationally expensive, making them more efficient and practical for implementation.
are predicted using dedicated classifiers. Figure 10a, b provide confusion matrices for the classification of L and h, respectively. These matrices reveal the precision of the model in distinguishing between closely related parameter values, demonstrating the effectiveness of the hierarchical approach in CPM-specific classification tasks. Various variants of SVMs, neural networks, and ensembles were used to train the classifier. However, decision trees and ensemble subspace KNN models produced promising results while being less computationally expensive, making them more efficient and practical for implementation.
Fig. 10.
Confusion matrix technique 1: hierarchical classification for (a) modulation order classification and (b) overlap factor classification.
The direct classification approach, i.e., technique 2 takes the whole dataset as input into a Neural Network classifier, which selects the appropriate modulation mode without any hierarchical breakdown. This method analyzes the dataset in a single stage, where a single model is responsible for evaluating all possible modes and classifying them. This approach achieves a mode classification accuracy of 98.35%. However, this approach can be computationally expensive as it demands substantial resources for a single model to process the entire dataset. In addition, using other variants of the models, such as decision trees and ensemble methods, in a direct approach, gave much lower accuracies of 59.3% and 12.9%, respectively, further highlighting the effectiveness of the hierarchical framework. However, Technique 2 was effective using neural networks, as illustrated by the ROC curve in Fig. 11.
Fig. 11.
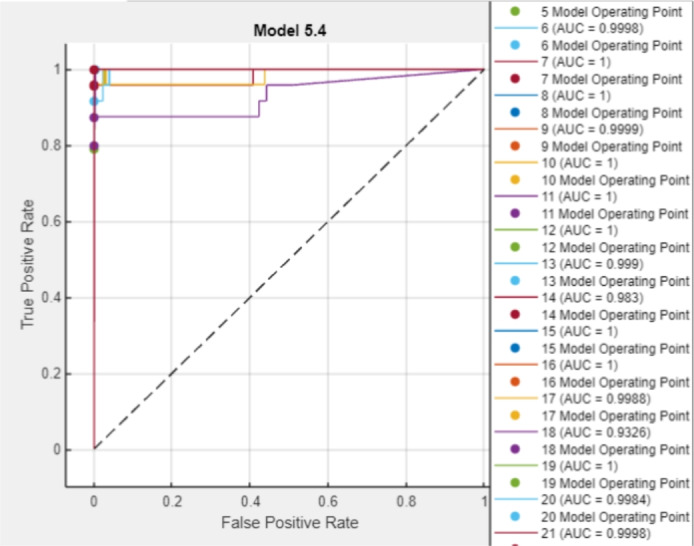
Technique 2: ROC curve analysis using the bi-layered neural network direct approach.
To provide a deeper analysis of Technique 2, the scatter plot of the unpredicted modes is shown in Fig. 12. Due to the confusion matrix containing approximately 168 values, it is challenging to visualize the results effectively in a single representation. To evaluate performance and design differences, both methodologies were compared based on their classification approaches, accuracy, and overall effectiveness. Technique 1 employs a hierarchical classification strategy, where the modulation types and their parameters (M, h, L, Mode) are sequentially classified using specialized classifiers. This stepwise breakdown allows for parameter-specific optimization, ensuring high accuracy for individual tasks such as FSK and CPM classifications.
Fig. 12.
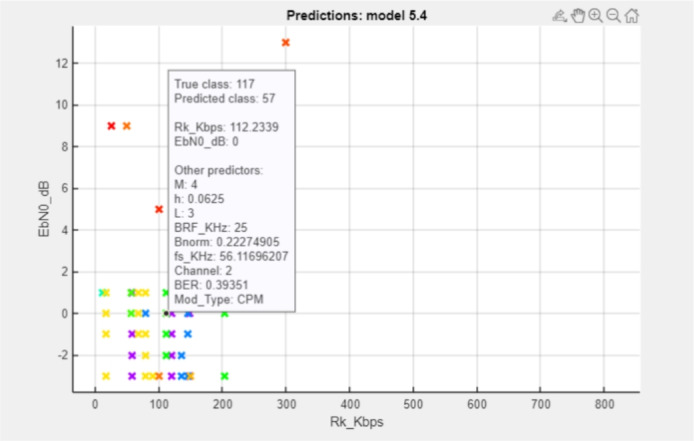
Technique 2: scatter plot illustrating misclassified predictions in direct approach.
In contrast, Technique 2 adopts a direct classification approach, in which the entire dataset is fed into a neural network classifier. This approach eliminates the need for hierarchical breakdowns and focuses on delivering a single-step classification for the modulation mode. While Technique 2 offers simplicity and faster implementation, Technique 1’s parameter-specific classifiers make it more flexible for detailed analysis. Hierarchical classifiers divide the classification problem into smaller and easier-to-understand steps. This helps researchers identify which modulation type or parameter is causing errors, allowing them to focus on improving those specific parts. The hierarchical classifier is flexible because new modulation types or parameters can be added without retraining the whole model, unlike direct classifiers. This makes them useful for dynamic systems like cognitive radios, where new modulation schemes may appear over time. In general, while direct classifiers may have higher accuracy, hierarchical classifiers are better in terms of being understandable, flexible, and adaptable, making them a more practical choice for many systems.
However, certain factors can lead to performance degradation. Class imbalance affects modes with lower occurrences (e.g., 44, 92, 93), resulting in misclassification due to insufficient training data. Similarly, overlapping feature distributions between certain modes (e.g., 133–138) introduce ambiguity, increasing classification errors. Edge cases, such as modes 35, 47, and 92, often yield lower confidence scores because they lie near decision boundaries. Moreover, the accuracy may drop at specific SNR, BER, or throughput values, where sensitivity of the features influences classification performance. These challenges highlight areas for further optimization, such as advanced data balancing techniques or improved feature separation strategies. The comparison of these methodologies, including classification accuracies and the types of classifier used, is summarized in Table 7.
Table 7.
Comparison of Technique 1 and Technique 2 for modulation scheme classification and parameter optimization.
| Aspect | Technique 1 | Technique 2 |
|---|---|---|
| Methodology | Hierarchical classification with primary and parameter-specific classifiers | Direct classification of full dataset without hierarchy |
| Primary classification accuracy | 98.18% (decision tree) | N/A |
| FSK, PSK M classification | 99.81% (decision tree) | N/A |
| CPM M classification | 99.81% (ensemble subspace KNN) | N/A |
| CPM L classification | 99.84% (ensemble subspace KNN) | N/A |
| CPM h classification | 99.91% (ensemble subspace KNN) | N/A |
| CPM mode classification | 99.3% (narrow neural network) | N/A |
| PSK/FSK mode classification | 99.8% (decision tree) | N/A |
| Overall mode classification accuracy | 99.41% (narrow neural network and decision tree) | 98.35% (bilayered neural network) for direct classification |
| Classifier types | Decision tree, narrow neural network and ensemble subspace KNN | Neural network |
| Approach | Hierarchical classification by modulation type and parameters (M, h, L, mode) | Single-step mode classification |
Comparative analysis and discussion
This section presents a comparative analysis of the proposed technique against existing research methodologies shown in Table 8 concentrated on different types of modulation. Our study analyzes M-PSK, M-FSK, and CPM through a hierarchical categorization framework that incorporates Decision Trees, Subspace KNN and Neural Networks. Our analysis encompasses a wider spectrum of parameters, including modulation orders  , spectral efficiency
, spectral efficiency 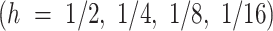 and overlap factors
and overlap factors  in various channel circumstances, such as AWGN and SUI (1 to 6). The proposed multimodal methodology improves the precision of classification compared to previous research while adeptly addressing the intricacies of modulation classification in practical contexts. Identifies modulation types and optimizes the parameters for picking each mode, illustrating the efficacy of our methodology.
in various channel circumstances, such as AWGN and SUI (1 to 6). The proposed multimodal methodology improves the precision of classification compared to previous research while adeptly addressing the intricacies of modulation classification in practical contexts. Identifies modulation types and optimizes the parameters for picking each mode, illustrating the efficacy of our methodology.
Table 8.
Comparison of classification performances.
| Ref. | Dataset (modulation types) | Channels considered | Method (classifier/features) | Acc. (%) | SNR (dB) |
|---|---|---|---|---|---|
| 19 | OOK, 4ASK, 8ASK, M-PSK(2,4,32), MAPSK(16-128), MQAM(16,64), SSBSC, DSBSC, FM, GMSK, OQPSK | OTA signals | Hierarchical SVM, HOSs | 95 | 5 |
| 31 | BPSK, PAM, QAM, 8PSK | AWGN | Hierarchical classification, cumulant-based | 70 | 5 |
| 32 | 2ASK, 4ASK, 8ASK, BPSK, QPSK, 8PSK | AWGN | Hierarchical, decision tree, higher-order cumulants | 96 | 10 |
| 33 | 4ASK, 8ASK, 2PSK, 4PSK, 8PSK, Star8QAM, V29, 32QAM, 64QAM | AWGN | Hierarchical SVM, higher order moments and cumulants | 96 | 3 |
| 15 | FSK, 2ASK, 4ASK, 8ASK, QPSK, 8PSK, 16QAM, 64QAM | - | Naive SVM, Hierarchical-local density | 97.29 | 16 |
| 34 | M-PSK(2,4,8), M-QAM(16,64,256) | AWGN, slow flat fading | Hierarchical polynomial classifier, cumulants | 86.52 | 5 |
| This work | M-PSK, M-FSK, CPM (M,h,L) | AWGN, SUI-1 to SUI-6 | Hierarchical decision trees, neural network | 98.57 | [-3,15] |
Significant values are in bold.
Table 8 shows that our proposed methodology is distinguished by its integration of a wide array of channels that encompass various terrains, from flat regions with sparse vegetation (SUI-1 to SUI-4) to hilly areas with dense tree cover (SUI-5, SUI-6). These results highlight its adaptability to real-world wireless environments with dynamic channel conditions. Our analysis utilized a feature vector with 15 finely chosen features, contrasting the methodology of19, which employs an extensive vector of 41 features with a fixed SNR of 5 dB. Having a reduced feature set, our model attains a remarkable accuracy of about 98.57% of efficiently classifying modes at various SNR levels ranging from -3 to 15 dB. This shows the resilience and adaptability of our model in simulating real-world situations through a combination of SUI channels and AWGN. The proposed framework goes beyond classifying the modulation type; it also identifies all the specific parameters associated with each modulation type. It effectively selects the optimal mode based on user requirements i.e. (QoS, Required Throughput, and SNR). By incorporating multiple modulation techniques and realistic channel conditions, the approach improves adaptability and suitability for real-time applications. The proposed hierarchical classifier significantly improves adaptive modulation, unlike conventional methods that require manual feature extraction, this model automates feature selection, reducing preprocessing time and computational complexity. By employing a stepwise classification approach, it ensures faster and more efficient decision-making. Additionally, its robustness is demonstrated by its ability to generalize across various modulation schemes and channel conditions. The classifier’s scalability allows seamless integration of new waveforms without necessitating complete model retraining, making it a flexible solution for evolving CRNs. However, misclassifications in high-order modulations (e.g., 8-PSK, 8-FSK) at low SNR’s can still lead to error propagation in parameter predictions, exacerbated by rapid SNR variations in SUI channels.
However, it was observed that the range of identified modulation types is frequently limited, and the channel effects are typically unrealistic. Unlike previous works compared in Table 9 that focus on isolated aspects of modulation adaptation, our approach combines these elements into a unified framework, offering improved flexibility and robustness in dynamic communication environments.
Table 9.
Comparison of various studies on adaptive modulation and hierarchical classification.
| Study | Adaptive modulation | Hierarchical classification | ML-based approach | Real-time adaptation | Modulation diversity |
|---|---|---|---|---|---|
| Adaptive modulation under Doppler effects14 | ✓ | ✗ | ✗ | ✗ | ✗ |
| HLD classification (Jajo et al.)15 | ✗ | ✓ | ✗ | ✗ | ✗ |
| SUI channel model (A. Hashib et al.)16 | ✓ | ✗ | ✗ | ✗ | ✗ |
| Cross-layer SDR Design (Shahzad et al.)17 | ✓ | ✗ | ✗ | ✓ | ✗ |
| AMR classifier (Ali et al.)18 | ✗ | ✓ | ✓ | ✗ | ✗ |
| Hierarchical SVM classifier19 | ✗ | ✓ | ✓ | ✗ | ✗ |
| Cognitive radio in satellite networks13 | ✗ | ✗ | ✓ | ✓ | ✗ |
| Our approach | ✓ | ✓ | ✓ | ✓ | ✓ |
Conclusion and future works
The proposed approach uses a hierarchical machine learning cognition engine to select the best-fit user-controlled mode of transmission based on SNR, QoS and throuhgput in varying channel conditions. It classifies and adjusts PSK, FSK, and CPM modulation schemes with varying parameters (M, h, L) over diverse frequency bands using MATLAB simulations. Our hierarchical ML approach improves flexibility and accuracy by automatically selecting modulation parameters based on SNR, BER, and throughput, removing the need for fixed rules or manual adjustments. Unlike traditional methods, it adapts to different frequency bands and complex channel conditions, achieving a high classification accuracy of 98.57%. It also supports various real-world environments, including flat and hilly terrains with different tree densities (SUI-1 to SUI-6). The classifier’s modular design makes it easy to add new modulation types without retraining old data, reducing computational effort. While the model effectively predicts modulation order and parameters, challenges remain in handling high-order modulations at low SNR and mitigating cascading errors in dynamic channel conditions. Future work can focus on improving hardware efficiency and error correction to enhance its use in cognitive radio systems and dynamic spectrum allocation. To improve this hierarchical framework, further research may include modulation methods, complex channel models like Rayleigh or Rician fading, and advanced neural network designs like CNNs or RNNs for channels that are NLOS (non-line of sight) or that change over time. In complex scenarios, reinforcement learning for adaptive parameter selection may enhance modulation accuracy by augmenting responsiveness to channel conditions.
Acknowledgements
The article processing charges of this manuscript is paid by Ajman University, United Arab Emirates.
Author contributions
F.I. collected the data, implemented the MATLAB simulations, and generated the results. S.G.K. conceptualized the research, supervised the study, and provided feedback on the methodology. A.M.K. provided guidance on data collection protocols, verification of data and machine learning methods. M.U.A. contributed to the development of the hierarchical machine learning classifier and assisted with result validation. A.S. and U.H.S contributed to the interpretation of the results. All authors contributed to the writing of the manuscript, reviewed the final draft, and approved the submission.
Data availability
The datasets used and/or analyzed during the current study is available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Ulversoy, T. Software defined radio: Challenges and opportunities. IEEE Commun. Surv. Tutor.12, 531–550 (2010). [Google Scholar]
- 2.Lee, D. et al. Neural episodic control-based adaptive modulation and coding scheme for inter-satellite communication link. IEEE Access9, 159175–159186 (2021). [Google Scholar]
- 3.Liu, X., Wang, Y., Bai, J., Li, H. & Wang, X. An imbalanced signal modulation classification and evaluation method based on synthetic minority over-sampling technique. In IGARSS 2023-2023 IEEE International Geoscience and Remote Sensing Symposium. 6224–6227 (IEEE, 2023).
- 4.Kulkarni, S. & Markande, S. Comparative study of routing protocols in cognitive radio networks. In 2015 International Conference on Pervasive Computing (ICPC). 1–5 (IEEE, 2015).
- 5.Shahzad, K., Farooq, M. U., Zeeshan, M. & Khan, S. A. Adaptive multi-input medium access control (AMI-MAC) design using physical layer cognition for tactical SDR networks. IEEE Access9, 58364–58377 (2021). [Google Scholar]
- 6.Chandhok, S., Joshi, H., Darak, S. J. & Subramanyam, A. V. LSTM guided modulation classification and experimental validation for sub-Nyquist rate wideband spectrum sensing. In 2019 11th International Conference on Communication Systems & Networks (COMSNETS). 458–460 (IEEE, 2019).
- 7.Park, J. H., Yun, D. W., Choi, J. P. & Lee, W. C. A novel case-based reasoning method for cognitive frequency allocation. In 2019 International Conference on Artificial Intelligence in Information and Communication (ICAIIC). 164–168 (IEEE, 2019).
- 8.Singh, K. & Nirmal, A. Overview of modulation schemes selection in satellite based communication. ICTACT J. Commun. Technol.11, 2203 (2020). [Google Scholar]
- 9.Park, H. C., Lee, K. & Feher, K. Continuous phase modulation of f-qpsk-b signals. In IEEE Transactions on Vehicular Technology. Vol. 56 (2007).
- 10.Munawar, T., Saleem, S., Hassan, S. A. & Zaidi, S. M. H. Estimation of modulation index for partial response cpm signal. IEEE Access6, 16052–16061 (2018). [Google Scholar]
- 11.Tonchev, K. et al. 25th International Symposium on Wireless Personal Multimedia Communications (WPMC). 75–79 (IEEE, 2022).
- 12.Peng, S., Sun, S. & Yao, Y.-D. A survey of modulation classification using deep learning: Signal representation and data preprocessing. In IEEE Transactions on Neural Networks and Learning Systems (2021). [DOI] [PubMed]
- 13.Mohammed, D. A. & Sadkhan, S. B. Cooperative cognitive radio sensing-optimization: Status, challenges and future trends. In 2021 1st Babylon International Conference on Information Technology and Science (BICITS). 164–169 (IEEE, 2021).
- 14.Rochmatika, R. A., Suryani, T. et al. Performance of adaptive modulation over frequency selective fading channel in vanet environment. In 2018 10th International Conference on Information Technology and Electrical Engineering (ICITEE). 400–405 (IEEE, 2018).
- 15.Jajoo, G., Kumar, Y., Kumar, A. & Yadav, S. K. Blind signal modulation recognition through density spread of constellation signature. Wirel. Pers. Commun.114, 3137–3156 (2020). [Google Scholar]
- 16.HashibSiddique, A., Arifuzzman, A. & Tarique, M. Performance study of IEEE 802.16 D under Stanford University Interim (SUI) channel. Int. J. Comput. Netw. Commun.5, 137 (2013).
- 17.Shahzad, K., Farooq, M. U., Zeeshan, M. & Khan, S. A. Adaptive multi-input medium access control (AMI-MAC) design using physical layer cognition for tactical SDR networks. IEEE Access9, 58364–58377 (2021). [Google Scholar]
- 18.Ali, A. K. & Erçelebi, E. Automatic modulation classification using different neural network and PCA combinations. Expert Syst. Appl.178, 114931 (2021). [Google Scholar]
- 19.Yalcinkaya, B., Coruk, R. B., Kara, A. & Tora, H. Hierarchical classification of analog and digital modulation schemes using higher-order statistics and support vector machines. Wirel. Pers. Commun.136, 827–847 (2024). [Google Scholar]
- 20.Hou, S. et al. Multi-domain-fusion deep learning for automatic modulation recognition in spatial cognitive radio. Sci. Rep.13, 10736 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xi, H. et al. Cross-attention mechanism-based spectrum sensing in generalized Gaussian noise. Sci. Rep.14, 23261 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Adardour, H., Meliani, M. & Hachemi, M. Estimation of the spectrum sensing for the cognitive radios: Test analysing using Kalman filter. Wirel. Pers. Commun.84, 1535–1549 (2015). [Google Scholar]
- 23.Muzaffar, M. & Sharqi, R. A review of spectrum sensing in modern cognitive radio networks. Telecommun. Syst.85, 347–363 (2024). [Google Scholar]
- 24.Adardour, H., Meliani, M. & Hachemi, M. Improved local spectrum sensing in cluttered environment using a simple recursive estimator. Comput. Electr. Eng.61, 208–222 (2017). [Google Scholar]
- 25.Solanki, S., Brahma, B. & Singh, Y. Automatic modulation classification for CR using deep learning. SN Comput. Sci.5, 1061 (2024). [Google Scholar]
- 26.Adardour, H. & Kameche, S. Enhancing the performance of spectrum mobility in cognitive radio local area networks using kf-abf-sre estimators. Wirel. Pers. Commun.104, 1321–1341 (2019). [Google Scholar]
- 27.Rahim, V. & Prema, S. A highly controllable cooperative automatic modulation classification. Wirel. Pers. Commun.131, 2081–2092 (2023). [Google Scholar]
- 28.Adardour, H. E. & Kameche, S. Predicting the primary signal sensing for cognitive radio users using an alpha-beta filter. In 2017 5th International Conference on Electrical Engineering - Boumerdes (ICEE-B) (IEEE, 2017).
- 29.Zeeshan, M. & Khan, S. A. A novel fuzzy inference-based technique for dynamic link adaptation in SDR wideband waveform. IEEE Trans. Commun.64, 2602–2609 (2016). [Google Scholar]
- 30.Proakis, J. G. & Salehi, M. Digital Communications (McGraw-Hill, 2008).
- 31.Swami, A. & Sadler, B. M. Hierarchical digital modulation classification using cumulants. IEEE Trans. Commun.48, 416–429 (2000). [Google Scholar]
- 32.Ali, A. & Yangyu, F. Higher-order statistics based modulation classification using hierarchical approach. In 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC). 370–374 (IEEE, 2016).
- 33.Geisinger, N. P. Classification of Digital Modulation Schemes Using Linear and Nonlinear Classifiers. Ph.D. Thesis, Monterey, California. Naval Postgraduate School (2010).
- 34.Abdelmutalab, A., Assaleh, K. & El-Tarhuni, M. Automatic modulation classification based on high order cumulants and hierarchical polynomial classifiers. Phys. Commun.21, 10–18 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study is available from the corresponding author on reasonable request.