Life-long sustained mortality advantage of siblings of centenarians

Abstract

Although survival to old age is known to have strong environmental and behavioral components, mortality differences between social groups tend to diminish or even disappear at older ages. Hypothesizing that surviving to extreme old age entails a substantial familial predisposition for longevity, we analyzed the pedigrees of 444 centenarian families in the United States. These pedigrees included 2,092 siblings of centenarians, whose survival was compared with 1900 birth cohort survival data from the U.S. Social Security Administration. Siblings of centenarians experienced a mortality advantage throughout their lives relative to the U.S. 1900 cohort. Female siblings had death rates at all ages about one-half the national level; male siblings had a similar advantage at most ages, although diminished somewhat during adolescence and young adulthood. Relative survival probabilities for these siblings increase markedly at older ages, reflecting the cumulative effect of their mortality advantage throughout life. Compared with the U.S. 1900 cohort, male siblings of centenarians were at least 17 times as likely to attain age 100 themselves, while female siblings were at least 8 times as likely.

Many centenarians live the majority of their exceptionally long lives in good health, demonstrating a rapid decline only near the end of life (1). Deciphering why centenarians markedly delay or in some cases even escape age-associated diseases could help in better understanding the pathogenesis of diseases such as stroke, heart disease, cancer, and Alzheimer's dementia, and the relative contributions of environment, behavior, and genetics in determining rates of aging and susceptibility or resistance to diseases that cause premature mortality (2).

Whereas survival to old age is known to have a strong environmental and behavioral component, mortality differences between social groups tend to diminish or even disappear at older ages (3–5). One explanation for this phenomenon is that genetic factors unrelated to social groupings play a predominant role in survival chances at older ages. If genetic factors are indeed an important component of longevity, there should be greater similarity of individual longevity within families or lineages than within the population as a whole. We have documented the familial component of longevity in a variety of ways, as part of a larger study of centenarians in the United States.

In a previous study, four families, impressive for the number of individuals achieving extreme old age, were identified (6). The question was explored as to whether such intrafamilial clustering could be attributed to chance alone, or if shared characteristics might be responsible for a collective ability to achieve extreme old age. A mathematical analysis was performed to determine the probability of families such as these occurring by random variation alone. Such probabilities were found to be extremely small (less than 1 per all of the families that exist in the world today), assuming that the very long-lived individuals of these families were exposed to the same environment as those who did not make it to extreme old age. This assumption could be wrong if, for example, longer-lived family members were also the more successful ones in socioeconomic terms, or if they lived in areas better protected from lethal epidemics. Nevertheless, this clustering of exceptional survival within families is suggestive of a familial component affecting mortality variation, especially at older ages.

Another piece of evidence about the familial component of extreme longevity comes from analyses of New England Centenarian Study data that compared siblings (n = 456) of centenarians with siblings (n = 240) of a control group. Controls were randomly chosen individuals from a similar birth cohort (born in 1896) who died of nontraumatic causes at the age of 73 (7). Compared with siblings of controls, the relative risk of survival for siblings of centenarians increased steadily with age, so that they had four times the probability of surviving to age 91. The relative probability of survival to a given age continued to rise beyond age 91, but these larger differences were not statistically significant because of the small number of siblings at these extreme ages. A study of Mormon pedigrees also observed that relatives of long-lived individuals had a higher probability of surviving to very old age than the relatives of those with average life spans (8).

These previous studies demonstrate a strong familial component to extreme longevity, but they do not further differentiate how much of that component is caused by environmental versus genetic factors that family members may have in common. Nor did these studies examine in detail the familial effect on mortality rates and survivorship across the life span that culminate in the achievement of exceptional longevity. Survival to exceptional old age may be associated with different mortality patterns across the life span (e.g., decreased early and/or late mortality, ref. 9). With the continued enrollment of subjects, the New England Centenarian Study reports here the analyses of more than four times the previously studied number of centenarians and their siblings. The larger sample size allows for an examination of age-specific mortality rates and survivorship in centenarian siblings up to age 100 and a comparison with a corresponding American birth cohort.

Methods

Since 1998, the New England Centenarian Study has conducted a nationwide recruitment of centenarian sibships. Pedigree data from these families have been compiled and analyzed in a variety of ways. The study received Institutional Review Board approval from Boston's Beth Israel Deaconess Medical Center's Committee on Clinical Investigations.

The pedigrees of 444 centenarian families revealed 2,092 siblings. If there were multiple centenarians in a family, the oldest living centenarian was considered the proband. Of the 444 centenarian probands, 289 (65%) were alive at the time of this analysis and 157 (35%) were deceased. Whether or not a proband was alive, all data about siblings were reported by the proband's next-of-kin, usually their child. The probands had a median of 5 reported siblings with a range of 1–15. In total, there were 1,017 male siblings (49%) and 1,075 female siblings (51%); at the time of this analysis, 1,784 siblings (85%) were already dead, leaving only 308 censored observations (15%).

Ninety-five percent of the centenarian probands were Caucasian, and their average year of birth was late 1896. Siblings were slightly younger, born on average in late 1898. For both centenarians and siblings, we recorded age at death or, for those still alive, age when last observed (i.e., age of censoring). Ages for all siblings still alive were determined within 6 months of the data analysis. A total of 96% of centenarian and sibling birth dates (for siblings aged 90 and older) were confirmed by birth certificates, and all others were corroborated by at least two forms of evidence, such as a marriage certificate and an old passport (10).

Because we focus on sibling mortality and survivorship, the centenarian probands are not included in the analysis described here. Death rates for siblings were computed from tabulations by age of sibling deaths and censored observations. Death rates are simply the ratio of deaths over the exposure-to-risk in a given age group. Exposure-to-risk for a single-year age group, E_x, was computed as the number of sibling survivors at the beginning of an age interval, N_x, minus half of the deaths, D_x, and censorings, W_x, over the same interval:

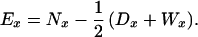Both death counts and exposure estimates were aggregated into n-year age groups (usually n = 5) before dividing to obtain death rates:

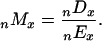Standard errors for sibling death rates were computed based on an assumption of Poisson variability (11):

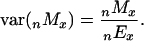Survival curves, S_x, were computed by combining observed survival probabilities for single-year age intervals: S_x = p₀ p₁ ⋅⋅⋅ p_x−1. Age-specific survival probabilities equaled the risk-set, R_x, minus the deaths over an age interval, divided by the risk-set:

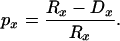The risk-set equaled the number of sibling survivors at the beginning of an age interval, minus half of the censorings over that interval:

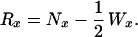Standard errors for sibling survival probabilities were computed based on an assumption of binomial variability (conditional on the observed collection of R_x values) by using Greenwood's formula (12):

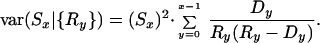Sibling death rates and survival probabilities were compared with the corresponding U.S. national statistics using the Social Security Administration's life table for the cohort born in 1900 (13). Data for the 1900 cohort were used to determine whether the siblings of centenarians had lower mortality and higher survival probabilities compared with the population as a whole. It is possible that there was some underreporting of sibling deaths, especially among siblings who died early in life. To minimize the effect of such errors, survival probabilities reported here are conditional on survival to age 20. In most cases, more than one family member was contacted to obtain family pedigree data.

Confidence intervals for relative death rates and survival probabilities are the estimated value plus or minus two times the standard error. For convenience (and with little loss of accuracy), data for the 1900 cohort were treated as fixed numbers (i.e., with zero variance) when computing the standard errors used for these intervals.

Results

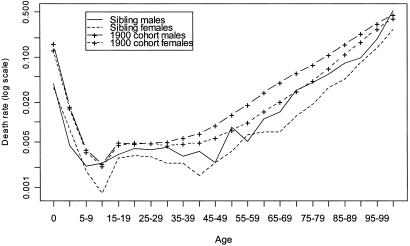
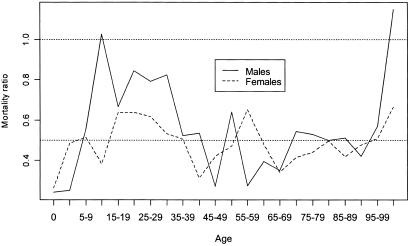
The mean age at death of male siblings of centenarians is 76.7 years, and for female siblings it is 70.4 years. In contrast, life expectancy for the U.S. 1900 cohort (thus, mean age at death corrected for migration) has been estimated at around 51.5 for males and 58.3 for females (U.S. Social Security Administration data, available at http://www.demog.berkeley.edu/wilmoth/mortality or http://www.lifetable.com). Age-specific death rates according to sex for siblings of centenarians and for the total U.S. population born in 1900 are depicted in Fig. 1. Death rates of the siblings of centenarians relative to the 1900 birth cohort are illustrated in Fig. 2. These relative death rates are recorded also in Table 1, which gives confidence intervals for the estimates.

Figure 1.

Age-specific death rates by sex. Siblings of centenarians and U.S. cohort born in 1900

Figure 2.

Relative death rates by sex. Siblings of centenarians versus U.S. 1900 cohort

Table 1.

Relative death rates with 95% confidence intervals (CI) of siblings of centenarians versus U.S. 1900 cohort

Age group	Male			Female
	Relative death rate	Lower 95% CI	Upper 95% CI	Relative death rate	Lower 95% CI	Upper 95% CI
0	0.24	0.17	0.32	0.26	0.17	0.35
1–4	0.25	0.13	0.37	0.48	0.31	0.65
5–9	0.56	0.21	0.90	0.51	0.17	0.86
10–14	1.03	0.42	1.63	0.38	0.00	0.76
15–19	0.67	0.33	1.00	0.64	0.30	0.98
20–24	0.84	0.46	1.23	0.64	0.31	0.97
25–29	0.79	0.42	1.17	0.62	0.29	0.95
30–34	0.83	0.45	1.20	0.53	0.21	0.85
35–39	0.52	0.24	0.80	0.50	0.20	0.81
40–44	0.53	0.27	0.80	0.31	0.08	0.55
45–49	0.27	0.11	0.43	0.42	0.17	0.67
50–54	0.64	0.43	0.85	0.47	0.24	0.71
55–59	0.27	0.16	0.39	0.65	0.40	0.90
60–64	0.40	0.28	0.51	0.48	0.30	0.65
65–69	0.35	0.26	0.44	0.34	0.21	0.47
70–74	0.54	0.45	0.64	0.41	0.29	0.53
75–79	0.53	0.44	0.62	0.44	0.33	0.55
80–84	0.50	0.42	0.58	0.50	0.40	0.59
85–89	0.51	0.44	0.58	0.42	0.34	0.50
90–94	0.42	0.35	0.49	0.48	0.39	0.56
95–99	0.57	0.47	0.67	0.51	0.40	0.61
100+	1.15	0.86	1.44	0.66	0.43	0.90

As seen in Fig. 2 and Table 1, female siblings of centenarians experienced lower mortality throughout life, at about one-half the national level. Male siblings also experienced a similar mortality advantage through most of life relative to the general population, but this advantage was diminished substantially during adolescence and young adulthood. Presumably, male siblings had a lesser advantage with respect to the violent causes of mortality that are characteristic of these ages (e.g., accidents and homicide; ref. 14). Above age 100, the estimated male mortality ratio exceeds 1, but this anomaly may be the result of random variation. Even in our expanded study population, relatively few male siblings are themselves centenarians, as reflected by the wide confidence interval for the mortality ratio among those beyond the age of 100.

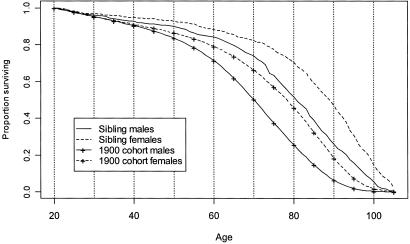
In addition to the above analysis of death rates, siblings of centenarians were compared with the 1900 cohort in terms of survival probabilities from age 20 onward. Survival curves by sex are compared in Fig. 3. Relative probabilities of survival from age 20 to higher age are plotted in Fig. 4 (which is published as supporting information on the PNAS web site, www.pnas.org) and noted in Table 2, which also provides confidence intervals. The chances of survival for the two groups do not differ substantially during early adulthood (relative survival probabilities are approximately 1), but they rapidly diverge after age 50 or 60. Fig. 4 shows that the overall gap in survival between older siblings and the 1900 cohort is quite large at very old ages. At age 100 years, for example, the relative probability of survival (from age 20) was about 17 for men and ≈8 for women.

Figure 3.

Survival probabilities from age 20. Siblings of centenarians and U.S. 1900 cohort

Table 2.

RSPs with 95% confidence intervals (CI) of siblings of centenarians versus U.S. 1900 cohort

Age	Males			Females
	RSP	Lower 95% CI	Upper 95% CI	RSP	Lower 95% CI	Upper 95% CI
20	1.00	1.00	1.00	1.00	1.00	1.00
25	1.00	0.99	1.01	1.01	1.00	1.02
30	1.01	1.00	1.02	1.02	1.01	1.03
35	1.01	1.00	1.03	1.03	1.01	1.04
40	1.03	1.01	1.05	1.04	1.02	1.06
45	1.04	1.02	1.06	1.06	1.04	1.07
50	1.08	1.05	1.10	1.08	1.06	1.09
55	1.10	1.07	1.13	1.10	1.08	1.12
60	1.18	1.15	1.21	1.12	1.09	1.14
65	1.29	1.25	1.33	1.16	1.13	1.19
70	1.48	1.42	1.53	1.24	1.21	1.28
75	1.68	1.60	1.77	1.36	1.31	1.41
80	2.03	1.90	2.16	1.54	1.47	1.60
85	2.69	2.47	2.91	1.83	1.73	1.93
90	4.08	3.62	4.54	2.56	2.39	2.74
95	8.35	6.98	9.71	4.15	3.73	4.57
100	16.95	10.84	23.07	8.22	6.55	9.90

These survival probabilities reflect mortality differences between siblings and the 1900 cohort for ages 20 and above only. Siblings of centenarians also show a mortality advantage below age 20. Although mortality ratios below age 20 may be biased downward because of underreporting of very young sibling deaths, it seems likely that the correct ratios are nevertheless below 1 in most cases. Therefore, the relative probability of survival from age 20 reported here is a plausible lower boundary for survival ratios from birth. We conclude that male siblings of centenarians were at least 17 times as likely to become centenarians themselves compared with the average person born in 1900, and female siblings were at least 8 times as likely.

Although the average birth year of the siblings of centenarians was 1898, there was a significant range of approximately 40 years (1873 to 1910) for birth years. Thus the question arises as to the appropriateness of comparing the survival experience of all these individuals against the experience of a single cohort, that is, the 1900 birth cohort. To determine the necessity of comparing the siblings' survival experience with a weighted average of U.S. cohort experiences, death rates for 1900–1927 were extrapolated backwards by using the Lee–Carter method to calculate age-specific death rates for cohorts beginning in 1873 (15). Weighted death rates were computed separately for men and women using the distribution of siblings by sex and birth year.

There were some differences between the weighted death rates and the actual death rates depicted in Figs. 1 and 2, especially for adolescents and young adults. However, the general pattern does not change at all. If anything, the differences using the weighted mortality rates are larger than those by using the 1900 cohort alone. Thus the results would not change using the weighted average versus the 1900 birth cohort experience for comparison with the siblings' survival experience.

Noting that 95% of the centenarian sample was Caucasian, we explored the possibility that racial or other associated sociodemographic factors might explain the observed survival advantage. Table 3 compares the distribution by sex, race, and education of the centenarian probands (born on average in 1896) to the U.S. population aged 90–94 in the 1990 census (born 1895–1900).

Table 3.

Distribution of centenarian probands versus U.S. national population by sex, race, and education

Group	Centenarian probands	Persons aged 90–94 in 1990*
Sex
Male	0.22	0.25
Female	0.78	0.75
Race
White	0.95	0.91
Non-White	0.05	0.09
Education
0–8 years	0.28	0.46
9–12 years	0.34	0.35
More than 12 years	0.38	0.19

^*For the category of education, years of education for the 1900 birth cohort was available from the U.S. census publication for the age group 85+ years (16). Education data for the age group 90–94 years (1895–1900 birth cohort) were kindly provided by Tori Velkoff, Chief of the Aging Studies Branch at the U.S. Census Bureau. 

As would be expected, because they are older, a greater proportion of the probands were female. However, more of the probands were also Caucasian and had more years of education. To answer the question if the differences in the distribution by race and education could explain the mortality differentials we observed for the siblings of the probands, relative mortality risks by race and education were determined by using National Longitudinal Mortality Study (NLMS) data for the period 1979–1985 noted in Sorlie et al. (4). The relative mortality risks for specific age groups according to race and years of education are noted in Table 4.

Table 4.

Estimated relative mortality risks by race and education according to age group, U.S. 1979–1985

Group	Male			Female
	25–44	45–64	65+	25–44	45–64	65+
Race
White	1.00	1.00	1.00	1.00	1.00	1.00
Black	2.07	1.68	1.00	2.15	1.72	1.11
Education
0–8 years	1.41–1.55	1.16–1.38	1.07–1.15	1.00–1.63	1.35–1.50	1.07–1.10
(0–8 midrange)	(1.48)	(1.27)	(1.11)	(1.32)	(1.43)	(1.09)
9–11 years	1.38	1.21	1.11	1.51	1.29	1.06
(9–12 weighted avg.)	(1.03)	(1.02)	(1.01)	(1.04)	(1.02)	(1.00)
12 years	1.00	1.00	1.00	1.00	1.00	1.00
More than 12 years	0.48–0.92	0.60–0.91	0.76–0.97	0.64–0.85	0.81–1.01	0.82–0.96
(>12 midrange)	(0.70)	(0.76)	(0.87)	(0.74)	(0.91)	(0.89)

Educational categories noted by Sorlie et al. (4) were consolidated into the categories 0–8 years and more than 12 years. The categories 9–11 years and 12 years were consolidated by using a weighted average (with weights of 0.08 and 0.92, since this is the breakdown of 90–94 year olds in these two educational categories in the 1990 census) and are shown in parentheses between the values for these two categories. The numbers derived in this fashion provide rough estimates of relative mortality levels by age and sex for the three educational categories in Table 3. Using the midrange of values for the most and least educated categories may have the effect of exaggerating the magnitude of mortality differentials by education, because it gives equal weight to small, extreme categories. This is the preferred strategy, however, in order to err on the side of exaggerating the amount of the sibling mortality advantage that could be explained by the sociodemographic characteristics of the study population. 

How much of the sibling mortality advantage could be explained by the distribution of the study population by race and education? Take the example of males aged 25–44 years. If we apply the racial distribution of the study population (Table 3) to the relative mortality risks (Table 4), we get a relative mortality level of 1.05 ( = 0.95 × 1.00 + 0.05 × 2.07). Making the same calculation using the racial distribution of persons aged 90–94 in 1990 yields a relative mortality level of 1.10 ( = 0.91 × 1.00 + 0.09 × 2.07). Therefore, on the basis of the racial distribution alone, we might expect that male siblings aged 25–44 would experience mortality rates that are 0.97 ( = 1.05/1.10) times the national level, or a 3% advantage.

Table 5 presents the results of calculating the relative mortality risks applied to males and females in three age groups by using the distributions of race and education noted among the centenarian sample. The last row indicates the relative mortality advantage if one were to combine the effects of race and education. The combined effect of race and education was computed by simply multiplying the relative mortality levels implied by racial and educational distributions considered individually. Such a calculation is correct only if race and education are independent—which of course they are not—and thus certainly exaggerates the combined impact of race and education on the sibling mortality advantage. For this reason, the estimates of the combined effect of the racial and educational distributions shown here may be considered as an upper boundary on the true effect of these sociodemographic characteristics on the mortality advantage of siblings. We conclude that the distribution of the study population by race and education yields a mortality advantage among siblings that is probably in the range of 5–10% and certainly no more than 15%. Therefore, it seems quite certain that the racial and educational characteristics of the study population do not account for the large sibling mortality advantage documented here (≈50%). Given the magnitude of the difference that remains after accounting for race and education, it appears unlikely that any combination of sociodemographic characteristics could explain the observed sibling mortality advantage.

Table 5.

Sibling mortality advantage implied by distribution of centenarian study sample by race and education, separately or together, expressed as a fraction of U.S. national mortality

	Male			Female
	25–44	45–64	65+	25–44	45–64	65+
Race	0.96	0.97	1.00	0.96	0.97	1.00
Education	0.89	0.92	0.96	0.91	0.93	0.97
Race and education	0.86	0.90	0.96	0.87	0.91	0.96

Relative mortality risks according to age group if one assumes the distributions of race and attained years of education experienced among the centenarian sample. The last row of this table presents an estimate of the relative mortality level of siblings that might be attributed to the combined effects of race and education. 

To summarize these findings in terms of life expectancy at birth, the siblings of centenarians in our study population had an average age at death of 76.7 and 70.4 years (females and males, respectively), compared to 58.3 and 51.5 years for the U.S. 1900 cohort. Adjusting for a 10% mortality advantage caused by the composition of the study population by race and education (as noted above) reduces the sibling values to 74.7 and 68.4 years, suggesting a net survival advantage of around 16–17 years compared to the general population. This result could be biased by under-reporting of early sibling deaths. However, even if 50% of sibling deaths under age 20 and 5% at all higher ages are missing from our analysis, and assuming a maximal 15% composition effect, the average age at death for siblings of centenarians would still be 67.4 and 61.4 years for females and males, respectively, or about 9–10 years above the national average.

Discussion

A striking finding of this study is that, with rather few exceptions, centenarian sibling mortality rates at all ages throughout life were roughly half of what was observed for the United States as a whole. It is perhaps unsurprising that siblings of centenarians are themselves relatively long-lived. It is the sustained, life-long nature of this mortality advantage that is truly remarkable. Ignoring uncertainties caused by random variation (for males in particular), the mortality differentials documented here are undiminished even at very old ages.

In contrast, almost every mortality differential that has been documented diminishes with age. It is quite common to observe a convergence at older ages of mortality differentials measured along various dimensions: sex (3), race (17), income (3, 4), education (5), physical activity (18), occupation (19), etc. In exceptional cases, mortality differentials may even reverse direction at very old ages, although a simple convergence is the rule.

Thus, to find a difference of such magnitude that endures over the full life course is quite unusual. The results imply that there is a substantial familial component to exceptional longevity. Obviously, a trait that is shared commonly within families could be environmental, behavioral, or genetic in origin. Neither previous studies nor the current one allow us to distinguish unambiguously between these competing explanations. However, given the rarity of life-long mortality differences between social groups defined in other ways, these findings may suggest an important role of genetics in differentiating exceptionally long-lived individuals from the rest of the population.

The survival experience of siblings of centenarians was clearly different from the general experience of their birth cohort. As shown, relative survival probabilities (RSPs) (from age 20) increased rapidly, especially at older ages. Whereas death rates (or hazard functions) reflect the current intensity of death (or failure) at a moment in time, a survival probability reflects the cumulative experience of death up to that moment in a cohort's life history. Thus, a relatively constant advantage from moment to moment (as seen in the relative death rates) is being translated into an increasing survival advantage over a lifetime (relative survival probabilities). From the analysis of death rates, we know that the siblings' mortality advantage does not grow as they get older. Rather, their relative probability of survival is a cumulative measure and reflects their life-long advantage over the general population born around the same time.

In Fig. 4 or Table 2, it is obvious that RSPs at older ages are much higher for male than for female siblings. However, this result does not reveal a meaningful difference by sex. As noted above, RSPs increase rapidly with age because the cumulative mortality advantage of siblings grows over a lifetime. At a given age, male survival ratios (siblings vs. the 1900 cohort) are higher than female ones because a larger fraction of males have died; thus, the male sibling's cumulative advantage (compared with the 1900 cohort) is greater than for females of the same age. It is easy to confirm that relative survival probabilities for males and females are quite similar if the comparison is made at a point where there are equivalent fractions of survivors, rather than equivalent ages.

As this discussion illustrates, relative death rates paint a much clearer picture of the mortality difference at various ages between siblings of centenarians and the U.S. 1900 cohort than do RSPs. On the other hand such elevated RSP values are important to consider when weighing the potential utility of performing a sibling linkage study to discover genetic loci (20, 21). Effects of some environmental and behavioral factors that siblings could have in common early in life may remain strong throughout life. Some of these effects might not become evident until older age. However, in general, environmental characteristics of siblings such as socioeconomic status, life styles and region of residence are likely to diverge as they grow older. Thus, if the survival advantage of the siblings of centenarians is mainly caused by environmental factors, the advantage should decline with age (22). Therefore, the stability of relative risk over the wide age range may suggest that the advantage is attributable more to genetic than environmental factors.

Although the relative difference in mortality rate remains stable throughout the lifespan, the absolute difference increases with age. The marked increase in RSP and sustained mortality advantage at extreme ages is consistent with the forces of demographic selection in which genes and/or environmental factors that predispose to longevity increase in prevalence with increasing age relative to those that are associated with premature or average mortality. Along these lines, Silverman and colleagues hypothesized that the siblings of cognitively intact nonagenarians would have an increased genetic resistance to Alzheimer's disease (AD) relative to younger individuals. Studying approximately 1,000 probands grouped into three age groups, all without AD, the cumulative survival without AD was noted to be greatest among the first-degree relatives of the oldest probands, ages 90–102 years (23). The importance of genetic protective factors is underscored by the United States 1990 Census finding that centenarians were more likely to be poor, widowed, and to have fewer years of education; all environmental factors that should otherwise predict decreased survival, not more (24). The fact that male centenarian siblings have substantially higher RSP values (compared with males in the 1900 birth cohort) than do female siblings (compared with females in the 1900 cohort) also suggests the powerful influence of demographic selection at work given men's higher age-specific mortality rates because of lethal age-related illnesses (2, 4).

Consistent with previous reports, this study noted that siblings of centenarians have a higher probability of surviving to exceptionally old age. Our findings differ in degree of survival advantage compared with earlier investigations by other groups but agree with the earlier study performed by the New England Centenarian Study (7). Studying pedigrees from the Utah Population Database, Kerber and colleagues (8) investigated the impact of family history on the longevity of 78,994 individuals who achieved at least the age of 65 years. The relative risk (λ_s) calculated for siblings of probands achieving the 97th percentile of “excess longevity” (for males this corresponded with an age of 95 years, and for women an age of 97 years) was 2.30.

The Utah study findings closely agree with a study of the Icelandic population in which first-degree relatives of those living to the 95th percentile of surviving age were almost twice as likely to also live to the 95th percentile compared with controls (25). Both these studies found a considerably lower RSP to advanced ages than we observed among centenarian siblings. The differences may be attributable to several factors. One of these may be the younger age of the probands compared with the probands in our sample who were all at least 100 years old. In addition, the Utah study measured survivorship after a different age (65 years) than the New England Centenarian Study. Other possible factors include the likely greater homogeneity of the populations in these studies, which may have lessened the contribution of confounding covariates that differ in frequency between centenarian families and the general population. In addition, the Utah study controlled for the effects of other environmental variables that could not be measured in the present study, and which may contribute to longevity. On the other hand it is possible that familial effects on mortality are truly weaker in the Utah and Icelandic populations that they are in the overall U.S. population. Nonetheless, both studies note that the range of recurrent relative risks that they observed indicated a substantial genetic component to exceptional longevity that supports the conduct of molecular genetic studies to locate longevity enabling genetic loci among sibling pairs.

The relative risks reported before the present study have been encouraging enough that several research groups have pursued molecular genetic studies to determine whether there are genetic loci among the sibships that could be linked to the exceptional longevity phenotype. Geneticists associated with the French Centenarian Study performed a linkage study of 558 individuals representing 188 nonagenarian sibships using seven polymorphic markers in the region of the ApoE gene (26). The study did not reveal significant linkage, and the authors concluded that such studies are unlikely to be successful if exceptional longevity is a chance event among individuals not carrying deleterious alleles that are quite common in the general population and rare among centenarians. On the other hand, rare alleles that significantly enhance the ability to survive to such old age would be sufficiently enriched among a centenarian sample that a nonparametric analysis of a genome wide scan for such excess allele sharing would be worth performing.

Puca et al. recently performed just such a study. A genome-wide scan for predisposing loci was conducted by studying 308 individuals belonging to 137 sibships demonstrating exceptional longevity. Using nonparametric analysis, significant evidence for linkage was noted for chromosome 4 locus at D4S1564 with a MLS of 3.65 (P = 0.044). The analysis was corroborated by a parametric analysis (P = 0.052). These linkage results indicated the significant likelihood that there exists a gene or genes exerting a substantial positive influence on the ability to achieve exceptional old age (27). The high relative survival probabilities for achieving exceptional old age reported in this current study would be consistent with a statistically significant linkage to a specific locus. These findings, however, do not suggest that only one genetic locus or gene is responsible for the familial advantage we have observed in achieving exceptional old age.

It is worth noting that the above evidence for a substantial and significant genetic effect on the likelihood of reaching exceptionally old age is not inconsistent with several twin studies indicating that the heritability of life span considered as a quantitative trait is between 20% and 30% (28–30). The results of these studies in which few subjects survived beyond age 85 should not be interpreted as an indication of the genetic contribution to achieving much older age, that is, the nonagenarian years and beyond. Centenarian families may have certain genetic characteristics that are highly advantageous but are also rare in the population at large. If so, these differences might have little impact on the total variation in human life span, even if their effect is quite significant for the relatively few individuals involved. Alternatively, these longevity-associated alleles could be more common than previously thought because their existence could be masked by infant mortality (which was high at the turn of the last century) and poor health habits that cause premature mortality.

Assuming genes do play an important role in the ability to achieve exceptional old age, there are probably two classes of genes at play. On the one hand, the probability of achieving exceptional old age is likely enhanced by lacking genetic polymorphisms that predispose to diseases that cause premature mortality (31, 32). The absence of a “disease gene” among centenarians is exemplified by the finding by several groups of the marked rarity of the apolipoprotein E ɛ-4 allele (33, 34) that has been associated with AD and cardiovascular disease. On the other hand, there might also be genes that slow aging at its most basic levels and therefore also confer resistance to age-related diseases (“longevity enabling genes”) (ref. 2 and http://sageke.sciencemag.org/cgi/content/full/sageke;2001/9/vp6 ).

Observations by several groups indicating the demographically select nature of centenarians as well as the familiality of exceptional longevity indicate the potential value of studying centenarians to discover genes affecting mortality and survival rates across the life span, and also to confirm or rule out the significance of polymorphisms of candidate genes discovered in lower organisms or implicated in human studies. Specifically, the findings reported here support the utility of conducting a sibling pair study searching for genetic factors these sibships might have in common that confer such a substantial survival advantage.

Abbreviations

RSP

relative survival probability

AD

Alzheimer's disease