Abstract
We address the stability of multicharged finite systems driven by Coulomb forces beyond the Rayleigh instability limit. Our exploration of the nuclear dynamics of heavily charged Morse clusters enabled us to vary the range of the pair potential and of the fissibility parameter, which results in distinct fragmentation patterns and in the angular distributions of the fragments. The Rayleigh instability limit separates between nearly binary (or tertiary) spatially unisotropic fission and spatially isotropic Coulomb explosion into a large number of small, ionic fragments. Implications are addressed for a broad spectrum of dynamics in chemical physics, radiation physics of ultracold gases, and biophysics, involving the fission of clusters and droplets, the realization of Coulomb explosion of molecular clusters, the isotropic expansion of optical molasses, and the Coulomb instability of “isolated” proteins.
The fragmentation of multiply charged finite systems driven by long-range Coulomb forces (1–33) or their analogue (34), i.e., nuclei (1–4), clusters (5–29), droplets (30–33), and optical molasses (34), raises some interesting questions regarding the energetics and dynamics of dissociation. How does a finite system respond to a large excess charge (1–33) or effective charge (34)? What are the topography and topology of the multidimensional energy landscape (4, 35) that guide the system's shape evolution and fragmentation? What are the fragmentation channels and under what conditions are they realized? What is the interplay between fission, i.e., instability toward dissociation, of the finite system into two (or a small number of) fragments and Coulomb explosion (17–29) into a large number ∼n (where n is the number of constituents) of ionic species? On the basis of molecular dynamics simulations of the fragmentation patterns of heavily charged Morse clusters we established that the Rayleigh instability limit (30) separates between nearly binary (or tertiary) spatially unisotropic fission and spatially isotropic Coulomb explosion into a large number of ionic fragments.
The ubiquity of fission phenomena of droplets (30–33), nuclei (1–4),
and clusters (5–16) was traditionally described by the liquid drop
model (LDM) of Lord Rayleigh (30), Meitner and Frisch (2), and Wheeler
and Bohr (1), where a classical charged drop deforms through elongated
shapes to form separate droplets. The fissibility parameter
X =
E(Coulomb)/2E(surface)
characterizes the relative contribution of repulsive (Coulomb) and
cohesive (surface) energies to the fission barrier, separating between
the bound initial states and the fission products. For
X < 1, thermally activated fission over the barrier
prevails. At the Rayleigh instability limit of X = 1,
the barrier height is zero (1, 30). Many features of nuclear and metal
cluster fission go beyond the physics of a classical liquid droplet and
require the incorporation of quantum shell structure and dynamics (4,
10). Nevertheless, the simple LDM expression X =
Z2e2/16πγR3
=
(Z2/n)/(Z2/n)cr
with
(Z2/n)cr
= 16πγr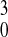 /e2
(where γ is the surface tension, Z the total charge,
R the system's radius, and
r0 the constituent radius) provided
the conceptual framework for the fission of charged finite systems. The
LDM accounts for the gross universal features of Coulomb instability of
finite systems, with
(Z2/n)cr ≃ 50 for
nuclei (1–3), (Z2/n)cr
≃ 0.40–0.50 for metal clusters (10), and
(Z2/n)cr ≃ 0.1 for
hydrogen-bonded clusters (31–33). The values of
(Z2/n)cr,
which correspond to the Rayleigh instability for the onset of
barrierless fission (X = 1), reflect on the
quantitative difference between the surface properties of nuclear
matter held by strong cohesive interactions and of molecular matter
held by chemical and van der Waals binding. All of the ubiquitous
phenomena of fission were experimentally realized for the fissibility
parameter below the Rayleigh instability limit of X =
1, i.e., nuclear fission (36), the fission of metal clusters (14, 15),
and of hydrogen-bonded clusters (31–33). In all these diversely
charged finite systems (with X <1), thermally activated
fission is dominated by the geometry and the topology of the potential
energy hypersurface (4). Beyond the fissibility limit
(X > 1), barrierless fission and other dissociative
channels can open up, but this barrierless domain was not yet explored.
In this context, Coulomb explosion of highly charged clusters and large
molecules induced by multielectron ionization in ultraintense,
ultrashort laser fields (18–29), as well as the expansion of ultracold
optical molasses (34), constitute new dissociative phenomena induced by
Coulomb instability of multicharged finite systems or their analogy for
finite ultracold gases (34), which were not yet related to fission.
/e2
(where γ is the surface tension, Z the total charge,
R the system's radius, and
r0 the constituent radius) provided
the conceptual framework for the fission of charged finite systems. The
LDM accounts for the gross universal features of Coulomb instability of
finite systems, with
(Z2/n)cr ≃ 50 for
nuclei (1–3), (Z2/n)cr
≃ 0.40–0.50 for metal clusters (10), and
(Z2/n)cr ≃ 0.1 for
hydrogen-bonded clusters (31–33). The values of
(Z2/n)cr,
which correspond to the Rayleigh instability for the onset of
barrierless fission (X = 1), reflect on the
quantitative difference between the surface properties of nuclear
matter held by strong cohesive interactions and of molecular matter
held by chemical and van der Waals binding. All of the ubiquitous
phenomena of fission were experimentally realized for the fissibility
parameter below the Rayleigh instability limit of X =
1, i.e., nuclear fission (36), the fission of metal clusters (14, 15),
and of hydrogen-bonded clusters (31–33). In all these diversely
charged finite systems (with X <1), thermally activated
fission is dominated by the geometry and the topology of the potential
energy hypersurface (4). Beyond the fissibility limit
(X > 1), barrierless fission and other dissociative
channels can open up, but this barrierless domain was not yet explored.
In this context, Coulomb explosion of highly charged clusters and large
molecules induced by multielectron ionization in ultraintense,
ultrashort laser fields (18–29), as well as the expansion of ultracold
optical molasses (34), constitute new dissociative phenomena induced by
Coulomb instability of multicharged finite systems or their analogy for
finite ultracold gases (34), which were not yet related to fission.
Multicharged Morse Clusters
We shall transcend the Rayleigh instability limit
(X = 1) for Coulomb instability of large finite
systems, demonstrating the prevalence of a qualitatively different
fragmentation pattern of Coulomb explosion beyond the Rayleigh
instability limit. We explored the fragmentation patterns and dynamics
of highly charged Morse clusters by varying the range of the pair
potential and of the fissibility parameters. The instability of
multicharged Morse clusters directly reflects on covalently or
dispersion-bound chemical and biophysical finite systems. We applied
classical (constant energy) molecular dynamics simulations to study the
stability, decay patterns, and fragmentation dynamics of multicharged
clusters (A+)n consisting
of singly charged A+ ions (with a mass of 100
atomic mass units), where the total cluster charge is Z
= n. The interionic pair potential
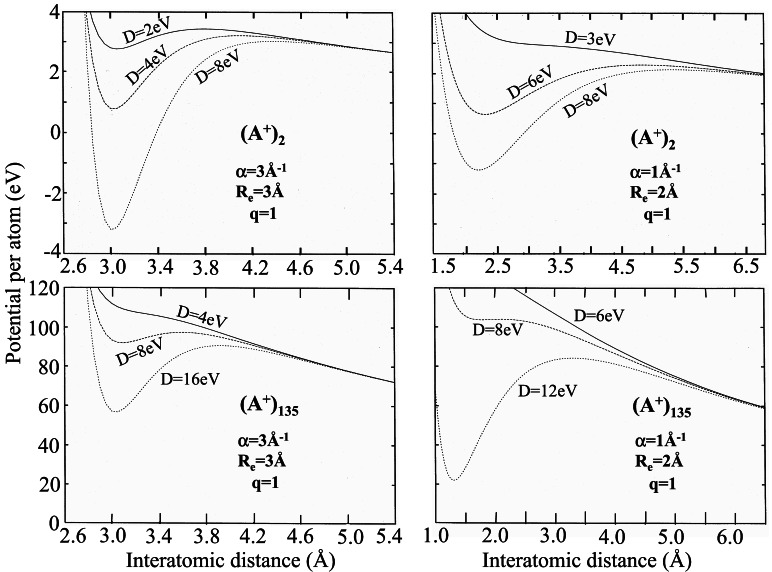
U(R) (Fig. 1)
consisted of an attractive Morse potential and a Coulomb repulsion,
with U(R) = DG(G
− 2) + Be2/R, where
G = exp[−α(R −
Re)], the parameters of the Morse
potential being D (dissociation energy), α (range
parameter), and Re (equilibrium pair
distance), while B = 14.385 eV/Å. The interionic
pair potential U(R) is purely repulsive for
D < D0 (α,
Re) and exhibits a minimum and a barrier
for D > D0 (Fig. 1).
Two sets of Morse potential parameters were considered. (i) Short-range
Morse potential, with α = 3Å−1 and
Re = 3Å, where
αRe = 9, so that the interaction between
nonneighboring atoms is negligibly small. (ii) Long-range Morse
potential, with α = 1Å−1 and
Re = 2Å, where
αRe = 2 and the contribution of
interactions between nonneighboring atoms is of significance. The total
potential energy (Fig. 1) of a multicharged
(A+)n cluster is
E = 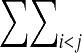 U(Rij), consisting of a
repulsive Coulomb component and an attractive Morse component. The
(A+)n clusters also exist
in a metastable state, with E being higher than the total
energy of products in some decay channels but separated from them by
barriers (Fig. 1). The equilibrium icosohedral cluster configuration
was determined by simulated annealing for the energy minimization. The
cluster potential energy for potential parameters (i) and (ii) at the
equilibrium configuration is positive, i.e., E > 0
(Fig. 1), reflecting on the existence of a metastable state. The
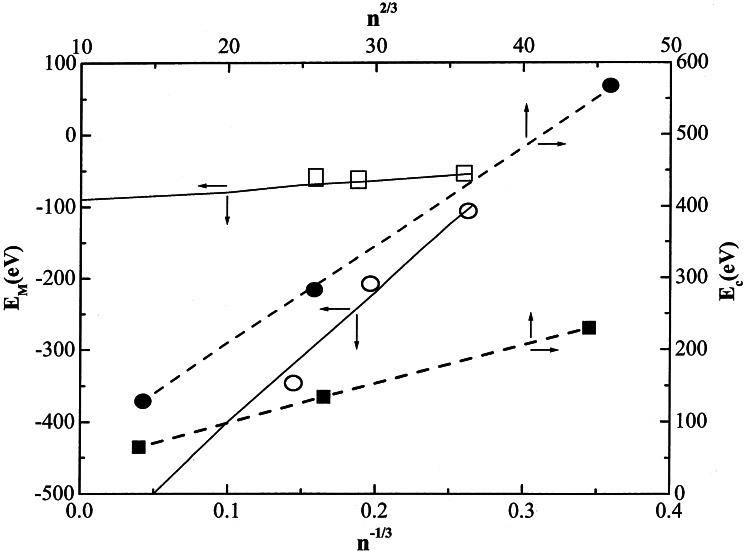
cluster energetics at the minimum was analyzed by the LDM, as shown in
Fig. 2. The potential energy (per
particle) is E/n =
EM +
Ec, where
Ec =
acn2/3 is the Coulomb
energy (per particle) while the Morse energy (per particle) is
EM =
Es +
Ev and where the surface energy (per
particle) is Es =
asn−1/3, while the
interior energy (per particle) is Ev =
−av. Here the parameters
ac, as, and
av are size-independent. The LDM analysis is
based on the calculation of Ec,
together with the simple relation for the Morse energy
EM =
(E/n) −
Ec ≡
asn−1/3 −
av. The size dependence of the potential energy
landscapes of the (A+)n
charged Morse clusters was calculated for short-range Morse potential
(i) with D = 14.2 eV and for long-range Morse potential
(ii) with D = 9.6 eV. From the cluster size dependence
of Ec and
EM (Fig. 2) we infer that for the
short-range Morse potential ac = 4.8 ± 0.1
eV, av = −80 eV, and as =
132 eV, while for the long-range Morse potential
ac = 10.8 ± 2 eV, av
= −600 eV, and as = 1900 eV. The one-order of
magnitude difference of the as parameters between
the long-range and the short-range potentials (while the
ac parameters differ only by a numerical factor
of 2 between the two classes of potentials) implies that the
fissibility parameter X =
(ac/as)n is
considerably larger for the short-range potential. The fissibility
parameters are X =
1.81⋅10−2n for the short-range
Morse potential and X =
2.82⋅10−3n for the long-range
Morse potential, which for the cluster size domain n =
55 − 321 corresponds to X ≅ 0.1 − 1.0 for the
long-range potential and X ≅ 1 − 7 for the short-range
potential. Our simulations revealed that the qualitative difference in
the size domain of the fissibility parameters between the charged
long-range and short-range Morse potential implies a qualitatively
different fragmentation dynamics driven by Coulomb instability of these
two classes of charged Morse clusters.
U(Rij), consisting of a
repulsive Coulomb component and an attractive Morse component. The
(A+)n clusters also exist
in a metastable state, with E being higher than the total
energy of products in some decay channels but separated from them by
barriers (Fig. 1). The equilibrium icosohedral cluster configuration
was determined by simulated annealing for the energy minimization. The
cluster potential energy for potential parameters (i) and (ii) at the
equilibrium configuration is positive, i.e., E > 0
(Fig. 1), reflecting on the existence of a metastable state. The
cluster energetics at the minimum was analyzed by the LDM, as shown in
Fig. 2. The potential energy (per
particle) is E/n =
EM +
Ec, where
Ec =
acn2/3 is the Coulomb
energy (per particle) while the Morse energy (per particle) is
EM =
Es +
Ev and where the surface energy (per
particle) is Es =
asn−1/3, while the
interior energy (per particle) is Ev =
−av. Here the parameters
ac, as, and
av are size-independent. The LDM analysis is
based on the calculation of Ec,
together with the simple relation for the Morse energy
EM =
(E/n) −
Ec ≡
asn−1/3 −
av. The size dependence of the potential energy
landscapes of the (A+)n
charged Morse clusters was calculated for short-range Morse potential
(i) with D = 14.2 eV and for long-range Morse potential
(ii) with D = 9.6 eV. From the cluster size dependence
of Ec and
EM (Fig. 2) we infer that for the
short-range Morse potential ac = 4.8 ± 0.1
eV, av = −80 eV, and as =
132 eV, while for the long-range Morse potential
ac = 10.8 ± 2 eV, av
= −600 eV, and as = 1900 eV. The one-order of
magnitude difference of the as parameters between
the long-range and the short-range potentials (while the
ac parameters differ only by a numerical factor
of 2 between the two classes of potentials) implies that the
fissibility parameter X =
(ac/as)n is
considerably larger for the short-range potential. The fissibility
parameters are X =
1.81⋅10−2n for the short-range
Morse potential and X =
2.82⋅10−3n for the long-range
Morse potential, which for the cluster size domain n =
55 − 321 corresponds to X ≅ 0.1 − 1.0 for the
long-range potential and X ≅ 1 − 7 for the short-range
potential. Our simulations revealed that the qualitative difference in
the size domain of the fissibility parameters between the charged
long-range and short-range Morse potential implies a qualitatively
different fragmentation dynamics driven by Coulomb instability of these
two classes of charged Morse clusters.
Figure 1.
Pair potentials [Upper images, marked (A+)2 ] and potential energy landscapes for the radical expansion of n = 135 clusters [Lower images, marked (A+)135] for the charged Morse clusters. The potential parameters (i) α = 3Å−1, Re = 3Å, and q = 1 correspond to the short-range Morse potential, while (ii) α = 1Å−1, Re = 2Å, and q = 1 correspond to the long-range Morse potential.
Figure 2.
Analysis of the energetics of icosohedral-charged Morse clusters at their equilibrium configuration by the LDM. The potential parameters are (i) short-range Morse potential with α = 3Å−1, Re = 3Å, D = 14.2 eV, q = 1 and (ii) long-range Morse potential with α = 1Å−1, Re = 2Å, D = 9.6 eV, q = 1. The Coulomb energy per particle is Ec = acn2/3 [■ for short-range Morse potential (i) and ● for long-range Morse potential (ii)], while the Morse energy per particle is EM = asn−1/3 − av [□ for short-range potential (i) and ○ for long-range Morse potential (ii)].
Dynamics of Fission and Coulomb Explosion
Constant energy molecular dynamics simulations (on time
scales of up to 1 ns) were performed for the fragmentation products and
dynamics of the icosohedral-charged Morse clusters
A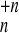 →
{A
→
{A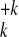 } (n =
55, 135, 321), which result in the fragments of charged clusters/ions
(1 ≤ k < n) of sizes
{nk} with
} (n =
55, 135, 321), which result in the fragments of charged clusters/ions
(1 ≤ k < n) of sizes
{nk} with 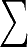 knk = n. As appropriate for
thermally activated fragmentation (at least for X <
1), the configurationally equilibrated cluster was subjected at
t = 0 to a temperature jump to a final temperature
T. The simulations were performed at the finite temperatures
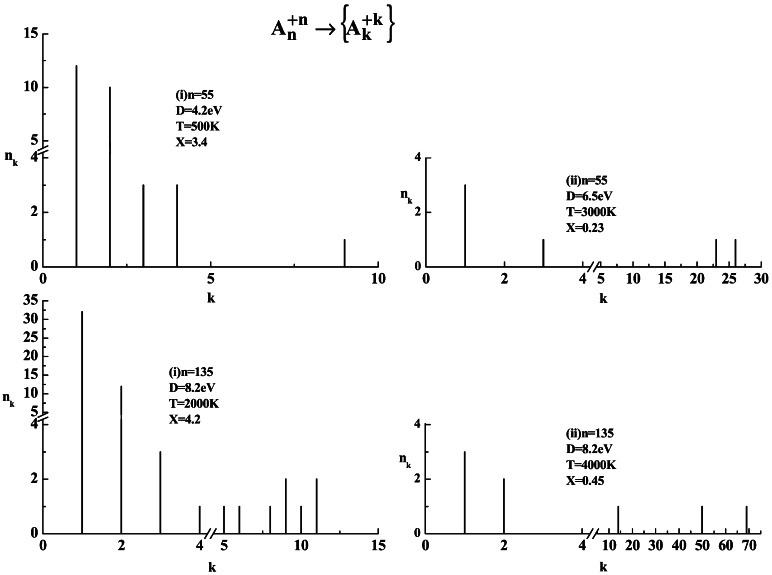
T = 500–10,000 K. Histograms of the ionic products,
i.e., nk vs. k, are presented
in Fig. 3. The corresponding values
of X were calculated from linear scaling as by the
dissociation energies D for Morse potentials (i) and (ii),
marked on Fig. 3. For long-range Morse potential (ii), a nearly binary
or tertiary cluster fission is exhibited (Fig. 3). The
n = 55 cluster (X = 0.23) reveals a
nearly symmetric fission, while the n = 135 cluster
(X = 0.45) reveals an asymmetric fission into three
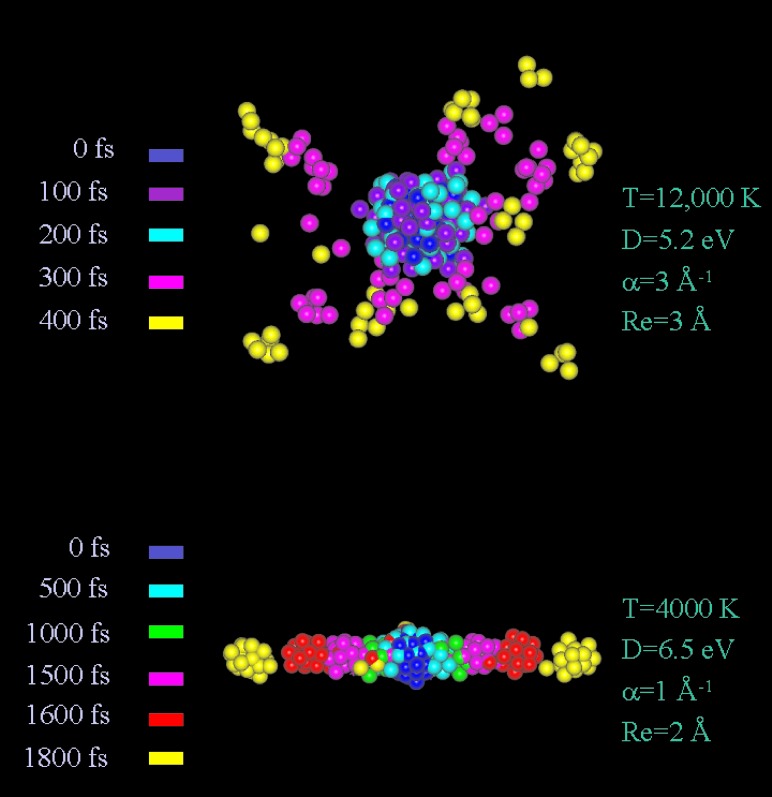
large clusters (Fig. 3). The fission process is spatially unisotropic,
with the deformation of the parent charged cluster occurring via
elongation to form separate clusters (Fig.
4). The situation is drastically and
qualitatively different for the short-range Morse potential (i)
(X = 3.4 for n = 55, and
X = 4.2 for n = 135), where the
fragmentation involves a large number of small ionic clusters, which
manifests Coulomb explosion (Fig. 3). The Coulomb explosion process is
spatially isotropic, with the small ionic fragments expanding radially
(Fig. 4). The dissociation dynamics were characterized by the (ps)
dissociation times, τD, which manifest the
incubation time for the attainment of the transition state for
fragmentation. For the long-range Morse potential (X <
1), the onset of fission exhibits a weak size dependence, i.e.,
τD = 1.0–0.3 ps for n = 55
(T = 3000–10,000 K), and τD =
0.8–3.6 ps for n = 135 (T =
2,000–10,000 K), while for the short-range Morse potential
(X > 1) the onset of Coulomb explosion manifests a
modest decrease of τD with increasing the
clusters size, i.e., τD = 1.5–1.8 ps for
n = 55 (T = 1,000–8,000 K) and
τD = 0.35–0.5 ps for n = 135
(T = 2,000–3,000 K).
knk = n. As appropriate for
thermally activated fragmentation (at least for X <
1), the configurationally equilibrated cluster was subjected at
t = 0 to a temperature jump to a final temperature
T. The simulations were performed at the finite temperatures
T = 500–10,000 K. Histograms of the ionic products,
i.e., nk vs. k, are presented
in Fig. 3. The corresponding values
of X were calculated from linear scaling as by the
dissociation energies D for Morse potentials (i) and (ii),
marked on Fig. 3. For long-range Morse potential (ii), a nearly binary
or tertiary cluster fission is exhibited (Fig. 3). The
n = 55 cluster (X = 0.23) reveals a
nearly symmetric fission, while the n = 135 cluster
(X = 0.45) reveals an asymmetric fission into three
large clusters (Fig. 3). The fission process is spatially unisotropic,
with the deformation of the parent charged cluster occurring via
elongation to form separate clusters (Fig.
4). The situation is drastically and
qualitatively different for the short-range Morse potential (i)
(X = 3.4 for n = 55, and
X = 4.2 for n = 135), where the
fragmentation involves a large number of small ionic clusters, which
manifests Coulomb explosion (Fig. 3). The Coulomb explosion process is
spatially isotropic, with the small ionic fragments expanding radially
(Fig. 4). The dissociation dynamics were characterized by the (ps)
dissociation times, τD, which manifest the
incubation time for the attainment of the transition state for
fragmentation. For the long-range Morse potential (X <
1), the onset of fission exhibits a weak size dependence, i.e.,
τD = 1.0–0.3 ps for n = 55
(T = 3000–10,000 K), and τD =
0.8–3.6 ps for n = 135 (T =
2,000–10,000 K), while for the short-range Morse potential
(X > 1) the onset of Coulomb explosion manifests a
modest decrease of τD with increasing the
clusters size, i.e., τD = 1.5–1.8 ps for
n = 55 (T = 1,000–8,000 K) and
τD = 0.35–0.5 ps for n = 135
(T = 2,000–3,000 K).
Figure 3.
Fragmentation patterns of charged Morse clusters
{A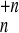 }
(n = 55 and 135). The distributions of the ionic
fragmentation products
{A
}
(n = 55 and 135). The distributions of the ionic
fragmentation products
{A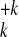 } are presented
in terms of the histograms of the product sizes
{nk}. (i)
Short-range Morse potential α = 3Å−1,
Re = 3Å, q = 1.
(ii) Long-range Morse potential α =
1Å−1, Re = 2Å,
q = 1, with the corresponding D and
X values marked on the images. Note the fission into a
small number of ionic fragments for case (ii) and the Coulomb explosion
into a large number of small ionic fragments for case (i).
} are presented
in terms of the histograms of the product sizes
{nk}. (i)
Short-range Morse potential α = 3Å−1,
Re = 3Å, q = 1.
(ii) Long-range Morse potential α =
1Å−1, Re = 2Å,
q = 1, with the corresponding D and
X values marked on the images. Note the fission into a
small number of ionic fragments for case (ii) and the Coulomb explosion
into a large number of small ionic fragments for case (i).
Figure 4.
Superimposed temporal patterns of the fragmentation of highly charged (A+)55 Morse clusters. The potential parameters are marked on the two images. Upper panel corresponds to short-range interactions with X = 4.2. Lower panel corresponds to long-range interactions with X = 0.23. The projections of the structures of the disintegrating clusters at different times (t = 0–1500 fs) are presented by different colors, marked on each image. The time t = 0 corresponds to the T jump to the final temperatures marked on the images. Note the dramatic distinction between the (spatially isotropic) Coulomb explosion (Upper) and the (spatially unisotropic) tertiary fission (Lower).
Epilogue
Our model calculations bridged between (spatially unisotropic) fission and (spatially isotropic) Coulomb explosion of highly charged, strongly bound, molecular clusters demonstrating the prevalence of finite temperature cluster fission into large ionic fragments for X < 1, while beyond the fissibility limit, i.e., X > 1, Coulomb explosion into elemental-charged constituents provides the dominant dissociation channel. While our results pertain strictly to covalently bound molecular matter, e.g., molecular clusters, large molecules or biomolecules, droplets, and also to finite ultracold gases (34), some general conclusions are inferred.
The majority of the currently available experimental information on the
Coulomb instability of nuclei, of droplets, and of metal clusters
pertains to the fission limit (X < 1). In the field of
nuclear physics, the fissibility parameter is X ≅ 0.7 for
235U and about X ≅ 0.9 for the
recently discovered Z = 114 element (36), while the
realization of higher fissibilities, inducing isotropic nuclear Coulomb
explosion, requires the nuclear synthesis of heavier elements, which
seems to be unattainable at present. For hydrogen-bonded finite systems
fission was recorded for droplets below the Rayleigh fissibility limit
(X = 1) at X = 0.7 (T. Leisner,
personal communication) and at X < 1 (31–33). For
multiply charged metal clusters, the maximal value of X
= 0.85 ± 0.07 for Na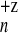 was recorded
(14, 15), although these clusters were not yet produced with a
sufficiently large enough charge to overcome the Rayleigh limit. A new
fragmentation pattern beyond cluster fission was experimentally
recorded (12) for highly charged Nan clusters
produced by collision with multicharged Xe20+
ions, with the emission of a large number of singly charged monomers
and leaving a single heavy residue of low charge. The production of the
light Na+ ions manifests Coulomb explosion for
X > 1. Information from Monte-Carlo simulations on
evaporation, fission, and multifragmentation of multicharged metal
clusters (12) provided information on their Coulomb instability. Our
results for molecular matter driven by Coulomb forces, which predict
isotropic Coulomb explosion for X > 1, concur with the
simulation results for the multifragmentation of
Na
was recorded
(14, 15), although these clusters were not yet produced with a
sufficiently large enough charge to overcome the Rayleigh limit. A new
fragmentation pattern beyond cluster fission was experimentally
recorded (12) for highly charged Nan clusters
produced by collision with multicharged Xe20+
ions, with the emission of a large number of singly charged monomers
and leaving a single heavy residue of low charge. The production of the
light Na+ ions manifests Coulomb explosion for
X > 1. Information from Monte-Carlo simulations on
evaporation, fission, and multifragmentation of multicharged metal
clusters (12) provided information on their Coulomb instability. Our
results for molecular matter driven by Coulomb forces, which predict
isotropic Coulomb explosion for X > 1, concur with the
simulation results for the multifragmentation of
Na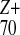 clusters, which for Z
> 8 (approximately corresponding to X > 1.8) manifest
Coulomb explosion into small fragments.
clusters, which for Z
> 8 (approximately corresponding to X > 1.8) manifest
Coulomb explosion into small fragments.
How can the Rayleigh limit for Coulomb instability of finite systems be
overcome? This can be accomplished either by a marked enhancement of
the repulsive Coulomb energy or by the dramatic reduction of the
cohesive surface energy. The increase of E(Coulomb) was
experimentally attained for cluster Coulomb explosion induced by
ultrashort (1–10 fs) multielectron ionization and nuclear dynamics
(10–100 fs) of molecular clusters, e.g.,
Xen,
(D2)n,
(D2O)n (n =
50–5,000), triggered by ultraintense laser fields (intensity
I = 1016–1018
Wcm−2) (17–29, 37–40). Femtosecond electron dynamics,
involving inner and outer cluster ionization (29), strips the cluster
atoms/molecules of their outer shell valence electrons, producing
highly charged clusters on a time scale shorter than nuclear motion.
For these highly charged molecular clusters X =
a(Z2/n),
whereupon X ≅ anq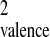 [where
a =
(Z2/n)
[where
a =
(Z2/n)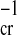 ≈ 1 for the interparticle van der Waals interaction, and
qvalence is the valence atomic charge]. The
relation X ≫ 1 is well obeyed for these highly charged
molecular clusters, with the dynamics of fragmentation corresponding to
the limit of Coulomb explosion. A novel application of this cluster
fragmentation mechanism beyond the Rayleigh instability limit
(X = 1) pertains to nuclear fusion induced by Coulomb
explosion of homonuclear and heteronuclear deuterium- or
tritium-containing molecular clusters (37–40), e.g.,
(D2)n,
(DT)n/2,
(D2O)n,
(DTO)n,
(CD4)n (n
= 400–104), stripped of all their valence
electrons by multielectron ionization in ultraintense laser fields
(I = 1016–1019
Wcm−2). The high energies (E = 1–20 keV)
of the D+ or T+ ions (d or
t nuclei) resulting from the Coulomb explosion of an assembly of
clusters fall in the energy domain of nuclear physics, driving dd or dt
nuclear fusion. An alternative way to obtain high values of the
fissibility parameter, which are far above the Rayleigh limit, involves
the drastic decrease of E(surface). This was achieved in
three-dimensional optical molasses (34), consisting of a cloud of
low-density (1010–1011 cm−3),
ultracold (T = 10–100 μK), neutral (Rb) atoms subjected to the
radiative trapping force, which is equivalent to the interatomic
Coulomb force, with an effective atomic charge q ≃
10−5e (34). The restoring surface
energy is vanishingly small, whereupon X ≫ 1, even for
these low values of q. The nuclear dynamics of optical
molasses, transcendenting the Rayleigh limit, manifests an isotropic,
radial, spatial expansion, in analogy with isotropic cluster Coulomb
explosion (34). The time scales for the isotropic expansion of optical
molasses [τM ≃ 1 ms for Rb (34)] and for
cluster Coulomb explosion [τM ≃ 100 fs for
(Xe+)n (27)]
differ by a numerical factor of 1010, in accord
with the theory of Coulomb explosion (34).
≈ 1 for the interparticle van der Waals interaction, and
qvalence is the valence atomic charge]. The
relation X ≫ 1 is well obeyed for these highly charged
molecular clusters, with the dynamics of fragmentation corresponding to
the limit of Coulomb explosion. A novel application of this cluster
fragmentation mechanism beyond the Rayleigh instability limit
(X = 1) pertains to nuclear fusion induced by Coulomb
explosion of homonuclear and heteronuclear deuterium- or
tritium-containing molecular clusters (37–40), e.g.,
(D2)n,
(DT)n/2,
(D2O)n,
(DTO)n,
(CD4)n (n
= 400–104), stripped of all their valence
electrons by multielectron ionization in ultraintense laser fields
(I = 1016–1019
Wcm−2). The high energies (E = 1–20 keV)
of the D+ or T+ ions (d or
t nuclei) resulting from the Coulomb explosion of an assembly of
clusters fall in the energy domain of nuclear physics, driving dd or dt
nuclear fusion. An alternative way to obtain high values of the
fissibility parameter, which are far above the Rayleigh limit, involves
the drastic decrease of E(surface). This was achieved in
three-dimensional optical molasses (34), consisting of a cloud of
low-density (1010–1011 cm−3),
ultracold (T = 10–100 μK), neutral (Rb) atoms subjected to the
radiative trapping force, which is equivalent to the interatomic
Coulomb force, with an effective atomic charge q ≃
10−5e (34). The restoring surface
energy is vanishingly small, whereupon X ≫ 1, even for
these low values of q. The nuclear dynamics of optical
molasses, transcendenting the Rayleigh limit, manifests an isotropic,
radial, spatial expansion, in analogy with isotropic cluster Coulomb
explosion (34). The time scales for the isotropic expansion of optical
molasses [τM ≃ 1 ms for Rb (34)] and for
cluster Coulomb explosion [τM ≃ 100 fs for
(Xe+)n (27)]
differ by a numerical factor of 1010, in accord
with the theory of Coulomb explosion (34).
In the realm of biophysics, highly charged peptides and proteins in the gas phase are interrogated by mass spectrometry (41, 42), providing significant information on the structure, reactivity, conformational changes, and folding of “isolated” anhydrous proteins (41). It is interesting to inquire whether charged isolated protein fission or Coulomb explosion can be realized. Typical protein sizes (specified in terms of the number, n, of residues) and total charges (Z) currently available correspond to rather low values of Z2/n, e.g., for cytochrome C (41), Z = 8–19, n = 104 (Z2/n ≃ 0.5–4) and for carbonic anhydrase (41, 42), Z = 45, n ≃ 260 (Z2/n ≃ 7), while for G-Actin (41) (with 46 basic residues) Z = 59, n ≃ 370 (Z2/n ≃ 9). Adopting a very crude description of the Coulomb instability of globular proteins, these low values of Z2/n ≃ 1–10 ≪ n, together with large surface energies (i.e., a ≃ 10−2–10−3), imply that the fissibility parameter for these charged gas phase proteins is low, i.e., X ≪ 1. Accordingly, only thermally activated protein fission over high barriers may be manifested, insuring the structural integrity of the charged protein in the mass-spectrometric experiments. Kinetic energy release studies (41, 42) of the melittin peptide (Z = 3, n = 26) reveal energetic ionic dissociation (ΔE = 1.25 eV) of small fragments, presumably induced by local Coulomb effects. Further experimental and computational studies of Coulomb instability of highly charged proteins are called for.
Acknowledgments
We thank Professor Chava Lifschitz for stimulating discussions, Dr. Claude Guet for inspiring correspondence, and Professor Thomas Leisner for prepublication information. This research was supported by the James–Franck German–Israeli Binational Program on Laser–Matter Interaction.
Abbreviation
- LDM
liquid drop model
References
- 1.Bohr N, Wheeler J A. Phys Rev. 1939;56:426–450. [Google Scholar]
- 2.Meitner L, Frisch O R. Nature (London) 1939;143:239–240. [Google Scholar]
- 3.Frenker S, Metropolis N. Phys Rev. 1947;72:914–925. [Google Scholar]
- 4.Möller P, Madland D G, Sierk A J, Iwamoto A. Nature (London) 2001;409:785–790. doi: 10.1038/35057204. [DOI] [PubMed] [Google Scholar]
- 5.Sattler K, Muhlbach J, Echt O, Pfau P, Recknagel E. Phys Rev Lett. 1981;47:160–164. [Google Scholar]
- 6.Bréchignac C, Cahuzac Ph, Carliez F, de Frutos M. Phys Rev Lett. 1990;64:2893–2896. doi: 10.1103/PhysRevLett.64.2893. [DOI] [PubMed] [Google Scholar]
- 7.Bréchignac C, Cahuzac Ph, Kebaili N, Leignier J, Sarfati A. Phys Rev Lett. 1992;68:3916–3919. doi: 10.1103/PhysRevLett.68.3916. [DOI] [PubMed] [Google Scholar]
- 8.Chandezon F, Guet C, Huber B A, Jalabert M, Maurel E, Monnand E, Ristori C, Rocco J C. Phys Rev Lett. 1995;74:3784–3787. doi: 10.1103/PhysRevLett.74.3784. [DOI] [PubMed] [Google Scholar]
- 9.Bréchignac C, Cahuzac Ph, de Frotos M, Kebaili N, Sarfati A. Phys Rev Lett. 1996;77:251–254. doi: 10.1103/PhysRevLett.77.251. [DOI] [PubMed] [Google Scholar]
- 10.Näher U, Bjornholm S, Fraundorf S, Gracias F, Guet C. Phys Rep. 1997;285:245–322. [Google Scholar]
- 11.Guet C, Biquard X, Blaise P, Blundell S A, Gross M, Huber B A, Jalabert D, Maurel M, Plague L, Rocco J C. Z Phys D. 1997;40:317–322. [Google Scholar]
- 12.Shapiro O, Kunz P J, Möhring K, Hervieux P A, Gross D H F, Madjet M E. Z Phys D. 1997;41:219–227. [Google Scholar]
- 13.Bréchignac E, Cahuzac Ph, Kebaili N, Leygnier J. Phys Rev Lett. 1998;81:4612–4615. doi: 10.1103/PhysRevLett.68.3916. [DOI] [PubMed] [Google Scholar]
- 14.Daligault J, Guet C. Phys Rev A. 2001;64:043203-1–043203-5. [Google Scholar]
- 15.Chandezon F, Tomita S, Cornier D, Grubling P, Guet C, Lebius H, Pesnelle A, Huber B A. Phys Rev Lett. 2001;87:153402-1– 153402-4. doi: 10.1103/PhysRevLett.87.153402. [DOI] [PubMed] [Google Scholar]
- 16.Chandezon F, Bergen T, Brenac A, Guet C, Huber B A, Lebius H, Pesnelle A. Phys Rev A. 2001;63:051201-1–051201-4. [Google Scholar]
- 17.Purnell J, Snyder E M, Wei S, Castleman A W., Jr Chem Phys Lett. 1994;229:333–339. [Google Scholar]
- 18.Ditmire T, Donnelly T, Rubenchik A M, Falcone R W, Perry M D. Phys Rev A. 1996;53:3379–3402. doi: 10.1103/physreva.53.3379. [DOI] [PubMed] [Google Scholar]
- 19.Ditmire T, Tisch J W G, Springate E, Mason M B, Hay N, Smith R A, Marangos J, Hutchinson M H R. Nature (London) 1997;386:54–56. [Google Scholar]
- 20.Ditmire T, Tisch J W G, Springate E, Mason M B, Hay N, Marangos J P, Hutchinson M H R. Phys Rev Lett. 1997;78:2732–2735. [Google Scholar]
- 21.Hutchinson M H R, Ditmire T, Springate E, Tisch J W G, Shao Y L, Mason M B, Hay N, Marangos J P. Philos Trans R Soc London A. 1998;356:297–315. [Google Scholar]
- 22.Ditmire T, Springate E, Tisch J W G, Shao Y L, Mason M B, Hay N, Marangos J P, Hutchinson M H R. Phys Rev A. 1998;57:369–382. [Google Scholar]
- 23.Springate E, Hay N, Tisch J W G, Mason M B, Ditmire G, Hutchinson M H R, Marangos J P. Phys Rev A. 2000;61:063201-1–063201-7. [Google Scholar]
- 24.Kou J, Nakashima N, Sakabe S, Kawato S, Ueyama H, Urano T, Kuge T, Izawa Y, Kato Y. Chem Phys Lett. 1998;289:334–337. [Google Scholar]
- 25.Card D A, Wisniewski E S, Folmer D E, Castleman A W., Jr J Chem Phys. 2002;116:3554–3567. [Google Scholar]
- 26.Lezius M, Dobosh S, Normand D, Schmidt M. Phys Rev Lett. 1998;80:261–264. [Google Scholar]
- 27.Last I, Schek I, Jortner J. J Chem Phys. 1997;107:6685–6692. [Google Scholar]
- 28.Last I, Jortner J. Phys Rev A. 1999;60:2215–2221. [Google Scholar]
- 29.Last I, Jortner J. Phys Rev A. 2000;62:013201-1–013201-9. [Google Scholar]
- 30.Lord Rayleigh L. Phil Mag. 1882;14:184–186. [Google Scholar]
- 31.Taflin D C, Ward T I, Davis E J. Langmuir. 1989;5:376–384. [Google Scholar]
- 32.Widman J F, Arrdahl C L, Davis E J. Aerosol Sci Technol. 1997;27:636–648. [Google Scholar]
- 33.Gomez I A, Tang K. Phys Fluids. 1993;6:404–409. [Google Scholar]
- 34.Pruvost L, Serre I, Duong H T, Jortner J. Phys Rev A. 2000;61:053408-1–053408-9. [Google Scholar]
- 35.Berry R S. In: Theory of Atomic and Molecular Clusters. Jellinek J, editor. Berlin: Springer; 1999. pp. 1–26. [Google Scholar]
- 36.Oganessian Y T, Yeremin A V, Popeko A G, Bogomolov S L, Buklanov G V, Chelnokov M L, Chepigin V I, Gikal B N, Gorshkov V A, Gulbekian G G, et al. Nature (London) 1999;400:242–245. [Google Scholar]
- 37.Zweiback J, Smith R A, Cowan T E, Hays G, Wharton K B, Yanovsky V P, Ditmire T. Phys Rev Lett. 2000;84:2634–2637. doi: 10.1103/PhysRevLett.84.2634. [DOI] [PubMed] [Google Scholar]
- 38.Zweiback J, Cowan T E, Smith R A, Hurtlay J H, Howell R, Steinke C A, Hays G, Wharton K B, Krane J K, Ditmire T. Phys Rev Lett. 2000;85:3640–3641. doi: 10.1103/PhysRevLett.85.3640. [DOI] [PubMed] [Google Scholar]
- 39.Last I, Jortner J. Phys Rev Lett. 2001;87:033401-1–033401-4. doi: 10.1103/PhysRevLett.87.033401. [DOI] [PubMed] [Google Scholar]
- 40.Last I, Jortner J. Phys Rev A. 2001;64:063201-1–063201-11. [Google Scholar]
- 41.Cherokee S, Hoaglund-Hyzer A, Counterman E, Clemmer D E. Chem Rev. 1999;99:3037–3079. doi: 10.1021/cr980139g. [DOI] [PubMed] [Google Scholar]
- 42.Laskin J, Lifshitz C. J Mass Spectrom. 2001;36:459–478. doi: 10.1002/jms.164. [DOI] [PubMed] [Google Scholar]