Aligning phenotypic and genetic trends: comparing trends from threshold and linear models in pigs

Abstract

This study aimed to compare phenotypic and genetic trends when genomic breeding values (GEBV) were computed using linear and threshold models or when GEBV were transformed to the probability scale for wean-to-finish mortality (WFM) and front leg structure (FLS). A total of 270,064 and 998,289 observations were available for WFM measured on crossbred and FLS measured on purebred, respectively. The total number of animals in the analyses was 577,947 for WFM and 1,079,080 for FLS. The number of purebred genotyped animals was 274,365 and 239,075 for WFM and FLS, respectively. Incidences were 9.71% for WFM and 13.31% for FLS. Heritabilities on the observed scale were 0.04 for WFM and 0.23 for FLS, whereas on the liability scale they were 0.08 and 0.38. When using linear models, we applied two approaches to convert GEBV to probabilities: (1) we standardized the GEBV deviated from the mean GEBV based on the additive genetic variance and then transformed them into probabilities; (2) we used an approximation to the liability scale and then transformed the approximated liabilities to the probability scale. Genetic and phenotypic trends were obtained by averaging GEBV and phenotypes based on the birth year for animals with phenotypes. Spearman correlations among raw and transformed GEBV within trait were all ≥0.98, suggesting minimal changes when selecting candidates based on GEBV from linear or threshold models and their transformation to probabilities. The slopes of genetic trends based on raw GEBV from linear models were significantly different from zero. The sign of the slopes suggests that selections have been directed toward desirable phenotypes. After the transformation into the probability scale, genetic trends computed based on GEBV from linear and threshold models aligned the phenotypic trend for FLS. For WFM, the genetic and phenotypic trends showed less alignment, possibly due to the lower trait incidence, low heritability, and susceptibility to environmental influences. The close association between genetic and phenotypic trends for FLS was also confirmed by the slopes of the regressions of GEBV on the probability scale or phenotypes on the year of birth. Results of the present study demonstrated that GEBV from the linear scale can be transformed into the probability scale with a strong alignment with GEBV transformed from the liability scale. Aligning genetic and phenotypic trends, however, depends on the model, heritability, and trait incidence.

Breeding values for categorical traits can be estimated using both threshold and linear models and can be transformed to probabilities. The alignment between genetic and phenotypic trends is a function of the used model and the heritability and incidence of the trait.

Introduction

Phenotypes considered in animal breeding schemes can be divided into continuous numerical values and categorical discrete classes. The former are usually analyzed using a linear model, whereas the latter using a threshold model (Hoeschele, 1988). In theory, discrete phenotypes should be analyzed with threshold models, especially when only two levels are represented, because they better account for the probability structure of categorical data (Gianola, 1982), and they consider the asymmetry and extreme incidence of some categories (Arango et al., 2005). Moreover, one advantage of threshold models is that transforming estimated breeding values (EBV) from the liability into the probability scale is straightforward. However, threshold models imply a nonlinear system of equations, and they are more expensive to be applied in terms of computing time and model implementation (Hidalgo et al., 2024a).

On the other hand, linear models, with their simpler computations and faster implementation, have opened a new avenue of research. Several studies have explored the potential of linear models in analyzing categorical data and compared them with threshold models (Ramirez-Valverde et al., 2001; Carlén et al., 2006; Silvestre et al., 2007). Abdel-Azim and Berger (1999) analyzed different aspects of threshold models in estimating variance components and accuracy of genetic predictions. The authors found that accuracy increased with normally distributed incidences, a larger number of categories, and more balanced data. While some studies found threshold models to outperform linear models (Meijering and Gianola, 1985; Hoeschele, 1988), others (e.g., Koeck et al., 2010; Cappelloni et al., 2022) reported very similar results between the two models in terms of transformed variance components and breeding values (i.e., very high Pearson and Spearman correlations). Recently, Hidalgo et al. (2024a) proposed some equations to convert EBV from the observed to probability scale. They found good agreement in the genetic evaluation of calving ease, with an incidence of assisted calvings of about 7%. Hidalgo et al. (2024b) analyzed health traits in U.S. Holsteins using linear and threshold models, and they tested the proposed transformation. These authors concluded that linear models led to a robust approximation to threshold models and, when the incidence of the trait is not very low, their proposed approximation from observed to liability and probability scale works well.

For traits with discrete phenotypes, having EBV in the probability scale can be helpful when comparing phenotypic and genetic trends. Phenotypic trends show how a particular trait changes over time. Assessing genetic trends is crucial for determining the effectiveness of breeding schemes and providing breeders with valuable insights to develop future selection programs (Hamadani et al., 2021). The study of genetic and phenotypic trends improves the understanding of the evolution of breeding programs. It helps to analyze the impact of genetic selection compared to previous generations and to check whether the results align with the expected ones, that is, if the breeding program is effective (Kuthu et al., 2017). Moreover, genetic trends give insights into the rate of improvement (Bosso et al., 2007). A good alignment between phenotypic and genetic trends indicates that genetic selection and phenotypic expression are going in the same direction, which is desirable to improve the population.

Traditionally, genetic trends were based on breeding values estimated using pedigree only, whereas more recently, they show how genomic breeding values (GEBV) change over time. Masuda et al. (2018) compared genetic trends from single-step genomic BLUP (ssGBLUP) and traditional BLUP models for milk production traits of U.S. Holsteins. These authors reported divergent trends and concluded that ssGBLUP better accounts for the effects of preselection that are not accounted for by traditional BLUP in populations undergoing genomic selection. According to Abdollahi-Arpanahi et al. (2021), the starting point of effective genomic selection can be inferred by the time when estimated genetic trends based on BLUP or ssGBLUP start to diverge. Thus, if a population is under genomic selection, the genetic trends should be based on GEBV to better represent the progress attained in the population.

Thus, this study aimed to compare phenotypic and genetic trends when GEBV were computed using linear and threshold models or when GEBV were transformed to the probability scale for wean-to-finish mortality (WFM) and front leg structure (FLS), which have different heritabilities and phenotypic incidences. A second objective was to compare GEBV transformed from the linear and liability scales into the probability scale.

Materials and Methods

Animal Care and Use Committee approval was not needed as data were obtained from preexisting databases.

The Pig Improvement Company (PIC, a Genus company, Hendersonville, TN) provided the datasets used in this study. The considered phenotypes were: (1) WFM scored as 1 for alive and 2 for dead; (2) FLS scored as 2 for values 1 to 4, and 1 for values 5 to 9. As reported in Figure 1, FLS were visually assessed. Animals with low (1 to 4) FLS values are undesirable, whereas the animals with larger values (5 to 9) are desirable because they have better FLS. We binarized FLS with the objective of testing the correspondence between linear and threshold models’ GEBV and the robustness of the approximation to liability scale under the stricter conditions. In addition, in this way, we evaluated two binary traits differing in incidence (9.71% for WFM vs. 13.31% for FLS) and could make conclusions about the impact of the trait incidence on the approximation to liability scale and the alignment between genetic–phenotypic trends.

Figure 1.

Visually assessed front leg scores. In a scale from 1 to 9, 1 to 4 is not desirable (binary phenotype = 2) and from 5 to 9 is desirable (binary phenotype = 1)

WFM was measured on crossbred animals produced by purebred terminal sire line A, whereas FLS in purebred animals from terminal sire line B. The number of animals with phenotypes was 270,064 (243,852 scored as 1 and 26,212 scored as 2) for WFM and 998,289 (865,411 scored as 1 and 132,878 scored as 2) for FLS. The numbers of genotyped purebred animals were similar for the two traits: 274,365 and 239,075 for WFM and FLS, respectively.

Both traits were analyzed using single-trait animal models that considered the mean as a fixed effect and the contemporary group, litter, and animal as random effects. In the analyses for WFM, Unknown Parent Groups were also considered as random effects. Variance components and heritabilities were computed using the gibbsf90+ software (Misztal et al., 2014) via a Gibbs sampling approach with 100,000 samples, a burn-in of 10,000, and saving one sample every 10. WFM had low heritability (0.04 ± 0.01 for linear and 0.08 ± 0.01 for threshold models) and low incidence (9.71% of undesirable scores = 2), whereas FLS had higher heritability (0.23 ± 0.01 for linear and 0.38 ± 0.01 for threshold models) and higher incidence (13.31% of undesirable scores = 2). Table 1 summarizes the analyzed datasets and reports the estimated variance components.

Table 1.

Description of the involved datasets

	Wean-to-finish mortality1	Front leg structure2
Phenotypes 1 (desirable) 2 (undesirable) Incidence	270,064 243,852 26,212 9.71%	998,289 865,411 132,878 13.31%
Total animals in pedigree	577,947	1,079,080
Genotypes3	274,365	239,075
Contemporary groups	426	30,895
Litters	28,263	187,696
Linear model
Variance contemporary group	0.0029	0.0065
Variance litter	0.0046	0.0022
Variance animal	0.0036	0.0247
Variance residual	0.0752	0.0731
Heritability	0.04 ± 0.01	0.23 ± 0.01
Threshold model
Variance contemporary group	0.1193	0.2940
Variance litter	0.1462	0.0724
Variance animal	0.1138	0.8439
Variance residual	1.000	1.000
Heritability	0.08 ± 0.01	0.38 ± 0.01

¹Records measured on crossbred animals.

²Records measured on purebred animals.

³Genotypes from purebred animals.

GEBV were estimated using single-step GBLUP (ssGBLUP; Legarra et al., 2009; Christensen and Lund, 2010) applying linear (LIN) and threshold (THR) models. GEBV were computed using blup90iod3 for the linear model and cblup90iod2 (Misztal et al., 2014) for the threshold model. Based on Hidalgo et al. (2024a), the raw breeding values from linear models, that is, GEBV on the observed scale, were transformed into probabilities of death (for WFM) or having bad leg structure (for FLS) using two methods:

(1) M1: transformation into probabilities using standardized breeding values deviated from the mean breeding value. The standardization was based on the additive genetic standard deviation (i.e., the square root of the additive genetic variance):

$${\displaystyle \begin{array}{l}{\displaystyle P_i=1-\mathrm{\Phi }\left(\frac{u_i-{\mu }_u}{{\sigma }_u}\right),}\end{array}}$$

where P_i is the probability of dying or presenting a bad FLS for animal $i$, $\mathrm{\Phi }$ is the standard cumulative distribution function, $u_i$ is the estimated breeding value of animal i; µ_i is the mean of EBV, and ${\sigma }_u$ is the genetic standard deviation.

(2) M2: approximation to the liability scale using the following formula from Hidalgo et al. (2024a).

$${\displaystyle \begin{array}{l}{\displaystyle GEB{V}_{i_l}\approx \frac{GEB{V}_{i_o}}{\sqrt{{\sigma }_{e_o}^2\ast (1-\frac{h_o^2}{h_l^2})}},}\end{array}}$$

where $GEBV$ are the genomic EBV for animal $i$ on the liability ($l$) and observed ($o$) scales, ${\mathrm{\sigma }}_{{\mathrm{e}}_{\mathrm{o}}}^2$ is the residual variance on the observed scale, and $h^2$ are heritabilities on the liability ($l$) and observed ($o$) scales.

After approximating the GEBV from the observed to the liability scale, probabilities were obtained using the following formula (Hidalgo et al., 2024a):

$${\displaystyle \begin{array}{l}{\displaystyle P_i=\mathrm{\Phi }\left(\frac{t-{\mu }_u-u_i}{{\sigma }_e}\right),}\end{array}}$$

where $t$ is the threshold, and ${\sigma }_e$ is the residual standard deviation. The remaining terms were defined before. In the M2 approach, the approximation to the liability scale was only needed for GEBV obtained with linear models; GEBV from threshold models, which were already on the liability scale, were transformed into probabilities directly using the latter formula.

Pearson correlations were computed between the phenotypes and the different sets of GEBV. Spearman correlations were used to evaluate potential differences in the ranking of animals according to the different GEBV.

Genetic trends were computed for both traits by averaging the GEBV of animals with phenotypes according to their birth year. Phenotypic trends were also computed by calculating the incidence of the trait by year of birth. Moreover, GEBV were regressed on the animals’ birth year, and the slopes of the regression were compared. Genetic trends were also analyzed for the sires of the animals with phenotypes to compare their slopes.

Results and Discussion

Correlations between GEBV in different scales

Table 2 shows the correlations between the phenotypes and GEBV in different scales. For FLS, Spearman correlations among GEBV were all ≥0.99, whereas for WFM, correlations were ≥0.98. GEBV for WFM were less correlated with the phenotype compared to GEBV for FLS (≥0.36 vs. ≥0.58; Table 2). These results align with the findings reported by Hidalgo et al. (2024b), who reported correlations among raw and approximated GEBV (i.e., M2 in the present study) ≥0.95 for four health traits in U.S. Holsteins. Cappelloni et al. (2022) computed EBV for respiratory and enteritis diseases in three pig breeds (i.e., Italian Large white, Italian Landrace, and Italian Duroc), and they reported Spearman correlation ≥0.97. Piwczyński and Kowaliszyn (2013) analyzed fertility traits in Merino sheep using linear and threshold models; these authors reported a high correlation (0.97) between rankings of EBV of animals estimated using the linear and threshold models. Hansen et al. (2004) reported similar predictions of transmitting abilities of sires for stillbirth in Danish Holsteins, which were estimated using threshold or linear models. Other studies also reported correlations between EBV from the threshold and linear models close to 1 (Carlén et al., 2006; Piwczyński and Mroczkowski, 2009). High correlations between GEBV estimated using linear and threshold models ensure that both would lead to similar choice of selection candidates and, therefore, genetic progress. The high correlations reported by several studies are the product of the robustness of linear models when the traits depart from normality and homogeneous variance assumptions. This strength increases as the number of records increases and when the incidence of the traits is not very extreme (i.e., it is not close to 0% or to 100%), reaching its maximum at 50% incidence, that is, when there is no asymmetry in the distribution of the binary phenotypes.

Table 2.

Pearson correlations between phenotypes and raw and transformed genomic breeding values (GEBV) and Spearman correlations among different sets of GEBV

	Phenotype	Threshold raw	Linear raw	Threshold M1	Linear M1	Threshold M2	Linear M2
Phenotype		0.61	0.66	0.58	0.66	0.63	0.61
Threshold raw	0.36		0.99	1.00	0.99	1.00	0.99
Linear raw	0.43	0.98		0.99	1.00	0.99	1.00
Threshold M1	0.36	1.00	0.98		0.99	1.00	0.99
Linear M1	0.41	0.98	1.00	0.98		0.99	1.00
Threshold M2	0.37	1.00	0.98	1.00	0.98		0.99
Linear M2	0.44	0.98	1.00	0.98	1.00	0.98

Values above the diagonal refer to front leg structure, whereas values below the diagonal to wean-to-finish mortality.

In the present study, the computing time for threshold models was around 10 h, whereas for linear models, it was less than 1 h. Thus, linear models delivered similar results at 10 times lower computing costs. Recently, Hidalgo et al. (2024a) analyzed calving ease and birth weight in Angus by comparing threshold and linear models: the authors reported that linear models were 5× faster to converge than threshold models. Computational cost became one of the most important parameters when dealing with breeding values estimation, especially with genomics, since the number of available genotypes reached millions in different species (Cesarani et al., 2022; Wiggans and Carrillo et al., 2022; Alvarenga et al., 2023). The greater computing time needed for threshold models could help understand why most categorical calving traits in dairy cattle are evaluated using linear models worldwide (Interbull, 2013).

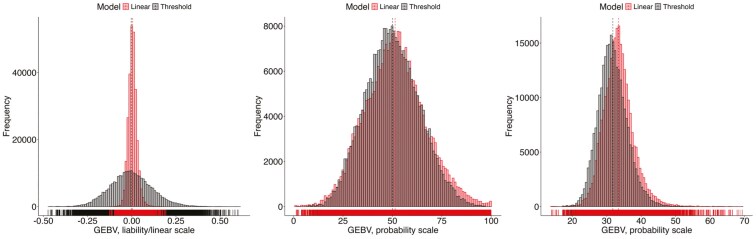
Figures 2 and 3 show the distributions of GEBV of animals with phenotypes on the observed and liability scales (i.e., raw breeding values estimated using linear and threshold models), and after the transformation into probabilities for WFM and FLS, respectively. An overlapping distribution would indicate a perfect alignment between linear and threshold models. Raw GEBV (on the left panel in Figures 2 and 3) had the most divergent distributions, as expected, because they are in different scales (i.e., observed and liability). However, the distributions overlapped noticeably on the probability scales (center and right panels in Figures 2 and 3). Contrasting WFM and FLS, the GEBV distributions in the probability scale from linear and threshold models presented a better agreement for WFM, even though FLS has a higher incidence and heritability. This was particularly true for M1 (center panel in Figures 2 and 3), whereas basically no differences were observed regarding M2 transformation (right panel in Figures 2 and 3). A possible explanation for this difference could be that the binarized leg score was derived from the original categorical scoring system from 1 to 9, which is inherently subjective and may lead to potential variation in classification, especially for adjacent scores.

Figure 2.

Breeding values distributions for wean-to-finish mortality on the observed and liability scale (i.e., raw breeding values, on the left panel), and on the probability scale of death using M1 (center panel) and M2 (right panel)

Figure 3.

Breeding values distributions for front leg structure on the observed and liability scale (raw breeding values, on the left panel), and on the probability scale of having bad leg structure using M1 (center panel) and M2 (right panel)

In practice, for selection, method 2 (i.e., the one involving the use of ${\sigma }_e$ or ${\sigma }_p$) should be preferred because the scale of GEBV in probability is close to the real probability. For example, in the probability of GEBV with ${\sigma }_u$, it can be +10%, but with ${\sigma }_e$ (${\sigma }_p$), it can be +1%. In reality, we can expect a 1% increase in incidence but not a 10% increase.

Genetic and phenotypic trends

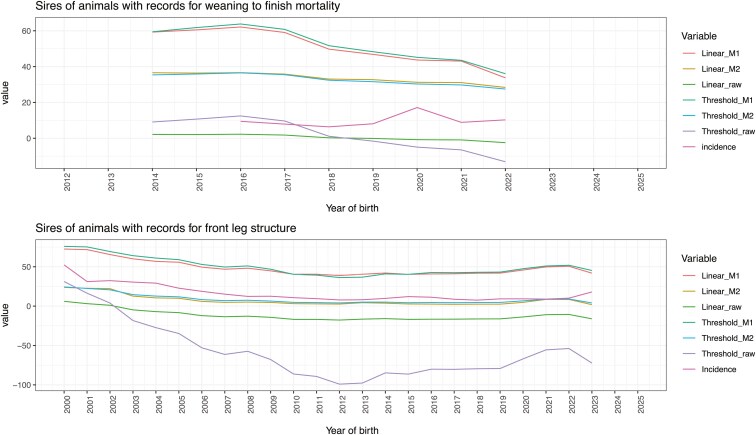
Genetic and phenotypic trends for WFM are reported in Figure 4. The genetic trends within transformation methods were very similar; however, the trajectory of the phenotypic incidence (i.e., the phenotypic trend) was less aligned with the genetic trends. The phenotypic trend for WFM showed variability, potentially reflecting the occurrence of environmental challenges: there was a decreasing phenotypic trend until 2018, followed by an increase that peaked in 2020; after that, the incidence slightly decreased the year later and reached a plateau of around 9%. The variation between phenotypic and genetic trends could be due to this trait’s very low incidence and genetic variability (i.e., heritability <0.05), suggesting that controlling the environment would help move phenotypes in the desirable direction. Genetic trends for sires of animals with phenotypic records reflect the results reported for phenotyped animals (Figure 6).

Figure 4.

Genetic trends and phenotypic incidence rate according to the year of birth of animals with records for wean-to-finish mortality. Raw GEBV were multiplied by 100 to align the scale of the other breeding values

Figure 6.

Genetic trends for sires of animals with records for wean-to-finish mortality (top) or front leg structure (bottom). Raw GEBV were multiplied by 100 to align the scale of the other breeding values

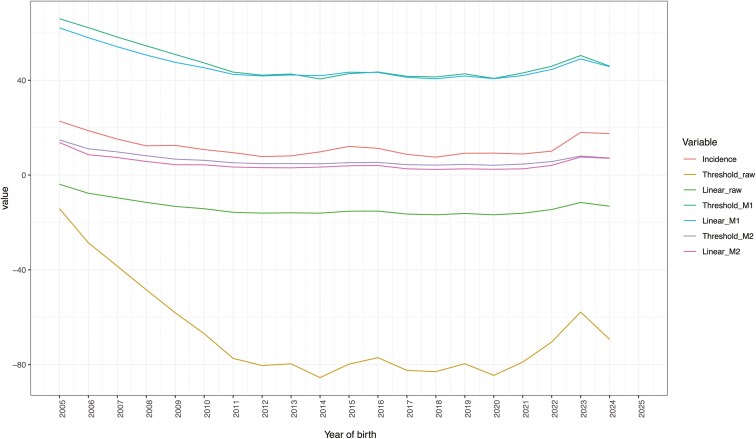
Figure 5 shows the genetic trends and phenotypic incidence across years of birth for animals with records for FLS. As observed in the correlations among GEBV, the genetic trends within transformed methods were also very similar, whereas a larger difference was observed between linear and threshold raw GEBV. Very similar genetic trends between threshold and linear models were already reported by previous studies (e.g., Silvestre et al., 2007). Estimated genetic trends obtained using linear or threshold models for clinical mastitis in Norwegian dairy cattle were compared by Heringstad et al. (2003). The latter authors reported that linear models yielded underestimated genetic trends; however, they compared the mean EBV on the probability scale (from threshold models) against the mean EBV in the observed scale (from linear models). In contrast, studying calving ease in the American Angus beef cattle population, Hidalgo et al. (2024a) compared the estimated genetic trends from linear and threshold models after transforming GEBV from both models into the probability scale, obtaining a good agreement. The transformation on the probability scale using M2 (Figure 5) provided GEBV that better followed the phenotypic trend because this transformation considers the estimated threshold value; the good alignment between genetic and phenotypic trends could also be favored by this trait’s higher incidence and moderate heritability. The transformation using M2 allowed to have genetic trends similar to phenotypic trend also for sires of the animals with phenotypic records (Figure 6).

Figure 5.

Genetic trends and phenotypic incidence rate according to the year of birth of animals born since 2005 with records for front leg structure. Raw GEBV were multiplied by 100 to align the scale of the other breeding values

Table 3 reports the results of the regression of GEBV on birth year: all slope values reported in Table 3 were significantly different from zero. According to the slope, GEBV for WFM decreased over time for both the animals with phenotypes and their sires, suggesting that selection has been directed toward reducing mortality despite the trait’s low heritability. For this trait, animals were scored as 1 for “alive” and 2 for “dead”, that is, the lower the GEBV, the better. As also observed in Figure 4, there is less alignment between the genetic trend and the phenotypic trend for WFM, possibly due to the trait’s very low heritability and varying environmental challenges. The slopes computed for FLS were all negative, suggesting that phenotypes and GEBV are both decreasing with the years: this means that the trait is improving since lower values are desirable (the animals were scored as 1 when they had good leg structures, and as 2 when they had bad leg structures). This result confirms what was already observed from the graphical representation of phenotypic and genetic trends, especially when considering GEBV transformed using M2 (Figure 5). Looking at the values computed for sires, slopes for transformed GEBV (M1 and M2) for both WFM and FLS were more negative (favorable) than those for animals with phenotypes, confirming that animals chosen as sires of the next generations are the best animals of the population.

Table 3.

Slope (standard errors in parentheses) of the regression of GEBV on the year of birth of all animals with records or their sires

	Animals with phenotypes		Sires
	WFM1	FLS	WFM	FLS
GEBV linear raw2	−0.33 (0.002)	−0.35 (0.002)	−0.63 (0.05)	−0.62 (0.03)
GEBV threshold raw2	−1.87 (0.01)	−2.14 (0.009)	−3.62 (0.25)	−3.27 (0.11)
GEBV linear method 1	−2.16 (0.01)	−0.65 (0.003)	−3.79 (0.28)	−0.93 (0.03)
GEBV threshold method 1	−2.18 (0.01)	−0.80 (0.003)	−3.88 (0.26)	−1.06 (0.03)
GEBV linear method 2	−0.59 (0.004)	−0.26 (0.002)	−1.12 (0.09)	−0.59 (0.03)
GEBV threshold method 2	−0.66 (0.004)	−0.29 (0.002)	−1.28 (0.09)	−0.57 (0.02)

¹WFM = wean-to-finish mortality; FLS = front leg structure.

²GEBV raw were multiplied by 100 to align the other scales.

Conclusion

WFM and FLS in pigs were analyzed using threshold and linear models. GEBV estimated with the two models were highly correlated, and their transformation into the probability scale allowed for a better alignment of their distribution. For categorical traits, comparing phenotypic trends with genetic trends from GEBV in observed or liability scales (i.e., raw GEBV from linear and threshold models, respectively) is improper because they are not on the same scale. The GEBV must be transformed to the probability scale prior to the comparisons. Genetic trends assessed based on the probability scale followed phenotypic trends closer for FLS than WFM because of the higher incidence and moderate heritability of the leg score. The transformation method based on M2 seems to be preferable to have a better alignment. Alignment between phenotypic and genetic trends is less expected for traits with low incidence and heritability, independently of the scale of the EBV.

Glossary

List of abbreviations:

EBV

pedigree-based estimated breeding values

GEBV

genomic estimated breeding value

WFM

wean-to-finish mortality

FLS

front leg structure

ssGBLUP

single-step genomic best linear unbiased predictor

LIN

linear model

THR

threshold model

M1

transformation into probabilities using standardized breeding values

M2

approximation to the liability scale

Author contributions

Alberto Cesarani (Formal analysis, Investigation, Methodology, Writing—original draft, Writing—review & editing), Jorge Hidalgo (Methodology, Writing—original draft, Writing—eview & editing), Matias Bermann (Methodology, Writing—review & editing), Shogo Tsuruta (Methodology, Software, Writing—review & editing), Ching-Yi Chen (Data curation, Resources, Writing—review & editing), Justin Holl (Data curation, Resources, Writing—review & editing), and Daniela Lourenco (Conceptualization, Funding acquisition, Project administration, Supervision, Writing—review & editing)

Conflict of interest statement

The authors declare no conflicts of interest.