Transitions between dynamical states of differing stability in the human brain

Abstract

What mechanisms underlie the flexible formation, adaptation, synchronization, and dissolution of large-scale neural assemblies from the 10¹⁰ densely interconnected, continuously active neurons of the human brain? Nonlinear dynamics provides a unifying perspective on self-organization. It shows that the emergence of patterns in open, nonequilibrium systems is governed by their stability in response to small disturbances and predicts macroscopic transitions between patterns of differing stability. Here, we directly demonstrate that such transitions can be elicited in the human brain by interference at the neural level. As a probe, we used a classic motor coordination paradigm exhibiting well described movement states of differing stability. Functional neuroimaging identified premotor (PMA) and supplementary motor (SMA) cortices as having neural activity linked to the degree of behavioral instability. These regions then were transiently disturbed with graded transcranial magnetic stimulation, which caused sustained and macroscopic behavioral transitions from the less stable out-of-phase to the stable in-phase movement, whereas the stable pattern could not be affected. Moreover, the strength of the disturbance needed (a measure of neural stability) was linked to the degree of behavioral stability, demonstrating the applicability of nonlinear system theory as a powerful predictor of the dynamical repertoire of the human brain.

Imaging of the living human brain routinely reveals patterns corresponding to the synchronized action of billions of neurons (1). The brain's formation of these large-scale distributed neural assemblies and the rapid transition between them is a striking example of self-organization. In complex systems far from equilibrium, nonlinear systems theory has proposed that the decisive parameter governing such collective emergent behavior is stability to small-scale disturbances; which dynamic patterns get selected from the vast array of possible combinations depends on their relative stability (2). Nonlinear systems exhibit pronounced susceptibility to small disturbances due to a hallmark property called “sensitive dependence on initial conditions,” meaning that minute changes to the system's state result in large-scale alterations.

A further fundamental prediction of this approach is that self-organization depends on the occurrence of sudden macroscopic transitions between states of differing stability (usually called phase transitions; ref. 3). Therefore, if the presence of transitions between differentially stable patterns could be established, this would uncover a fundamental determinant of the dynamic repertoire of the central nervous system (4). Consequently, transition, synchronization and stability phenomena in neuronal membranes, cells, and small assemblies have been studied intensively (5–7). In humans, correlative evidence comes from the observation of electrophysiological changes as a consequence of alterations of stability in motor behavior, an area to which this theory has been applied with particular success (8–10). However, a direct demonstration of the applicability of nonlinear dynamics to the brain would require the reverse finding, showing that interference at the neural level can cause large-scale transitions in behavior.

The goal of the present study was to use this strategy for a characterization of neural activation patterns of differing stability and the direct demonstration of transitions between stable and unstable states in the intact human brain. For this, it was necessary to (i) have two clearly distinct behavioral states of differing stability, (ii) map out the neural activation patterns underlying these states, (iii) demonstrate differing stability of these patterns by interfering at the neural level, and (iv) attempt to induce transitions between them, again by introducing neural disturbance. For steps iii and iv, the associated behavior served as the target measure; changes in behavior were monitored to quantify the effects of the introduced neural interference.

In the used motor experiment (11) subjects performed continuous repetitive metronome-paced movements of the index fingers of both hands simultaneously in one of two simple patterns: either in mirror (fingers moving in phase, alternatingly toward or away from the midline) or parallel (out of phase, with one finger moving toward and the other away from the midline). The parameter varied was the movement frequency, which affected the two patterns differentially. Previous work with this well established paradigm has shown that both movements were equally stable at low frequency; when the frequency was increased, the mirror pattern showed no change, whereas the parallel pattern destabilized and switched to the mirror pattern (11). Stability and transition properties of the movement studied in this experiment have been extensively analyzed mathematically on the behavioral level (12–14). One simple model (13) describes the coordination law governing the relative phase of hand movement, φ, by the differential equation φ̇ = −sin φ − (b/a)sin 2φ.

The parameter a can be interpreted as the movement frequency, while b can be seen to describe the degree to which changes in frequency affect the system's behavior (thus summarizing the neural and mechanical properties of the studied phenomenon). Analysis of this equation shows that only two fixed points exist, corresponding to the mirror, in-phase (φ = 0) and the parallel, out-of-phase (φ = π) movement. The relative stability of these patterns is governed by the term b/a. With low values of a (high values of b/a), both movement modes are comparably stable; as a is increased, the basin of attraction at φ = π becomes increasingly more shallow, leading to differential stability to disturbances of the system. Once a is increased enough that b/a reaches a critical value (0.5 in the equation quoted), the antiphase state becomes so unstable that a spontaneous transition into the mirror-mode movement occurs. The existence of a critical frequency is well established experimentally (11). Since spontaneous switches would have created a confound in our experiments that had to be avoided, we used a frequency range safely below this critical value but wide enough to result in clear changes in stability of the parallel pattern. Because varying one control parameter (frequency) differentially affected the stability of the two movement patterns while leaving all other movement parameters the same, this created an ideal situation for the neuroimaging experiment.

In a first step, we used functional neuroimaging to map out cortical areas with activity that was related to the degree of behavioral instability. During performance of the motor task, regional cerebral blood flow (rCBF) was measured with positron emission tomography. Then, transcranial magnetic stimulation (TMS; ref. 15) was used to create, via neuronal depolarization and discharge induced by magnetic induction, a transient localized disturbance of neural activity (16). This technique was used to probe cortical areas while the subjects performed parallel or mirror movements. The motor behavior now served as the target measure: We hypothesized that a disruptive stimulus applied to areas at which neuroimaging demonstrated an instability interaction effect should be able to differentially affect behavior patterns of differing stability. Specifically, since the mathematical formulation predicts the existence of only two fixed points, such an effect should take the form of pushing the less stable pattern (out-of-phase) into the stable mirror pattern but not vice versa. In our formulation of the model, the TMS stimulus should create a transient decrease in the parameter b, which describes the neural stability properties of the system, with the effect that a switch from the less stable to the mirror pattern could be observed at values of the frequency parameter a, which otherwise would be too low for this to occur. We further hypothesized that decreasing behavioral stability by increasing the frequency of the out-of-phase movement would be associated with increased susceptibility to disturbance by TMS in the neural domain (i.e., lower TMS intensities should be necessary to affect behavior). Since it is known that TMS can introduce (nonspecific) errors and changes in the temporal organization of movement performance (17), it was an essential feature of the paradigm to have two clearly and macroscopically distinct movement patterns to define and measure transitions between them and to distinguish such events from simple errors. Because TMS-induced error rates may be greater with complex movements (17), it was important also that both patterns were similarly simple and easy to perform, as ascertained by subject ratings.

Methods

Subjects.

For neuroimaging, six strongly left-handed and six strongly right-handed subjects (Edinburgh handedness scale scores of 100 or −100, respectively), age 23–41, male/female 7:5, were studied according to National Institutes of Health guidelines. Ten of these subjects were available for the TMS studies (one moved out of the area, and one became pregnant). All subjects gave written informed consent.

Neuroimaging Procedure.

Thirty-two scans per subject were acquired after injection of 10 mCi (1 Ci = 37 GBq) H₂¹⁵O during parallel and mirror movements at four frequencies (1, 1.5, 1.7, and 2 Hz) on a General Electric Advance 3D scanner in three-dimensional mode (156-cm axial field of view). Subjects were instructed to closely attend to the movement at all times and accurately perform the pattern they were assigned to do during the trial. The task order was pseudorandomized and balanced between subjects. No deviation from the proscribed movement (mirror or parallel) occurred during any trial of the positron emission tomography experiment. Data were acquired over 1 min per scan, corrected for attenuation, and reconstructed into 32 image planes (resolution, 6.5 mm). After subtraction of background activity and reorientation (18), further image processing was performed with SPM96 software (Wellcome Department of Cognitive Neurology, London). Images were normalized to an average positron emission tomography template and smoothed with a 10-mm³ Gaussian kernel filter.

All measurements per condition were averaged across subjects. State-dependent differences in global blood flow were removed using proportional scaling. Main effects as well as the interaction between movement pattern and frequency were assessed with contrasts of the adjusted task means using t statistics transformed into the z statistic. Resulting values reflecting a significance level of P < 0.001 were corrected for multiple comparisons on the cluster level as described by Friston et al. (19). Localization of maximal rCBF responses are reported within the standard space of the atlas of Talairach and Tournoux (20). Statistical maps are shown rendered on an average MRI template image.

A possible confound of the present analysis would be (nonspecific) task difficulty and concomitant differences in perceived motor or attentional effort. To investigate this, subjects rated the difficulty of each performed movement after scanning on a line marked with the numbers 1 (very easy) to 6 (very difficult). Responses were analyzed by ANOVA with movement pattern (mirror, parallel, two levels) and frequency (four levels) as factors.

TMS Procedure.

We used a figure-eight coil (5-cm wing diameter) connected to a Cadwell high-speed magnetic stimulator (Cadwell Laboratories, Kennewick, WA). Over primary sensorimotor cortex (M₁/S₁) and premotor area (PMA) the coil was oriented with handle pointed backward and 45° away from the midline. The small coil dimension and the orientation secured selective stimulation of the PMA (or M₁/S₁) of one hemisphere. Orientation over supplementary motor area (SMA) was with backward-pointing handle and coil junction in the midline. Stimulation was by double pulse (50-msec interval), with randomized onset between 4 and 8 sec after commencement of movements. Ten trials of 16 sec were performed for each studied condition.

Movement was monitored continuously by accelerometers placed on the tips of both index fingers. Their signal was numerically integrated twice, discarding linear drifts, to yield finger position. The relative phase angle of the finger positions then was calculated by the method of Schmidt et al. (21) for the entire duration of the trial.

TMS-induced changes in movement parameters were then computed for a time window of three movement cycles. Since the present experiments were concerned with sustained changes of motor behavior, but the TMS pulse induced in some cases an immediate jerk-like movement effect, the prepulse time window was aligned to end 20 msec before the first TMS pulse, and the post-TMS window started 250 msec after the second TMS pulse. The effect of TMS then was assessed by the difference between the relative phase before and after the pulse. A switch event was defined as a change in phase of at least 3 rad. As a second criterion, the pre-postphase change had to be sustained for at least one movement cycle.

Prepulse data were analyzed to evaluate adequate performance of the movement (as measured by the mean phase) and its stability (as reflected in the standard deviation of the phase). To quantify immediate movement effects of the TMS pulse, motor-evoked potentials were calculated from electromyography data (first dorsal interosseus muscle) high pass-filtered at 100 Hz and averaged relative to TMS-stimulus onset.

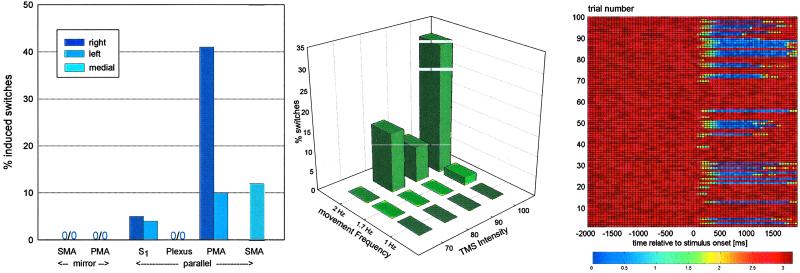
In the first TMS experiment, pulses of maximum intensity were administered to the following sites: left and right PMA, SMA, left and right brachial plexus (Erb's point), and left and right M₁/S₁. Target areas (PMA and SMA) were chosen on the basis of the neuroimaging results (below). The reason for stimulation of a peripheral (brachial plexus) site was to control for any noncortical, direct movement effects (motor-evoked potentials) caused by the procedure. To demonstrate regional specificity within the cortex, a cerebral control region was chosen also. Based on the results of the neuroimaging study (see below), we selected the primary somatosensory hand area, M₁/S₁, closely adjacent to PMA and SMA. Target sites (PMA and SMA) were investigated during parallel and mirror movements at 2 Hz, and control sites were investigated only during parallel 2-Hz movement. Effects of TMS stimulation were assessed by subjecting the number of induced switch events, as defined above, to repeated-measures nonparametric analysis of variance, the factors being stimulus condition (10 levels corresponding to the stimulus location and movement pattern combination described, as plotted in Fig. 2) and repetition (10). Planned comparisons were performed using appropriate contrasts.

Fig 2.

(Left) Number of switch events after maximum intensity TMS pulse by stimulation location and movement pattern. (Center) Number of induced switches after TMS stimulation of varying intensity of the right PMA during parallel movement of varying frequency. (Right) Color-coded raster plot of relative phase 2 sec before and after right PMA 100% TMS pulse (at 0 sec) for all subjects, 10 consecutive trials per subject, taken from experiment 2. Note the induction of sustained switches into mirror mode (phase near 0) in a proportion of trials.

The second TMS experiment was designed to explore parametrically the relationship between behavioral (in)stability and the reaction to neural disturbance. For this, we chose the right PMA as our stimulation site and performed a parametric study in which we analyzed the effect of varying the intensity of the TMS pulse (strength of neural disturbance) and the movement frequency (degree of behavioral and, by inference, neural instability) on our target behavior measure. Parallel movements at 1, 1.7, and 2 Hz were subjected to TMS stimulation at intensities of 70, 80, 90, and 100% of maximum stimulator output in a fully factorial design. Analysis of switch events was by ANOVA, the factors being movement frequency (three levels: 1, 1.7, and 2 Hz), TMS intensity (four levels: 70, 80, 90, and 100% of maximum), and repetition (10 levels).

Results

Behavioral Parameters.

Subjective difficulty increased with movement frequency [F(30,3) = 7.8, P < 0.001]. There was no difference in the subjective difficulty of the mirror and the parallel pattern [F(10,1) = 1.8, P > 0.2] and no interaction between frequency and pattern [F(30,3) = 0.7, P > 0.58]. Overall, movements were regarded as easy and effortless (range of mean ratings from 1.2 to 1.9 on a scale from 1 to 6). The analysis of the relative phase and the standard deviation of the movement as calculated from accelerometer readings demonstrated adequate performance and a significant effect of frequency on the stability (as ascertained by the standard deviation of the phase) of the out-of-phase pattern only [F(30,3) = 8.1, P < 0.001, ANOVA, mean relative phase 0.1 ± 0.05 rad for mirror movements, and 3.11 ± 0.08, 3.10 ± 0.09, and 3.12 ± 0.18 rad for parallel at 1, 1.7, and 2 Hz]. There was no significant difference between left- and right-handers.

Neuroimaging Experiment.

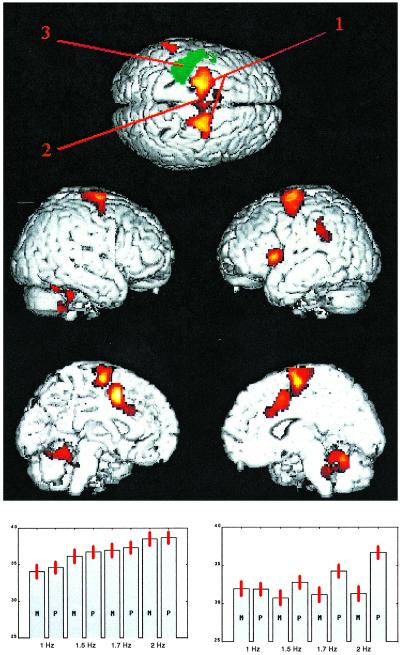
Blood flow that increased with increasing instability (i.e., during parallel but not mirror movement as frequency increased) was seen in PMA and SMA, cingulate, Broca's area, the left supramarginal gyrus, and cerebellum (Table 1 and Fig. 1 Upper and Bottom Right). No such effect was present in the M₁/S₁, which only showed monotonically increasing blood flow with frequency regardless of pattern (Fig. 1 Bottom Left). Handedness had no significant effect.

Table 1.

Maximal rCBF changes for pattern by frequency interaction contrast

Extent significance	Intensity significance, Z	Talairach space x, y, z coordinates, mm	Anatomical description (Brodmann area)
P < 0.001	6.09	−24, −12, 58	Left dorsal premotor area (BA 6)
P < 0.001	5.27	24, −8, 72	Right dorsal premotor area (BA 6)
P < 0.001	5.83	−2, 6, 48	Cingulate gyrus (BA 24)
P < 0.001	4.66	26, −56, −28	Right cerebellar hemisphere
P < 0.001	4.38	0, −52, −14	Cerebellar vermis
P < 0.001	3.79	2, −10, 62	Supplementary motor area (BA 6)
P < 0.001	3.50	0, −2, 76	Supplementary motor area (BA 6)
P < 0.002	5.62	−42, 12, 4	Broca's area (BA 45)
P < 0.03	4.14	−56, −38, 34	Left supramarginal gyrus (BA 40)

All tabulated activations were significant at the level of P < 0.001 (uncorrected). Multiple comparison corrections for cluster extent (column 1) and voxel intensity (column 2) are shown.

Fig 1.

Brain areas showing a significant (P < 0.001, corrected, voxel-level; P < 0.02, corrected, cluster-level) interaction of movement pattern and frequency. No areas showed decreased blood flow in this contrast. The Upper (superior) view also marks the sites chosen for the TMS experiment labeled 1 (PMA), 2 (SMA), and 3 (M₁/S₁). Since the latter area did not show the interaction effect, a green rendering of the main effect of frequency in this area has been added (same statistical parameters). (Bottom Left) Normalized (to a whole-brain average of 50 mm³/min) blood flow averaged for all subjects for the four used frequencies and two patterns (M, mirror; P, parallel) from a voxel (−32,−30,60) from M₁/S₁ (no interaction). (Bottom Right) A voxel (24,−12,58) typical for PMA/SMA with a pronounced frequency–pattern interaction.

TMS Experiments.

Experiment 1.

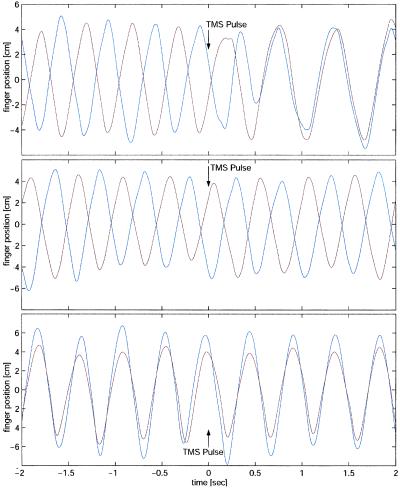
Relative to the motor potential evoked over the PMA (100%), the amplitudes of the motor-evoked potentials were 115% (M₁/S₁), 48% (SMA), and 216% (Erb), averaged for all subjects and between left- and right-sided stimulation where applicable. Comparisons of movement phase before and after stimulation during mirror (stable) movement only showed a slight change in phase centered on zero. In contrast, during parallel movement and stimulation of the PMA, SMA or to a lesser degree M₁/S₁, sustained phase changes near 3 rad occurred in a proportion of trials (Fig. 2 Right). These trials corresponded to a switch from parallel (before the TMS disturbance) to mirror movement (after). Fig. 3 shows representative finger position data from single trials in the same subject stimulated at 100% at the right PMA illustrating these findings: a tracing with no effect during 2-Hz mirror movement, a tracing in which TMS during 2-HZ parallel movement had no effect, and one in which the TMS pulse induced a sustained switch from 2-Hz parallel movement before the stimulus to in-phase movement after the pulse. In individual cases the induced mirror-movement pattern was sustained for more than 30 cycles. Average latency from TMS pulse to the onset of relative phase deviation was 175 ± 22 msec over the PMA (averaged between left and right stimulation) and 185 ± 25 msec when the SMA was stimulated.

Fig 3.

Representative data traces from single trials in the same subject, stimulated at maximum intensity at the right PMA, showing left (red) and right (blue) finger displacement. (Bottom) 2-Hz mirror movement, showing no effect. (Middle) A trial during 2-Hz parallel movement without effect of TMS stimulation. (Top) A trial in which TMS stimulation during 2-Hz parallel movement leads to sustained switch into mirror movement pattern. The time points of TMS stimulation are marked with arrows.

Switch events that were sustained for more than one complete movement cycle were counted, quantified, and analyzed using nonparametric ANOVA (Table 2 and Fig. 2 Left). The main effect of stimulation condition was highly significant [F(5,45) = 7.04, P < 0.0001]. The repetition factor was not significant. TMS disturbance of the SMA and PMA produced no switch events during mirror movement, in contrast to stimulation over the same sites during parallel movement, a highly significant difference [F(3,27) = 7.90, P < 0.0007]. Stimulation of the SMA and the PMA had significantly greater effect than stimulation at the plexus and M₁/S₁ control sites [F(3,27) = 11.6, P < 0.0001]. PMA effects were significantly greater than SMA effects [least-squares difference (LSD) test, P < 0.01], and switch events there were of the longest duration. On post hoc testing, no significant differences between the control sites and conditions were observed (LSD test). Right-sided stimulation at the PMA had a significantly more robust effect than left-sided stimulation (LSD test, P < 0.02). No other laterality effects were evident on post hoc testing.

Table 2.

TMS experiment 1: Number and mean duration of switches induced by TMS stimulation at the studied sites

Stimulation location/movement pattern	% switches (switch duration mean ± SE)
SMA mirror	0
Right PMA mirror	0
Left PMA mirror	0
Right M1/S1 parallel	5 (1.44 ± 0.05)
Left M1/S1 parallel	4 (1.19 ± 0.02)
Right plexus parallel	0
Left plexus parallel	0
Right PMA parallel	41 (2.04 ± 0.02)
Left PMA parallel	10 (2.35 ± 0.08)
SMA parallel	12 (1.21 ± 0.04)

Experiment 2.

The results are summarized in Table 3 and Fig. 2 Center. At the slowest movement frequency and stimulation of the right PMA, switches could not be induced at any TMS intensity level; at the intermediate level of behavioral instability, the highest intensity levels were needed, and at the highest frequency, low intermediate stimulus levels sufficed to induce behavioral transitions. This was reflected in a highly significant frequency by stimulation-intensity interaction in the ANOVA [F(6,54) = 10.6, P < 0.00001]. Also significant were the main effects of movement frequency [F(2,18) = 11.2, P < 0.0.008] and TMS intensity [F(3,27) = 11.2, P < 0.0002].

Table 3.

TMS experiment 2: Number and mean duration of switches induced by TMS stimulation at the right PMA as a function of stimulus intensity (70–100% of maximum) and movement frequency (1, 1.7, or 2 Hz)

Movement frequency, Hz	TMS stimulus intensity
	70%	80%	90%	100%
1	0	0	0	0
1.7	0	0	0	2 (1.57 ± 0.10)
2	0	15 (1.70 ± 0.06)	9 (1.53 ± 0.08)	32 (2.40 ± 0.02)

Discussion

The goal of the neuroimaging experiment was to map out cortical regions with a neural activity that was related to the degree of behavioral instability. Because increasing movement frequency decreases the stability of the parallel pattern but leaves the mirror pattern unaffected, the interaction of frequency and pattern was explored as the primary statistical target measure. Based on previous work showing that synaptic firing rate increases as the system nears the transition point (22) and that changes in rCBF parallel changes in synaptic firing (23), we hypothesized that differential increases of blood flow would be found as movement frequency increased. Analysis of the data with statistical parametric mapping confirmed this prediction.

The area most strongly associated with the target interaction effect was the dorsal PMA bilaterally, in accordance with previous work comparing in-phase and antiphase movements at single movement frequencies (24, 25). Convergent evidence from a multitude of studies shows that the PMA is pivotal in motor feedback control. It has been implicated in the timing, selection, preparation, and temporal control of movements (26–28). Theoretical formulations have ascribed to the PMA a central role in the maintenance of “motor set.” Lesions in this area impair motor control (29). The effect seen in the medial wall, comprising the posterior (behind the anterior commissure) SMA and a locus in the cingulate gyrus bilaterally, again is in accordance with results of previous nonparametric neuroimaging studies (24, 30, 31). SMA lesions have been shown to impair bimanual coordination (32, 33).

The analysis also uncovered unilateral effects in Broca's area and the left supramarginal gyrus. Activation in both regions has been found associated with movement preparation (34). The supramarginal gyrus has been implicated also in motor output timing, and activation of the left supramarginal gyrus has been reported when switching between bimanual motor programs, suggesting that it becomes increasingly necessary in providing timing information when movement becomes more unstable (25, 35).

While differing in details, most mathematical models of this experiment (12–14) include parameters that can be interpreted to describe neural feedback as a delayed coupling parameter between the oscillators representing hand movements. This is in good accordance with our neuroimaging findings of bilateral activation of motor feedback control centers with hand area representations that are strongly coupled transcallosally (36). In view of the fact that instability and transition phenomena can even be elicited when synchronization is attempted between the limbs of two persons, necessitating an integration of visual and proprioceptive information, it is noteworthy that the PMA receives strong multimodal, including visual, afferent input (37).

The neuroimaging findings established evidence of regionally specific correlations between behavioral instability and cortical blood flow. This set the stage for the next step of the experiment, an investigation of whether the observed rCBF changes indeed reflect differential stability on a neural level.

The first TMS experiment showed that the mirror-movement pattern could not be disturbed significantly by the neural intervention. In marked contrast, during the out-of-phase pattern, the TMS disturbance induced, in a proportion of trials, a macroscopic transition from one coordinated movement pattern (parallel) to another (mirror). These switch events were characterized by a sustained change of phase from parallel to mirror and thus represented a large-scale behavioral reorganization, a qualitatively different phenomenon from previous studies using different motor paradigms and TMS in these areas, which reported errors in movement performance and sequencing (17, 38). Errors typically induced by repetitive TMS of the SMA in these studies, such as interruption or cessation of motor output or unilateral “extra” movements, were not observed. The results thus conform completely with the prediction of the mathematical model cited above that only two stable states (at φ = 0 and φ = π) exist. Stimulation over the brain regions showing the stability effect in neuroimaging resulted in a significantly greater number of switches than did stimulation at either control site. The finding that peripheral stimulation did not evoke any switches (despite producing a large immediate movement effect, as shown by the comparison of the motor-evoked potentials) showed that the observed effect was cortical in origin and not related to any immediate movement effects of the procedure. The observation that stimulating M₁/S₁ evoked some switches might be due to the close proximity of this area to the target regions coupled with insufficient regional specificity of the TMS procedure and the limitations arising from using a standard anatomical atlas as a reference.

The first experiment confirmed our main hypothesis; TMS disturbance succeeded in disrupting only the behaviorally less stable but not the stable movement when applied specifically over the PMA and SMA, the regions that showed blood-flow changes indicative of a stability effect. This demonstrated differential stability of the neural activity patterns underlying these behavioral states. What is more, TMS pulses were shown to be able to elicit phase transitions from parallel to mirror movement by pushing the system's state from the shallow basin of attraction (out-of-phase movement) to the stable state but not vice versa.

The observed 175-msec delay between TMS pulse and onset of movement disturbance is in good agreement with previous TMS studies of PMA involvement in reaction-time tasks (39, 40). It closely corresponds to the estimated “feed-forward” time of the motor system, defined as the time that elapses before a sensory feedback input can affect motion, confirming the interpretation of our result as a TMS-induced disturbance of a motor feedback system (41).

After the first TMS experiment had demonstrated that large-scale behavioral transitions could be evoked during performance of the out-of-phase movement, we were able to use this phenomenon to study the prediction that increasing behavioral instability should be associated with increased susceptibility for disturbance in the neural domain. This was possible since (i) the paradigm enabled us to differentially manipulate behavioral (in)stability by changing frequency during parallel movement and (ii) the TMS stimulus could be applied in graded intensity, providing a relative measure of the strength of the disruption induced. Using the right PMA as our stimulation site, we performed a parametric study in which we analyzed the effect of varying the intensity of the TMS pulse (strength of neural disturbance) and movement frequency (degree of behavioral and, by inference, neural instability) on our target behavior measure (Table 2). At the slowest frequency, switches could not be induced at any TMS intensity level; at the intermediate level of behavioral instability, the highest intensity levels were needed; and at the highest movement frequency, low intermediate stimulus levels sufficed to induce behavioral transitions (Fig. 2 Center). This demonstrated that, as hypothesized, the degree of instability of the pattern predicted the strength of the pulse needed to elicit a phase transition. In other words, increasing behavioral instability was shown to correspond to increased susceptibility to disturbance on the neural level and thus, increasing neural instability. This result precisely corresponded to the effect predicted by the mathematical model: Since TMS was conceptualized as a transient decrease in the parameter b and the stability of the movement pattern is governed by the term b/a, smaller decreases of b should be necessary to induce a transition as the frequency a increases.

It is noteworthy that an isolated double pulse was sufficient in our paradigm to induce a large-scale effect on the out-of-phase movement, since this mode of stimulation results in a comparatively minor disruption compared with the much more enduring alterations induced by repetitive TMS paradigms commonly necessary to evoke measurable changes when stimulating SMA and PMA (17, 42). This demonstrates how the experimental manipulation succeeded in making the basin of attraction of the parallel-movement mode shallow. Similarly, the second TMS study demonstrated that highly significant changes in switch-induction rates could be induced and resulted when the initial conditions were changed slightly by varying movement frequency and stimulus intensity. The most compelling indication of differential susceptibility to disturbance on the neural level, however, comes from the observation that repetition trials of the TMS experiment, in which all experimental conditions were held constant, sometimes resulted in macroscopic behavioral (and by inference neural) transitions and sometimes in no significant change. This dichotomous, stochastic behavior of the system under the same stimulus and movement parameters demonstrated that even minute variations in the initial conditions occurring in a trial-by-trial repetition could lead to macroscopically differing neural consequences.

In conclusion, this combined neuroimaging–TMS study demonstrated neuronal dynamics that conformed to the predictions of nonlinear systems theory. We were able to characterize neural activity patterns of differing stability and induce switches between two clearly defined and distinct modes of behavior by intervention on the neural level. From the point of view of classical neuroscience, the results are best described as a motor-control feedback system placed under different demands by mirror and parallel movements, leading to an increased susceptibility to disturbance during the latter by TMS. The present analysis shows these two interpretations to be entirely consistent, underscoring the potential of nonlinear dynamics as a unifying account of large-scale behavior of complex systems.

Abbreviations

• rCBF, regional cerebral blood flow

• TMS, transcranial magnetic stimulation

• M₁/S₁, primary sensorimotor cortex

• PMA, premotor area

• SMA, supplementary motor area