Interchain vs. intrachain energy transfer in acceptor-capped conjugated polymers

Abstract

The energy-transfer processes taking place in conjugated polymers are investigated by means of ultrafast spectroscopy and correlated quantum-chemical calculations applied to polyindenofluorenes end-capped with a perylene derivative. Comparison between the time-integrated luminescence and transient absorption spectra measured in solution and in films allows disentangling of the contributions arising from intrachain and from interchain energy-migration phenomena. Intrachain processes dominate in solution where photoexcitation of the polyindenofluorene units induces a rather slow energy transfer to the perylene end moieties. In films, close contacts between chains favors interchain transport of the excited singlet species (from the conjugated bridge of one chain to the perylene unit of a neighboring one); this process is characterized by a 1-order-of-magnitude increase in transfer rate with respect to solution. This description is supported fully by the results of quantum-chemical calculations that go beyond the usual point-dipole model approximation and account for geometric relaxation phenomena in the excited state before energy migration. The calculations indicate a two-step mechanism for intrachain energy transfer with hopping along the conjugated chains as the rate-limiting step; the higher efficiency of the interchain transfer process is mainly due to larger electronic coupling matrix elements between closely lying chains.

Energy transfer is a key process in the working mechanism of a number of opto-electronic devices based on conjugated materials. This is the case for instance in electroluminescent displays where one can take advantage of energy transfer to tune the color of the emitted light when the active layer includes several materials with different optical gaps (1–5). In addition to providing an efficient technique for internal color conversion, polymer–polymer and polymer–dye blends have been shown also to lead to a significant improvement in photoluminescence (PL) and electroluminescence (EL) quantum efficiencies (6–8). Since most conjugated polymers are characterized by the presence of a distribution of segments with distinct conjugation lengths, optical absorption in the inhomogeneously broadened density of states usually leads to unidirectional energy migration to lower energy sites (9). Thus, controlling the flow of excitations across the polymer material is of importance to limit luminescence quenching due to energy transfer to defects.

In the case of solar cells, charge generation usually requires the migration of the electronic excitations induced by light absorption toward dissociation zones (such as interfaces in blends made of different materials) (10, 11). Research in this field aims at mimicking the powerful antenna machines that nature has designed through evolution to harvest solar light and funnel the energy to the photosynthetic reaction centers (12).

A most striking demonstration of ultrafast energy transfer in conjugated polymers is the recent discovery of highly sensitive biological and chemical sensors based on reversible fluorescence quenching in a polyanionic poly(p-phenylenevinylene) (13). The use of a conjugated polymer was found to lead to a greater than 1 million-fold amplification of the sensitivity to luminescence quenching relative to that of small molecules with similar structures. The work by Chen et al. (13) has raised a considerable amount of interest in developing a detailed understanding of the mechanisms for energy migration in conjugated polymers. One of the main issues concerns the relative efficiencies of interchain versus intrachain energy-transfer processes. This problem has been elegantly tackled by Schwartz and coworkers, who have demonstrated recently that in an alkoxy-substituted poly(p-phenylenevinylene), exciton diffusion along the chain is slow in an environment where interchain interactions are inhibited (through incorporation of single conjugated chains in the pores of a silica matrix) due to weak dipole coupling of the excitations along the chain direction (14, 15).

At this stage, it is worth stressing that by intrachain energy migration we mean hopping of electronic excitations along a single polymeric chain that adopts a rigid rod-like conformation in the absence of any chain–chain contact. Depending on the chemical structure of the conjugated polymer and its “history” (sample preparation parameters, nature of solvent, etc.), various conformations can form such as the defect cylinder or defect coil where π–π interactions stem from the collapse of single conjugated chains (16). For instance, experimental investigations using single-molecule spectroscopy have suggested the presence of multiple funnels associated with chain folding in an alkoxy poly(p-phenylenevinylene) derivative; these funnels form “a landscape for pseudo intrachain energy transfer,” which drives the excitons toward quenching sites (16).

Guest–host systems are also attractive materials for investigating energy-migration processes. Recent steady-state PL measurements by List et al. have demonstrated that in a solid-state blend of ladder-type poly-p-phenylene (L-PPP, host) and a molecular energy acceptor (guest), energy transfer occurs in a two-step process (17). The first is thermally activated migration of the exciton within the donor polymer to a point sufficiently close to the acceptor that resonance energy transfer from the host to the guest can occur. The latter step is described most often in the framework of the Förster model (18). This model is based on the weak coupling limit of radiationless transition theory, i.e., it is assumed that the energy-transfer process occurs after vibrational relaxation in the donor-excited state; in addition, the electronic coupling matrix element involved in the expression of the transfer rate is usually approximated using the point–dipole model. Note that recent time-resolved fluorescence data are consistent with dispersive relaxation dynamics of the photoexcitations in a polyfluorene film via incoherent hopping among localized states (19).

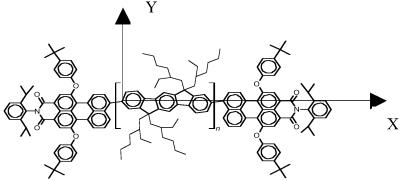
Here, we have adopted another strategy to assess intrachain and interchain transfer processes in luminescent conjugated polymers, which is based on the design of covalently linked donor–acceptor systems. The conjugated material investigated in this work is α,ω-bis[N-(2,6-diisopropylphenyl]-1,6-bis(4-t-butylphenoxy)-3,4-dicarbonicacidimide-9-perylene-poly2,8-(6,6,12,12-tetraethylhexyl)indenofluorene, hereafter abbreviated as PEC-PIFTEH (see chemical structure in Fig. 1). The molecules consist of red-emitting perylene monoimide (PEC) derivatives, covalently grafted at the ends of a blue-emitting derivative of polyindenofluorene (PIF), with ≈5% mole fraction. We can expect that incoherent exciton-hopping along the PIF chains is the main energy-migration channel in solution. Since PEC-PIFTEH is a rigid system, in a good solvent such as p-xylene, no interactions due to chain folding should occur between the perylene end caps and the conjugated segments in contrast to what is found in poly(p-phenylenevinylene) derivatives (16). Therefore, exciton migration before energy transfer is expected to occur primarily along one chain. We will show below that intramolecular energy-transfer rates in this polymer are slow compared with the excited-state depopulation rate. In contrast, energy transfer is found to be very efficient in a solid film of the same material.

Fig 1.

Molecular structure of PEC-PIFTEH. The reference frame is also defined (the z axis is out of plane).

The experimental results are interpreted in the framework of a theoretical approach based on an improved Förster model, wherein the electronic matrix elements for energy transfer are calculated from a multicentric atomic representation of the transition moments, i.e., under the form of atomic transition densities (20–22). We have successively considered the case of intramolecular energy transfer, where exciton transport takes place via hopping along the PIF chains followed by transfer to the perylene end caps, and intermolecular energy transfer, simulated by considering two molecules in close contact. In both cases, the roles of geometric relaxation and local interactions between the atomic transition densities are emphasized. Our combined experimental/theoretical investigation points to the interchain channel as the most efficient pathway for excitation transfer.

Experimental Procedures

The synthesis of the materials studied here has been reported elsewhere (ref. 23 and D. Marsitzky, S. Becker, S.S., K.M., J. D. Mackenzie, and R.H.F., unpublished data). Polymer samples were dissolved in anhydrous p-xylene in a nitrogen environment using standard syringe techniques to avoid contact of either polymer or solvent with air. Films (≈150-nm thickness) were prepared in a dry nitrogen-filled glove box by spin-coating the polymer solution onto Spectrosil substrates. Samples were stored in the glove box before use and kept under dynamic vacuum (<10⁻⁵ mbar) during experiments to prevent photooxidation. Absorption spectra were measured with a Hewlett Packard 8453 diode-array spectrophotometer.

The femtosecond transient absorption apparatus used in these studies has been described in detail previously (24). Briefly, <100-fs full width at half maximum femtosecond pulses at 780-nm central wavelength and 1-kHz repetition rate were derived from a home-built, dye-amplified Ti:sapphire laser system. The pump beam at 390 nm (3.18 eV) was focused in the sample to an ≈125-μm spot. The weaker probe beam, consisting of a single-filament white-light continuum, was focused to a much smaller spot in the same region of the sample after passing through a computer-controlled variable optical delay. Both pump and probe beams were horizontally linearly polarized. Spectrally resolved measurements of the fractional change in probe transmission due to the pump pulse (ΔT/T) were performed with a 0.25-m spectrometer and Peltier-cooled charge-coupled device (CCD) camera. The chirp across the white-light continuum was corrected numerically by using an empirical determination of the dispersion. Time-integrated PL spectra were measured by exciting the polymer at 3.18 eV and dispersing the resulting luminescence in the spectrograph and onto the CCD camera.

Theoretical Modeling of Intrachain and Interchain Energy Transfer

Because of their different chemical natures and the large torsion angle [≈56° at the Austin model 1 (AM1) level] between a perylene cap and the PIF chain, the two moieties are decoupled in PEC-PIFTEH as evidenced by the measured optical absorption spectrum of the polymer (which, to a good approximation, can be described as the superimposition of the PIFTEH and PEC absorptions). We have therefore investigated first the geometric and electronic structures of the individual units; we then have assembled them to explore intrachain and interchain energy-transfer processes. The ground-state (excited-state) geometries of a methyl-substituted PIF model chain and of the perylene derivative were optimized at the AM1 (25) (AM1/configuration interaction) (26) level assuming fully planar conformations for each. (In this approach, a subset of electronic configurations is selected using perturbation theory from the list generated by a full configuration interaction over a defined window of molecular orbitals {active space}; the active space is increased until convergence of the results.) For the simulation of intermolecular energy transfer, the interchain structural parameters were first optimized at the molecular mechanics (27) level, and the intrachain geometries were then refined using the AM1 approach.

The optimized geometries then are used as input for excited-state calculations performed by means of the intermediate neglect of differential overlap (28)/single configuration interaction formalism. As an output of these calculations, we obtain the excitation energies and transition dipole matrix elements from the ground state to the lowest excited states, as well as the corresponding atomic transition densities.

In Förster theory, the electronic coupling V_da that promotes energy transfer from one molecule to another is usually calculated on the basis of a point–dipole model. Such an approach averages away the shapes of the donor and acceptor units and is valid when the size of the molecules is small with respect to intermolecular separations. This is, however, hardly the case in polymeric materials, where the calculation of the long-range (dominant) Coulombic interactions should take into account the local character of the molecules in interaction. The distributed monopole method (20–22), wherein the total electronic coupling is estimated as the sum over atomic transition charges, takes into account the spatial shape of the donor and acceptor via the transition densities. It has been used here to calculate V_da:

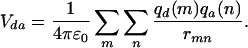In Eq. 1, the summations run over all sites m[n] on the donor [acceptor], r_mn denotes the distance between m and n, and q_d(m) [q_a(n)] is the intermediate neglect of differential overlap/single configuration interaction atomic transition density on site m[n] calculated for the lowest optical g → e excitation on the donor [acceptor].

Our aim here is to provide a qualitative description of intrachain versus interchain energy transfer in conjugated materials. Our analysis is based on a simple model that assumes that, for the donor, energy is localized over one segment of the polymer chain. Conformational motion leads to localization of the excitations over spatial domains corresponding to conformational subunits. Here, these are simply taken to be planar segments of finite sizes (thereby simulating the distribution of conjugation lengths associated with the different conformers present in solution or in the films). For the acceptor in an intrachain energy-migration process, we also assume that electronic interactions between neighboring acceptor conformational subunits are small enough that the acceptor density of states is not perturbed by electronic coupling between subunits. We recognize that this can be a rather severe approximation for a quantitative treatment of intrachain energy migration (29); however, in the linear chain model where there is no critical dependence on spectral overlap (e.g., the donor and acceptor densities of states are broad), this approximation will allow us to provide an upper bound on the fastest intrachain energy-transfer hopping rate (30).

With the transfer rate, k_da, expressed in ps⁻¹ and the electronic coupling, V_da, in cm⁻¹, we use Eq. 2 for the donor-to-acceptor hopping rate (31):

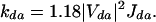J_da, the overlap factor, is calculated on the basis of the simulated (normalized) donor emission and acceptor absorption spectra, obtained assuming a single-mode displaced harmonic oscillator model. In such a simple model, the intensity from the zero vibrational level in the ground state to vibrational level p in the excited state follows a Poisson distribution, I_0−p ∝ (S^p exp(−S/p!), with S being the Huang-Rhys factor (that can be directly related to the calculated changes in coordinates when going from the ground state to the excited state). S is proportional to the geometric relaxation energy (E_rel) in the excited state, S = E_rel/hν, where ν denotes the frequency of the vibrational mode coupled to the excitation (32, 33). Here, a single vibrational mode at 0.18 eV is considered, and the relaxation energies are calculated from intermediate neglect of differential overlap/single configuration interaction vertical excitation energies, as obtained on the basis of the AM1 ground-state and excited-state optimized geometries. The absorption and emission spectra are then convoluted by means of Lorentzian functions. The full width at half maximum of these Lorentzians is fixed at 0.07 eV, thereby accounting for the spectral inhomogeneity of the conformational subunit absorptions that are obscured within the broad polymer absorption band (we note that the overlap and transfer rates only weakly depend on the choice of the line width, which was obtained from a fit to the experimental spectra). Thus, since we use transition densities to calculate the electronic couplings, our analysis differs significantly from the usual application of Förster theory to energy transfer involving conjugated polymers.

Results and Discussion

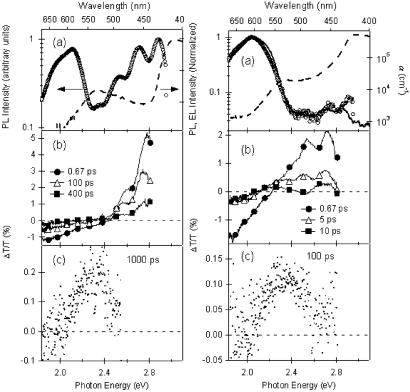
The absorption spectrum of PEC-PIFTEH in 1.7 g/liter solution in anhydrous p-xylene is displayed in Fig. 2a Left. It corresponds to a linear superposition of the PIFTEH homopolymer (peak at ≈3.0 eV) (ref. 23 and D. Marsitzky, S. Becker, S.S., K.M., J. D. Mackenzie, and R.H.F., unpublished data) and PEC (peak at ≈2.3 eV) (34) spectra. The spectral overlap of the PIFTEH PL spectrum with the PEC absorption spectrum ensures resonance energy transfer from PIFTEH to PEC. Excitation in the blue region of the spectrum (3.18 eV for all the spectra reported here) accesses the π–π* transition in the PIFTEH backbone, with essentially no direct excitation of the PEC units; the latter have an absorption maximum in the green region (2.33 eV). The time-integrated PL spectrum is displayed as open circles in Fig. 2a. Approximately equal contributions of emission from the polymer chain (2.3–3.0 eV) and dye end caps (1.8–2.3 eV) are observed, indicating that exciton transfer from the polymer to the dye occurs in competition with radiative and nonradiative decay on the polymer.

Fig 2.

(Left) Absorption (dashed line) and PL (open circles) spectra of PEC-PIFTEH in 1.7 g/liter solution in p-xylene (a); femtosecond transient absorption spectra of the same solution for various pump-probe delays (b); and transient absorption spectrum at a pump-probe delay of 1,000 ps (c). (Right) Absorption (dashed line), EL (solid line), and PL (open circles) of an ≈150-nm-thick PEC-PIFTEH film (a); femtosecond transient absorption spectra of the same film for various pump-probe delays (b); and transient absorption spectrum at a pump-probe delay of 100 ps (c).

This competition is demonstrated in Fig. 2b Left, which shows femtosecond transient absorption spectra at various pump-probe delays. At early times after photoexcitation (0.67 ps), only transient absorption features assigned to PIFTEH singlet (1B_u) excitons are evident. Probe-induced stimulated emission of photoexcited chromophores is observed in the region of the polymer PL, while photoinduced absorption of the same species is observed to the red of 2.46 eV (35). The decay of these spectral signatures occurs in an ≈500-ps time scale. Concomitant with this decay, a small positive feature, which peaks at 2.34 eV, grows in a comparable time scale and decays on a nanosecond time scale. This is assigned to photobleaching of the ground state of PEC as a result of exciton transfer from the polymer. This assignment is made by comparison of the transient data at long delays after excitation (Fig. 2c Left), when no exciton density remains in the polymer, and with the steady-state absorption spectrum in the corresponding spectral region (Fig. 2a).

Fig. 2a Right shows the linear absorption, PL, and EL spectra of a PEC-PIFTEH film. Both the time-integrated PL and EL are dominated by PEC emission. The femtosecond-resolved transient absorption dynamics of the thin-film sample is displayed in Fig. 2b Right. Within 10 ps, ≈60% of the initial amplitude of the stimulated emission signal from the polymer has decayed, and a significant perylene ground-state photobleaching signal (see Fig. 2c Right) is evident. Note that exciton diffusion within the host is expected to play a significant role only if the local guest concentration is low as a result of phase segregation effects. In a PEC-PIFTEH film, where PEC units are coupled covalently to the polymer backbone such that there is a high surface area of PIFTEH/PEC intermolecular interactions, there is a high yield of direct resonance energy transfer without the need for excitons to diffuse near an acceptor. Even with a relatively low acceptor density, nearly complete energy transfer is achieved.

In the following, we model intrachain versus interchain exciton-migration processes to rationalize the difference in dynamics observed in solution and in films. From the ratio between PIFTEH and PEC absorptions in Fig. 2a, we expect an average polymer length of 50–100 indenofluorene units; direct experimental determination of M_n indicates a lower degree of polymerization, on the order of 30 units. The actual conjugation length, i.e., the length between two kinks along the conjugated path (most likely limited by conformational disorder), has been estimated to lie in the range of 5–7 repeat units from extrapolation of the absorption and emission spectra of well defined oligo(indenofluorenes) to those of the homopolymer (23). Since the conjugation length is much shorter than the real length of the PEC-PIFTEH chains, it is likely that excitation of one PIF segment in solution first induces exciton-hopping along the main chain before energy transfer to the perylene end caps. Thus, we first explored this scenario.

For that purpose, we applied Eq. 2 to the computation of the electronic couplings, spectral overlaps, and energy-transfer rates for intramolecular energy transfer (i) among PIF-conjugated segments [hereafter denoted (PIF)_n, where n is the number of repeat units] and (ii) from PIF segments to the PEC end groups. The results are reported in Tables 1 and 2 for a number of donor/acceptor couples differing by the size of the indenofluorene segments participating in the energy-transfer process. In both cases, we find that the electronic couplings for intrachain energy migration (and the corresponding transfer rates) drop quickly with the size of the donor and acceptor groups. This arises from the increased intersite separations in Eq. 1 together with a concomitant decrease in transition density at the edges of the subunits. We stress that these results are obtained on the basis of the relaxed donor excited-state geometry; when considering the unrelaxed ground-state geometries, a somewhat smaller chain-length dependence is found. This behavior stems from the localization of the atomic transition densities around the center of the conjugated chains upon lattice relaxation in the excited state (36). In our calculations, we make the assumption that the time scales of nuclear relaxation are fast compared with energy transfer. If this were not the case, a much more complicated theoretical framework would be required to account for the entanglement of electronic interactions and electron–phonon coupling (37–39).

Table 1.

Electronic matrix elements (V_da), spectral overlaps (J_da), and rates (k_da) for exciton hopping along (PIF)_n conjugated chains and interchain PIF-to-PIF energy migration

Donor	Acceptor	R, Å	Vda, cm−1	Jda, eV−1	kda, ps−1
Intrachain
(PIF)2	(PIF)2	25.0	413	1.14	29
(PIF)2	(PIF)4	36.1	225	1.44	11
(PIF)2	(PIF)6	50.0	149	1.39	4.5
(PIF)2	(PIF)8	63.5	111	1.33	2.4
(PIF)4	(PIF)4	50.1	96	1.36	1.8
(PIF)4	(PIF)6	64.0	67	1.48	0.97
(PIF)4	(PIF)8	76.5	52	1.53	0.61
(PIF)6	(PIF)6	76.5	37	1.52	0.30
(PIF)6	(PIF)8	90.0	29	1.61	0.20
(PIF)8	(PIF)8	103.2	18	1.65	7.8 × 10−2
Interchain
(PIF)2	(PIF)2	5	903	1.14	139
(PIF)2	(PIF)4	5	412	1.44	37
(PIF)2	(PIF)6	5	201	1.39	15
(PIF)2	(PIF)8	5	111	1.33	2.4
(PIF)4	(PIF)4	5	394	1.36	30
(PIF)4	(PIF)6	5	222	1.48	11
(PIF)4	(PIF)8	5	135	1.53	4.1
(PIF)6	(PIF)6	5	232	1.52	12
(PIF)6	(PIF)8	5	147	1.61	5.1
(PIF)8	(PIF)8	5	149	1.65	5.3

n is the oligomer length, and R is the center-to-center donor-acceptor separation.

Table 2.

Electronic matrix elements (V_da), spectral overlaps (J_da), and rates (k_da) for intrachain and interchain PIF-to-PEC energy transfer (see text)

Donor	Acceptor	R, Å	Vda, cm−1	Jda, eV−1	kda, ps−1
Intrachain
(PIF)2	PEC	17.5	689	0.61	42
(PIF)4	PEC	29.9	231	0.95	7.4
(PIF)6	PEC	42.4	106	1.02	1.7
(PIF)8	PEC	54.9	55	1.04	0.46
Interchain
(PIF)2	PEC	4.18	836	0.61	62
(PIF)4	PEC	4.18	556	0.95	43
(PIF)6	PEC	4.18	503	1.02	38
(PIF)8	PEC	4.18	489	1.04	36

R is the center-to-center donor-acceptor separation.

From Table 1, the typical electronic couplings for exciton-hopping between two adjacent segments with sizes ranging from 4 to 6 repeat units (i.e., close to the actual conjugation length) are on the order 20–100 cm⁻¹. This translates into transfer rates on the order of a few hundreds of ns⁻¹ for a single hop event. We stress that, since only hopping to the nearest neighbor has been considered here, this provides an upper limit to the actual rate of homopolymer energy-motion process; an attempt to a more quantitative description will be given below. Note also that we have neglected the role of the collective excitation of coupled acceptors, which is a reasonable approximation when the donors and acceptors are coupled linearly (29). At this stage, it is instructive to compare these results to the values obtained within a simple point–dipole model. Although such a model correctly reproduces the qualitative evolution of V_da with donor-acceptor separation, it strongly underestimates (by roughly 1 order of magnitude) the electronic couplings and transfer rates in comparison to the description provided on the basis of the atomic transition densities. This large discrepancy arises from the fact that the point–dipole model cannot adequately account for the spatial distribution of the excitations over nearby donor and acceptor. Such considerations are especially important for linear molecules (21).

Compared with exciton motion along the conjugated chains, energy transfer from an indenofluorene segment to an attached perylene derivative is calculated to be 1–2 orders of magnitude faster. This marked difference in transfer rates is mainly due to larger electronic couplings for intrachain heteromolecular transfer with respect to homomolecular hopping (see Tables 1 and 2), the overlap factors being of comparable magnitude. The differences in V_da values are due to a compromise between large oscillator strength and short intersite distance, which is favorable to PIF–PEC transfer. As in the case of on-chain hopping, the electronic couplings calculated within the point–dipole approximation are ≈1 order of magnitude smaller.

At this stage, we can conclude that, in situations where intermolecular processes are unlikely (such as for step-ladder-type polymer chains dissolved in “good” solvents), the step determining the energy-transfer rate in PEC-PIFTEH corresponds to the slowest hopping process along the conjugated main chains. To quantify the speed of intrachain energy migration, we have performed Monte Carlo simulations on long PIF strands composed of sequential conjugated segments of different lengths (assuming some input distribution). A random sequence of segments is first generated, and the average time for the exciton to hop from a donor end site (here a short PIF unit) to the acceptor end site (the perylene derivative) is calculated (by averaging over all simulated pathways, with back energy transfer allowed); the procedure then is repeated to ensemble average over a large number of sequences. For bridge lengths in the range of 30–100 repeating units, the total time for the exciton to reach the acceptor is calculated to be on the order of 0.1–1 ns. These results thus indicate that intramolecular exciton motion along individual rigid-rod conjugated chains is an intrinsically slow process, with a characteristic time comparable to that of exciton radiative decay (i.e., in the nanosecond time scale).

Next, we turn to the discussion of interchain PIF–PEC energy transfer that we expect to be significant in polymer films. This process has been modeled by considering a complex formed by a perylene derivative lying on top of a poly(indenofluorene)-conjugated chain. To explore the sensitivity of the transfer rates on the relative orientations of the donor and acceptor molecules, we have considered the effects of both longitudinal (along the x axis, see Fig. 1) and lateral (along the y axis) displacements of the PEC unit with respect to the conjugated PIF bridge as well as rotations along the packing axis (z). A detailed analysis of the results will be given elsewhere. The main findings can be summarized as follows:

• (i)  As expected, V_da is maximized when the center of the perylene derivative lies on top of the middle part of the conjugated chain and the long axes of the two molecules are oriented in a parallel fashion.

• (ii)  The dependence of V_da on translational motion along the chain axis is particularly pronounced when allowing the PIF geometry to relax before energy migration; this is a consequence of the confinement of the excited-state wavefunction and hence of the transition density around the center of the PIF segment that we discussed earlier.

• (iii)  The electronic couplings follow more or less a cosine function of the rotation angle between the PIF and PEC long axes, as predicted by a simple point–dipole model. However, V_da remains surprisingly large in an orthogonal orientation of the donor and acceptor molecules, provided the center of the perylene derivative is displaced significantly either longitudinally or laterally with respect to the center of the poly(indenofluorene) chain. Such a result is in clear contradiction with the conventional point–dipole model and emphasizes the need for taking into account local interactions between different parts of the molecules involved in the energy-transfer process. Similar conclusions apply when modeling the dynamics of donor-to-acceptor energy transport in aggregated molecular assemblies (30).

Switching from a point–dipole model (where the electronic coupling vanishes for orthogonal orientations and decreases quickly as 1/R³ with R the center-to-center donor-acceptor distance) to a multicentric monopole model therefore appears to smooth out the dependence of V_da and hence k_da on fluctuations in the relative orientations of the perylene derivative end caps and the poly(indenofluorene)-conjugated chains. Additionally, covalent linking between the two partners is expected to provide an optimal interaction surface area in films. We therefore expect interchain energy transfer to be an efficient process in the solid state.

To quantify this statement, we have repeated the calculations described above for a number of PIF donor chains ranging in size from 2 to 8 repeat units. The maximal values of the electronic couplings (corresponding to cofacial arrangement and minimal intermolecular distance from center to center) together with the corresponding transfer rates are listed in Table 2. We find that V_da rapidly saturates with donor size to reach values as large as ≈500 cm⁻¹, which translate into exciton-transfer rates on the order of a few tens of ps⁻¹. Again, this is likely to be an upper limit for the intermolecular migration frequency, since close contacts between the PIF-conjugated chain and the PEC end unit of a neighbor chain have been assumed in the simulations. Most importantly, the dynamics of intermolecular energy migration is found to be fast in comparison to the time scale for exciton-hopping between localized states on the donor polymer, which is consistent with the experimental data.

Finally, we have considered the case of two interacting poly(indenofluorene) chains to model intermolecular chain–chain energy transport. The chains were packed in a cofacial arrangement with a center-to-center distance of 5 Å (depending on the nature of the side groups and conformation of the chains, molecular mechanics calculations yield average intermolecular distances ranging from 4 to 5 Å) (40). As in the case of heteromolecular PIF-to-PEC energy transfer, the electronic couplings and transfer rates calculated for the PIF–PIF cofacial complexes are always found to be larger than the corresponding on-chain couplings (owing to the reduced center-to-center distance; see Table 1). Thus, it clearly appears that close contacts between molecules should provide an efficient pathway for energy migration in conjugated materials as a result of increased donor–acceptor electronic couplings. Note also that in contrast to the case of intrachain exciton migration, V_da is largely overestimated when considering only the dipolar contribution to the interchain interaction energy.

Synopsis

We have explored the mechanisms for energy transfer in a poly(indenofluorene) (donor) end-capped with a perylene derivative (acceptor). Time-resolved experiments have been conducted in solution and in films to unravel the relative roles of intrachain and interchain exciton motion channels. While in solution the energy-transfer process competes with radiative decay of the singlet excitons photogenerated on the donor-conjugated chains (in the nanosecond range), it is found to be much faster (a few tens of ps) in the solid state where donor emission becomes completely quenched. We conjectured that these different dynamical behaviors stem from the emergence of a new efficient channel for energy transfer in films likely related to direct contact between the donor and acceptor parts of two adjacent molecules.

To check this hypothesis, we have modeled the elementary steps involved in both intrachain and interchain energy migrations. In the former case, this implies calculating the electronic couplings and transfer rates for exciton-hopping along the conjugated segments, which is followed by energy transfer to the acceptor sites. The energy-transfer electronic matrix elements have been computed by using an exciton approach going beyond the usual point–dipole approximation through an explicit treatment of local interchain interactions; such an approach, which is based on a monopole multicentric expansion of the transition moment, has been shown to be successful in describing the exciton splitting in a number of molecular systems (21, 22). In addition, geometry relaxation phenomena in the excited state have been analyzed; they were found to impact strongly the electronic couplings, and such calculations also provide the reorganization energies associated to energy transfer, which were included in the calculation of the transfer rates by assuming that the time scales of the geometric relaxation are fast compared with energy transfer.

We found that the limiting step for the intrachain mechanism is the incoherent transport of the electronic excitations among localized segments along poly(indenofluorene) polymer chains. The rather slow rate of this process, estimated from Monte Carlo simulations to be in the range of 1 ns⁻¹ in long chains, is due essentially to modest electronic couplings. In contrast, direct contact between a conjugated segment of one macromolecule and the perylene moiety attached to a neighbor chain or between two conjugated PIF chains leads to both large electronic matrix elements and good spectral overlap for intermolecular energy transfer. Within the exciton approach used here, the electronic couplings show a rather weak dependence on the relative geometric arrangement of the donor–acceptor pair and remain significant even in a priori unfavorable situations such as orthogonal orientations. These results highlight the limitations inherent to the conventional point–dipole approximation. Overall, the qualitative picture emerging from the theoretical modeling confirms the observed increase in energy-transfer rate when going from a solution (of the rigid-rod macromolecules) to the solid state due to an efficient interchain hopping process (provided, as assumed here, that donor–acceptor pairs with short intermolecular contacts are present in the film). These results indicate that in the case of solutions of conjugated macromolecules that can coil, such as the biosensors developed by McBranch and coworkers (13), the fast energy-transfer rate has to be related to hops between stacked conjugated segments of the same chain rather than hops along the chain.

Further developments of the model described here would include namely a proper handling of the shape of the absorption and emission spectra by including inhomogeneous broadening and the role of donor or acceptor aggregation (due, for instance, to chain folding). Chain-packing effects have been demonstrated to be significant in related PEC-PIFTEH ultrafast measurements of resonance energy heterotransfer (34).

Abbreviations

• PL, photoluminescence

• EL, electroluminescence

• PEC-PIFTEH, α,ω-bis[N-(2,6-diisopropylphenyl]-1,6-bis(4-t-butylphenoxy)-3,4-dicarbonicacidimide-9-perylene- poly2,8-(6,6,12,12-tetraethylhexyl)indenofluorene

• PEC, perylene monoimide

• PIF, polyindenofluorene

• AM1, Austin model 1