FAST CARS: Engineering a laser spectroscopic technique for rapid identification of bacterial spores

Abstract

Airborne contaminants, e.g., bacterial spores, are usually analyzed by time-consuming microscopic, chemical, and biological assays. Current research into real-time laser spectroscopic detectors of such contaminants is based on e.g., resonance fluorescence. The present approach derives from recent experiments in which atoms and molecules are prepared by one (or more) coherent laser(s) and probed by another set of lasers. However, generating and using maximally coherent oscillation in macromolecules having an enormous number of degrees of freedom is challenging. In particular, the short dephasing times and rapid internal conversion rates are major obstacles. However, adiabatic fast passage techniques and the ability to generate combs of phase-coherent femtosecond pulses provide tools for the generation and utilization of maximal quantum coherence in large molecules and biopolymers. We call this technique FAST CARS (femtosecond adaptive spectroscopic techniques for coherent anti-Stokes Raman spectroscopy), and the present article proposes and analyses ways in which it could be used to rapidly identify preselected molecules in real time.

There is an urgent need for the rapid assay of chemical and biological unknowns, such as bioaerosols. Substantial progress toward this goal has been made over the past decade. Techniques such as fluorescence spectroscopy (1, 2) and UV resonant Raman spectroscopy (3–7) have been successfully applied to the identification of biopolymers, bacteria, and bioaerosols.

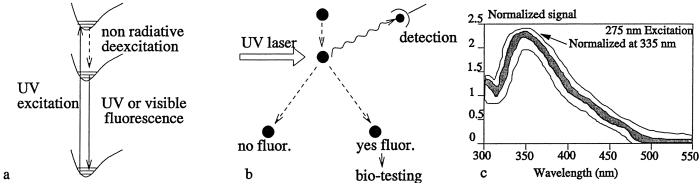
At present, field devices are being engineered (1) that will involve an optical preselection stage based on, e.g., fluorescence radiation as in Fig. 1. If the fluorescence measurement does not give the proper signature then that particle is ignored. Most of the time the particle will be an uninteresting dust particle; however, when a signature match is recorded, then the particle is selected for special biological assay (see Fig. 1b). The relatively simple fluorescence stage can very quickly sort out some of the uninteresting particles whereas the more time-consuming bio-tests will be used for only the “suspects.”

Fig 1.

(a) UV excitation radiation promotes molecules from ground state to an excited-state manifold. This excited-state manifold decays to the ground state via nonradiative processes to a lower manifold, which then decays via visible or UV fluorescence. (b) A scenario in which a UV laser interacts with dust particles and biospheres of interest. When, for example, a bacterial spore is irradiated, fluorescence will be emitted signaling that this particular system is to be further tested. In principle, uninteresting particles are deflected one way; but when fluorescence takes place, the particles are deflected in another direction and these particles are then subjected to further biological tests. (c) The shaded area displays the signal range for the fluorescence spectrum of a number of biological samples, Bacillus subtilis, Bacillus thuringiensis, Escherichia coli, and Staphylococcus aureus. It is not possible to distinguish between the different samples based on such a measurement (see ref. 2 for more details).

The good news about the resonance fluorescence technique is that it is fast and simple. The bad news is that although it can tell the difference between dust and bacterial spores it cannot differentiate between spores and many other organic bioaerosols (see Fig. 1c).

However, despite the encouraging success of the above-mentioned studies, there is still interest in other approaches to, and tools for, the rapid identification of chemical and biological substances. To quote from a recent study (8):

“Current [fluorescence-based] prototypes are a large improvement over earlier stand-off systems, but they cannot yet consistently identify specific organisms because of the similarity of their emission spectra. Advanced signal processing techniques may improve identification.”

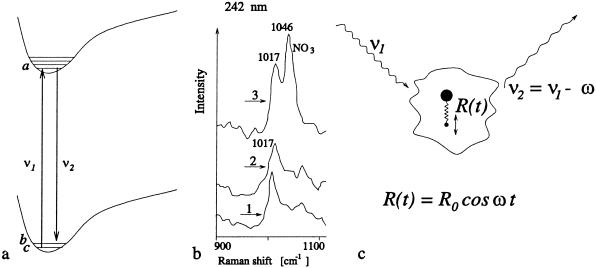
Resonant Raman spectra hold promise for being spore specific as indicated in Fig. 2b. This is the good news, the bad news is that the Raman signal is weak and it takes several minutes to collect the data of Fig. 2b. Because the through-put in a set-up such as that of Fig. 1b is large, the optical interrogation per particle must be essentially instantaneous.

Fig 2.

(a) Resonant Raman scattering in which radiation ν₁ excites the atom from |c> to |a> and the Stokes radiation is emitted taking the molecule from |a> to |b>. (b) Detail of UV resonance Raman spectra of spores of B. megaterium (trace 1), Bacillus c. (trace 2), and calcium dipicolinate (trace 3), all excited at 242 nm; adapted from ref. 4 (see also Fig. 6). (c) A more physical picture of Raman scattering in which a single diatomic molecule, consisting of a heavy nucleus and a light atom, scatters incident laser radiation at frequency ν₁. The vibrational degrees of freedom associated with the diatomic molecule are depicted here as occurring with amplitude R₀ oscillating at frequency ω. The scattered radiation from this vibrating molecule is at frequency ν₂ = ν₁ − ω for the Stokes radiation.

The question then is: Can we increase the resonant Raman signal strength and thereby reduce the interrogation time per particle? If so, then the technique may also be useful in various detection scenarios.

The answer to the question of the proceeding paragraph is a qualified yes. We can enhance the Raman signal by increasing the coherent molecular oscillation amplitude R₀ indicated in Fig. 2c. In essence this means maximizing the quantum coherence between vibrational states |b> and |c> of Fig. 2a.

Our point of view derives from research in the fields of laser physics and quantum optics that have concentrated on the utilization and maximization of quantum coherence. The essence of these studies is the observation that an ensemble of atoms or molecules in a coherent superposition of states represents, in a real sense, a new state of matter aptly called phaseonium (9–11).

In particular, we note that matter in thermodynamic equilibrium has no phase coherence between the electrons in the molecules making up the ensemble. This is discussed in detail later. When a coherent superposition of quantum states is involved, things are very different, and based on these observations, many interesting and counterintuitive notions are now a laboratory reality. These include lasing without inversion (12–15), electromagnetically induced transparency (16, 17), light having ultra-slow group velocities on the order of 10 m/sec (18–23), and the generation of ultra-short pulses of light based on phased molecular states (24, 25).

Another emerging technology central to the present paper is the exciting progress in the area of femtosecond quantum control of molecular dynamics originally suggested by Judson and Rabitz (26). This progress is described and reviewed in the articles by Kosloff et al. (27), Warren et al. (28), Gordon and Rice (29), Zare (30), Rabitz et al. (31), and Brixner et al. (32). Other related work on quantum coherent control includes the quantum interference approach of Brumer and Shapiro (33), the time-domain (pump-dump) technique proposed by Tannor et al. (34), and the stimulated Raman adiabatic passage (STIRAP) approach of Bergmann et al. (35) to generate a train of coherent laser pulses. The preceding studies teach us how to produce pulses having arbitrary controllable amplitude and frequency time dependence. Indeed the ability to sculpt pulses by the femtosecond pulse shaper provides an important new tool for all of optics [see the pioneering works by Heritage et al. (36), Weiner et al. (37), Wefers and Nelson (38), and Weiner (39)].

A promising approach is to use learning algorithms so that knowledge of the molecular potential energy surfaces and matrix elements between surfaces are not needed. Precise taxonomic marker frequencies may not be known a priori; however, by using a pulse shaper coupled with a feedback system, complex spectra can be revealed.

Thus, we now have techniques at hand for controlling trains of phase-coherent femtosecond pulses so as to maximize molecular coherence. This process allows us to increase the Raman signal while decreasing the undesirable fluorescence background, which has much in common with the CARS spectroscopy (40) of Fig. 3, but with essential differences as we now discuss.

Fig 3.

(a) Ordinary resonant Raman spectroscopy in which a drive laser of amplitude ɛ₁ generates a weak signal field having an amplitude ɛ₂. The incident signal consists of one pulse at ν₁, and the pulse structure after interaction with the molecular medium consists of two pulses at ν₁ and ν₂. (b) The coherent Raman process associated with CARS is depicted in which two fields at frequency {ν₁} and {ν₂} are incident with amplitudes ɛ₁ and ɛ₂. The third radiated anti-Stokes signal field at frequency ν₃ is indicated. (c) FAST CARS configuration in which maximal coherent Raman spectroscopy is envisioned. The preparation pulses ɛ₁ and ɛ₂ prepare maximum coherence between states |b> and |c>. Next the probe laser ɛ₃ interacts with this oscillating molecular configuration and the anti-Stokes radiation is generated.

The presently envisioned improvement over ordinary CARS is based on enhancing the ground-state molecular coherence. However, we note that molecules involving a large number of degrees of freedom will quickly dissipate the molecular coherence among these degrees of freedom. This difficulty is well known and is addressed in the present work from several perspectives. First of all, when working with ultra-short pulses, we have the ability to generate the coherence on a time scale that is small compared with the molecular relaxation time. Furthermore, we are able to tailor the pulse sequence in such a way as to mitigate and overcome key limitations in the application of conventional coherent anti-Stokes Raman spectroscopy (CARS) to trace contaminants. The key point is that we are trying to induce maximal ground-state coherence, as opposed to the usual situation within conventional CARS where the ground-state coherence is not a maximum as is shown later in this paper. With FAST CARS (femtosecond adaptive spectroscopic techniques applied to CARS) we can prepare the coherence between two vibrational states of a molecule with one set of laser pulses and use higher frequency visible or UV to probe this coherence in a coherent Raman configuration. This process will allow us to capitalize on the fact that maximally coherent Raman spectroscopy is orders of magnitude more sensitive than incoherent Raman spectroscopy.

Having stated our goals and our approach toward attaining these goals, we emphasize that the present article represents essentially an engineering endeavor. We propose to draw heavily on the ongoing work in quantum coherence and quantum control as mentioned earlier. For example, the careful experiments and analysis of the Würzburg group on the generation and probing of ground-state coherence in porphyrin molecules (41) by femtosecond-CARS (fs-CARS) are very germane to our considerations. However, ground-state coherence is not maximized in these experiments. In another set of beautiful experiments (42) they investigate the selective excitation of polymers of diacetylene via fs-CARS. They control the timing, phase, and frequency (chirp) content of their preparation pulses. In these experiments it was necessary to focus attention on the evolution of the excited-state molecular dynamics. We hope to avoid this complication as is explained later.

Perhaps closest to our approach is the recent joint work of the Garching Max-Planck and Würzburg groups (43). Their paper is a prime example of a FAST CARS experiment. However, they concentrate on producing highly excited states of the “vibrational motion of a certain bond.” The application of their technique to the production of maximum coherence between states |b> and |c> of Fig. 2a in a specific vibrational mode of their molecule would be of great interest to us and is underway.

Finally, we want to draw the reader's attention to the useful collection of articles in a recent special issue of the Journal of Raman Spectroscopy dedicated to fs-CARS (44). Likewise the recent work of Silberberg and coworkers (45, 46) in which they show that it is possible to excite one of two nearby Raman levels, even when they are well within the broad fs pulse spectrum, is another excellent example of the power of the FAST CARS technique.

The present work focuses on utilization of a maximally phase-coherent ensemble of molecules, i.e., molecular phaseonium, to enhance Raman signatures. This will be accomplished via the careful tailoring of a coherent pulse designed to prepare the molecule with maximal ground-state coherence. Such a pulse is a sort of “melody” designed to prepare a particular molecule. Once we know this molecular melody, we can use it to set that particular molecule in motion and this oscillatory motion is then detected by another pulse; this is the FAST CARS protocol depicted in Fig. 3c.

In the next section, the status of Raman spectroscopy applied to biological spores is reviewed. Then, we compare various types of Raman spectroscopy with an eye to the recent successful applications of quantum coherence in laser physics and quantum optics. Then, we present several experimental schemes for applying these considerations to the rapid identification of macromolecules, in general, and biological spores, in particular. Finally, we propose several scenarios in which FAST CARS could be useful in the rapid detection of bacterial spores. The various appendixes referred to are to be found in our extended paper, which is published as supporting information on the PNAS web site, www.pnas.org. As stated earlier, the present article is an engineering science analysis of a promising approach to the problem of bacterial spore detection.

Pico-Review of Raman Spectroscopy Applied to Bacterial Spores

The bacterial spore is an amazing life form. Spores thousands of years old have been found to be viable. One textbook (48) reports that “endospores trapped in amber for 25 million years germinate when placed in nutrient media.”

A key to this incredible longevity is the presence of dipicolinic acid (DPA) and its salt calcium dipicolinate in the living core that contains the DNA, RNA, and protein as shown in Fig. 4.

Fig 4.

Sketch of spore indicating that the DPA and its salts, e.g., Ca-DPA, are contained in the core and are in contact with the spore-specific DNA ribosomes and cell proteins.

A major role of the calcium DPA complex seems to be the removal of water, as per the following quote (49): “The exact role of these [DNA] chemicals is not yet clear. We know, for instance, that heat destroys cells by inactivating proteins and DNA and that this process requires a certain amount of water. Since the deposition of calcium dipicolinate in the spore removes water … it will be less vulnerable to heat.”

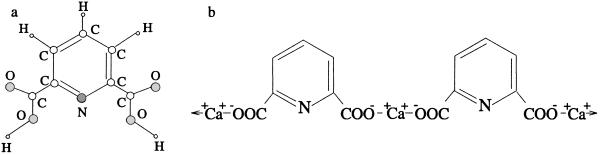
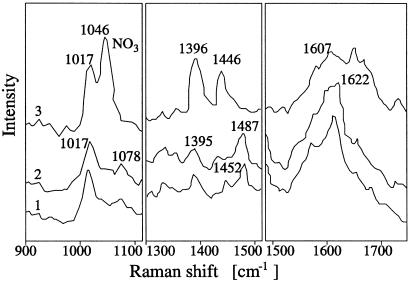
Hence, one of the major components of bacterial spores is DPA and its ion as depicted in Fig. 5. Calcium dipicolinate can contribute up to 17% of the dry weight of the spores. A definitive demonstration (3) of this conjecture was made by comparing the 242-nm excitation spectra of calcium dipicolinate with spore suspensions of Bacillus megaterium and Bacillus cereus. From Fig. 6, it is seen that good matches were noted at 1,017 cm⁻¹ with further matches being found at 1,396, 1,446, and 1,607 cm⁻¹ peaks of the calcium dipicolinate.

Fig 5.

(a) DPA [2,6-pyridinedicarboxylic acid, C₅H₃N(COOH)₂]. (b) The Ca²⁺ DPA complex.

Fig 6.

Shown are UV resonance Raman spectra of spores of B. megaterium (trace 1), spores of B. cereus (trace 2), and calcium dipicolinate (trace 3) in three spectral regions. All samples are excited at 242 nm. Figure adapted from ref. 4.

As has been shown in previous work by, e.g., Carmona (3) and Nelson and coworkers (4–7), the presence of DPA and its calcium salt gives us a ready-made marker for endospores. As has been mentioned earlier and as will be further discussed later, this is the key to Raman fingerprinting of the spore.

We note, however, that fluorescence spectroscopy was one of the first methods used for detection of bacterial taxonomic markers and is still used for detection where high specificity is not required. This technique is an important addition to the tool kit of scientists and engineers working in this area.

A possible FAST CARS protocol is as follows: First, we obtain size and fluorescence information. If this information is consistent with the presence of a particular bacterial spore we could then automatically perform a FAST CARS analysis sensitive to DPA so as to further narrow the number of suspects.

It is important to note that just as resonant Raman is some 10⁶ times more sensitive than nonresonant, coherent Raman yields a much stronger signal than ordinary incoherent Raman spectroscopy. This makes it possible to collect the Raman spectra much more rapidly via FAST CARS, which is very important in the ultimate scheme of things.

We will generate quantum coherence in macromolecules by working with the now available femtosecond pulse trains in which phase coherence exists between the individual pulses. In this way, one can enhance coherent Raman signatures. The utilization of “molecular music” to generate maximal phase coherence holds promise for the identification and characterization of macromolecules and biomolecules.

Overview of Raman Spectroscopy

Raman scattering is an inelastic scattering of electromagnetic fields off vibrating molecules. The origin of Raman scattering dates back to a theoretical paper in Naturwissenschaften by A. Smekal in 1923 entitled (translated) “The quantum theory of dispersion” (50). It was followed by another paper in a 1923 Physical Review (by A. Compton) entitled “A quantum theory of the scattering of x-rays by light elements” (51). Some historians feel that these two papers gave C. V. Raman the idea for the experiments that were performed with K. S. Krishnan and led to the discovery of the effect in more than 60 liquids. Raman and Krishnan published their results entitled “A new type of secondary radiation” in Nature on March 28, 1928 (52). It was soon followed by the landmark paper of G. Landsberg and L. Mandelstam who found the same effect in quartz and published a paper entitled (translated) “A novel effect of light scattering in crystals,” which appeared on July 13, 1928 in Naturwissenschaften (53). By the end of 1928 dozens of papers had already been published on the Raman effect.

Raman scattering is an optical phenomenon in which there is a change of frequency of the incident light. Light with frequency ν₁ scatters inelastically off the vibrating molecules such that the scattered field has frequency ν₂ = ν₁ ± ω_bc, where ω_bc is the frequency of the molecular vibrations. The field with down-shifted frequency ν₂ = ν₁ − ω_bc is called Stokes field, whereas the frequency up-shifted radiation is called the anti-Stokes.

There are two basic Raman processes: the so-called spontaneous and stimulated Raman scattering. Spontaneous scattering occurs if a single laser beam with intensity below a certain threshold illuminates the sample. In condensed matter, in propagating through 1 cm of the scattering medium, only approximately 10⁻⁶ of the incident radiation is typically scattered into the Stokes field (see, e.g., ref. 54). Stimulated scattering that occurs with a very intense illuminating beam is a much stronger process in which several percent of the incident laser beam can be converted into the other frequencies.

For spontaneous Stokes scattering, the intensity of the scattered field is roughly proportional to the length traveled by the incident field in the medium. On the other hand, the stimulated process becomes dominant and the scattered field intensity can increase exponentially with the medium length.

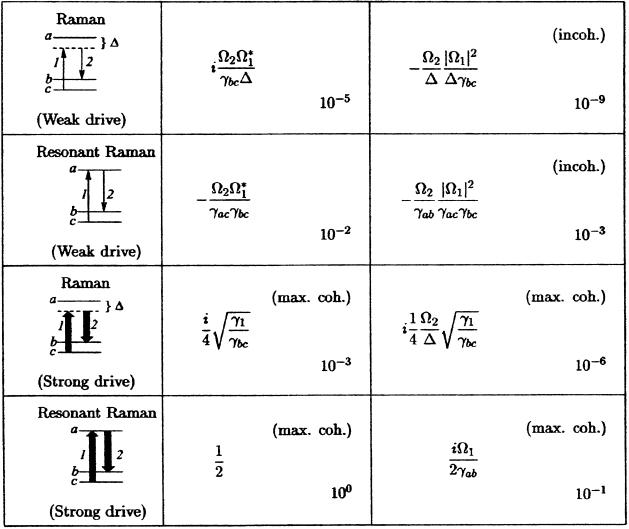
The resonant Raman process (appearing when the frequency of the incident radiation coincides with one of the electronic transitions) is much richer than the nonresonant, and we now turn to a discussion of the resonant problem. Resonant Raman radiation is governed by the oscillating dipole between states |a> and |b> (Stokes) and/or |a> and |c> (anti-Stokes) in the notation of Fig. 3 and Table 1. In the Stokes case, the steady-state coherent oscillating dipole P(t), divided by the dipole matrix element ρ_ab = e <a|r|b>, is the important quantity. That is ρ_ab(t) ≡ P(t)/ρ_ab is

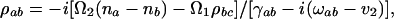where the Raman coherence is ρ_bc. In Eq. 1, ω_ab is the transition frequency between the electronic states a and b, n_a and n_b are the populations of levels a and b, ν₂ is the frequency of the generated field, and the other quantities are defined in the legend of Table 1.

Table 1.

Comparison of different Raman spectroscopic techniques as derived in Appendix A, which is published as supporting information on the PNAS web site

Process         Raman coherence ϱcb         Dipole coherence ϱab

The density matrix element ρ_bc governs the amplitude of coherent vibration, whereas the element ρ_ab is proportional to the electronic polarization responsible for emission of radiation. Ω_1,2 are the Rabi frequencies, Δ is the detuning of the electronic transition, γ_ab, γ_ac are the decay rates of the optical transitions, γ_bc is the decoherence rate of the vibrational states, and γ₁ is the decay rate from level b to c. The approximated values (shown in the lower right corner) were obtained for γ_ab ≈ γ_ac ≈ γ_bc ≈ 10¹²s⁻¹, γ₁ ≈ 10⁶s⁻¹, Δ ≈ 10¹⁵s⁻¹, and Ω_1,2 ≈ 10¹¹s⁻¹ for weak driving and Ω_1,2 ≈ 10¹²s⁻¹ for strong driving. Note that Ω ≈ 10¹¹s⁻¹ corresponds to a 10-ns pulse with 0.1 mJ energy focused on a square millimeter spot if the electronic transition dipole moment is ℘ ≈ 10⁻¹⁹C × 10⁻¹⁰m.

The main advantage of resonant Raman scattering is that the signal is very strong—up to a million times stronger compared with the signal of nonresonant scattering (4, 5). It is also very useful that only those Raman lines corresponding to very few vibrational modes associated with strongly absorbing locations of a molecule show this huge intensity enhancement. On the other hand, the resonance Raman spectra may be contaminated with fluorescence. However, this problem can be avoided by using UV light so that most of the fluorescence appears at much longer wavelengths than the Raman scattered light and is easily filtered out.

Fast Cars

Generation of Atomic Coherence.

The purpose of this section is to demonstrate the utility of pulse shaping as a mechanism for generating maximal coherence. The Raman signal is optimized at the condition of maximal molecular coherence. When in this state, each of the molecules oscillates at a maximal amplitude, and all molecules in an ensemble oscillate in unison. Here we discuss several methods for the preparation of maximal coherence state.

Adiabatic rapid passage via chirped pulses.

A particularly simple and robust approach to the generation of the maximal coherence is to use a detuning δω, which is largely independent of inhomogeneous broadening and variations in matrix elements (Fig. 7).

Fig 7.

Energy level schematics for a three-level system to generate maximum coherence between the levels |b> and |c> via fields ɛ₁ and ɛ₂. These fields are off-resonant with the electronic detuning δω and possibly also with the Raman detuning Δω, which can vary in time, thus chirping the pulses. After preparing the coherence ρ_bc with fields ɛ_1,2 the probe field ɛ₃ gives rise to the anti-Stokes field ɛ₄.

Such multilevel molecular system can be described in terms of an effective two-by-two Hamiltonian (55). Diagonalization of this Hamiltonian (see Appendix C, which is published as supporting information on the PNAS web site) allows us to analyze the evolution of the system by drawing analogies to two-state systems. If the excitation is applied resonantly (Δω = 0), such that the initial state of the system (the ground state |c> is projected onto the new basis formed by the eigenvectors |+> and |−>, the system undergoes a sinusoidal Rabi flopping between states |b> and |c>. In this situation one can choose to apply a π/2 pulse to create the maximal coherence |ρ_bc| = 0.5. Alternatively, one can apply an excitation at a finite detuning Δω, to allow all population, which is initially in the ground state, to follow the eigenstate |+> adiabatically.

Fractional STIRAP.

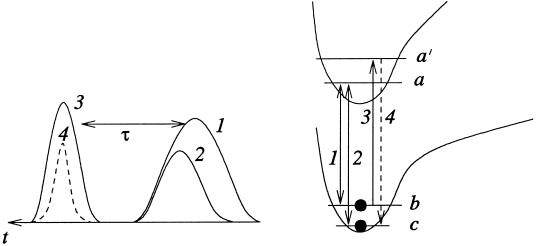
In an all-resonant Λ scheme (Fig. 8, with δω = Δω = 0) maximal coherence can be prepared between the levels b and c in a fractional STIRAP set up by a counterintuitive pulse sequence (35, 56, 57), such that the population of the upper state a is always zero and fluorescence from this state is eliminated. This can be accomplished via a counterintuitive sequence of two pulses at frequencies ω_ab and ω_ac. Under the condition of adiabatic passage, the molecule in the initial state |b> is transformed into a coherent state (|b> − |c>)2^−1/2.

Fig 8.

Energy-level schematics for the generation of maximum coherence between the levels |b> and |c> via fractional STIRAP by counterintuitive pulses 1 and 2. After a time delay of τ the pulse resonant with |a′> → |b> transition produces a signal at ω_a′c.

The principle behind a STIRAP process is the adiabatic theorem as applied to the time-varying Hamiltonian H(t). If the system at time t₀ is in an eigenstate of H(t₀), and the evolution from t₀ to t₁ is sufficiently slow, then the system will evolve into the eigenstate of H(t₁). The three-level atomic system driven by two fields has three eigenstates, one of which is a linear superposition of only the lower levels b and c. The time-dependent amplitudes of this eigenstate depend on the pulse shapes of the fields at frequencies ω_ab and ω_ac. Thus, by an appropriate pulse shaping, it should be possible to prepare a maximally coherent superposition of states b and c as shown in Fig. 8. The expressions for the Hamiltonian and the corresponding eigenstates are given in Appendix D, which is published as supporting information on the PNAS web site.

Comparing different schemes for the preparation of maximal coherence, we note that the required laser power is much lower for the all-resonant scheme, but in the case of biomolecules, UV lasers are required. The far-detuned scheme will work with more powerful infrared lasers, up to the point of laser damage. As for the comparison of adiabatic and nonadiabatic regimes, we should note that the adiabatic scheme may turn out to be more robust, because it does not rely on a particular pulse area and works for inhomogeneous molecular ensembles and nonuniform laser beams.

Femtosecond pulse sequences.

In a series of beautiful experiments K. Nelson and coworkers (58) have generated coherent molecular vibration via a train of femtosecond pulses. They nicely describe their work as: “Timed sequences of femtosecond pulses have been used to repetitively ‘push’ molecules in an organic crystal … , in a manner closely analogous to the way a child on a swing may be pushed repetitively to reach oscillatory motion.”

An interesting aspect of this approach is the fact that the individual pulses need not be strong. Only the collective effect of many weak pulses is required. This may be helpful if molecular “break-up,” caused by strong ɛ₁ and ɛ₂, is a problem. This will be further discussed elsewhere.

Adaptive Evolutionary Algorithms.

So far we described how one-photon and two-photon resonant pulse sequences can be used to produce a coherent molecular superposition state. The idea is that once this state is created a delayed pulse can be applied to produce Raman scattering, which will bear the signature of the molecular system. The Raman signal is expected to be optimized when the molecular coherence is maximal. In general, however, things are too complicated to enable us to work with simple predetermined laser pulses. For large biomolecules the level structure is not only very complex, but usually unknown. We now consider how search algorithms can be used to find the optimal pulse sequence for a complicated molecule with an unknown Hamiltonian. This approach will eventually lead to an efficient generation of “molecular fingerprints.”

To achieve this goal we will need to (i) use a technique for preparation of complex-shaped pulse sequences, and (ii) find the particular pulse sequences, required for the excitation of the particular biomolecules and the production of spectral signatures, which will allow one to distinguish (with certainty) the target biological agent from any other species.

Pulse-shaping techniques already exist; they are based on spectral modification. First, a large coherent bandwidth is produced by an ultra-short pulse generation technique¶¶ (59–61). Then, the spectrum is dispersed with a grating or a prism, and each frequency component is addressed individually by a spatial light modulator [a liquid crystal array (62, 63) or an acoustic modulator (64)]. This way, individual spectral amplitudes and phases can be adjusted independently. Finally, the spectrum is recombined into a single beam by a second dispersive element and focused onto the target. This technique allows synthesis of arbitrarily shaped pulses right at the target point and avoids problems associated with dispersion of intermediate optical elements and windows.

A particular shaped pulse sequence can be represented by a three-dimensional surface in a space with frequency-amplitude-phase axes. Each pulse shape, which corresponds to a particular three-dimensional surface, produces a molecular response. The problem is to find the optimal shape. The search space is too large to be scanned completely. Besides, many local optima may exist in the problem. The solution is offered by global search algorithms (such as adaptive evolutionary algorithms) (32, 65). In this approach the experimental output is included in the optimization process. This way, the molecules subjected to control are called on to guide the search for an optimal pulse sequence within a learning loop (26). With the proper algorithm, automated cycling of this loop provides a means of finding optimal pulse shapes under constraints of the molecular Hamiltonian and the experimental conditions. No prior knowledge of the molecular Hamiltonian and the potential energy surfaces is needed in this case.

This adaptive technique was developed for coherent control of chemical reactions (32). The idea is that the pulses can be optimized to produce desired chemical products. In our problem we want to optimize Raman generation. In this case both preparation and reading pulses can be adaptively shaped to maximize the signal. Fig. 9 shows schematics for the experimental setup that implements these ideas.

Fig 9.

(a) Experimental setup for the implementation of adaptive techniques. (b) Depiction of amplitude of possible optimized Raman preparation pulse sequence ɛ₁* ɛ₂. Not indicated is the fact that the reading pulse ɛ₃ can also be profitably considered as a learning algorithm variable.

Generated spectra will be different for different molecular species. And our task is not only to maximize Raman generation, but also to identify spectral patterns characteristic of particular species and maximize the difference in the spectrum produced by the target biomolecule from spectra produced by any other biomolecules. The key idea here is to apply the same adaptive algorithms to learn these optimal molecular fingerprints or perhaps better said molecular melody.

We note that the complexity of the molecular level structure is not so much a problem as a solution to a problem. We should take advantage of the richness of the molecular structure, and the infinite variety of possible pulse shapes, to distinguish different species.

Possible FAST CARS Measurement Strategies for Detection of Bacterial Spores

Having presented the FAST CARS concept in some detail we now return to the question of its application to fingerprinting of macromolecules and bacterial spores. Some aspects of the technique seem fairly simple to implement and would seem to hold relatively immediate promise. Others are more challenging but will probably be useful at least in some cases. Still other applications, e.g., the stand-off detection of bioaerosols in the atmosphere present many open questions and require careful study. In the following we discuss some simple FAST CARS experiments that are underway and/or being assembled in our laboratories.

Preselection and Hand-Off Scenarios.

At present, field devices are being engineered that will involve an optical preselection stage based on, e.g., fluorescence tagging. If the fluorescence measurement does not match the class of particles of interest then that particle is ignored. When many such particles are tested and a possible positive is recorded, the particle is subjected to special biological assay. Such a two-stage approach can substantially speed up the detection procedure. The relatively simple fluorescence stage can very quickly sort out many uninteresting scattering centers whereas the more sophisticated Raman scattering protocol will be used only for the captured suspects.

The properly shaped preparation pulse sequence will be determined by, e.g., the adaptive learning algorithm approach. The amplitude and phase content of the pulse that produces maximum oscillation may be linked to a musical tune. Each spore will have a song that results in maximum Raman coherence. A correctly chosen melody induces a characteristic response of the molecular vibrations—a response that is as unique as possible for the bacterial spores to be detected. Playing a melody rather than a single tone is a generalization that enables us to see a multidimensional picture of the investigated object. We note that the optimization can (and frequently will) include not only the preparation pulses 1 and 2 (see Fig. 9b), but also the probe pulse 3, in particular, its central frequency and timing. Analysis of the response to such a complex input is a complicated signal processing problem. Various data mining strategies may be used in a way similar to speech analysis.

However, taking into account the fact that we work with femtosecond pulses chained in picosecond to nanosecond pulse trains, the whole analysis can be very short. In particular, if we recall the long sampling time of the complete fluorescence spectra of ref. 6 being ≈15 min, our estimation of a microsecond analysis is a very strong argument for the chosen approach.

Possible Further Raman Characterization.

After a suspect particle has been targeted, it may be subject to a whole variety of investigative strategies. Raman scattering off a flying particle can be very fast, but not necessarily the most accurate method. It will be very useful to pin the particle on a fixed surface and cool it down to maximize the decoherence time T₂ so that the characteristic lines are narrowed down. The particle can be deflected by optical means (laser tweezers, laser ionization, etc.) and attached to a cooled conducting surface. Cooling to liquid helium temperature should enable us to enhance the dephasing time from T₂ ≤ 10⁻¹² sec at room temperature to perhaps a few picoseconds (or more) at a few degrees Kelvin.

Possible Spore-Specific FAST CARS Detection Schemes.

We conclude with some speculative observations for long-range (stand-off) measurements. The chemical state of DPA in the spore is of special interest to us because the stuff we hang on the DPA molecule will determine its characteristic Raman frequency. To this end, we quote from an article (66) by Murrell on the chemical composition of spores: “When DPA is isolated from spores it is nearly always in the Ca-CDPA chelate but sometimes as the chelate of other divalent metals [e.g., Zn, Mn, Sr, etc.] and perhaps as a DPA-Ca amino complex.”

Thus, because each different type of spore would have its own unique mixture of metals and amino acids, it may be the case that the finer details of the Raman spectra would contain spore specific fingerprints. This conjecture is supported by Fig. 2b where the difference between the DPA Raman spectra of the spores of B. cereus and B. megaterium is encouraging.

The extent to which the DPA Raman spectra are sensitive to its environment is an open question. That we might be able to achieve spore specific sensitivity is consistent with the well-known fact that substituents, e.g., NO₂ experience a substantial shift of their vibrational frequencies when bound in different molecular configurations. Furthermore, recent NMR experiments (47) show spore-specific fingerprints.

Clearly there are many opportunities and open questions implicit in the FAST CARS molecular melody approach to real-time spectroscopy. However it plays out, this combination of quantum coherence and coherent control is a rich field.

Abbreviations

• CARS, coherent anti-Stokes Raman spectroscopy

• FAST CARS, femtosecond adaptive spectroscopic techniques for CARS

• STIRAP, stimulated Raman adiabatic passage

• DPA, dipicolinic acid