Y genetic data support the Neolithic demic diffusion model

Abstract

There still is no general agreement on the origins of the European gene pool, even though Europe has been more thoroughly investigated than any other continent. In particular, there is continuing controversy about the relative contributions of European Palaeolithic hunter-gatherers and of migrant Near Eastern Neolithic farmers, who brought agriculture to Europe. Here, we apply a statistical framework that we have developed to obtain direct estimates of the contribution of these two groups at the time they met. We analyze a large dataset of 22 binary markers from the non-recombining region of the Y chromosome (NRY), by using a genealogical likelihood-based approach. The results reveal a significantly larger genetic contribution from Neolithic farmers than did previous indirect approaches based on the distribution of haplotypes selected by using post hoc criteria. We detect a significant decrease in admixture across the entire range between the Near East and Western Europe. We also argue that local hunter-gatherers contributed less than 30% in the original settlements. This finding leads us to reject a predominantly cultural transmission of agriculture. Instead, we argue that the demic diffusion model introduced by Ammerman and Cavalli-Sforza [Ammerman, A. J. & Cavalli-Sforza, L. L. (1984) The Neolithic Transition and the Genetics of Populations in Europe (Princeton Univ. Press, Princeton)] captures the major features of this dramatic episode in European prehistory.

It is widely accepted that the onset of agriculture in the Near East triggered a cultural change that brought farming and associated technologies across Europe about 10,000 years ago (1). Two alternative demographic scenarios have been proposed to account for this transition, documented in the archaeological record (2). In the demic diffusion model (DDM; ref. 1), the spread of technologies involved a massive movement of people, which implies a significant genetic input of Near Eastern genes from Neolithic farmers. Under the cultural diffusion model (CDM; refs. 3 and 4), on the contrary, the transition to agriculture is regarded essentially as a cultural phenomenon, involving the movement of ideas and practices rather than people. Consequently, it would not imply major changes at the genetic level.

Proponents of both models acknowledge that there is a spectrum of intermediate scenarios, which are essentially admixture models: settlements were founded by a mixture of farmers whose ancestors originally came from the Near East and indigenous hunter-gatherers. The question is, therefore, whether the dispersing farmers were few, (as in the CDM) or many (as in the DDM).

The DDM seemed to explain the major geographic trends detected in allele frequencies at conventional marker loci, such as blood groups and enzymes (5, 6). Conversely, recent mtDNA data have been interpreted in favor of the CDM, thereby generating a controversy (7–15). Similarly, Semino et al. (16) have used their results from the non-recombining Y-chromosome region (NRY) to argue that the genetic contribution of Neolithic people may have been as low as 22%. This figure represents the proportion in Europe of the four haplotypes (Eu4, -9, -10, and -11), which were singled out because they show a distinct gradient from the epicenter of the agricultural revolution in the Levant. Although this gradient may well have been established during the Neolithic transition, it is not clear that the proportion of these haplotypes should provide an estimate of admixture proportions. Indeed, admixture is a demographic process, and, as such, it affects the entire genome. In particular, simulation studies demonstrated that only a limited fraction of alleles will exhibit a clinal pattern after expansion and introgression (1), and only a fraction of these will be visible thousands of years later.

The best way to quantify the relative contributions of different populations is far from trivial (see refs. 17–19). The limited genetic differentiation between human populations indicates that traces of ancient population movements will be uncovered only by efficient statistical methods (20). Although indirect evidence, such as correlations between genetic and non-biological information (archaeology, linguistics), can be persuasive, the full use of genetic data requires explicit models of the admixture process (21). In particular, we argue that it is necessary to base the analysis on estimates of the ancestral allele frequencies in each population. By doing so, it becomes possible to distinguish the relative contribution of genetic drift and admixture. Because the ancestral frequencies cannot be known exactly, the calculations must take into account the range of possible histories (19).

Recent innovations in computational statistics, such as the extension of importance sampling and Markov chain Monte Carlo (MCMC) exploration to genealogical models, allow inferences about demographic history by using likelihood-based methods. In this paper, we make use of a MCMC method that we developed (19) to estimate the genetic contributions, p₁ and (1 − p₁), of two parental populations, P₁ and P₂, into a third, hybrid population, H, and applied it to the NRY data of Semino et al. (16).

We use the method to estimate the change from place to place in Europe of admixture proportions of “Neolithic” and “Palaeolithic” genes. Importantly, the method does not require us to define these “Palaeolithic” or “Neolithic” alleles. It requires only the definition of parental populations, which is fortunately one of the few points on which there is a broad agreement (8, 16). The method takes into account, and quantifies, the effect of genetic drift since the time of admixture in each population. This innovation in the method is important because the populations are expected to have expanded after acquiring agriculture and, consequently, to have experienced a reduction in genetic drift. Because the archaeological data suggest that the timing of this transition varied from place to place in Europe, the method should be able to pick up a signature of this sequence in the genetic data.

Materials and Methods

Populations Used.

We have used the genetic data of Semino et al. (16) comprising 22 binary markers from the NRY in a large number of European populations (n = 1,007 chromosomes from 25 samples, Table 1). These markers are considered to be the result of unique mutational events and are called unique-event polymorphisms (UEPs; refs. 21 and 22). They are thought to be rare enough to have occurred only once in the recent history of human populations. The presence of these UEPs in different populations is thus unlikely to indicate recurrent mutation but rather common ancestry, migration, or admixture events. These data are therefore particularly appropriate for our admixture analysis.

Table 1.

Estimated Palaeolithic contribution across Europe

Population	Mode	Median	90% CI	50% CI
Greece	0.000	0.289	0.027–0.745	0.139–0.467
Albania	0.000	0.263	0.024–0.750	0.121–0.453
Macedonia	0.000	0.311	0.030–0.838	0.151–0.520
Georgia	0.194	0.360	0.041–0.870	0.183–0.580
Croatia	0.176	0.437	0.052–0.919	0.228–0.677
Calabria	0.373	0.392	0.045–0.808	0.215–0.576
Hungary	0.084	0.398	0.039–0.899	0.194–0.630
Poland	0.335	0.478	0.054–0.936	0.244–0.725
Northern Italy	0.591	0.542	0.074–0.935	0.321–0.741
Ukraine	0.811	0.562	0.068–0.956	0.303–0.783
Catalunia	0.865	0.610	0.086–0.960	0.365–0.811
Netherlands	0.942	0.588	0.086–0.961	0.336–0.804
Germany	0.854	0.601	0.077–0.960	0.351–0.805
France	0.766	0.620	0.105–0.957	0.392–0.804
Czechoslovakia	0.790	0.622	0.123–0.958	0.406–0.809
Andalusia	0.904	0.690	0.185–0.969	0.477–0.849
Sardinia	1.000	0.845	0.425–0.987	0.711–0.931

^*These intervals represent the values between the 0.05 and 0.95, and the 0.25 and 0.75 quantiles for p₁, respectively.

The method requires that we define two populations as the descendants of the original parental populations. Our choice is based on current archaeological, linguistic, and genetic knowledge and is similar to the conventions found in the literature. To represent descendants of Near Eastern Neolithic farmers, previous studies (e.g., refs. 8, 16, and 23) have used available samples from Turkey, Iraq, Iran, Lebanon, or Syria. The Y chromosome data of Semino et al. (16) had three samples from these areas: Turkey (n = 30), Lebanon (n = 31), and Syria (n = 20). Given their limited size, and because they had similar heterozygosity (H_e = 0.83 for Turkey and Lebanon and H_e = 0.87 for Syria, whereas H_e ranged between 0.38 and 0.83 in the European samples) and essentially the same haplotypes in similar frequencies, it seemed sensible to pool them. This choice also aids comparisons with previous studies and with the interpretation of the same data by Semino et al. (16).

Under the CDM, all European populations are mostly derived from local Palaeolithic ancestors. As a consequence, under this hypothesis, any European sample could have been used to represent the Y-chromosomes of the Palaeolithic parental population. We used the two Basques samples (n = 45 + 22) because linguistic, archaeological, and genetic data agree in suggesting a persistence of pre-Neolithic features in the Basque country (24). This choice was cross-validated by comparison with an analysis using the Sardinians as an alternative approximation of the parental population (see Results and Discussion).

Three samples were not analyzed in the present study because of their geographical location: these were the Saami (n = 24), Udmurt (n = 43), and Mari (n = 46) samples. These samples come from Uralic-speaking populations of North-Eastern Europe and are well away from the supposed route of Neolithic immigrants. The admixture model is therefore unlikely to hold, given the parental populations used.

The Admixture Model and Estimation Methodology.

Our method assumes a simple admixture model in which two independent parental populations, P₁ and P₂, of size N₁ and N₂, have contributed a proportion p₁ and p₂ (p₂ = 1 − p₁) of the genes of a third “hybrid” or “admixed” population, H of size N_h, T generations ago. At the time of the admixture event, the gene frequencies are given by the vectors x₁ and x₂ in the two parental populations and by p₁x₁ + p₂x₂ in the hybrid population. After the admixture event, the three populations are isolated from each other and diverge because of genetic drift, the magnitude of which is determined by t₁ = T/N₁, t₂ = T/N₂, and t_h = T/N_h. The assumption of independent drift implies negligible gene flow between the populations after time T, which is reasonable given the large geographical distances between them. We assess this assumption in Results.

Full details of the derivation of the calculation are given in ref. 19. In outline, the likelihood for a sample of size n₁ from P₁ (or any other) is the product of three components. It depends on the number of coalescent events, c₁, between the present and the time of admixture T, the probability of which is p(c₁ | T/N₁, n₁). The number of coalescent events determines the number of lineages in the ancestral population that have left descendants, and hence the number of each allele with descendants, f₁. The probability of a particular vector of counts, p(f₁ | x₁, c₁), additionally depends on the ancestral allele frequencies x_1. Finally, the probability of the observed counts of allele in the present sample, p(a₁ | f₁) can be calculated from f₁. Because the three populations are assumed to be independent, the probability of the full data set D is obtained from the product of the three probabilities above for each of the three populations. The value must be summed over all possible values of c_i and f_i:

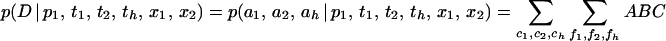where

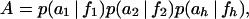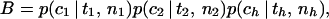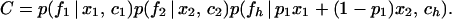The likelihood specified by Eq. 1 is difficult to evaluate directly, and we estimate it by using the Griffiths and Tavaré (25) scheme, as described in ref. 19. Having obtained the likelihood, it is useful to be able to make inferences about parameters without assuming any particular value of the others. This result can be achieved by using the Metropolis-Hastings algorithm (e.g., ref. 26), which allows us to obtain samples from the posterior distribution of p₁, T/N₁, T/N₂, T/N_h, x₁, and x₂. Posterior distributions of each parameter, independent of the values of the others (in particular independent of the “nuisance parameters' x₁ and x₂), can be obtained by simply looking at the samples corresponding to the parameter of interest.

We chose flat priors for p₁, T/N₁, T/N₂, and T/N_h. For x₁ and x₂, we chose a prior in which all possible allele frequencies have equal probability; this prior is given by a uniform Dirichlet distribution (19). The posterior distributions generated by the MCMC scheme described above are therefore proportional to the likelihood curves.

Principle and How Drift Is Taken into Account.

The MCMC method reconstructs ancestral allelic configurations compatible with the data while estimating the probability of the observed (present-day) allelic configurations for different values of the admixture parameter (p₁), of the times because admixture (T/N₁, T/N₂, T/N_h), and of the parental allelic distributions just before admixture (x₁, x₂). The T/N_i values measure genetic drift since admixture. For example, if one of the ancestral populations has remained relatively small since admixture (as might be the case for the Basques) it is expected to deviate more from its ancestral frequencies than a community that has grown in size. Because the T/N_i and x_i values are not constrained, the method encompasses different demographic scenarios before admixture (leading to different x_i distributions) and allows for the three populations to experience different amounts of drift after admixture (leading to different T/N_i distributions). This aspect of the analysis is important and allows the effect of pure drift and of admixture to be distinguished. For example, two populations may have similar allelic compositions, as a result of genetic drift, yet the method can still detect large differences in their admixture proportions (see Discussion).

The method assumes a model of pure drift without mutations. In practice, it means that mutations since the time of admixture have negligible effect on our estimate. This assumption is reasonable for these NRY data because the admixture events we are studying can be dated by the archaeological record to less than 10⁴ years ago (2) and the mutation rate for these markers appears to be less than 10⁻⁸ per site per year (27). Furthermore, the small effective size of Y-linked loci enhances the effect of drift (16, 21).

Regression Analysis.

A linear regression approach was used to detect, quantify, and assess the significance of any geographical trend in admixture proportions across Europe. By combining information across locations, this procedure reduces the uncertainty in admixture proportions at each distance. As in Semino et al. (16), the geographic distance was calculated from the middle point between Syria and Lebanon.

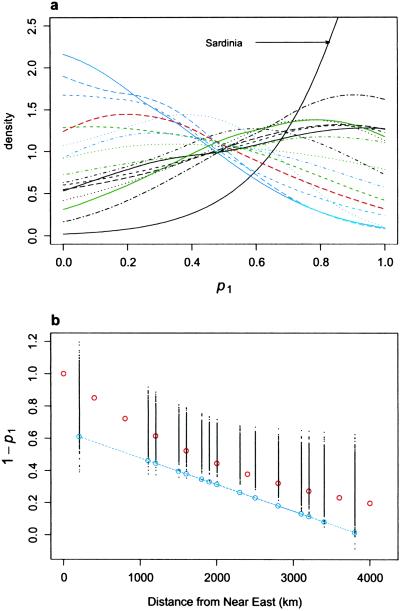
We could have obtained the regression of average p₁ values against distance. We rejected such an approach because it would have ignored the error on each p₁ estimate. We therefore assessed the uncertainty in the regression estimate by repeatedly sampling from the p₁ distributions in the following manner. For each of the European samples, one p₁ value was randomly sampled from the corresponding posterior distribution (Fig. 1a). A linear regression was then calculated between this set of values and geographic distance. This process was repeated 1,000 times to obtain the empirical distribution of regression curves shown in Fig. 1b. A similar approach was used for T/N_h.

Fig 1.

Palaeolithic and Neolithic contributions across Europe. (a) Posterior distributions of p₁ for all European populations. The colors correspond to the following populations. Blue: Albania (solid), Macedonia (dashed), Calabria (dotted), Croatia (dot-dash), and Greece (long-dash). Green: Czech Republic (solid), Hungary (dashed), Poland (dotted), and Ukraine (dot-dash). Black: Holland (solid), Germany (dashed), France (dotted), North Italy (dot-dash), Catalunia (long-dash), Andalusia (two-dash), and Sardinia (solid, see arrow). Red: Georgia (solid). The Sardinian posterior distribution is markedly sharper. Archaeological evidence also suggests that it is unlikely to have experienced introgression from Near Eastern farmers. (b) Linear regression of p₁ against geographic distance from the Near East. The geographic distance was calculated from the midpoint of Syria and Lebanon. The distribution of points was generated by sampling one p₁ value from each of the posterior distributions in a and then by calculating the linear regression between this set of values and geographic distances. The fitted values are plotted for each of 1,000 replicates. As fitted values are plotted, they can occur outside the range (0–1). Note that some samples were at very similar geographic distances from Near East, so the distributions are overlaid. It is possible to fit the simple stepping-stone model described in the text to this distribution. For instance, the values shown by the red circles are the expected proportions for n = 10 admixture events in which the contribution of the farming community, P_N was 0.85. There is a range of other combinations, which fit equally well. However, for large n values, the relationship becomes very curvilinear and requires large values of P_N to explain the trend and average contribution of 50% (or 65% by using the Sardinian). The dotted blue line with the circles represents the regression obtained by Semino et al. (16) by using Eu4, -9, -10, and -11. It is significantly different from the regressions we obtain by using all of the allelic information (P < 0.001).

Results

Admixture Proportions.

Table 1 shows summary statistics for the posterior distributions for p₁, the Palaeolithic contribution to 17 European populations (represented in Fig. 1a). The modes correspond to the most probable values (equivalent to the maximum likelihood estimates in a classical likelihood framework). The distributions are clearly rather wide, as expected from simulations (19). For instance, even for populations as far from the Levant as France or Germany, Palaeolithic (hunter-gatherers) contributions as low as 20% are within the 90% most probable values. Similarly, for Greece and Albania, p₁ values as high as 70% cannot be rejected (Table 1). Thus, our approach highlights that estimates of admixture in a particular population made from a single locus are often imprecise.

Despite uncertainty on p₁ for specific populations, there is a clear trend across Europe, with the proportion of Neolithic genes decreasing from modal values around 85–100% in Albania, Macedonia or Greece to around 15–30% in France, Germany, or Catalunia. The statistical significance of this trend can be assessed and quantified by combining information from the individual populations and their geographic distance from the Near East and by plotting the regressions as shown in Fig. 1b. Using the same data, Semino et al. (16) obtained the regression represented by the blue dotted line in Fig. 1b, which is significantly different from the 1,000 regressions obtained by our randomization approach (see Fig. 1 legend and Materials and Methods). This approach allows us to reject both the regression and the associated 22% estimate for the Neolithic contribution (P < 0.001).

Note that the regression analysis might be biased if the information from adjacent populations were non-independent because of local gene flow. However, previous work by Sokal and collaborators (e.g., ref. 28) has shown that such effects are found over scales less than 300 km, whereas the current samples were more widely spaced than this. We checked the plot of residuals from the regression and found no evidence of non-independence. Thus, it appears that the linear regression is a reasonable approximation and although gene flow might have had some influence locally, it cannot explain the trend in admixture proportions observed across Europe.

Geographical patterns cannot be completely summarized by one average value. Nevertheless, it is instructive to estimate the average p₁ value across Europe to compare it with the value given by Semino et al. (16). The estimate was obtained by averaging p₁ values drawn from the distributions shown in Fig. 1a. We found an average Neolithic contribution of 50% across all samples, 56% for the Mediterranean subset and 44% in non-Mediterranean samples. Thus, whichever region of Europe is considered, we find that the average value is more than twice that suggested by Semino et al. on the basis of the more readily apparent trends.

Another important result of the admixture analysis is the p₁ distribution obtained for the Sardinian sample. Sardinia appears as a clear outlier from other European samples, showing a very tight distribution compared with other populations, with a peak at p₁ = 1, indicating a high proportion of genes derived from the Palaeolithic inhabitants of Europe. This point is discussed below.

Drift.

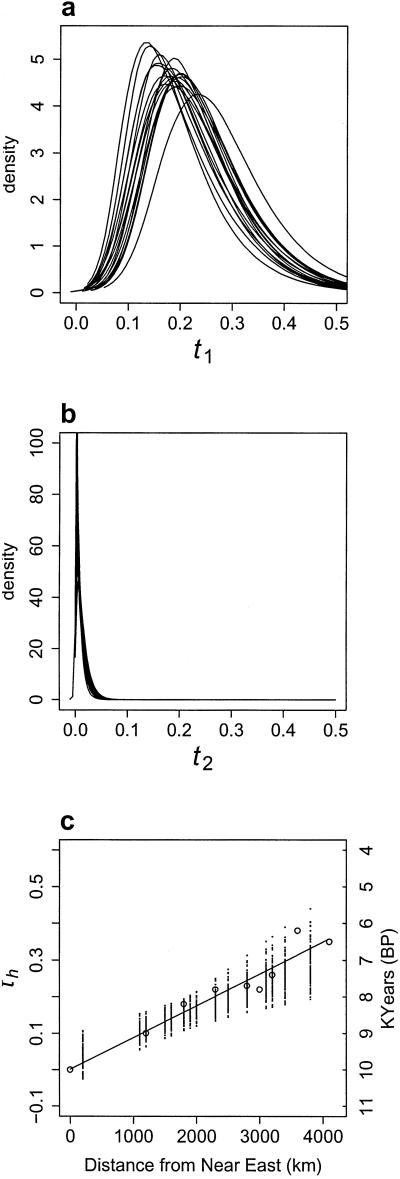
The method also generates estimates of the t_i = T/N_i values (T/N₁, T/N₂, T/N_h), which indicate the amount of genetic drift since admixture. Fig. 2 shows the posterior distributions for the two parental populations. Remember that the same two parental populations are used but that there are 17 European samples, and therefore 17 estimates for T/N₁ and T/N₂. Each curve in Fig. 2a (showing T/N₁) or b (showing T/N₂) thus corresponds to an estimate of the effects of drift among the Basques and the Near Easterners, respectively, obtained from the analysis of a particular hybrid (European) population. It is expected that T/N₁ and T/N₂ curves should be different because Basques and Near Eastern populations acquired agriculture at different times and therefore were subjected to different amounts of drift. This result is indeed, what we see with T/N₂ curves being almost identical (Fig. 2b), suggesting limited drift, and hence rather large long-term population size for the Near East population. For the Basques (Fig. 2a), the T/N₁ distributions are much wider and more variable, although all modes but one fall in the interval between 0.1 and 0.2. This effect is expected because simulations have shown that, as drift increases, T/N_i distributions both become wider and have variable modal values (19). Such a variation suggests a smaller population size and some level of differentiation among the hunter-gatherers that originally contributed to the pre-Neolithic gene pool (see below). The difference observed between T/N₁ and T/N₂ distributions is to be expected when an expanding population (here, the one from the Near East) disperses into scarcely populated areas (whose descendants are here represented by the Basque sample).

Fig 2.

Distribution of the T/N_is for all populations. (a) Posterior distributions of T/N₁. The different curves represent the amount of scaled time (generations divided by population size) between the present-sample of Basques used and the ancestral population of hunter-gatherers who interbred with arriving farmers. Different T/N₁ distributions are expected if the early European populations were highly differentiated from each other. This result is not what we observe. This outcome shows that the present-day samples of the Basques represent a non-biased sample of the original distribution and/or that the amount of differentiation between hunter-gatherer populations was not very high compared with drift since the admixture. The large and highly significant difference with b shows that the method is indeed sufficiently sensitive to detect different values of T/N_i. (b) Posterior distributions of T/N₂. Scaled times (as in a), but for the Near East populations. (c) Linear regression of T/N_h against geographic distance. For each of the admixed population samples, one T/N_h value was randomly sampled from the corresponding posterior distribution (not shown). A linear regression was then calculated between this set of values and the set of geographic distances from the Near East. Fitted values are plotted for each of 1,000 replicates. The calibrated radiocarbon dates represent the 95% limit for the earliest date of arrival of agriculture. These dates are based on locations for which there were more than 30 available data points (S. Shennan, personal communication).

The T/N_h would be expected to show a geographical trend because of the change in population size as agriculture arrived. To test this effect, T/N_h values were randomly drawn from the T/N_h distributions and were regressed against geographical distance. Fig. 2c shows that the T/N_h values increase as distance from the Near East increases. In other words, drift was greater where the archaeological record suggests a later arrival of agriculture, in agreement with the idea that demographic growth started when food began to be produced. To obtain an absolute dating scale for this geographic trend, we have plotted calibrated radiocarbon dates (S. Shennan, personal communication) of the first arrival of agriculture in a number of populations across Europe. A good fit between the absolute dates and the T/N_h values is obtained when we assume a starting date around 10,000 years B.P. and an average rate of 1 km/yr, both figures being widely accepted (1, 6). These values are in agreement with our current knowledge of human history.

Discussion

Admixture and Drift.

Europe-wide gradients of allele frequencies have repeatedly been described since the early work of Ammerman and Cavalli-Sforza (1, 5, 12, 13, 28). They were originally interpreted as a consequence of the admixture between low-density local hunter-gatherers and the large numbers of newcoming farmers from the Near East.

A number of studies based on mtDNA have recently criticized this view and suggested that the Neolithic contribution could have been much smaller, perhaps around 15%. This assertion has generated a controversy (9, 11, 15, 29, 30) over the interpretation of mtDNA data. Y chromosome data on the contrary appeared to confirm previous work on nuclear genes (23, 31).

It therefore came as a surprise when Semino et al. (16) analyzed the largest set of NRY data at the time and proposed that Y chromosome data also favor limited contribution from Near Eastern farmers.

One basic reason for the discrepancy between our and Semino et al.'s interpretation is that they used only a subset of information from selected haplotypes. Such an approach could make inefficient use of the data, or introduce bias. Conversely, the likelihood calculations on which our method is based can take advantage of all of the information present in the allelic distributions, without preselection of any allele. For instance, haplotype Eu17 is observed twice in the Near Eastern and Calabrian samples and once in the Georgian, Greek, Andalusian, and Hungarian samples. Although Eu17 and other similar haplotypes are unlikely to show any visible spatial pattern such as those shown by Eu4, -9, -10, and –11, they may convey relevant information. A closer look at Semino et al.'s table 1 shows that 60% of non-empty cells are singletons, doublets, or triplets. The total frequency of these “rare” haplotypes represents approximately 17%. This calculation is given here as an illustration and should not be used to estimate how much information was lost because such a computation is not trivial.

A particular innovation of our approach is that it estimates the trend in the Neolithic contribution directly, rather than evaluating it indirectly from the clines in allele frequencies.

One of the most striking results was obtained for the Sardinian sample (Fig. 1). Semino et al.'s ordination of the haplotype frequencies showed the Sardinian sample clustering with Greek and Albanian samples, far removed from the Basque samples. That result appeared at odds with archaeological data that suggest a limited Neolithic immigration in Sardinia (e.g., ref. 32). Conversely, in Fig. 1a, Sardinia appears as an outlier with a significantly high proportion of Palaeolithic genes. This result suggests that the Y-chromosome differentiation observed between Basques and Sardinians today is due to drift from common Palaeolithic ancestors, with little input of genes from the Near East, rather than to a greater Neolithic immigration in Sardinia. This result shows the importance in separating drift from admixture in the analysis of ancient demographic events.

This result prompted us to carry out a reanalysis of the data by using the Sardinian sample to represent descendants of the Palaeolithic people instead of the Basques. Although this was not our original choice, it is consistent with the archaeological evidence and provides and interesting comparison. Indeed any SE-NW geographical trend of p₁ values could not be attributed to geographic proximity to Sardinia. This new analysis confirms and strengthens the results obtained with the Basque samples. The regression of the Neolithic contribution against geographic distance is very similar to that in Fig. 1b (not shown), and the proportions are again significantly higher (P < 0.001) than estimates of Semino et al. Indeed, the average value of the Neolithic contribution is actually higher, ≈65%.

Our analysis also showed differences between Mediterranean and non-Mediterranean samples, which are in agreement with archaeological evidence for an earlier development of farming communities along the Mediterranean shores and with mitochondrial studies suggesting a greater introgression of Near Eastern genes in Southern European populations (30).

It is worth stressing again that the analyses presented here rest on the use of Basques (or Sardinians) as descendants of Palaeolithic people. Because the Basques are likely to contain an unknown proportion of Neolithic genes, there is reason to believe that the Palaeolithic contribution has actually been overestimated, even though we cannot say by how much.

Preadmixture Population Structure and Selection.

The existence of population structure in Europe before the arrival of farmers might influence our admixture estimates (and any other published estimates, in fact). For instance, it has been suggested that geographic diversity of mtDNA reflects population contractions and expansions, occurring in response to movements of the ice sheet, before and after the last glacial maximum, i.e., in the Mesolithic period. Whereas the relative importance of differentiation during this period is uncertain, it is very likely that hunter-gatherer population exhibited some level of genetic differentiation, and this has to be accounted for.

As explained in Materials and Methods, our analysis does not require the allele frequencies among hunter-gatherers to be uniform across Europe. If the initial European populations resembled the ancestral Basques in some cases and were more differentiated in others, then this would generate different T/N₁ estimates. The 17 T/N₁ estimates shown in Fig. 2a are similar to each other, suggesting that the hunter-gatherers were not dramatically different compared with the amount of drift in the last 5,000 to 10,000 yr.

An additional point that needs to be considered is whether the observed patterns can be attributed to the action of natural selection. This is an important issue because this could mean that estimation of genetic admixture may not properly represent demographic admixture. In other words, a selective sweep might lead us to overestimate the overall demographic impact. Conversely, balancing selection would lead to underestimates of the demographic impact. Whereas the data from a single locus cannot exclude the possibility of selection, we do have background information from other studies that suggest that selection may not be a significant issue. First, assuming that drift has been more important in the last 10,000 yr for the Y chromosome is in line with most population-based studies and therefore should not bias our study more than previous ones tackling similar questions (16). Second, and more importantly, the patterns observed here are in agreement with those observed at a number of independent loci and are therefore most likely to reflect demographic rather than selective processes (5, 12). A recent review by Harpending and Rogers also indicates that selection is likely to act on other sets of loci (33). Finally, we have applied a similar approach to a set of mtDNA data, and the preliminary results indicate that similar trends are emerging. This finding again would argue for the signal of a demographic event.

Implications for the DDM vs. CDM Controversy.

Our analysis clearly suggests that the contribution of genes from the Near East to Europe was substantial. The average values are 50% and 65% by using Basques and Sardinians as references, respectively, and these are likely to be underestimates. It is however important to realize that the CDM/DDM controversy is not directly and simply related to such average values. In particular, they do not represent the relative proportions of farmers and hunter-gatherers during the initial formation of settlements, but rather the proportion of genes that can be traced back to ancestors in the Near East. This very important distinction has been neglected in much of the recent literature, even though it was clearly made by Ammerman and Cavalli-Sforza (1).

By way of clarification, consider a simple “stepping-stone” model that assumes that admixture took place, across Europe, in the form of a series of steps, where farmers migrated to areas occupied by hunter-gatherers and mixed to create new communities of farmers. If we call P_N the proportion of farmers in the admixed populations, the Neolithic contribution in each location will decrease geometrically from P_N to P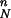, where n is the number of steps or admixture events taking place as populations move toward Western Europe. When n is large, the Neolithic contribution will appear to decrease very quickly and then stay at low values across most of Europe. Indeed, farmers could contribute as much as 90% at each settlement, yet with n = 20 the westernmost populations will have only 12% of Neolithic genes, and the average contribution will be only 100 × (P_N + P 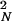+ ⋯ + P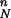)/n ≈ 40%. Thus, high P_N values are required to maintain a cline across the whole of Europe and even low averages can correspond to high P_N values.

Although the model is clearly a simplification, and many different combinations of P_N and n are compatible with the data, it is instructive to look at the implications for extreme values. A minimum Neolithic contribution at each event can be found by fitting P_N and n values to the trend obtained in Fig. 1b, for low n values. In the extreme case of n = 3, it would require P_N ≈ 0.7 to explain the observed trend (mean and slope). Because the archaeological evidence suggests a much more gradual expansion across Europe (i.e., larger n values) as shown by the radiocarbon dates plotted in Fig. 2c, it appears that P_N must have been larger than 0.7. More reasonable values of n suggest P_N values between 0.8 and 0.95 (see legend of Fig. 1b). These values are in agreement with previous estimates obtained in simulation studies, showing that, to generate gradients similar to those observed in proteins, the genetic contribution of Neolithic farmers had to be between 65 and 100% (34, 35).

Conclusion

In summary, our results provide direct estimates of the Neolithic contribution in Europe, and suggest that large movements of people accompanied the introduction of farming to Europe. Of course, farming practice may have spread concurrently by imitation and cultural transmission. Different processes are likely to have been important at different localities and at different times. Nevertheless, the broad picture produced by our method has led to diametrically different conclusions from the previous interpretations of the same data. We therefore argue that drawing inferences indirectly from the clines in haplotype frequency could be misleading. We suggest that data from other independent loci should be analyzed by using a similar approach to separate the effects of demography and selection. Our assessment of the demographic impact of the Neolithic expansion into Europe is largely independent from, but appears consistent with, archaeological evidence, simulations, and classical studies of allele frequencies. Despite some reports of its demise, the original model proposed by Ammerman and Cavalli-Sforza is more alive than ever.

Abbreviations

• DDM, demic diffusion model

• CDM, cultural diffusion model

• NRY, non-recombining region of the Y chromosome

• MCMC, Markov chain Monte Carlo