Extinction rates under nonrandom patterns of habitat loss

Abstract

Most models that examine the effects of habitat conversion on species extinctions assume that habitat conversion occurs at random. This assumption allows predictions about extinction rates based on the species–area relationship. We show that the spatially aggregated nature of habitat conversion introduces a significant bias that may lead species-loss rates to exceed those predicted by species–area curves. Correlations between human activity and major compositional gradients, or species richness, also alter predicted species extinction rates. We illustrate the consequences of nonrandom patterns of habitat conversion by using a data set that combines the distribution of native vascular plants with human activity patterns in California.

Humans have caused numerous species extinctions (1–9) primarily through the conversion of natural habitat into land dominated by agriculture and other anthropogenic activities (3, 10–14). Despite attempts to conserve global biological diversity, habitat conversion rates are accelerating, particularly in tropical countries (14). Policies for the preservation of global biodiversity rely on accurate predictions of the effects of habitat conversion on species distributions (15–17).

Attempts to estimate the relationship between habitat loss and extinction rates have focused on species–area relationships (6, 18–22) and metapopulation models (23–28). Although these methods differ in their predictions about the types of species that are most at risk and the delay between conversion of habitat and extinction (i.e., the “extinction debt”) (29), both approaches assume random habitat loss (26, 29). This assumption ignores two related biases. First, the distribution of species is influenced by underlying habitat characteristics such as rainfall, soil quality, and elevation. Secondly, these characteristics influence the rate at which areas are converted to human-dominated land uses. Specifically, humans have clear habitat preferences for coastal or other low-lying lands with adequate supplies of water (30, 31). The rate of habitat conversion is significantly faster in these areas than in areas less suitable for agriculture (26). Consequently, habitat-loss rates may be correlated with gradients of species composition and diversity (Fig. 1).

Fig 1.

Percentage of area in urban or agricultural land use (A), population density in 1990 (km⁻²) (B), and species richness of native plants (C) in each of 93 regions in California.

Furthermore, extinction rates will be sensitive to the specific distribution of species across the landscape as well as the spatial configuration of habitat conversion (32–34). A correlation between habitat-loss rate and species richness may cause extinction rates to deviate from the predictions of the species–area relationship. If species-rich areas are lost first, we would expect that initial species extinction rates to exceed those predicted under the assumption of random habitat loss.

The systematic nature of anthropogenic habitat conversion also changes the relationship between species extinctions and habitat loss, because species turnover tends to increase with geographic distance (32, 35, 36). If habitat conversion is spatially aggregated, then the average distance between remnant patches will be lower than when patches are randomly distributed. Because of the proportional relationship between distance and species turnover (36), we expect lower species turnover rates among aggregated patches than among randomly distributed patches. Accordingly, a system in which remnant habitat is aggregated will have fewer species than we would expect in a collection of widely scattered patches of equivalent total area.

There is excellent theory on the effects of spatial aggregation of habitat loss and correlation of habitat loss with endemism (32–34). In addition, there are compelling observational studies looking at correlation of population density with local diversity metrics such as richness and endemism (37, 38). However, our study is the first (of which we are aware) to link actual species distributions (as opposed to local diversity metrics) with observed patterns of habitat loss; as we discuss, habitat loss and population density are not always correlated.

Here, we explicitly incorporate realistic patterns of habitat conversion and species distributions into a model framework that links our empirical results to theory. We use this model to demonstrate the degree to which observed patterns of habitat conversion in California modify the predicted species extinction rates based solely on the species–area relationship. In addition, we use this model to examine the effects of three general processes that can alter predicted species extinction rates: spatial aggregation of loss, variance in loss rates among regions, and covariance between loss rates and local species richness.

Methods

California's diverse vascular-plant community provides an excellent opportunity to test for nonrandom patterns of habitat loss and their implications for rates of biodiversity loss. California contains more than 20% of all of the vascular plant species in the United States and 4% of the worldwide total (39). Nearly 30% of these species are endemics (39). California also spans a wide range of abiotic conditions and levels of human activity. California encompasses habitats that range over 4,000 m in elevation and 10° of latitude, and covers more than 40 million hectares (ha). Habitat loss within the regions in this study varies from less than 1% to more than 95% area converted to urban and agricultural land uses. In addition, most anthropogenic change in California has occurred over the last 50–100 years (40), a time scale comparable with current predictions for habitat conversion in the tropics (13, 20).

We used a public data set that lists the native species (and recognized subspecies) in each of 93 regions in California (http://elib.cs.berkeley.edu/calflora/). These regions were constructed by subdividing the 58 counties at biologically meaningful points (e.g., the crest of the Sierra Mountains) (41). These data include species already extirpated in portions of their range, so that they are not biased by extinctions resulting from recent anthropogenic activities. In our analysis, we used the most conservative list of species occurences. Use of more inclusive ranges did not qualitatively affect any results.

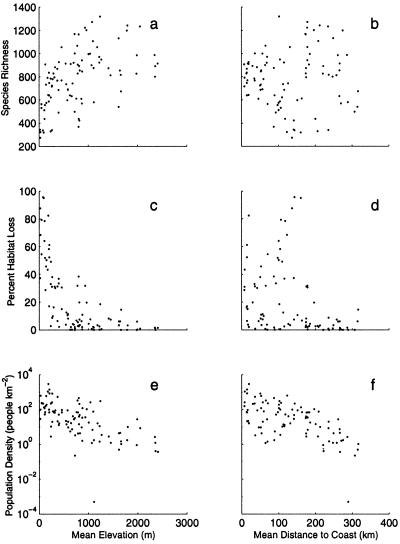
We looked for biophysical factors that were correlated with the intensity of human impact (measured as percent cover of agriculture or urban land use and population density in 1990 and 2020). We tested the relationship between the following geographical and human impact levels in California: mean elevation, distance to coast, mean July temperature (42), January temperature (42), annual precipitation (43), mean latitude, and potential plant productivity (44). Habitat loss was defined as the percent of the area converted to urban or agricultural land use (45). We included 1990 population density and projected 2020 population density (46). We present the 1990 population density, but these variables are highly correlated (r = 0.99; P < 0.0001). Population density and habitat loss also are correlated (r = 0.46; P < 0.0001) in California as in other areas (14). However, there are agricultural regions, such as the Central Valley, where high levels of habitat conversion have occurred in areas with low human population densities (Figs. 1 and 2).

Fig 2.

Species richness and the level of human impact in California relative to elevation (a, c, and e) and distance to the coast (b, d, and f). Human impact is measured as the projected population density in 1990 and the percent habitat loss, i.e., the land in either urban or agricultural uses. Each point represents a single subcounty region (n = 93).

The Model.

The relationship between species diversity and area is one of the clearest empirical laws in ecology (47). This relationship can be stated as

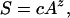where S is the number of species, A is area, c is a constant, and z is the exponent. The exponent usually ranges from 0.2–0.3 for oceanic islands, and slightly less in empirical studies of habitat islands (48, 49). The species–area extrapolations based on this relationship assume that conversion of habitat occurs at random with respect to the distribution of species.

To examine the implications of nonrandom habitat loss on extinction rates, we explore a range of habitat-loss scenarios. To do this, we sort the regions according to the order of interest (e.g., from high to low elevation) and assume that, over time, habitat conversion proceeds systematically from the first to the nth region, such that the proportion of habitat remaining in the jth region is given by the relationship

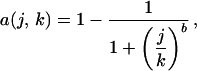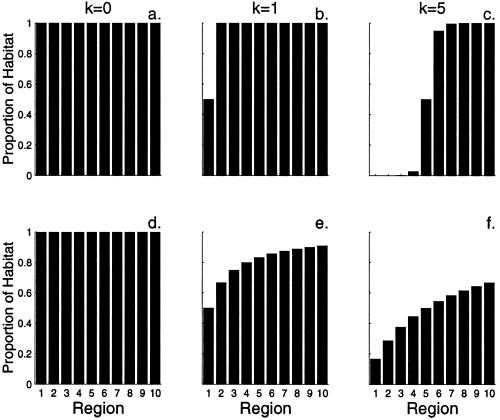
in which k is an arbitrary index that runs from 0 (no loss has occurred) until all habitat is converted. It should be noted that k is assigned arbitrary units without loss of generality, as the final analysis is autonomous of k. If b = 1.0, habitat-loss rates are fairly similar across all regions. If b ≫ 1.0, habitat-loss rates are variable among regions, and most of the habitat in the first region is converted before habitat conversion begins in subsequent regions (Fig. 3). We assume that species loss within a region follows a species–area relationship (Eq. 1). The number of species in the jth region (S_jk) for any given value of k will be

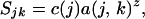where c(j) is the number of species in the jth region before any habitat conversion (k = 0). In our analyses, we set z = 0.25. Qualitative results were not affected by altering z within reasonable bounds (0.1–0.4) (50). For any given value of k, the proportion of the area remaining in the system, A_k, is current area summed across all regions divided by the total area in the system when k = 0, such that

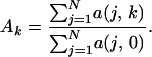If there is no overlap in species composition among regions, the proportion of the species in the system, S_k, is

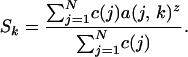In our data set, there is overlap in species composition among regions, and we calculated S_k by tallying the number of species with at least one occurrence across all regions. The change in total diversity with area can be seen by plotting S(k), against A(k) with k running from 0 until S(k) = 0.

Fig 3.

Proportion of habitat remaining in a landscape composed of 10 regions. Habitat conversion begins in region 1 and proceeds sequentially through the landscape as the index k runs from 0 until all habitat is converted. The variance in loss rates among regions is determined by the slope of the loss function (b in Eq. 2). When b = 16, the pattern of loss resembles a step function (a–c). When b = 1, loss rates are more even across the landscape (d–f).

We assume that species with small ranges (i.e., those present in a small number of regions) are the first to go extinct, because these species are likely to have lower mean population density (51–53). It is interesting to note that the assumption that extinction risk is a species trait greatly increases predicted loss rates. If the order in which species are lost is random but the same in each patch, there is little effect on the model predictions. However, if the order in which species are lost is independent in each patch, very few species become extinct until nearly all habitat is converted.

We used this model to investigate the effects of spatial aggregations of habitat conversion, variance in loss rates (i.e., b), and covariance between loss rates and species richness. To test the effects of spatial aggregation, we compare predicted loss rates when regions are ordered randomly with rates when loss is contiguous. We model contiguous loss by randomly selecting a region; habitat conversion proceeds from this seed region to all others in order of increasing distance (region 2 is the closest region to the seed point, region 3 is the next closest, etc.). We present the results of 100 simulations using randomly selected seed locations.

Results

We used canonical correlation analysis to look for the linear combination of the four human impacts and the six geographical factors that had the highest correlation (Table 1). The first human impact axis was dominated by the percent agricultural land and the second was a combination of population density and percent urban land use. The first biophysical axis was a contrast between elevation and July temperature, and the second biophysical axis was a combination of January temperature, elevation, distance to coast, and latitude. These results illustrate that urban and agricultural land uses are most intense at low elevations and in areas with high temperatures. In addition, urbanization and population density are highest in coastal areas (Fig. 2). The temperature effects arise because of the strong negative correlation between elevation and temperature (January r = −0.88; P < 0.0001; July r = −0.57; P < 0.0001). Similarly, distance to coast is negatively correlated with January temperature (r = −0.51; P < 0.0001).

Table 1.

Results of canonical correlation analysis

Variable	Axis 1	Axis 2
Human impact variables
Percent croplands	−0.9630	0.1780
Percent urban	0.1027	0.7935
2020 population density	0.1226	0.8908
1990 population density	0.1184	0.8410
Biophysical variables
Elevation	0.5627	−0.7346
Distance to coast	0.0216	−0.7282
July temperature	−0.4297	0.3022
January temperature	−0.2366	0.8350
Latitude of centroid	−0.1735	−0.6425
Plant productivity (potential NDVI)	0.2456	−0.2519

The table shows the correlation between the original variables and the first two axes extracted from human impact and biophysical variables. The correlation between the first human impact and biophysical axes (r² = 0.51) and the second human impact and biophysical axes (r² = 0.32) are significantly greater than 0.0 (P < 0.001).

The results of our analysis (Table 1) suggest two habitat-loss scenarios: (i) development proceeds from low to high elevations, and (ii) development proceeds from the coast to the inland areas. In addition to these empirically based scenarios, we look at three additional factors each of which is likely to be operating: (i) the variability in loss rates among regions (the shape of the loss function; Eq. 2, Fig. 3), (ii) the level of spatial aggregation of the loss, and (iii) the level of covariance between local richness and loss rate.

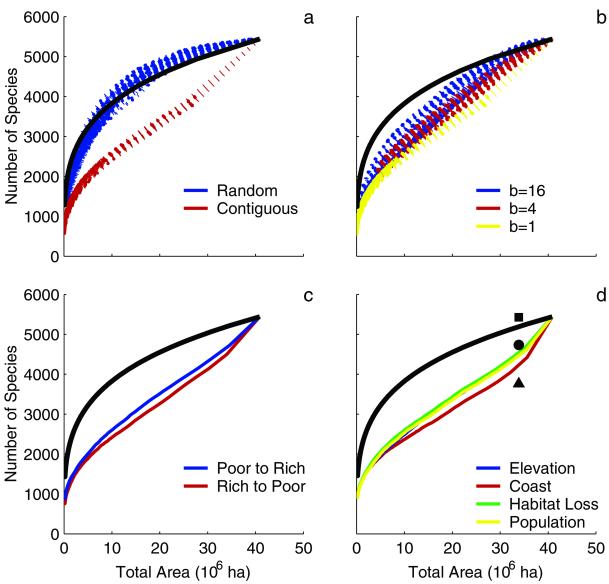
We found that spatially aggregated habitat loss led to increased extinction rates, mainly because species ranges also tend to be contiguous (Fig. 4a). In contrast, under the assumption of random loss, species can persist in portions of their range even when there is little habitat remaining in the system. Predicted extinction rates increased when habitat-loss rates became more similar among regions (b = 1) (Fig. 4b). In these cases, species with restricted ranges are rapidly lost from each region, and the overall species pool declines rapidly. There is an interaction between the effects of spatial aggregation of habitat loss and the variance in habitat-loss rates among regions (b), such that spatial aggregation only affects extinction rates when loss rates are variable among regions (e.g., when b = 16). When habitat-loss rates were similar among regions (b = 1) extinction rates are high for both the random and spatially aggregated scenarios. Removing the species-rich regions first increased predicted rate of species loss. However, the strength of the this effect was small relative to the effects of spatial variability and aggregation (Fig. 4c).

Fig 4.

Effects of nonrandom habitat loss on predicted species extinction rates of native vascular plants in California. In all panels, the solid black line shows the species–area relationship with z = 0.25. (a) The effects of spatial aggregation on predicted species-extinction rates (b = 16) based on 100 random permutations of the data. (b) Predicted extinction rates when habitat loss is contiguous and b ranges from 1 (habitat-loss rates are similar among regions) to 16 (habitat-loss rates vary greatly among regions). Results are shown for 100 random permutations of the data. (c) Sites are removed either from low richness to high richness (blue) or high to low richness (red). (d) We show the predicted species extinction rates under four habitat-loss scenarios: low to high elevation (Elevation), coastal to inland (Coast), high to low current habitat loss (Habitat Loss), and high to low 1990 population density (Population). The symbols shows the current area of California not in urban or agricultural land use and the current number of species that are not extinct (▪) or are not designated by state or federal agencies (•) or The Nature Conservancy (▴) as being in danger of extinction.

All of the realistically ordered scenarios had loss rates that were more rapid than species–area predictions (Fig. 4d). A comparison of two scenarios provides insight into the mechanism leading to the accelerated species-loss predictions. First, note that species diversity is positively correlated with elevation (r = 0.51 ; P < 0.0001) but not distance from the coast (r = 0.04 P = 0.683; Figs. 1 and 2 A and C). Thus, in the coastal to inland scenario, the accelerated loss of species results from the species turnover effect. In contrast, in the elevational scenario, the local richness effect should slow species loss rates, because the low diversity (i.e., low elevation) sites are converted first. Nevertheless, the elevational scenario also predicts accelerated species loss, suggesting that the species-turnover effect is stronger than the local diversity effect (Fig. 4).

Although we cannot test our model with a time series of species extinctions, we can gain a general impression of the validity of these predictions by looking at the current status of plant species in California. Most plant species that currently have federal or state status are very close to extinction. Half of the endangered plant species in the United States are known from only five or fewer locations and have population sizes of less than 100 individuals (54, 55). If we compare the ability of the different models to predict the number of species that are extinct (n = 14) or very close to extinction (709 species listed or proposed for state or federal listing), then our more detailed models give a closer match to the observed data than the standard species–area projection (Fig. 4). A species area curve fitted to the actual number of extinctions has a slope of 0.01, which is an unrealistically small value. A species area curve fitted through the number of imperiled species has a slope of 0.63, which is an equally unrealistic number (49).

It should be noted that The Nature Conservancy considers even more species (1,679) to be at risk of extinction in California (39). These currently imperiled or extinct species are not distributed randomly in the landscape. There is a positive relationship between the number of imperiled species and the proportion of urban land (r = 0.29; P = 0.292). In addition, there are more imperiled species in habitats that have experienced the most habitat conversion near the coast (r = 0.57; P < 0.0001) and at low elevations (r = 0.30; P = 0.0034).

Discussion

Until this time, we are aware of only a few attempts to examine the effects of nonrandom habitat loss on species extinction rates (32, 34). The predictions of these nonrandom models have never, to our knowledge, been tested against actual species distributions. Here we show that the assumption of random habitat loss is likely to strongly bias models of species extinctions. If habitat loss is negatively correlated with local richness, as in California, there are cases when the rates may be slower than the species–area curve predictions. Conversely, a positive relationship will create a bias that causes the species area relationship to significantly underestimate the ultimate rate of extinction.

It is likely that the effects of local richness will be masked by the effects of spatial aggregation on species turnover. Spatially aggregated loss dramatically increased the predicted rate of species loss. It is also likely, that the effects of aggregation are more general than the effects of local richness. Given that humans have clear preferences for certain habitats (30), it is likely that human activity will often be spatially aggregated. The degree to which spatially aggregated habitat conversion increases species extinctions will depend on the distribution of endemic species within the areas of high habitat conversion (34, 38).

All of the results of this paper suggest that estimates of extinction rates from species–area extrapolations are likely to be wrong when applied to species data from a large geographical area. We have shown three processes that lead to differences between the expected species–area loss rate and more realistic loss rates: variability in loss rates among regions, spatial aggregation in loss, and covariance between loss rates and local species richness. Why then do species-area predictions seem to provide an accurate prediction? First, it seems likely that they have mainly been applied to relatively restricted geographical locations. Secondly, any prediction of species loss is distorted by the time delay between when the habitat is lost and when the species finally declines to extinction (29). Thirdly, attempts to protect threatened species will slow the extinction rate. This seems to be particularly important in California, where relatively few plant species have actually gone extinct, but many are protected in the one or two locations where their last persisting populations survive. Similar levels of protection are essentially nonexistent in the tropics.

This analysis has a number of implications for reserve design. The presence of biodiversity “hotspots” suggests that conservation efforts should focus on areas of higher-than-average local richness (56). Our results illustrate the pitfalls of focusing too highly on within-site species richness rather than complementarity among sites. Specifically, the preservation of vascular-plant diversity in California is likely to be more dependent on the preservation of a wide range of complementary sites along the elevational and coastal gradients than on selecting solely on the basis of local species richness. On a larger scale, in the United States, 50% of endangered plant species could be conserved with less than 2% of the land area. However, the remaining species are found in only one location and conserving all endangered plants requires 9.6% of the land area (56).

Rates of anthropogenic habitat conversion are currently at their historical maximum (13, 57). Most of this habitat conversion is occurring in the lowland tropics and is converting forest and savannah into agriculture and urban land to feed the human population of over six billion people. It seems unlikely that the rate of habitat conversion will slow in the near future given current projects that human population will increase by 50% to approach nine billion in the next 50 years (13, 57). If this process of habitat conversion expands further into the biologically rich lands that are currently only threatened, then rates of extinction will rapidly increase.

The major successes of conservation in the last 20–50 years have come from the protection of wilderness, usually in high elevation areas, that are unsuitable for agriculture or human development. For example, in the United States most of the habitat loss occurs in low-lying areas, while most of the protected land is restricted to high elevations (58). Unfortunately, these lands contain less than 10% of the nation's biological diversity. The biggest challenge now facing conservation biology is to conserve the 90% of biodiversity residing on low-lying lands that are often privately owned. It is here that rates of habitat loss are increasing most rapidly. Understanding the relationship between habitat loss and the loss of biological diversity is central to the development of sound conservation policy. The analysis presented here suggests that models that do not account for the nonrandom nature of habitat loss will provide biased projections of future extinctions.