An improved genetic model generates high-resolution mapping of QTL for protein quality in maize endosperm

Abstract

The genetic mapping of polymorphic markers in a cross between two inbred plant lines has proven to be a powerful method for detecting quantitative trait loci (QTL) underlying complex traits. However, existing methods of QTL mapping were developed for disomic inheritance of both marker and QTL loci in a diploid population. To map QTL influencing traits expressed in the endosperm, a triploid embryo-nourishing tissue resulting from double fertilization, existing QTL mapping models require modification to consider the trisomic inheritance of the endosperm and the generation difference between the mapping population and the endosperm. Such a model requires simultaneous use of two successive generations, which theoretically can lead to an increase in resolution for QTL mapping compared with the use of a single backcross or F₂ generation. Using a newly developed model based on these considerations, we demonstrate the improved resolution of QTL, influencing protein quality traits in maize endosperm. The increased resolution made possible with this approach makes identified QTL accessible to positional cloning.

The evolutionary success of flowering plants is to a certain extent due to the occurrence of double fertilization (1). Double fertilization involves two sperm cells: one fuses with the egg cell to form a diploid zygote; the other fuses with the binucleated central cell to give rise to the triploid primary endosperm nucleus (2). The endosperm has classically been assigned the function of nourishing the embryo and providing hormones thought to regulate embryo growth (2, 3). The endosperm is largely or partially responsible for many grain quality traits, including protein (amino acid) and carbohydrate content (4), that are of paramount importance to the health of humans. Unfortunately, the essential amino acids needed for building proteins and other molecules are generally present at low concentrations in seeds of crop plants. Genomics-based strategies for breeding and genetic modification provide a powerful means for developing nutritionally improved cultivars of crop plants (5).

The improvement of many crop quality traits relies on the identification of genes responsible for endosperm-specific traits. The endosperm is a triploid tissue with four possible genotypes at one gene locus AAA, AAa, Aaa, and aaa versus the three AA, Aa, and aa for a usual diploid tissue. Also, because the endosperm is a product of a reproductive process, it represents a new generation as compared with its maternal sporophytic tissue. Finally, for the endosperm, the progeny of a cross between two different genotypes will vary between the reciprocal crosses. For these reasons, statistical strategies for genetic mapping of endosperm traits should be qualitatively different from those for mapping a diploid tissue (6, 7). To this end, we have extended and improved existing genetic models to map quantitative trait loci (QTL) affecting endosperm traits in maize.

Using this improved model, we mapped QTL influencing two measures of grain protein quality in maize (Zea mays): the protein synthesis factor elongation factor 1α (eEF1A) and free amino acid (FAA) content (8). It is well established that the concentration of eEF1A is consistently highly correlated with the lysine content of maize endosperm flour (9), which has much nutritional value for humans and monogastric animals. A great deal of research has been performed to explain the increased level of FAA in opaque-2 (o2) mutants that nearly double the Lys content of maize endosperm (10). These two traits have been used as indicators of the lysine content of the endosperm (9). The genetic basis of eEF1A and FAA content, which could provide an approach for selecting crop genotypes with better protein quality, has been investigated using quantitative and molecular genetic approaches (11–13). As will be seen below, however, the underlying genetic factors or QTL for these two traits can be identified more precisely by using our improved statistical model.

Statistical Theory

Mixture Model.

A mixture model forms a basic framework for modeling putative QTL genotypes (6). In this model, each observation y is assumed to have arisen from one of k (k possibly unknown but finite) genetic components, each component being modeled by a density from the parametric family f:

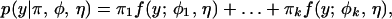where π = (π₁, . . . , π_k) are the mixture proportions which are constrained to be non-negative and sum to unity; φ = (φ₁, . . . , φ_k) are the component specific parameters, with φ_i being specific to component i and η a parameter that is common to all components.

A genetic mapping study built on such a mixture model contains two major tasks: (i) Derive the mixture proportions (π₁, . . . , π_k), denoted as the frequencies of QTL genotypes, and the density functions specified by gene effects of putative QTL (φ₁, . . . , φ_k) and the common residual variance (σ²); (ii) estimate the unknown QTL parameters included in the mixture model, based on observed markers and phenotypes. The first task relies on experimental designs, marker types, meiotic configurations, population structures, and reproductive behaviors contained in the mixture proportions, as well as gene actions and interactions contained in the normal distribution density. The second task needs powerful statistical and computational algorithms; for example, the EM algorithm for maximum likelihood method (14, 15).

Differences of Diploid and Triploid Mapping.

Suppose there is a segregating QTL (Q) with two alleles Q and q. For a usual diploid F₂ population, the components in the mixture model of Eq. 1 correspond to three groups of QTL genotypes QQ, Qq, and qq. Phenotypic observations within each of the three genotype groups are assumed to follow a normal distribution in which the expected QTL genotypic values (μ_j, j = 0, 1, 2 denotes the number of allele Q), composed of the overall mean (μ) and additive (a) and dominant effects (d), are modeled by

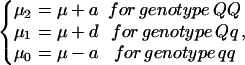and the common residual variance is denoted by σ². The mixture proportion of each QTL genotype is the conditional probability of the QTL genotype, on a marker genotype, which is derived on the basis of linkage analysis model as used in ref. 6.

For the triploid endosperm, there are four possible QTL genotypes, QQQ, QQq, Qqq, and qqq, whose expected genotypic values (μ_j) contain the additive effect (a) due to the substitution of allele q by Q and two dominant effects of alleles QQ over q (d₁) and allele Q over qq (d₂):

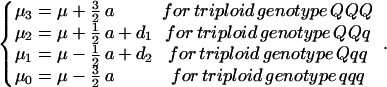In addition, the mixture proportions in endosperm mapping are the conditional probabilities of each of the four endosperm QTL genotypes on the marker genotypes of diploid F₂ plants. For a QTL located in a marker interval ℳ₁ − ℳ₂, these conditional probabilities are derived and described in Table 3, which is published as supporting information on the PNAS web site, www.pnas.org. It is seen that the conditional probabilities of the QTL genotypes on a given marker genotype are different between the F₂ and endosperm models.

Statistical Algorithm.

In endosperm mapping, there are six unknown parameters to be estimated, which are the overall mean (μ), additive effect (a), dominant effects (d₁ and d₂), residual variance (σ²), and QTL position (θ). The maximum-likelihood estimates (MLEs) of the unknown vector Ω = (μ a d₁ d₂ σ² θ)^T under the endosperm model can be computed by implementing an EM algorithm (14, 15). The log-likelihood of Eq. 1 for N endosperms derived from the F₂ generation is given by

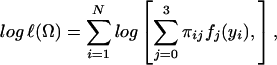with derivatives

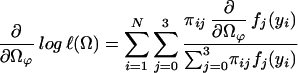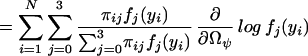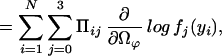where we define

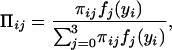which could be thought of as a posterior probability that the endosperm from the ith F₂ plant has a QTL genotype j. We then implement the EM algorithm with the expanded parameter set {Ω, Π}, where Π = {Π_ij}. Conditional on Π, we solve for the zeros of ∂log ℓ(Ω)/∂Ω_ϕ to get our estimates of Ω (the M step). The estimates are then used to update Π (the E step), and the process is repeated until convergence. The values at convergence are the maximum-likelihood estimates (MLEs).

It is assumed above that an additive effect (a), along with two different dominant effects (d₁, QQ versus q, and d₂, qq versus Q), determines QTL-genotypic values of an endosperm (Eq. 3; three-effect triploid model). In some case, the two dominant effects can be collapsed into one (d₁ = d₂ = d; two-effect triploid model). Thus, whereas the three-effect model is more general, the two-effect model is computationally simpler. Because these two models are not nested, a better model to fit a triploid endosperm data set can be selected on the basis of Akaike's (16) information criterion (AIC)

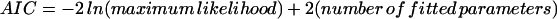The model with the smallest AIC is chosen as the most parsimonious.

Materials and Methods

An F₂ population of 106 plants was derived from a cross between two contrasting maize inbred lines, Oh51Ao2 (high eEF1A and low FAA content) and Oh545o2 (low eEF1A and high FAA content). The F₂ and F_2:3 progeny from this cross were prepared for genotypic and phenotypic analyses as described (11, 12).

DNA was extracted from young leaves of the F₂ plants, whereas grain protein quality traits were measured from the F₃ kernels of the F₂, as described (11–13). Simple sequence repeat (SSR) primers were selected from the Maize Microsatellite-RFLP consensus map. The primer sequences were described in the Maize Genome Database. The procedures for generating SSR markers were described in refs. 11 and 12. A linkage map of 83 SSR markers of the F₂ plants was constructed (11), based on the known order of SSR markers on maize chromosomes.

Results

The eEF1A and FAA values for the endosperm of the F₂ plants and their original parents were previously reported (11, 12) and found to display remarkable variation in the population. It is not uncommon to detect F₂ transgressive segregants whose phenotypic values are beyond those of both parents. The marker information of the genetic map constructed is associated with the phenotypic values of the endosperm in the F₂ by using a statistical model. For comparison, we used both the current diploid model (6) and our newly developed triploid model, described in the Statistical Theory.

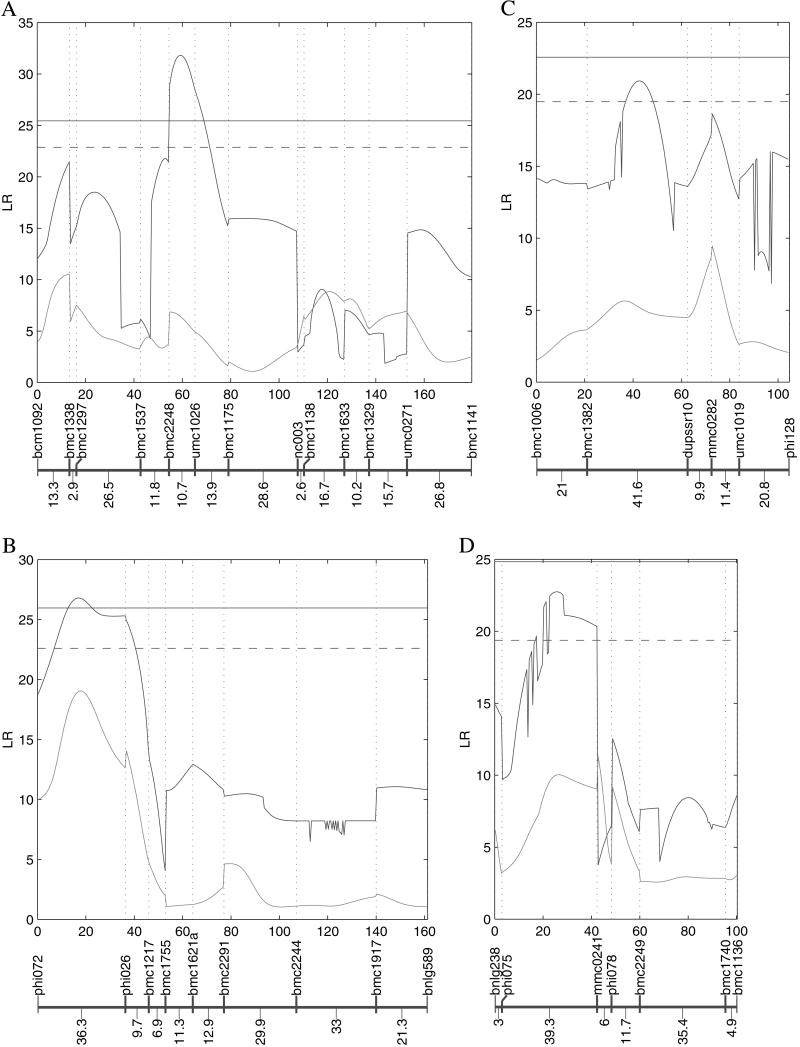
The diploid model detected two suggestive QTLs (P = 0.05) for eEF1A content, but did not detect a significant QTL (P = 0.01; ref. 11). However, our triploid model detected two suggestive QTLs and two significant QTLs for the same trait (Table 1, Fig. 1). The two significant QTLs for eEF1A content were detected on chromosomes 2 and 4, respectively. The log-likelihood ratio (LR) test statistics calculated for these two QTLs were 31.82 and 26.84, greater than the critical threshold values at P = 0.01, 25.45, and 25.97, respectively, calculated from 1,000 permutation tests (17). As shown in Fig. 1A, interval mapping of a significant QTL on chromosome 2 indicated a narrow peak spanning about 10 cM between markers bmc2248 and umc1026. This finding suggests that our triploid model provides high resolution for QTL mapping of endosperm traits. The second significant QTL was detected on the short arm of chromosome 4 at 16.7 cM from the first marker phi072 (Fig. 1B). Although this QTL was also detected at a similar location by Lander and Botstein's diploid interval mapping (6), the diploid mapping model had considerably lower power compared with our triploid mapping model, as indicated by the difference of the LR profiles between the two models (Fig. 1B). Wang et al. (11) observed that this QTL was linked with a cluster of 22-kDa α-zein coding sequences, confirming the biological relevance of our triploid model.

Table 1.

MLEs of chromosome locations and effects of QTL affecting eEF1A and FAA contents in maize endosperm

Chromosome	Location	LR	Threshold		a	d1	d2
			P = 0.05	P = 0.01
eEF1A content
2S	bmc2248 –umc1026	31.82	22.88	25.45	0.10	−0.47	−0.60
4S	phi072 –phi026	26.84	22.61	25.97	−0.07	−0.07	0.41
5S	bmc1382 –dupssr10	20.93	19.49	22.58	−0.23	−0.23	−0.14
6S	phi075 –mmc0241	22.75	19.37	24.83	−0.28	−0.30	0.20
FAA content
1L	phi037 –mmc0041	28.29	22.92	27.33	−6.17	−6.17	−11.87
2S	bmc1537 –bmc2248	42.37	22.22	26.04	0.48	17.19	−0.48
2L	bmc1633 –bmc1329	42.75	22.22	26.04	5.93	−11.19	−5.93
3S	bmc2136 –bmc1452	41.22	21.61	23.84	6.18	−12.76	−6.18
4L	bmc1217 –bmc1755	45.09	23.04	28.31	−5.80	−5.80	−12.51
5L	dupssr10 –mmc0282	23.52	21.17	23.50	0.13	17.09	−0.13
6L	bmc2249 –bmc1740	20.45	19.88	24.16	8.69	−14.62	−8.69
7L	dupssr13 –bmc2328b	38.25	21.65	27.70	5.93	−11.31	−5.93
8S	phi119 –phi115	34.95	19.60	24.15	−5.98	−5.98	−10.94
9S	phi028 –bnlg244	26.03	18.63	24.83	5.73	−11.30	−5.73
10S	bmc1655 –bmc1074	24.74	22.52	25.62	0.02	16.83	−0.02

The location of QTLs is described by two flanking markers. The threshold is calculated on the basis of 1,000 permutation tests (17). a is the additive effect of a QTL, and d₁ and d₂ are the dominance effects due to the dominance of QQ over q or Q over qq, respectively. Significant QTLs (P = 0.01) are expressed in boldface.

Fig 1.

The profiles of the LR test statistics for testing the QTL affecting eEF1A content calculated as a function of genome position on chromosomes 2 (A), 4 (B), 5 (C), and 6 (D). The blue curves are associated with our triploid model, whereas the pink curves with Lander and Botstein's diploid model. The significance threshold values for the triploid model [indicated by the solid (P = 0.01) and dashed (P = 0.05) horizontal lines] were estimated with 1,000 permutations (17). Except for the QTL on chromosome 4, all of the QTL detected are fit better by the three- rather than two-effect triploid model. Marker names and map distances (in cM) are given below each profile (11).

The two suggestive QTLs were detected between markers bmc1382 and dupssr10 on chromosome 5 (Fig. 1C) and between markers phi075 and mmc0241 on chromosome 6 (Fig. 1D), respectively, and both displayed steep peaks for the profile of the LR values as a function of the length of linkage group. Each QTL detected by our model independently explains about 20% of the variance for eEF1A content. The four QTLs detected display strong allelic interaction effects because of the dominance of QQ over q or the dominance of Q over qq (Table 1). The QTL detected near the centromere of chromosome 7 by the diploid model (11) was not confirmed by the triploid model.

More striking genetic mapping results were obtained for FAA content. The new triploid model identified ten significant QTLs and one suggestive QTL, located on all ten chromosomes (Table 1), whereas only four suggestive QTLs were detected by the diploid model (8). Although the additive effects of the QTL detected are significant for the FAA content of the endosperm, two types of dominant effects (QQ versus q and Q versus qq) play a more important role in affecting this trait. In all cases, the Akaike's information criterion (AIC) values calculated showed that the three-effect triploid model better fit the data than the two-effect model.

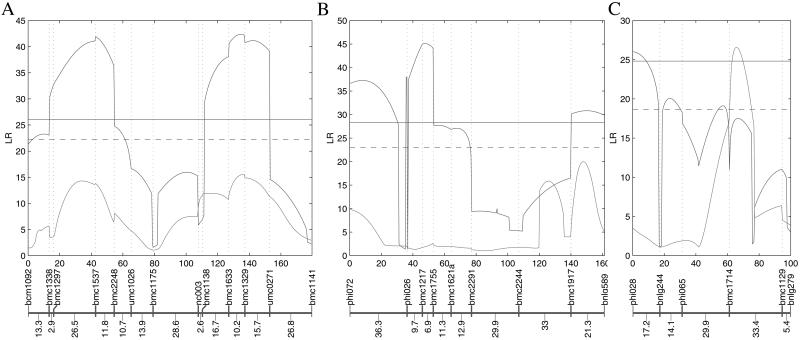
The most pronounced examples of loci affecting FAA content are two QTL, one on chromosome 2 (Fig. 2A) and the other on chromosome 4 (Fig. 2B). These two QTL were detected with high LRs (42.4 and 45.1) and, more importantly, exhibited high mapping resolution—i.e., their mapping intervals are 7–10 cM. The QTL at marker interval bmc1633–bmc1329, located on the long arm of chromosome 2, was also detected by the diploid model (ref. 12; Fig. 2A). This strong QTL is coincident with genes encoding a monofunctional Asp kinase 2 and a bifunctional Asp kinase-homo-Ser dehydrogenase-2 (13), which are enzymes controlling important steps in metabolic pathways for amino acid biosynthesis and Lys degradation. The gene corresponding to this QTL has now been cloned (X.W. and B.A.L., unpublished work), which further validates our triploid model. On chromosome 2, a second significant QTL bracketed by bmc1537 and bmc2248 was also detected by the triploid model (Fig. 2B). But its existence can be tested more precisely by modeling multiple QTL for the endosperm-specific traits.

Fig 2.

The profiles of the LR test statistics for testing the QTL affecting FAA content calculated as a function of genome position on chromosomes 2 (A), 4 (B), and 9 (C). The blue curves are associated with our triploid model, whereas the pink curves with Lander and Botstein's diploid model. The significance threshold values for the triploid model [indicated by the solid (P = 0.01) and dashed (P = 0.05) horizontal lines] were estimated with 1,000 permutations (17). According to AIC (16), all of the QTL detected for FAA content are fit better by the three- rather than two-effect triploid model. Marker names and map distances (in cM) are given below each profile (11).

Another interesting finding in this study is that a QTL at marker interval bmc1714–bmc1129 on chromosome 9 was observed by the diploid model, whereas a QTL at a different marker interval on the same chromosome was detected by the triploid model (Fig. 2C). Because the triploid model built on the quantitative inheritance of the endosperm (18) provides a more precise approach for QTL mapping in the endosperm, this difference suggests that the result from the diploid model, as can be used in the current literature, may deviate from biological reality. The QTL detected on chromosomes 1, 3, 5, 6, 7, 8, and 10 are shown as Fig. 3, which is published as supporting information on the PNAS web site.

Simulation

We performed a simulation study to examine the robustness and power of the triploid model for detecting QTL affecting endosperm-specific traits. This simulation study mimics the conditions of the maize endosperm experiment by assuming the same sample size (n = 106), a similar marker interval (10 cM) and similar gene effects. The simulation study includes three different schemes describing a variety of inheritance modes of a QTL expressed in the endosperm: (i) a = 0.5, d₁ = d₂ = 0.05 (additive model); (ii) a = 0.5, d₁ = 2.0 and d₂ = 0 (one dominant-effect model); and (iii) a = 0.5, d₁ = d₂ = 2.0 (two dominant-effect model).

Assume that a QTL affecting an endosperm-specific trait is located at 3 cM from the left one of the two flanking markers. Given the conditional probabilities of endosperm QTL genotypes (see supporting information), a total of 106 endosperm phenotypes were simulated on the basis of a normal distribution with the mean as the genotypic value of a particular QTL genotype (Eq. 3) and the residual variance corresponding to the broad-sense heritability of 0.15.

We used both the triploid and diploid models to detect the hypothesized QTL from the simulated phenotypic data for the endosperm under the three different schemes. In any case, the triploid model displayed greater power (or probability) of detecting a significant QTL among 500 simulation replicates (0.23–0.42) than the diploid model (0.20–0.36; Table 2). The map location of the QTL detected was also estimated more precisely from the triploid model (±1.0 cM) than from the diploid model (±3.5 cM). Under the diploid model, the estimate of the additive genetic effect of the endosperm QTL had a significantly greater sampling error (by over 50%) than under the triploid model (Table 2). This finding thus suggests that the estimate of the QTL additive effect is questionable when the conventional diploid model is used to map QTL segregating in the endosperm. The triploid model can estimate two different dominant effects (d₁, the dominance of QQ over q, and d₂, the dominance of Q over qq) occurring in the endosperm inheritance, whereas the diploid model mixes the estimates of these two dominant effects. When the dominant effect of a QTL is small (Scheme 1 in Table 2), the triploid model appeared to overestimate this effect (Table 2). But the triploid model provided an accurate estimate of a large dominant effect, although a large sampling error may occur. The inaccurate estimate of the dominant effect from the triploid model may occur because of the small sample size simulated. When the sample size is increased to 400, both the accuracy and precision of the dominant-effect estimate can be significantly increased from the triploid model, whereas the diploid model still displays a poor estimate of the dominant effect as obtained from a small sample size (data not shown). A similar result is achieved when different sets of values are hypothesized.

Table 2.

The MLEs of genetic parameters, their sampling errors (SE), and the power of detecting a significant QTL segregating in the endosperm from the triploid and diploid models under different simulation schemes

Model	MLE (±SE)			Power
	â	d̂1	d̂2
Scheme 1: Additive model	0.5	0.05	0.05
Triploid	0.49 (0.1473)	0.33 (0.9376)	−0.16 (0.9091)	0.416
Diploid	0.51 (0.2330)	0.04 (0.3689)		0.364
Scheme 2: One dominant-effect model	0.5	2.0	0
Triploid	0.49 (0.2387)	1.86 (1.3778)	0.10 (1.6118)	0.182
Diploid	0.49 (0.3680)	0.53 (0.5944)		0.120
Scheme 3: Two dominant-effect model	0.5	2.0	2.0
Triploid	0.50 (0.2575)	2.43 (1.1899)	1.47 (1.7075)	0.234
Diploid	0.52 (0.3927)	1.06 (0.5961)		0.198

a, d₁, and d₂ are the additive genetic effect, the dominant genetic effect of QQ over q, and the dominant genetic effect of Q over qq, respectively, for a QTL expressed in the endosperm. The triploid model estimates the dominant effects d₁ and d₂ separately, whereas the diploid model estimates the mixture of these two effects.

Discussion

The past 10–15 years have witnessed tremendous progress in the development of innovative molecular techniques and the application of these techniques to dissect complex, quantitatively inherited traits into QTL components in a variety of organisms (19, 20). Statistical inference has played a pivotal role in the successful dissection of quantitative traits (6, 7). The statistical principle for QTL mapping originally proposed by Lander and Botstein (6) has been extended to different experimental designs, different mapping populations, and different marker types. However, no statistical strategy has been developed to specifically map disomically inherited quantitative traits expressed in the triploid endosperm, despite the fact that the endosperm is an embryo-nourishing tissue carrying grain quality traits of great economical importance.

In this study, we have proposed an improved QTL mapping model built on the segregation and transmission of genes from a diploid sporophytic mother to triploid endosperm and used it to map QTLs affecting grain quality traits in maize endosperm. Our model takes account of the nature of quantitative inheritance in the endosperm (18) and the difference between the generation of the endosperm and the generation of its mother sporophytic plant. As compared with Lander and Botstein's model (6) developed for mapping diploid tissues, our triploid model displays three advantages. First, our model can increase the power of detecting a QTL affecting endosperm traits (reduced type II errors). In our maize example, many more significant QTL have been identified by the triploid than by the diploid model. Second, the triploid model can increase mapping resolution. For example, a QTL for FAA content was mapped to an interval of <7 cM. Third, our model increases the precision of QTL mapping. At least one QTL detected by our model corresponds to candidate genes encoding enzymes important to amino acid biosynthesis (13). Fourth, because the genetic mechanism underlying endosperm formation is embedded in our model, it has increased potential to detect correct QTL (reduced type I errors).

It is expected that the triploid endosperm has more possibilities to generate strong dominance effects than usual diploid tissues because of its larger number of gene combinations (18). In this study, we observed strong dominance effects of QTL on eFF1A and FAA contents in maize endosperm, suggesting that dominance effects are important for the genetic improvement of grain quality traits. However, given the modest sample size used in this study, the estimates of dominance effects should be interpreted with caution. Based on our simulation study, we found that the precise estimate of dominance effects on endosperm traits requires 400 genotypes. When the sample sizes used are limited, other measures, as we recommended in our other study (21), can be used to enhance the estimates of QTL positions and effects in the endosperm. These measures include (i) a two-stage hierarchical design for genotyping both the maternal plants and their embryos to extract more information about gene transition and segregation, (ii) appropriate sampling schemes for allocating samples between the F₂ and their seeds, and (iii) multiple replicates used to increase heritability levels of an endosperm trait.

In this study, we ignored the effect of the maternal genome on the endosperm. Despite many QTL detected for the two protein traits, our current triploid model may be insufficient to capture all information about the inheritance of the endosperm. For example, the QTL located near the centromere of chromosome 7 was detected by the diploid model (11), but not by the triploid model. This difference can be explained by a possibility that this QTL is derived from the maternal genome. It is interesting to investigate how maternal genomes (F₂) interact with offspring genomes (endosperm) to determine the phenotypes of seed- and endosperm-specific traits. This issue is similar to gene interactions from maternal effects in animals (22) and should be fundamentally important to simultaneously improve seed yield (mostly determined by parental genomes) and seed quality (mostly determined by offspring genomes) in plants (4, 5). The model reported in this study, however, provides a necessary platform for unlocking the genetic secrets underlying seed and endosperm formation and, ultimately, designing an efficient marker-assisted selection plan for the genetic improvement of grain yield and quality traits in crop plants.

Abbreviations

• QTL, quantitative trait locus

• FAA, free amino acid

• LR, log-likelihood ratio