Stepwise contribution of each subunit to the cooperative activation of BK channels by Ca²⁺

Abstract

BK channels (Slo1) are widely distributed K⁺ channels that control Ca²⁺-dependent processes and cellular excitability. Their activation by intracellular Ca²⁺ (Ca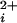) is highly cooperative, with Hill coefficients of typically 2–5. To investigate the cooperativity contributed by each of the four α subunits that form the BK channel, we studied single channels comprised of mixtures of functional subunits and subunits with a mutation to disrupt a key site (Ca-bowl) required for activation by low concentrations of Ca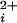. As the number of functional subunits increased, we found a stepwise increase in the Hill coefficient of 0.3–0.8 per functional subunit and a stepwise decrease in the Ca 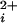required for half activation (K_d). These results show directly that BK channels can open with 0, 1, 2, 3, or 4 functional Ca-bowls, and that each subunit with a functional Ca-bowl contributes a stepwise increase to both the cooperativity of activation and the apparent Ca²⁺ affinity. A model with 0–4 high-affinity allosteric activators and four low-affinity allosteric activators was examined. In this model, Ca²⁺ bindings were independent of one another and the cooperativity arose from the joint action of the allosteric activators on the open–closed equilibrium. Although this model described well the major features of the experimental data, some differences between the observed and predicted results indicated that additional factors not included in the model also contribute to the cooperativity.

Large conductance Ca²⁺-activated K⁺ (BK) channels (Slo1) are activated in a highly synergistic manner by elevations in intracellular Ca²⁺ (Ca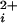) and depolarization (1, 2). When activated, the efflux of K⁺ out of the cell hyperpolarizes the membrane potential, shutting down voltage-dependent Ca²⁺ and Na⁺ channels. In this guardian role of controlling Ca²⁺ influx and excitability, BK channels modulate many processes, such as spike broadening in neurons (3), smooth muscle contraction (4), neurotransmitter release (5), and the electrical tuning of hair cells (6, 7). The activation of BK channels by Ca 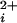typically occurs with Hill coefficients of 2–5 (1, 8–11), indicating that Ca 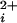acts in a highly cooperative manner. These coefficients suggest that a minimum of 2–5 Ca²⁺ must be bound to allosteric activators to maximally activate the channel. Consistent with this necessity, BK channels are tetramers (12), with each of the four pore-forming α subunits having at least two Ca²⁺-binding sites (13–18). One of these sites is a high-affinity (<10 μM) Ca²⁺-binding site and the other is a low-affinity (>100 μM) site that binds Ca²⁺ and Mg²⁺ (17, 18).

A candidate for the high-affinity Ca²⁺ activator site has been termed the Ca-bowl by Schreiber and Salkoff (14). The Ca-bowl is located in the C terminus and includes five consecutive negatively charged aspartic acid residues. Disruption of the Ca-bowl by mutations in the Ca-bowl or by replacement of the tail of the channel that includes the Ca-bowl with a tail from Slo3, a Ca²⁺ insensitive BK-like channel, greatly decreases the Ca²⁺ sensitivity (11, 14, 15, 19) and also decreases the Hill coefficient for Ca²⁺ activation from 4.5 to 1.3 at +50 mV (11). Fragments of the C terminus that include the Ca-bowl (the last ≈230 or ≈280 aa residues of the channel) bind Ca²⁺ (11, 16). The location of the low-affinity nonselective site is not clear, but it is closer to the core of the channel than the Ca-bowl (17).

An important step toward understanding the mechanism for the cooperative activation of BK channels by Ca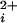, would be to determine the cooperativity contributed by each of the four individual subunits. Such information could place constraints on which types of gating mechanisms are consistent with the observed cooperativity and indicate at which steps in the activation process the cooperative interactions occur. Considerable insight into the mechanism of cooperativity has been obtained by detailed kinetic analysis, which has suggested that the activation of BK channels by Ca²⁺ and by voltage occurs through separate allosteric mechanisms that modulate the channel opening–closing transitions independently of one another (10, 17, 18, 20–25). However, because the gating of BK channels is so complex, it has been necessary in these studies to either make simplifying assumptions about the particular types of the cooperative interactions (10, 17, 18, 20–22, 25) or to analyze simplified models with fewer assumptions (7, 23, 24).

To overcome these difficulties, we now examine directly the cooperativity contributed by each individual subunit during Ca²⁺-activation of BK channels. This was done by studying single channels comprised of mixtures of functional and nonfunctional subunits in which the high-affinity allosteric activator was knocked out by mutating the Ca-bowl. The stoichiometry of each channel was determined from the single channel current amplitude by introducing a mutation to a tetraethylammonium (TEA) sensitive site (12, 26). Our results show directly that BK channels can open with 0, 1, 2, 3, or 4 functional Ca-bowls, and that each subunit with a functional Ca-bowl contributes a similar stepwise increase to the cooperativity. Although our results can be approximated by a model in which each subunit with a functional Ca-bowl serves as an independent allosteric activator to modulate the open–closed transition (17, 18), they also suggest that additional cooperative interactions are involved.

Materials and Methods

Expression of BK Channels.

Human embryonic kidney (HEK 293) cells were transiently transfected by using the Lipofectamine Reagent (Life Technologies), as described previously (27). Transfection was with an expression vector encoding the green fluorescent protein (Plasmid pGreen Lantern-1; GIBCO/BRL) to allow identification of transfected cells and an expression vector (pcDNA3) encoding either the wild type α subunit or a mutated α subunit of mouse BK channels (mSlo1). The original mSlo1 gene was cloned by Pallanck and Ganetzky (28). The construct we used was kindly provided by Merck Research Laboratories (29), who removed all 5′ noncoding sequence up to the second potential translation initiation site (1–940 was removed). Using this wild type construct, we generated constructs for two additional types of subunits. For one subunit we mutated a pore site in the channel to decrease TEA sensitivity (Y334V: GYGDVYAKT to GYGDVVAKT), based on the work of MacKinnon and Yellen (30) and Shen et al. (12). For the other subunit we mutated the Ca-bowl (deletion of D965 and D966: FLDQDDDDDPD to FLDQ_DDDPD). This mutation was used to disrupt the Ca-bowl, as it had the greatest effect on decreasing the Ca²⁺ sensitivity over a range of Ca²⁺ of all of the mutations examined by Schreiber and Salkoff (14). The indicated residue numbers are those in the GenBank accession no. U09383 before modification by Merck. Mutations were made by using the Stratagene QuickChange Site-Directed Mutageneis kit and checked by sequencing. When expressing channels with mixed subunits, the cDNA for the two types of subunits was applied in a 1:1 ratio.

Electrophysiology.

The transfected HEK 293 cells were cultured and recordings were made within 2–3 days after transfection, as detailed (27, 31). Single-channel currents were recorded from BK channels at room temperature (20–25°C) from inside-out patches containing single BK channels using the patch clamp technique (32). Endogenous channels in the HEK 293 cells were seldom observed under the conditions of our experiments and could be excluded from analysis because their properties differed from the channels observed after transfection with wild-type or mutated BK channels. The pipette solution contained 150 mM KCl and 5 mM TES. TEA chloride (1.5 mM) was added to the pipette when indicated. The intracellular solution contained 150 mM KCl, 5 mM TES, 1 mM EGTA, 1 mM HEDTA, and added CaCl₂ to obtain the desired free Ca²⁺ concentrations of 1–1000 μM (27). All solutions were adjusted to pH 7.0.

Analysis.

The single-channel current records were sampled with pClamp8 at 200 kHz and filtered to 1–5 kHz (−3 dB). The open probability (Po) was determined by dividing the total open time by the sum of the open and closed times, and/or by fitting the all points histograms of the current record with Gaussian distributions, with Po given by the fractional area of the open distribution. Fitting of the equations in the text to the Po versus Ca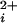 data were accomplished with the nonlinear least squares fitting routines in SIGMAPLOT 2000.

If Po versus Ca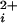 data are averaged from multiple channels before fitting, then the natural variation in the K_d's among BK channels (9) flattens the dose-response curves, underestimating the Hill coefficients (33, 34). To overcome this problem, the K_d and Hill coefficient were estimated for each single-channel patch by fitting the data from that patch with the Hill equation (see Results). The average K_d's and Hill coefficients for each type of channel were then given by the average of all of the individually determined values for that type of channel. To present all of the individual data points from all of the channels in the Po versus Ca 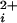plots (rather than presenting averaged data), the experimental data points from each individual channel where shifted an equal amount on the log Ca 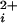axis until the K_d of the shifted data were identical to the K_d for the averaged data for all channels of that type. Aligning the data in this way did not change the average K_d and preserved the slopes of the dose-response data from the individual channels.

Results

Construction of Channels with 0–4 Functional Ca-bowls.

To investigate the contribution of each of the four α subunits to the cooperative Ca²⁺-activation of BK channels, we studied channels in which 0–4 of the subunits were replaced with subunits in which a key site (Ca-bowl) required for activation by low Ca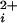 was disrupted by mutation. Because it was not possible to directly construct tandem subunits to give channels of the desired stoichiometry (the C terminus and N terminus of the α subunit of BK channels are on opposite sides of the membrane), we coexpressed subunits with functional Ca-bowls together with subunits with disrupted Ca-bowls, and then determined the stoichiometry of each studied channel. Identification was possible because each subunit with a functional Ca-bowl also had a mutation in the pore of the channel to render the channel relatively insensitive to block by TEA_O (30). The number of functional Ca-bowls in each studied channel could then be inferred from the single-channel current amplitude in the presence of TEA_O, similar to the approaches used by Shen et al. (12) and Liu et al. (26).

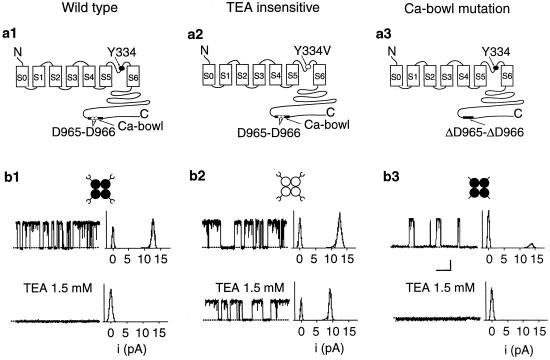
Fig. 1a1-3 presents schematic diagrams of the three types of α subunits used in this study: wild type (Fig. 1a1), after a pore mutation (GYGDVYAKT to GYGDVVAKT) (12) to remove most of the TEA_O sensitivity (Fig. 1a2), and after a deletion mutation in the Ca-bowl (FLDQDDDDDPD to FLDQ_DDDPD) (14) to disrupt the Ca-bowl (Fig. 1a3). Cartoons of the homotetrameric channels that would be obtained from expressing each type of subunit are presented in Fig. 1b1-3, together with single-channel currents recorded at +50 mV from these homotetrameric channels in the absence (Fig. 1b1–3 Upper) and presence (Fig. 1b1–3 Lower) of 1.5 mM TEA_O. (Channel opening is upward and the all-points current histograms are to the right of the traces.) TEA_O fully blocked both wild-type BK channels (Fig. 1b1) and also BK channels with disrupted Ca-bowls (Fig. 1b3). In contrast, BK channels with a pore mutation to remove most of the TEA_O sensitivity still carried robust currents of only slightly reduced amplitude (Fig. 1b2). Consequently, because currents comprised of subunits with disrupted Ca-bowls were fully blocked by TEA_O (Fig. 1b3), and currents from channels formed with subunits with functional Ca-bowls and pore mutations were little affected by TEA_O (Fig. 1b2), we used the single-channel current amplitude to deduce the subunit stoichiometry of channels formed from mixed subunits.

Fig 1.

Both wild-type and Ca-bowl mutated BK channels were totally blocked by TEA_O, whereas BK channels with the TEA_O binding site mutated were only partially blocked. (a) Schematic representation of a wild type subunit (a1), a Y334V subunit in which the TEA-binding site was mutated (a2), and a ΔD965–ΔD966 mutated subunit in which two critical residues in the Ca²⁺-bowl were deleted (a3). (b) Diagrams of the three types of homotetrameric BK channels that would be formed from the subunits represented above, together with single-channel currents and all-points amplitude histograms of the currents in the absence and presence of 1.5 mM TEA_O. The dotted lines show the closed current level. Horizontal bar, 30 ms; vertical bar, 5 pA. +50 mV.

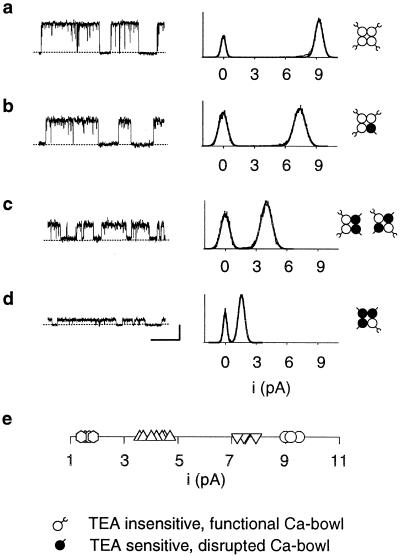
After expressing mixed subunits and recording with 1.5 mM TEA_O, the single-channel current amplitude remained constant for each given channel, but differed among channels, falling into four distinct classes. Representative single-channel currents from the four classes are shown in Fig. 2 a–d. A one-dimensional scatter plot of the single-channel current amplitudes observed in 18 patches containing a single channel showed that the unitary currents clustered into four discrete levels with TEA_O of 1–2 pA, 3.5–5 pA, 7–8 pA, and 8.8–9.5 pA (Fig. 2e). These different classes of current level were not seen in the absence of TEA_O, either in the absence or presence of disrupted Ca-bowls. Thus, neither the mutations to the TEA site nor mutations to the Ca-bowl induced these different classes of current level. Instead, they arose from differential block of the current by TEA_O because of differences in the number of subunits with a functional TEA site.

Fig 2.

Determination of subunit stoichiometry from the single-channel current amplitude. Coexpression of TEA insensitive (Y334V) and Ca-bowl mutated (ΔD965–ΔD966) subunits yields BK channels whose current amplitudes fall into one of four levels in the presence of 1.5 mM TEA_O. (a–d) Representative single-channel recordings and all-points amplitude histograms for the four levels of observed currents. The stoichiometry for each of these channels, as deduced from the single-channel current amplitudes, is shown at the right. (e) A one-dimensional scatter plot of the current amplitude recorded from each of 18 channels shows clustering into four distinct current levels. Ca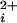 adjusted for a–d to obtain a high Po. Horizontal bar, 100 ms; vertical bar, 5 pA. +50 mV.

Because the highest current level with 1.5 mM TEA_O for expressing mixed subunits was ≈ 9.2 pA, the same as observed for homotetrameric channels in which each subunit had the TEA-binding site destroyed by mutation (as in Fig. 1b2), then the ≈9.2 pA current level would indicate that all four subunits had a mutated TEA-binding site. Because each subunit with a mutated TEA-binding site also had a functional Ca-bowl, then channels with a ≈9.2-pA current level would have four functional Ca-bowls. Progressively reduced current levels would then indicate channels with 3, 2, or 1 subunits with destroyed TEA-binding sites and, consequently, 3, 2, or 1 functional Ca-bowls. The inferred channel stoichiometry for each current level is indicated in Fig. 2 a–d. Channels with no functional Ca-bowls would have four functional TEA sites and conduct no current with TEA_O. Consequently, we studied this type of channel by expressing only subunits with no functional Ca-bowls, and then recording in the absence of TEA_O, as in Fig. 1b3 Upper.

The Ca²⁺-Sensitivity of Activation Increases with the Number of Functional Ca-Bowls.

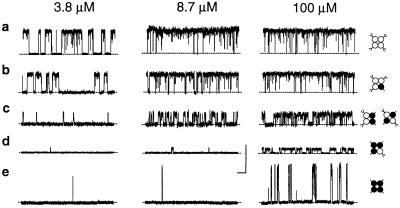
Previous studies have shown that BK channels without functional Ca-bowls have both reduced Ca²⁺ sensitivity and reduced Hill coefficients for activation by Ca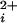 (11, 14–16, 19). To examine the contribution of each individual functional subunit to the Ca²⁺ sensitivity and cooperative activation of BK channels, we examined the Ca²⁺ activation of BK channels with 0–4 functional Ca-bowls, using the methods shown in Figs. 1 and 2 to identify the stoichiometry. Fig. 3 presents representative currents from such channels at three different Ca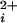. The deduced channel stoichiometry for each channel is indicated to the right. All five classes of channels were Ca²⁺ sensitive, increasing their activity with increases in Ca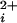. 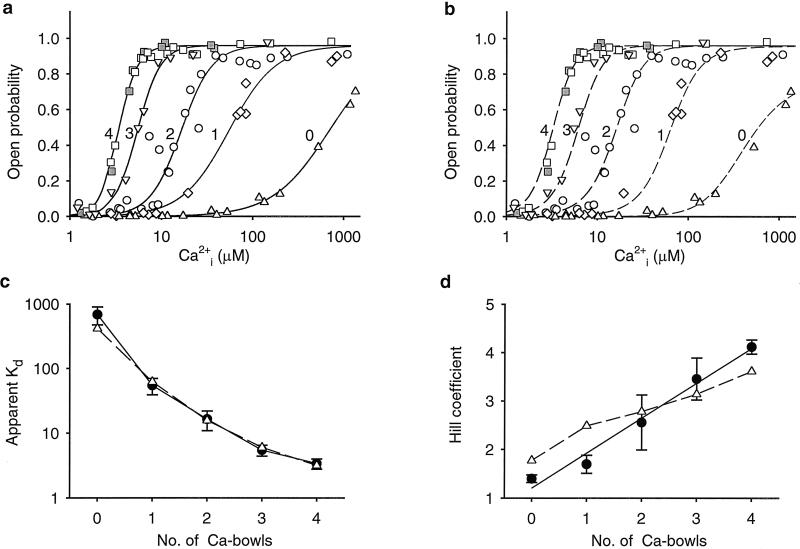The dose-response relationships, as plots of Po versus Ca, for a series of such experiments are plotted in Fig. 4a (see Materials and Methods). The lines through the data are fits with the Hill equation, and are discussed below. Increasing the number of functional Ca-bowls from 0–4 both shifted the response to the left and increased the slope. Thus, a lower Ca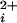 and a smaller fractional change is Ca 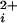was required to fully activate the channel as the number of Ca-bowls increased.

Fig 3.

The apparent Ca²⁺ sensitivity of BK channels decreased as the number of active Ca-bowls was reduced from 4 to 0. (a–d) Representative recordings from single-channel patches after the coexpression of TEA-insensitive and Ca-bowl mutated subunits. TEA_O (1.5 mM) was present. The stoichiometry of each channel (right diagrams) was deduced from the single-channel current amplitudes. (e) Representative recordings from a homotetrameric BK channel with mutated Ca-bowls in the absence of TEA_O. Horizontal bar, 100 ms; vertical bar, 10 pA. +50 mV.

Fig 4.

Stepwise increases in the Hill coefficient and stepwise decreases in the apparent K_d as the number of functional Ca bowls increase from 0 to 4. (a) Dose-response curves for channels with 0–4 functional subunits, as indicated (upright triangles = 0, diamonds = 1, circles = 2, upside down triangles = 3, squares = 4). For each curve, data from 3–6 single-channel patches are plotted as described in Materials and Methods. The lines are fits with the Hill equation (Eq. 1), as described in Materials and Methods. All recordings had 1.5 mM TEA_O except for the filled squares, which were obtained from homotetrameric wild-type channels, and the upright triangles, which were obtained from homotetrameric Ca-bowl mutated channels. (b) A model with 0–4 high-affinity allosteric activators to match the number of subunits with a functional Ca-bowl, four low-affinity allosteric activators, independent Ca²⁺ binding, and cooperativity arising from joint action of the allosteric activators on the opening–closing equilibrium, could approximate the data (dashed lines calculated with Eq. 2) where L(V) = 2500, K_(H)C = 63.9 (±45.9) μM, K_(H)O = 0.55 (±0.12) μM, K_(L)C = 325 (±91) μM; K_(L)O = 30.4 (±9.6) μM. The numbers in brackets indicate the uncertainty in the parameter values from the fitting and were not used in calculating the dashed lines. L(V) was fixed based on the observed Po in the absence of Ca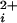. (c and d) Plots of K_d and the Hill coefficient versus the number of subunits with a functional Ca-bowl for the experimental data (continuous lines through filled circles) and the predictions of Eq. 2 (dashed lines through open triangles). The filled circles in c and d plot the parameters for fits of Eq. 1 to the data in a. The continuous lines in a plot these fits. The triangles in c and d plot the parameters for fits of Eq. 1 to the dashed lines in b. The fits of Eq. 1 to the dashed lines in b are not shown because they were essentially identical to the dashed lines generated by Eq. 2. The bars represent SEM.

To determine whether differences in the Ca²⁺-dependent activation of the channel may be influenced by the number of functional TEA-binding sites, we compared channels with four functional TEA-binding sites to those with four mutated TEA sites. Both types of channels had four functional Ca-bowls. The similarity in response (filled and open squares in Fig. 4a) indicated that mutating the TEA sites had little effect on the Ca²⁺ sensitivity.

The observation of Ca²⁺-dependent channel activity in the absence of functional Ca-bowls (Figs. 3e and 4a) indicates that BK channels have Ca²⁺ binding sites that can operate the channel in the absence of functional Ca-bowls. The half activation at ≈690 μM Ca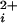 with no functional Ca-bowls (Fig. 4a) indicates that these additional sites are of low apparent affinity. The presence of low-affinity sites that can bind either Ca²⁺ or Mg²⁺ separately from the Ca-bowl has been reported previously (11, 14–18).

Stepwise Increase in the Hill Coefficient and Stepwise Decrease in the Apparent K_d with the Number of Functional Ca-Bowls.

To quantitate the contribution of each functional Ca-bowl to the Ca²⁺ sensitivity, the data were fit with a form of the Hill equation (35)

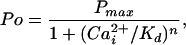where P_max is the maximum Po for BK channels, typically 0.96, K_d is the Ca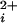 required for half activation, and n is the Hill coefficient that reflects the slope of the dose–response relationship. The Hill coefficient n also gives a measure of cooperativity, as it indicates the minimal number of functional allosteric activators that work jointly to maximally activate the channel by Ca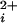. The value of K_d decreased 200-fold, from 690 μm with no functional Ca-bowls to 3.4 μM with four functional Ca-bowls (Fig. 4c), and the Hill coefficient increased from 1.4 with no functional Ca-bowls to 4.1 with four functional Ca-bowls (Fig. 4d). Each additional Ca-bowl added a step increase to the Hill coefficient of 0.3 to 0.8. The overall stepwise additions of cooperativity could be approximated by a straight line with a slope of 0.72 per functional subunit. As a first approximation, then, these observations suggest that the contribution by each Ca-bowl to the cooperative activation is relatively independent of the number of functional Ca-bowls.

To explore whether such a model is consistent with the gating of BK channels, we examined whether a model drawn from the models of Zhang et al. (18) and Shi and Cui (17), which incorporates assumptions of independent Ca²⁺-binding sites, could account for our experimental observations. These models extend previous models for the gating of BK channels (22–24, 36, †) by incorporating four low-affinity Ca²⁺-binding sites in addition to the four high-affinity Ca²⁺-binding sites. Eq. 2 summarizes the steady-state predictions of such a model at a constant voltage:

where P_max is the maximum open probability of typically 0.96, L(V) is the allosteric gating factor (36) in the absence of Ca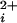 at the indicated voltage, n is the number of functional high-affinity allosteric activators (the number of functional Ca-bowls), K_(H)C and K_(H)O are the high-affinity equilibrium constants for the binding of Ca²⁺ to each high-affinity binding site for the closed and open states, the exponent 4 indicates four low-affinity allosteric activators, and K_(L)C and K_(L)O are the low-affinity equilibrium constants for binding of Ca²⁺ to the low-affinity binding site for the closed and open states. Because we are predicting Po at a single voltage, the action of the four voltage sensors of BK channels is included in L(V). We used this model to simultaneously fit all of the data in Fig. 4a by setting n, the number of high-affinity allosteric activators, to 0, 1, 2, 3, and 4 for the data obtained with 0, 1, 2, 3, and 4 functional Ca-bowls, respectively. All of the curves were predicted by using the same allosteric gating factor and equilibrium constants, with the only difference in parameters being the value of n, which was fixed by the determined stoichiometry of each channel type.

The model described by Eq. 2 closely approximated the shifts and slope changes in the dose-response relationship with 0–4 functional Ca-bowls (dashed lines, Fig. 4b). To determine the apparent K_d's and Hill coefficients predicted by the model, the predicted response (dashed lines in Fig. 4b) were then fitted with the Hill equation. The determined parameters show that the model closely predicted the step changes in apparent K_d as the number of functional Ca-bowls increased (dashed lines through triangles, Fig. 4c), but over predicted the cooperativity (n) for 0 and 1 functional Ca-bowls, and under predicted the cooperativity for 3 and 4 functional Ca-bowls (dashed lines through triangles, Fig. 4d). In addition, the average stepwise increase in cooperativity added by each functional subunit (the average slope of the dashed line in Fig. 4d) was also under predicted by the model.

Discussion

We examined the gating of BK (Slo1) channels with 0–4 functional Ca-bowls to determine directly the contribution of each of the four subunits to the cooperative Ca²⁺ activation of the channel. We found that each functional subunit led to a stepwise increase in the Hill coefficient of ≈0.3–0.8 and also a stepwise increase in the apparent Ca²⁺ affinity (≈1/K_d). Under the conditions of our experiments (+50 mV), the Hill coefficient was 1.4 with no functional Ca-bowls and increased to 4.1 with four functional Ca-bowls. Thus, the addition of four functional Ca-bowls increased the Hill coefficient by 2.7. Our findings thus show that the majority of the cooperativity in activation of BK channels under the conditions of our experiments requires functional Ca-bowls.

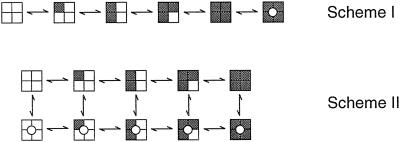
Our observations reveal directly a key gating property of BK channels only inferred previously from kinetic analysis and the observation of openings in the absence of Ca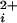 (7, 9, 20–24, 31, 36–41). Our findings show directly that BK channels can gate with 0–4 functional high-affinity allosteric activators. The implications of this conclusion can best be seen by considering two highly simplified gating mechanisms for BK channels given by Schemes I and II, where each shaded subunit indicates that a Ca²⁺ is bound to the high-affinity allosteric activator, and channels in the closed and open states have closed and open pores, respectively. These highly simplified models represent gating at low concentrations of Ca 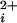so that the secondary binding sites are excluded, and at a fixed voltage so that the contributions to the gating by movement of the four voltage sensors are condensed into one state. Including the voltage sensors would expand Scheme II to at least 50 states (22–25), and further including the secondary sites would expand the 50 state model to 250 states (18).

Figure a.

Schemes I and II

In Scheme I, all allosteric sites must be activated before the channel can open. In Scheme II, which is the MWC model (42), the channel can open with from 0–4 activated allosteric sites. Clearly, our data are more consistent with Scheme II, as BK channels opened with from 0–4 functional high-affinity allosteric activator sites. Complete opening–closing transitions with 0–4 functional Ca-bowls (Figs. 1–3) suggest that the high-affinity allosteric activators modulate the channel activity allosterically (18, 25) rather than by forming the gate itself.

A question that arises is whether the allosteric activators act independently of one another. To approach this question, we examined whether a model with independent allosteric activators (17, 18) could describe the Ca²⁺ dependence of Po for channels with 0–4 functional Ca-bowls. In this model (Eq. 2), the equilibrium constants for the binding of Ca²⁺ to both the high and low-affinity allosteric activator sites are independent of the number of bound Ca²⁺. The cooperativity in activation arises because each allosteric activator acts on the opening–closing equilibrium by multiplying the allosteric gating factor L(V), shifting the equilibrium further toward the open states (36). In terms of this model, our experiments changed the number of effective allosteric activators, the value of n, in Eq. 2 by changing the number of functional Ca-bowls.

Eq. 2 closely approximated the dose–response curves of the data obtained with from 0–4 functional Ca-bowls and predicted the observed step decreases in K_d as the number of effective allosteric activators increased. In addition, Eq. 2 predicted an increase in the Hill coefficient as the number of allosteric activators increased. However, Eq. 2 first over predicted and then under predicted the total cooperativity, and the total predicted increase was only 67% of the observed increase. These observations suggest that there are cooperative factors in the gating not incorporated into the model described by Eq. 2. These may involve interactions among the subunits or additional Ca²⁺-binding sites and associated allosteric activators. The suggestion in our study of cooperative interactions not included in Eq. 2 is also inferred from kinetic analysis in previous studies (9, 20, 23–25, †).

Interestingly, the greatest variability in the K_ds and Hill coefficients among individual channels of the same type occurred for channels with two functional Ca-bowls. This finding suggests that the cooperative properties may be different depending on whether the functional subunits are adjacent or diagonal to each other. Such differences would also require cooperative factors not included in Eq. 2. Differences in properties of channels depending on whether altered subunits are adjacent or diagonal have been observed (26, 43, 44).

Nevertheless, the fact that Eq. 2 could approximate the Ca²⁺ dependence of Po for channels with different numbers of functional Ca-bowls simply by changing the number of allosteric activators n suggests that the assumptions incorporated into Eq. 2 capture many of the features of the gating. To a first approximation, then, the stepwise increase in cooperativity added by each subunit with a functional Ca-bowl arises because the allosteric activators act cooperatively (jointly) on a common step controlling the opening–closing transitions. Our observation that the single-channel current amplitude in the absence of TEA_O was independent of the number of functional Ca-bowls, as indicated by two prominent current levels, open and closed, in Fig. 1, supports the idea that the allosteric activators are not the gates, but act by modulating the opening–closing transitions. In this regard, the Ca²⁺ activation of BK channels thus appears similar to the allosteric activation of other channels (26, 34, 44–48). Although the opening–closing transitions being modulated appear to involve the concerted movement of the gating machinery of the subunits, as the current transitions between the open and closed states generally occurred without obvious steps, in reality, the final “concerted” transition may involved several steps, and the gates of the four subunits may not move exactly synchronously (49, 50).

By what mechanisms could the Ca-bowl act to impart cooperativity? It has been suggested that the tail of BK channels normally inhibits channel activity, and that the binding of Ca²⁺ to the Ca-bowl then activates the channel by removing inhibition (19). In this case, each Ca-bowl and associated tail region of the subunit would become an allosteric activator that shifts the transition barriers between the open and closed states to favor the open states on the binding of Ca²⁺. Although it has been shown that a tail fragment of BK channels that includes the Ca-bowl can bind Ca²⁺ (11, 16), it has not been directly established that the Ca-bowl is the functional high-affinity Ca²⁺-binding site, nor has it been established that it is the only high-affinity site. It is possible that mutations in the Ca-bowl disrupt the high-affinity allosteric activator indirectly by blocking Ca²⁺ binding elsewhere or by disrupting, uncoupling, or jamming the action of the allosteric activator. Nevertheless, the interpretation of our findings is independent of whether mutating the Ca-bowl blocks the function of a high-affinity allosteric activator either directly by preventing Ca²⁺ binding, or indirectly by changing structure. In either case, a subunit with a mutated Ca-bowl has lost considerable function. By assembling channels with different numbers of functional subunits, we have been able to determine the contribution of each individual subunit to the cooperativity for activation by Ca²⁺.

Abbreviations

• BK, large conductance Ca²⁺ and voltage-activated K⁺ channel

• TEA, tetraethylammonium