Enhancing body fat prediction with WGAN-GP data augmentation and XGBoost algorithm

Abstract

Background and Objective

Machine learning models offer a practical approach for estimating body fat percentage from simple anthropometric data. However, the scarcity of biomedical data frequently leads to model overfitting, compromising predictive accuracy. Generative data augmentation presents a promising strategy to address this limitation. This study develops and evaluates a generative data augmentation framework to enhance body fat prediction from limited anthropometric data.

Methods

A public dataset comprising 249 male subjects was partitioned into development (80%) and test (20%) sets. The fidelity of Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP), random noise injection, and mixup was compared to select the optimal method. Subsequently, XGBoost, Support Vector Regression, and Multi-layer Perceptron models were trained and validated, comparing performance with and without the selected augmentation. Final model generalization was assessed on the independent test set using the coefficient of determination (R²), Mean Absolute Error, and Root Mean Squared Error.

Results

Among the evaluated augmentation techniques, the WGAN-GP generated synthetic data with the highest fidelity. On the original data, the baseline XGBoost model achieved a R² of 0.67; this performance increased to 0.77 on the test set when using WGAN-GP augmentation. Feature importance analysis of the final model identified abdominal circumference as the most significant predictor of body fat percentage.

Conclusion

The WGAN-GP is a highly effective method for generating realistic synthetic anthropometric data. Integrating these synthetic samples into the training pipeline substantially improves the generalization and predictive accuracy of machine learning models. This methodology offers a robust solution for developing more accurate and accessible predictive health models in data-scarce environments.

Introduction

Accurate assessment of body composition is fundamental to clinical health evaluation and disease risk management. Body fat percentage, in particular, serves as a key indicator of metabolic status. However, gold-standard measurement techniques are often resource-intensive, limiting their feasibility in large-scale or routine clinical settings. Simple anthropometric measurements thus provide a practical and accessible alternative. Therefore, developing robust computational models that accurately estimate body fat percentage from this readily available data is of critical importance.

Various modeling approaches have been developed to address this challenge. Historically, research centered on establishing linear prediction equations using multiple regression.^1–3 These statistical models provided simple and interpretable formulas for estimating body composition.^4,5 However, such linear methods often fail to capture the complex, non-linear relationships inherent in physiological data. ⁶ To overcome these limitations, the field has progressively adopted machine learning (ML) techniques. Algorithms like Support Vector Regression (SVR), Random Forests, and Multi-layer Perceptrons (MLP) have shown improved predictive power by effectively modeling these non-linearities.^7,8 More recently, advanced ensemble methods, particularly gradient boosting machines (GBMs), have gained prominence for their superior performance.^9,10 Models such as XGBoost are now widely recognized for their high accuracy and robustness in handling the structured tabular data typical of clinical prediction tasks. ¹¹

Despite the high performance of models like XGBoost, their predictive power is fundamentally dependent on large and diverse training datasets. In biomedical research, however, acquiring extensive data is often challenging due to high costs, complex logistics, and patient privacy considerations.^12–14 This common issue of data scarcity creates a significant risk of model overfitting.^15,16 Overfitting occurs when a model learns statistical noise from the small training set rather than the true underlying patterns, leading to poor generalization on new, unseen data.^17–19 Data augmentation has emerged as a powerful strategy to address data limitations and improve model robustness.^20,21 While highly successful in fields like computer vision, its application to complex, structured tabular data is an active area of investigation. Methodologies range from simple noise injection to sophisticated deep learning approaches. Among these, Generative Adversarial Networks (GANs) have shown considerable potential for creating realistic synthetic tabular data.^22–24 Specifically, advanced architectures like the Wasserstein GAN (WGAN) have proven effective at generating high-fidelity data that preserves complex feature distributions, showing promise in various domains including medicine.^25–28

Therefore, this study aimed to develop and validate a data augmentation framework for improving body fat percentage prediction from limited anthropometric data. A Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP) was systematically compared against simpler augmentation methods, including random noise injection and mixup. The superior augmentation technique was then integrated with XGBoost, SVR, and MLP to evaluate its impact on predictive performance. This approach uses a generative model to create high-fidelity synthetic data, enabling predictive models to learn more robust features and mitigate overfitting from small sample sizes. It was hypothesized that models trained with WGAN-GP augmented data would achieve significantly higher predictive accuracy than those trained only on the original dataset. This research provides a validated methodology to enhance clinical prediction models when faced with data scarcity, potentially enabling more accurate and accessible health assessment tools.

Material and method

Database

The “Body Fat Prediction Dataset” utilized in this study was obtained from Kaggle ²⁹ and originates from foundational research conducted by Penrose et al. ³⁰ at the Human Performance Research Center, Brigham Young University, Provo, UT, USA. Notably, this dataset, comprising measurements from 252 male subjects, was previously employed by Penrose and colleagues ³⁰ to successfully develop and validate generalized body composition prediction equations using traditional statistical methods, establishing its relevance and utility within the field. While the original publication ³⁰ details the study location, it does not specify the nationality or detailed ethnic breakdown of the participants. Recognizing this, we utilize this established dataset primarily as a case study to demonstrate the efficacy of our proposed WGAN-GP augmentation and XGBoost modeling approach, particularly for enhancing predictions from anthropometric data that may lack extensive demographic annotation. It comprises data on the percentage of body fat, which was calculated based on the density determined by underwater weighing, along with various body circumference measurements from 252 men, covering a total of 15 features.

In preparation for analysis, the dataset underwent a thorough cleaning process. This included the identification and removal of duplicate entries, handling of missing values by deleting records with missing data, exclusion of outliers, and conversion of weight to kilograms and height to meters. To identify and remove multivariate outliers, we employed the EllipticEnvelope algorithm from the scikit-learn library (version 1.2.0). ³¹ This method robustly estimates the data covariance assuming an underlying Gaussian distribution and identifies outliers based on their Mahalanobis distance. We specified an expected outlier proportion by setting the contamination parameter to 0.05, reflecting an assumption of approximately 5% anomalous data points in the dataset. Points exceeding the Mahalanobis distance threshold derived from this contamination factor were removed, enhancing the robustness of subsequent analyses. Post-cleaning, the refined dataset consisted of 249 valid entries, with no remaining missing values. The detailed summary of the processed data is presented in Table 1, and the distribution of the key variables is illustrated in Figure 1. As the primary objective of this study is to develop a body fat prediction method based on data augmentation, the density feature will not be considered in subsequent data augmentation and regression model building.

Table 1.

Original data descriptive statistics (N = 249).

Features	Mean ± SD	Features	Mean ± SD
Density	1.06 ± 0.02	Hip circumference (cm)	99.67 ± 6.45
BodyFat (%)	19 ± 8.3	Thigh circumference (cm)	59.27 ± 4.91
Age (years)	44.8 ± 12.6	Knee circumference (cm)	38.54 ± 2.32
Weight (kg)	80.8 ± 12.28	Ankle circumference (cm)	23.03 ± 1.51
Height (m)	1.79 ± 0.07	Biceps (extended) circumference (cm)	32.22 ± 2.93
Neck circumference (cm)	37.95 ± 2.29	Forearm circumference (cm)	28.67 ± 2.03
Chest circumference (cm)	100.67 ± 8.17	Wrist circumference (cm)	18.22 ± 0.92
Abdomen circumference (cm)	92.3 ± 10.23

Figure 1.

Overall study workflow diagram.

To ensure a robust and unbiased evaluation of the models while preventing data leakage, the cleaned dataset (N = 249) was partitioned prior to any data augmentation or model training. A stratified splitting strategy was employed based on the target variable (Figure 1), ‘Bodyfat’, to divide the data into a development set (80%, n = 199) and a final test set (20%, n = 50). This stratification ensures a similar distribution of body fat percentages in both subsets. The development set was exclusively used for all model development activities, including data augmentation, hyperparameter tuning, and cross-validated training. The final test set was held out and used only once for the terminal performance evaluation of the best-performing model, thereby providing a truly independent assessment of its generalization capability.

Data augmentation

To address the limited sample size of the development set, three distinct data augmentation techniques were employed and compared. These methods were WGAN-GP, Random Noise Injection, and Mixup. Each technique was used to generate new, synthetic samples based on the original development set. The optimal method was then selected by comparing the fidelity of the synthetic data generated by each technique.

WGAN-GP model

The WGAN-GP model was implemented to learn the underlying multivariate distribution of the data. The architecture consisted of a generator and a critic, both constructed as MLP. The generator network was designed to map a 100-dimensional latent vector to the feature space of the dataset. The critic network evaluated the authenticity of the generated samples. The model was trained by optimizing the Wasserstein distance with a gradient penalty, minimizing the critic's loss function:

$$L_{\mathrm{Critic}}=\mathbb{E}[C(x_{\mathrm{fake}})]-\mathbb{E}[C(x_{\mathrm{real}})]+{\lambda }_{gp}\mathbb{E}[{({\mathrm{\nabla }}_{\hat{x}}C{(\hat{x})}_2-1)}^2]$$ (1)

Here, x_real and x_fake represent real and generated samples, respectively. C(⋅) is the critic's output, and $\hat{x}$ is a sample interpolated between real and fake data. Key hyperparameters included a gradient penalty coefficient (λ_gp) of 10, a learning rate of 5×10⁻⁵, and five critic updates per generator update. The model was trained using the Adam optimizer for 10,000 epochs.

Random noise injection

Random noise injection created new instances by perturbing existing ones. For each new sample, a random data point was selected from the development set. Gaussian noise was then added to each feature of this selected point. The noise was drawn from a normal distribution with a mean of zero. The standard deviation of the noise was set to 5% of the standard deviation of the corresponding feature in the original development set.

Mixup

Mixup generated synthetic samples via linear interpolation of two distinct, randomly chosen samples from the development set. For a pair of samples, (x_i, y_i) and (x_j, y_j), a new sample ( $\hat{x}$ , ŷ) was created as follows:

$$\hat{x}=\lambda x_i+(1-\lambda )x_j$$ (2)

$$\hat{y}=\lambda y_i+(1-\lambda )y_j$$ (3)

The interpolation coefficient, λ was drawn from a symmetric Beta distribution, Beta(α,α). The hyperparameter α, which controls the interpolation strength, was set to 0.2.

Following the generation process for each method, a post-processing step was applied to ensure the plausibility of the synthetic data. The values for each feature in the generated samples were clipped. The allowable range for each feature was defined by its minimum and maximum values in the original development set, expanded by 1% of the feature's total range. This constrained the synthetic data to a realistic feature space.

To select the optimal augmentation method, a dual-criterion assessment was performed. The fidelity of individual feature distributions was first visually inspected using Kernel Density Estimate (KDE) plots. This was complemented by a quantitative, multivariate evaluation using a ML-based discriminator test, which measures the distinguishability between real and synthetic data. The technique yielding the lowest classifier Area Under the Curve (AUC) score, indicating the highest data realism, was chosen for the subsequent modeling phase.

Predictive modeling pipeline and model evaluation

Predictive modeling pipeline

Three distinct regression models were developed to predict body fat percentage: Extreme Gradient Boosting (XGBoost), SVR, and a MLP. The modeling pipeline for each followed a unified structure, incorporating the optimal data augmentation technique selected in the previous section. The pipeline consisted of hyperparameter optimization (HPO), model validation using cross-validation with dynamic data augmentation, and final evaluation on an independent test set (Figure 2).

Figure 2.

Detailed predictive model development and validation pipeline.

HPO for each model was conducted using a 5-fold randomized search cross-validation on the development set. For this process, the development set was first expanded by combining the original samples with an equal number of synthetic samples generated by the selected augmentation method. This combined dataset was used exclusively for identifying the best hyperparameter configurations. The search space for XGBoost included n_estimators (100–400), max_depth (3–7), learning_rate (0.01–0.1), subsample (0.7–1.0), and regularization parameters. For SVR, the search explored kernel (linear, poly, rbf), C (0.1–500), gamma (0.001–0.1), and epsilon (0.01–0.3). The MLP optimization tuned hidden_dims (e.g. [64], [64, 32]), learning_rate (0.0005–0.005), dropout_rate (0.2–0.5), and weight_decay (1×10⁻⁵ to 1×10⁻³).

Model performance and robustness were assessed using a 5-fold cross-validation scheme on the original development set. A dynamic augmentation strategy was employed within this process. For each fold, the training partition was augmented with synthetic data doubling its size, while the validation partition remained unmodified. This ensured that the model was validated against original, unseen data in every iteration. For the SVR and MLP models, features were standardized using a StandardScaler fitted only on the respective training data of each fold.

The XGBoost model was implemented as a standard gradient boosting regressor. The SVR model was constructed within a pipeline that first applied feature scaling. The MLP was a fully-connected neural network using ReLU activation functions and included dropout layers for regularization. Final models were then trained on the entire development set combined with a larger set of synthetic data, using the optimal hyperparameters identified previously. The generalization ability of these final models was assessed on the held-out test set, which was not used at any stage of model training or optimization.

For direct comparison, baseline versions of each model were also developed using an identical methodological pipeline, but applied to the original, non-augmented data. To prevent data leakage, the development set (199 samples) was first partitioned into a main training set (159 samples) and a final hold-out test set (40 samples) for all modeling approaches.

Model evaluation

Model performance was consistently quantified using Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and the coefficient of determination (R²). These metrics served distinct purposes throughout the pipeline. During HPO, a single metric was used as the scoring function to identify the optimal parameter set. In the cross-validation stage, all three metrics were calculated on each validation fold to assess the robustness and estimated generalization error of the configured models.

The definitive, unbiased performance of the final trained models was assessed on the final test set. This test set was strictly held-out and was not used in any preceding training, augmentation, or HPO stages, ensuring a true evaluation of the models’ predictive capabilities on unseen data.

Results

Evaluation of data augmentation methods

The fidelity of the three data augmentation methods was evaluated against the original development set. The assessment consisted of a visual comparison of data distributions and a quantitative ML-based distinguishability test.

Visual inspection of the KDE plots showed that all three methods produced distributions that closely approximated the original data (Figure 3). Notable differences were observed in features with more complex distributions. For the Ankle feature, the distribution generated by WGAN-GP closely mirrored the sharp peak of the original data (red line), whereas the Mixup and Noise Injection methods produced smoother, broader peaks. A similar pattern was observed for the “BodyFat” feature, where the WGAN-GP distribution replicated a subtle secondary mode present in the original data, a feature not captured by the other two techniques.

Figure 3.

KDE plots of selected feature distributions. Original (red line), Mixup (green line), NoiseInjection (blue line), and WGAN-GP (purple line). Each subplot represents one feature, with values on the x-axis and probability density on the y-axis.

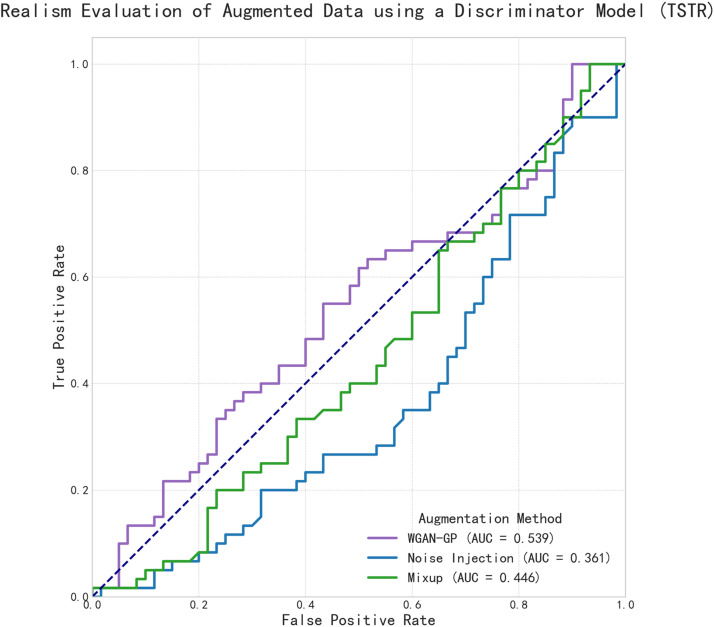
A quantitative assessment using a ML discriminator provided an AUC score for each method's realism (Figure 4). The resulting AUC scores were 0.539 for WGAN-GP, 0.446 for Mixup, and 0.361 for Noise Injection. The Receiver Operating Characteristic (ROC) curve for WGAN-GP was positioned closest to the no-skill diagonal, followed by the curve for Mixup, and then Noise Injection.

Figure 4.

Discriminator-based evaluation of data augmentation realism. ROC curves for LightGBM classifiers trained to distinguish between original data and data generated by three different augmentation techniques. The AUC score quantifies the distinguishability of each augmented dataset. A lower AUC score indicates that the synthetic data is more realistic and harder for the classifier to differentiate from the original data, signifying a higher-fidelity augmentation method. The dashed line represents the performance of a random-guess classifier (AUC = 0.5).

As WGAN-GP demonstrated the highest fidelity in replicating the complex characteristics of the original data, both visually and quantitatively, it was selected as the sole augmentation method for the subsequent modeling pipeline.

Predictive modeling performance

Model performance on original development set

To establish a performance baseline, each model was also trained using the original, non-augmented dataset. Final performance was assessed on a consistent hold-out test set (40 samples), which was partitioned from the initial 199-sample development set to ensure an unbiased evaluation.

The optimal SVR model utilized a radial basis function (RBF) kernel with C = 500 and γ = 0.001. For XGBoost, key parameters included a learning rate of 0.05, a maximum depth of 3, and 200 estimators. The selected MLP architecture consisted of three hidden layers with dimensions [128, 64, 32], a dropout rate of 0.3, and a weight decay of 0.002.

Table 2 summarizes the final performance metrics on the held-out test set. During the optimization phase, SVR achieved the lowest cross-validation MAE (3.67). However, in the final evaluation on the test set, XGBoost demonstrated the strongest generalization. It achieved the lowest MAE of 3.71 and the highest R² score of 0.67. The SVR and MLP models yielded comparable results to each other, with SVR producing an R² of 0.62 and MLP resulting in an R² of 0.60.

Table 2.

Performance of baseline models on the original development set.

Model	Best CV MAE	Test set MAE	Test set RMSE	Test set R²
XGBoost	3.93	3.71	4.47	0.67
SVR	3.67	4.00	4.83	0.62
MLP	3.8	4.05	4.96	0.60

Figure 5 provides a visual representation of these outcomes. The scatter plots show that predictions from the XGBoost model (Figure 6) exhibit a slightly tighter distribution around the perfect prediction line, which aligns with its superior quantitative metrics.

Figure 5.

Distribution of original data.

Figure 6.

Scatter plots of predicted versus actual BodyFat values for the baseline models on the original development set. The dashed line in each plot represents a perfect prediction (y = x). Subplots display the performance for (a) the XGBoost model, (b) the SVR model, and (c) the MLP model.

Model performance with data augmentation

This section presents the performance of the models when trained with the WGAN-GP dynamic data augmentation strategy. The models were re-optimized on the augmented dataset to identify hyperparameters suited to the enhanced data distribution. The optimized XGBoost model used parameters such as a subsample rate of 0.8 and a gamma of 0.2. The optimal SVR configuration remained consistent with a high regularization value (C = 500) and an RBF kernel. The MLP architecture was refined to two hidden layers ([128, 64]) with a low weight decay of 0.0001.

The quantitative results of this process are summarized in Table 3. During the HPO phase, all three models achieved a similar best MAE of approximately 2.9. In the final evaluation on the hold-out test set, XGBoost again yielded the highest performance. It achieved an R² score of 0.77 and an MAE of 3.39. The SVR model followed with an R² of 0.72, while the MLP model produced an R² of 0.68.

Table 3.

Performance of models with WGAN-GP data augmentation.

Model	Best HPO MAE	Test set MAE	Test set RMSE	Test set R²
XGBoost	2.93	3.39	4.03	0.77
SVR	2.96	3.75	4.47	0.72
MLP	2.91	3.91	4.73	0.68

The predictive accuracy of the three models is visually detailed in Figure 6. These scatter plots illustrate the relationship between the actual and predicted values on the test set for each model. The predictions from the XGBoost model show the tightest clustering around the perfect prediction line, corresponding to its superior quantitative metrics (Figure 7).

Figure 7.

Scatter plots of predicted versus actual values for the final models on the hold-out test set, trained on WGAN-GP augmented data. The dashed line represents a perfect prediction (y = x). Subplots show the performance for (a) the XGBoost model, (b) the SVR model, and (c) the MLP model.

To identify the most influential predictors, a feature importance analysis was performed on the final augmented XGBoost model. The results, calculated using the Gain metric, are presented in Figure 8. The analysis reveals that the Abdomen measurement is the most dominant predictor, with an importance score greater than 0.40. The Chest measurement ranks as the second most significant feature. A distinct gap in importance separates these top two predictors from a subsequent group of moderately influential features, which includes Height, Hip, and Wrist. The remaining features demonstrate comparatively minor contributions to the model's predictive power.

Figure 8.

Top 13 feature importances for the final XGBoost model trained with WGAN-GP augmentation, calculated using the Gain metric.

Discussion

This study demonstrates the efficacy of data augmentation for enhancing body fat percentage prediction. A WGAN-GP proved effective for generating high-fidelity synthetic data from limited anthropometric measurements. This approach surpassed traditional augmentation techniques by more accurately replicating the complex, multimodal distributions present in the original dataset. The application of augmented data yielded a significant improvement in predictive model performance. Specifically, the XGBoost model trained on the enhanced dataset exhibited substantially improved accuracy and generalization. Furthermore, the feature importance analysis confirmed that abdominal circumference is the most influential predictor for body fat estimation, aligning with established physiological principles.

This study's findings indicate that WGAN-GP possesses a distinct advantage in generating high-fidelity synthetic anthropometric data. This superiority stems from its core mechanism, as GANs learn to approximate the complex data manifold of the original dataset. ³² Instead of simply transforming existing points, GANs capture the deep, non-linear correlations among features.^33,34 This capability contrasts sharply with methods like Mixup or random noise, which often fail to preserve the multivariate statistical properties of the original data when augmenting dataset size. ³⁵

This mechanistic difference explains the observations in this study. For instance, WGAN-GP successfully replicated the complex, multi-modal distributions of features such as ‘Ankle circumference’ and ‘BodyFat’, whereas simpler methods tended to over-smooth the data, leading to a loss of key statistical characteristics. The success of WGAN-GP is also attributable to its stable training framework. The use of Wasserstein distance provides a smoother and more meaningful loss metric, which promotes stable convergence.^36,37 Furthermore, the gradient penalty term acts as an effective regularizer. This ensures the critic network satisfies the Lipschitz continuity constraint, which is critical for preventing mode collapse and guaranteeing the diversity of the generated samples.^38,39

These findings are consistent with a growing body of research demonstrating the efficacy of GAN-based models for generating complex tabular data across various domains. For instance, Park et al. (2024) reported that a WGAN-GP-based scheme effectively generated tabular data for photovoltaic power forecasting, significantly improving the performance of downstream models. ²⁵ Similarly, its utility has been confirmed in cybersecurity for enhancing intrusion detection systems with high-quality synthetic data. ³⁹ The application of such generative models is particularly relevant in the biomedical field, where data scarcity is a critical and persistent challenge.^40,41 Studies have successfully employed GANs to generate synthetic health records that preserve patient privacy while improving the accuracy of decision-making models, ⁴² and to create realistic tabular data for cardiovascular health research. ⁴³ Medical datasets are often characterized by intricate interdependencies among variables^33,44 and the results of this study confirm that WGAN-GP is a powerful tool for handling such complexity.

This study demonstrates that data augmentation with WGAN-GP substantially enhances predictive model performance. The most notable improvement was seen in the XGBoost model, where the R² on the test set increased from 0.67 to 0.77. This outcome aligns with a primary goal of data augmentation: the mitigation of model overfitting, which is a common risk when training on limited datasets.^45,46 By enriching the training data with high-fidelity synthetic samples, the model is compelled to learn more robust and generalizable decision boundaries rather than memorizing the noise inherent in a small sample.^47,48

The effectiveness of this approach is consistent with findings from other domains. For instance, studies have reported significant performance gains by combining synthetic and real data for hydrological forecasting ⁴⁹ and for predicting clinical outcomes in intensive care. ⁵⁰ Specifically, Noguer et al. (2022) also showed that GAN-generated data improved ML model performance for predicting hypoglycemic events in patients with diabetes. ⁵¹ Furthermore, the performance gains in this study were observed across all three distinct model architectures—XGBoost, SVR, and MLP. This consistent improvement suggests that the benefit is a fundamental consequence of the enhanced data quality and not an artifact of a specific learning algorithm. This is particularly relevant as data augmentation strategies are continually being adapted for diverse and complex regression tasks.^52,53

The value of this methodology is especially pronounced in fields like body composition analysis, where a key goal is to develop computational models that can reduce the time and expense associated with resource-intensive experimental procedures. ⁵⁴ Acquiring gold-standard measurements for body fat, for instance, is a costly process that inherently restricts dataset size. ⁵⁵ The challenges of building reliable AI models from limited or non-representative biomedical data are well-documented.^56,57 Therefore, using a robust generative model to augment these valuable but scarce datasets offers a practical pathway to develop more accurate and accessible predictive tools.

Across all experimental conditions, the XGBoost model consistently demonstrated superior predictive performance compared to both SVR and MLP. This robust performance is largely attributable to the inherent strengths of GBMs in handling structured, tabular data.^58,59 Tree-based ensembles like XGBoost are adept at capturing complex, non-linear relationships and high-order feature interactions directly from the data. ⁶⁰ This aligns with other comparative studies where XGBoost has proven to be a top-performing model for regression tasks.^61,62 Furthermore, its built-in L1 and L2 regularization helps control model complexity, which is a crucial advantage for preventing overfitting, particularly when working with datasets of limited size.

In contrast, the other models faced distinct challenges. The performance of SVR is highly sensitive to the meticulous selection of its kernel function and hyperparameters.^63,64 While SVR can be powerful, achieving optimal results often requires complex, dedicated optimization procedures that may not be fully resolved within a standard hyperparameter search. ⁶⁵ The MLP also exhibited limitations, which is a recognized phenomenon when applying deep learning to tabular data. ⁶⁶ Deep learning models are often “data-hungry” and may underperform compared to classical ML methods on smaller datasets. ⁶⁷ Even with data augmentation, the final sample size in this study may have been insufficient for the MLP to develop a feature representation that could surpass the efficiency and power of the XGBoost framework.

An analysis of the final XGBoost model revealed that abdominal circumference was the most dominant predictive feature for body fat percentage. The strong predictive power of central adiposity, often quantified by waist circumference, for determining overall body composition is well-established in clinical research.^6,68 The significance of this finding lies in the model's ability to independently learn and prioritize this key anthropometric marker from the data. It demonstrates that the algorithm is not simply fitting to statistical noise but is successfully capturing patterns that are physiologically meaningful. This alignment between the model's internal feature weighting and established biomedical domain knowledge is essential. It enhances the trustworthiness and interpretability of its predictions, a crucial step for applying ML in medical contexts, where XGBoost and interpretability methods are increasingly combined to build reliable diagnostic tools.^69,70

This research presents a robust framework for enhancing predictive models from limited biomedical tabular data. The proposed pipeline, combining WGAN-GP for data augmentation with an XGBoost regressor, offers a promising route to develop more accurate and accessible clinical tools from simple, low-cost anthropometric measurements. Nevertheless, several limitations must be acknowledged. The study was conducted on a single, historical dataset comprising only male participants. This constrains the direct clinical generalizability of the specific body fat model to modern, diverse populations, including women, various ethnicities, and different age groups. It is important to note that this work was designed primarily as a proof-of-concept to validate the data augmentation and modeling methodology itself, using the dataset as a case study. Therefore, a critical direction for future research is to apply and validate this successful framework on larger, contemporary, and more heterogeneous datasets. Future efforts should focus on assessing the model's performance and fairness across diverse demographic cohorts to develop more equitable and widely applicable predictive tools. Furthermore, exploring more advanced generative architectures and performing external validation on completely independent clinical data are essential next steps for eventual real-world implementation.

Conclusion

This study investigated the use of generative data augmentation to enhance the accuracy of body fat percentage prediction models built from limited data. Using a publicly available dataset of anthropometric measurements from male subjects, three data augmentation techniques were compared: WGAN-GP, random noise injection, and mixup. The most effective method was then used to augment the training data for three distinct regression models: XGBoost, SVR, and a MLP. The performance of models trained with augmented data was systematically evaluated against baseline models trained only on the original data.

Among the augmentation techniques, the WGAN-GP proved most effective for creating high-fidelity synthetic anthropometric data. The application of this method significantly improved the performance of an XGBoost regression model, increasing its R² on the test set from 0.67 to 0.77. These findings confirm that combining advanced generative models with robust ML algorithms provides a powerful framework for mitigating the effects of data scarcity. This approach enhances model generalization by enriching the training data with realistic samples, thereby reducing overfitting. Future research should focus on validating this methodology on larger, more heterogeneous datasets to ensure its applicability across diverse populations.