Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2025 Jul 29;16(31):7960–7967. doi: 10.1021/acs.jpclett.5c01673

Symmetric Ligand Binding Pathways and Dual-State Bottleneck in [NiFe] Hydrogenases from Unbiased Molecular Dynamics

Farzin Sohraby 1, Ariane Nunes-Alves 1,*
PMCID: PMC12337149  PMID: 40729627

Abstract

[NiFe] hydrogenases make up a family of enzymes that can be used to produce biofuel, thus making them important for industrial applications. In this work, we utilized unbiased molecular dynamics simulations to capture binding and unbinding events of the substrate, H2, to and from the [NiFe] hydrogenases from two different organisms. We obtained multiple (un)­binding events and reproduced experimental association rate constants. We observed symmetry between the binding and unbinding pathways used by H2 to access and leave the catalytic site. Moreover, we found that the main bottleneck for ligand binding, the distance between residues V74 and L122, can shift between two states with different bottleneck widths, a feature which can be exploited to modulate the access of small molecules to the catalytic site. The pathway probabilities presented here can be used to benchmark enhanced sampling methods which investigate protein–ligand binding.

graphic file with name jz5c01673_0006.jpg

graphic file with name jz5c01673_0005.jpg

It has been established in recent years − that binding kinetic rates should be taken into consideration in drug design efforts, since in some cases residence times can have a strong correlation with drug efficacy. − This has led to the development of many computational methods which can be used to predict binding kinetic rates for protein–ligand complexes and investigate the associated (un)­binding paths. − Kinetic rates are nonequilibrium properties, and their values depend on the paths for ligand binding and unbinding. Therefore, a fundamental aspect of understanding and predicting ligand binding kinetics is the characterization of binding and unbinding paths and associated probabilities. Knowledge of binding pathways can also be explored in biotechnology and enzyme engineering. For instance, mutant enzymes can be rationally designed to block or promote access of substrate or inhibitor molecules to the catalytic site. −

Investigating protein–ligand binding using unbiased molecular dynamics (UMD) simulations is challenging, because the time scales for the occurrence of (un)­binding events are usually longer in comparison to the ones achieved by UMD simulations. , Microsecond-long UMD simulations were performed by D. E. Shaw research to investigate the binding of small molecule inhibitors to Src kinase and G protein-coupled receptors (GPCRs). , Observing binding events with UMD simulations was an important achievement, but only a few events could be captured, preventing sound estimation of kinetic rates or pathway probabilities. Additionally, very few people have access to computing clusters like Anton, , used to perform such UMD simulations. In recent years, researchers started to combine MD simulations with methods to enhance sampling, − such as τ-Random Acceleration Molecular Dynamics (τRAMD) or metadynamics, to obtain a large number of unbinding events, which enable them to estimate kinetic rates and pathway probabilities. While computed kinetic rates can be compared to experimental ones to benchmark new enhanced sampling methods, there is no clear data set or reference to benchmark the observed pathways and associated probabilities. In previous reviews, , we showed that authors using different enhanced sampling methods obtain different unbinding paths for systems such as T4 lysozyme, kinases, and trypsin. For T4 lysozyme, reasonable predictions of the kinetic rates can be obtained as long as the main pathway is sampled. However, a complete understanding of binding paths with high and low probabilities can enable the rational design of mutant proteins with new or modified paths to either block or facilitate ligand binding, as done before for haloalkane dehalogenase and ABCG transporters. ,−

In this work, we propose as a data set to benchmark the pathway probabilities obtained from enhanced sampling methods the pathway probabilities for binding and unbinding of H2 to and from two different [NiFe] hydrogenases, the hydrogenase from Desulfovibrio fructosovorans (Df hydrogenase) and the hydrogenase from Megalodesulfovibrio gigas (Mdg hydrogenase), obtained from a total of 18.75 μs of UMD simulations (75 replicas of 250 ns) for each hydrogenase. Df hydrogenase and Mdg hydrogenase are both O2-sensitive hydrogenases and they have low sequence identity, 65.5%, despite the fact that the two enzymes have an almost identical secondary structure (Figure ). We chose hydrogenase as a model system because for small gas molecules such as H2 the binding rates are fast, and it is feasible to capture a reasonable number of (un)­binding events using UMD simulations. Additionally, data analysis of the UMD simulations revealed that there are two states for the bottleneck identified by us and others ,− as one of the major factors which regulates ligand binding in Df hydrogenase, the distance between residues at positions 74 and 122 in the large subunit of Df hydrogenase (Figure ). This dual-state bottleneck mechanism could be exploited to engineer mutants of hydrogenases that are resistant to inhibitors such as CO and O2.

1.

1

Open in a new tab

Aligned crystallographic structures of Df hydrogenase and Mdg hydrogenase (PDB ID 1YQW and 1YQ9, respectively) show the high similarity of the secondary structures of the two hydrogenases. The small subunits of Df hydrogenase and Mdg hydrogenase are shown in blue and green, and the large subunits are in yellow and magenta, respectively. The catalytic site and the position of the residues of the bottleneck for ligand binding, V74 and L122, are shown in the inset.

We put 100 H2 molecules in the simulation box randomly and let the gas molecules diffuse independently, explore the tunnels inside the enzymes, and eventually reach the hydrogenase active site, the [NiFe] center. Since we are using a conventional force field, no covalent bond is formed between the [NiFe] center and H2 once it approaches the active site. The bound state was achieved when H2 reached a distance of 5 Å or lower from the center of mass of the [NiFe] center, and it was also near the interface of the Ni and Fe atoms of the [NiFe] center. The unbound state was achieved when H2 was fully solvated and displayed no contact with any of the atoms of the enzyme (a contact was formed when the atom–atom distances were below 4 Å).

Using UMD simulations, we could obtain 43 and 100 binding events of H2 to Df hydrogenase and Mdg hydrogenase, respectively, and 41 and 99 unbinding events of H2 from Df hydrogenase and Mdg hydrogenase, respectively (). For Df hydrogenase, experimentally measured Michaelis constant (Km) and catalytic constant (k cat) values for H2 were reported by Liebgott et al., leading to an experimental k on value calculated to be 1.9 × 106 M–1·s–1 (see equations in ). With 100 H2 molecules in the simulation box, leading to a concentration of 119.7 mM, and a mean first passage time (FPT) of 89.6 ± 69.2 ns, calculated from the binding events from UMD simulations, the computational k on was calculated to be 9.3 ± 1.2 × 107 M–1·s–1, which is in close agreement to the experimental k on value. The computational k off value was calculated to be 2.2 ± 0.3 × 108 s–1, but there is no experimental k off value reported for comparison.

We performed the same UMD simulations for the inhibitors O2 and CO binding to Df hydrogenase, as we did for the substrate H2. However, the number of (un)­binding events obtained was low, 4 and 2 binding and 4 and 1 unbinding events for O2 and CO, respectively, even with double the amount of simulation time for CO (37.5 μs). The pathways for O2 and CO can be found in .

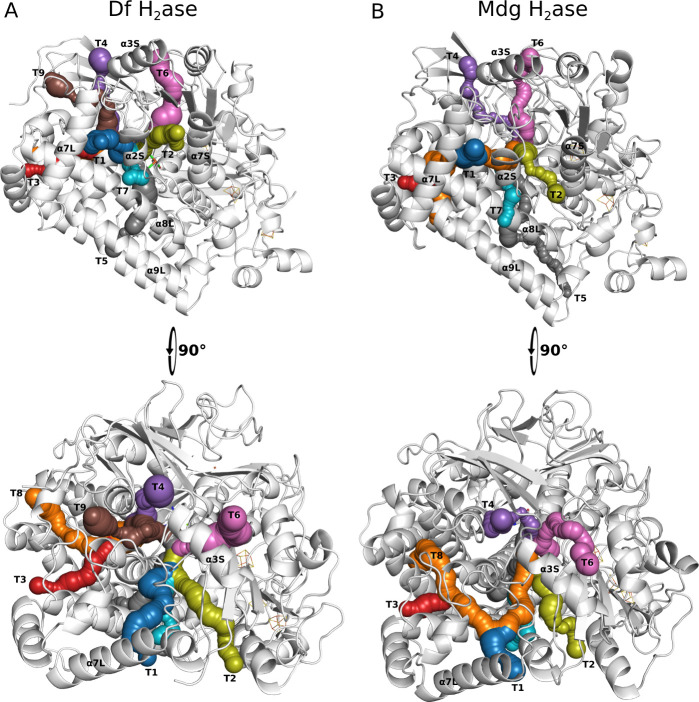
We mapped the tunnels for gas diffusion in the crystallographic structures of both Df and Mdg hydrogenase using CAVER 3.0 (Figure ) to later map the tunnels to the (un)­binding events identified in UMD simulations, following our previous works. , We found that the tunnels are similar for the different enzymes except for the fact that T9 in Df hydrogenase is not present in Mdg hydrogenase. There are also changes in tunnels T3 and T8 in the Mdg hydrogenase, which have common parts with T1, in contrast to tunnels T3 and T8 in Df hydrogenase, which are independent of T1. The binding and unbinding events obtained from UMD for Df and Mdg hydrogenase were identified following the definitions of bound and unbound states above and manually assigned to the tunnels identified (Figure , ). The assignment was based on matching of entry (for binding events) and exit points (for unbinding events) between (un)­binding events and tunnels. We use the term “pathway” to refer to a tunnel used for (un)­binding in the UMD simulations.

2.

2

Open in a new tab

Tunnels identified in the crystallographic structures of A) Df hydrogenase (Df H2ase, PDB ID 1YWQ ) and B) Mdg hydrogenase (Mdg H2ase, PDB ID 1YQ9 ) using the CAVER 3.0 plugin in Pymol. , Nine tunnels (T1-T9) and eight tunnels (T1-T8) were identified in Df and Mdg hydrogenase, respectively. The secondary structures are named according to order of appearance in the primary structure and subunits (S for small and L for large). Example: α2S, second α-helix from the small subunit.

3.

3

Open in a new tab

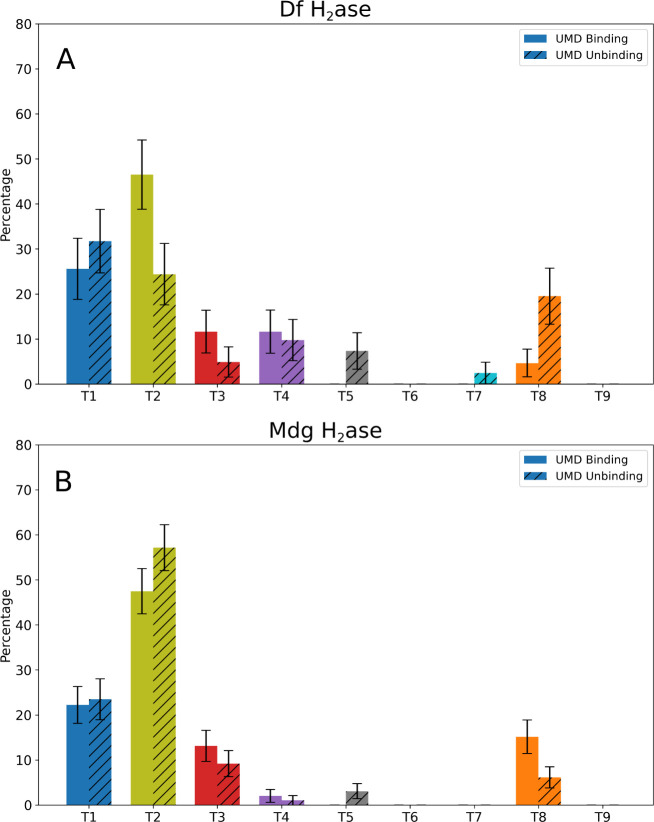
Pathway probabilities are symmetric for H2 binding and unbinding in A) Df hydrogenase (Df H2ase) and B) Mdg hydrogenase (Mdg H2ase). The colors of each pathway match the colors of the associated tunnels in Figure . The standard error for each bar comes from bootstrapping. The p-values obtained from the chi-square test were 0.053 and 0.121 for Df and Mdg hydrogenase, respectively, indicating that there is no significant difference between the binding and unbinding pathway probabilities (considering a threshold of 0.05).

For the two enzymes, pathways T1 and T2 were the most probable paths for binding and unbinding (Figure ), in overall agreement with our previous works, where we used τRAMD to investigate unbinding of H2, CO, and O2 from Df hydrogenase and Mdg hydrogenase. , Pathways T1 and T2 are similar, sharing the region close to the [NiFe] center (Figure , bottom panels) and bifurcating close to helix α2S. It is also notable that some tunnels, like T6 and T9, were not used for (un)­binding events.

Next, we tested whether there was symmetry of the binding and unbinding pathways for the two hydrogenases or, in other words, if the pathway probabilities for binding and unbinding were the same. Pathway symmetry is expected for equilibrium processes, based on the principle of detailed balance or microscopic reversibility proposed by Boltzmann. , A chi-square test was conducted, and the p-values obtained were 0.053 and 0.121 for Df hydrogenase and Mdg hydrogenase, respectively (Tables S5 and S6), which indicates that the differences in pathway usage between binding and unbinding events in each hydrogenase are not statistically significant (using a p-value of 0.05 as a threshold). The p-value for Df hydrogenase is near the threshold, and this can be traced to the differences in the populations of paths T5 and T8 (). Paths T5 and T8 have a lower probability in binding events. Such differences can be the result of a limited number of (un)­binding events.

In previous works, , we used τRAMD to simulate unbinding of H2, CO, and O2 from Df and Mdg hydrogenases. τRAMD is an enhanced sampling technique which applies a force of constant magnitude and random orientation on the center of mass of the ligand to facilitate ligand unbinding. The relative residence times obtained with τRAMD, from tens of unbinding events for one protein–ligand complex, can be compared with experimental values for benchmarking and can be used to rank multiple ligands or different mutants of a protein. We performed τRAMD simulations for 10 different mutants of Df hydrogenase, using a force with a magnitude of 1 kcal/(mol·Å) and 75 unbinding events to estimate relative residence times, and we could successfully reproduce the ranking of absolute residence times measured experimentally (R = 0.79, ρ = 0.75).

We compared the unbinding pathway probabilities obtained from our previous works using τRAMD , with the pathway probabilities obtained here using UMD and found that they are significantly different according to the chi-square test. We obtained p-values of 0.013 and 1.7e–15 for Df hydrogenase and Mdg hydrogenase, respectively (, ). In Df hydrogenase, the differences can be mainly attributed to path T2 (), which has a lower probability in τRAMD. In Mdg hydrogenase, the differences can be attributed mostly to paths T2 and T5 (), which have lower and higher probability in τRAMD, respectively. For the case of Df hydrogenase, differences between the pathway probabilities could have arisen from the number of unbinding events, which is larger in τRAMD. In Df hydrogenase, UMD simulations have similar probabilities for paths T1 and T2, while in τRAMD the probabilities are higher for path T1. Since paths T1 and T2 are similar, they can potentially be grouped together, which would lead to more comparable probabilities. Differences may also arise from the longer UMD simulations (hundreds of nanoseconds), which may have captured long time scale dynamics not observed in short τRAMD simulations (tens of nanoseconds), and from the use of a force in τRAMD to speed up unbinding, which can potentially affect unbinding and the associated pathway probabilities, as observed before for ligand unbinding in GPCRs. Despite the differences, τRAMD was able to identify path T1 as one of the most probable paths for H2 unbinding from Df and Mdg hydrogenase.

Additionally, we performed data analysis to investigate the dynamics of the main bottleneck for ligand unbinding, located between two evolutionary conserved hydrophobic residues, V74 and L122 (Df hydrogenase sequence numbering), in the UMD simulations. The bottleneck distance was identified by us and others ,, as one of the main factors modulating the residence times for CO bound to different mutants of Df hydrogenase. In our previous work, we identified a strong correlation between the distances between residues V74 and L122 and the experimentally measured residence times, suggesting that these two residues act as a bottleneck for gas transit to the catalytic site. Equilibrium properties such as free energy landscapes (FELs) should not be directly computed from an ensemble of short independent simulations. Therefore, we constructed a Markov state model (MSM; details in the Supporting Information in ) and used it to compute a reweighted FEL (Figure B). UMD simulations revealed that the bottleneck distances have two populated states in Df hydrogenase: open and closed (Figure ). The minimum distance between residues V74 and L122 can range from ∼ 4 up to ∼ 10 Å (Figure ). Part of this variation can be attributed to dihedral changes in L122 (Figure ) and part to changes in the secondary structure in the region around residue L122, which switches between 310-helix, extended strand and turn according to the DSSP analysis (). While the crystallographic structure is in the closed state, UMD simulations suggest that the open state is the most stable state for Df hydrogenase. In the τRAMD simulations from previous work, we only observed the open state of the bottleneck (). We also investigated the presence of the open and closed states in Mdg hydrogenase. In this case, while the FEL indicates the presence of two states, there are only minor structural changes in the regions including V74 and L122 (), and the range of distances sampled in the UMD simulations is narrower (Figure A), indicating that the bottleneck in Mdg hydrogenase is in the closed state. The kinetic diameter of gas molecules (H2, CO, and O2) ranges between 2.9 and 3.8 Å (). While these diameters are lower than the minimum width of the bottleneck in the two hydrogenases, it is expected that motions in the bottleneck can hinder or facilitate gas transit. Information about the dual-state bottleneck can be exploited to engineer mutant enzymes that block the passage of larger gas molecules, such as CO and O2, which inhibit some hydrogenases. It remains to be tested whether the dual-state bottleneck is part of the dynamics of other hydrogenases, contributing to the regulation of residence times and access of the gas molecules to the catalytic site.

4.

4

Open in a new tab

Dual-state bottleneck in Df hydrogenase (Df H2ase) observed in unbiased molecular dynamics simulations. A) Probability density of lowest distance values between residues V74 and L122 in Df hydrogenase and Mdg hydrogenase (Mdg Df H2ase). The distance values in the crystallographic structures are shown as traced lines. B) Free energy landscape of the V74-L122 bottleneck in Df hydrogenase computed using a Markov state model (details in the ). Two main states were identified: open and closed. C) Representative snapshots of Df hydrogenase in the open (cyan residues) and closed (green residues) states of the V74-L122 bottleneck. The location of the snapshots in the free energy landscape in panel B is indicated with green and cyan stars.

It has long been believed that the mechanism of tolerance in [NiFe] hydrogenases is due to the proximal and distal FeS centers, which are located in the small subunit and can reduce the [NiFe] center following an O2 or a CO attack. However, recent experiments using chimeric forms of Escherichia coli [NiFe] hydrogenases found that sensitivity to the inhibitor CO can be set by the large subunit and that specific structural determinants in both subunits contribute to inhibitor tolerance in the enzymes. This is evidence that structural information about the binding pathways and associated bottlenecks is an important factor in the tolerance mechanism. Recently, Grinter et al. revealed the energy extraction mechanism of the O2-tolerant Huc hydrogenase from Mycobacterium smegmatis using experiments and MD simulations. The authors obtained H2 and O2 (un)­binding events using UMD simulations and found that only H2 could enter the binding site, while O2 was sterically excluded by a series of bottlenecks present in the tunnels. O2 could reach the active site only in mutants where the bottlenecks were relieved. This is another evidence that the bottlenecks in the binding pathways can be exploited to achieve inhibitor-tolerance and optimized enzymes. Taking into consideration the mechanistic insights obtained here for Df hydrogenase, we propose introducing mutations in the region around the α-helix containing L122 to limit the motions of the residues in the bottleneck for ligand binding and lock the bottleneck in the closed state, restricting the access of inhibitors such as O2 and CO, which have diameters larger than those of H2, to the catalytic site. This may increase the tolerance of the enzyme to inhibitors.

In this work, we utilized UMD simulations for sampling binding and unbinding events of H2 to and from two different [NiFe] hydrogenases, Df hydrogenase and Mdg hydrogenase. The computed k on value reproduced the experimental k on value for the association of H2 to Df hydrogenase. We characterized path probabilities for binding and unbinding and found that there is symmetry between the binding and unbinding pathways for both enzymes. We also compared the path probabilities from this work using UMD simulations with the ones obtained in our previous works using τRAMD, and we found that τRAMD can identify the most probable pathways for H2 dissociation from hydrogenases. We expect this observation to be true for other systems, as long as large protein conformational changes are not required for ligand dissociation. Data analysis revealed that the main bottleneck that controls the access of ligands to the catalytic site can have two states in Df hydrogenase. The pathway populations obtained from UMD simulations can be used as a data set to benchmark enhanced sampling methods that aim to investigate ligand binding. Additionally, the mechanistic insights obtained for the gating of ligand access to the catalytic site of Df hydrogenase can lead to novel strategies to modulate gas diffusion inside hydrogenases.

Computational Methods

The crystallographic structures of Df hydrogenase and Mdg hydrogenase (PDB IDs 1YQW and 1YQ9, respectively) were obtained from the Protein Data Bank. The force field bonded parameters and the partial charges of the metal centers were obtained from the works of Smith et al. and Teixeira et al., respectively. The protonation states of the residues at pH 7, the pH used for measuring experimental kinetic rates, were determined using Propka version 3.5.2, − as implemented in the program pdb2pqr version 2.1.1. , The force field parameters of H2 (bonded parameters, Lennard-Jones parameters, and partial charges) were obtained from Wang et al. The protein was placed in the center of a cubic box with a distance of 1.5 nm from all edges, and then 100 H2 molecules were added to the box randomly (minimum distance of 1 nm from the hydrogenase) with a concentration of ∼ 120 mM. Finally, the system was solvated with the TIP3P water model. Then, sodium and chloride ions were added to produce an ionic strength of 118 mM, which was adopted to reproduce the conditions used for the protein film voltammetry experiments to obtain kinetic rates. All of the MD simulations were unbiased and were performed by GROMACS 2024.2 and the Amber ff99SB force field. We kept the force field and, when possible, all of the parameters the same as the simulations performed previously with τRAMD for Df hydrogenase and Mdg hydrogenase , to make a fair comparison between results from τRAMD simulations and UMD simulations. In total, we performed 75 replicas for each of the two hydrogenases, and each simulation had a duration of 250 ns, leading to a total simulation time of 18.75 μs for each hydrogenase. The MD simulations have been performed using two types of GPUs, Nvidia 1080 and 2080, on multiple nodes available at the High Performance Computer (HPC) of the Technical University of Berlin, and the performance for this system size, with 110,000 atoms, was roughly 40 ns/day on average. More details of the methods can be found in the .

Supplementary Material

jz5c01673_si_001.pdf (2.9MB, pdf)
jz5c01673_si_002.pdf (3MB, pdf)

Acknowledgments

Funding from DFG under Germany’s Excellence Strategy – EXC 2008/1-390540038 – UniSysCat is gratefully acknowledged. The authors thank Dr. Marius Horch (Free University Berlin), Prof. Maria Andrea Mroginski (Technical University of Berlin), and Dr. Jing-Yao Guo (Technical University of Berlin) for helpful discussions.

The data to reproduce the UMD simulations (input files, starting structures and topologies) and the trajectories obtained are uploaded on Zenodo in 4 separate parts (‘10.5281/zenodo.15521025’, ‘10.5281/zenodo.15520947’, ‘10.5281/zenodo.15520978’, ‘10.5281/zenodo.15521025’); the code to analyze the data, the code for building and validating the MSM and the Pymol session files containing the Df and Mdg hydrogenase tunnels identified by CAVER can be found on Github: https://github.com/FarzinSohraby/SI-H2ase-UMD.

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.5c01673.

  • 1) Description of the methods used for the UMD simulations and for data analysis. 2) Equations to calculate k on values using experimental data and mean first passage times (MPFTs) from UMD simulations. 3) Paths and MFPTs obtained from UMD simulations (Tables S1–S3). 4) Percentages of paths used for binding and unbinding in Df and Mdg hydrogenases (Table S4). 5) Contribution of pathway probabilities to the results of the chi-square tests (Tables S5–S8). 6) Comparison between pathway probabilities for unbinding obtained from τRAMD and UMD simulations (Figure S1 and S2). 7) Markov state model building and validation (Figures S3–S8). 8) DSSP analysis of the region around residue L122 in Df hydrogenase (Figure S9). 9) Comparison between probability densities of the bottleneck widths in τRAMD and UMD simulations (Figure S10). 10) Breck’s kinetic diameter of small gas molecules (Table S9). 11) Free energy profile, snapshots of representative structures and DSSP analysis of the residues in the V74-L122 bottleneck in Mdg hydrogenase (Figure S11). See also Data Availability Statement (PDF)

  • Transparent Peer Review report available (PDF)

The authors declare no competing financial interest.

References

  1. Knockenhauer K. E., Copeland R. A.. The Importance of Binding Kinetics and Drug-Target Residence Time in Pharmacology. Br. J. Pharmacol. 2024;181(21):4103–4116. doi: 10.1111/bph.16104. [DOI] [PubMed] [Google Scholar]
  2. Seow V., Lim J., Cotterell A. J., Yau M.-K., Xu W., Lohman R.-J., Kok W. M., Stoermer M. J., Sweet M. J., Reid R. C., Suen J. Y., Fairlie D. P.. Receptor Residence Time Trumps Drug-Likeness and Oral Bioavailability in Determining Efficacy of Complement C5a Antagonists. Sci. Rep. 2016;6(1):24575. doi: 10.1038/srep24575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Lu H., Tonge P. J.. Drug-Target Residence Time: Critical Information for Lead Optimization. Curr. Opin. Chem. Biol. 2010;14(4):467–474. doi: 10.1016/j.cbpa.2010.06.176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Lee K. S. S., Yang J., Niu J., Ng C. J., Wagner K. M., Dong H., Kodani S. D., Wan D., Morisseau C., Hammock B. D.. Drug-Target Residence Time Affects in Vivo Target Occupancy through Multiple Pathways. ACS Cent. Sci. 2019;5(9):1614–1624. doi: 10.1021/acscentsci.9b00770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Liu H., Zhang H., IJzerman A. P., Guo D.. The Translational Value of Ligand-receptor Binding Kinetics in Drug Discovery. Br. J. Pharmacol. 2024;181(21):4117–4129. doi: 10.1111/bph.16241. [DOI] [PubMed] [Google Scholar]
  6. Voss J. H., Crüsemann M., Bartling C. R. O., Kehraus S., Inoue A., König G. M., Strømgaard K., Müller C. E.. Structure-Affinity and Structure-Residence Time Relationships of Macrocyclic Gαq Protein Inhibitors. iScience. 2023;26(4):106492. doi: 10.1016/j.isci.2023.106492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Zhang R., Monsma F.. The Importance of Drug-Target Residence Time. Curr. Opin. Drug Discovery Devel. 2009;12(4):488–496. [PubMed] [Google Scholar]
  8. Sohraby F., Nunes-Alves A.. Advances in Computational Methods for Ligand Binding Kinetics. Trends Biochem. Sci. 2023;48(5):437–449. doi: 10.1016/j.tibs.2022.11.003. [DOI] [PubMed] [Google Scholar]
  9. Nunes-Alves A., Kokh D. B., Wade R. C.. Recent Progress in Molecular Simulation Methods for Drug Binding Kinetics. Curr. Opin. Struct. Biol. 2020;64:126–133. doi: 10.1016/j.sbi.2020.06.022. [DOI] [PubMed] [Google Scholar]
  10. Zhang Q., Zhao N., Meng X., Yu F., Yao X., Liu H.. The Prediction of Protein-Ligand Unbinding for Modern Drug Discovery. Expert Opin. Drug Discovery. 2022;17(2):191–205. doi: 10.1080/17460441.2022.2002298. [DOI] [PubMed] [Google Scholar]
  11. Ahmad K., Rizzi A., Capelli R., Mandelli D., Lyu W., Carloni P.. Enhanced-Sampling Simulations for the Estimation of Ligand Binding Kinetics: Current Status and Perspective. Front. Mol. Biosci. 2022;9:899805. doi: 10.3389/fmolb.2022.899805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Brezovsky J., Babkova P., Degtjarik O., Fortova A., Gora A., Iermak I., Rezacova P., Dvorak P., Smatanova I. K., Prokop Z., Chaloupkova R., Damborsky J.. Engineering a de Novo Transport Tunnel. ACS Catal. 2016;6(11):7597–7610. doi: 10.1021/acscatal.6b02081. [DOI] [Google Scholar]
  13. Sohraby F., Nunes-Alves A.. Characterization of the Bottlenecks and Pathways for Inhibitor Dissociation from [NiFe] Hydrogenase. J. Chem. Inf. Model. 2024;64(10):4193–4203. doi: 10.1021/acs.jcim.4c00187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kokkonen P., Bednar D., Pinto G., Prokop Z., Damborsky J.. Engineering Enzyme Access Tunnels. Biotechnol. Adv. 2019;37(6):107386. doi: 10.1016/j.biotechadv.2019.04.008. [DOI] [PubMed] [Google Scholar]
  15. Kong X.-D., Yuan S., Li L., Chen S., Xu J.-H., Zhou J.. Engineering of an Epoxide Hydrolase for Efficient Bioresolution of Bulky Pharmaco Substrates. Proc. Natl. Acad. Sci. U. S. A. 2014;111(44):15717–15722. doi: 10.1073/pnas.1404915111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Bernetti M., Masetti M., Rocchia W., Cavalli A.. Kinetics of Drug Binding and Residence Time. Annu. Rev. Phys. Chem. 2019;70(1):143–171. doi: 10.1146/annurev-physchem-042018-052340. [DOI] [PubMed] [Google Scholar]
  17. Ziada S., Diharce J., Raimbaud E., Aci-Sèche S., Ducrot P., Bonnet P.. Estimation of Drug-Target Residence Time by Targeted Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022;62(22):5536–5549. doi: 10.1021/acs.jcim.2c00852. [DOI] [PubMed] [Google Scholar]
  18. Shan Y., Kim E. T., Eastwood M. P., Dror R. O., Seeliger M. A., Shaw D. E.. How Does a Drug Molecule Find Its Target Binding Site? J. Am. Chem. Soc. 2011;133(24):9181–9183. doi: 10.1021/ja202726y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dror R. O., Pan A. C., Arlow D. H., Borhani D. W., Maragakis P., Shan Y., Xu H., Shaw D. E.. Pathway and Mechanism of Drug Binding to G-Protein-Coupled Receptors. Proc. Natl. Acad. Sci. U. S. A. 2011;108(32):13118–13123. doi: 10.1073/pnas.1104614108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Karmani, R. K. ; Agha, G. ; Squillante, M. S. ; Seiferas, J. ; Brezina, M. ; Hu, J. ; Tuminaro, R. ; Sanders, P. ; Träffe, J. L. ; Geijn, R. A. ; Träff, J. L. ; Geijn, R. A. ; Sander, M. B. ; Gustafson, J. L. ; Dror, R. O. ; Young, C. ; Shaw, D. E. ; Lin, C. ; Lee, J.-K. ; Chang, R.-G. ; Kuan, C.-B. ; Kollias, G. ; Grama, A. Y. ; Li, Z. ; Whaley, R. C. ; Vuduc, R. W. ; Anton, A. . Special-Purpose Molecular Simulation Machine. In Encyclopedia of Parallel Computing; Padua, D. , Ed.; Springer US: Boston, MA, 2011; pp 60–71. 10.1007/978-0-387-09766-4_199. [DOI] [Google Scholar]
  21. Shaw, D. E. ; Adams, P. J. ; Azaria, A. ; Bank, J. A. ; Batson, B. ; Bell, A. ; Bergdorf, M. ; Bhatt, J. ; Butts, J. A. ; Correia, T. ; Dirks, R. M. ; Dror, R. O. ; Eastwood, M. P. ; Edwards, B. ; Even, A. ; Feldmann, P. ; Fenn, M. ; Fenton, C. H. ; Forte, A. ; Gagliardo, J. ; Gill, G. ; Gorlatova, M. ; Greskamp, B. ; Grossman, J. P. ; Gullingsrud, J. ; Harper, A. ; Hasenplaugh, W. ; Heily, M. ; Heshmat, B. C. ; Hunt, J. ; Ierardi, D. J. ; Iserovich, L. ; Jackson, B. L. ; Johnson, N. P. ; Kirk, M. M. ; Klepeis, J. L. ; Kuskin, J. S. ; Mackenzie, K. M. ; Mader, R. J. ; McGowen, R. ; McLaughlin, A. ; Moraes, M. A. ; Nasr, M. H. ; Nociolo, L. J. ; O’Donnell, L. ; Parker, A. ; Peticolas, J. L. ; Pocina, G. ; Predescu, C. ; Quan, T. ; Salmon, J. K. ; Schwink, C. ; Shim, K. S. ; Siddique, N. ; Spengler, J. ; Szalay, T. ; Tabladillo, R. ; Tartler, R. ; Taube, A. G. ; Theobald, M. ; Towles, B. ; Vick, W. ; Wang, S. C. ; Wazlowski, M. ; Weingarten, M. J. ; Williams, J. M. ; Yuh, K. A. . Anton 3: Twenty Microseconds of Molecular Dynamics Simulation before Lunch. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis; ACM: St. Louis, Missouri, 2021; pp 1–11. 10.1145/3458817.3487397. [DOI] [Google Scholar]
  22. Votapka L. W., Stokely A. M., Ojha A. A., Amaro R. E.. SEEKR2: Versatile Multiscale Milestoning Utilizing the OpenMM Molecular Dynamics Engine. J. Chem. Inf. Model. 2022;62(13):3253–3262. doi: 10.1021/acs.jcim.2c00501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jagger B. R., Ojha A. A., Amaro R. E.. Predicting Ligand Binding Kinetics Using a Markovian Milestoning with Voronoi Tessellations Multiscale Approach. J. Chem. Theory Comput. 2020;16(8):5348–5357. doi: 10.1021/acs.jctc.0c00495. [DOI] [PubMed] [Google Scholar]
  24. Ray D., Stone S. E., Andricioaei I.. Markovian Weighted Ensemble Milestoning (M-WEM): Long-Time Kinetics from Short Trajectories. J. Chem. Theory Comput. 2022;18(1):79–95. doi: 10.1021/acs.jctc.1c00803. [DOI] [PubMed] [Google Scholar]
  25. Shao Q., Zhu W.. Exploring the Ligand Binding/Unbinding Pathway by Selectively Enhanced Sampling of Ligand in a Protein-Ligand Complex. J. Phys. Chem. B. 2019;123(38):7974–7983. doi: 10.1021/acs.jpcb.9b05226. [DOI] [PubMed] [Google Scholar]
  26. Ray D., Andricioaei I.. Weighted Ensemble Milestoning (WEM): A Combined Approach for Rare Event Simulations. J. Chem. Phys. 2020;152(23):234114. doi: 10.1063/5.0008028. [DOI] [PubMed] [Google Scholar]
  27. Miao Y., Bhattarai A., Wang J.. Ligand Gaussian Accelerated Molecular Dynamics (LiGaMD): Characterization of Ligand Binding Thermodynamics and Kinetics. J. Chem. Theory Comput. 2020;16(9):5526–5547. doi: 10.1021/acs.jctc.0c00395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wang J., Miao Y.. Ligand Gaussian Accelerated Molecular Dynamics 2 (LiGaMD2): Improved Calculations of Ligand Binding Thermodynamics and Kinetics with Closed Protein Pocket. J. Chem. Theory Comput. 2023;19(3):733–745. doi: 10.1021/acs.jctc.2c01194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wang J., Miao Y.. Ligand Gaussian Accelerated Molecular Dynamics 3 (LiGaMD3): Improved Calculations of Binding Thermodynamics and Kinetics of Both Small Molecules and Flexible Peptides. J. Chem. Theory Comput. 2024;20(14):5829–5841. doi: 10.1021/acs.jctc.4c00502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kokh D. B., Amaral M., Bomke J., Grädler U., Musil D., Buchstaller H.-P., Dreyer M. K., Frech M., Lowinski M., Vallee F., Bianciotto M., Rak A., Wade R. C.. Estimation of Drug-Target Residence Times by τ-Random Acceleration Molecular Dynamics Simulations. J. Chem. Theory Comput. 2018;14(7):3859–3869. doi: 10.1021/acs.jctc.8b00230. [DOI] [PubMed] [Google Scholar]
  31. Tiwary P., Limongelli V., Salvalaglio M., Parrinello M.. Kinetics of Protein-Ligand Unbinding: Predicting Pathways, Rates, and Rate-Limiting Steps. Proc. Natl. Acad. Sci. U. S. A. 2015;112(5):E386-E391. doi: 10.1073/pnas.1424461112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kokkonen P., Sykora J., Prokop Z., Ghose A., Bednar D., Amaro M., Beerens K., Bidmanova S., Slanska M., Brezovsky J., Damborsky J., Hof M.. Molecular Gating of an Engineered Enzyme Captured in Real Time. J. Am. Chem. Soc. 2018;140(51):17999–18008. doi: 10.1021/jacs.8b09848. [DOI] [PubMed] [Google Scholar]
  33. Kaushik S., Marques S. M., Khirsariya P., Paruch K., Libichova L., Brezovsky J., Prokop Z., Chaloupkova R., Damborsky J.. Impact of the Access Tunnel Engineering on Catalysis Is Strictly Ligand-specific. FEBS J. 2018;285(8):1456–1476. doi: 10.1111/febs.14418. [DOI] [PubMed] [Google Scholar]
  34. Pakuła K., Sequeiros-Borja C., Biała-Leonhard W., Pawela A., Banasiak J., Bailly A., Radom M., Geisler M., Brezovsky J., Jasiński M.. Restriction of Access to the Central Cavity Is a Major Contributor to Substrate Selectivity in Plant ABCG Transporters. Cell. Mol. Life Sci. 2023;80(4):105. doi: 10.1007/s00018-023-04751-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sohraby F., Guo J.-Y., Nunes-Alves A.. PathInHydro, a Set of Machine Learning Models to Identify Unbinding Pathways of Gas Molecules in [NiFe] Hydrogenases. J. Chem. Inf. Model. 2025;65(2):589–602. doi: 10.1021/acs.jcim.4c01656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Liebgott P.-P., Dementin S., Léger C., Rousset M.. Towards Engineering O 2 -Tolerance in [Ni-Fe] Hydrogenases. Energy Env. Sci. 2011;4(1):33–41. doi: 10.1039/C0EE00093K. [DOI] [Google Scholar]
  37. Wang P., Blumberger J.. Mechanistic Insight into the Blocking of CO Diffusion in [NiFe]-Hydrogenase Mutants through Multiscale Simulation. Proc. Natl. Acad. Sci. U. S. A. 2012;109(17):6399–6404. doi: 10.1073/pnas.1121176109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wang P., Best R. B., Blumberger J.. Multiscale Simulation Reveals Multiple Pathways for H2 and O2 Transport in a [NiFe]-Hydrogenase. J. Am. Chem. Soc. 2011;133(10):3548–3556. doi: 10.1021/ja109712q. [DOI] [PubMed] [Google Scholar]
  39. Volbeda A., Martin L., Cavazza C., Matho M., Faber B. W., Roseboom W., Albracht S. P. J., Garcin E., Rousset M., Fontecilla-Camps J. C.. Structural Differences between the Ready and Unready Oxidized States of [NiFe] Hydrogenases. JBIC J. Biol. Inorg. Chem. 2005;10(3):239–249. doi: 10.1007/s00775-005-0632-x. [DOI] [PubMed] [Google Scholar]
  40. Liebgott P.-P., Leroux F., Burlat B., Dementin S., Baffert C., Lautier T., Fourmond V., Ceccaldi P., Cavazza C., Meynial-Salles I., Soucaille P., Fontecilla-Camps J. C., Guigliarelli B., Bertrand P., Rousset M., Léger C.. Relating Diffusion along the Substrate Tunnel and Oxygen Sensitivity in Hydrogenase. Nat. Chem. Biol. 2010;6(1):63–70. doi: 10.1038/nchembio.276. [DOI] [PubMed] [Google Scholar]
  41. Chovancova E., Pavelka A., Benes P., Strnad O., Brezovsky J., Kozlikova B., Gora A., Sustr V., Klvana M., Medek P., Biedermannova L., Sochor J., Damborsky J.. CAVER 3.0: A Tool for the Analysis of Transport Pathways in Dynamic Protein Structures. PLoS Comput. Biol. 2012;8(10):e1002708. doi: 10.1371/journal.pcbi.1002708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Schrödinger, LLC . The PyMOL Molecular Graphics System, Version 1.8; Schrödinger, 2015. [Google Scholar]
  43. Lewis G. N.. A New Principle of Equilibrium. Proc. Natl. Acad. Sci. U. S. A. 1925;11(3):179–183. doi: 10.1073/pnas.11.3.179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Bhatt D., Zuckerman D. M.. Beyond microscopic reversibility: Are observable non-equilibrium processes precisely reversible? J. Chem. Theory. Comput. 2011;7(8):2520–2527. doi: 10.1021/ct200086k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Kokh D. B., Wade R. C.. G Protein-Coupled Receptor-Ligand Dissociation Rates and Mechanisms from τRAMD Simulations. J. Chem. Theory Comput. 2021;17(10):6610–6623. doi: 10.1021/acs.jctc.1c00641. [DOI] [PubMed] [Google Scholar]
  46. Kabsch W., Sander C.. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-bonded and Geometrical Features. Biopolymers. 1983;22(12):2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
  47. Scherer M. K., Trendelkamp-Schroer B., Paul F., Pérez-Hernández G., Hoffmann M., Plattner N., Wehmeyer C., Prinz J.-H., Noé F.. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015;11(11):5525–5542. doi: 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
  48. Fasano A., Guendon C., Jacq-Bailly A., Kpebe A., Wozniak J., Baffert C., Barrio M. D., Fourmond V., Brugna M., Léger C.. A Chimeric NiFe Hydrogenase Heterodimer to Assess the Role of the Electron Transfer Chain in Tuning the Enzyme’s Catalytic Bias and Oxygen Tolerance. J. Am. Chem. Soc. 2023;145(36):20021–20030. doi: 10.1021/jacs.3c06895. [DOI] [PubMed] [Google Scholar]
  49. Grinter R., Kropp A., Venugopal H., Senger M., Badley J., Cabotaje P. R., Jia R., Duan Z., Huang P., Stripp S. T., Barlow C. K., Belousoff M., Shafaat H. S., Cook G. M., Schittenhelm R. B., Vincent K. A., Khalid S., Berggren G., Greening C.. Structural Basis for Bacterial Energy Extraction from Atmospheric Hydrogen. Nature. 2023;615(7952):541–547. doi: 10.1038/s41586-023-05781-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Berman H. M.. The Protein Data Bank. Nucleic Acids Res. 2000;28(1):235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Smith D. M. A., Xiong Y., Straatsma T. P., Rosso K. M., Squier T. C.. Force-Field Development and Molecular Dynamics of [NiFe] Hydrogenase. J. Chem. Theory Comput. 2012;8(6):2103–2114. doi: 10.1021/ct300185u. [DOI] [PubMed] [Google Scholar]
  52. Teixeira V. H., Baptista A. M., Soares C. M.. Pathways of H2 toward the Active Site of [NiFe]-Hydrogenase. Biophys. J. 2006;91(6):2035–2045. doi: 10.1529/biophysj.106.084376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Li H., Robertson A. D., Jensen J. H.. Very Fast Empirical Prediction and Rationalization of Protein pKa Values. Proteins Struct. Funct. Bioinforma. 2005;61(4):704–721. doi: 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
  54. Bas D. C., Rogers D. M., Jensen J. H.. Very Fast Prediction and Rationalization of pKa Values for Protein-Ligand Complexes. Proteins Struct. Funct. Bioinforma. 2008;73(3):765–783. doi: 10.1002/prot.22102. [DOI] [PubMed] [Google Scholar]
  55. Olsson M. H. M., Søndergaard C. R., Rostkowski M., Jensen J. H.. PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical p K a Predictions. J. Chem. Theory Comput. 2011;7(2):525–537. doi: 10.1021/ct100578z. [DOI] [PubMed] [Google Scholar]
  56. Unni S., Huang Y., Hanson R. M., Tobias M., Krishnan S., Li W. W., Nielsen J. E., Baker N. A.. Web Servers and Services for Electrostatics Calculations with APBS and PDB2PQR. J. Comput. Chem. 2011;32(7):1488–1491. doi: 10.1002/jcc.21720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Dolinsky T. J., Nielsen J. E., McCammon J. A., Baker N. A.. PDB2PQR: An Automated Pipeline for the Setup of Poisson-Boltzmann Electrostatics Calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wang S., Hou K., Heinz H.. Accurate and Compatible Force Fields for Molecular Oxygen, Nitrogen, and Hydrogen to Simulate Gases, Electrolytes, and Heterogeneous Interfaces. J. Chem. Theory Comput. 2021;17(8):5198–5213. doi: 10.1021/acs.jctc.0c01132. [DOI] [PubMed] [Google Scholar]
  59. Mark P., Nilsson L.. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A. 2001;105(43):9954–9960. doi: 10.1021/jp003020w. [DOI] [Google Scholar]
  60. Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., Lindahl E.. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX. 2015;1–2:19–25. doi: 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  61. Ponder, J. W. ; Case, D. A. . Force Fields for Protein Simulations. In Advances in Protein Chemistry; Elsevier, 2003; Vol. 66, pp 27–85. 10.1016/S0065-3233(03)66002-X. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz5c01673_si_001.pdf (2.9MB, pdf)
jz5c01673_si_002.pdf (3MB, pdf)

Data Availability Statement

The data to reproduce the UMD simulations (input files, starting structures and topologies) and the trajectories obtained are uploaded on Zenodo in 4 separate parts (‘10.5281/zenodo.15521025’, ‘10.5281/zenodo.15520947’, ‘10.5281/zenodo.15520978’, ‘10.5281/zenodo.15521025’); the code to analyze the data, the code for building and validating the MSM and the Pymol session files containing the Df and Mdg hydrogenase tunnels identified by CAVER can be found on Github: https://github.com/FarzinSohraby/SI-H2ase-UMD.

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES