Abstract
Photoacoustic tomography (PAT) combines high optical contrast with deep acoustic penetration, making it valuable for biomedical imaging. However, all-optical systems often face challenges in measuring the acoustic wave-induced displacements on rough and dynamic tissues surfaces. We present an all-optical PAT system enabling fast and high-resolution volumetric imaging in vivo. By integrating holographic microscopy with a soft cover layer and coherent averaging, the system detects ultrasound-induced surface displacements over a 10 × 10 mm² area with 0.5 nm sensitivity in 1 s. A novel backpropagation algorithm reconstructs a depth-selective pressure image from two consecutive displacement maps. The coherent summation of these depth-selective pressure images enables the reconstruction of a 3D acoustic pressure image. Using adaptive multilayer backpropagation, we achieve imaging depths of up to 5 mm, with lateral and axial resolutions of 158 µm and 92 µm, respectively, demonstrated through in vivo imaging of mouse vasculature and chicken embryo vessels.
Keywords: Photoacoustic tomography, Holography, In vivo imaging, Backpropagation
1. Introduction
Photoacoustic tomography (PAT) offers volumetric imaging with high optical contrast and long acoustic imaging depth, making it a vital tool for biomedical applications and industrial inspections [1]. Its principle involves irradiating short laser pulses onto light-absorbing objects embedded in a scattering medium, where short-duration acoustic waves, called photoacoustic waves, are induced by photo-thermal expansion at the absorption sites. By acquiring the 2D pressure profiles of these acoustic waves at the surface of a specimen over time, the 3D distribution of the objects within the specimen can be visualized [2], [3]. Essentially, PAT can selectively visualize the objects having high optical absorption at the wavelength of excitation laser [4], [5].
Since the advent of PAT, ultrasound transducers have been widely used to detect the acoustic pressures induced by photoacoustic waves [6]. When using a single-element transducer, scanning over an area is required, making tomographic reconstruction time-consuming. For efficient volumetric imaging, various forms of transducer arrays have been employed [7], [8], [9], [10], [11]. However, ultrasound transducers face intrinsic limitations, including low spatial sampling bandwidth due to the finite sensor size, which is often larger than the acoustic wavelength, a limited number of sensor elements packable in a device, and difficulty in securing an optical beam path for excitation laser pulses.
Various optical detection systems have been proposed to address the limitations associated with conventional ultrasound transducers [12], [13], [14], [15], [16]. These methods employ the optical detection of the surface displacements induced by photoacoustic waves, allowing for optical-resolution spatial sampling of acoustic waves and providing optical windows for the excitation laser pulses. For example, Jathoul et al. used a Fabry-Perot polymer film, composed of partially reflective glasses and a polymer spacer, to enhance pressure sensitivity beyond that of conventional transducers [16]. While early versions suffered from slow imaging speeds, mainly due to lateral scanning of the probe laser focus, recent studies have significantly improved the acquisition speed, reducing it to seconds or even hundreds of milliseconds by employing a multichannel detection scheme [17]. To enhance the surface profiling speed, wide-field detection methods have been developed, enabling the acquisition of surface displacement maps over a large area at once [18], [19], [20], [21], [22]. Nuster et al. utilized a phase contrast imaging technique to measure the acoustic pressure integrated along the probe beam direction [18], [19]. However, this method requires transmission-based measurements, making it difficult to apply to in vivo imaging, where reflection-based measurements are essential. Buj et al. applied an off-axis holography-based optical interferometric system, operating in a pump-and-probe mode, to capture 2D snapshot images of propagating photoacoustic waves [22]. While the study demonstrated the feasibility of imaging a silicon tube phantom placed under porcine skin, imaging in live tissues has remained out of reach mainly because the system’s sensitivity was insufficient to capture photoacoustic waves on a rough and dynamic tissue surface. Furthermore, the 3D image reconstruction was performed in the spatio-temporal frequency domain, requiring the recording of a complete set of surface displacement maps over a time span of the photoacoustic wave propagation. Thus, most of the all-optical PAT systems developed so far either lack the sensitivity needed for in vivo imaging or are too complex and time-consuming.
Here, we present an all-optical photoacoustic tomography system that provides high-speed volumetric imaging with high sensitivity for live tissue imaging. The detection system is based on full-field holographic microscopy, and a soft and transparent cover layer is applied on the tissue surface to provide an optically smooth surface for displacement measurements. Coherent averaging of multiple holograms is employed to further enhance the signal-to-noise ratio (SNR) of the phase detection. As a result, our system achieves 0.5 nm vertical displacement sensitivity at each 31 µm optical resolution spot, offering pressure sensitivity comparable to an ultrasound transducer of the same size, while profiling the surface displacements over a 10 × 10 mm² area in just 1 s. Furthermore, we propose a temporal backpropagation algorithm that can reconstruct a volumetric image from a single surface pressure map, generated from two consecutive displacement maps, enabling rapid and depth-selective volumetric imaging. This algorithm incorporates adaptive multilayer backpropagation, adjusting acoustic velocities in situ across different media and correcting the angle-dependent transmittance caused by impedance mismatches between the cover layer and the tissue medium. Our system achieves imaging depths of up to 5 mm, with 158 µm lateral and 92 µm axial resolutions, demonstrated through in vivo volumetric imaging of mouse hindlimb vasculature and chicken embryo blood vessels.
2. Results
2.1. All-optical full-field imaging of photoacoustic wave propagation
Optical imaging of photoacoustic waves in a living specimen is challenging due to the extremely small surface displacements caused by acoustic pressure waves, often just a few nanometers or less [23]. These minute deformations are easily masked by the inherent surface roughness of biological tissues, which can range from tens to hundreds of micrometers. Additionally, the continuous movement of living tissues further complicates the wave detection. To address these issues, we apply an optically transparent and smooth cover layer on the tissue surface (Fig. 1(a)). In our experiments, we have used polydimethylsiloxane (PDMS), a biocompatible material commonly used in wearable technology, as the cover layer [24], [25]. This cover layer allows clear optical access to the excitation light while significantly improving the measurement sensitivity of surface displacements. However, the acoustic impedance mismatch between the cover layer and the biological tissue complicates the reconstruction process. As we shall explain later on, we have developed a specialized multilayer backpropagation algorithm to reconstruct the initial photoacoustic pressure induced at the time of optical excitation.
Fig. 1.
Schematic of full-field optical interferometric imaging of photoacoustic waves at the specimen surface. (a) When an excitation pulse with a beam size of several millimeters is irradiated to the specimen, each absorber inside the specimen absorbs light energy and generates a pulse of acoustic wave. (b) The photoacoustic wave propagates toward the surface and induces displacement at the top surface of the cover layer, at . (c) By adjusting the time delay between the excitation and the probe pulses, the 2D displacement maps are captured in a time sequence. Color bars: phase in radians. (d) By taking time derivative with the acquired displacement maps, the pressure maps are calculated. These maps visualize the expansion or propagation of pressure waves with time. Color bar: scaled pressure. Scale bars in (c)-(d): 2 mm.
Our experimental system employed a pump-and-probe configuration to capture temporal snapshots of the surface displacements induced by photoacoustic wave propagation (see supplementary material Section 1). An excitation laser pulse from a Nd:YAG laser (wavelength: 532 nm, pulse width: 8 ns, repetition rate: 20 Hz) is irradiated onto light-absorbing objects embedded in a host medium (Fig. 1(a)). The generated photoacoustic wave deforms the specimen surface at the depth (Fig. 1(b)) and further propagates to the top surface of the cover layer at , where it induces surface displacements. A probe pulse from a pulsed laser diode (PLD; wavelength: 905 nm, pulse width: 20 ns, repetition rate: 40 Hz) is used to measure the induced surface displacements. An off-axis holography system records the 2D interferogram between the probe pulse reflected from the top surface of the cover layer and the reference pulse. By applying the Hilbert transform to each interferogram, we obtain the complex-field map—i.e., amplitude and phase maps—of the interferogram. From the phase map , the surface displacement map can be calculated simply using the relation , where is the optical wavelength of the probe pulse.
The excitation beam had a 5 mm diameter and a fluence of 15 mJ/cm², adhering to the American National Standards Institute (ANSI) laser safety standards. The probe beam, with a diameter of 16 mm, covered a field of view of 10 × 10 mm² in the holographic imaging system. The optical resolution was set to 31 μm, approximately six times smaller than the typical photoacoustic wavelength (∼200 μm), providing sufficient spatial sampling bandwidth. This setup achieved spatial sampling with over 104,000 effective elements in each single-shot recording, far exceeding the 256–1024 elements typically used in conventional transducer arrays [10].
To capture the time evolution of the photoacoustic waves, we recorded the surface displacement maps by incrementally adjusting the probe delay for each excitation pulse (Fig. 1(c)). With a 50 ns interval over a 5 μs time span, we could sample acoustic frequencies up to 10 MHz and reconstruct the photoacoustic image to a depth of up to 5 mm. Although we measured the surface displacement induced by the acoustic wave, it is the acoustic pressure that satisfies the wave equation. Therefore, we obtained the pressure map (Fig. 1(d)) at first by taking time derivative of the displacement map as:
| (1) |
Here, is the acoustic impedance of the medium [12], [26]. As we shall explain below, we reconstructed the initial volumetric pressure image by spatio-temporally backpropagating these pressure waves measured at the specimen surface.
To minimize the effect of dynamic surface fluctuations, we employed a differential measurement technique, normalizing the complex-field maps recorded with and without the excitation pulse. This method allowed us to isolate the surface displacements induced solely by the photoacoustic wave (Fig. 1(c)). Since the probe pulse repetition rate was twice that of the excitation pulse, a single differential measurement could be made per each excitation laser pulse, enabling the acquisition of one wide-field displacement map every 0.05 s. However, during in vivo experiments, single displacement map was often insufficient for detecting weak photoacoustic waves. To enhance the phase detection sensitivity, we utilized coherent averaging of the complex-field maps, improving the SNR in proportion to the number of averaged maps. By typically averaging 20 displacement maps over 1 s, we achieved a displacement sensitivity of 0.5 nm, corresponding to a pressure sensitivity of approximately 15 kPa. This sensitivity level is comparable to that of the ultrasound transducer having a size similar to the optical lateral resolution [16].
2.2. Single-sheet multilayer backpropagation algorithm
The goal of photoacoustic imaging is to reconstruct the 3D spatial distribution of acoustic pressure at the time of excitation , known as the initial volumetric pressure image, , which reflects the positions and densities of molecules absorbing the optical excitation pulse. In the case of measuring the pressure on a flat surface, the initial pressure distribution can be reconstructed by backpropagating the acoustic waves using angular spectrum analysis [27], [28]. In this approach, the spatio-temporal spectrum of the acoustic waves is obtained by the Fourier transform of the surface pressure maps, , in both time and space (lateral). Each spectral component is then backpropagated according to its temporal frequency. The initial volumetric pressure image is reconstructed by superposing the backpropagated waves across the entire spatiotemporal spectrum [27], [28], [29]. While this reconstruction process is straightforward, it requires the recording of all time-sequential measurements, potentially limiting its application for imaging dynamic samples.
To overcome this limitation and enable rapid imaging, we have devised a reconstruction algorithm termed the single-sheet backpropagation (SSB) method, which backpropagates the 2D surface pressure map taken at each time delay into a 3D volume image. For each surface pressure map taken at a specific time , the lateral spatial spectrum is obtained by applying the Fourier transform with respect to lateral coordinates:
| (2) |
This spatial spectrum represents the amplitude of the acoustic wave having a lateral spatial wave vector . Let us first consider a backpropagation to the bottom surface of the cover layer at . Since the photoacoustic wave is a pulse, the wave packet having a specific lateral wave vector is composed of many plane waves with different temporal frequencies and, thus, with different longitudinal wave vector component , called the propagation constant (Fig. 2(a)). Here, and are related by the dispersion relation via the acoustic velocity of the cover layer:
| (3) |
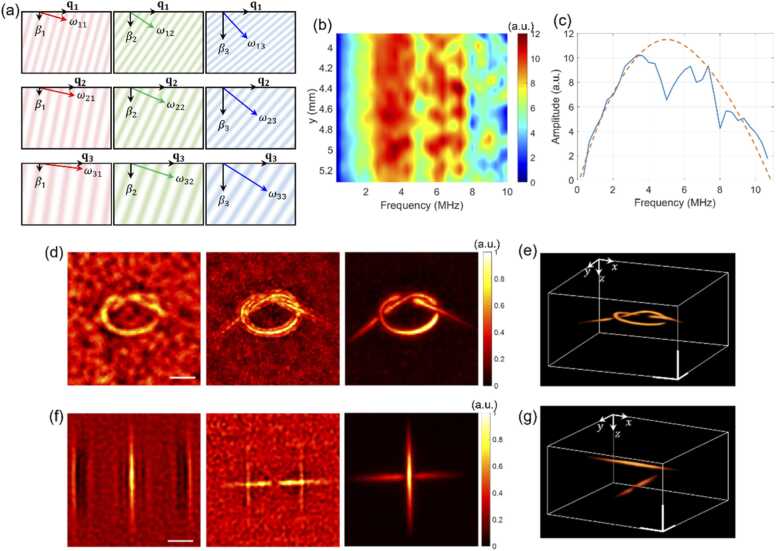
Fig. 2.
The single-sheet backpropagation (SSB) method for 3D reconstruction from a single surface pressure map. (a) Each row illustrates that the wave having a same lateral spatial frequency can be decomposed with multiple plane waves having different propagation constant ’s (different columns). (b) Temporal frequency spectra of surface pressure maps obtained with a line-shaped PET fiber embedded in PDMS. (c) The spectrum (blue solid line) averaged along the direction (-direction) of the PET fiber and fitted with a parabola (red dotted curve). (d) Maximum intensity projection images of a knot-shaped phantom reconstructed using 1, 3, and 20 surface pressure maps with the proposed SSB method, and (e) a 3D view reconstructed using 20 maps. (f) For objects located crosswise with a depth difference of 1 mm, a depth-selective thin-volume image was reconstructed by using a single pressure map (first, second) taken at different times, and the full-volume image by using 40 pressure maps (third). (g) The 3D view reconstructed using 40 pressure maps. Scale bars in (d)-(g): 1 mm.
Then, each plane wave constituting the wave packet of a same lateral wave vector can be backpropagated spatially to the depth with various and temporally to the time with :
| (4) |
Here, is the intensity of the temporal spectrum of the photoacoustic wave, calibrated from a prior measurement (Fig. 2(b) and (c)). Since the complex amplitude of each acoustic plane wave in the right-hand side of Eq. 4 evolves over time with its temporal frequency , we obtain the wave at a previous time by backpropagating it for a time duration of . The main assumption in Eq. 4 is that the calibrated spectrum remains the same or similar for different target specimens in the same medium.
To find the initial volumetric pressure image within the medium, the acoustic wave of each lateral wave vector should be propagated further back to a depth within the medium:
| (5) |
Here, is the propagation constant in the host medium of the specimen. Since the temporal frequency of a plane wave does not change with propagation, and the lateral spatial frequency remains constant due to continuity at the boundary, is determined by the acoustic velocity in the medium and :
| (6) |
Finally, the initial volumetric pressure image is calculated by taking the inverse Fourier transform of the lateral spectrum obtained by backpropagating in time to the moment of in Eq. 5:
| (7) |
The SSB algorithm enables the reconstruction with a single surface pressure map taken at any specific time . This relieves the need for taking a full set of pressure maps captured in a time series, making it more suitable for imaging dynamic biological processes. It is noteworthy that the reconstruction finds the initial pressure map distribution around a specific depth range associated with because only the photoacoustic waves captured at the surface can be involved in the reconstruction process. Waves that have not yet reached the surface or have already passed away at the time are not involved in the reconstruction (see supplementary material Section 2 for detailed mathematical description). We can increase the imaging volume by the coherent superposition of multiple images backpropagated from surface pressure maps taken at other time delays, which also leads to the increased SNR at the overlapped region (see supplementary movie S1).
Supplementary material related to this article can be found online at doi:10.1016/j.pacs.2025.100753.
The following is the Supplementary material related to this article Video S1.
Video S1
Fig. 2 illustrates the concept of the proposed SSB method. Fig. 2(a) shows the backpropagation of each wave packet of a lateral wave vector constituting the acoustic wave captured at a specific time . The images in each row depict the backpropagation of waves having the same , but with different and . In the figure, represents the temporal angular frequency of the plane wave with -th and -th . The initial pressure distribution is reconstructed by reversing the time evolution of all these plane waves from the captured moment back to the time of excitation. During time reversal, the phase of each plane wave evolves according to its temporal frequency. The spectrum of the generated photoacoustic waves was estimated by sequentially measuring a set of photoacoustic waves emanating from a line-shaped object. Fig. 2(b) shows the temporal spectra calculated along the object's length (see supplementary material Section 3). The spectrum in Fig. 2(c) (blue solid curve) was obtained by averaging along the vertical direction, and the red dotted curve shows the curve fitting.
Fig. 2(d) shows normalized maximum intensity projection images of a knot-shaped object, reconstructed using 1, 3, and 20 surface pressure maps acquired at 50 ns intervals from 1.35 μs to 2.30 μs. The 3D view of the object, reconstructed with 20 maps, is shown in Fig. 2(e). Even with a single pressure map, the target object could be reconstructed, though the SNR was improved with additional maps. To validate the tomographic reconstruction capability, a phantom consisting of two line-shaped objects with a 1 mm depth separation was imaged. The first two sub-images in Fig. 2(f), reconstructed from two single surface pressure maps taken at different time delays, separately visualized the upper and lower objects. The third image, reconstructed with 40 maps over a 2 μs time span (from 2.8 μs to 4.75 μs), shows both objects. Its 3D view is presented in Fig. 2(g), confirming that the reconstruction depth can be expanded by increasing the number of pressure maps used. Prior to reconstruction, the power spectral density (PSD) profile of the photoacoustic wave is acquired for each sample. Although the PSD may exhibit slight spatial variation, this does not significantly affect reconstruction quality. Additionally, the acoustic velocity—potentially varying between specimens—is adaptively estimated by maximizing image sharpness in the post processing. Although the SSB method enables rapid 3D reconstruction from single pressure maps, it inherently suffers from limited lateral resolution and depth-related artifacts due to restricted angular information. However, as shown in our experiments (Fig. 2, supplementary material Section 4, and supplementary movie S2), both resolution and artifact suppression improve markedly as more pressure maps are coherently accumulated over time delays.
Supplementary material related to this article can be found online at doi:10.1016/j.pacs.2025.100753.
The following is the Supplementary material related to this article Video S2.
Video S2
2.3. PAT in scattering media by coherent averaging and adaptive backpropagation
The proposed method was experimentally verified by imaging the objects embedded within an optically thick scattering medium. Several pieces of black polyethylene terephthalate (PET) fibers, each with a diameter of 200 μm, were arranged in the form of ‘AOL’ alphabet characters (top of Fig. 3(a)). The PDMS medium was prepared by mixing silicone and curing agent in a 10:1 ratio and adding 0.3 % by weight of TiO2 particles. Due to multiple light scattering in the medium, the embedded PET fibers were not optically visible (bottom of Fig. 3(a)). Since the size of the ‘AOL’ object was larger than the size of the excitation beam spot, four sub-regions were individually imaged and stitched together after reconstruction. The total imaging area is indicated by the green box in Fig. 3(a).
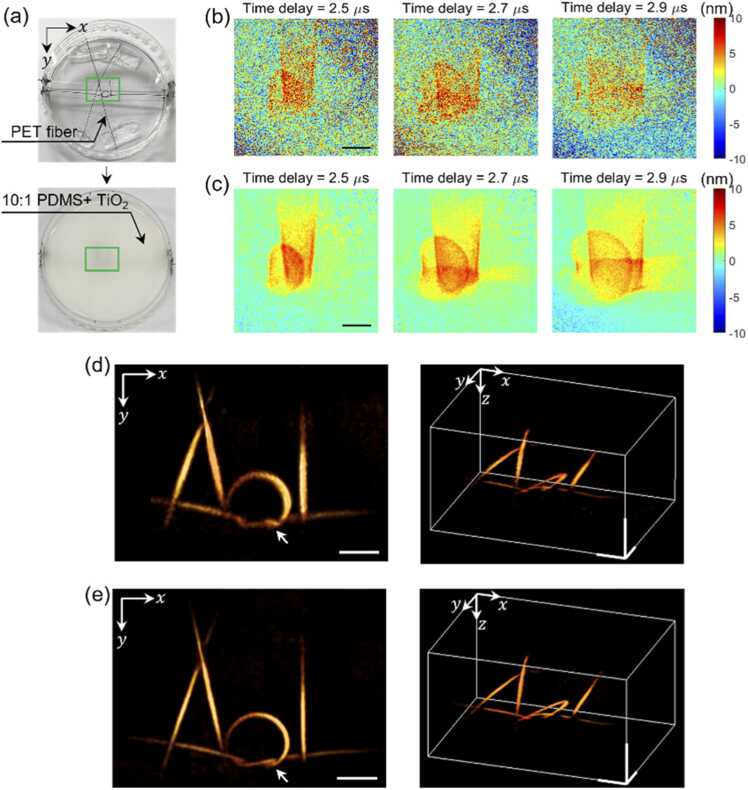
Fig. 3.
Experimental demonstration of coherent averaging and adaptive backpropagation. (a) An ‘AOL’ shape structure was made with a black PET fiber of 200 μm diameter (top), which was embedded within an optically opaque PDMS made by mixing with 0.3 % weight TiO2 particles (bottom). (b) The 2D displacement maps captured at the PDMS surface for different time delays. (c) The map coherently averaged with 20 displacement maps, after compensating for the overall phase drift. (d) The 3D image reconstructed by using the acoustic velocity of 1076 m/s, a literature value for the 10:1 ratio PDMS. (e) The image reconstructed by applying adaptive backpropagation algorithm for finding the proper acoustic velocity. At the velocity of 1045 m/s, we could reconstruct the image with optimal contrast and resolution. Scale bars in (b)-(e): 2 mm.
Fig. 3(b) shows a few representative time-evolving displacement maps selected from a set of 51 time delay captured between 2.0 μs to 4.5 μs. Photoacoustic waves with nanometer-scale displacement traversing the surface were identified; however, there was substantial noise. To reduce the noise, 50 complex-field maps were captured at each time delay and coherently averaged after compensating for the overall phase drift that occurred during the multiple measurements (see supplementary material Section 4). This increased the SNR from 6 to 12 dB (Fig. 3(c)). The achieved phase sensitivity was 6.9 mrad, corresponding to a displacement amplitude of 0.5 nm. The SNR increased with the number of images used for averaging but saturated at around 20 images. Therefore, 20 displacement maps were recorded at each time delay in all the photoacoustic imaging results presented in this study.
In backpropagation, the proper setting of the acoustic velocity is critical for achieving appreciable resolution and contrast in reconstruction [30], [31], [32], [33]. The velocity depends on the type of medium and the frequency through the dispersion relation [34]. For in vivo experiments, determining the acoustic velocity is challenging because the medium is a heterogeneous mixture of various biomolecules. To address this, we developed an adaptive backpropagation algorithm to find the acoustic velocities in situ. Specifically, we expanded the velocity in the medium to the first order of :
| (8) |
We then find the coefficients in such a way as to maximize the image sharpness metric defined as [35], [36], [37]:
| (9) |
The choice of the metric is somewhat flexible, depending on factors such as the structure of the object and the quality of experimental data.
The reconstructed image was somewhat blurred (Fig. 3(d)) when we used the acoustic velocity of 1076 m/s, an estimated value from the literature for PDMS with a 10:1 ratio [38]. After applying the adaptive backpropagation algorithm, the acoustic velocity was determined to be 1045 m/s. The reconstructed image shown in Fig. 3(e) visualizes the fine structure, particularly near the knot part indicated by a white arrow. The measured width of the 200 μm diameter PET fiber was 262 μm with a velocity of 1076 m/s, but it was reduced to 204 μm with 1045 m/s. It should be noted that, due to the round shape of the fiber, only a small portion of its cross-section contributed to the photoacoustic wave generation.
The velocity estimated by the adaptive backpropagation algorithm was independently verified using a simple trigonometric method. Specifically, by measuring the distance between counter-propagating photoacoustic waves emanating from a line-like object, the velocity was calculated to be 1044 m/s, which is close to the in situ optimized velocity (see supplementary material Section 5). We also found that played a more important role than in Eq. 8, suggesting that the effect of dispersion was not significant. When applying the adaptive backpropagation to a multilayer sample with a cover layer, the algorithm has been designed to determine the optimal values of and in each medium.
2.4. Multilayer acoustic backpropagation for cover-layered phantoms
As mentioned earlier, we introduced a cover layer to smooth out the rough and dynamically fluctuating surface of the specimen, enabling precise optical mapping of photoacoustic waves. Among various materials considered—such as acrylic, glass, and quartz—we selected a PDMS plate for the cover layer due to its biocompatibility, mechanical flexibility [24], [25], and proper acoustic impedance matching. In our experiment, we placed two pencil leads with a diameter of 300 μm in a cross pattern inside a petri dish filled with deionized water (Fig. 4(a)). The dynamic fluctuations of the water surface made the photoacoustic wave mapping challenging, but by placing a 3.44-mm-thick PDMS block on top of the water-filled dish, we were able to stabilize the surface and capture the displacement maps (Fig. 4(b)).
Fig. 4.
Experimental demonstration of the multilayer acoustic backpropagation algorithm. (a) Two 300 μm diameter pencil leads were placed orthogonal to each other in a petri dish at a depth difference of about 1 mm. The dish was filled with DI water and covered with a 3.44-mm-thick PDMS block. (b) The hologram taken at the top surface of the block (left) and the extracted surface displacement map (right). (c) Same as (b), but taken at the bottom surface of the PDMS block. The white and black scale bars in (b)-(c): 200 μm and 2 mm, respectively. (d) Sharpness metric calculated with various acoustic velocities and . (e) The 3D image reconstructed without accounting for the propagation angle-dependent attenuation due to acoustic impedance mismatch. (f) The same image but reconstructed after compensating the propagation angle-dependent attenuation. Scale bars in (e)-(f): 2 mm.
The photoacoustic waves were recorded at the top surface of the PDMS cover layer rather than the bottom. This preference is due to the higher contrast in the holograms at the top surface (Fig. 4(b)), which translates to enhanced phase detection sensitivity. The optical reflectivity at the top surface (air vs. PDMS) is 48 times larger than that at the bottom surface (PDMS vs. water), making the top surface more suitable for optical measurement (Fig. 4(c)). Additionally, the irregular surface of the specimen at the bottom negatively affected the optical reflectivity distribution. Despite all these benefits, measurements at the top surface required multilayer backpropagation for accurate image reconstruction, as discussed earlier.
Fig. 4(e) presents a 3D image reconstructed using our adaptive multilayer backpropagation algorithm, based on data acquired with a 30 time delay set captured from 4.90 μs to 6.35 μs. The acoustic velocities were optimized based on the sharpness metric in Fig. 4(d), where = 1020 m/s in the cover layer and = 1541 m/s in DI water yielded the highest sharpness. The reconstructed 3D image clearly visualized the two pencil leads; however, slight blurring remained even after correcting for the acoustic velocities. This was attributed to the acoustic Fresnel reflections at the cover-specimen boundary. Due to the impedance mismatch, waves with higher propagation angles experienced more pronounced Fresnel reflection, resulting in increased attenuation. To address this, a correction factor was applied to compensate for the angle-dependent attenuation, the transmissivity of an acoustic plane wave depending on its propagation angle. As shown in Fig. 4(f), this adjustment significantly improved the image sharpness, reducing the reconstructed diameter of the pencil lead from 349 μm to 232 μm.
2.5. In vivo vasculature imaging of mouse hindlimb and chicken embryo
To validate the utility of the proposed all-optical photoacoustic imaging method, we conducted vasculature imaging of a living mouse. We prepared a 5-week-old nude mouse (Fig. 5(a)) and placed a 2.28-mm-thick PDMS block on its hindlimb, using ultrasound gel—commonly employed in photoacoustic imaging—to fill out the air gap between the skin and the cover layer. The measurement was made at the top surface of the PDMS block. Our adaptive reconstruction algorithm identified acoustic velocities of 1030 m/s for the cover layer and 1540 m/s for the mouse tissues.
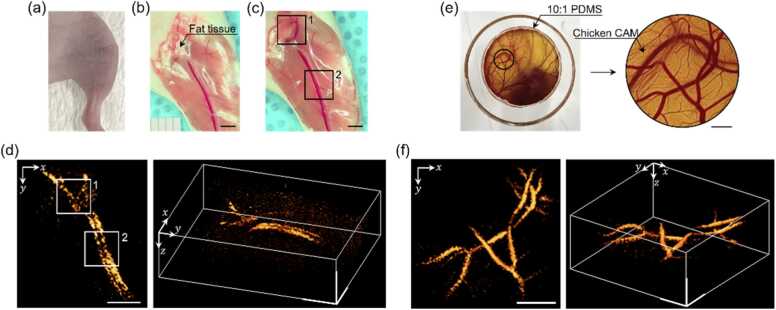
Fig. 5.
In vivo imaging of vasculatures in mouse hindlimb leg and chicken embryo’s CAM. (a) A 5-week-old nude mouse placed in the sample arm of the all-optical PAT system for in vivo imaging through the intact skin. (b) A photograph of the blood vessels in the hindlimb, taken after imaging session, which was used as ground truth. (c) A photograph taken after further removing the fat tissue revealing vascular structures underneath (area 1). Two vessels of artery and vein are distinctly visible in area 2. (d) The 3D image of the mouse hindlimb reconstructed with the multilayer backpropagation method. Scale bars in (b)-(d): 2 mm. (e) A photograph and its enlarged image of the blood vessels formed in the CAM of chicken embryo incubated for 11 days. Scale bar: 1 mm. (f) Reconstructed volumetric vasculature image of the CAM. Scale bar: 2 mm.
Fig. 5(d) presents the reconstructed volumetric image of the vasculature based on the data set acquired with 30 time delays, from 2.50 μs to 3.95 μs. We successfully visualized the main blood vessels distributed at depths ranging from 1.2 to 2 mm beneath the skin. The figure clearly shows two major blood vessels running parallel to each other, along with additional vascular features in the upper-side of the image. To validate the imaging results, we dissected the skin of the mouse immediately after the photoacoustic imaging. Fig. 5(b) reveals that fat tissues were situated beneath the skin layer, overlaying the upper part of the main blood vessels. After removing the fat tissues, we could observe the specific blood vessels designated as area 1 in Fig. 5(c). In imaging area 2, we observed that the blood vessels consisted of the femoral artery and vein. The photoacoustic image in Fig. 5(d) was in excellent agreement with the anatomical findings in Fig. 5(b) and (c). Interestingly, the photoacoustic image was able to visualize the vasculature even beneath the fat tissues, which were optically too opaque to reveal any blood vessels in a photograph. These results validate the accuracy and utility of our approach for in vivo applications.
As another application, we performed in vivo blood vessel imaging on a chicken embryo’s chorioallantoic membrane (CAM). Fig. 5(e) shows a photograph of an 11-day-old chicken embryo. Zooming into the region of interest, indicated by the black circle in the left-side image of Fig. 5(e), reveals well-developed blood vessels on the CAM. Measuring surface displacement in this environment was particularly challenging due to the dynamically fluctuating surface, which was susceptible to external vibrations and biological factors such as heartbeats. This issue was resolved by placing a 2.42-mm-thick PDMS cover layer on top of the CAM. A gap of approximately 1–2 mm between the cover layer and the CAM surface was filled with normal saline to prevent the blood vessels from rupturing due to osmotic pressure. We adaptively identified acoustic velocities of 1035 m/s in the cover layer and 1560 m/s in the normal saline, based on data acquired with a 52 time delay set from 2.45 μs to 5.0 μs. The reconstructed image in Fig. 5(f) shows the complex vasculature of the CAM with high contrast, which closely matches the photographic evidence in Fig. 5(e).
3. Discussion
In this study, we proposed a photoacoustic tomography technique designed to detect acoustic waves on rough and dynamic tissue surfaces with high sensitivity and speed. Although direct optical measurement on such surfaces remains difficult, we addressed this limitation by introducing a soft and optically smooth cover layer. This approach enabled stable and reliable signal acquisition even on uneven or dynamic biological tissue surfaces. The cover layer effectively mitigates issues caused by surface roughness while allowing optical access to the excitation and detection processes. To further improve sensitivity, we applied coherent averaging of phase maps, which made in vivo imaging feasible. The proposed method achieved surface profiling across a 10 × 10 mm² field of view with a spatial resolution of 31 µm and 0.5 nm vertical displacement sensitivity, enabling surface pressure mapping with sensitivity comparable to that of an ultrasound transducer of a similar size with the optical resolution. This system provides approximately 105 sampling elements, two orders of magnitude more than conventional ultrasound transducer arrays. Moreover, the system captures one full-field image, including coherent averaging, in just one second, offering a sampling rate of 105 per second—over ten times faster than beam-scanning methods, assuming the same excitation laser repetition rate [16].
Additionally, we have devised a new 3D reconstruction method named single-sheet backpropagation (SSB). Traditional backpropagation requires measuring the full-time span of photoacoustic wave propagations to initiate the reconstruction. In contrast, our method allows image reconstruction from each temporal snapshot. While the imaging depth range depends on the time span, our approach is better suited for imaging dynamic samples especially when investigating specific depth ranges. We further developed methods to identify acoustic velocities within different media during post-processing and to correct for angle-dependent attenuation caused by impedance mismatch between layers, optimizing the reconstruction contrast and resolution.
One of the key features in this study is the application of a soft PDMS cover layer that renders the rough tissue surface optically smooth. While we also experimented with acrylic, glass, and quartz plates, the PDMS cover layer produced the best reconstruction images. This is because the other plates had higher acoustic impedance than the tissues, causing total internal reflection (TIR) to the high-angle photoacoustic waves and limiting their propagation into the cover layer. Experimentally, some interesting phenomena related to TIR have been observed with the cover layers of acrylic, glass and quartz, thus, systematic analysis is being prepared. Additionally, the higher acoustic velocity in these plates led to repeated reflections of the photoacoustic waves within the cover layer, producing duplicated and overlapped images. The proposed use of a PDMS cover layer not only improves optical smoothness and acoustic coupling but also provides practical advantages over conventional transducer-based approaches. In traditional ultrasound systems, acoustic contact is typically achieved through direct coupling with a bulky transducer array or by immersing the specimen in a water tank. In contrast, our method requires only a soft, optically smooth film gently placed on the tissue surface, while measurements are performed remotely through air via optical interferometry. As a result, physical interference with the specimen is minimal, and the setup imposes far less discomfort or constraint. Furthermore, the optical transparency of the PDMS layer allows unobstructed delivery of the excitation beam to the target. It is also noteworthy that perfect optical flatness is not required; as long as the surface is optically smooth within the coherence length of the probe beam (∼100 μm in our system), reliable holographic detection can be achieved.
Looking ahead, several improvements could further enhance the proposed photoacoustic tomography technique. Although object motion can introduce artifacts during in vivo imaging, we minimized these effects in the current study through temporary measures such as anesthesia for mice. However, these are not fundamental solutions. A more robust approach would be to employ a high-repetition-rate excitation laser [16], [17], which would dramatically shorten acquisition times and thereby reduce susceptibility to motion. Together with the SSB method, these strategies could significantly expand the technique’s utility for real-time in vivo imaging and dynamic tissue monitoring. In addition, advancements in adaptive algorithms for reconstructing images in more complex and heterogeneous media could allow for higher accuracy and deeper imaging depth in challenging environments, such as through-skull imaging. This system can also be optimized for broader biomedical applications, such as functional imaging to assess tissue oxygenation, molecular imaging, or tumor detection with high optical contrast. Additionally, the technique has potential applications beyond biomedicine, such as in industrial non-destructive testing (NDT), where it could be used for detecting flaws in semiconductor wafers, inspecting civil structures, or remotely monitoring the integrity of high-voltage electrical equipment [39]. With further refinement and expansion, the proposed all-optical PAT system could become a versatile tool across various fields, offering high-resolution imaging with unprecedented speed and sensitivity.
4. Methods
4.1. Experimental setup
A Nd:YAG laser (Quantel, Ultra 50, France) with a wavelength of 532 nm and a pulse width of 8 ns was used for photoacoustic excitation. Köhler illumination was employed to uniformly irradiate the excitation beam onto the target objects embedded in the specimen medium [40], [41]. To probe the surface displacement, a fiber-pigtailed pulsed diode laser (PLD; LASER COMPONENTS, 905D2S3J09FP-40, Germany), with a wavelength of 905 nm and a pulse width of 20 ns, was used. An off-axis holography system was implemented by introducing a tilted reference mirror. Each interferogram, called a digital hologram, was captured by a sCMOS camera (scientific complementary metal-oxide-semiconductor camera; Andor, Zyla 4.2, Japan) with 1024 × 1024 elements and a pixel size of 6.5 μm. The captured hologram was Fourier transformed to obtain its spatial frequency spectrum, and one of the twin cross-correlation parts of the spectrum was spatially filtered and re-centered. Finally, the complex field recorded in the hologram was retrieved by taking the inverse Fourier transform. By extracting the phase part of the complex field and multiplying it by the optical wavelength of the probe beam, the 2D surface profile of the specimen was obtained. The net surface displacement map, induced solely by the photoacoustic waves, was extracted by taking the difference between the maps captured with and without the excitation beam. The phase change of 2π radians was treated as the displacement corresponding to half the wavelength of the probe beam, accounting for its round trip.
The PLD was operated at 40 Hz to sequentially capture holograms with and without excitation. The sCMOS camera was synchronized to the trigger of the Nd:YAG laser, which was operating at 20 Hz. In our experiment, the probe delay was incremented in 50 ns steps, providing an axial resolution of approximately 77 μm, assuming an acoustic velocity of 1540 m/s. While the axial resolution is determined by the delay step size, the total number of delay steps defines the acquisition time window and thus the imaging depth range [42].
4.2. Animal preparation
4.2.1. Nude mouse
A 5-week-old nude mouse was prepared for small animal vascular imaging. To minimize mouse movement during the experiment, the mouse was anesthetized using an intraperitoneal injection of Zoletil/Xylazine at a dose of 60/10 mg/kg body weight. Then the animal was placed on a heating plate for imaging. After the experiment, the mouse was returned to its cage and placed on another heating pad to aid recovery. A light-dark cycle of 12 h was established, and conditions were maintained to ensure a stable body temperature. The animal experiments followed the protocol approved by the Institutional Animal Care and Use Committee (IACUC) of Gwangju Institute of Science and Technology (GIST).
4.2.2. Chicken embryo
To image the blood vessels of the chicken embryo's CAM, fertilized eggs were purchased in a market and incubated for 11 days in an incubator. The temperature and humidity within the incubator were maintained at 37°C and 60 %, respectively. Following incubation, the chicken embryo exhibited a heart rate of 126 beats per minute at room temperature (25°C). To minimize the movement caused by heartbeats, the embryos were placed in a refrigerator of 5°C for 30 min. This decreased the heart rate down to 60 beats and slowed down the body movement. To expose the CAM, a small section of the outer shell and the inner membrane of the air cell were removed, and a PDMS cover layer was positioned atop the remaining outer shell. The gap between the outer shell and the cover layer was filled with normal saline to prevent blood vessels from rupturing due to osmotic pressure.
CRediT authorship contribution statement
Wonshik Choi: Writing – review & editing, Validation, Methodology, Funding acquisition. Byeongha Lee: Writing – review & editing, Validation, Methodology, Funding acquisition, Conceptualization. Euiheon Chung: Resources, Funding acquisition. Taeil Yoon: Writing – original draft, Visualization, Validation, Software, Project administration, Investigation, Formal analysis, Data curation. Hakseok Ko: Investigation, Data curation. Jeongmyo Im: Resources.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We would like to express our gratitude to Dr. Soongho Park for initiating this study and to Hansol Lee for conducting the proof-of-concept study of the acoustic backpropagation. This work was supported by National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. RS-2024–00461205, RS-2024–00442818, RS-2023–00302281) and the Technology Innovation Program (20021979, Development of health monitoring system for gas-insulated switchgears by using optical sensing modalities) funded by the Ministry of Trade, Industry and Energy (MOTIE, Republic of Korea).
Biographies

Taeil Yoon is a post-doctoral researcher at the Korea University, Korea. He received his bachelor’s degree in Electrical and Electronics Engineering from Chung-ang University in 2017 and his doctoral degree in Electrical Engineering and Computer Science from the Gwangju Institute of Science and Technology (GIST) in 2024. His research interests include photoacoustic tomography and optical coherence tomography.

Hakseok Ko is a post-doctoral researcher at the Korea Advanced Institute of Science and Technology (KAIST), Korea. He received his bachelor’s, master’s, and doctoral degrees in Physics from Korea University in 2013, 2015, and 2020, respectively. His research interests include optical imaging.

Jeongmyo Im is a Ph.D. candidate at the Gwangju Institute of Science and Technology (GIST), Korea. She received her bachelor’s degree in Biomedical Engineering at Konkuk University in 2021. Her research interests include laser speckle contrast imaging.

Euiheon Chung is a professor in the Department of Biomedical Science and Engineering at the Gwangju Institute of Science and Technology (GIST), Korea. He received his bachelor’s and master’s degrees in Aerospace Engineering with a minor in Physics from the Korea Advanced Institute of Science and Technology (KAIST) in 1996 and 1998, and a doctoral degree in Medical Engineering from the Harvard-MIT Division of Health Sciences and Technology 2007. His research focuses on developing translational neurophotonic technologies to address unmet clinical needs using biomedical engineering approaches.

Wonshik Choi is a professor in the Department of Physics at Korea University, Korea. He received his bachelor’s, master’s, and doctoral degrees in Physics from Seoul National University in 1997, 1999, and 2004, respectively. His research focuses on developing super-depth optical methodologies for imaging, sensing, and manipulating light in scattering media.

Byeongha Lee is a professor in the Department of Electrical Engineering and Computer Science at Gwangju Institute of Science and Technology (GIST), Korea. He received his bachelor’s and master’s degrees in Physics from Seoul National University in 1984 and 1989, respectively, and his doctoral degree in Physics from the University of Colorado at Boulder in 1996. His research focuses on developing novel optical system for sensing and imaging. Optical coherence tomography and photoacoustic imaging are in his main fields. Highlight is seeing acoustic waves with optics, enabling non-contact photoacoustic imaging.
Contributor Information
Wonshik Choi, Email: wonshik@korea.ac.kr.
Byeongha Lee, Email: leebh@gist.ac.kr.
Data availability
Data will be made available on request.
References
- 1.Wang X., Xu Y., Xu M., Yokoo S., Fry E.S., Wang L.V. Photoacoustic tomography of biological tissues with high cross-section resolution: Reconstruction and experiment. Med. Phys. 2002;29:2799–2805. doi: 10.1118/1.1521720. [DOI] [PubMed] [Google Scholar]
- 2.Wang L.V., Hu S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science. 2012;335:1458–1462. doi: 10.1126/science.1216210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hoelen C.G.A., de Mul F.F.M., Pongers R., Dekker A. Three-dimensional photoacoustic imaging of blood vessels in tissue. Opt. Lett. 1998;23:648. doi: 10.1364/OL.23.000648. [DOI] [PubMed] [Google Scholar]
- 4.Greening G.J., Istfan R., Higgins L.M., Balachandran K., Roblyer D., Pierce M.C., Muldoon T.J. Characterization of thin poly(dimethylsiloxane)-based tissue-simulating phantoms with tunable reduced scattering and absorption coefficients at visible and near-infrared wavelengths. J. Biomed. Opt. 2014;19 doi: 10.1117/1.JBO.19.11.115002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Park E.-Y., Park S., Lee H., Kang M., Kim C., Kim J. Simultaneous Dual-Modal Multispectral Photoacoustic and Ultrasound Macroscopy for Three-Dimensional Whole-Body Imaging of Small Animals. Photonics. 2021;8:13. doi: 10.3390/photonics8010013. [DOI] [Google Scholar]
- 6.Yao J., Wang L.V. Photoacoustic tomography: fundamentals, advances and prospects. Contrast Media Mol. 2011;6:332–345. doi: 10.1002/cmmi.443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xiang L., Wang B., Ji L., Jiang H. 4-D Photoacoustic Tomography. Sci. Rep. 2013;3:1113. doi: 10.1038/srep01113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Abdolali A., Barati Sedeh H., Fakheri M.H., Shen C., Sun F. Breaking the acoustic diffraction limit with an arbitrary shape acoustic magnifying lens. Sci. Rep. 2021;11 doi: 10.1038/s41598-021-92297-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Patricio Rodrigues E., Francisco de Oliveira T., Yassunori Matuda M., Buiochi F. Development of a 2-D Array Ultrasonic Transducer for 3-D Imaging of Objects Immersed in Water. Sensors. 2021;21:3501. doi: 10.3390/s21103501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lin L., Hu P., Tong X., Na S., Cao R., Yuan X., Garrett D.C., Shi J., Maslov K., Wang L.V. High-speed three-dimensional photoacoustic computed tomography for preclinical research and clinical translation. Nat. Commun. 2021;12:882. doi: 10.1038/s41467-021-21232-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li L., Zhu L., Shen Y., Wang L.V. Multiview Hilbert transformation in full-ring transducer array-based photoacoustic computed tomography. J. Biomed. Opt. 2017;22 doi: 10.1117/1.JBO.22.7.076017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Speirs R.W., Bishop A.I. Photoacoustic tomography using a Michelson interferometer with quadrature phase detection. Appl. Phys. Lett. 2013;103 doi: 10.1063/1.4816427. [DOI] [Google Scholar]
- 13.Eom J., Park S.J., Lee B.H. Noncontact photoacoustic tomography of in vivo chicken chorioallantoic membrane based on all-fiber heterodyne interferometry. J. Biomed. Opt. 2015;20 doi: 10.1117/1.JBO.20.10.106007. [DOI] [PubMed] [Google Scholar]
- 14.Zhang X., Fincke J.R., Wynn C.M., Johnson M.R., Haupt R.W., Anthony B.W. Full noncontact laser ultrasound: first human data. Light Sci. Appl. 2019;8:119. doi: 10.1038/s41377-019-0229-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lengenfelder B., Mehari F., Hohmann M., Heinlein M., Chelales E., Waldner M.J., Klämpfl F., Zalevsky Z., Schmidt M. Remote photoacoustic sensing using speckle-analysis. Sci. Rep. 2019;9:1057. doi: 10.1038/s41598-018-38446-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jathoul A.P., Laufer J., Ogunlade O., Treeby B., Cox B., Zhang E., Johnson P., Pizzey A.R., Philip B., Marafioti T., Lythgoe M.F., Pedley R.B., Pule M.A., Beard P. Deep in vivo photoacoustic imaging of mammalian tissues using a tyrosinase-based genetic reporter. Nat. Photon. 2015;9:239–246. doi: 10.1038/nphoton.2015.22. [DOI] [Google Scholar]
- 17.Huynh N.T., Zhang E., Francies O., Kuklis F., Allen T., Zhu J., Abeyakoon O., Lucka F., Betcke M., Jaros J., Arridge S., Cox B., Plumb A.A., Beard P. A fast all-optical 3D photoacoustic scanner for clinical vascular imaging. Nat. Biomed. Eng. 2024;9:638–655. doi: 10.1038/s41551-024-01247-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nuster R., Zangerl G., Haltmeier M., Paltauf G. Full field detection in photoacoustic tomography. Opt. Express. 2010;18:6288. doi: 10.1364/OE.18.006288. [DOI] [PubMed] [Google Scholar]
- 19.Nuster R., Slezak P., Paltauf G. High resolution three-dimensional photoacoustic tomography with CCD-camera based ultrasound detection. Biomed. Opt. Express. 2014;5:2635. doi: 10.1364/BOE.5.002635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Balogun O., Regez B., Zhang H.F., Krishnaswamy S. Real-time full-field photoacoustic imaging using an ultrasonic camera. J. Biomed. Opt. 2010;15:1. doi: 10.1117/1.3420079. [DOI] [PubMed] [Google Scholar]
- 21.Buj C., Horstmann J., Münter M., Brinkmann R. Speckle-based off-axis holographic detection for non-contact photoacoustic tomography. Curr. Dir. Biomed. Eng. 2015;1:356–360. doi: 10.1515/cdbme-2015-0088. [DOI] [Google Scholar]
- 22.Buj C., Münter M., Schmarbeck B., Horstmann J., Hüttmann G., Brinkmann R. Noncontact holographic detection for photoacoustic tomography. J. Biomed. Opt. 2017;22:1. doi: 10.1117/1.JBO.22.10.106007. [DOI] [PubMed] [Google Scholar]
- 23.Payne B.P., Venugopalan V., Mikić B.B., Nishioka N.S. Optoacoustic tomography using time-resolved interferometric detection of surface displacement. J. Biomed. Opt. 2003;8:273. doi: 10.1117/1.1559727. [DOI] [PubMed] [Google Scholar]
- 24.Li Y.-Q., Zhu W.-B., Yu X.-G., Huang P., Fu S.-Y., Hu N., Liao K. Multifunctional Wearable Device Based on Flexible and Conductive Carbon Sponge/Polydimethylsiloxane Composite. ACS Appl. Mater. Interfaces. 2016;8:33189–33196. doi: 10.1021/acsami.6b11196. [DOI] [PubMed] [Google Scholar]
- 25.Wang L., Dou W., Chen J., Lu K., Zhang F., Abdulaziz M., Su W., Li A., Xu C., Sun Y. A CNT-PDMS wearable device for simultaneous measurement of wrist pulse pressure and cardiac electrical activity. Materials Science Engineering C. 2020;117 doi: 10.1016/j.msec.2020.111345. [DOI] [PubMed] [Google Scholar]
- 26.Paltauf G., Schmidt-Kloiber H., Frenz M. Photoacoustic waves excited in liquids by fiber-transmitted laser pulses. J. Acoust. Soc. Am. 1998;104:890–897. doi: 10.1121/1.423334. [DOI] [Google Scholar]
- 27.Schoonover R.W., Anastasio M.A. Image reconstruction in photoacoustic tomography involving layered acoustic media. J. Opt. Soc. Am. A. 2011;28:1114. doi: 10.1364/JOSAA.28.001114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Stepinski T. An Implementation of Synthetic Aperture Focusing Technique in Frequency Domain. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2007;54:1399–1408. doi: 10.1109/TUFFC.2007.400. [DOI] [PubMed] [Google Scholar]
- 29.Köstli K.P., Frenz M., Bebie H., Weber H.P. Temporal backward projection of optoacoustic pressure transients using Fourier transform methods. Phys. Med. Biol. 2001;46:1863–1872. doi: 10.1088/0031-9155/46/7/309. [DOI] [PubMed] [Google Scholar]
- 30.Anderson M.E., McKeag M.S., Trahey G.E. The impact of sound speed errors on medical ultrasound imaging. J. Acoust. Soc. Am. 2000;107:3540–3548. doi: 10.1121/1.429422. [DOI] [PubMed] [Google Scholar]
- 31.Napolitano D., Chou C.-H., McLaughlin G., Ji T.-L., Mo L., DeBusschere D., Steins R. Sound speed correction in ultrasound imaging. Ultrasonics. 2006;44:e43–e46. doi: 10.1016/j.ultras.2006.06.061. [DOI] [PubMed] [Google Scholar]
- 32.Zangerl G., Haltmeier M., Nguyen L.V., Nuster R. Full Field Inversion in Photoacoustic Tomography with Variable Sound Speed. Appl. Sci. 2019;9:1563. doi: 10.3390/app9081563. [DOI] [Google Scholar]
- 33.Jeon S., Choi W., Park B., Kim C. A Deep Learning-Based Model That Reduces Speed of Sound Aberrations for Improved In Vivo Photoacoustic Imaging. IEEE Trans. Image Process. 2021;30:8773–8784. doi: 10.1109/TIP.2021.3120053. [DOI] [PubMed] [Google Scholar]
- 34.Chintada B.R., Rau R., Goksel O. Spectral Ultrasound Imaging of Speed-of-Sound and Attenuation Using an Acoustic Mirror. Front. Phys. 2022;10 doi: 10.3389/fphy.2022.860725. [DOI] [Google Scholar]
- 35.Hillmann D., Spahr H., Hain C., Sudkamp H., Franke G., Pfäffle C., Winter C., Hüttmann G. Aberration-free volumetric high-speed imaging of in vivo retina. Sci. Rep. 2016;6 doi: 10.1038/srep35209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Pande P., Liu Y.-Z., South F.A., Boppart S.A. Automated computational aberration correction method for broadband interferometric imaging techniques. Opt. Lett. 2016;41:3324. doi: 10.1364/OL.41.003324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kumar A., Drexler W., Leitgeb R.A. Subaperture correlation based digital adaptive optics for full field optical coherence tomography. Opt. Express. 2013;21:10850. doi: 10.1364/OE.21.010850. [DOI] [PubMed] [Google Scholar]
- 38.Tsou J.K., Liu J., Barakat A.I., Insana M.F. Role of Ultrasonic Shear Rate Estimation Errors in Assessing Inflammatory Response and Vascular Risk. Ultrasound Med. Biol. 2008;34:963–972. doi: 10.1016/j.ultrasmedbio.2007.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Selim H., Trull J., Delgado Prieto M., Picó R., Romeral L., Cojocaru C. Fully Noncontact Hybrid NDT for 3D Defect Reconstruction Using SAFT Algorithm and 2D Apodization Window. Sensors. 2019;19:2138. doi: 10.3390/s19092138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grieve K., Paques M., Dubois A., Sahel J., Boccara C., Le Gargasson J.-F. Ocular Tissue Imaging Using Ultrahigh-Resolution, Full-Field Optical Coherence Tomography. Invest. Ophthalmol. Vis. Sci. 2004;45:4126. doi: 10.1167/iovs.04-0584. [DOI] [PubMed] [Google Scholar]
- 41.Thouvenin O., Apelian C., Nahas A., Fink M., Boccara C. Full-Field Optical Coherence Tomography as a Diagnosis Tool: Recent Progress with Multimodal Imaging. Appl. Sci. 2017;7:236. doi: 10.3390/app7030236. [DOI] [Google Scholar]
- 42.Feldman M.K., Katyal S., Blackwood M.S. US Artifacts. RadioGraphics. 2009;29:1179–1189. doi: 10.1148/rg.294085199. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Video S1
Video S2
Data Availability Statement
Data will be made available on request.