Population Structure in Admixed Populations: Effect of Admixture Dynamics on the Pattern of Linkage Disequilibrium

Abstract

Gene flow between genetically distinct populations creates linkage disequilibrium (admixture linkage disequilibrium [ALD]) among all loci (linked and unlinked) that have different allele frequencies in the founding populations. We have explored the distribution of ALD by using computer simulation of two extreme models of admixture: the hybrid-isolation (HI) model, in which admixture occurs in a single generation, and the continuous-gene-flow (CGF) model, in which admixture occurs at a steady rate in every generation. Linkage disequilibrium patterns in African American population samples from Jackson, MS, and from coastal South Carolina resemble patterns observed in the simulated CGF populations, in two respects. First, significant association between two loci (FY and AT3) separated by 22 cM was detected in both samples. The retention of ALD over relatively large (>10 cM) chromosomal segments is characteristic of a CGF pattern of admixture but not of an HI pattern. Second, significant associations were also detected between many pairs of unlinked loci, as observed in the CGF simulation results but not in the simulated HI populations. Such a high rate of association between unlinked markers in these populations could result in false-positive linkage signals in an admixture-mapping study. However, we demonstrate that by conditioning on parental admixture, we can distinguish between true linkage and association resulting from shared ancestry. Therefore, populations with a CGF history of admixture not only are appropriate for admixture mapping but also have greater power for detection of linkage disequilibrium over large chromosomal regions than do populations that have experienced a pattern of admixture more similar to the HI model, if methods are employed that detect and adjust for disequilibrium caused by continuous admixture.

Introduction

The identification and characterization of genes influencing complex diseases and traits is a major goal of human geneticists. One approach to the identification of these genes is to search for linkage in families. However, in the case of complex diseases or traits it may be difficult to obtain enough informative pedigrees to elucidate underlying genetic factors, especially in the case of adult-onset traits, in which accurate multigenerational phenotypic data may be particularly difficult to obtain. An alternative approach to family-based linkage analysis is to search for allelic association between a marker and phenotype. Although individuals in a population-based association analysis are often considered “unrelated,” many are actually members of extremely large pedigrees of unknown structure. In this type of study, affected individuals are hypothesized to share predisposing or causal alleles that are identical by descent (IBD) from a common ancestor.

It has been suggested that association analyses may have more power to detect susceptibility genes underlying a complex disease than do linkage analyses (Risch and Merikangas 1996; Camp 1997). However, association studies rely on the presence of detectable linkage disequilibrium (LD) between a marker and a causal locus. The extent of LD across chromosomal regions determines the marker density required for sufficient power in a genomewide association-mapping study. In practice, the extent of LD over chromosomal regions appears to be heterogeneous and highly dependent on both gene and population histories. Without sufficient LD between a marker and a functional locus, an association study cannot detect association between a causal locus and the phenotype of interest. Additionally, genetic structure can lead to LD between unlinked loci, causing false-positive linkage signals. An additional complication in the mapping of complex disease genes arises when there is heterogeneity in the etiology of the disease; that is, when the disease has multiple genetic origins, association analyses that rely on the assumption that trait-influencing genes are IBD may fail to identify influential genes, since the association will be divided between multiple loci in the sample of affected individuals. To avoid these hazards, some researchers have focused on association mapping in isolated populations that are more genetically homogeneous than larger cosmopolitan populations. Such isolated populations are often preferred, for two reasons. First, drift can create large amounts of LD, which can be used for mapping genes in populations of constant size (Laan and Pääbo 1998; Terwilliger et al. 1998). Second, small founding populations are more likely to produce populations that have only one genetic etiology for a given trait. However, for common traits and diseases, predisposing alleles (those that increase risk but do not directly cause a phenotype) probably exist at frequencies much higher than that of the trait or disease, thereby increasing the probability of multiple genetic sources of the trait, even in relatively young and homogeneous populations (Terwilliger and Weiss 1998). Additionally, recent work has suggested that these isolated populations may not exhibit amounts of LD that are significantly greater than those in more heterogeneous populations (Boehnke 2000; Eaves et al. 2000; Taillon-Miller et al. 2000).

Admixture mapping (AM) is a type of association study that uses admixed populations (those formed by gene flow between two or more genetically distinct populations) to map genes. Theoretical and experimental studies have shown that AM is a potentially powerful method for the identification of genes that elude other mapping methods (Briscoe et al. 1994; Stephens et al. 1994; Parra et al. 1998; Lautenberger et al. 2000). The power of AM comes from the fact that the admixture process itself creates LD between all loci (linked and unlinked) that have different allele frequencies in the parental populations. However, as with any population study, the results of an AM study will be affected by the demographic history of the population. In particular, we show here, through computer simulation, that the pattern of LD resulting from admixture—and, therefore, the power and applicability of AM—is highly dependent on admixture dynamics (i.e., the way in which admixture occurs). Additionally, we present the admixture proportions of two African American population samples and compare the observed LD patterns to the simulation results.

Subjects and Methods

Population Samples

Two African American population samples (one from Jackson, MS, and one from coastal South Carolina) were typed for a panel of markers (shown in table 1) that were selected on the basis of their high allele-frequency differences between Africans and Europeans (Shriver et al. 1997; Parra et al. 1998). The Jackson sample consists of 987 African American individuals participating in ongoing genetic studies in Jackson of cardiovascular disease and its risk factors. The South Carolina sample is a subset of the population described in detail by Parra et al. (in press) and consists of 541 African American women from the low country (Berkeley, Charleston, Colleton, and Dorchester counties) of coastal South Carolina who participated in a lead determination study.

Table 1.

Population-Associated Alleles

		Average Allele Frequencya			Average Allele Frequency
Marker	Chromosomal Location	African	European	δ	Jackson	South Carolinab
Fy-Null*1	1q22-q23	.001	1.000	.999	.175	.094
OCA2*1	15q11.2-q12	.112	.769	.657	.208	.162
GC*1Fc	4q12-q13	.841	.156	.685	.726	.785
GC*1Sc	4q12-q13	.069	.607	.538	.157	.125
AT3*1	1q23-q25	.859	.279	.580	.747	.755
RB1*1	13q14.3	.923	.333	.590	.819	.810
LPL*1	8p22	.972	.486	.486	.876	.904
APOA1*1	11q23	.420	.927	.507	.510	.501
SB19.3*1	19	.410	.910	.500	.478	.522
D11S429*1	11	.079	.541	.462	.143	.132
ICAM1*1	19p13.3-p13.2	.753	1.000	.247	.770	.755

^aData are unweighted allele frequencies from Parra et al. (1998, and in press)

^bData are weighted allele frequencies from Parra et al. (in press)

^cTwo independent alleles of a three-allele locus.

Allele frequencies for the parental populations (European and African), given in table 1, represent the average frequency observed in European samples from England, Ireland, and Germany and in African samples from the Central African Republic, Nigeria, and Sierra Leone (both Mende and Temne; for detailed allele-frequency information, see Parra et al. [1998, and in press]). A measure of allele-frequency difference, δ, is defined as the absolute value of the frequency difference between African and European populations. High δ values increase the amount of LD created during the admixture process and thereby increase the likelihood that association between loci will be detected. The δ values for the population-associated alleles (PAAs) used in this study are presented in table 1, and have a range of .25–.999, with a mean .57. Although our focus has been on markers that have δ values ≳.50 (∼5% of diallelic markers), ICAM (δ=.25) was included in the panel because one of its alleles is found only in African populations, making it more informative for ancestry than are other markers with similar δ values.

Laboratory Methods

The laboratory methods used to type the DNA samples have been described in detail elsewhere (see Parra et al. 1998, and in press). In brief, these PAAs were typed from genomic DNA by standard PCR and electrophoretic separation of DNA fragments. APOA1 and Sb19.3 are Alu polymorphisms; AT3 is a 68-bp insertion/deletion polymorphism; and FY, ICAM1, LPL OCA2, RB1, GC, and D11S429 are all restriction-site polymorphisms. The primers and methods used for these markers have been described by Parra et al. (1998, and in press).

Simulation Methods

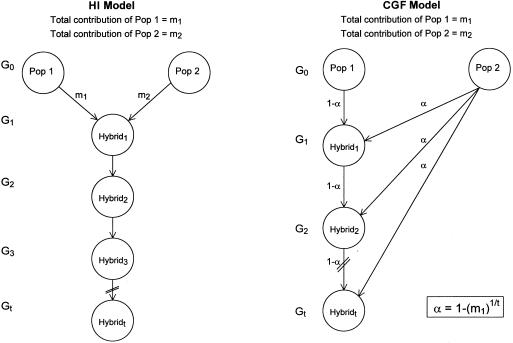
We have developed a population simulation program that creates an admixed population based on the two distinct patterns of admixture diagrammed by Long (1991) (fig. 1). In the hybrid-isolation (HI) model, admixture occurs in a single generation and is followed by recombination and drift, with no further genetic contribution from either parental population. In the continuous-gene-flow (CGF) model, admixture occurs at a steady but reduced rate in every generation, such that the cumulative amount of admixture is equal to that in the HI model, allowing comparison of the two models. In both admixture models, the original founding populations contribute alleles rather than genotypes or haplotypes. In subsequent generations, contributions from the admixed population are in the form of haplotypes. This design ensures that the LD observed in the admixed population is the result of admixture and drift rather than the retention of LD from the parental populations. At the end of each simulation run, a random sample of individuals is chosen, and LD (D) is calculated by comparison of the haplotype frequency observed in the sample versus that expected on the basis of the allele frequencies in the sample. Power for each set of parameters is reported as the proportion of simulations that demonstrate significant LD (χ²>3.84, 1 df; P<.05). Each round of simulations was run using a panel of markers resembling those given in table 1, and using the average African and European frequencies shown as the founding population frequencies. Populations of 100,000 individuals were created, and samples of 1,000 individuals were collected at the end of each simulation round.

Figure 1.

Schematic of the two models of admixture used in computer simulations (adapted from Long [1991])

It is possible to calculate the amount of LD expected under each model of admixture, given a set of population parameters. For the HI model, the LD expected at generation t is

where θ is the recombination fraction between loci and D₀ is the amount of LD present in the admixed population immediately after the admixture event (i.e., the amount generated by admixture, when it is assumed that there is no LD in the founding populations). D₀ is calculated as

where m is the proportion of admixture from population 1, 1-m is the proportion of admixture from population 2, and δ_A and δ_B are the allele-frequency differences between the parental populations, at loci A and B, respectively (Chakraborty and Weiss 1988). The amount of LD expected under the CGF model of admixture is calculated as

where α is the contribution of population 2 in each generation, 1-α is the contribution of the admixed population in each generation, δ_A,t and δ_B,t are the allele-frequency differences between the parental populations, in generation t, at loci A and B, respectively, and D_t-1 is the amount of LD in the previous generation. The simulation programs were validated by comparison of the amount of LD observed in the simulated population, at various points in time, versus that expected on the basis of these theoretical equations (data not shown).

Statistical Methods

Admixture proportions for population samples were estimated with the program ADMIX, provided by Dr. Jeffrey Long, which implements a least-squares method (Long 1991). This algorithm was validated by comparison of estimated population-admixture proportions of a simulated population sample versus the known population-admixture proportions (data not shown). Haplotype frequencies for population samples were estimated with the program 3LOCUS, provided by Dr. Long, which implements an expectation-maximization algorithm (Long et al. 1995). This algorithm was validated by comparison of estimated two-point haplotype frequencies to the known frequencies. No significant differences between estimated and known frequencies were observed (data not shown). LD in the population samples was reported as the likelihood ratio (G), as described by Long et al. (1995). The G distribution approximates a χ² distribution when sample size is large (for a comprehensive discussion of the G-test compared with the χ² test, see Sokal and Rohlf [1995]). It is important to point out that LD was measured for 36 pairs of markers in each sample population (fig. 2). These comparisons test a joint hypothesis: (a) that admixture does not vary between individuals (i.e., there is no genetic structure) and (b) that the marker is not informative for ancestry. If either of these null hypotheses is true, the marker will not show allelic association with other markers. If allelic association between two unlinked markers is detected, then both null hypothesis a, which applies to the entire sample, and null hypothesis b, which applies to the two markers studied, are rejected. The two markers are then expected to show allelic association with any other markers that are informative for ancestry. Since these hypotheses are not independent, a Bonferroni correction cannot be applied. Linear-regression lines, confidence intervals (CIs), and P values were obtained with SPSS (version 10.0).

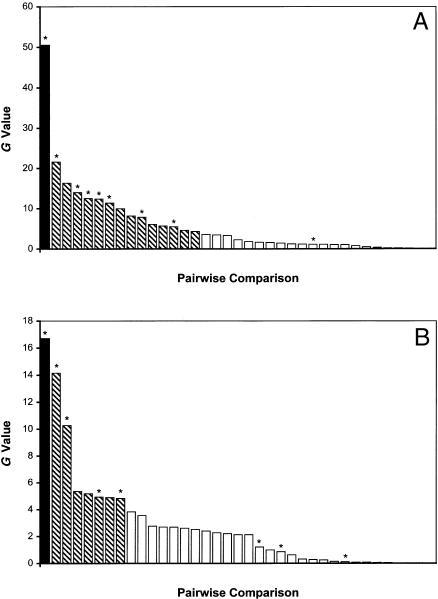
Figure 2.

Observed association statistics between PAAs for Jackson (A) and South Carolina (B). Each bar represents the association statistic observed between a pair of PAA markers listed in table 1. The FY-AT3 pair, linked at 22 cM, is shown as a black bar, marker pairs that are unlinked but in association (G>3.84, P<.05) are shown as hatched bars, and unlinked pairs that are not associated (P>.05) are shown as unblackened bars. Marker pairs containing the FY locus are indicated by asterisks (*).

Results

Population Results

The allele frequencies observed in the Jackson sample and the South Carolina sample for the 10 markers analyzed are also given in table 1. The frequencies for the South Carolina sample, reported by Parra et al. (in press), represent the weighted frequencies (by sample size) for the samples from the low country and have been reprinted here for convenience. The estimated amount of European ancestry is 16.9% (95% CI 14.7%–18.8%) for the Jackson sample and 11.6% (95% CI 8.84%–14.36%) for the South Carolina sample (as reported by Parra et al. [in press]).

To test for the presence of genetic structure (as indicated by LD between unlinked loci) in the Jackson sample and the South Carolina sample, association between all pairs of loci given in table 1 was measured. The results of these pairwise comparisons are presented in figure 2. Both African American samples demonstrate significant association between the two loosely linked (θ=.22) markers, FY and AT3 (G=50.54, P=1.16751×10^-12 for Jackson sample; and G=16.7, P=4.3781×10^-5 for the South Carolina sample). However, both samples also exhibit significant association between pairs of unlinked markers (37% of unlinked pairs in the Jackson sample and 20% in the South Carolina sample). In each case, the LD observed between unlinked markers is in the positive direction; that is, the alleles in association are from the same ancestral population, as would be expected if the LD were caused by admixture. In both populations, a large proportion of the unlinked marker pairs found in significant association include FY (88% of FY comparisons in the Jackson sample and 63% in the South Carolina sample; indicated by asterisks in fig. 2). The significant number of associations observed between unlinked loci indicates the presence of genetic structure in these population samples and could result in a high rate of false positives in an actual AM study.

Simulation Results

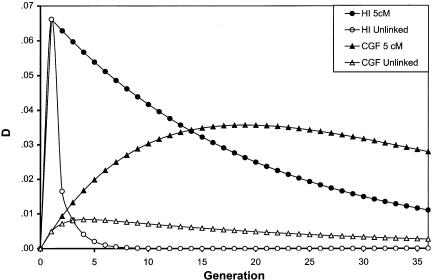
As shown in figure 3, the HI and CGF models of admixture have different expectations for the distribution of LD between unlinked markers. In the HI model, LD is generated in a single generation and then progressively decays in each successive generation, as a result of independent assortment and recombination between loci. In the CGF model, the amount of LD observed increases during the first few generations as continual admixture generates more disequilibrium than is broken down by independent assortment and recombination. After a few generations, the amount of LD begins to decay, although at a rate much slower than that observed in the HI model. The decay of LD in the CGF model occurs as the admixed population begins to resemble the parental population from which it receives continual genetic contributions. The rate at which the admixed population becomes similar to the parental population depends on the rate of gene flow from the parental population to the admixed population.

Figure 3.

Amount of ALD expected under each model of admixture for unlinked loci and loci linked at 5 cM. The results shown are for two loci with δ = .54 and .49, and with 50% admixture in the first generation, for the HI model, and 36 generations of 1.9% admixture, for the CGF model (equivalent to 50% total).

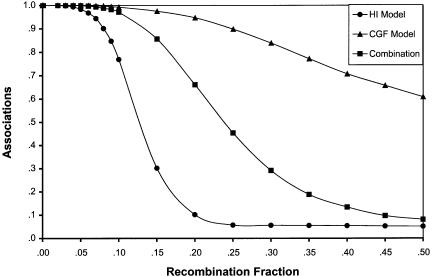
Figure 4 shows the average proportion of simulation rounds that demonstrated significant results under each model of admixture when a panel of markers with the characteristics of those shown in table 1 was used. The two models result in very different association patterns. In the HI model, the number of simulations exhibiting association declines rapidly as θ increases. The overall number of associations between unlinked loci (θ=.50) is low (∼5%) for the HI model. The CGF model, on the other hand, exhibits a much more gradual decline in association as recombination distance increases, and it displays a notable number of associations between unlinked loci (∼60%). These associations are the result of LD generated by recent admixture rather than by true physical linkage and would therefore constitute false-positive results in an actual mapping study. Figure 4 also shows the results of a combined admixture model, in which the population is simulated with 12 generations of CGF, followed by three generations of random mating. This type of model represents the effect when individuals with recent admixture—for example, those with a parent, grandparent, or great-grandparent from the introgressing parental population—are excluded from an admixture study sample. This model is intermediate between the HI and CGF models, demonstrating moderate power to detect loosely linked loci and a low (∼8%) frequency of associations between unlinked loci.

Figure 4.

Average proportion of simulation rounds demonstrating significant association for HI (▒), CGF (▴), and combination (▪)models, for a panel of population-association alleles with characteristics of those listed in table 1. Simulations were run such that the total amount of admixture in each model was 17%. The simulation parameters were as follows: 1,000 rounds of simulation, population size 100,000, sample size 1,000, significance level 5%, and 15 generations of admixture (the combination model was run with 12 generations of CGF, followed by 3 generations of random mating).

Controlling for False Positives

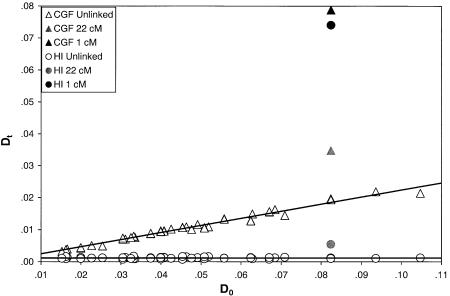
The large proportion of unlinked loci that demonstrated significant association in both the Jackson sample and the South Carolina sample signifies the presence of genetic structure, indicating that, to use these populations in AM studies, methods that can detect and adjust for these false-positive signals must be developed. The initial amount of LD created by admixture, D₀, can be calculated algebraically for each pair of markers, on the basis of the admixture proportion and the δ values at each locus (see eq. [2]). It is important to point out that D₀, as defined here, represents only the LD resulting from admixture and does not account for any preexisting LD in the parental populations. The amount of LD observed, D_t, represents some portion of that created by admixture. Because LD decays as a function of time and chromosomal distance, the ratio D_t/D₀ will be higher for linked loci than for unlinked loci, thereby allowing for the distinction between true linkage and false positives. The simulation of the D_t/D₀ ratio is shown in figure 5. The two admixture models clearly show distinct patterns for unlinked loci. In the CGF model, the amount of LD observed, D_t, is directly related to the amount generated by the admixture process, which is a function of the magnitude of the allele-frequency differences in the parental populations. In contrast, in the HI model for unlinked markers there is no relationship between D₀ and D_t; in other words, the slope of the line D_t/D₀ is not significantly different from 0 in the HI model but is >0 in the CGF model. However, both models demonstrate an excess of LD in the presence of linkage at 22 cM (shown for two markers with δ values equal to those of FY and AT3).

Figure 5.

Simulated results of D_t compared with calculated (D₀) for both the HI and the CGF models. For these simulations, D₀ is calculated according to equation (2), for both models of admixture. In this case, D_t is the observed LD value, rather than the theoretical value predicted by equation (1).

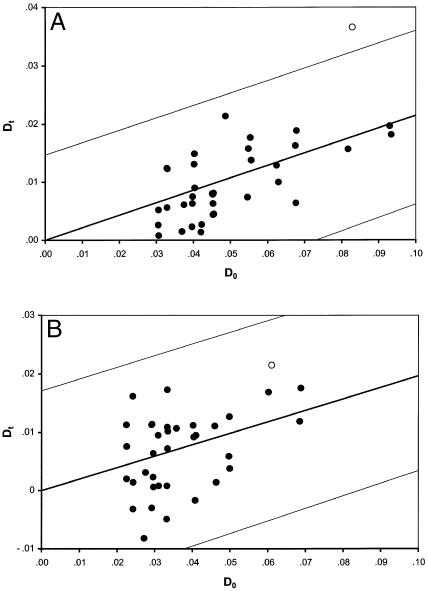
The D_t/D₀ results for the Jackson sample and the South Carolina sample are shown in figure 6. In both populations, the slope of the regression is significantly different from 0 (P<.001 in the Jackson sample and P=.004 for South Carolina). In the Jackson sample, the FY-AT3 pair is an outlier, falling outside the 99% CI. However, in the South Carolina sample the FY-AT3 association does not show a deviation from the pairs of unlinked loci.

Figure 6.

Comparison of observed D_t/D₀ ratios for two African American sample populations, from Jackson (A) and South Carolina (B). Unlinked pairs of markers are shown as blackened circles (░), and the FY-AT3 pair is shown as an unblackened circle (○). D₀ is calculated according to equation (2).

A more powerful method of distinguishing between true signals and false positives has been developed recently (McKeigue 1998; McKeigue et al. 2000). This method differentiates between allelic association due to shared ancestry and association due to linkage, by adjusting for the variation in admixture between individuals. The test for association is based on a hybrid of Bayesian and frequentist approaches. The posterior distribution of ancestry at all marker loci, conditional on the observed marker genotype data and assuming all loci to be unlinked, is generated by Markov-chain simulation. A score test for association of ancestry between each pair of loci is then obtained by averaging over this posterior distribution. A useful feature of this method is that it yields an estimate of the proportion of information (about association) that is extracted by the markers used. The results of this test, applied to the Jackson sample and the South Carolina sample, are presented in table 2. As seen in the table, conditioning on admixture identifies a significant association between FY and AT3, which is independent of admixture (and, therefore, is an indication of linkage), whereas all other pairs of markers are no longer significant once the adjustment has been made.

Table 2.

Conditioning on Parental Admixture

	Jackson			South Carolina
Marker	Score	Z	Pa	Score	Z	Pa
FY-AT3	14.83	3.39	.0003	3.62	1.89	.03
FY-ICAM1	3.38	1.53	.06	−.01	−.02	.51
FY-LPL	6.16	1.34	.09	−2.94	−1.68	.95
FY-D11S429	.73	.23	.41	−1.25	−1.09	.86
FY-Sb19.3	.56	.20	.42	−.82	−.76	.78
FY-GC	.13	.03	.49	.84	.49	.31
FY-OCA2	−.80	−.21	.58	2.76	1.53	.06
FY-RB1	−2.97	−.71	.76	.96	.51	.31
FY-APOA1	−4.92	−1.92	.97	1.46	1.14	.13

^aValues are one-tailed.

Discussion

As is the case with many mapping methods, AM can be confounded by complex population and evolutionary history. The diverse geographic origins of enslaved Africans brought to the United States during the 17th, 18th, and 19th centuries could hinder AM studies if allele frequencies were significantly different between African regions, thereby generating, within the African American population, ALD that is separate from the ALD caused by European admixture. However, the allele frequencies for the PAAs analyzed here demonstrate similar frequencies in various geographic regions of western Africa (Parra et al. 1998, and in press). Although several other forces can also cause LD, it is clear that the LD between pairs of unlinked loci observed in the Jackson sample and the South Carolina sample is the result of admixture, rather than other recent evolution, for two reasons. First, most other sources of LD, such as mutation or natural selection, cause LD between linked loci, not between pairs of unlinked loci as observed here. For example, it has been suggested that, in Africa, the FY locus has undergone selection for resistance to the malarial pathogen Plasmodium vivax (for a recent discussion of the evidence for natural selection at the FY locus, see the work of Hamblin and Di Rienzo [2000]). In the Jackson sample and the South Carolina sample, a large proportion of the pairs of unlinked markers that include the FY locus are in association (88% of FY comparisons in the Jackson sample and 63% in the South Carolina sample, indicated by asterisks in fig. 2). This persistence of LD between FY and unlinked markers is most likely a result of the extraordinarily high allele-frequency differential of the FY locus (δ=.999). Although natural selection could explain the high δ level, it is not expected to generate or retain LD between FY and unlinked markers. Some sources of LD, such as epistasis, can cause LD between unlinked loci, but they are unlikely to generate LD between so many pairs of unlinked loci throughout the genome. Second, the significant LD observed between unlinked marker pairs in the Jackson sample and the South Carolina sample is always in a positive direction (the alleles in association are from the same ancestral population), which is expected of ALD but not of LD generated by other mechanisms.

The simulation results shown in figure 4 are in accordance with the theoretical predictions of the distribution of ALD, under both models. The results for the HI model are quite promising for AM studies. They suggest that high-δ (>.35) markers provide 80% power to detect association at distances of ∼10 cM. These results are consistent with the results of previous studies (Stephens et al. 1994), which predict that ALD will extend over a total distance of 20 cM (10 cM on each side of a marker). Additionally, the HI results demonstrate a low (∼5%) proportion of detected association between unlinked loci (i.e., false positives). The frequency of these false positives correlates with the specified significance level of 5% (G>3.84) and would be reduced by an increase in the stringency of the association test, as would be appropriate for a genomewide mapping study.

Like the HI model, the CGF model exhibits very high power to detect association when the distance between markers is small. However, the CGF model also demonstrates significant association between loosely linked (.10<θ<.50) and unlinked (θ=.50) markers. In these simulations, >60% of all pairwise comparisons of unlinked markers demonstrate significant association, verifying that a CGF pattern of admixture can be a source of genetic structure. The extent of the genetic structure indicates that the use of CGF populations for AM may result in a high frequency of false-positive results.

The results of pairwise comparisons of markers in the two African American samples (fig. 2) indicate that these populations have most likely experienced a CGF pattern of admixture. The observed pattern of association resembles the results from simulation of the CGF model, in three respects. First, the significant number of pairs of unlinked markers that are in association (37% in the Jackson sample and 20% in the South Carolina sample) is not expected under the HI model. Second, the strength of the association between FY and AT3 (G=50.54, P=1.16751×10^-12 for Jackson and G=16.7, P=4.3781×10^-5 for South Carolina) is indicative of a CGF pattern rather than a HI pattern. This distinction is a result of the decay of LD between unlinked loci in an HI model of admixture. Specifically, under the HI model, after 12 generations of admixture (a reasonable estimate for the admixture history of African American populations) only ∼5% of the ALD between two markers separated by 22 cM is expected to remain. Such a low level of remaining LD is unlikely to generate a highly significant association statistic. It is important to note that the relative strength of the LD between FY and AT3 has been observed by Lautenberger et al. (2000), who also noted that “recurring” admixture between European and African American populations would explain the retention of LD over large (⩾10 cM) chromosomal regions. Third, the slope of the D_t/D₀ line is significantly >0, indicating a positive relationship between the δ levels of two markers and the LD observed between them. This relationship is indicative of CGF populations but not of HI populations. These results have two important implications for the use of admixed populations for mapping genes. First, they demonstrate that, in CGF populations, it is possible to detect, between loosely linked loci, association that would most likely not be detectable in HI populations. However, they also show that a simple analysis of association data in these populations will yield a high rate of false positives. It is important to point out that CGF between the admixed population and one parental population is only one possible explanation for the genetic structure observed in these two population samples. A model in which the admixed population receives genetic contribution from both parental populations in each generation may reflect more accurately the history of the African American population. The effect of CGF from both parental populations would most likely be an elevation of the level of genetic structure, above that observed in the simple CGF. Since the degree of structure observed in the simple CGF model exceeds that observed in the real populations, it is unlikely that addition of CGF from both parental populations to the simulation models will be informative. Additionally, assortative mating and/or population subdivision might also lead to similar LD patterns. However, regardless of its origin, such a high amount of genetic structure has the potential to impede AM studies. Therefore, methods that can detect and, where necessary, correct for association between unlinked loci must be implemented, in order to avoid false-positive results.

A straightforward method of controlling for spurious associations caused by CGF is to exclude from an AM study sample individuals with recent admixture. Although the ideal AM study design involves collection of only individuals who have not had any recent admixture (usually via questionnaire criteria), there are many existing data sets that have the potential to be useful in AM studies but for which parental and grandparental ancestries are unavailable. Additionally, for many populations there will be a number of people who are unaware of the true level of admixture in their ancestors. Thus, it is important to develop statistical methods that use molecular data, to identify and control for the associations that are expected between unlinked markers in some admixed populations. In addition, these methods can easily be used to verify ancestry information obtained by questionnaire.

One possible molecular method of distinguishing between association caused by true linkage and association between unlinked loci is to adjust D_t, according to the characteristics of the loci being compared. The amount of admixture-generated LD between any two loci (A and B) depends on four parameters: the proportion of admixture from population 1 (m₁), the proportion of admixture from population 2 (m₂), the δ level at locus A (δ_A), and the δ level at locus B (δ_B). Since m₁ and m₂ are the same, on average, for each locus in the data set, the variation in the amount of generated ALD depends on δ_A and δ_B. Therefore, adjustment of D_t by D₀ will equalize comparisons of different pairs of markers. It is then possible to examine whether there are outliers demonstrating an excess of association; that is, a higher D_t than is generally seen for unlinked marker pairs. Figure 5 shows the D_t/D₀ relationship for both linked and unlinked markers, under the HI and CGF models of admixture. As discussed previously, the two models of admixture show distinct patterns for the expectation of LD between unlinked loci, and both models show higher levels of association between linked markers than between unlinked markers. When the D_t/D₀ ratios are plotted for pairs of markers in the two African American population samples, the results are varied. Both samples show significant slopes, indicating the presence of genetic structure, as expected under a CGF model of admixture. In the Jackson sample, all pairs of markers fall within the 99% CI, except for the FY-AT3 pair; as expected with two linked markers, the FY-AT3 pair demonstrates a significant excess of association, compared with the amount of association expected for unlinked markers. However, the South Carolina sample shows a different pattern, in which none of the pairs of markers demonstrate a significant excess of association. This lack of association may result from the smaller size of the sample (n=541), since power to detect association between loci increases with sample size. The lack of association may also be a result of a reduced amount of recent admixture in the South Carolina sample compared to the Jackson sample, or it may reflect the lower amount of overall population admixture in the South Carolina sample relative to the Jackson sample (11.6% vs. 16.9%). It is important to point out that the distance between FY and AT3, 22 cM, is a relatively large chromosomal distance in terms of LD. Shorter distances between markers are expected to generate higher D_t/D₀ levels, as the simulations in figure 5 show. Therefore, examining the D_t/D₀ ratio for loci that are more closely linked may be a relatively quick method for identification of the most promising signals, in the presence of genetic structure.

One way to control for the effects of genetic structure in an AM study would be the use of a transmission/disequilibrium test (TDT). The TDT tests for disequilibrium in the transmission of a marker allele from heterozygous parents to affected offspring, in the presence of linkage. An excess of transmission is evidence of linkage between the marker and the trait locus (Ewens and Spielman 1995). For admixed populations, the greatest statistical power is achieved by selection of affected individuals who are the grandchildren of mixed unions (McKeigue 1997). However, the TDT takes advantage of only a portion of the available information, since many parents of affected individuals in the admixed population may not be heterozygous at the loci of interest. A more powerful method for differentiation between association due to shared ancestry and that due to linkage has been developed recently (McKeigue 1998; McKeigue et al. 2000). This method adjusts for the genetic structure that is expected in admixed populations, by testing for gametic disequilibrium, between alleles at two loci, that is independent of admixture. It can be shown that testing for association between loci, conditional on admixture, is a direct test for linkage (McKeigue 1998). This method has been applied successfully to both of these data sets. As shown in table 2, the FY-AT3 association is retained in both populations once the adjustment has been made, whereas all other pairwise comparisons are no longer significant.

These results indicate that, in AM studies, it is possible to use populations that have undergone CGF, as long as methods that can control for genetic structure are implemented. In fact, for mapping studies that rely on the extension of LD over relatively large chromosomal regions, CGF populations may be preferable to HI populations, since CGF reintroduces LD between loci in every generation. Because recombination breaks down LD between loosely linked markers more quickly than it breaks down LD between tightly linked markers, HI populations may be less amenable to the mapping of loosely linked loci but may be preferred for higher-resolution gene mapping.

Conclusions

LD between both linked and unlinked markers is formed by the process of admixture. The success of an AM study depends on the extent of LD between linked and unlinked loci and on the ability to differentiate between association due to linkage and association between unlinked loci that is due to genetic structure. The extent of ALD depends on several factors, including the allele frequencies in the parental populations, the amount of admixture, the admixture pattern, and the time since admixture.

The HI and CGF models are two simple models of admixture that are reasonable for admixed U.S. populations. These models yield very different patterns of association between markers. The HI model shows a steep drop in significant ALD, with increasing genetic distance. The CGF model shows a gradual decline in association, with increasing distance between markers, retaining significant association between unlinked markers.

In addition to strong association between two linked markers (FY and AT3), real data from two African American samples demonstrate a significant number of associations between unlinked markers, as expected under CGF. Two different methods have been used to differentiate between association due to true linkage and association due to genetic structure (i.e., false positives). These results indicate that it is possible to use populations that have experienced CGF, as long as methods that can control for spurious associations are implemented. Therefore, as efforts are made to use admixed populations in the mapping of complex-trait genes, methods should be used that can test for genetic structure (see Pritchard and Rosenberg 1999) and that, when necessary, can control for such structure (see McKeigue 1998; McKeigue et al. 2000).