Multi Electron Spin Cluster Enabled Dynamic Nuclear Polarization with Sulfonated BDPA

Abstract

Dynamic nuclear polarization (DNP) can amplify the solid-state nuclear magnetic resonance (NMR) signal by several orders of magnitude. The mechanism of DNP utilizing α,γ-Bisdiphenylene-β-phenylallyl (BDPA) variants as Polarizing Agents (PA) has been the subject of lively discussions on account of their remarkable DNP efficiency with low demand for microwave power. We propose that electron spin clustering of SA-BDPA is responsible for its DNP performance, as revealed by the temperature-dependent shape of the central DNP profile and strong electron-electron (e-e) crosstalk seen by Electron Double Resonance. We demonstrate that a multi-electron spin cluster can be modeled with three coupled spins, where electron J (exchange) coupling between one of the e-e pairs matching the NMR Larmor frequency induces the experimentally observed absorptive central DNP profile, and the electron T_1e modulated by temperature and magic angle spinning alters the shape between an absorptive and dispersive feature. Understanding the microscopic origin is key to designing new PAs to harness the microwave power-efficient DNP effect observed with BDPA variants.

Graphical Abstract

Despite the transformative success of dynamic nuclear polarization (DNP) for solid-state nuclear magnetic resonance (NMR) in the past decade, broadly used molecular families for polarizing agents (PA) are surprisingly limited. DNP is a technique employed to enhance the sensitivity of NMR signal by transferring spin polarization from highly polarized unpaired electron spins of a polarizing agent (PA) to the nuclear spins of the analyte that has orders of magnitude lower polarization than electron spins at the same conditions^1,2. The transfer is facilitated by microwave irradiation at or near the electron paramagnetic resonance (EPR) line. DNP can be accomplished by several mechanisms: the solid effect (SE)^3,4, Overhauser effect (OE)^5,6, cross effect (CE)^7-12, and thermal mixing (TM)^11-14, to name the four most prominent mechanisms each of which has unique advantages and limitations. The most effective three-spin (e-e-n) CE for ¹H DNP relies predominantly on the g anisotropy of coupled nitroxide biradicals to meet the CE conditions, with only select bis-nitroxide radical variants commercially available. The CE relies on the coupling between nitroxides with different orientations relative to the main magnetic field, and hence dissimilar EPR frequencies such that the difference matches the nuclear Larmor frequency of a coupled nuclear spin⁷. The CE is less efficient at high magnetic fields and its efficiency has a strong dependence on microwave power and temperature. Although gyrotrons generate microwave power on the order of several to tens of watts and offer significant DNP enhancements, they rely on specialized hardware requiring a separate superconducting magnet to operate the gyrotron cavity. Additionally, they typically necessitate field tunability of the main NMR magnet. This is because the narrow frequency bandwidth of gyrotrons, typically much less than 1 GHz (up to 3 GHz has been reported to date^15,16), makes it difficult to meet resonance conditions for DNP, thereby limiting their broad accessibility. As a result, DNP requiring a gyrotron source cannot be readily implemented in an existing NMR system. In contrast, a solid-state microwave source can be used to turn an existing NMR system into a DNP-operable instrument, given that its frequency is widely tunable (e.g., easily over 10 GHz) to meet the resonance conditions for the desired DNP effect. While the power performance of solid-state microwave sources is improving at a rapid pace, it still generates microwave power that is an order of magnitude lower¹⁷. Nevertheless, solid-state microwave sources offer unparalleled advantages to gyrotrons, klystrons, and other vacuum-based microwave sources. These advantages include wide tunability, programmability, frequency and phase control, exceptional mechanical stability, lightweight and compact design, operation in CW and pulsed mode, as well as cost-effectiveness. Consequently, the availability of polarizing agents (PAs) capable of producing significant DNP effects at lower microwave power levels, as provided by solid-state sources, can greatly broaden the applicability and accessibility of DNP, as well as the use of PA beyond stable radicals with g~2. The limitations and opportunities of current solid-state microwave sources underscore the need to develop new PAs with higher efficiency and lower power requirements for solid-state DNP.

The underlying hypothesis of our study is that a cluster of strongly coupled electron spins offers hitherto unrecognized opportunities for DNP in terms of performance at high magnetic fields, low microwave power requirements, and widened sample scope. The current literature actively engages in the study of the solid-state DNP mechanism specifically observed in narrow-line radicals, emphasizing their role as PAs with low microwave power requirements. Notably, these narrow-line radical PAs have been recently used at high concentrations to induce ¹H NMR signal enhancements, with the ¹H NMR Larmor frequency corresponding to multiple of the EPR linewidth^11-14,18-20. The use of BDPA as PAs for ¹H DNP has received significant attention in recent years owing to low power requirements and high efficiency at high magnetic fields up to 21.1 T, and at temperatures ranging from 1.2 K to 115 K ^13,19,21,22. High ¹H DNP enhancements have also been reported using Trityl-OX063 at similarly high radical concentrations ranging from 40- to 200-mM^13,22. Recently, Radaelli et. al reported on a new DNP effect of coexisting and inter-dependent TM and SE DNP for ¹³C DNP using SA-BDPA at 60- and 120-mM concentrations, at 6.7 Tesla and 1.1 K, driven by the dipolar spin bath of coupled SA-BDPA²⁰.

To harness the fascinating benefit of PAs with low microwave power requirement, it is critical to understand the microscopic origin of the DNP effect. The competing hypotheses are that the effect originates from an Overhauser DNP effect that requires dynamic coupling between one electron and one nuclear spin (e-n) vs. a multi-electron spin effect requiring a strongly coupled electron spin cluster (ESC) and a weakly coupled narrow-line radical coupled to a nuclear spin. The latter can be described using the TM-DNP framework, but to emphasize the critical role of Electron Spin Clusters of narrow-line radicals to generate an Asymmetric Polarization Elevation (ESCAPE) by microwave irradiation at a select frequency, we refer to it as ESCAPE- or in short ESC-DNP. In Overhauser DNP, frequency matching is achieved by the fluctuation frequency of the e-n hyperfine coupling matching the electron Larmor frequency, i.e. 200 GHz at 7 Tesla. In contrast, ESC-DNP achieves resonance matching by the dipolar and/or exchange (J) coupling within the strongly coupled ESCs matching or encompassing the nuclear Larmor frequency, i.e. 300 MHz for ¹H at 7 Tesla. If hyperfine fluctuations contribute to ESC-DNP, owing to electron spin exchange (J) coupling, the relevant frequency would be of the order of the NMR Larmor frequency, unlike in Overhauser DNP that requires hyperfine fluctuations of the order of the EPR Larmor frequency.

TM and CE DNP have been described by Wenckebach as two limits of the same physical phenomenon that is driven via triple spin flips of two electron spins and one nuclear spin (e-e-n)^11,12. ESC-DNP is a sub-category of TM-DNP and is connected to the indirect cross effect (iCE)²³. Another related mechanism is the truncated CE (tCE)²⁴. At a practical level, TM-^13,14, CE-^8,9, iCE-²³ or tCE-DNP²⁴ have been achieved typically with mono- or bi-radicals, relying on g anisotropies of one or both radicals, except in recent studies that propose clustering of narrow line radicals to generate TM-DNP effects. So, by referring to ESC-DNP, we are explicitly hinting at the microscopic structure consisting of electron spin clusters to generate an asymmetric polarization, or polarization gradient, and to achieve resonance matching with D and J couplings of the ESCs. Of note, tCE-DNP requires a specific ESC architecture, in which the strongly clustered ESC and the weakly coupled narrow line radical have a frequency difference matching the nuclear Larmor frequency, and the former has orders of magnitude shorter T_1e relaxation times compared to the latter, so that a polarization gradient can be generated and maintained with minimal microwave power saturation. However, tCE conditions can also be met with metal centers or fast-relaxing radicals that are not electron spin clusters²⁴. Previous studies of Trityl-OX063 and BDPA clusters referring to TM-DNP are still consistent with the hereby presented concept,^13,25 but the finer-grained naming conventions can be helpful for DNP practitioners.

Turning our attention to a pivotal aspect often employed in literature to delineate the DNP mechanism: the shape of the central DNP feature. Accordingly, the mostly dispersive feature seen with high concentrations of Trityl-OX063 has been readily ascribed to the thermal mixing DNP effect without much controversy¹³ unlike the DNP effect using BDPA at equally high concentrations that give rise to closer to an absorptive central DNP feature²⁵. Thermal mixing DNP typically describes systems with strong dipolar couplings between the electron spins, such that microwave irradiation of allowed off-centered EPR transitions, gives rise to a dispersive DNP profile, with positive and negative enhancements with respect to the central EPR resonance frequency. In contrast, OE utilizes microwave excitation of the allowed SQ spin transitions that give rise to enhancement when subsequent spontaneous DQ or ZQ cross-relaxation between an electron and a nuclear spin (e-n) is dominant (if the DQ and ZQ relaxivity is balanced, Γ_1,DQ = Γ_1,ZQ, there is no net enhancement). The resulting feature caused by OE would be purely absorptive with either positive or negative sign depending on whether Γ_1,ZQ > Γ_1,DQ or Γ_1,DQ > Γ_1,ZQ, respectively. However, it is increasingly becoming evident that the shape of the central DNP profile is not a sufficiently unique determinant of DNP mechanisms. TM-DNP can give rise to either a dispersive or absorptive central DNP profile, while a recent study of diamond P1 centers demonstrated that tCE can give rise to positive absorptive or negative absorptive DNP profiles, indistinguishable from the Overhauser DNP profile²⁶.

In this study, we focus on the question of whether the DNP effect originates from a coupled one electron-one nuclear (e-n) spin system, as assumed for Overhauser DNP, or from an ESC-DNP effect of an asymmetric electron spin cluster weakly coupled to an isolated electron spin and one or more nuclear spins. To achieve a more comprehensive understanding of the DNP mechanism, a direct exploration from both the EPR and NMR perspectives is imperative. The active discourse in the current literature hints at the opportunities of utilizing high concentrations of narrow-line radicals as polarizing agents for solid-state DNP^25,27-29. Notably, this study will show that ESC-DNP can give rise to positively or negatively absorptive or dispersive central DNP features, or asymmetric features in between absorptive and dispersive shapes, contingent on the exact coupling strengths and relaxation times of the ESCs coexisting with a weakly coupled electron spin.

This study examines the mechanism of the water-soluble BDPA variant sulfonated BDPA (SA-BDPA)²⁹ for ¹H NMR DNP in the solid state. Griffin and coworkers originally debuted SA-BDPA as a water-soluble variant to replicate the success of BDPA for high-field DNP requiring low microwave power. SA-BDPA serves as an interesting model system to clarify outstanding questions on DNP mechanisms that have consequences on the design principles for new PAs. To elucidate the multi-spin effect in DNP using SA-BDPA, we perform DNP profile measurements as a function of temperature between 10-100 K under both static and MAS conditions. Pump-probe ELDOR measurements were conducted to examine whether there is significant crosstalk between electron spin sub-ensembles whose EPR frequency differences exceed the resonance linewidth of SA-BDPA and potentially approach the NMR frequency. Another focus is to see whether hyperpolarization of an electron spin sub-ensemble can be induced with SA-BDPA under conditions used to induce DNP—hyperpolarization of strongly coupled electron spins reported before with high concentration BDPA or Trityl as PAs^13,25. It is critical to perform DNP and EPR experiments under the same experimental conditions, including the magnetic field strength, because parameters critical to the DNP mechanisms such as T_1e and electron and nuclear Larmor frequencies are sensitively dependent on temperature and the magnetic field. All experiments presented here are performed using a dual DNP-EPR instrument at 7 Tesla under static and MAS conditions^30,31. Finally, we perform quantum mechanical simulations using two (e-e-n) (as demonstrated in Figure S7) and three-coupled (e-e-e-n) electron spins to one nuclear spin to understand the consequence of coupled multi-spin architectures on the DNP profile shape. We could replicate the pattern of an experimental DNP profile by using a pair of strongly coupled electron spins as a model for an ESC that is weakly coupled to a third electron spin and a nuclear spin. Obtaining a microscopic understanding will aid in the design of future PAs with increased sensitivity and stability as well as having low microwave power requirement.

Experimental

Synthesis of SA-BDPA⁻

Oleum (1 mL, 19.6 mmol) was added in one portion to BDPAH (101 mg, 0.24 mmol) and heated to 85 °C in an oil bath for 5 min. The reaction mixture was brought to room temperature and water (20 mL) was added dropwise, with caution, to the stirring solution. The peach solution was left to stir at room temperature overnight and then filtered to remove residual insoluble material. A NaOH solution (16.5 mL, 2.5 M) was added dropwise to the filtrate to obtain a deep blue solution (pH ~ 10). The solution of SA-BDPA^– was condensed, and a blue powder was isolated via vacuum filtration and washed with DCM (~3). The resulting solid was dissolved in minimal MeOH, and the insoluble salts were filtered off. The filtrate was condensed to yield a deep blue powder (λ_Max = 630 nm and 507 nm) (Figure 1B)

Figure 1:

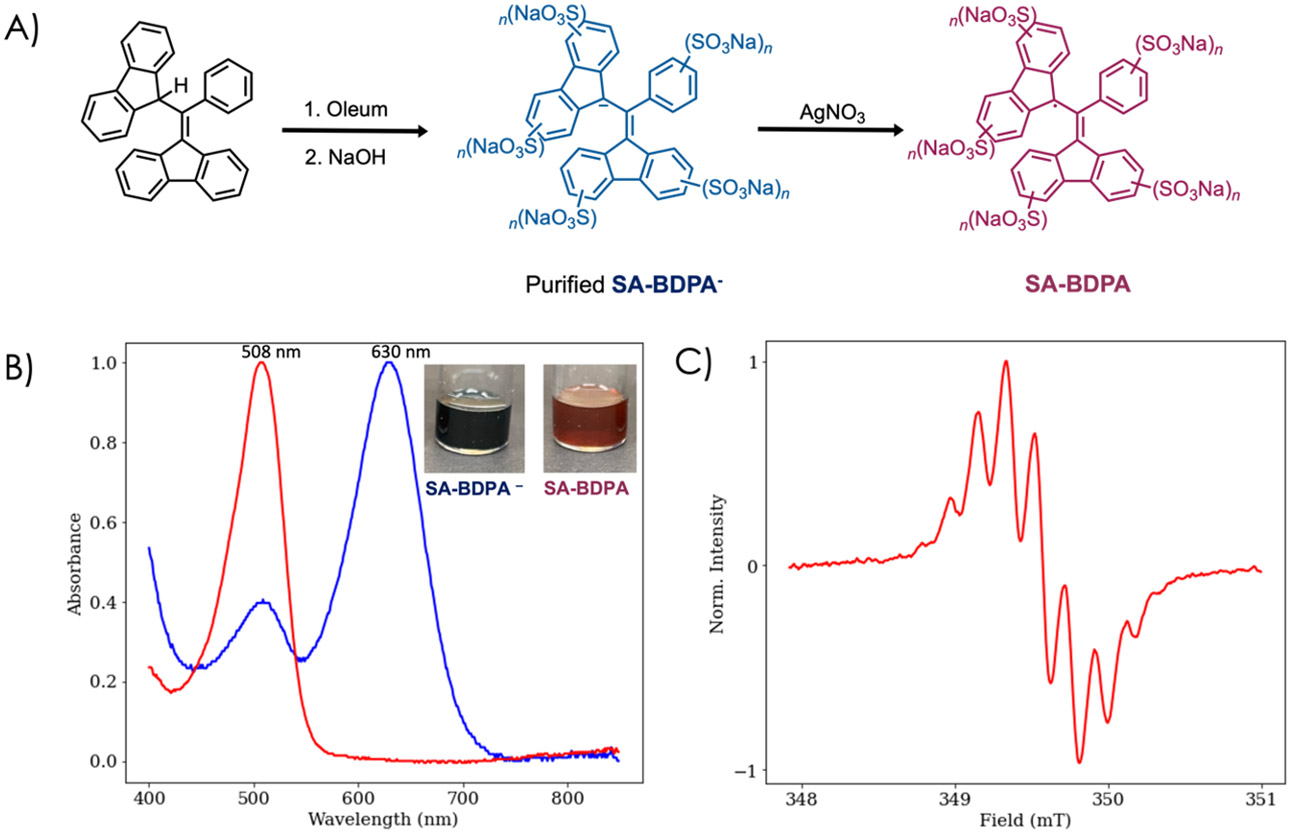
A) BDPAH was synthesized using the previously reported literature procedure. B) depicts the UV-VIS spectra of 100-mg of SA-BDPA- (blue) and SA-BDPA (red) dissolved in 3-mL of water. C) EMX EPR spectrum of 1-mg of SA-BDPA dissolved in 1-mL of water. Note that the first small hump at ~508 nm in the SA-BDPA salt is from auto oxidation to the radical in air.

Synthesis of SA-BDPA

AgNO₃ (101 mg, 0.59 mmol) was added to a stirring solution of SA-BDPA⁻ (100 mg) in water (3 mL). After 1 h, the reaction mixture was passed through celite to remove residual silver salts/particles and the filtrate was condensed to obtain sulfonated 1,3-bisdiphenylene-2-phenylallyl (SA-BDPA) as a dark red solid (λ_Max = 507 nm).

Sample preparation for DNP and EPR experiments

37-mg of freshly made SA-BDPA was dissolved in 100-μL in 60/40 v/v% d₈-Glycerol/D₂O (a fully deuterated DNP juice) glassing agent to create a 0.37 mg/μL solution. It is worth noting that although the solution is fully deuterated, some protons are still present as impurities, and these are utilized for measuring DNP. 20-μL of the BDPA solution along with 30-mg of KBr (for temperature sensing) were packed into a 4-mm MAS rotor (purchased through Revolution NMR LLC.).

Operation of Static DNP and EPR experiments at 7 Tesla

A 6.9 T wide-bore magnet system with a Bruker Avance DSX spectrometer was used. The spectrometer was equipped with a home-built μw bridge operating with a Virginia Diode Inc. (VDI) tunable μw source with a frequency range across 193-201 GHz and a μw irradiation power up to 350 mW. A homebuilt cryogen-free high field dual EPR and DNP probe as described in Tagami Et. Al.³⁰ was used for measurements. The transmitted μw beam was guided through a quasi-optical (QO) bridge setup and guided to the sample position through a corrugated waveguide as detailed in previous publications. Cryogenic temperatures down to ~10 K were achieved using He free cryostat from Janis Research Co. LLC. A sample cup was made from commercially available parts. The sample cup was made from Teflon tube with 4.6 mm OD 3.2 mm ID with a length of ~30 mm. A thread of ~ 7 mm in length was drilled into the Teflon tube using a 6.35 mm tap drill. The sample was centered into the sample cup using a 9.5mm in length and 3.1 mm diameter aluminum cap along with a 6.35 mm in length 3.1 mm diameter Teflon cap.

Operation of MAS DNP experiments at 7 Tesla

A 6.9 T wide-bore magnet system with a Bruker Avance DRX spectrometer was used. The NMR probe used was a custom designed 4 mm DNP probe from Revolution NMR LLC. Inspired by the design of Tycko Et. Al.^32,33, a VDI μw source with a frequency range tunable across 193-201 GHz and a μw irradiation power of up to 350 mW was used. The transmitted μw beam was guided through a quasi-optical (QO) bridge setup and guided to the sample position through a corrugated waveguide as has been detailed in previous publications^33,34. All experiments were performed at 3 kHz magic angle spinning (MAS) using room temperature nitrogen with a consumption rate of 10 liter/hour. Experiments were done in a temperature regime of 25 K to 100 K using liquid helium for cooling with an average flow consumption rate of ~3-4 liter/hour. A 4mm OD, 2.36mm ID zirconia rotor with a length of 46 mm fixed with Teflon inserts obtained from Revolution NMR was used for sample preparation. Rotor was packed with ~40-mg of KBr for temperature monitoring through the measurement of ⁷⁹Br T_1n as shown by Thurber et al.³⁵

This study is aimed at investigating the effect of multi-electron spin clusters in DNP when using SA-BDPA, a water-soluble narrow-line radical, as the PA. Our sample was prepared in a glassing agent and using a nominal SA-BDPA concentration of 60 mM, commonly used to achieve ¹H DNP using narrow-line radicals as described in the literature^20,29,36. To compare our results with prior studies, we begin our investigation by measuring the DNP enhancement as a function of microwave frequency at 100 K, as shown in Figure 2A under static conditions and Figure 2B under MAS conditions.

Figure 2:

DNP frequency profiles and Power sweep of 0.37-mg/μL SA-BDPA in 60/40 (v/v) d8-glycerol/D2O. The Figure demonstrates the effect of temperature under A) Static and B) MAS at 3 kHz conditions. The 1H DNP frequency profiles were obtained by measuring the 1H DNP signal enhancements as a function of the 350 mW irradiation frequency, swept from 193.1 GHz to 194.2 GHz with a 10 s saturation time. Figures C) and D) demonstrate the effect on epsilon as a function of microwave irradiation power from 0 to 350 mW whilst at microwave irradiation frequency fixed at C) 193.325 GHz and D) 193.625 GHz at various experimental temperatures in static condition.

Notably, we confirm the presence of distinct features revealing positive and negative enhancements at 193.325 GHz and 193.875 GHz, respectively, corresponding to the ZQ and DQ transitions associated with the SE DNP. Remarkably, these transitions align with the nuclear Larmor frequency, positioned approximately ±294 MHz away from the center of the EPR line at 193.625 GHz. The SE signatures persist at all temperatures under static (Figure 2A) and MAS (Figure 2B) conditions.

A central absorptive feature, commonly described as OE DNP in the literature, was also observed in the DNP profile, with the center of the feature spanning the BDPA EPR line, and a linewidth of ~150 MHz at the base for the central DNP feature. The central feature has a similar appearance under MAS and static conditions at 60 K and 100 K, respectively, except the absorptive feature is more asymmetric under MAS conditions. In fact, skewness of the central DNP profile is seen under both static conditions (below 50 K) and under MAS conditions visible at all temperatures examined in this study (see Figure S5). When extrapolating these observations to cryogenic temperatures above 90 K where prior literature studies of DNP mechanisms are performed, our results are in accordance with what has been reported in the literature, featuring SE DNP together with a central absorptive feature at around 100 K.

Next, we focus on studying the effect of temperature on the line shape of the DNP profile. Pylaeva et al.^37,38 and Delage-Laurin et al.³⁹ proposed intramolecular charge transfer mediated by the mixed-valence nature of BDPA as the source of electron–nuclear hyperfine fluctuations of the order of the EPR Larmor frequency in the sub-THz range, which are furthermore suggested to be temperature independent down to 1.2 K⁴⁰. Consequently, the effectiveness of the OE relying on this charge transfer mechanism in BDPA variants has been proposed to be temperature independent, which would be consistent with the observation of the apparent OE DNP features across a wide range of temperatures between 1.2 K and 90 K, as well as higher temperatures^39-41. Furthermore, both the SE and OE DNP effect should increase with increasing saturation, i.e. decreasing electron spin polarization, unless a slower T_1e limits the replenishing rate of polarized electron spins. Hence, the OE DNP effect is expected to either minimally change or increase with decreasing temperature. In contrast, the temperature dependence of the ESC-DNP is more complex since it sensitively depends on the balance between achieving saturation of the weakly coupled electron spin and maintaining a polarization differential between the weakly coupled electron spin and the ESC. This is because ESC-DNP relies on an inhomogeneously broadened EPR spectrum to generate and maintain an electron spin polarization gradient across the EPR frequencies under microwave saturation that is then transferred to the coupled nuclear spins, giving rise to DNP enhancements. As a result, ESC-DNP relies on maintaining partial saturation of the electron spin ensemble, with the extent of saturation increasing at lower temperature since spin dynamics is slowed down and longer electron T_1e and T_2e relaxation is observed. However, saturation and crosstalk between electron spin populations at lower temperature may obliviate the selective saturation condition between spin populations needed to maintain a maximum electron spin polarization differential. We measured the DNP profile with decreasing temperature from 100 K to 10 K to investigate how the SE and the central feature change with temperature.

The SE DNP exhibited the expected behavior of increasing DNP enhancements with decreasing temperature from 100 K to 10 K, presumably due to enhanced saturation (Figure 2A). To verify this hypothesis, we also measured the power-dependent DNP build-up for the SE signatures and confirm that a linearly power-limited regime is observed at all temperatures. Interestingly, we observe a steeper increase in DNP enhancement with power at lower temperatures, hinting at a greater extent of ZQ or DQ saturation at lower temperatures (Figure 2C and Figure S6A). These results correlate with the SE DNP effect increasing with decreasing temperatures.

Interestingly, the central absorptive feature attributed to OE DNP under static conditions maintains a largely absorptive feature, but shows a slight increase in skewness towards lower temperature, and significant decrease in intensity with decreasing temperature. However, OE DNP is not expected to decrease in amplitude with decreasing temperature, given that the OE DNP in BDPA has been suggested to be temperature independent under saturating conditions, while saturation should increase at lower temperature. We, therefore, examined whether the central feature is observed under saturating or power-limiting conditions by measuring the power-dependent DNP build-up of the central features (Figure 2D and Figure S6B). Unlike the SE DNP feature, the central feature is indeed obtained under low power conditions. This by itself is a remarkable finding that a solid-state microwave source with ~350 mW output at 6.9 T, without the use of a resonant microwave structure, is sufficient to achieve saturation of the DNP effect, confirming that saturation should not affect the temperature-dependent OE DNP effect.

Under MAS conditions, the central feature undergoes a change in shape with decreasing temperature, transitioning from an absorptive to a dispersive profile, and an overall smaller enhancement. If the central feature were a combination of both absorptive and dispersive components, the results would indicate that the absorptive feature linked to "OE DNP" is decreasing with temperature, as observed for the central absorptive feature under static conditions.

The factor other than saturation that dictates OE DNP efficiency is the dynamics causing e-n hyperfine fluctuations. So far, changes observed in the central DNP feature with decreasing temperature are inconsistent with the anticipated temperature independence of the e-n hyperfine fluctuations originating from the mixed valence nature of BDPA. In case there are dynamics that have not been accounted for leading to e-n hyperfine fluctuations, that decrease in amplitude with decreasing temperature between 100 K and 25 K, an additional strategy is needed to test whether the observed features are due to modulation in e-n dynamics or saturation. This can be achieved by comparing the DNP profile of the same sample under MAS and static conditions, since MAS at a low spinning rate between 0 and 3 kHz cannot alter the e-n hyperfine fluctuation dynamics in any relevant way for OE DNP at 7 Tesla that is proposed to be of the order of 200 GHz (EPR frequency), but will have dramatically different effects on the selective saturability of the inhomogeneously broadened EPR spectrum. The SA-BDPA spectrum is influenced by g anisotropy and further distorted due to inhomogeneous dipoler coupling of SA-BDPA. Surprisingly, we see drastically different intensities and shapes for the central feature between the two conditions, but at otherwise comparable conditions (e.g., the central DNP feature at 48 K under MAS and that at 50 K under static conditions, Figure 2A-B). Interestingly, the central feature has much greater overall intensity under MAS conditions but is much more dispersive compared to static conditions. Since the e-n hyperfine fluctuations should be independent of the MAS frequency of 0, 3, or 5 kHz spinning, these results suggest a much more dominant role of multi-electron spin effects and crosstalk that is modulated by MAS under CW μw irradiation. This is because under monochromatic CW irradiation over several rotor periods (and longer), the microwave excitation energy with MAS crosses multiple energy-matching conditions for ESC-DNP that includes truncated CE and TM DNP¹⁰.

If ESC-DNP is responsible for the central DNP feature, why does it become more dispersive and asymmetric at lower temperatures and under MAS? The presence of a central DNP feature relies on a heterogenous distribution of strongly coupled ESCs and weakly coupled electron spins. When the T_1e relaxation time of the strongly coupled ESC is short, the tCE condition is fulfilled and the central DNP feature is absorptive. Conversely, when the T_1e relaxation time of the strongly coupled ESC is long, the central DNP feature is dispersive. The T_1e of the ESC is longer at lower temperature and under MAS, and hence the dispersive central profile becomes more pronounced. The idea that the SA-BDPA sample consists of a multi-electron spin system is further supported by the microwave power trend shown in Figure 2D. There is a clear indication that full saturation is achieved of the central DNP features at microwave powers near or below 50 mW and at 50 K and lower temperatures, indicating a synergistic effect due to multi-electron couplings. The central feature demonstrated a favorable DNP power saturation, which was already achieved at the highest temperature investigated in this study, reaching 100 K (Figure 2D). Similar findings were also reported in the literature^29,42.

It is important to acknowledge that the effective SA-BDPA concentration is lower than the nominal concentrations due to the instability of SA-BDPA under experimental conditions. Therefore, there may be sample-to-sample variations leading to differences in the DNP efficiency with different SA-BDPA samples. However, the changes in the principal features for the DNP profiles with temperature and MAS were consistent from sample to sample, indicating that the nominal SA-BDPA concentration is not as critical to the DNP mechanism. The tendency of clustering in SA-BDPA seems to be intrinsic to the radical system. Consistent with this hypothesis, Eaton and coworkers have reported on the clustering of BDPA at concentrations as low as 12.5 μM using X-Band (9.5 GHz) CW EPR measurement experiments⁴³.

To understand whether there is inter-electron spin crosstalk between isolated and clustered SA-BDPA populations, we employed a technique known as the Electron Double Resonance (ELDOR) experiment to evaluate the presence of heterogeneously coupled multi-electron spin clusters experimentally. ELDOR involves irradiating the EPR spectrum with microwaves at a given pump frequency and detecting changes in the EPR signal amplitude at a different probe frequency. Figure 3A shows the echo-detected EPR spectrum of SA-BDPA at 30 K. ELDOR is performed with the pump frequency set at various frequencies across the EPR spectrum and the echo intensity measured at a given probe frequency (indicated in Figure 3A). Essentially, ELDOR allows for the detection of crosstalk between different electron spin ensembles separated in frequencies corresponding to the pump and probe frequencies.

Figure 3:

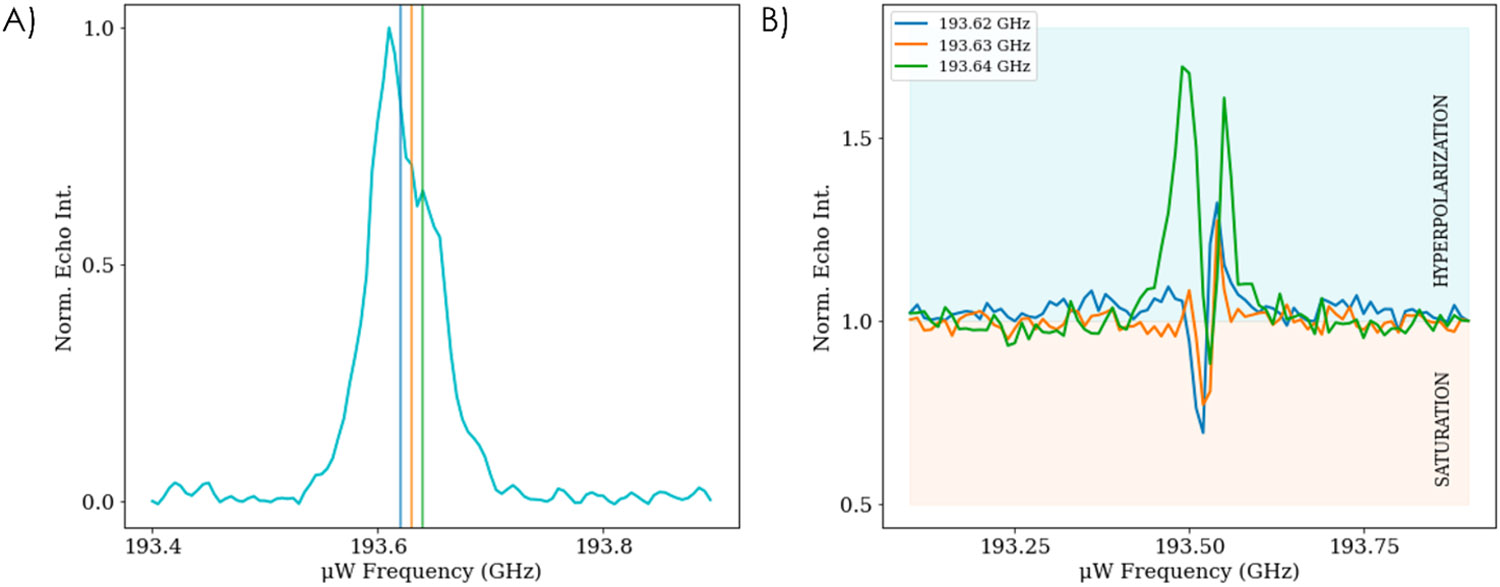
(A) Echo-detected EPR line featuring vertical lines at 193.2 GHz (blue), 193.63 GHz (orange), and 193.64 GHz (green), representing the probe frequencies employed for pump-probe ELDOR measurement and (B) pump-probe ELDOR of 0.37-mg/μL 60/40 v/v d8-glycerol/D2O. The EPR frequency profile measured echo signal intensity as a function of 350mW irradiation frequency swept from 193.4 GHz to 194 GHz. The pump-probe ELDOR profile demonstrates the electron-electron crosstalk of electrons at the probe frequencies, 193.62 GHz (blue), 193.63 GHz (orange), and 193.64 (green) to those at the pump frequencies.

We performed three sets of ELDOR measurements at different probe frequencies (193.62, 193.63. 193.64 GHz) while stepping through the pump frequencies across the EPR spectrum. At each of the three probe frequencies, we observed an intense negative dip in the EPR echo signal at the corresponding probe frequency, indicating saturation of the electron spins when the pump frequency is in the vicinity of the probe frequency (Figure 3B). Strikingly, we detected an echo intensity much greater than 1 (Boltzmann or Thermal polarization) at a pump frequency, e.g., 193.593 GHz off resonance from the probe frequency of 193.64 GHz, by approximately ±10 to 40 MHz depending on the probe frequency. An echo signal intensity above Boltzmann is evidently representative of hyperpolarization of the electron spins. Such electron spin hyperpolarization is observed across all three probe frequencies at this off-center pump frequency. Such electron spin hyperpolarization has been previously observed in other systems, such as Trityl-OX063¹³ and BDPA,²⁵ and is a recognized indicator of strong electron-electron (e-e) couplings, of the presence of a heterogeneous electron spin ensemble as well as a signature of TM DNP^44-46. The detailed mechanism underlying strong e-e coupling leading to hyperpolarization will be discussed in a separate publication. In short, this is due to the conversion of Zeeman order to dipolar order, fulfilled under selective μw irradiation of a broadened EPR line. What is significant about the observed ELDOR results is that the extent of electron spin hyperpolarization is very sensitive to the frequency of the probe pulse, varied over a narrow range of 20 MHz from 193.62 GHz to 193.64 GHz, falling within the 100 MHz baseline linewidth of SA-BDPA (by considering the g anisotropy), see Figure 3A. In fact, this makes sense if μw irradiation by the pump pulse is generating a hyperpolarized dipolar order and the probe pulse is converting it to an observable signal. Here, the hyperpolarized echo intensity rising above 1 is maximal when the probe frequency is set near the offset frequency where the hyperpolarized dipolar order is maximal.

Given these results, rationalizing the absorptive and dispersive shape of the central feature and its width in terms of ESC-DNP mechanisms is not intuitive nor trivial. We sought to obtain a more intuitive understanding of the role of ESCs and their spin dynamics on the DNP frequency profile through quantum mechanical calculations of a multi-electron spin system with systematically tuned parameters. Our objective is to understand whether the coupling, electron relaxation and geometry of a multi-electron spin system under physically viable conditions, without the considerations of e-n hyperfine fluctuations, is sufficient to generate both absorptive and dispersive DNP profiles at the central frequency spanning the width of the SA-BDPA EPR spectrum.

Quantum mechanical (QM) simulations were performed using the SpinEvolution software⁴⁷ using parameters that resemble the experimental conditions, including the external magnetic field, relaxation times, and MAS. A three-electron one-proton (e-e-e-¹H) spin system with highly uneven e₁-e₂ and e₁-e₃ vs. e₂-e₃ couplings was explored based on our hypothesis that a strongly coupled ESC weakly coupled to an isolated electron spin population is needed to replicate the experimentally observed DNP profile. Here, e₁ represents the isolated electron spin weakly coupled to e₂ and/or e₃ and e₂-e₃ represents a minimal model of a strongly coupled ESC, such that the three-electron spin system models the coexistence of a weakly coupled electron spin with an ESC. A depiction of such a e-e-e-¹H coupling network is shown in Figure 4A.

Figure 4:

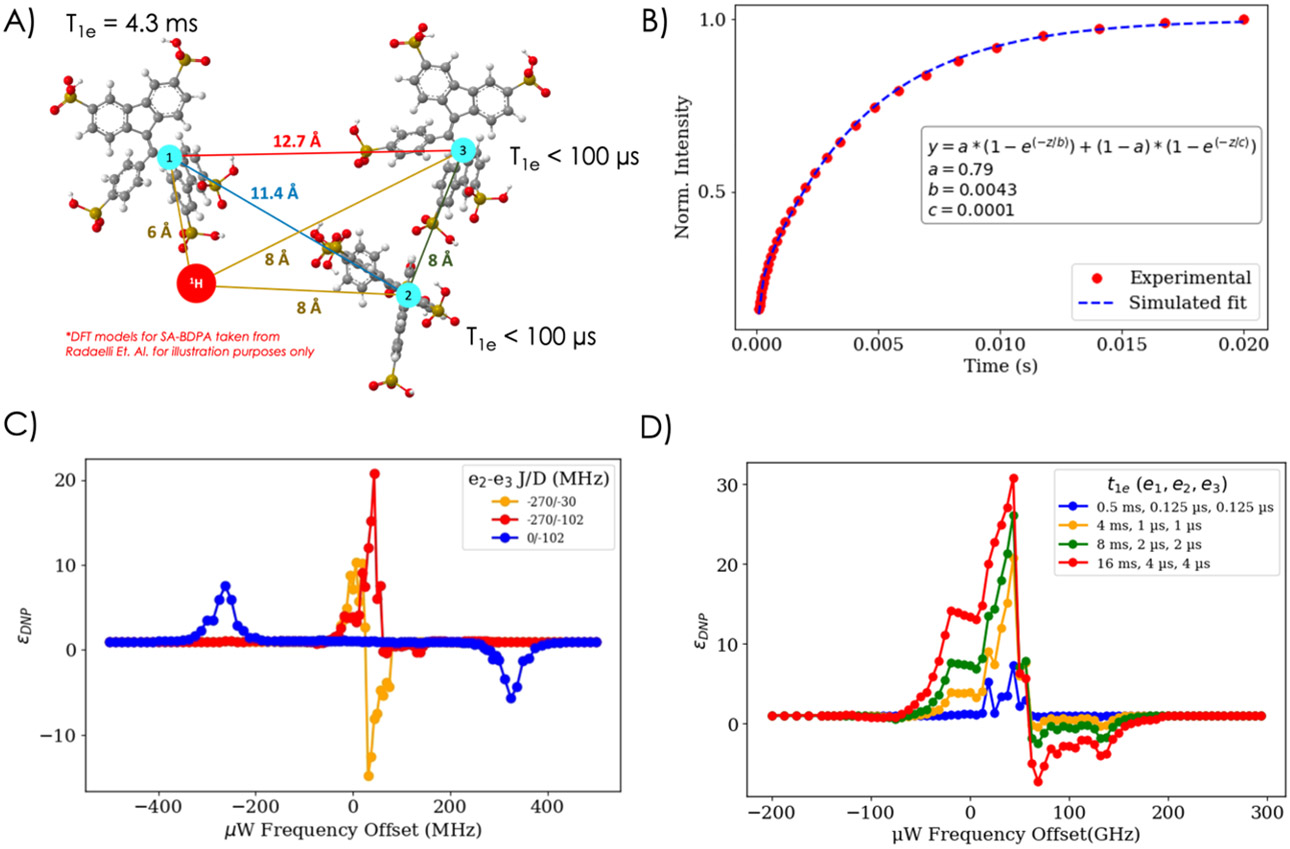
(A) 3-spin SA-BDPA structure reproduced from Radaelli, A.; Yosihara, H. A. I.; Nonaka, H.; Sando, S.; Ardenkjaer-Larsen, J. H.; Gruetter, R.; Capozzi, A. 13C Dynamic Nuclear Polarization Using SA-BDPA at 6.7 T and 1.1 K: Coexistence of Pure Thermal Mixing and Well-Resolved Solid Effect. J. Phys. Chem. Lett. 2020, 11 (16), 6873–6879. Copyright © 2020 American Chemical Society. B) Echo detected T_1e while microwave irradiating at 193.6 GHz at 10 K. C) The simulated DNP profile for three different scenarios, depending on the J and D couplings. In blue is the scenario where the J couplings for all e-e pairs are zero and the e₂-e₃ electron pair are 8 Å apart (-102 MHz D coupling), the shortest expected e-e distance. In orange is the scenario where the J couplings are on for all e-e pairs and is –270 MHz for e₂-e₃, but the e₂-e₃ distance is 12 Å (30 MHz D coupling), further apart than 8 Å. In red is the scenario in orange except for the e₂-e₃ distance at 8 Å. D) DNP profile simulations of a three-electron BDPA system with all electron t_1e's being varied, using the same D and J couplings as shown in red in Figure 4C.

Several parameters can be varied for the three-electron spin system: three T_1e’s, three dipole-dipole coupling and three J-coupling strengths. This results in a large parameter space that cannot be fully explored without a dedicated data science approach that is outside the scope of our study at the present time. Therefore, empirical SA-BDPA parameters together with reasonable assumptions were used to limit the simulation parameter space. The g tensor of [g_x, g_y, g_z] = [2.0028, 2.0026, 2.0025] reported for BDPA¹⁹ was used for all simulations. We model BDPA with two types of electron spin populations, weakly coupled and slow relaxing (e₁) and strongly coupled and fast relaxing (e₂-e₃), and spatially arrange the spins in a plausible geometry. The minimum e-e distance reported for two proximally associated SA-BDPA is 8 Å according to Radaelli and coworkers, giving rise to a dipolar cut-off frequency of 91 MHz^20,49. This value gives rise to a total span of the dipolar coupling of the order of 300 Mhz. Hence, this distance of 8 Å was assumed for the shortest e₂-e₃ distance for all e-e-e-¹H. The T_1e for SA-BDPA measured at 10 K under static conditions is biexponential, with a slow component relaxing at T_1e = 4.3 ms and a fast component relaxing at T_1e = 1 μs (See Figure 4B). Accordingly, this T_1e = 4.3 ms was assigned to the slower relaxing electron spin, e₁. Meanwhile, the faster relaxing e₂ and e₃ are assumed to be coupled together strongly, such that their relaxation times are identical to each other, and the short T_1e value of 1 μs was assigned. The distances between e₁-e₂ and e₁-e₃ are assumed to be 11.4 and 12.7 Å, respectively, which is relatively close to the e-e distance required for cross-effect radicals such as AMUPOL^50,51. These distances are assumed to be only slightly different to account for inherent asymmetry expected to be found in clustered systems. Clustering due to stacking of conjugated systems, such as BDPA, is known to induce high J-coupling. However, there is no study on the magnitude and distribution of J-couplings from through-space coupling of two BDPA molecules. The J-coupling between two conjugated molecules at 8 Å distances can easily exceed −270 MHz depending on the exact orientation and solvent condition. Of note, the total span of D-coupling between two BDPAs at 8 Å separation is about 300 MHz, given the dipolar coupling constant of ~-102 MHz. The J-couplings for the weakly coupled pairs are assumed to be small such as −15 MHz for e₁-e₂ and −5 MHz for e₁-e₃^50-53. Negative J-coupling values were chosen to retain the same sign as the negative e-e dipolar coupling constants. It is important to highlight that the specific J- and D- coupling values listed here are coupling constants. When these constants are integrated with powder averaging over 50 or so orientations, it leads to a distribution of J and D couplings, as reflected in our simulations. An e⁻¹H distance between 6 Å to 8 Å is assumed to be a reasonable e-¹H distance in BDPA.

SpinEvolution simulations performed with the just discussed parameters are illustrated in Figure 4C. Under the constraint parameters and in the presence of D (coupling constant – 102 MHz) and J coupling (of the order −270 MHz) between e₂-e₃, we replicate a prominent absorptive central feature as witnessed in experiments (Figure 4C, red). Conversely, the solid effect is quenched under these conditions, likely due to substantial J coupling between e₂-e₃, leaving no decoupled e-n pair. When the J coupling between e₂-e₃ is turned off, but the 8 Å distance between e₂-e₃ is maintained, this still gives rise to a dipolar cut-off frequency of 91 MHz, yet the central DNP feature disappears (Figure 4C, blue). Instead, the solid effect now reemerges, likely because there is not enough energy matching to enable triple e-e-n spin flips. When the J coupling between e₂-e₃ is maintained, but the dipolar coupling turned low by increasing the e₂-e₃ distance to 12 Å, the central DNP feature becomes dispersive (Figure 4C, orange). This is because the EPR frequency of the strongly coupled e₂-e₃ systems is not shifted sufficiently with respect to the center resonance without both the J and D couplings present, so that resonance matching occurs with ESCs to either side of the central frequency, giving rise to a dispersive pattern. We can also construct a scenario where J coupling alone will give rise to a central absorptive DNP feature, but this requires near exact energy matching between the J coupling and the ¹H Larmor frequency of −294 MHz at 6.9 Tesla (Figure S9). We learn that the shape of the central feature, e.g., the skewness and whether it is positive or negative, is heavily influenced by the strength of the J-coupling, mixing with D-coupling and its proximity to the nuclear Larmor frequency (Figure S10).

Now that absorptive features can be reliably replicated by computer simulations using strong electron-electron coupling, the next step is to determine if the absorptive-to-dispersive transition with decreasing temperature as seen experimentally (see Figure 2B) can be simulated. To mimic the experimental result, we can assume that changing temperature has no influence on the coupling of the e-e-n spin network as the sample is prepared in a glassing agent and is not dynamically evolving, but only influences electron spin relaxation. Specifically, electron T_1e becomes longer with decreasing temperature. We illustrate in Figure 4D the simulated DNP profiles as a function of electron T_1e, from 0.5 ms to 16 ms for e₁ and 0.125 μs to 4 μs for e₂ and e₃. Note that all other spin parameters have been preserved as shown in Figure 4A and 4C (red).

The simulated DNP profile mimics remarkably well the experimentally obtained temperature-dependent trends for the DNP profiles, with the relative absorptive and dispersive contribution in the central feature of the profile changing with T_1e electron spin relaxation. At short T_1e’s (i.e., higher temperatures) the profile appears to be more absorptive and at long T_1e’s (i.e., lower temperatures) the profile appears to be more dispersive.

A central DNP feature requires ESC-DNP mechanisms that utilize an inhomogeneous electron spin network. Hence, such features cannot be replicated with a two-electron e-e-n spin network (SpinEvolution calculations of DNP profiles of e-e-n spin systems are shown in Figure S7). The minimal ESC comprises of three coupled electron spins, with two electron spins experiencing strong J and D couplings, weakly coupled to a third electron spin and a nuclear spin, as modeled here. For a four coupled ESC, many more combinations of parameters can give rise to the observed phenomena. Exchange or J coupling between the electron spins within the ESC can give rise to hyperfine fluctuation frequencies of the same order of magnitude as the coupling, that will generate a central absorptive DNP profile if it matches the ¹H NMR Larmor frequency. Hence the relevant hyperfine fluctuations that contribute to ESC-DNP are in the NMR frequency range, unlike Overhauser DNP that requires hyperfine fluctuations near the EPR Larmor frequency.

To obtain an absorptive ¹H DNP profile for SA-BDPA clusters, multiple conditions must be fulfilled. The strongly coupled ESCs need to not only experience exchange, or J, coupling matching the ¹H NMR Larmor frequency, but also experience rapid T_1e so that their EPR signatures cannot be readily saturated. D coupling can principally achieve the same effect as J coupling, but the e₂-e₃ distance in the three-electron spin system would need to be < 5-6 Å. However, the presence of D coupling of proximal electron spins, e₂-e₃, of 8 Å in addition to J coupling renders the observed central absorptive feature more robust with respect to small changes in the dipolar coupling, J coupling, and g factor orientation. For the ESCs to effectively contribute to DNP, they must also crosstalk with the rest of the weakly coupled electron spin populations. This has been verified by ELDOR experiments. Remarkably, the electron spin system subjected to a selective pump pulse of an ELDOR pulse sequence gives rise to electron spin hyperpolarization. This is a signature of the generation of dipolar order from Zeeman order by selective saturation and is only observed in the presence of strong e-e couplings. Finally, the weakly coupled, narrow-line, electron spin population must be subject to relatively weak D and J coupling and have relatively long T_1e so that its EPR signature can be easily saturated and give rise to power-efficient DNP effects with an absorptive central feature. This set of conditions that give rise to an absorptive central ESC-DNP feature also satisfies the tCE condition in which the EPR envelope of the narrow-line radical dictates the DNP profile, given that the very short T_1e of the strongly coupled ESCs renders their saturation prohibitive, such that their contribution is only visible via the saturation of the narrow-line EPR populations in crosstalk with the ESCs.

Quantum mechanical calculations provide an intuitive, microscopic-level understanding of the multi-electron spin system architecture giving rise to an absorptive DNP feature with low microwave power requirements. Extensive computational explorations revealed the type of spin cluster design and dynamics that gives rise to the experimentally observed DNP features. Such calculations are well suited to predict the dependence of these effects on the ESC design, magnetic field and MAS frequency, as further described in Figure S11 and Figure S12.

This study highlights a new opportunity to use strongly coupled ESCs of narrow-line paramagnetic species for power-efficient DNP with potentially dramatic signal enhancements. A cluster of conjugated radicals with exchange coupling matching the ¹H NMR frequency (exchange coupling of up to 1 GHz is readily reached), and D coupling of 100s of MHz offering margins of error, weakly coupled to a narrow-line radical, is the new PA archetype worth exploring. The development of power-efficient DNP mechanisms that can be maximized with microwave power available from a solid-state source at high field will be a game changer for DNP that can significantly expand the accessibility and applicability of DNP-enhanced NMR spectroscopy to a wider array of research and applications.

Highlights:

• Multi electron spin cluster driven ¹H DNP observed with Sulfonated BDPA (SA-BDPA)

• Multi electron spin cluster-dependent DNP effects vary with electron T_1e relaxation.

• Low power requirement for electron spin cluster-driven DNP using SA-BDPA

• Quantum mechanical simulations using three coupled electron spins can replicate key DNP features observed in experiments with SA-BDPA