After BRCA1 and BRCA2—What Next? Multifactorial Segregation Analyses of Three-Generation, Population-Based Australian Families Affected by Female Breast Cancer

Abstract

Mutations in BRCA1 and BRCA2 that cause a dominantly inherited high risk of female breast cancer seem to explain only a small proportion of the aggregation of the disease. To study the possible additional genetic components, we conducted single-locus and two-locus segregation analyses, with and without a polygenic background, using three-generation families ascertained through 858 women with breast cancer diagnosed at age <40 years, ascertained through population cancer registries in Melbourne and Sydney, Australia. Extensive testing for deleterious mutations in BRCA1 and BRCA2, to date, has identified 34 carriers. Our analysis suggested that, after other possible unmeasured familial factors are adjusted for and the known BRCA1 and BRCA2 mutation carriers are excluded, there appears to be a residual dominantly inherited risk of female breast cancer in addition to that derived from mutations in BRCA1 and BRCA2. This study also suggests that there is a substantial recessively inherited risk of early-onset breast cancer. According to the best-fitting model, after excluding known carriers of mutations in BRCA1 and BRCA2, about 1/250 (95% confidence interval [CI] 1/500 to 1/125) women have a recessive risk of 86% (95% CI 69%–100%) by age 50 years and of almost 100% by age 60 years. Possible reasons that our study has implicated a novel strong recessive effect include our inclusion of data on lineal aunts and grandmothers, study of families ascertained through women with early-onset breast cancer, allowance for multiple familial factors in the analysis, and removal of families for whom the cause (i.e., BRCA1 or BRCA2) is known. Our findings may have implications for attempts to identify new breast cancer–susceptibility genes.

Introduction

Various studies have shown that family history is an important risk factor for female breast cancer, especially if close relatives have early-onset disease (Newman et al. 1988; Claus et al. 1990, 1991; Colditz et al. 1993; Slattery et al. 1993; McCredie et al. 1998). The increased risk associated with an affected first-degree female relative varies from about 1.5-fold to 3-fold or more, depending on the age at onset of the relative and the age of the unaffected at-risk woman (Pharoah et al. 1997). To explain this extent of familial aggregation, there must exist a very strong underlying familial risk factor, or multiple familial risk factors of moderate risk (Peto 1980; Hopper and Carlin 1992). Deleterious mutations in the recently discovered genes BRCA1 (MIM 113705) and BRCA2 (MIM 600185) that cause a dominantly inherited high risk appear to explain <20% of familial aggregation of female breast cancer at age <55 years (Peto et al. 1999). Currently identified environmental risk factors, as measured by questionnaires, that are correlated within relatives are unlikely to explain >10% (Hopper and Carlin 1992). Therefore, there is still much to be learned about why female breast cancer tends to run in families more often than would be predicted by chance alone.

Prior to the discovery of BRCA1 and BRCA2, most segregation analyses of female breast cancer family data modeled familial aggregation by a single mode of inheritance and, without measuring actual genetic variants, supported the role of rare, highly penetrant, and dominantly inherited genetic factors (Bishop and Gardner 1980; Newman et al. 1988; Hall et al. 1990; Claus et al. 1991; Iselius et al. 1991; Eccles et al. 1994; Essioux et al. 1995). Some more recent segregation analyses, however, have suggested that a recessive or codominant pattern of inheritance may also be plausible (Goldstein and Amos 1990; Chen et al. 1995; Baffoe-Bonnie et al. 2000).

In this article we have conducted segregation analyses to investigate models of familial aggregation of female breast cancer that consider together different modes of inheritance—dominant, recessive, and polygenic—using three-generation population-based families from Australia that are affected by breast cancer (Hopper et al. 1994, 1999a, 1999b; McCredie et al. 1998). These families have been ascertained through incident cases of breast cancer in women diagnosed before age 40 years (probands). We have conducted analysis with and without excluding families on the basis of a proband already found to carry a deleterious mutation in BRCA1 or BRCA2, following extensive sequencing and mutation testing carried out over the past 5 years.

Subjects and Methods

Subjects

Each family was ascertained through a woman who had been recently diagnosed with breast cancer at age <40 years, reported to the Victoria or New South Wales cancer registry and living in Melbourne or Sydney, respectively. Between 1992 and 1995, a total of 467 such families were studied (McCredie et al. 1998), and from 1996–1999 a further 391 such families have been studied as part of the NIH-funded Cooperative Family Registry for Breast Cancer Studies (Hopper et al. 1999b), giving a total of 858 case families.

For each such proband, a face-to-face interview was used to collect information on a range of known or putative risk factors. Prior to interview, each proband was told that we wished to know about any cancers in each of her adult first- and second-degree relatives. She was also informed that we wished to interview her adult living relatives (i.e., her mother, siblings, both maternal and paternal grandparents, and lineal aunts), and her cooperation in approaching those relatives was sought. The same questions asked of the proband—including “any cancers in relatives?”—were also asked of these relatives, usually by a telephone interview. That is, the family's history of cancer was gathered from a number of relatives and over a period of time, usually several months, during which they were encouraged to investigate their family’s cancer history. For all relatives for whom there was a report of a cancer, questions about age and place of residence at diagnosis, as well as age at time of interview and age at death (if appropriate), were asked. Censored age was defined as the lesser of the latter two ages. Verification of all reported family cancers was sought through cross-linking with cancer registries, death certificates, and medical records (see McCredie et al. 1998). Blood samples were collected from the probands and some relatives. Further details about the design and conduct of this breast cancer case/control family study can be found in work by Hopper et al. (1994), McCredie et al. (1998), and Hopper et al. (1999a). Although the full study also involved control families, ascertained through unaffected women chosen by use of the Australian electoral rolls and studied by identical processes, the following segregation analyses use only the data from those families ascertained through an affected proband (i.e., case families).

Statistical Analysis

The cumulative probability of breast cancer in a defined cohort of relatives of the probands, F(t)=1-S(t), where S(t) is the survivor function, was estimated by the Kaplan-Meier product-limit method (Kaplan and Meier 1958), on the basis of disease status and censored age, and was calculated by use of the statistical software STATA (STATA 1999). The variance of the product-limit estimator was estimated by Greenwood’s formula (Greenwood 1926) and was used to calculate confidence intervals. This was performed separately for sisters, mothers, and combined maternal and paternal lineal aunts.

Complex segregation analyses were performed using breast cancer status, age at diagnosis or age at interview or death, and vital status for the proband and her adult first- and second-degree relatives (see our fig. 1 and fig. 1 of Cui and Hopper [2000]), by use of the software MENDEL (Lange and Weeks 1988). Under maximum-likelihood theory, we fitted what traditionally have been called single-locus and two-locus models of “major gene” effects with different modes of inheritance (dominant, recessive, and codominant). We also fitted a hypergeometric polygenic model following Lange (1997), with and without a single-locus major-gene effect (Antoniou et al. 2000). To adjust for ascertainment, the likelihood for each pedigree was conditioned on the proband being affected at her age at diagnosis of breast cancer.

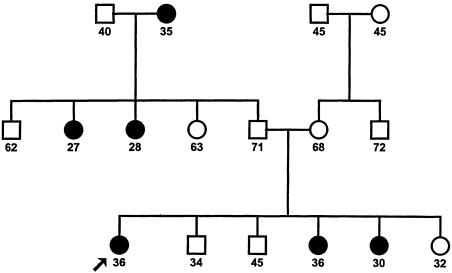
Figure 1.

Three-generation family, ascertained through a proband with breast cancer at age <40 years, showing age at onset, death, or interview, that gives most support for a recessively inherited risk of breast cancer. The proband has not been found to carry a germline mutation in either BRCA1 or BRCA2.

For a single-locus model, let a represent a disease allele and assume Mendelian mode of transmission. Let p=1-q be the population frequency of all disease alleles at this locus and assume random mating and Hardy-Weinberg equilibrium at this locus (Elandt-Johnson 1971). Note that, despite its traditional name, this model may also represent effects with the same mode of inheritance at multiple loci—provided that, at each of these loci, the at-risk group (i.e., Aa or aa for dominant inheritance or aa for recessive inheritance) is so rare that it is highly unlikely that more than one locus is contributing to this mode of inheritance of genetic risk within the same family.

In accordance with Claus et al. (1993) and Ford et al. (1998), a proportional hazards model was assumed in which the hazard function of developing breast cancer at age t for an individual with i disease alleles, i=0, 1, 2, is given by

We set HR₀(t)=1, so that HR_i(t) is the genetic hazard ratio for individuals with i alleles, compared with that of noncarriers (i.e., individuals with no disease alleles) at age t. We use the term “hazard ratio,” instead of “relative risk” or “relative hazard,” to be consistent with the entry in Encyclopedia of Biostatistics (Benichou 1997, pp. 11–27). We modeled HR_i(t) as a step function, constant within age groups (t_j-1, t_j), where j=1, 2,⋅⋅⋅. Because the focus of this article is female breast cancer and no cases of male breast cancer were reported to us in the studied families, we have assumed for the sake of simplicity that, in males, λ_i(t)=0 for all values of i.

Let λ(t) be the population incidence of female breast cancer at age t (Australian Institute of Health and Welfare 1999). Then the hazard function for noncarriers is given by

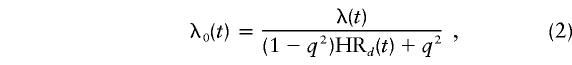under dominant inheritance, where HR₁(t)=HR₂(t)=HR_d(t); by

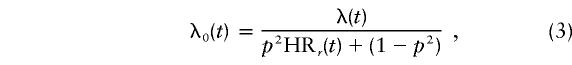under recessive inheritance, where HR₁(t)=1 and HR₂(t)=HR_r(t); and by

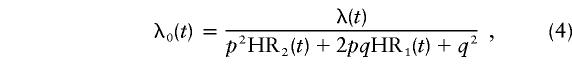under the codominant model, where HR₁(t) and HR₂(t) are not necessarily equal to HR₀(t) or each other. In MENDEL (Lange and Weeks 1988), we used ln(p), ln(HR₁(t)), and ln(HR₂(t)) as unknown parameters, as their distributions are close to normal. Their variance estimates were obtained from the asymptotic covariance matrix.

The probability that a female with i disease alleles develops breast cancer at age t is given by

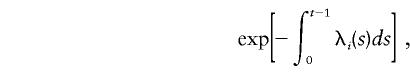and the probability that a female does not develop breast cancer before age t is given by

where i=0, 1, 2 indicates the number of disease alleles.

For a two-locus model, without loss of generality, we assumed dominant inheritance for the first locus and recessive inheritance for the second. The interaction between the effects of these two loci was allowed to be multiplicative or additive. Under a multiplicative model, the hazard ratio of carriers of both a dominant and recessive risk is given by HR_d×HR^′_r , where HR_d is the hazard ratio for carriers of the dominant risk and HR^′_r the hazard ratio for carriers of the recessive risk. Under an additive model, the hazard ratio is HR_d+HR^′_r . The correlations between the estimates of pairs of model parameters, e.g. the dominant and recessive allele frequencies, and the dominant and recessive hazard ratios, were estimated from the asymptotic correlation matrix calculated by MENDEL (Lange and Weeks 1988).

We also fitted models that included a single-locus “major-gene” effect plus a hypergeometric finite gene component, following Cannings et al. (1978), Fernando et al. (1994), Antoniou et al. (2000), and Lange (1997). This approach emulates incorporation of a classic “polygenic liability model” based on an underlying polygenically determined liability. The approach thus attempts to model familial effects other than those caused by the putative major-gene effects of a given mode of inheritance. The hypergeometric polygenic model (Cannings et al. 1978) proposes n independent and additive loci, each with two equally likely alleles (positive or negative), and genotypes with the same number of positive alleles are assumed to be equivalent. Thus, there are 2n+1 possible genotypes. The genotype of an offspring is determined by independently sampling n alleles, without replacement from the genotypes of each parent. The value of these polygenotypes is given by

where X is the number of positive alleles out of 2n and has a binomial distribution with parameter  1/2, so that SD is the standard deviation of the polygenic component. In this analysis, we used n=3, following Antoniou et al. (2000). Further details about this method can be found in Lange (1997) and Fernando et al. (1994).

Because of the computational demands of performing this modeling, the hazard ratio for the single locus was assumed to be a constant over all ages. Again, the mode of inheritance of the major-gene effect was allowed to be dominant, recessive, or codominant. The age-specific hazard function was then assumed to be λ_i(t)e^P, where λ_i(t) is given by equation (1), with λ₀(t) given by (2), (3), or (4), respectively.

Nested models were compared using the likelihood ratio criterion. Otherwise we used the Akaike’s information test (Akaike 1974), defined as AIC=2(−maximum log-likelihood + number of parameters estimated). It serves as a measure for assessing the relative fits of unnested models by adding a penalty to each log-likelihood, to reflect the number of parameters estimated under a particular model. The most parsimonious model is taken to be that with the smallest AIC. To identify the families most likely to be contributing to a particular major-gene effect (dominant, recessive, or codominant), we calculated the change in log-likelihood for each family when that effect was included in the model.

Testing for Mutations in BRCA1 and BRCA2

A considerable amount of testing for mutations in BRCA1 and BRCA2 has been undertaken in the probands of these families. For a random sample of 93 probands from the 1992–1995 study, stratified by family history, the full coding region of BRCA1 was manually sequenced (Southey et al. 1999). For all 408 probands in the 1992–1995 study for whom a blood sample was taken, protein-truncation testing was undertaken for exon 11 of BRCA1 and exons 10, 11, and 27 of BRCA2 (Hopper et al. 1999a), which cover about two-thirds of the combined coding regions of BRCA1 and BRCA2. These probands were also screened for BRCA1 duplication 13 (the Alu-mediated 6-kb duplication in BRCA1; see Puget et al. 1999), and for the three ancestral Ashkenazi mutations (185delAG and 5382insC in BRCA1 and 6174delT in BRCA2). The same mutation testing has been undertaken for the 358 probands in the 1996–1999 study from whom a blood sample was obtained. In addition, manual sequencing of the entire coding region of BRCA1 and BRCA2 has been completed for 73 probands with two or more first- or second-degree relatives with breast cancer.

At the time of the segregation analyses reported in this article, a deleterious mutation had been identified in 34 probands (18 had mutations in BRCA1 only, 15 had mutations in BRCA2 only, and 1 had both a BRCA1 and a BRCA2 germline mutation; see Tesoriero et al. 1999). A modified segregation analysis of the families of the 18 probands in the 1992–1995 study found to carry a protein-truncating mutation in the defined exons above suggested that the average penetrance of these mutations was equivalent to a cumulative risk, to age 70 years, of ∼40% (Hopper et al. 1999a). To evaluate the effect of genetic susceptibility besides that caused by deleterious mutations in BRCA1 and BRCA2, we conducted the segregation analyses outlined above both on the full set of families and on the subset of families excluding the 34 mutation-carrying probands and their relatives.

Results

Descriptive Statistics and Analysis of Cohorts of Relatives

The total of 858 families (identified on the basis of 380 probands living in Sydney at diagnosis and of 478 living in Melbourne) contained 13,805 individuals. There were 6,289 female relatives of the probands, of whom 361 (6%) had been diagnosed with breast cancer. The family size, including the proband, was 7–39 individuals, with a median of 15. One quarter of the families had >20 members, and another quarter had <13 members. Only 5% of families had >25 members, and another 5% had <10 members. About one-third (245) of the probands had no sisters, one-third (294) had only one, and one-third (319) had more than one. On average, there were ∼1.7 maternal or paternal lineal aunts per family.

Table 1 shows the number and percentage of the probands by the number of relatives with breast cancer for different categories of relationship to the proband, and table 2 shows the number and percentage of women with breast cancer by age at diagnosis for different categories of family members. Of the probands, ∼70% (590/858) did not have any first- or second-degree female relatives with breast cancer. Five probands had two affected sisters, and one proband had three affected lineal aunts. Two probands had five affected relatives, and one proband had four.

Table 1.

No. of Probands by Number of Relatives with Breast Cancer, for Different Categories of Relationship to the Proband

	No. (%) of Probands with Affected Female Relatives
No. ofRelativeswithBreastCancer	Mother	Sister	Aunt	Grandmother	First Degree	Second Degree	Any
0	776 (90.4)	831 (96.8)	736 (85.8)	761 (88.6)	757 (88.2)	657 (76.6)	590 (68.8)
1	82 (9.6)	22 (2.6)	98 (11.4)	94 (11.0)	90 (10.5)	162 (18.9)	199 (23.2)
2	…	5 (0.6)	23 (2.7)	3 (0.4)	9 (1.1)	32 (3.7)	50 (5.8)
3	…	…	1 (0.1)	…	2 (0.2)	7 (0.8)	16 (1.9)
4	…	…	…	…	…	…	1 (0.1)
5	…	…	…	…	…	…	2 (0.2)

Table 2.

No. of Women with Breast Cancer, by Age at Diagnosis, for Different Categories of Family Members

	No. (%) of Affected Women
Age(years)	Proband(n=858)	Mother(n=858)	Sister(n=1,113)	Aunt(n=2,602)	Grandmother(n=1,716)
<30	84 (9.8)	1 (1.2)	2 (6.2)	6 (4.1)	1 (1.0)
30–39	774 (90.2)	11 (13.4)	11 (34.4)	25 (17.0)	4 (4.0)
40–49	…	21 (25.6)	18 (56.3)	35 (23.8)	19 (19.0)
50–59	…	24 (29.3)	1 (3.1)	42 (28.6)	24 (24.0)
60–69	…	21 (25.6)	…	28 (19.0)	18 (18.0)
70–79	…	4 (4.9)	…	10 (6.8)	23 (23.0)
⩾80	1858…8581	828…828	323…323	1 (0.7)	11 (11.0)
Total	858	82	32	147	100

Of mothers, ∼10% (82/858) had been diagnosed with breast cancer, as had 3% (32/1113) of sisters, 6% (147/2602) of lineal aunts, and 6% (100/1716) of grandmothers. The median age at diagnosis of breast cancer was 36 years (mean 35, SD 3.6) for the probands, 41 years (mean 40, SD 5) for the affected sisters, 51 years (mean 52, SD 11) for the affected mothers, 52 years (mean 51, SD 13) for the affected lineal aunts, and 60 years (mean 61, SD 15) for the affected grandmothers.

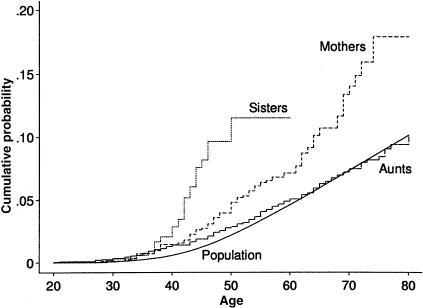
Figure 2 shows the cumulative probability of breast cancer for the Australian population, and for cohorts defined by sisters, mothers, and lineal aunts of the proband. Of Australian women, ∼7% are diagnosed with breast cancer before age 70 years, and 2% are diagnosed with breast cancer by age 50 years (Australian Institute of Health and Welfare 1999). For the sisters, however, ∼10% (95% confidence interval [CI] 7%–14%) were affected by age 50 years. For mothers, almost 14% (95% CI 11%–18%) were affected by age 70 years. There appeared to be a small excess risk in lineal aunts, at least up to age 50 years, with ∼3% affected by age 50 years (95% CI 2%–4%).

Figure 2.

Age-specific cumulative probability of breast cancer for the population, and for sisters, mothers and lineal aunts of the probands who had breast cancer before age 40 years.

Segregation Analyses: Single-Locus Models

Table 3 shows the fits for single-locus models on data from all 858 families. Under dominant inheritance alone, the allele frequency was estimated to be small (.001). When estimated as a constant, the hazard ratio was 63 (95% CI 45–89). When allowed to vary by age, the estimated hazard ratio decreased markedly with age, although this trend was of marginal statistical significance (P=.04). On the basis of the age-specific hazard-ratio estimates, the cumulative probability of breast cancer in carriers of at least one copy of the disease allele was 49% (95% CI 39%–59%) and 71% (95% CI 57%–85%) at age 50 and 70 years, respectively. On the basis of the constant hazard-ratio estimate, it was 58% and 87%, respectively.

Table 3.

Segregation Analysis of Single-Locus Models, Based on All 858 Families

Model	Allele Frequency(95% CI)	Age(years)	Hazard Ratio (95% CI)	Log-Likelihood	Akaike’sInformationCriterion
Null	0	⩾20	1	−2581.49	5162.98
Dominant	.0010 (.0004–.0024)	20–29	157.87 (108.78–229.10)	−2523.58	5061.16
		30–39	60.98 (35.56–104.19)
		40–49	27.18 (14.64–50.23)
		50–59	20.16 (8.54–47.50)
		60–69	10.11 (2.55–40.03)
		⩾70	6.96 (1.34–36.11)
Recessive	.0721 (.0541–.0961)	⩾20	116.26 (68.39–197.62)	−2526.85	5057.71
Codominant	.0667 (.0432–.1031)	⩾20	2.06 (1.06–4.01)a	−2526.35	5058.64
			142.22 (108.08–187.09)b

^aHeterozygote mutation carriers compared with normal homozygotes.

^bHomozygote mutation carriers compared with normal homozygotes.

Under recessive inheritance alone, the allele frequency was .07 and the hazard ratio was 116, independent of age. The cumulative probability of breast cancer in homozygote carriers was 80% (95% CI 65%–100%) at age 50 years and virtually 100% at age 70 years. Under codominance alone, the allele frequency was close to that estimated by the recessive model, as was the hazard ratio for homozygote carriers. The hazard ratio for heterozygote carriers was small and of marginal significance. On the basis of the AIC, the recessive model was the most parsimonious.

Table 4 shows corresponding estimates based on the 824 families with the known BRCA1 and BRCA2 mutation carriers and their relatives excluded. Under dominant inheritance, the allele frequency was reduced by ∼20%, but the hazard-ratio estimates, and hence the age-specific cumulative probabilities of disease, were little changed. Exclusion of the known mutation carriers and their relatives had little influence on the parameters estimated under recessive or codominant inheritance. As in table 3, the recessive model still had the smallest AIC value. The allele frequency under recessive inheritance was .07, showing that it was insensitive to exclusion of families in which a known dominantly inherited risk was segregating.

Table 4.

Segregation Analysis of Single-Locus Models, Based on 824 Families with Known BRCA1 and BRCA2 Mutation Carriers and Their Relatives Excluded

Model	Allele Frequency(95% CI)	Age(years)	Hazard Ratio (95% CI)	Log-Likelihood	Akaike’sInformationCriterion
Null	0	⩾20	1	−2431.04	4862.08
Dominant	.0008 (.0003–.0019)	20–29	179.73 (123.35–259.77)	−2376.92	4767.84
		30–39	68.31 (39.47–118.19)
		40–49	29.96 (15.74–57.04)
		50–59	19.79 (7.61–51.52)
		60–69	11.73 (2.85–48.52)
		⩾70	6.42 (1.25–37.46)
Recessive	.0653 (.0501–.0852)	⩾20	131.69 (77.47–223.87)	−2379.79	4763.58
Codominant	.0579 (.0385–.0871)	⩾20	2.82 (1.15–5.59)a	−2378.91	4763.82
			161.80 (125.41–208.75)b

^aHeterozygote mutation carriers compared with normal homozygotes.

^bHomozygote mutation carriers compared with normal homozygotes.

Segregation Analyses: Two-Locus Models

Table 5 shows the fits of the two-locus models: one with dominant inheritance of risk and the other with recessive inheritance of risk. As computation of maximum-likelihood estimates was very time consuming, we constrained the hazard-ratio estimates to be a constant for both the dominant and recessive effects. As judged by likelihood-ratio tests, the two-locus models clearly gave a better fit than did the single-locus models. Furthermore, the fits were better if it was assumed that the interaction effects were multiplicative rather than additive, especially when the known mutation carriers were excluded.

Table 5.

Segregation Analyses of Two-Locus Models, Assuming the Interaction Effect is Multiplicative or Additive, Based on All 858 Families and on the 824 Families with Known BRCA1 and BRCA2 Mutation Carriers and Their Relatives Excluded

Interaction,No. of Families,and Model	Allele Frequency(95% CI)	Hazard Ratio (95% CI)	Log-Likelihood	Akaike’sInformationCriterion
Multiplicative:
858:
Dominant	.0014 (.0008–.0022)	13.24 (3.57–49.03)	−2509.22	5026.44
Recessive	.0652 (.0404–.1052)	142.23 (108.52–186.41)
824:
Dominant	.0011 (.0003–.0045)	10.09 (3.02–50.34)	−2361.57	4729.14
Recessive	.0629 (.0445–.0888)	161.26 (111.99–232.19)
Additive:
858:
Dominant	.0004 (.0001–.0426)	28.34 (11.96–67.13)	−2509.56	5027.12
Recessive	.0608 (.0284–.1301)	161.63 (123.56–211.42)
824:
Dominant	.0003 (.0001–.0013)	5.92 (1.66–53.17)	−2362.83	4733.66
Recessive	.0652 (.0304–.1401)	166.87 (117.26–237.46)

Comparison of tables 3 and 5 shows that estimates of the parameters describing the recessive effect were virtually unchanged by addition of a dominant effect, under either the multiplicative or the additive assumption for interaction effects, or when the known mutation carriers were included or excluded. The cumulative probability for carriers of the recessive effect was still 99% to age 70 years. The comparison also shows that the strength of the dominant effect was reduced by adding a recessive effect to the model. Under the multiplicative assumption, the hazard ratio went from 63 to 13, and the cumulative probability of breast cancer to age 70 years in carriers of at least one disease allele from 87% (95% CI 69%–100%) to 56% (95% CI 45%–67%). The estimated allele frequency of the recessive effect was stable, ∼.06, irrespective of the model specification.

Also shown in table 5 are the results of segregation analyses of the two-locus model based on the 824 families with known BRCA1 and BRCA2 mutation carriers and their relatives excluded. As previously seen from comparing the single-locus models with and without mutation carriers (tables 3 and 4), the estimated allele frequency for the dominant effect was reduced by ∼20%. Under the assumption of multiplicative interaction effects, for both the dominant and recessive effects, the estimates of hazard ratio were little changed, and the allele frequency for the recessive effect was also relatively stable.

The correlation coefficients between the estimates of the dominant and recessive allele frequencies were small and not statistically significant, varying between .02 and .18 depending both on whether the mutation carrier families were included or excluded and on whether the interaction effect was assumed to be multiplicative or additive. Similarly, the correlation coefficients between the two estimated hazard ratios, when each fitted as a constant independent of age, were also not significant and between −.07 and 0.17 across the four scenarios above.

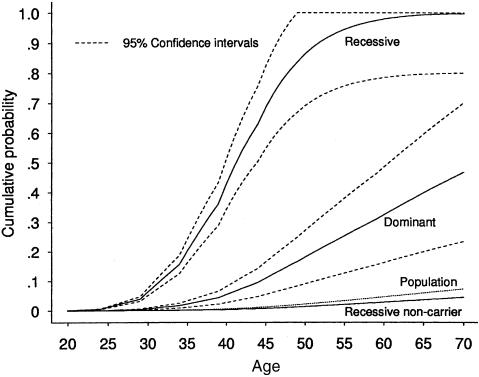
Figure 3 shows the age-specific cumulative probability of breast cancer for carriers of a recessively inherited and a dominantly inherited risk, under the assumptions of multiplicative interaction effect between the two loci, on the basis of the 824 families excluding the known BRCA1 or BRCA2 mutation carrier families. The recessive penetrance increased rapidly from 43% to 86% to 98% and 99%, at ages 40, 50, 60, and 70 years, respectively. The corresponding dominant penetrance estimates were 5%, 18%, 32%, and 48%, respectively. From equations (2) and (3), the hazard rate of breast cancer for noncarriers of the dominant risk was λ₀(t)=λ(t)/1.02, which is almost identical to the population hazard. The hazard rate for noncarriers of the recessive risk was λ₀(t)=λ(t)/1.63, and its corresponding cumulative probability curve is shown in figure 3.

Figure 3.

Age-specific cumulative probabilities of breast cancer for the population, for carriers of a dominantly inherited and a recessively inherited risk, and for noncarriers of the recessively inherited risk, with 95% CIs, on the basis of the 824 families with known BRCA1 and BRCA2 mutation carriers and their relatives excluded, under the multiplicative two-locus model.

Segregation Analyses: Hypergeometric Polygenic Models

Table 6 shows the results of fitting models with a hypergeometric polygenic effect, with or without a major-gene effect. The SD estimated under the polygenic effect–only model provides a general measure of familial aggregation. It can be seen that SD decreased more when a recessive effect was included than when a dominant effect was included, whether or not the known mutation carrying families were included. Furthermore, although a codominant effect gives a reduced SD, the additional decrease in log-likelihood was small and the AIC suggests that the mixed polygenic and recessive model was preferable. Note also that the parameter estimates that best describe the recessive effect when a polygenic effect is included were not dissimilar to the corresponding estimates from the single-locus recessive model or the two-locus recessive and dominant model (tables 3 and 5).

Table 6.

Segregation Analyses of Hypergeometric Polygenic Model, with and without a Single-Locus Effect, Based on All 858 Families and on 824 Families with Known BRCA1 and BRCA2 Mutation Carriers and Their Relatives Excluded

Model andNo. ofFamilies	AlleleFrequency	HazardRatio	SD ofGeneticComponent	Log-Likelihood	Akaike’sInformationCriterion
Polygenic only:
858	…	…	1.578	−2529.65	5061.3
824	…	…	1.533	−2386.07	4774.14
Mixed dominant:
858	.0002	187.9	1.456	−2497.47	5000.94
824	.0002	197.4	1.306	−2351.95	4709.9
Mixed recessive:
858	.0779	108.2	.837	−2488.92	4983.84
824	.0716	123.2	.726	−2344.05	4694.1
Mixed codominant:
858	.0572	2.3a	.433	−2487.88	4983.76
		173.8b
824	.0538	2.3a	.277	−2342.90	4695.8
		186.9b

^aHeterozygote mutation carriers compared with normal homozygotes.

^bHomozygote mutation carriers compared with normal homozygotes.

Exclusion of the known mutation-carrying families reduced the variance (SD²) of the polygenic effect by just 100×[1.578²-1.533²]/1.578²=6%. Of the polygenic variance remaining after these families had been excluded, 100×[1.533²-0.754²]/1.533²=76% was explained by addition of the recessive effect, or 100×[1.533²-1.118²]/1.533²=47% by addition of the dominant effect.

Table 7 shows the women with breast cancer, their relationship to the proband, and their age at diagnosis, for the 10 families for whom the change in log-likelihood was greatest from adding a recessive major-gene effect to a null model with no recessive effect, after the known mutation-carrying families were excluded. All five families with two sisters affected with breast cancer, as well as all three families with four or more affected relatives, are in this table. In none of these families has breast cancer been shown to be due to a mutation in BRCA1 or BRCA2, despite the probands having been fully sequenced for both genes.

Table 7.

Ages at Diagnosis of All Affected Members of the 10 Families for Whom the Change in Log-Likelihood was Greatest When a Recessive Effect Was Added to the Null Model

	Age at Diagnosis(years)
Family ID	Proband	Mother	Sister(s)	Aunt(s)	Grandmother	ΔLLa
M3808	36	…	36, 30	27, 28 (paternal)	35 (paternal)	12.47
S80242	32	47	…	38, 39 (maternal)	…	5.21
M3622	35	…	36, 44	…	…	4.93
M3133	27	…	…	30, 35 (paternal)	…	4.89
M3785	34	…	37, 43	…	…	4.53
M3511	37	69	37, 40	54, 68 (paternal)	…	4.43
M3138	29	34	34	…	…	4.32
S80117	29	38	…	37 (maternal)	50 (maternal)	4.19
S80050	34	37	…	36 (maternal)	…	3.42
S80225	38	…	42, 46	66 (maternal)	…	3.23

^aChange in log-likelihood between null model and recessive model.

Discussion

Two major conclusions arise from our analyses of three-generation population-based families with breast cancer. First, there appear to be residual dominantly inherited risks for breast cancer in addition to those derived from mutations in BRCA1 and BRCA2, even when additional recessive or polygenic effects are allowed for. Over all families, the dominant effect was represented by a hazard ratio of 13 (95% CI 4–49), equivalent to a cumulative risk, to age 70 years, of 56% (95% CI 45%–67%), and allele frequency of .0014 (95% CI .0008–.0022). Analysis of the family history of breast cancer for the first 18 BRCA1 and BRCA2 mutation carriers detected in this sample (Hopper et al. 1999a) suggested that the increased risk in carriers was nine-fold (95% CI 4%–23%), with cumulative risk, to age 70 years, of 40% (95% CI 15%–65%). Reanalysis including the additional 16 carriers made little difference to this point estimate (analyses not shown). That is, the hazard-ratio estimates from the segregation analyses are consistent with the analyses based on known mutation-carrying families. After excluding the currently known mutation carriers, the estimate of hazard ratio was 10 (95% CI 3–50), and the allele frequency was reduced by ∼20%.

This suggests that there is still substantial dominantly inherited risk not explained by BRCA1 and BRCA2. This could be because our mutation testing has yet to detect all BRCA1 and BRCA2 mutation carriers in these families. It is likely that we have detected more than two-thirds of the protein-truncating mutations, given that they appear to be widely scattered across the coding regions of these genes. Although we have tested for the large duplication in BRCA1 (Puget et al. 1999), it is possible that there are other types of deleterious mutations that we have yet to test for. The average sensitivity of past testing methodologies, as applied to the Breast Cancer Linkage Consortium, has been historically estimated to be ∼70%. Nevertheless, there could also be genes other than BRCA1 and BRCA2 that are associated with a dominantly inherited risk of breast cancer but have yet to be discovered (see, e.g., Kainu et al. 2000).

Perhaps of more importance is the suggestion that there is a substantial recessively inherited risk of early-onset breast cancer. This effect was evident, and its parameter estimates were stable, whether or not we included a dominant effect or a polygenic effect. Cohort analysis of the relatives of probands (fig. 2) showed that the increased risk to sisters of these early-onset probands was greater than the increased risk to mothers (P=.0005). Although this could be explained, in part, by the mothers being parous by definition and, therefore, at reduced risk of post-menopausal breast cancer, the difference in risk between mothers and sisters was evident in the premenopausal years, when the mothers were not necessarily at reduced risk of breast cancer (McCredie et al. 1998), and, furthermore, a large proportion (77%) of the sisters were parous anyway. The observation by us and others of a higher risk to sisters of cases than to mothers has been interpreted elsewhere as suggesting an underlying recessive mode of inheritance for breast cancer (Pharoah et al. 1997).

Table 7 shows the families providing the most evidence for a recessive effect. First, these families have not been found to carry a mutation in BRCA1 or BRCA2, despite being fully sequenced. Second, they have either multiple sisters affected, or multiple lineal aunts affected, if not both. In four of the five families in which the mother was affected, at least one lineal aunt was also affected. In the two families with an affected grandmother, she had at least one affected daughter. Third, the age at onset in these families was early, with ∼90% at or before age 50 years. Nevertheless, the average age at diagnosis of the affected mothers and lineal aunts in these families was 43 years, nearly a decade younger than the average age of the affected mothers and lineal aunts in the study, which was 52 years. The average age at diagnosis of these affected sisters was 39 years, compared to 40 years for all affected sisters in the study. Finally, as the families shown in table 7 are those most likely to segregate a recessively inherited risk of breast cancer, they could contribute to searches for novel recessively inherited breast cancer–susceptibility genes using classic linkage analysis and the parameter estimates from our fits.

The estimated allele frequency of .063 suggests that 1/250 (95% CI 1/500 to 1/125) women have a recessively inherited risk, compared to our estimate of 1/350 (95% CI 1/225 to 1/625) for having a dominantly inherited risk, including that due to mutations in BRCA1 and BRCA2. That is, recessive risk carriers may be at least as common in the population as dominant risk carriers. According to our fitted model, the risk in women with a recessive risk was higher than in those with a dominant risk (see fig. 3), reaching 50% by age 40 years and near certainty by age 60 years.

Our finding of a high recessively inherited risk at young age, as well as a dominantly inherited risk, is supported, to some extent, by the recently published analysis of 389 Icelandic multigeneration pedigrees with, on average, 19 female members (Baffoe-Bonnie et al. 2000). The researchers fitted regressive logistic models that incorporated a background effect caused by the mother being affected, plus a single-locus “major gene” effect. They found that codominant inheritance was preferable to dominant or recessive inheritance alone, and predicted that the risk of breast cancer to age 60 years was ∼40% in homozygous carriers and >20% in heterozygous carriers.

The finding of a recessively inherited risk is also supported by segregation analyses of population-based families from the United Kingdom (Antoniou et al. 2000). These families were ascertained through 1,484 women diagnosed with breast cancer before age 55 years, and was limited to their first-degree relatives. As in our study, extensive testing for mutations in BRCA1 and BRCA2 had been carried out, in this instance using multiplex heteroduplex analysis. The penetrances of mutations in BRCA1 and BRCA2 were assumed to be that estimated from previous analyses of multicase families. A third major-gene effect was fitted, with and without a hypergeometric polygenic effect. The best major-gene effect was a recessively inherited risk with a disease-allele frequency of .24 (95% CI .12–.42) and a cumulative risk, to age 70 years, of 42% (HR=21; 95% CI 12–36). The polygenic model, however, gave a similarly good fit.

A number of single-locus analyses in earlier studies suggested that dominant inheritance was the most plausible. These studies, such as the Cancer and Steroid Hormone Study, typically used data from nuclear families only and had little power to detect recessive inheritance or to discriminate between different modes of inheritance. In addition to the new United Kingdom study and the multigeneration Icelandic study described above, there have been other reports supporting recessive or codominant inheritance. An interesting feature of those analyses was that they used data from families ascertained through women with particular features, namely bilateral breast cancer (Goldstein et al. 1987) and ductal cancer (Goldstein and Amos 1990).

Therefore, there are three possible reasons why our study has implicated such a strong recessive effect that does not appear to have been reported previously in the literature. Our study has been constructed multigenerationally by inclusion of both lineal aunts and grandmothers of the probands, giving it more power to detect recessive effects. Second, it has been based on women with early-onset disease (<10% of Australian women who develop breast cancer are diagnosed before the age of 40), for which it is known that the familial risk to relatives is stronger than for later-onset diseases (Pharoah et al. 1997; McCredie et al. 1998). Furthermore, the sort of recessive effect suggested by our analyses may not be detectable in families ascertained through probands with later-onset disease, given the high estimated risk at young ages, and near-full penetrance, by age 60 years, of this predicted recessive risk. Third, we have fitted multiple factors, including both recessive and dominant modes of inheritance, and allowed for background familial effects as well. This reflects the realization that there are likely to be many sources of familial aggregation of breast cancer. Future analyses of this data set will attempt to incorporate measured risk factors from the questionnaire, as well as other measured genetic variants possibly associated with breast cancer, such as a polymorphism in the CYP17 gene (Spurdle et al. 2000).