Dynamics of self assembly of magnetized disks rotating at the liquid–air interface

Abstract

This paper is a theoretical study of dynamic self assembly in a system of millimeter-sized magnetized disks floating at a liquid–air interface and spinning under the influence of a rotating magnetic field. Equations of motions are derived that account for the hydrodynamic and magnetic forces acting in the system. Numerical integration of these equations predicts formation of ordered structures of spinning disks; the simulated structures reproduce the patterns observed experimentally.

The formation of ordered structures by self assembly is interesting both theoretically and practically, with implications for chemistry (1, 2), physics (3–5), materials science (6–9), and biology (10–12). Although self assembly and self organization in systems operating at or near thermodynamic equilibrium are relatively well understood, the theoretical description of dynamic self-assembling systems (13, 15)—those that operate away from equilibrium and develop order only when dissipating energy—is incomplete. In the absence of a general analytical description of such systems, numerical analysis is a convenient (and often the only) method for studying their dynamics.

In previous work (16, 17), we described a dynamic self-assembling system composed of a limited number (<40) of millimeter-sized magnetized disks floating on a liquid–air interface and subject to an external magnetic field produced by a rotating permanent magnet with a dipole length much larger (∼6 cm) than the radii (∼0.5 mm) of the disks. In the presence of the rotating external field, the disks spin around their axes with angular frequency equal to that of the external magnet (ω ∼200–1,200 rpm). All disks are attracted toward the axis of rotation of the magnet and are repelled by one another by hydrodynamic interactions associated with the motion of the fluid surrounding the disks. The interplay between attractive magnetic and repulsive hydrodynamic interactions in this system leads to the formation of macroscopic patterns. We quantified both the hydrodynamic repulsive force between the disks and the central magnetic force acting on all disks. On the basis of the experimental data for the simplest case of two interacting disks, we derived the equations that describe the forces acting in the system (17) and proposed that interactions in aggregates composed of a larger number of disks can be treated pairwise.

This work describes the equations of motion of the rotating disks and uses them to model self organization of different numbers of such disks in ordered aggregates. The simulated patterns are in excellent agreement with those observed experimentally. Our model not only correctly predicts the symmetry and dimensions of the aggregates at various rotational speeds but also allows estimation of the frequencies of occurrence of polymorphic patterns (i.e., different patterns that arise in the same system). We identify dimensionless parameters that control the formation of the aggregates and compare and contrast the results of our simulations with those for systems of two-dimensional point vortices (18–20).

Derivation of the Equations of Motion

In the experimental system (Fig. 1a), all disks are fully immersed in a fluid of viscosity μ, uniform density ρ (∼1.1 g/cm³ for the mixtures of ethylene glycol and water used in most experiments), and kinematic viscosity ν = μ/ρ (typically ∼10 cP), and they rotate around their axes with angular velocity ω. In aggregates composed of two or more disks, the fluid motion associated with spinning results in repulsive hydrodynamic interactions between them. In our previous analysis (16), we approximated each spinning disk i by a rigid sphere of radius a_i equal to that of the disk§ and suggested that the repulsive force between the spheres is a low-Reynolds-number effect. If the motions of the liquid around the rotating spheres were modeled as zero-Reynolds-number flows, then—because of symmetry considerations—there would be no net hydrodynamic force on either of the two particles. Because the experiments clearly demonstrate the existence of such force, we hypothesized that it is a consequence of the fluid inertia (finite Reynolds numbers).

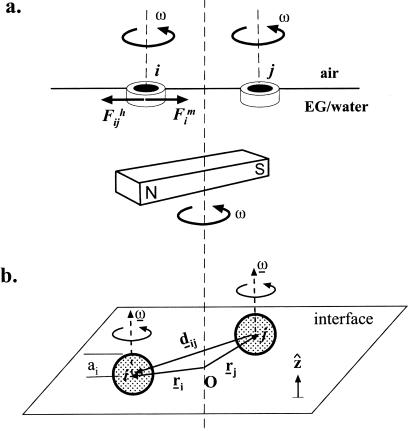
Figure 1.

a illustrates the experimental arrangement. Circular disks were made of hollow polyethylene tubing (∼1 mm in diameter) filled with poly(dimethylsiloxane) (Dow-Corning) doped with magnetite (15% by weight). The disks were placed at an ethylene glycol–water (3:1 by volume)/air interface, so that they were fully immersed in the liquid except for their top surface. A permanent bar magnet (IKA Labortechnik, Staufen, Germany) of dimensions L ∼ 5.6 cm × W ∼ 4 cm × T ∼ 1 cm was placed ∼3 cm below the interface and rotated with angular velocity ω. The magnet was magnetized along its longest dimension and had magnetization M ∼ 1,000 G/cm³. Magnetic force F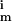 attracts disk i towards the axis of rotation of the magnet. The spinning disks repel each other by pairwise hydrodynamic forces F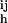. The entire aggregate slowly precesses at Ω ∼ 5 rpm around the axis of rotation of the magnet. The schematic in b defines the parameters used in the calculations. Disks composing an aggregate are approximated by rigid spheres; the radius of sphere i is equal to that of a corresponding disk. The position vectors r originate at the intersection of the axis of rotation of the magnet and the plane of the interface O and are confined to the plane of the interface.

We considered (16, 17) a neutrally buoyant sphere of radius a₁ in a shear flow produced by a larger sphere of radius a₂. The smaller sphere experiences a lift force perpendicular to the local direction of flow. The magnitude of this force, F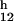 = O(μa₁u Re_G), is proportional to the viscosity of the liquid μ, the size of the particle a₁, its typical velocity u ∼ ωa₁, and its Reynolds number Re_G = ρGa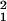/μ, which is based on the local shear rate G. Because the shear rate produced by particle 2 in the neighborhood of particle 1 is G = O(ωa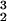/d³), where d is the distance between the centers of the spheres, our analysis predicts an inertially generated lift force F 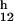= O(ρω²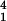aa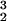/d³). For arbitrary particles i and j, the repulsive hydrodynamic interaction between them can be written in vectorial notation (Fig. 1b), as F 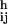= c_hρω²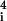aa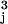(r_i − r_j)/d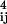), where c_h is a constant of proportionality, and d_ij = |r_i − r_j|. The force on sphere i acts along the direction of d_ij and away from sphere j.

The magnetic force acting on a sphere i is directed towards the axis of rotation of the magnet, varies approximately linearly with the distance |r_i| from this axis and depends on the volume of the sphere, F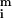 = −c_m|r_i|a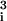, where c_m is a constant.

Under the influence of the hydrodynamic and magnetic forces, the spheres move in the fluid. Because in our experiments the flow about a particle is in the low-Reynolds-number regime, the particle moves relative to the fluid at a velocity U_i proportional to the net force acting on it: U_i = ξ⁻¹ (F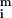 + ∑_j≠iF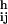), where ξ = 6πμa_i for a sphere. In addition, each sphere moves in the flow created by the other spinning spheres composing an aggregate. Because a single sphere j creates a velocity field u_j(x) = a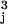ω × x/x³ (where x is the position vector measured from the sphere's center; Fig. 1b), the velocity V_i at which any sphere i translates is given by the sum of velocity fields produced by the remaining spheres at the location of i: V_i = ∑_j≠iu_j(r_i − r_j).

Adding the component velocities U_i and V_i, the equations of motion describing the dynamics of an aggregate composed of N spinning spheres can be written as

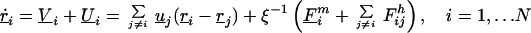1

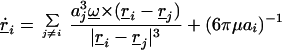2

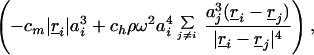Introducing dimensionless parameters r̃_i = r_i/a₀, t̃ = tω, and β_i = a_i/a₀ (a₀ is the radius of the smallest particle in an aggregate), the equations of motion can be written in nondimensional form:

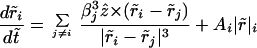3

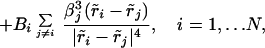where A_i = −(c_maβ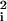/6πμω) and B_i = (c_hρωaβ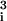/6πμ).

Pattern Formation

(i) Calibration of Parameters Used in the Simulation.

The formation of ordered aggregates of spinning disks was studied by numerical integration of the equations of motion. The relative value of the magnitudes of the constants c_h and c_m characterizing the hydrodynamic and magnetic interactions, respectively, was found from the experimental dependence of the separation d of two 1.27-mm disks on the angular speed ω. Because the stable aggregate formed by two disks is symmetric with respect to the origin, the magnitudes of the position vectors of the disks are equal (i.e., |r₁| = |r₂|) and, consequently, d = 2|r₁| = 2|r₂|. Using this relationship and equating the magnitudes of hydrodynamic and magnetic forces at equilibrium, we obtain c_m/c_h = 2ρω²a⁴/d⁴, which on substitution of the numerical values characteristic of the experiment (16, 17) was found to be ∼17. The magnitude of c_m was estimated by placing one 1.27-mm disk at specified distances |r| from the origin and measuring the distance in the radial direction the disk covered in one second; the value of the constant was c_m ∼ 0.32 (g⋅mm⁻³ s⁻²).

(ii) Unique Patterns.

Fig. 2 summarizes the results of simulations performed for N = 2–9 identical disks, 1.27 mm in diameter and rotating at ω = 500 rpm. We have previously performed experiments (17) using disks of this size for values of ω ranging from 300 to 900 rpm; thus, the patterns that emerged from modeling could be compared directly with the experimental ones. For identical disks, all β_is were equal to 1, so that only two parameters, A = −0.00131 and B = 0.21088, were necessary to describe the dynamics of the system. The initial positions of the disks were chosen randomly within 20 disk diameters from the center of the magnetic field, and the system was allowed to evolve for 10,000 steps; the patterns shown in Fig. 2 are stable configurations reached at the end of the dynamics run. These patterns were unique, that is, no other arrangements of the disks (polymorphs) were recorded when the simulations were repeated several (∼20) times with different initial conditions. This finding agreed with the experimental observation that for N < 10, groups of disks always evolved to a unique structure. The experimental and simulated patterns were isomorphic.

Figure 2.

Simulated stable aggregates of N = 2–9 disks 1.27 mm in diameter, rotating at angular velocity ω = 500 rpm. The dimensionless parameters used in the calculations were A = −0.00131 and B = 0.21088. The simulations were started from random initial positions of the disks within 20 disk diameters from the origin. Each run consisted of 10,000 steps. For each N, 20 runs were performed. The patterns presented here were unique, i.e., no other final configurations of the disks were observed. In addition to each disk rotating around its axis, the entire aggregate precesses around its center.

The simulations correctly reproduced not only the ordering but also the dimensions of the aggregates. For N = 2, the distance between the centers of the disks was 2.78 mm, compared to the experimental value of 2.8 mm. For N > 2, the average distance between the nearest-neighbor disks agreed with the experimental value to within 0.1 mm. For N = 6, the simulation correctly predicted the distance between the central disk and the disks in the first shell to be longer by a factor of 1.13 (∼1.1 in the experiments) than the distance between the nearest-neighbor disks within the shell. The model also accounted for the opposite trend in the aggregate with N = 8, in which the ratio of these distances was 0.85 (∼0.8 in the experiments). Finally, for N = 9, the distance between the two central disks was shorter than between the disks of the outer shell by 20%, again in good agreement with the experiment.

(ii) Polymorphic Patterns.

We have previously demonstrated experimentally (16, 17) that for certain values of N > 9, the disks can evolve into more than one stable configuration. We wished to reproduce the formation of these polymorphic patterns in our simulations. We modeled the dynamics of the aggregates composed of N = 10 to N = 16 disks (1.27 mm in diameter) at two rotational speeds, ω = 500 rpm and ω = 700 rpm. To quantify the frequencies of occurrence of the polymorphs, we performed 100 runs for each value of N (with different initial conditions) and recorded how many times a given configuration was achieved. Fig. 3 shows the stable configurations observed in the simulations. In two cases, for N = 11 and N = 13, only one pattern was observed at both values of ω; these patterns were also unique in the experiments. Other numbers of disks produced polymorphs. For N = 10, the structure with a pair of disks in its center (denoted {2,8}, where the numbers give the occupations of, respectively, the inner and the outer shells within the aggregate) was seen more frequently than the structure with a triangular “core,” {3,7}. In the experiments, both structures appeared with roughly equal frequencies at 700 rpm, but at 500 rpm, {2,8} was observed in ∼90% of cases. We note that the simulations, in agreement with the experiment, predicted the inner two disks in the {2,8} aggregate to precess a bit slower than the outer ring (the outer ring is “sliding” past the inner pair). In simulations with N = 12 disks, the {4,8} polymorph formed slightly more frequently than the {3,9} one. In reality, the {4,8} structure was the predominant one at 700 rpm. At 500 rpm, the two structures interconverted in time, and after ∼30 min usually (though not always) equilibrated into the {3,9} structure.

Figure 3.

Simulated stable aggregates of N = 10–16 disks 1.27 mm in diameter, rotating at angular velocity ω = 500 rpm (A = −0.00131 and B = 0.21088, two columns on the left), and ω = 700 rpm (A = −0.000936 and B = 0.2952, two columns on the right). For N = 11, 13, the stimulated patterns were unique. For N = 10, 12, 14, 15, 16, polymorphs were observed. The relative frequencies of occurrence of the polymorphs are given by the numbers above the patterns; these numbers are based on 100 simulation runs (10⁴ steps, random initial positions) for each N. Each of the aggregates shown precesses around its center.

For N = 14, the {4,10} structure was the only one observed at ω = 700 rpm, in both the simulations and in the experiment. Two structures, {4,10} and {5,9}, were predicted to be stable at ω = 500 rpm, and both were achieved experimentally, the {4,10} aggregate being the more frequently observed. For N = 15, only one structure, {5,10}, was formed in the simulations at ω = 500 rpm; this structure was also unique in the experiments. The {5,10} aggregate was also the exclusive product of the experiments at ω = 700 rpm. The simulations at this angular speed resulted in the {5,10} structure in 91 runs, but in 9 runs, a {1,5,9} aggregate, not seen in the experiments, was formed. Finally, for N = 16, all forms shown in Fig. 3 were seen in the experiments, with frequencies close to those predicted by the modeling.

As in the case of smaller assemblies (N < 9), modeling was successful in correctly reproducing the sizes of the experimental aggregates at both values of the rotational speed. The simulations correctly predicted the dominant polymorphs and, with one exception—{1,5,9}—all structures obtained in the simulations were observed in the experiments. On the other hand, the frequencies of occurrence obtained from the modeling should be taken only as approximate measures of the frequencies of occurrence of the experimental structures: they are significant when one polymorph is a dominant one, but not when the stability of polymorphs is similar (e.g., interconverting patterns for N = 12 at 500 rpm).

(iii) Patterns of Low Symmetry.

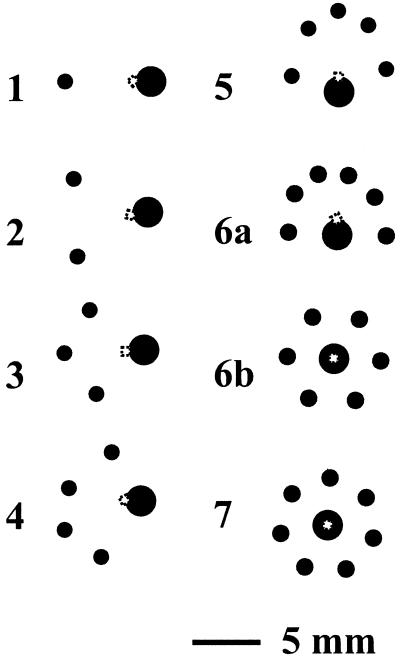
Some of the most intriguing patterns observed in our experiments were those formed when one disk was substantially larger than the remaining ones: these patterns often had only one plane of symmetry. We wanted to investigate whether our model would account for the existence of such low-symmetry structures. Specifically, we modeled the system of one large disk (2.42 mm in diameter) and N = 1–7 smaller disks (1.27 mm) rotating at ω = 500 rpm; we chose this system because we had complete experimental data for it.

Fig. 4 shows the simulated aggregates. For N < 6, the small disks moved in a “train” on an orbit around the large disk. The nearest-neighbor distance between the small disks was ∼6 mm for N = 2 and decreased to ∼3 mm for N = 5; this distance was shorter (by ∼10–35%) between the disks in the center of the “train” than between those near its edges. The large disk precessed around the axis of rotation of the magnet (center of the magnetic field) and the distance between its center and that of any of the small disks was ∼4.2 mm. All these observations were in excellent agreement with the experiments (17).

Figure 4.

Simulated low-symmetry patterns in aggregates composed of one large disk (2.42 mm in diameter) and N = 1–6 small disks (1.27 mm in diameter) rotating at ω = 500 rpm. For N = 1–5, the patterns were stable. For N = 6, the trailing small disk moves slower than the remaining small disks, and the morphology of the aggregate changes periodically in time. All simulations were done for 10,000 steps. The small white squares indicate the location of the origin (that is, the axis of rotation of the external magnetic field) around which the aggregates precess.

For N = 6, there were two stable structures: one, in which the small disks formed a closed shell around the large disk, and a second, in which the small disks organized into a “train.” Both of these structures were observed in experiments. For N = 7, the small disks formed a closed shell around the large disk—again, in agreement with experiment.

We briefly mention that analytical studies of systems of point vortices of unequal strengths (21, 22) indicate that the symmetric forms (that is, structures in which small disks are distributed equally along the perimeter of the circle along the central vortex) become unstable at certain values of controlling parameters. Yet, as we have verified, the ideal, point–vortex equations of motion do not evolve randomly positioned vortices into low-symmetry structures such as those obtained in our simulations.

Comparison with the Point–Vortex Model.

Because the interactions between the spinning particles in our system are mediated by vortices produced by these particles in the surrounding fluid, it might appear that a simple model of two-dimensional interacting point–vortices would be sufficient to describe the dynamics of our disks. Although the point–vortex model predicts stable patterns of vortices graphically similar to those formed by the spinning disks, its quantitative predictions are not in agreement with our experiments. In particular, this model fails to account for: (i) the dependence of the spacing between the spinning disks on the parameters A and B describing the system, and (ii) the evolution of disks to the experimentally observed structures. According to calculations based on the point–vortex model (20), the assemblies of our disks sometimes correspond to the high free-energy polymorphs, whereas we do not observe the calculated low free-energy forms. For example, for N = 9, we never observed, either in the experiments or in the simulations, the {1,8} structure that the point–vortex model predicts to be the lowest-energy configuration for this number of vortices (the complete table of the free energies of stable configurations of point vortices up to N = 19 can be found in ref. 20).

The differences between the results of our simulations and those based on the point–vortex model reflect different physical assumptions underlying both approaches. The point–vortex model assumes infinitely small vortex core, inviscid fluid, and no central potential; these assumptions do not hold in our system.

We suggest that our theoretical description is adequate for systems of interacting vortices (i) that are subject to a central confining potential, (ii) in which the dimensions of the core of the vortex are of a size similar to the spacing between the vortices, and (iii) in which the length of the vortex filament is comparable to its width.

Conclusion

The nondimensionalized equations of motion allow the study of self assembly at different values of phase-space parameters A and B. With the aid of these equations, the morphologies of the aggregates can be predicted a priori for various radii of the disks, and their rotational speeds and magnetic contents.

This study suggests that our experimental system, to a good approximation, is deterministic: polymorphic patterns and low-symmetry structures are not emergent but can be deduced from the equations of motion and initial positions. More recent experimental results with magnetized plates of low symmetries (e.g., comma-shaped plates; B.A.G. and G.M.W., unpublished work) show that the hydrodynamic interactions can be made multibody, and the entire system can exhibit qualitatively different behaviors (e.g., shape-selective aggregation of spinners). In other words, relatively small adjustments of the shapes of individual spinners can lead to large-scale changes in the aggregates. We hope that the equations we developed here, with necessary adjustments, will be applicable to the dynamics of systems of plates of lower symmetry. Even if they cannot faithfully reproduce their behaviors, they might prove valuable in assessing the limits of deterministic modeling of interacting vortex flows.