Abstract
Considerable effort in instrument development has made possible detection of picosecond fluorescence lifetimes by time-correlated single-photon counting. In particular, efforts have been made to narrow markedly the instrument response function (IRF). Less attention has been paid to analytical methods, especially to problem of discretization of the convolution integral, on which the detection and quantification of short lifetimes critically depends. We show that better discretization methods can yield acceptable results for short lifetimes even with an IRF several times wider than necessary for the standard discretization based on linear approximation (LA). A general approach to discretization, also suitable for nonexponential models, is developed. The zero-time shift is explicitly included. Using simulations, we compared LA, quadratic, and cubic approximations. The latter two proved much better for detection of short lifetimes and, in that respect, they do not differ except when the zero-time shift exceeds two channels, when one can benefit from using the cubic approximation. We showed that for LA in some cases narrowing the IRF beyond FWHM = 150 ps is actually counterproductive. This is not so for quadratic and cubic approximations, which we recommend for general use.
Full text
PDF





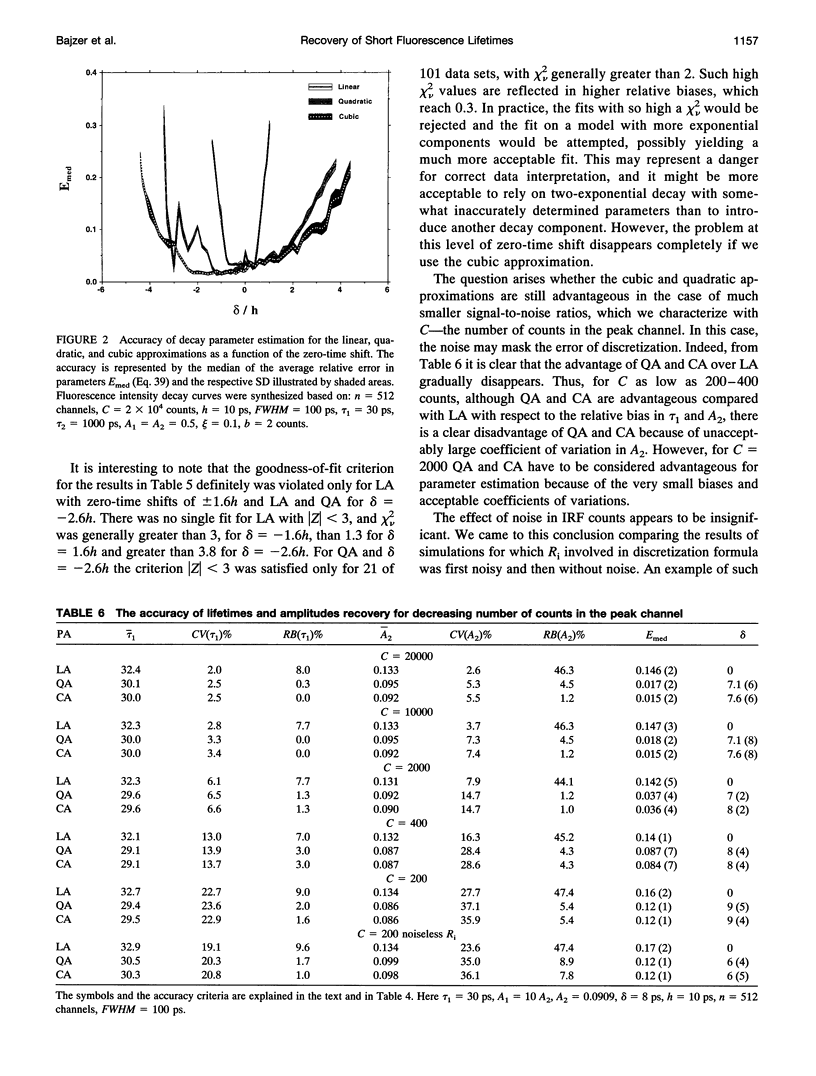

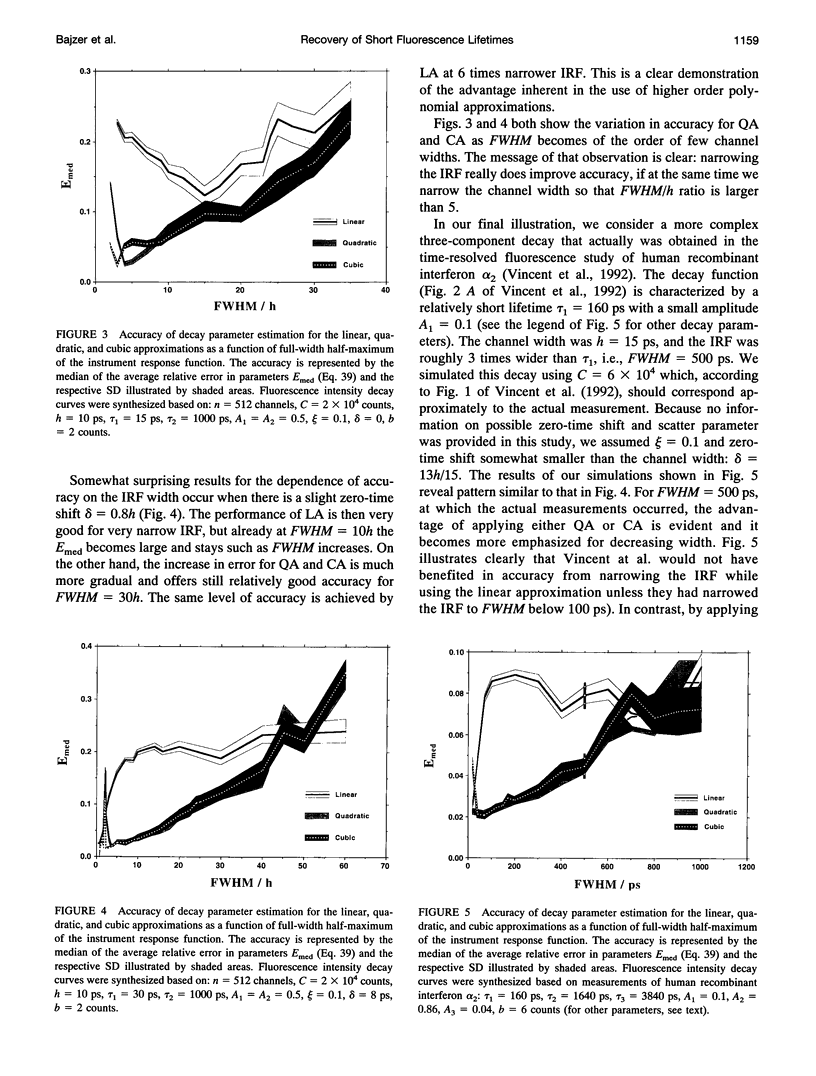


Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bajzer Z., Prendergast F. G. Maximum likelihood analysis of fluorescence data. Methods Enzymol. 1992;210:200–237. doi: 10.1016/0076-6879(92)10012-3. [DOI] [PubMed] [Google Scholar]
- Bajzer Z., Sharp J. C., Sedarous S. S., Prendergast F. G. Padé-Laplace method for the analysis of time-resolved fluorescence decay curves. Eur Biophys J. 1990;18(2):101–115. doi: 10.1007/BF00183269. [DOI] [PubMed] [Google Scholar]
- Eisenfeld J., Ford C. C. A systems-theory approach to the analysis of multiexponential fluorescence decay. Biophys J. 1979 Apr;26(1):73–83. doi: 10.1016/S0006-3495(79)85236-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinvald A., Steinberg I. Z. On the analysis of fluorescence decay kinetics by the method of least-squares. Anal Biochem. 1974 Jun;59(2):583–598. doi: 10.1016/0003-2697(74)90312-1. [DOI] [PubMed] [Google Scholar]
- Klafter J., Shlesinger M. F. On the relationship among three theories of relaxation in disordered systems. Proc Natl Acad Sci U S A. 1986 Feb;83(4):848–851. doi: 10.1073/pnas.83.4.848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livesey A. K., Brochon J. C. Analyzing the distribution of decay constants in pulse-fluorimetry using the maximum entropy method. Biophys J. 1987 Nov;52(5):693–706. doi: 10.1016/S0006-3495(87)83264-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Periasamy N. Analysis of fluorescence decay by the nonlinear least squares method. Biophys J. 1988 Nov;54(5):961–967. doi: 10.1016/S0006-3495(88)83032-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent M., Li De La Sierra I. M., Berberan-Santos M. N., Diaz A., Diaz M., Padron G., Gallay J. Time-resolved fluorescence study of human recombinant interferon alpha 2. Association state of the protein, spatial proximity of the two tryptophan residues. Eur J Biochem. 1992 Dec 15;210(3):953–961. doi: 10.1111/j.1432-1033.1992.tb17500.x. [DOI] [PubMed] [Google Scholar]
- Wahl P. Analysis of fluorescence anisotropy decays by a least square method. Biophys Chem. 1979 Jul;10(1):91–104. doi: 10.1016/0301-4622(79)80009-5. [DOI] [PubMed] [Google Scholar]