Abstract
Under a stretching force, the sugar ring of polysaccharide molecules switches from the chair to the boat-like or inverted chair conformation. This conformational change can be observed by stretching single polysaccharide molecules with an atomic force microscope. In those early experiments, the molecules were stretched at a constant rate while the resulting force changed over wide ranges. However, because the rings undergo force-dependent transitions, an experimental arrangement where the force is the free variable introduces an undesirable level of complexity in the results. Here we demonstrate the use of force-ramp atomic force microscopy to capture the conformational changes in single polysaccharide molecules. Force-ramp atomic force microscopy readily captures the ring transitions under conditions where the entropic elasticity of the molecule is separated from its conformational transitions, enabling a quantitative analysis of the data with a simple two-state model. This analysis directly provides the physico-chemical characteristics of the ring transitions such as the width of the energy barrier, the relative energy of the conformers, and their enthalpic elasticity. Our experiments enhance the ability of single-molecule force spectroscopy to make high-resolution measurements of the conformations of single polysaccharide molecules under a stretching force, making an important addition to polysaccharide spectroscopy.
Single molecule force spectroscopy has become an important tool to examine the conformations of proteins and polysaccharide molecules under a stretching force (1–12). Recent experiments have demonstrated that a force field can trigger conformational changes in these molecules that cannot be observed by traditional NMR or x-ray crystallographic techniques. Force spectroscopy involves measuring the force required to extend a molecule by a certain amount (2–10). The data are compiled into a force–extension relationship that gives a characteristic fingerprint for the conformational transitions of the molecule under study. For example, force–extension relationships of polysaccharides such as amylose and dextran (13, 14) display a characteristic plateau (2, 4) that marks forced transitions of the glucose monomers from their chair conformation to the boat-like conformation (4). Similarly, two distinct plateaus in the force-extension curve of pectin (13, 14) report a transition of the galactose rings from the chair conformation to the boat conformation and a subsequent flip of the boat to the inverted chair conformation (5). These observations provide an interesting perspective on the behavior of polysaccharides under mechanical tension (15) and suggest that fingerprints of forced conformational transitions can be used as a means for identifying single polysaccharides molecules in solution (9).
In the most typical atomic force microscopy (AFM) experiment, a single molecule adsorbed between a substrate and the cantilever tip is extended vertically at a constant rate while the resulting force is measured (2–10). Although it may seem that these experiments can be completed equally by controlling either the extension or the force applied to the molecule, these two modes can yield quite different results (e.g., see ref. 16). It is now understood that force drives new conformations by reducing the activation energy of conformations that are not populated at room temperature (17–20). Hence, by controlling the applied force, we directly increase (or decrease) the transition probability (17–20). However, when the molecule's end-to-end distance is the variable under control the actual force applied to the molecule usually cannot be predicted because it varies with the extension of the molecule in a complicated manner (2, 4, 21, 22) and is only known after the experiment. Although analytical treatments of the rupture of bonds stretched under a controlled extension have been developed (18, 23), no analytical function has been proposed to describe the conformational transitions of a stretched polysaccharide molecule. This lack of an analytical model has prevented the utilization of the AFM data for the analysis of the chair to boat transition. Here we demonstrate that when polysaccharides are stretched under force ramp conditions, a simple two-state model can describe the changes in length resulting from the chair-to-boat transitions of the monomers. The variables of this model are determined directly from the experimental data, allowing us to analytically predict the extension of a polysaccharide molecule under force, without the use of free parameters.
Materials and Methods
Force-Ramp AFM.
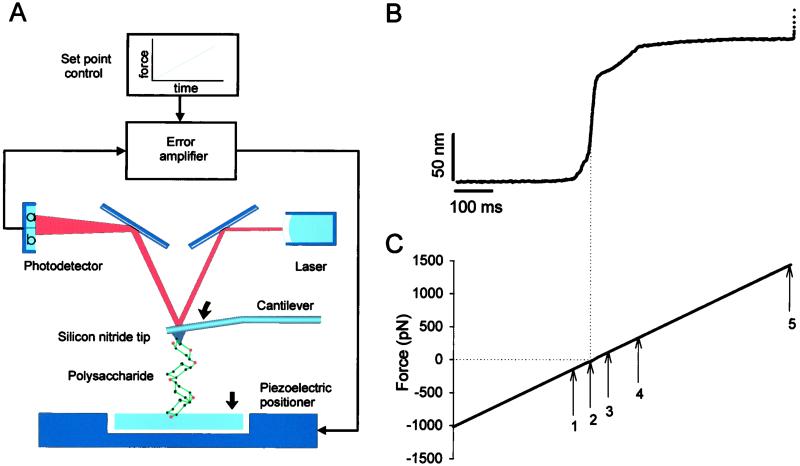
We have described in detail our AFM set-up (3) and the recent implementation of its force-clamp and force-ramp modes of operation elsewhere (16). Briefly, to control the force exerted on a polysaccharide chain during stretching we used a feedback system that compared the signal generated on deflection of the AFM cantilever with a computer-controlled set point(s) and fed the error signal back to the piezoelectric positioner. The feedback system was adjusting the length of the molecule being stretched (by moving the piezoelectric stage) in such a way that the molecule's tension (sensed by the cantilever deflection) had to correspond to the predetermined value at each point during the stretch (Fig. 1A). The spring constant of each individual AFM cantilever (Si3N4 tip, TwinTips, Digital Instruments, Santa Barbara, CA, or microlevers from Thermomicroscopes, Sunnyvale, CA) was calibrated in solution, using the equipartition theorem (24). The step time response of our force-clamp/ramp system was ≈20 ms and the uncertainty of the force magnitude during the ramp, because of the cantilever drift, was <50 pN (16).
Figure 1.
Stretching single polysaccharides under the force-ramp mode of AFM. (A) Schematic of the AFM apparatus used to stretch polysaccharides under the force-ramp mode (16). Single polysaccharide molecule adsorbed at both ends to the substrate and the cantilever tip can be stretched by using a force-ramp mode of AFM. In this mode, force F, measured from the laser deflection (a − b)/(a + b), is detected by a split photodiode and is compared with a set point (force-ramp control). This comparison generates an error signal that is fed to a proportional, integral, and differential amplifier (PID) whose output is connected directly to the piezoelectric positioner. The positioner moves in such a way that the force exerted on the cantilever increases at a constant rate. (B) Time dependence of the extension of a carboxymethylamylose (CMA) molecule stretched under the force-ramp mode of AFM. (C) The applied force increased linearly at the rate of 2.5 pN/ms. The arrows mark the characteristic points of the recording (see text).
Polysaccharides.
Dextran [α-(1→6)-D-glucan; T500, T2000, Pharmacia]; carboxymethylamylose [CMA, α-(1→4)-D-glucan, C-4947, Sigma] are linear or >95% linear (dextran) homopolymers of D-glucopyranose. Pectin (P-9135, from citrus fruits; Sigma) contains linear sequences of galacturonic acid and its idealized structure is represented as α-(1→4)-D-galactouronan. Dextran, CMA, and pectin were dissolved in water at a concentration of 0.001–10% (wt/vol). A drop of these solutions was placed onto glass coverslips for drying followed by extensive rinsing. This procedure leaves a layer of polysaccharide molecules tightly adsorbed to the glass surface (7). The measurements were carried out in water or in PBS.
Single-Molecule Recordings.
To pick polysaccharide molecules, an AFM tip was pressed down for 1–3 s onto the sample at forces of 1–40 nN. On retracting the sample from the cantilever, polysaccharide molecules that adhered to the tip were stretched with the linearly increasing force (a force-ramp mode). Typically, the probability of picking up molecules was below one in ten attempts (9). Therefore, in most cases, we measured force–extension relationships that were characteristic of single molecules.
Two-State Model of Length Transitions in Single Polysaccharides Under a Stretching Force.
The elasticity of polysaccharide molecules has been modeled by combining the entropic extensibility of the chain with length transitions caused by the applied force (20). These simulations were performed using the Monte Carlo method to explain data obtained under length-clamp conditions (20). By contrast, here we seek to explain data obtained using the force-clamp method, where we can ignore the entropic elasticity of the chain and derive an analytical expression for the force-driven transitions of the polysaccharide molecule.
In our model, a polysaccharide (e.g., amylose) is composed of nS short segments that are characterized by the resting separation of the glycosidic oxygens, lS = OiO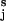 and nL long segments characterized by the extended separation lL = OiO
and nL long segments characterized by the extended separation lL = OiO . For example, in amylose, short segments correspond to the chair conformation of the glucopyranose ring while long segments represent a boat-like conformation (4). We assume that at any point during the stretch the chain is at equilibrium. This assumption is based on the observation that the stretching of a polysaccharide chain is fully reversible—i.e., the relaxing of a prestretched molecule accurately follows the stretching path in the force-extension space. Following the approach used to model the dissociation of a noncovalent bond placed under an external force (17, 18, 23, 25) we assume that the rate constants of the short-to-long (α) and the long-to-short (β) transitions depend exponentially on the applied force, F, and on the distance to the transition state, Δx: α(F) = α0exp(FΔx/kBT), β(F) = β0exp(−FΔx/kBT); α0 and β0 are the spontaneous rate constants determined by the height of the energy barrier, ΔGT, and the relative energy of the conformers, ΔG; kB is the Boltzmann constant. The number of monomers in both conformations can, at equilibrium, be calculated as follows: nS(F) = Nβ/(α+β); nL(F) = N − nS(F), where N is the number of all of the monomers.
. For example, in amylose, short segments correspond to the chair conformation of the glucopyranose ring while long segments represent a boat-like conformation (4). We assume that at any point during the stretch the chain is at equilibrium. This assumption is based on the observation that the stretching of a polysaccharide chain is fully reversible—i.e., the relaxing of a prestretched molecule accurately follows the stretching path in the force-extension space. Following the approach used to model the dissociation of a noncovalent bond placed under an external force (17, 18, 23, 25) we assume that the rate constants of the short-to-long (α) and the long-to-short (β) transitions depend exponentially on the applied force, F, and on the distance to the transition state, Δx: α(F) = α0exp(FΔx/kBT), β(F) = β0exp(−FΔx/kBT); α0 and β0 are the spontaneous rate constants determined by the height of the energy barrier, ΔGT, and the relative energy of the conformers, ΔG; kB is the Boltzmann constant. The number of monomers in both conformations can, at equilibrium, be calculated as follows: nS(F) = Nβ/(α+β); nL(F) = N − nS(F), where N is the number of all of the monomers.
The freely jointed chain (FJC) model of entropic elasticity (21, 22) predicts that polysaccharides like amylose or dextran (the Kuhn length estimated from the fits of the FJC model to the force-extension curves is of the order of ≈1 nm) should be stretched to >95% of the contour length at forces >100 pN. We therefore assume that at forces close to the conformational transition region (F > 100 pN) all of the virtual bonds OiO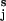 are already aligned in the direction of the applied force. Under these conditions the end-to-end distance is simply the algebraic sum of the lengths of all of the virtual bond vectors OiO
are already aligned in the direction of the applied force. Under these conditions the end-to-end distance is simply the algebraic sum of the lengths of all of the virtual bond vectors OiO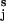 . This approximation holds for flexible polysaccharides like dextran, but may be less accurate for polysaccharides like amylose, which have a preferred pseudohelical trajectory (26). These constraints could be corrected by taking into account the angle between the force vector and the virtual bond vector OiO
. This approximation holds for flexible polysaccharides like dextran, but may be less accurate for polysaccharides like amylose, which have a preferred pseudohelical trajectory (26). These constraints could be corrected by taking into account the angle between the force vector and the virtual bond vector OiO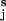 for a given chain structure.
for a given chain structure.
The end-to-end length x(F) of the filament subjected to stretching forces is then solely determined by the partition of the monomers between the two conformations: x(F) = nS(F)lS + nL(F)lL or
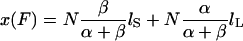 |
1 |
By ignoring variations in the mutual orientation of the residues we also tend to underestimate their number, N. For example, the length of an amylose dimer calculated as an algebraic sum of virtual bond lengths is 2 × 4.5 Å = 9 Å. However, if the residues are in an antiparallel orientation, as suggested by the molecular dynamics simulation of Heymann and Grubmüller (27), the length of the amylose dimer is 8.4 Å. In this case, the effective length of a residue is only 4.2 Å, leading us to underestimate the number of residues by ≈7% when we divide the contour length by 4.5 Å.
We calculate the first and the second force derivative of x(F) (Eq. 1) and assume a symmetrical energy barrier, Δx = 0.5(lL − lS) to find that dx/dF reaches a maximum when α(F) = β(F). This occurs at a force, Fα=β equal to
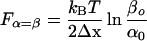 |
2 |
We further find that at Fα=β, the width of the energy barrier, 2Δx, is related to dx/dFα=β by a simple formula:
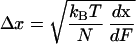 |
3 |
We conclude that by differentiating the extension–force relationship around the transition region we can measure the two important parameters characterizing the conformational transition: the width of the energy barrier, 2Δx, is determined by the maximum value of the derivative (Eq. 3), and the relative energy of the two conformers, ΔG = kBTln(β0/α0) is determined by Δx, and by the value of the force, Fα=β, at which the derivative attains its maximum (Eq. 2).
Results and Discussion
Stretching Polysaccharides Under the Force-Ramp Mode of AFM.
To determine the relationship between the force applied to a polysaccharide and the distribution of the monomers among the chair and boat conformations, we measured the end-to-end length of single polysaccharide molecules stretched by a linearly increasing force (force ramp). An advantage of this protocol is that it generates a complete set of data over a wide range of forces in a single experiment, minimizing the impact of cantilever drift (16). Fig. 1B shows the time course of the end-to-end length of a CMA molecule stretched with the force ramp depicted in Fig. 1C. The initial flat region of this curve in Fig. 1B (0–337 ms) indicates that the cantilever remains in contact with the substrate. In this part of the recording we apply a negative force to keep pressure on the polysaccharide substrate, and the molecules do not experience a stretching force. At 337 ms (Fig. 1C, arrow 1) the curve rises steeply as the tip and the substrate begin to separate; however, until 385 ms (Fig. 1C, arrow 2) the force on the cantilever tip remains negative. This part of the extension-time curve represents the decompression of the polysaccharide layer that coats the surface of the substrate. At 385 ms (Fig. 1C, arrow 2) the force clamp changes from a negative force to a positive force and a single amylose molecule is stretched. We observed that as soon as the stretching force was applied, the molecule elongated by a large amount. After this rapid elongation we observe a large decrease in the slope of the curve when the extension approached the contour length of the molecule. Up to the point marked by arrow 3 the elastic behavior of a single CMA molecule is fairly typical of a freely jointed chain (21, 22). At the point marked by arrow 3 the molecule undergoes conformational transition that ends at the point marked by arrow 4, when the molecule's compliance decreases dramatically and remains almost constant to the end of the stretch. At the point marked by arrow 5 the molecule detaches either from the glass substrate or from the tip freeing the cantilever from the force feedback control. We note that under force-ramp conditions the entropic phase of the stretch cycle is completed quickly and the measurement is focused on the postentropic events dominated by conformational transitions within the molecule.
Conformational Transitions in Polysaccharides Stretched Under the Force-Ramp Mode of AFM.
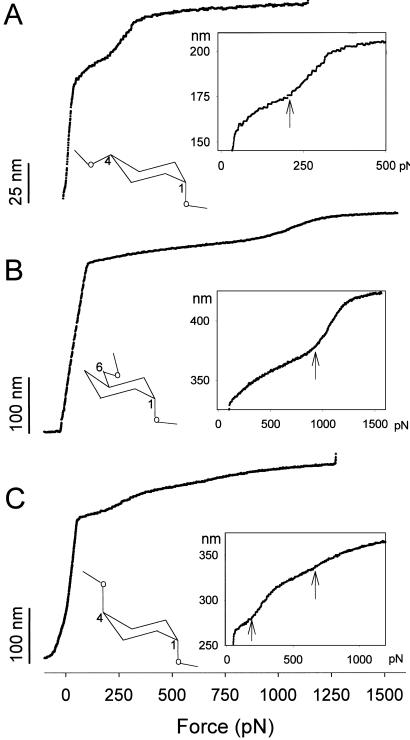
Fig. 2 shows plots of the end-to-end length versus force for three polysaccharide molecules: CMA (2A), dextran (2B), and pectin (2C). These plots are constructed from recordings similar to the one shown in Fig. 1 B and C and represent, in each case, a single experiment performed on a single molecule. The characteristic features observed in these curves are reproduced in other single-molecule recordings (Fig. 3).
Figure 2.
The extensibility of single amylose, dextran, and pectin molecules under the force-ramp mode of AFM. (A) The extension-force curve of amylose (CMA) shows the characteristic shape resulting from the forced lengthening of the amylose chain upon the chair-to-boat transition (arrow) of the glucopyranose rings. Ramp rate: 2.5 pN/ms. (Inset) A simplified α-d-glucopyranose ring with the amylose-type linkages, 1→4, and the transition region at high resolution. The arrow marks the beginning of the transition. (B) The extension-force curve of dextran reveals a similar transition (arrow) but at a higher force (1,000 vs. 200 pN). Ramp rate: 1.5 pN/ms. (Inset) A simplified α-d-glucopyranose ring with the dextran linkages, 1→6, and the transition region at high resolution. (C) Pectin, stretched under the force-ramp mode, reveals a two-step transition (arrows, chair-boat-inverted chair). Ramp rate: 3 pN/ms. (Inset) A simplified α-d-galactopyranose ring with the pectin-type linkages, 1→4, and the two transitions region at high resolution.
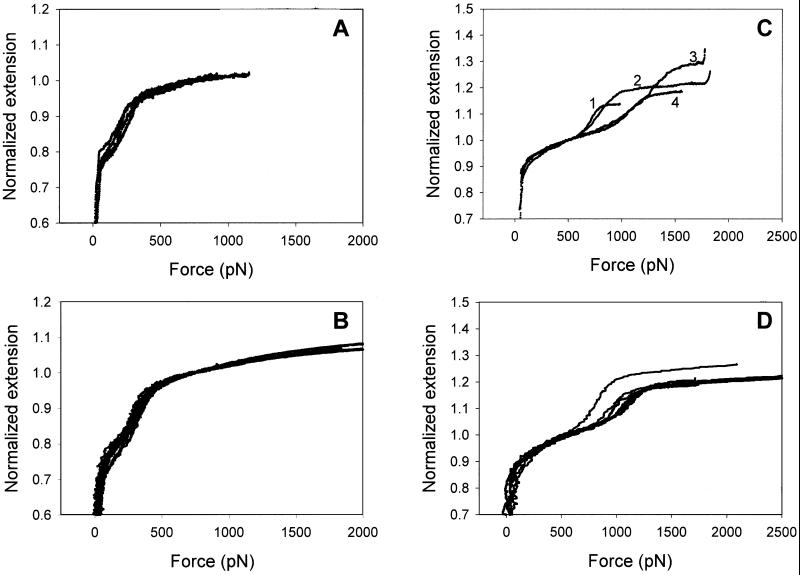
Figure 3.
A comparison of force-extension recordings of CMA (A), amylose (B), and dextran (C and D) obtained under the force-ramp (A and C) and the extension-ramp (B and D) protocols. All four graphs reveal variations among normalized recordings, which preclude a direct quantitative comparison of individual curves obtained under different AFM stretching protocols. In A and B the extension was normalized by the length of the molecule determined at 750 pN and in C and D the extension was normalized by the length of the molecule determined at 500 pN. To convert the recordings obtained under the extension ramp protocol into extension-force curves (B and D) we plotted the extension of the molecule versus the force, which was determined at that extension.
The CMA plot (Fig. 2A) can be divided into four regions (compare with Fig. 1B). At forces below ≈50 pN, the curve rises steeply consistent with the entropic extensibility of the polymer (see above). This entropic phase continues between 50 and 200 pN, albeit with the greatly reduced compliance of the molecule because at these forces the extension approaches the contour length. At approximately 200 pN (arrow in the Inset) the slope of the curve increases abruptly (compliance increases) because of the extra elongation of the chain resulting from the chair-boat transition of the pyranose rings (4). At around 350 pN this transition is complete and the chain is now composed of the rings in the boat-like conformation. This chain is stretched further but the small additional extensions come only from deforming the rings and bending the glycosidic linkages (intrinsic enthalpic elasticity of the segments) and this decreased extensibility is reflected in the greatly reduced slope of the extension-force curve.
Consistent with our earlier results (4), dextran stretched with the force ramp mode of AFM (Fig. 2B) shows a similar behavior to that of amylose; however, the transition occurs at a higher force (600–1,000 pN) (2, 4). Pectin (Fig. 2C) shows two transitions (≈200 and ≈650 pN) that reflect the lengthening of the chain by the two-step chair inversion transition (5). The initial extension of dextran and pectin in Fig. 2 B and C deviates from the FJC model of entropic elasticity. On application of any stretching force, a FJC polymer should reach its equilibrium length instantaneously. However, because of the limited slew-rate of the feedback mechanism, the observed initial extension deviates from the expected FJC model. This effect is smaller for the CMA molecule shown in Fig. 2A because this molecule was significantly shorter than those shown in Fig. 2 B and C, and it took less time to extend it. The slew-rate of the apparatus does not distort the postentropic range where the rate of extension of the molecules is given by the rate of increase in the applied force and is typically 10–100 times slower than the maximum rate allowed by the feedback system. For example, in Fig. 2B, the initial elongation of the molecule occurs at a maximal rate of 3.3 nm/ms, whereas in the postentropic region, the maximal slope occurs during the chair-boat transition and is 0.2 nm/ms, more than ten times slower than the instrumentation.
It is assumed that the conformational dynamics of the pyranose ring are, by analogy with the dynamics of cyclohexane (28), very fast compared with the time scale of our experiment and therefore stretching polysaccharides proceeds in equilibrium. In principle, force–extension relationships obtained under the extension ramp conditions can therefore be converted into extension–force relationships that should be equivalent to those obtained under the force ramp conditions. In Fig. 3 we converted the force-extension recordings of amylose and dextran (4, 9) into extension-force curves and compared these curves with the recordings registered under the force-ramp conditions. It is clear that the data obtained under both protocols are indeed similar. However, there are substantial variations among recordings in all four sets of the data that preclude a direct quantitative comparison of individual recordings obtained under different stretching protocols. These variations are greater for dextran than for amylose and their origin is unclear. It is possible that individual molecules are not always stretched vertically but at some angle that is less than 90° relative to the substrate surface. This can happen when a molecule is picked up by the AFM tip at a location away from its attachment point on the substrate. This pulling geometry can affect the force of the transition and its width. This effect was found negligible for proteins (29) but can be more significant for polysaccharides that are less compact than proteins and more likely to be picked up and stretched at an angle.
Two-State Model Fits the Data in the Vicinity of the Conformational Transition.
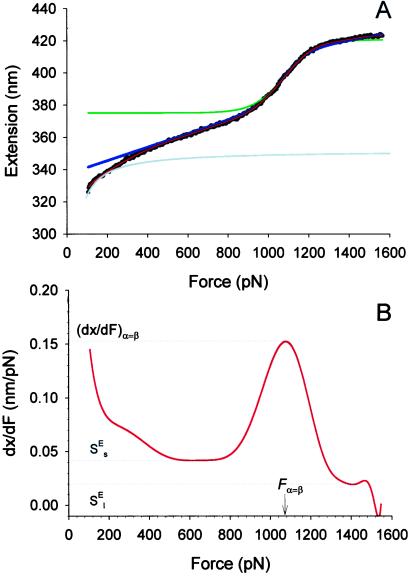
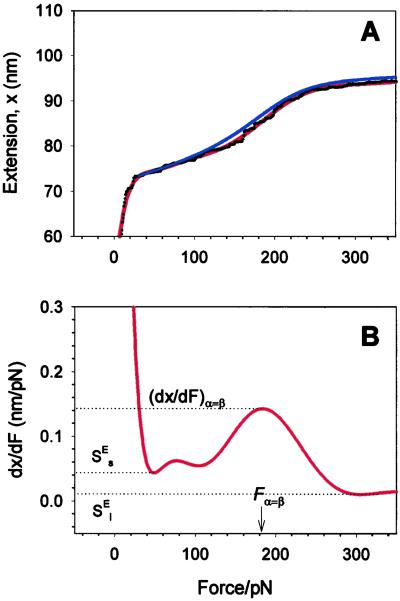
Fig. 4A shows recording 4 from Fig. 3C (black dots) in the vicinity of the conformational transition region. The gray line represents the extension-force curve of a hypothetical, purely entropic chain (a FJC) composed of segments in a single conformation state. We see that at forces >200 pN the entropic extensibility of this chain is small and therefore above ≈200 pN we neglect the entropic elasticity of dextran as compared with the extensibility arising from the conformational transition. The physical parameters characterizing this transition can be obtained from the force derivative of the extension–force relationship (see Materials and Methods). We show this derivative in Fig. 4B, and by inspecting it find that, in the region of the conformational transition, it reaches a local maximum of dx/dFα=β = 0.1513 nm/pN; this maximum is attained at a force Fα=β 1,075 pN. We calculate the number of monomers, N, from the length of the chain at the onset of the transition (≈375 nm; Fig. 4A), by assuming that at this extension all of the segments are still in the chair conformation with lS = 0.45 nm (4). Using Eqs. 3 and 2 we find Δx = 0.029 nm and ΔG = 15kBT. Using these parameters, we now generate a plot of x(F) given by Eq. 1 (green line, Fig. 4A). This line fits well the extension of dextran over the transitional region. However, the model deviates from the data above and below the transition. These deviations result from assuming that the pyranose ring is a rigid structure with only two possible lengths; which are given by either the chair or boat conformations. However, we know that the pyranose ring possesses an intrinsic enthalpic elasticity (4). We will show now that by including the intrinsic elasticity of the conformers, a full analytical fit of the data can be obtained.
Figure 4.
The two-state model correctly predicts the enthalpic elasticity of dextran and its forced-conformational transition. (A) The red line is the polynomial fit to the experimental data (black dots). The green line represents the fit of the two-state model without the segment elasticity. The blue line is the fit of the two-state model with the segment elasticity. The blue line was generated using n = 747 (recalculated using S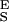 ), Δx = 0.034 nm, β0/α0 = 55 × 106, S
), Δx = 0.034 nm, β0/α0 = 55 × 106, S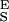 = 17,900 pN/nm and S
= 17,900 pN/nm and S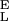 = 32,500 pN/nm. The gray line is the fit of the purely entropic FJC model to the data before the transition. (B) The force derivative of the dextran extension obtained from the polynomial fit in A. The maximum of the derivative (dx/dFα=β) occurs at a force Fα=β, at which the “chair-boat” and the “boat-chair” rate constants become equal. From the values of the derivative marked by the dotted lines the segment elasticity of each conformer can be determined (see text). We note that the final part of the derivative at F > 1,500 pN is unphysical when it becomes negative because of noise in the data.
= 32,500 pN/nm. The gray line is the fit of the purely entropic FJC model to the data before the transition. (B) The force derivative of the dextran extension obtained from the polynomial fit in A. The maximum of the derivative (dx/dFα=β) occurs at a force Fα=β, at which the “chair-boat” and the “boat-chair” rate constants become equal. From the values of the derivative marked by the dotted lines the segment elasticity of each conformer can be determined (see text). We note that the final part of the derivative at F > 1,500 pN is unphysical when it becomes negative because of noise in the data.
The Enthalpic Elasticity of the Monomers.
The intermediate range of forces above the entropic region and below the conformational transition is dominated by the enthalpic elasticity of the polysaccharide chain. We incorporate this enthalpic elasticity (2, 4) into our two-state model by assigning the conformers effective hookean spring constants, S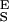 and S
and S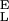 for short and long segments, respectively. Eq. 1, after supplementing it with the enthalpic elasticity, assumes the following form:
for short and long segments, respectively. Eq. 1, after supplementing it with the enthalpic elasticity, assumes the following form:
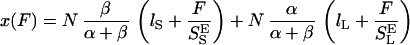 |
4 |
An inspection of Eq. 4 indicates that the segment elasticity of the short and long conformer determines the slope of the extension–force relationship at low and high forces, respectively, where α ≪ β and α ≫ β: dx/dFα≪β → N/S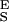 and dx/dFα≫β → N/S
and dx/dFα≫β → N/S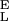 . We also find that the force derivative of Eq. 4 yields a quadratic equation for the half width of the energy barrier, Δx, when α = β. Now, Δx depends not only on dx/dFα=β (compare with Eq. 3) but also on S
. We also find that the force derivative of Eq. 4 yields a quadratic equation for the half width of the energy barrier, Δx, when α = β. Now, Δx depends not only on dx/dFα=β (compare with Eq. 3) but also on S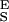 and S
and S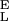 . To find this new value of Δx we first determine S
. To find this new value of Δx we first determine S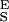 and S
and S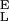 from the slopes of the extension–force relationship. These slopes are directly measured from the values of dx/dF before and after the conformational transition, as shown in Fig. 4B. We measure the enthalpic elasticity of the pyranose ring before and after the transition to be 17,870 pN/nm and 32,478 pN/nm, respectively. Using these values we find now Δx = 0.034 nm, and ΔG = 17.8 kBT. Using these new parameters and Eq. 4 we generate an extension-force curve shown as the blue line in Fig. 4A. As shown by the figure, we can now describe, analytically, the length versus force relationship, without the use of free parameters. This description is valid in the force range above 200 pN, where the entropic behavior of the chain can be neglected. Similarly, we analyzed recordings 1, 2, and 3 from Fig. 3C and we calculated the following parameters: 1, S
from the slopes of the extension–force relationship. These slopes are directly measured from the values of dx/dF before and after the conformational transition, as shown in Fig. 4B. We measure the enthalpic elasticity of the pyranose ring before and after the transition to be 17,870 pN/nm and 32,478 pN/nm, respectively. Using these values we find now Δx = 0.034 nm, and ΔG = 17.8 kBT. Using these new parameters and Eq. 4 we generate an extension-force curve shown as the blue line in Fig. 4A. As shown by the figure, we can now describe, analytically, the length versus force relationship, without the use of free parameters. This description is valid in the force range above 200 pN, where the entropic behavior of the chain can be neglected. Similarly, we analyzed recordings 1, 2, and 3 from Fig. 3C and we calculated the following parameters: 1, S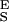 = 16,530 pN/nm, S
= 16,530 pN/nm, S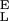 = 34,000 pN/nm, Δx = 0.041 nm, ΔG = 14 kBT; 2, S
= 34,000 pN/nm, Δx = 0.041 nm, ΔG = 14 kBT; 2, S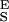 = 9,500 pN/nm, S
= 9,500 pN/nm, S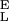 = 47,000 pN/nm, Δx = 0.049 nm, ΔG = 16.5 kBT; 3, S
= 47,000 pN/nm, Δx = 0.049 nm, ΔG = 16.5 kBT; 3, S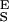 = 14,400 pN/nm, S
= 14,400 pN/nm, S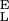 = 36,950 pN/nm, Δx = 0.044, ΔG = 27 kBT.
= 36,950 pN/nm, Δx = 0.044, ΔG = 27 kBT.
The derivative of the extension-force curve of dextran displays a “hump” between 200 and 400 pN (Fig. 4B). The feature responsible for this hump can be identified, after a closer inspection, in the extension-force curve (Fig. 4A). We speculate that this hump may correspond to an earlier force-induced conformational transition such as a torsional transition in the C5–C6 rotamers from a preferred gg or gt state to the more energetic tg conformation (30).
Using the above procedure we also analyzed the experimental extension-force curves obtained from single CMA molecules (Fig. 5). We measured the enthalpic elasticity of the conformers to be S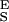 = 3,973 ± 1,045 pN/nm and S
= 3,973 ± 1,045 pN/nm and S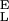 = 29,800 ± 11,200 pN/nm; the distance to the transition state to be Δx = 0.057 ± 0.006 nm; and the free-energy difference between the chair and the boat-like conformers to be ΔG = 6.4 ± 1.2 kBT (n = 5). This last value is similar to our earlier result obtained on native amylose (4) and to the classical data obtained for the chair-boat transition in cyclohexane (19, 28). The value of Δx is close to one half of the increase in the separation of the glycosidic oxygen atoms upon the chair-boat transition of the glucopyranose ring calculated ab initio (0. 044 nm; ref. 4). In contrast to CMA, Δx determined for dextran (0.042 ± 0.005) is smaller than the corresponding value calculated ab initio (0. 064 nm; ref. 4). It is possible that this difference is related to the greater complexity of the conformational transition in dextran than in amylose.
= 29,800 ± 11,200 pN/nm; the distance to the transition state to be Δx = 0.057 ± 0.006 nm; and the free-energy difference between the chair and the boat-like conformers to be ΔG = 6.4 ± 1.2 kBT (n = 5). This last value is similar to our earlier result obtained on native amylose (4) and to the classical data obtained for the chair-boat transition in cyclohexane (19, 28). The value of Δx is close to one half of the increase in the separation of the glycosidic oxygen atoms upon the chair-boat transition of the glucopyranose ring calculated ab initio (0. 044 nm; ref. 4). In contrast to CMA, Δx determined for dextran (0.042 ± 0.005) is smaller than the corresponding value calculated ab initio (0. 064 nm; ref. 4). It is possible that this difference is related to the greater complexity of the conformational transition in dextran than in amylose.
Figure 5.
The two-state model describes the elasticity of single CMA molecules. (A) The thin red line is the polynomial fit to the experimental data (black dots). The blue line is the fit of the two-state model with the segment elasticity. The blue line was generated using n = 159, Δx = 0.065 nm, ΔG = 6.1 kBT, S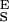 = 2,900 pN/nm, and S
= 2,900 pN/nm, and S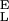 = 18,240 pN/nm. (B) The force derivative of the amylose extension obtained from the polynomial fit in A. The analysis of this derivative produced the parameters used to generate the two-state model line in A (compare with Fig. 4).
= 18,240 pN/nm. (B) The force derivative of the amylose extension obtained from the polynomial fit in A. The analysis of this derivative produced the parameters used to generate the two-state model line in A (compare with Fig. 4).
Similar to dextran, the derivative of the extension-force curve of amylose displays a “hump” before the main chair-to-boat transition at forces around 70 pN (Fig. 5B). We speculate that this feature of the force spectrogram reports on a conformational transition that occurs in the process of lining up the amylose monomers with the force vector, which involves the surmounting of torsional barriers.
We also note that the enthalpic elasticity of CMA segments before the transition is ≈7-fold lower than after the transition. There are several factors that may contribute to this difference as they are related to the overall mechanics of the polysaccharide chain and the mechanics of pyranose rings in various conformations. The extra extensibility of the CMA chain, observed at low stretching forces, could be related to forced changes in the mutual orientation of the monomers. In addition, and as shown by Joshi and Rao (31), the chair conformation of the pyranose ring is flexible because there are several distorted chair conformations that are of equal conformational energy but have very different torsional and bond angles. Hence, these conformers will make the chair conformation highly flexible because changes in the length of the O1O4 distance can occur without changing the conformational energy. By contrast, stretching the pyranose ring into the boat conformation limits the possible boat conformers to only that that gives the largest O1O4 distance. From this point of view, the elasticity changes are due to the reduced conformational space of the stretched boat compared with the relaxed chair forms. This evidently suggests that the two-state model that we use here is an oversimplification. However, incorporating multiple chair conformers at this stage is beyond the scope of this paper. We can estimate the order of magnitude of the enthalpic elasticity of a stretched boat conformer by considering the bending energy term in the CHARMM force-field parameterization of the glucopyranose ring. Ha et al. (1988) provided kθ ≈90 kcal/(mol rad2) for the bending of a C—OE—C bond (32), where OE is the ring oxygen. This is equivalent to an enthalpic elasticity of ≈60,000 pN/nm. The extension-force curve of amylose in the high force range (boat conformations) gives an enthalpic elasticity of ≈30,000–40,000 pN/nm, which is of the same order of magnitude as the value obtained from the CHARMM estimate.
The pectin data were not analyzed here by the simple two-state model because a more complex three-state model would be required, greatly increasing the complexity of the analysis with the obvious difficulties in determining the segment elasticity and energy barriers for each state.
Acknowledgments
This work was supported by grants from the National Science Foundation and the National Institutes of Health (to P.E.M. and J.M.F.).
Abbreviations
- CMA
carboxymethylamylose
- FJC
freely jointed chain
- AFM
atomic force microscopy
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Fisher T E, Marszalek P E, Fernandez J M. Nat Struct Biol. 2000;7:719–724. doi: 10.1038/78936. [DOI] [PubMed] [Google Scholar]
- 2.Rief M, Oesterhelt F, Heymann B, Gaub H E. Science. 1997;275:1295–1297. doi: 10.1126/science.275.5304.1295. [DOI] [PubMed] [Google Scholar]
- 3.Oberhauser A F, Marszalek P E, Erickson H P, Fernandez J M. Nature (London) 1998;393:181–185. doi: 10.1038/30270. [DOI] [PubMed] [Google Scholar]
- 4.Marszalek P E, Oberhauser A F, Pang Y-P, Fernandez J M. Nature (London) 1998;396:661–664. doi: 10.1038/25322. [DOI] [PubMed] [Google Scholar]
- 5.Marszalek P E, Pang Y P, Li H, Yazal J E, Oberhauser A F, Fernandez J M. Proc Natl Acad Sci USA. 1999;96:7894–7898. doi: 10.1073/pnas.96.14.7894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Marszalek P E, Lu H, Li H, Carrion-Vazquez M, Oberhauser A F, Schulten K, Fernandez J M. Nature (London) 1999;402:100–103. doi: 10.1038/47083. [DOI] [PubMed] [Google Scholar]
- 7.Li H, Rief M, Oesterhelt F, Gaub H E. Adv Mater. 1998;3:316–319. [Google Scholar]
- 8.Li H, Rief M, Oesterhelt F, Gaub H E, Zhang X, Shen J. Chem Phys Lett. 1999;305:197–201. [Google Scholar]
- 9.Marszalek P E, Li H, Fernandez J M. Nat Biotechnol. 2001;19:258–262. doi: 10.1038/85712. [DOI] [PubMed] [Google Scholar]
- 10.Xu Q, Zou S, Zhang W, Zhang X. Macromol Rapid Commun. 2001;22:1163–1167. [Google Scholar]
- 11.Hugel T, Seitz M. Macromol Rapid Commun. 2001;22:989–1016. [Google Scholar]
- 12.Isralewitz B, Gao M, Schulten K. Curr Opin Struct Biol. 2001;11:224–230. doi: 10.1016/s0959-440x(00)00194-9. [DOI] [PubMed] [Google Scholar]
- 13.Whistler R L, BeMiller J N. Industrial Gums: Polysaccharides and their derivatives. 3rd Ed. San Diego: Academic; 1993. [Google Scholar]
- 14.Rao V S R, Qasba P K, Balaji P V, Chandrasekaran R. Conformation of Carbohydrates. Amsterdam: Harwood Academic Publishers; 1998. [Google Scholar]
- 15.Brant D A. Curr Opin Struct Biol. 1999;9:556–562. doi: 10.1016/s0959-440x(99)00005-6. [DOI] [PubMed] [Google Scholar]
- 16.Oberhauser A F, Hansma P K, Carrion-Vazquez M, Fernandez J M. Proc Natl Acad Sci USA. 2001;98:468–472. doi: 10.1073/pnas.021321798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bell G I. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 18.Evans E, Ritchie K. Biophys J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.O'Donoghue P, Luthey-Schulten Z A. J Phys Chem B. 2000;104:10398–10405. [Google Scholar]
- 20.Rief M, Fernandez J M, Gaub H E. Phys Rev Lett. 1998;81:4764–4767. [Google Scholar]
- 21.Flory P J. Principles of Polymer Chemistry. Ithaca, NY: Cornell Univ. Press; 1953. [Google Scholar]
- 22.Smith S B, Finzi L, Bustamante C. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 23.Seifert U. Phys Rev Lett. 2000;84:2750–2753. doi: 10.1103/PhysRevLett.84.2750. [DOI] [PubMed] [Google Scholar]
- 24.Florin E L, Rief M, Lehmann H, Ludwig M, Dornmair K, Moy V T, Gaub H E. Biosens Bioelectron. 1995;10:895–901. [Google Scholar]
- 25.Evans E, Ritchie K. Biophys J. 1999;76:2439–2447. doi: 10.1016/S0006-3495(99)77399-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Perico A, Mormino M, Urbani R, Cesaro A, Tylianakis E, Dais P, Brant D A. J Phys Chem B. 1999;103:8162–8171. [Google Scholar]
- 27.Heymann B, Grubmüller H. Chem Phys Lett. 1999;305:202–208. [Google Scholar]
- 28.Pickett H M, Strauss H L. J Am Chem Soc. 1970;92:7281–7290. [Google Scholar]
- 29.Carrion-Vazquez M, Marszalek P E, Oberhauser A F, Fernandez J M. Proc Natl Acad Sci USA. 1999;96:11288–11292. doi: 10.1073/pnas.96.20.11288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bock K, Duus J Ø. J Carbohydr Chem. 1994;13:513–543. [Google Scholar]
- 31.Joshi N V, Rao V S R. Biopolymers. 1979;18:2993–3004. [Google Scholar]
- 32.Ha S N, Giammona A, Field M, Brady J W. Carbohydr Res. 1988;180:207–221. doi: 10.1016/0008-6215(88)80078-8. [DOI] [PubMed] [Google Scholar]