Computational mapping identifies the binding sites of organic solvents on proteins

Abstract

Computational mapping places molecular probes—small molecules or functional groups—on a protein surface to identify the most favorable binding positions. Although x-ray crystallography and NMR show that organic solvents bind to a limited number of sites on a protein, current mapping methods result in hundreds of energy minima and do not reveal why some sites bind molecules with different sizes and polarities. We describe a mapping algorithm that explains the origin of this phenomenon. The algorithm has been applied to hen egg-white lysozyme and to thermolysin, interacting with eight and four different ligands, respectively. In both cases the search finds the consensus site to which all molecules bind, whereas other positions that bind only certain ligands are not necessarily found. The consensus sites are pockets of the active site, lined with partially exposed hydrophobic residues and with a number of polar residues toward the edge. These sites can accommodate each ligand in a number of rotational states, some with a hydrogen bond to one of the nearby donor/acceptor groups. Specific substrates and/or inhibitors of hen egg-white lysozyme and thermolysin interact with the same side chains identified by the mapping, but form several hydrogen bonds and bind in unique orientations.

The mapping of a protein by experimental or computational tools involves placing molecular probes—small organic molecules or functional groups—around the protein surface to determine the most favorable binding positions. Larger molecules that are candidates for high affinity ligands can be constructed by combining the probes at (or near) their optimal binding sites. This site-mapping and fragment-assembly strategy provides an important approach to drug design (1–6). Experimental approaches to mapping include x-ray crystallography (7–10) and NMR techniques (11, l2). In the multiple solvent crystal structure method (7–10), the x-ray structure of a protein is repeatedly solved in a variety of organic solvents, each representing a different functional group. In NMR methods, the binding of small molecules in aqueous solution is detected by chemical shifts of the protein and by the observation of intermolecular nuclear Overhauser effects (NOEs) between protons of the protein and the ligand (11).

Because the probes are generally unrelated to any natural substrate of the protein, one would expect largely nonspecific binding. However, both x-ray crystallography (7–10) and NMR (11) reveal only a limited number of bound ligand positions, and a pocket of the active site tends to form a consensus site that binds many ligands, irrespective of their sizes and polarities. An NMR study by Liepinsh and Otting (11) shows that methanol, methylene chloride, acetonitrile (CCN), acetone (ACN), DMSO, isopropanol (IPA), t-butanol, and urea all bind to the specificity-determining site (site C) of the hen egg-white lysozyme (HEWL). Recent multiple solvent crystal structure studies of thermolysin (TLN) (9, 10) show that IPA, ACN, CCN, and phenol (IPH) bind preferentially to subsite S₁′ of the active site.

A number of methods have been developed to perform mapping computationally rather then experimentally, including the drug design program grid (1) and the multiple copy simultaneous search (MCSS) strategy (13–15). As emphasized by Mattos and Ringe (7), the major problem with approaches exemplified by grid and MCSS is that they result in hundreds of energy minima on the surface of the protein, and it is difficult to determine which of the minima are actually relevant. Thus, these mapping methods are unable to explain the origin of consensus sites.

In the present article we describe a three-step mapping algorithm that avoids the large number of irrelevant local energy minima and identifies the consensus sites. In all cases we have studied so far, the consensus binding site is a major subsite of the protein active site, which can accommodate most small ligands in a number of rotational states, frequently with one or two hydrogen bonds with polar groups in the pocket.

Methods

Empirical Free Energy Functions.

We calculate the conformation-dependent portion of the binding free energy by using an expression of the form

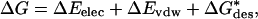1

where ΔE_elec denotes the direct (coulombic) part of the electrostatic energy, ΔE_vdw is the change in the van der Waals energy after binding, and ΔG^*_des is the desolvation free energy. The asterisk emphasizes that the latter term includes the change in the solute-solvent van der Waals interaction energy.

In the first step of the mapping procedure, we use a simplified form of the free energy expression (ΔG_s) in which we assume that the intermolecular van der Waals interactions in the bound state are balanced by solute-solvent interactions in the free state (16–18). This so-called “van der Waals cancellation” implies that both ΔE_vdw and the van der Waals contributions to the desolvation free energy can be removed and the binding free energy reduces to

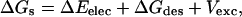2

where the desolvation free energy, ΔG_des, does not include the solute-solvent van der Waals term, and V_exc is an excluded volume penalty term such that V_exc = 0 if the ligand does not overlap the protein.

A continuum electrostatics model (19, 20) is used throughout the procedure, with ɛ = 4 and ɛ = 78 for the protein and the water, respectively. However, some of the free energy terms are evaluated differently at different stages of the mapping. In the first step, we calculate the electrostatic field Φ of the solvated protein by a finite difference Poisson-Boltzmann method (19, 20). The (direct) electrostatic energy is then obtained by the expression ΔE_elec = ∑ Φ_iq_i, where q_i is the charge of the ith probe atom, and Φ_i is the field value at that point. The desolvation free energy, ΔG_des, is calculated by an empirical contact potential of the form ΔG_des = ∑ ∑ e_ij, where e_ij denotes the atomic contact potential (ACP) of interacting atoms i (of the probe molecule) and j (of the protein), with the double sum taken over all protein-probe atom pairs that are less than 6 Å apart (21, 22).

In the second step, both solute–solute and solute–solvent van der Waals interactions are taken into account, i.e., the free energy is calculated by using Eq. 1. The sum ΔE_elec + ΔG*_des is obtained by the analytic continuum electrostatics method of Schaefer and Karplus (23) as implemented in version 27 of charmm (24). The solute-solvent van der Waals energy, ΔE_vdw, is also calculated by using charmm.

Mapping Algorithm.

The probes are modeled by using the quanta/charmm program (Molecular Simulations, Waltham, MA). The mapping procedure is identical for each probe molecule and is accomplished by using three computational steps as follows.

Step 1: Rigid body search for regions with favorable electrostatics and solvation.

Protein coordinates are read from the Protein Data Bank (PDB) files (PDB ID codes 2lym and 2tlx for HEWL and TLN, respectively). Ligand molecules are placed as probes at 222 initial points, evenly distributed in the first water layer over the entire protein surface. A multistart simplex minimization method (25, 26) is used to move the probes toward nearby minima of ΔG_s. During the course of the minimizations, the protein atoms are held fixed and the ligand molecules travel an average distance of 3.2 Å around the protein surface under the influence of electrostatic and desolvation forces.

Step 2: Free energy refinement and final docking.

Step 1 of the mapping produces 6,660 protein–ligand complexes at various local minima of ΔG_s. In the second step of the algorithm, the free energy of each of these complexes is minimized by using ΔG (Eq. 1) as the target function. The minimization is performed for each protein-probe complex by using an adopted basis Newton–Raphson method as implemented in charmm (24). During the minimization the protein atoms are held fixed, whereas the atoms of the probe molecules are free to move.

Step 3: Clustering, scoring, and ranking.

The minimized probe conformations from Step 2 are grouped into clusters based on Cartesian coordinate information. The method creates an appropriate number of clusters such that the maximum distance between the hub of a cluster and any of its members (the cluster radius) is smaller then half of the average distance among all of the existing hubs. We have slightly modified this algorithm by introducing an explicit upper bound U on the cluster radius to account for the physical dimensions of the different probe molecules. U is set equal to 2.0 Å for methanol, whereas a value of 4.0 Å is used for the other ligands. Very small clusters (n < 20) are excluded from consideration. For each of the remaining clusters we calculate the probability p_i = Q_i/Q, where the partition function Q is the sum of the Boltzmann factors over all conformations, Q = Σ_j exp (−ΔG_j/RT), and Q_i is obtained by summing the Boltzmann factors over the conformations in the ith cluster only. The Boltzmann average of a property x for the ith cluster is calculated by 〈x〉_i = Σ_j p_ij x_j, where p_ij = exp (−ΔG_j/RT)/Q_i, and the sum is taken over the members of the ith cluster. We calculate the average free energy terms 〈ΔG〉, 〈ΔE_elec〉, 〈ΔE_vdw〉, and 〈ΔG*_des〉 for each cluster (all free energies are given in kcal/mol).

Subcluster Analysis.

For each ligand, the cluster with the minimum average free energy, 〈ΔG〉, is divided further into subclusters by using pairwise rms deviation and absolute energy difference (AED) values among all members of the cluster. The AED between two probes i and j is calculated as AED_ij = |ΔG_i −ΔG_j|. Each set of pairwise numbers is scaled on the range 0 to 1 by using the maximum and minimum values within the cluster, and the scaled values for each pair of probes are summed yielding a pairwise scaled comparative value (PSCV). The lowest free energy probe in the cluster is denoted the hub of subcluster 1, and the PSCV of all other cluster members relative to it are checked. Those falling below a certain limit are grouped into the first subcluster. This procedure is repeated iteratively with the remaining probe molecules, with the lowest free energy probe among these denoted the hub of the next subcluster. The subclusters of the ith cluster are ranked on the basis of the probabilities p_ij = Q_ij/Q_i, where Q_i is the sum of the Boltzmann factors over all conformations of the ith cluster, and Q_ij is obtained by summing the Boltzmann factors over the conformations in the jth subcluster only.

Results and Discussion

Mapping HEWL.

The algorithm has been used to find the binding sites for methanol, methylene chloride, CCN, ACN, IPA, t-butanol, urea, and DMSO on HEWL in aqueous solution. NMR data by Liepinsh and Otting (11) show that all eight molecules bind to site C, with a few additional weak NOEs at the rim of site C for IPA and ACN. In addition, methanol and methylene chloride show NOEs with protons located in the interior of HEWL, indicating some penetration into the hydrophobic core (11).

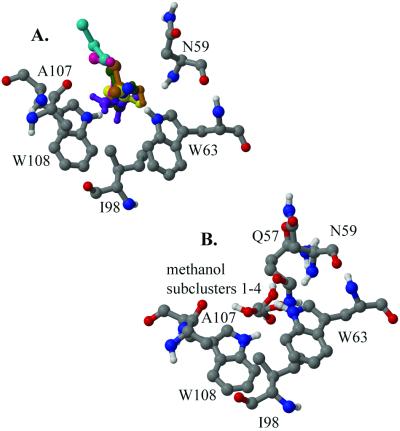
Table 1 lists a number of the low average free energy clusters for each ligand. As shown in Fig. 1A and confirmed by the distance of the ligand from site C in the last column of Table 1, the lowest average free energy cluster is always at site C. DMSO (pink) and methylene chloride (cyan) are not as deeply inside the pocket as the other ligands. Further details are given in Table 2, which lists the experimentally observed NOEs between the protons of seven of the eight ligands (no NOE data were published for t-butanol), and the nine protons located in site C of HEWL (11), as well as the computationally derived shortest distances (Å) among the same nine HEWL protons and those of each ligand in its lowest free energy cluster. Because an NOE can be detected experimentally if two protons are closer than about 5 Å, and a strong NOE requires a separation of around 3 Å, there is fairly good agreement between the experimentally observed NOEs and the calculated distances. We note that the mapping finds the consensus site, but not other locations that bind only certain ligands (e.g., the internal site that binds methanol and methylene chloride).

Table 1.

Lowest average free energy clusters of the eight organic ligands bound to HEWL

Ligand	Cluster	Size	p	〈ΔG〉	〈ΔEelec〉	〈ΔEvdw〉	〈ΔG*des〉	D,† Å
Methanol	1	97	0.74	−7.18	−0.87	−8.26	1.95	2.3
	2	98	0.14	−6.60	−3.87	−7.59	4.87	3.7
	3	51	0.00	−5.68	−1.88	−6.71	2.91	7.6
IPA	1	51	0.92	−11.60	−1.04	−12.82	2.27	2.8
	2	50	0.01	−8.94	−0.97	−10.04	2.07	2.3
	3	37	0.00	−8.81	−1.94	−9.85	2.98	16.9
t-butanol	1	76	0.48	−17.53	0.45	−16.85	−1.13	2.0
	2	72	0.47	−16.90	−3.00	−16.18	2.29	2.1
	3	275	0.03	−14.32	−0.99	−13.44	0.12	6.9
DMSO	1	100	0.51	−14.05	−0.72	−12.82	−0.51	2.7
	2	44	0.46	−13.76	−0.09	−12.81	−0.86	2.9
	3	263	0.01	−10.69	−1.68	−9.44	0.43	6.8
ACN	1	139	1.00	−13.14	−1.00	−13.56	1.42	2.2
	2	63	0.00	−9.45	−0.72	−10.04	1.30	11.0
CCN	1	26	0.28	−10.18	−0.82	−8.19	−1.17	2.4
	2	154	0.39	−9.41	−3.85	−6.60	1.04	3.2
	3	40	0.04	−8.81	−4.46	−6.16	1.81	7.7
Urea	1	40	0.91	−12.10	−0.79	−15.38	4.07	2.2
	2	94	0.06	−10.54	−5.93	−13.36	8.75	2.6
	3	21	0.00	−9.65	−0.37	−12.39	3.11	8.1
Methylene chloride	1	63	0.28	−3.70	−3.01	−4.27	3.57	3.5
	2	373	0.40	−2.91	−2.74	−3.60	3.43	6.8

^† Shortest distance between any ligand atom and any protein atom in site C of HEWL. 

Figure 1.

(A) The lowest free energy positions of eight organic solvents bound to HEWL. The color scheme used for the ligands is red, methanol; dark green, IPA; yellow, ACN; purple, urea; blue, CCN; ochre, t-butanol; cyan, methylene chloride; and pink, DMSO. For the protein we use the standard atom colors, i.e., carbon, gray; oxygen, red; nitrogen, blue; and hydrogen, white. Only polar hydrogen atoms are shown. (B) The four highest probability subclusters of the lowest average free energy cluster for methanol. Only polar hydrogen atoms are shown.

Table 2.

Intermolecular NOEs and calculated shortest intermolecular proton–proton distances for organic solvents in site C of HEWL

Ligand		Protons with intermolecular NOEs
		N59 NH	W63 CδH	W63 NɛH	I98 CγH	I98 CδH	A107 CβH	W108 CδH	W108 CζH	W108 NɛH
Methanol*	E†	Y‡	Y	Y	Y	Y	Y	Y	Y	Y
	M†	2.24	2.50	2.55	2.38	2.36	2.69	3.27	2.96	1.97
	M†	3.97	5.92	6.28	6.15	6.28	4.87	2.71	6.82	4.62
IPA	E	Y	Y	Y	Y	Y	Y	Y	Y	Y
	M	2.30	2.63	2.27	2.89	2.68	3.22	2.66	3.93	3.22
t-butanol*	M	1.72	2.06	2.02	1.98	2.00	1.86	2.97	3.68	2.77
	M	2.28	3.27	2.25	2.05	2.39	2.94	2.60	3.72	2.57
DMSO*	E	N	Y	Y	Y	Y	Y	Y	Y	Y
	M	2.59	3.72	3.62	2.98	3.06	3.32	2.48	4.11	2.78
	M	1.95	2.79	2.07	2.11	2.13	2.51	3.00	3.67	2.69
ACN	E	Y	Y	Y	Y	Y	Y	Y	Y	Y
	M	2.04	2.72	2.76	2.40	2.67	2.90	3.44	3.92	3.23
CCN*	E	N	N	W	Y	Y	Y	Y	W	Y
	M	2.47	3.65	3.91	2.41	2.32	3.13	3.14	3.76	3.12
	M	4.44	6.10	6.34	5.54	5.79	5.37	2.55	6.12	3.95
Urea	E	N	N	Y	Y	Y	Y	Y	N	Y
	M	1.73	2.22	1.85	1.86	1.83	2.03	2.92	2.51	2.05
Methylene chloride*	E	N	N	N	W	N	Y	Y	Y	Y
	M	2.46	3.81	4.00	2.30	2.75	3.05	2.88	4.13	2.85
	M	5.49	6.78	6.92	7.91	8.21	7.22	6.56	9.45	7.60

^*The two lowest free energy clusters. 

^† E, experimental (NMR [11]); M, mapping. 

^‡ Y, NOE is observed; N, no NOE; W, weak NOE. 

The minimum average free energy cluster for each ligand is divided further into subclusters as described in Methods. Table 3 lists the highest probability subclusters for each ligand, where the number in parentheses indicates the total number of subclusters. The table shows that site C accommodates each molecule in a number of rotational states. The hydrophobic part of the ligand is in a pocket formed by I98 and the nonpolar portions of the W62, W63, and W108 side chains. This pocket is surrounded by six polar groups: N59 NH, Q57 O, A107 O, W62 N^ɛ1, W63 N^ɛ1, and W108 N^ɛ1. All ligands (with the exception of methylene chloride) bind in a number of conformations, in many cases forming a hydrogen bond with one of these groups, and the polar parts of the ligands point toward various polar patches on the protein even in cases where no explicit hydrogen bonds are formed. For example, the methyl group of the methanol is almost completely invariant, whereas the hydroxyl group is found in four different states, forming a hydrogen bond with N59 NH, Q57 O, W108 N^ɛ1, or A107 O (Fig. 1B).

Table 3.

Selected subclusters of the minimum 〈ΔG〉 clusters of the 8 ligands bound to HEWL

Ligand (N)†	SC	Size	p	〈ΔG〉	〈ΔEelec〉	〈ΔEvdw〉	〈ΔG*des〉	H-bond(s)‡
Methanol (5)	1	39	0.63	−7.35	−0.38	−8.35	1.38	N59 NH
	2	24	0.22	−7.01	−1.77	−7.98	2.73	N59 NH, Q57 O
	3	7	0.07	−7.10	−2.03	−8.73	3.66	W108 Nɛ1
	4	21	0.05	−6.24	−1.53	−7.57	2.86	A107 O
IPA (8)	1	6	0.37	−11.73	−0.55	−13.05	1.87
	2	3	0.35	−12.07	−0.90	−13.01	1.84	Q57 O
	3	3	0.11	−11.41	0.06	−12.83	1.36	A107 O
	4	18	0.07	−10.10	−2.63	−11.83	4.36	A107 O, V109 NH
	5	17	0.05	−9.98	−3.03	−11.54	4.59	D52 Oδ1
t-butanol (7)	1	8	0.88	−17.75	0.66	−17.04	−1.37	N59 NH
	2	13	0.09	−16.18	−1.09	−15.80	0.72	A107 O
DMSO (8)	1	15	0.84	−14.36	−0.39	−13.13	−0.85
	2	54	0.08	−12.12	−3.08	−10.09	1.87
ACN (6)	1	25	0.61	−13.55	−1.15	−13.95	1.55	N59 NH
	2	85	0.36	−12.55	−0.86	−12.93	1.24
CCN (5)	1	20	0.89	−10.23	−0.85	−8.25	−1.13
	2	3	0.06	−9.72	−0.47	−7.64	−2.54
Urea (7)	1	10	0.71	−12.36	−0.36	−15.71	3.71	N59 NH
	2	11	0.16	−11.46	−3.18	−14.49	6.21	N59 NH
	3	8	0.12	−11.47	−0.05	−14.73	3.31
Methylene chloride (3)	1	57	0.98	−3.73	−3.08	−4.26	3.62

^† Total number of subclusters. 

^‡ Intermolecular hydrogen bonds. Protein donor or acceptor atoms are shown. 

Tables 1 and 3 also show the Boltzmann average values for the free energy components ΔE_elec, ΔE_vdw, and ΔG*_des, and these provide further information on the nature of the binding site. The lowest average free energy clusters are located deep in site C, and these clusters also have the lowest average van der Waals energy among all clusters. Furthermore, the average van der Waals energy is lower for all subclusters of the lowest average free energy cluster than for any cluster outside site C, suggesting that the pocket should be able to accommodate the ligand in a number of conformations with favorable shape complementarity. Charge–charge interactions do not seem to be very important. In fact, such interactions would imply large (favorable) ΔE_elec, compensated for the most part by large (unfavorable) ΔG*_des values. However, for most ligands the magnitudes of these free energy terms are smaller inside site C than outside it.

There are two low free energy clusters in site C for methanol, t-butanol, DMSO, and CCN. There are also a few fairly large clusters located outside side C (e.g., for methylene chloride, t-butanol and DMSO), but apart from methylene chloride these clusters have very low probabilities (Table 1). It is interesting to study how the energetics of binding at these locations differs from that at site C. We consider t-butanol as an example. The lowest free energy cluster is dominated by a single subcluster, which hydrogen bonds with N59 NH. In this position the nonpolar part of the ligand is in an extremely hydrophobic environment, resulting in very weak (and unfavorable) electrostatic interactions (〈ΔE_elec〉 = 0.45 kcal/mol) and a negative desolvation free energy for the cluster as a whole (Table 1). Table 3 shows that this is true only for the dominant subcluster. The second subcluster, which hydrogen-bonds with A107 O, is located in a slightly less hydrophobic environment, but the electrostatic interactions are still weak. The second t-butanol cluster is also in site C, and has a van der Waals term comparable to cluster 1, but more favorable electrostatics (〈ΔE_elec〉 = −3.0 kcal/mol), and positive desolvation. Both the electrostatics and the van der Waals interactions are weaker in cluster 3, just outside the pocket, suggesting that these two forces may steer the ligand toward cluster 2, whereas the transition to cluster 1 is governed by short-range desolvation and van der Waals forces.

According to the probabilities in Tables 1 and 3, the different clusters and subclusters represent a finite number of well defined conformations, with generally only a few dominating the distribution. The NOE spectroscopy spectra of these states overlap, and it is possible that the observed NOEs come from different conformations. In fact, because the NOEs vary as 1/r⁶ with the proton–proton distance r, these represent only the shortest proton–proton distances occurring in a population.

Mapping TLN.

English et al. (9, 10) determined high resolution crystal structures of TLN, generated from crystals soaked in aqueous solutions of IPA, ACN, CCN, and IPH, and found that the main substrate specificity pocket (S₁′) of the active site binds all four molecules. IPA also binds to the other three subsites of the active site, and additional sites have been observed for IPA, ACN, and IPH as the concentration of organic solvents in the soaking solution increases. In general, x-ray mapping shows more binding sites than NMR (11). Potential explanations for this include crystal contacts and weak binding that would not necessarily be seen in solution. For example, the bound sites IPA 9–12 are observed only in 100% IPA, four sites (IPA 6, IPA 7, IPA 10, and IPA 12) are at crystal contacts, IPA 4 interacts with a bound DMSO, and IPA 9 interacts with IPA 1. IPA 2 is almost completely buried in a hydrophobic pocket. For ACN, ACN 1 is in the S₁′ subsite, ACN 2 is in the buried pocket, ACN 3–5 are at crystal contacts, and the binding at ACN 6 is observed only at 80% ACN concentration. CCN shows a single probe bound at S₁′, whereas IPH has two probes bound at S₁′ and the buried subsite. Apart from the conformations buried in the hydrophobic pocket, the bound molecules are fairly mobile, generally with B factors around 60, and the existence of several possible binding modes has been postulated by the crystallographer (9, 10).

We emphasize that mapping considers a single solvated protein (i.e., surrounded by a high dielectric medium) and searches for locations at which a probe will replace water. Thus, we do not expect to find sites that are at crystal contacts or ones that occur only at high ligand concentrations, because the latter would require using a lower dielectric constant and possibly accounting for ligand–ligand interactions. We also neglect a number of factors such as the flexibility of the protein, a Zn²⁺ ion bound in the active site, and a number of crystallographic waters that interact with the bound ligands. Nevertheless, as shown in Table 4, the clusters with the lowest average free energies identify the bound probes in the active site for IPA, CCN, and IPH.

Table 4.

Lowest average free energy clusters of the four organic ligands bound to TLN

Ligand	Cluster	Size	p	〈ΔG〉	〈ΔEelec〉	〈ΔEvdw〉	〈ΔG*des〉	Mol†	D‡; rmsd§
IPA	1	129	0.40	−10.71	−2.74	−12.44	4.48	IPA 8	0.6; 1.1
	2	30	0.06	−10.49	−2.32	−12.81	4.64	IPA 1	0.7; 2.1
	3	132	0.26	−10.31	−2.03	−12.23	3.96	IPA 5	1.0; 3.4
	4	90	0.06	−10.01	−1.29	−11.07	2.36	IPA 8	13.6; 15.9
ACN	1	69	0.77	−13.10	−1.37	−14.15	2.41	ACN 2	12.8; 14.6
	2	104	0.15	−11.89	−5.59	−13.23	6.92	ACN 1	3.2; 5.0
	3	251	0.06	−10.96	−1.92	−12.26	3.22	ACN 1	5.4; 7.1
	4	30	0.01	−10.75	−0.16	−13.26	2.67	ACN 1	0.6; 1.4
	5	98	0.01	−10.19	−0.63	−11.53	1.97	ACN 6; 1	17.6; 18.8
CCN	1	241	0.63	−10.42	−7.01	−7.14	3.73	CCN 1	2.0; 4.6
	2	75	0.06	−9.90	−1.60	−7.64	−0.66	CCN 1	18.4; 20.8
IPH	1	134	1.00	−28.43	−3.35	−18.05	−7.03	IPH 1	2.6; 3.0
	2	30	0.00	−25.58	−1.57	−18.05	−5.97	IPH 1	0.4; 1.9
	3	62	0.00	−23.33	−2.20	−8.70	−12.44	IPH 1	13.1; 16.0

^† Experimental molecule (10). 

^‡ Shortest distance (Å) between any ligand atom and the corresponding experimentally determined ligand atom (10). 

^§ Shortest rms deviation (Å) between any ligand molecule and the corresponding experimentally determined ligand molecule (10). 

For IPA the three lowest free energy clusters are in the active site, very close to IPA 8, IPA 1, and IPA 5, respectively (Table 4). The only deviation from the experiment is that IPA 8 has slightly lower free energy than IPA 1, although IPA 5 and IPA 8 bind only at 90% IPA concentration. However, in view of the simplifying assumptions we described it seems remarkable that the three lowest free energy clusters identify the three major subsites. As mentioned, mapping is not expected to find binding sites that are at crystal contacts or those that occur only at high IPA concentration. Furthermore, the search focuses on relatively open surface regions with favorable electrostatics and desolvation, and hence it was not surprising that we did not find IPA 2, which is almost completely buried in a hydrophobic pocket.

For CCN, the mapping places a large cluster with the lowest average free energy in the S₁′ subsite, close to CCN 1 (Table 4). For IPH the two lowest free energy clusters are in S₁′, the second only 0.4 Å away from IPH 1. The mapping does not find the buried site that binds IPH 2. For ACN, clusters 2–4 are all in the active site, one of them only 0.6 Å away from ACN 1; however, the lowest average free energy cluster is at a location not seen in the x-ray structure. The predicted site is highly plausible, because it is the second largest pocket after the active site (the third largest is the buried pocket that binds IPA 2 and IPH 2) and is surrounded by partially exposed hydrophobic groups from the side chains of Y83, F172, L175, and Y179. In addition to Y83 and Y179, the pocket includes R260 and D261, which can form hydrogen bonds with ligands. It is not clear whether the mapping yields a false positive or the ACN at this site is simply missed in the crystal structure. In fact, crystallographic methods can identify only organic solvent molecules that bind in a relatively ordered manner; otherwise, the extra electron density is usually interpreted as a bound water molecule. The site contains three crystallographic waters, one of which is only 1.1 Å from the free energy minimum we have found for ACN. Whether ACN binds in this pocket or not is immaterial—because it is not a consensus site—the mapping does not show low energy positions for the other ligands in this region.

Table 5 lists the highest probability subclusters of the lowest energy clusters contacting the experimental positions of the four ligands. The table confirms the existence of several rotational states in most cases. Because the rotations affect the rms deviation from the experimental positions, Table 4 includes both this value and the shortest distance between probe atoms in the cluster and the closest experimental ligand atom position. The subclusters at the three lowest energy minima for IPA correspond to the S₁′, S₁, and S₂ subsites of the TLN active site. The S₁′ subsite forms a distinct cavity that is lined with hydrophobic residues (F130, L133, V139, I188, V192, Y193, and L202). Toward the edge of the pocket are several polar residues (N112, E143, and R203). As in HEWL, some of the ligands form a hydrogen bond with one or two of these groups, most frequently with R203 N^η2H1. The S₁ and S₂ pockets, which respectively bind IPA 8 and IPA 5, are contiguous and the corresponding IPA clusters are very close to each other. The nonpolar residues defining these pockets are F114, W115, and Y157, and hydrogen bonding occurs with the side chains of E143, D150, Y157, and E166, and with the backbone atoms of residues A113 and W115.

Table 5.

Selected subclusters of the minimum 〈ΔG〉 clusters contacting experimentally determined small molecules bound to TLN

Mol†	(N‡)	SC	Size	p	〈ΔG〉	〈ΔEelec〉	〈ΔEvdw〉	〈ΔG*des〉	H-bond(s)§
IPA 1	(11)	1	3	0.39	−11.00	−1.99	−13.05	4.05	R203 Nη2H1
		2	9	0.17	−9.87	−1.57	−12.49	4.19	R203 Nη2H1
		3	2	0.15	−10.69	−1.81	−13.66	4.79
		4	3	0.12	−10.31	−5.05	−11.90	6.64
		5	2	0.08	−10.32	−1.26	−13.06	4.00	R203 Nη2H1
IPA 5	(12)	1	47	0.61	−10.52	−2.68	−12.48	4.64	D150 Oδ2
		2	61	0.32	−9.99	−0.89	−11.83	2.73	W115 O
IPA 8	(14)	1	16	0.34	−11.06	−3.87	−12.61	5.41	E166 Oɛ2, Y157 Oη
		2	39	0.29	−10.51	−2.30	−12.33	4.12	W115 O
		3	14	0.22	−10.94	−1.75	−12.76	3.57	E143 Oɛ1, W115NH
		4	20	0.06	−9.94	−1.22	−11.61	2.89	E143 Oɛ1, A113 O
		5	14	0.06	−10.13	−4.44	−12.03	6.35
ACN 1	(6)	1	99	1.00	−11.90	−5.60	−13.23	6.94	Y157 OηH
ACN 1	(9)	1	162	0.90	−11.02	−2.07	−12.22	3.27
ACN 1	(4)	1	10	0.48	−10.81	−0.65	−13.55	3.39	R203 Nη2H1
		2	8	0.29	−10.65	−0.49	−12.58	2.42
		3	5	0.23	−10.79	1.26	−13.53	1.49	R203 Nη2H1
CCN 1	(5)	1	237	1.00	−10.43	−7.02	−7.15	3.74
IPH 1	(13)	1	12	0.65	−28.35	−3.71	−17.59	−7.05	E166 Oɛ2, Y157 Oη
		2	6	0.35	−28.63	−2.73	−18.93	−6.98
IPH 1	(10)	1	7	1.00	−25.59	−1.57	−18.05	−5.97	E143 Oɛ2

^† Experimentally determined ligand molecule (10). 

^‡ Total number of subclusters. 

^§ Intermolecular hydrogen bonds. Protein donor or acceptor atoms are shown. 

Why Do All Ligands Bind at the Active Site?

Mattos and Ringe (7) first reported the existence of a limited number of sites that attract many different organic molecules, regardless of their sizes and polarities. Analyzing multiple solvent crystal structures of the porcine elastase (8), they observed that the regions to which small molecules bind contain a number of partially exposed hydrophobic residues that interact with the nonpolar fragments of the ligands. We have shown that the consensus sites in HEWL and TLN are defined by a number of hydrophobic residues.

Our results suggest two further properties of consensus sites that bind many different ligands. First, such sites should be fairly large pockets that can accommodate many different ligands in a number of conformations while consistently providing favorable van der Waals interactions. Second, the sites must be surrounded by a number of groups that can serve as hydrogen-bond donors or acceptors. Because most ligands have polar groups, burying these in a hydrophobic environment would be energetically unfavorable. As shown in Tables 3 and 5, most ligands bind in a number of conformations, in many cases forming one or two hydrogen bonds. Enzyme active sites always satisfy these conditions. Indeed, substrates can replace water and bind with high affinity only in pockets that are lined with at least some hydrophobic patches. More importantly, because these pockets have developed to perform appropriate chemistry, they generally include a sufficient number of polar residues.

It is interesting to examine how interactions change as we proceed from the weakly specific binding of small probes to the highly specific binding of native substrates and inhibitors. HEWL recognizes its substrate, polymeric carbohydrates from bacterial cell walls, by the 2-N-acetylglycosamine (NAG) residues in the carbohydrate chain. NAG binds in site C and forms four hydrogen bonds with N59 NH, W62 N^ɛ 72, W63 N^ɛH, and A107 O. As discussed, the probes tend to form hydrogen bonds with the same groups.

The binding of substrates, products, and inhibitors to TLN always involves the largely hydrophobic S₁′ subsite, with longer inhibitors extending toward subsites S₁ and S₂. At least four hydrogen bonds are formed in each complex, most frequently with the side chains of R203, E143, Y157, N112, and D226, and with the polar backbone atoms of Y115, A113, and N111. As shown in Table 5, computational mapping with the four probes identifies all but the N112 and D226 bonds. Thus, sites that are favorable for the binding of highly specific ligands also tend to bind small organic molecules that comprise both polar and nonpolar portions and vice versa.

Conditions for Successful Mapping.

The mapping algorithm described here differs from MCSS and other traditional methods in three major respects. (i) The van der Waals interactions are introduced only after the probes have congregated to regions of the protein surface with favorable electrostatics and desolvation, providing a better sampling. (ii) The scoring potential includes a desolvation term. (iii) The docked ligand positions are clustered, with ranking based on the average cluster energies. Although all three factors help to avoid irrelevant local minima, they are not independent, and hence their relative importance is difficult to estimate. For example, without the desolvation term ΔG^*_des, which is not included in MCSS and GRID calculations, the mapping yields a number of isolated false positives, i.e., conformations with very favorable van der Waals and electrostatic interactions that are not located near any experimentally observed binding site. Accounting for desolvation generally removes these local minima, and frequently there is no need for clustering, i.e., the hubs of the lowest free energy clusters are themselves the lowest free energy conformations. However, most false positives can also be removed by simply clustering and evaluating the average energy for each cluster. The use of all three factors is a strong safeguard against isolated local minima, but alternative mapping strategies may exist.

Conclusions

We present a mapping algorithm that can identify the consensus-binding site of organic solvents on protein surfaces. The algorithm has been applied to HEWL and to TLN, interacting respectively with eight and four different ligands. In both cases the search finds a consensus site to which all molecules bind, in good agreement with NMR and x-ray data, whereas other positions that bind only certain ligands are not necessarily found.

These sites can accommodate each ligand in a number of rotational states such that (i) the van der Waals energy remains low in all states, indicating favorable shape complementarity. (ii) The nonpolar part of the ligand is in a hydrophobic region of the pocket. (iii) Charge–charge interactions do not substantially contribute to binding. (iv) Hydrogen bonds or polar interactions can be formed in a number of rotational states. For enzymes these conditions are generally met at subsites of the active site. The residues interacting with the probes also interact with the specific substrates and inhibitors of the enzyme, but these bind in unique orientations and form several hydrogen bonds.

Abbreviations

HEWL

hen egg-white lysozyme

NOE

nuclear Overhauser effect

TLN

thermolysin

MCSS

multiple copy simultaneous search

IPA

isopropanol

ACN

acetone

CCN

acetonitrile

IPH

phenol