Mirror-symmetry breaking in the Soai reaction: A kinetic understanding

Abstract

Kinetic modeling using nonlinear differential equations is proposed to analyze the spontaneous generation of enantiomeric excess in the autocatalytic addition of diisopropylzinc to prochiral pyrimidine carbaldehydes (Soai reaction). Our approach reproduces experimentally observed giant chiral amplification from an initial enantiomeric excess of <10^–6% to >60%, high sensitivity and positive response to the presence of minute amounts of chiral initiator at concentrations <10^–14 M, and spontaneous absolute asymmetric synthesis from achiral starting conditions. From our numerical simulations using kinetic schemes derived from the Frank model, including stereospecific autocatalysis and mutual inhibition, we have shown that it is possible to reproduce the mirror-symmetry-breaking behavior of the Soai reaction under batch conditions leading to a bimodal enantiomeric product distribution. Mirror-symmetry breaking was found to be resistant to a loss of stereoselectivity up to 30%. While the mutual inhibition between enantiomers seems to originate from the presence of dimerization equilibria, the exact nature of the autocatalytic stereoselective process still remains to be revealed. From the kinetic viewpoint, simple autocatalysis involving monomers as the catalytic species is consistent with all reported experimental effects of the Soai reaction.

Asymmetric synthesis usually requires the intervention of chiral chemical reagents or catalysts. Few examples are known in which the generation of enantiomerically enriched products occurs from achiral precursors without the involvement of such auxiliaries. These cases, known as absolute asymmetric synthesis (1, 2), have been mostly observed in the combination of spontaneous resolution and enantioselective catalysis (3) as well as by the influence of external chiral factors such as circularly polarized light (4) or vortex motion (5). Some cases were reported in which no obvious chiral inductor was used and, nevertheless, high enantiomeric excess (ee) has been obtained systematically. These examples display the signature of mirror-symmetry breaking (6), i.e., a process in which a small random ee is greatly amplified, whereas the chirality sign remains unpredictable for each individual experiment. The generation of small random ee occurs practically in any chiral system for statistical reasons alone in which the ee is inversely proportional to the square root of the number of molecules, ee ∝ n^–1/2 (7). However, this value remains negligible as long as a large number of molecules is involved, so an amplification mechanism is needed to increase such minute ee to a macroscopic level.

Mirror-symmetry breaking in chemical systems is typically associated to autocatalytic kinetics, i.e., a feedback mechanism in which one or several reaction products directly increase the overall rate of the chemical reaction. Hence in the specific case of chiral autocatalysis, the enantiomeric product could act as an asymmetric catalyst of its proper formation. This is one of the fundamental aspects to observe spontaneous growth of ee during the course of an asymmetric process. However, as Frank (8) stated in his early theoretical work, chiral autocatalysis alone is not sufficient, but additionally a type of mutual inhibition between the enantiomers is needed to achieve sustained amplification of the ee.

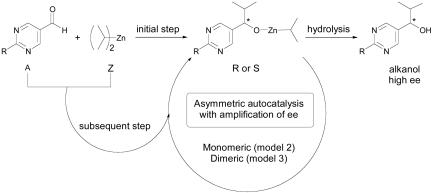
A clear-cut practical example of mirror-symmetry breaking in chemical systems was observed during the stirred crystallization of sodium chlorate by Kondepudi et al. (9), who also established the theory of chiral symmetry-breaking transitions in terms of nonequilibrium thermodynamics (10, 11). In 1995, Soai et al. (12) reported an example of spontaneous chiral amplification in organic chemistry that resulted in the formation of an asymmetric carbon and that essentially proceeds under homogeneous reaction conditions (13). As outlined in Scheme 1, the Soai reaction involves the addition of diisopropylzinc (Z) to a prochiral pyrimidine carbaldehyde (A) yielding isopropylzinc alkoxide (R or S) that, after hydrolysis, is converted into a stable chiral pyrimidyl alkanol.

Scheme 1.

The Soai reaction. R = H, CH₃, t-Bu–CC–, or (CH₃)₃Si–CC–.

The reaction is accelerated upon initial addition of the pyrimidyl alkanol, which has been also shown to perform as an effective chiral auxiliary that is generated in situ. This system was later shown to give rise to a nearly bimodal product distribution between left- and right-handed enantiomers in repeated experiments when started with the pyrimidine carbaldehyde and the diisopropylzinc alone, i.e., without adding any chiral substance (14–16). This intriguing result manifests the emergence of stochastic behavior in asymmetric synthesis in which the obtained ee originates from the statistical imbalance of racemates. Hence the Soai reaction shows the characteristics of mirror-symmetry breaking, i.e., does not require any chiral additive to generate significant ee.

These phenomena have attracted close attention from those interested in the still-disputed origin of biomolecular homochirality (17, 18). Although the Soai reaction, performed with organometallic reagents in anhydrous solvents, is hardly realistic from a prebiotic point of view, it remains of great conceptual importance for this field as a unique example of chiral autocatalysis in organic chemistry so far.

From the various attempts of kinetic modeling (19–23), it appears that autocatalysis and mutual inhibition are the necessary ingredients for the Soai reaction to describe the observed chiral amplification. However, reports using these approaches have not discussed the origin of the experimentally observed mirror-symmetry breaking so far. The purpose of this work is to analyze the foundation of mirror-symmetry breaking by focusing on closely related and more recently discovered properties of the Soai reaction such as astonishingly strong amplification starting from extremely small chiral imbalances (24) or the tremendous sensitivity of propagating the chirality sign starting with only a few thousand chiral molecules as an initiator (15). We will show that simple kinetic models are sufficient to understand the possible origin of these striking features.

Kinetic Models

Kinetic modeling was used for a better understanding of the reaction mechanism. To approach chemical realism and to check several mechanistic hypotheses, three kinetic models that involve chiral autocatalytic steps and mutual inhibition have been examined.

Model 1. This skeleton model has been derived from the Frank mechanism (8) considering batch conditions§ and a racemic outcome in the uncatalyzed product formation. While remaining entirely general from the chemical point of view, its purpose is to display the minimal processes that reproduce qualitatively the main features of the Soai reaction:

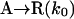[1]

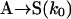[2]

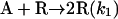[3]

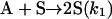[4]

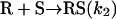[5]

Model 2. For more realism, the presence of the organozinc reactant Z has been included with the uncatalyzed steps as well as with the autocatalytic processes. We have also assumed a reversible formation of homochiral and heterochiral zinc alkoxide dimers. This idea is in accordance with Noyori and coworkers (25, 26), who reported the formation of zinc alkoxide dimers during the amino alcohol-catalyzed alkylzinc addition to benzaldehydes. For this reason, five more steps, 6–10, have been added to the model:

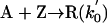[1′]

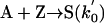[2′]

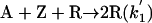[3′]

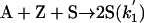[4′]

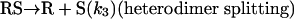[6]

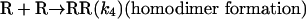[7]

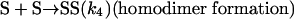[8]

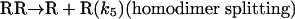[9]

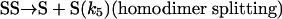[10]

Model 3. Kagan and coworkers (27, 28) introduced the concept of dimer catalysis to explain amplification or depletion of ee during enantioselective catalysis with partially resolved chiral auxiliaries. We examined this possibility by replacing the monomer-catalyzed steps 3′ and 4′ by the following dimer-catalyzed steps:

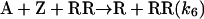[11]

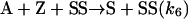[12]

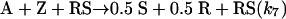[13]

Model 3 includes steps 1′, 2′, and 5–13.

Methods

Kinetic Modeling. We tried to avoid ad hoc assumptions or approximations and, instead, considered the full range of coupled dynamics given by foremost chemically realistic steps. The whole variety of involved species has been taken into account in the model, the coexistence of slow and fast processes as well as equilibria that were not approximated as preestablished. These measures were necessary in view of the highly nonlinear nature of the model systems with expected complex dynamic behavior.

A typical set of differential equations as used for the numerical simulations is given, for example, for model 1: d[A]/dt = –2r₀ – r₁ – r₂; d[R]/dt = r₀ + r₁ – r₃; d[S]/dt = r₀ + r₂ – r₃; and d[RS]/dt = r_3; where r₀ = k₀[A]; r₁ = k₁[A][R]; r₂ = k₁[A][S]; and r₃ = k₂[R][S].

Model calculations were carried out with the simulation-adjustment program sa3 (noncommercial software written by D. Lavabre, Laboratoire des Interactions Moléculaires et Réactivité Chimique et Photochimique, Université Paul Sabatier). The general algorithm for the numerical integration of the differential equations was based on the semiimplicit fourth-order Runge–Kutta method with stepwise control for stiff ordinary differential equations (29). In the optimization procedures, when used, the minimization algorithm was of the Powell type. Fitted rate parameters were automatically and iteratively returned to the numerical integration until a minimum in the residual error was reached. The robustness of the solutions was evaluated by showing that, whatever the guessed initial values were, either singly valued parameters or defined parameter ranges were delivered at convergence. The final concentrations of the enantiomeric species have been considered as the combined total amount of R- or S-matter such as [R]_total = [R] + [RS] + 2[RR] and for [S]_total respectively, i.e., ee = ([R]_total – [S]_total)/([R]_total + [S]_total). The pyrimidyl alcohol that is usually added to the reaction mixture as chiral initiator has been assumed to be instantly converted into isopropylzinc alkoxide (R or S) without any changes in chiral configuration. Hence initial concentrations of the alcohol in the experiment were regarded as initial concentrations of R or S in the kinetic modeling. For the simulation of reaction heat flows, it has been assumed that the achiral substrate consumption is the only exothermic process. Thus the heat flows have been taken proportional to d[A]/dt.

Semiempirical Calculations. PM-3 calculations (spartan, Wave-function, Irvine, CA) were performed to estimate the heats of formation of the expected dimer species. For both monomers and dimers a large number of conformers exist; for this reason we applied Monte Carlo simulations to find the optimum conformer and to check that the enantiomers displayed the same energies. We found that the closed [ZnO]₂ ring structure provided the most stable geometries, which is in agreement with a recent study of Gridnev et al. (30) and with the majority of other reported organozinc dimer structures (31). These lengthy calculations would be difficult to achieve with more advanced ab initio methods. On the other hand, because of the inherent limitations of the semiempirical methodology used, our results must be viewed as preliminary.

Results and Discussion

Properties of Model 1. Similar to the remarkable experimental results of Singleton and Vo (15), simulations of model 1 with arbitrarily chosen k₀ = 1 × 10^–3 s^–1, k₁ = 1 M^–1·s^–1, k₂ = 100 M^–1·s^–1, and [A]₀ = 1 M show the extreme sensitivity in propagating the chirality sign. The catalyst chirality sign was systematically maintained until the initial concentration of the enantiomerically pure catalyst was as low as 10^–14 M. The threshold concentration depends on the parameter values; especially when k₀ increases the concentration threshold increases. This increase is due to the production of the opposite enantiomer by the uncatalyzed formation of R and S. Table 1 demonstrates strong chiral amplification analogous to that observed in the Soai reaction (24). It also indicates that the amplification strength depends on the k₂/k₁ ratio, especially at very small initial ee.

Table 1. Amplification of ee by model 1.

	ee0
	10-9	10-8	10-7	10-6	10-5	10-4	10-3	10-2	10-1
eef(10)	0.004	0.024	0.047	0.074	0.117	0.187	0.296	0.467	0.721
eef(100)	0.663	0.695	0.727	0.762	0.798	0.835	0.875	0.916	0.958

[A]₀ = 1 M, [R]₀ + [S]₀ = 10^-2 M, k₀ = 10^-6 s^-1, k₁ = 1 M^-1·s^-1, ee₀ = initial ee, ee_f = final ee. (10), k₂ = 10; (100), k₂ = 100.

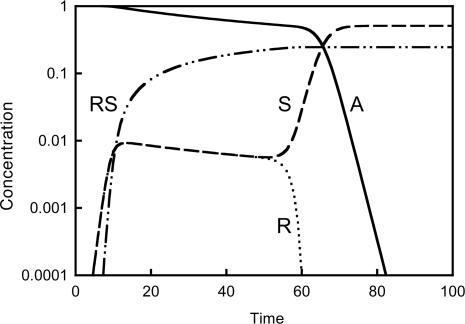
Regarding mirror-symmetry breaking, one may expect that if our simulations were started under achiral conditions, the system would be driven systematically into a racemic state. Surprisingly, this was not always the case. For selected parameter values, we observed the spontaneous generation of ee. Fig. 1 shows such a typical development into a chirally broken state from achiral conditions in which, after an almost racemic lag period, one of the two product enantiomers is suddenly subjected to rapid exhaustion while its optical antipode accumulates with increasing rate and, simultaneously, the achiral substrate is fast consumed.

Fig. 1.

Time evolution of the involved species in model 1, illustrating the consequence of mirror-symmetry breaking in a typical simulation starting from achiral conditions and by using an appropriate set of parameters: [A]₀ = 1 M, [R]₀ = [S]₀ = 0, k₀ = 10^–6 s^–1, k₁ = 1 M^–1·s^–1, and k₂ = 100 M^–1·s^–1.

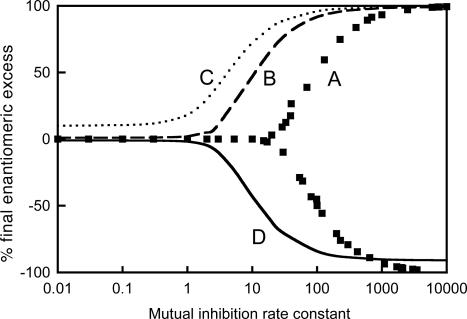
Moreover, unpredictability of the chirality sign was noticed. Although each computational run was perfectly reproducible by using the same internal calculation parameters, it occurred that a slight variation of some of them, such as the maximal integration step size, was sufficient to induce small numerical shifts triggering the system into either a positive or a negative final ee. This effect is a consequence of dynamic instabilities in model 1. It can be understood by recalling that in the original Frank model the ee increases exponentially. In fact, we observed a bifurcation scenario under batch conditions (Fig. 2) in which any kinetic parameter or achiral substrate concentration can drive the system into either a racemic or an optically active state from completely achiral initial conditions. Beyond the bifurcation threshold, the outcome of a positive or negative ee remains unpredictable, while its absolute value results in an expected pitchfork bifurcation behavior (32).¶

Fig. 2.

Mirror-symmetry breaking and amplification of ee in model 1. [A]₀ = 1 M, k₀ = 10^–6 M^–1·s^–1, k₁ = 1 M^–1·s^–1 and μ = 1. Curve A, [R]₀ = [S]₀ = 0 (no catalyst added); curve B, [R]₀ = 5.05 × 10^–3 M and [S]₀ = 4.95 × 10^–3 M (1% of catalyst, ee = 1%); curve C, [R]₀ = 5.50 × 10^–3 M and [S]₀ = 4.50 × 10^–3 M (1% of catalyst, ee = 10%); curve D, [R]₀ = 4.95 × 10^–2 M and [S]₀ = 5.05 × 10^–2 M (10% of catalyst, ee = –1%; note that because of a dilution effect by the high autocatalyst concentration the final ee does not reach –100%). For the sake of clarity data points corresponding to curves B, C, and D have been smoothed.

Our simulations resulted in total in an almost equal distribution of predominantly either R or S product species in the multiple runs. This finding emphasizes the stochastic nature of this effect and represents a striking similarity to the already observed laboratory experiments (9, 14–16) leading to bimodal product distributions. The values of the kinetic parameters affect the bifurcation occurrence. Table 2 shows the results of various simulations in which the parameter space of model 1 has been tentatively explored. It is indicated that bifurcation scenarios become increasingly stronger when k₀/(k₁[A]₀) (spontaneous reaction) is decreased and k₂/k₁ (mutual inhibition) is increased simultaneously.

Table 2. Final enantiomeric ratio (er) = major enantiomer/minor enantiomer obtained from achiral initial conditions in model 1.

	log(k2/k1)
log{k0/(k1[A]0)}	1	2	3	4	5
-2	1	1	1	1.41	1.01
-3	1	2	10	18	19
-4	1	2	24	96	164
-5	1	3	28	237	908
-6	1	2	29	285	740

Here, er has been used instead of ee to exemplify the effect of chiral amplification, er = (1 + ee)/(1 - ee).

It also appears that there is a threshold limit for mirror-symmetry breaking given by each of the parameters independently. Mirror-symmetry breaking and amplification of ee are related, but amplification of ee can take place in a parameter range where mirror-symmetry breaking still does not occur. As shown in Fig. 2, the position where the amplification arises depends on the value of the initial ee. The higher the initial ee the lower can be the rate constant k₂ (R + S → RS) to obtain an amplification effect. The lack of amplification of ee for low k₂ values (left side of Fig. 2) shows that without mutual inhibition amplification of ee cannot occur. This result is noteworthy, because it was recently shown by Lente (33) in a discrete modeling approach that a final ee ≠ 0 can be obtained with the same autocatalytic model but omitting the mutual inhibition step. However, there is no contradiction between this result and ours because this discrepancy is only apparent. In the discrete approach, there is no amplification of ee at all because the reproduction of a unique molecule is considered and, obviously, a single chiral molecule always is enantiopure. Our deterministic simulations of model 1 can also generate this effect by taking appropriate parameter values in accordance with the simulations of Lente.∥

Furthermore, we examined the occurrence of mirror-symmetry breaking in respect to imperfect stereoselectivity in the autocatalytic steps 3 and 4. This has been accomplished by introducing μ as a stereoselectivity parameter in the autocatalytic process by replacing A + R → 2R with A + R → (1 + μ) R + (1 – μ) S, where μ = 1 corresponds to stereospecificity and μ = 0 to the total lack of stereoselectivity. It was found that even at μ = 0.3 bifurcation behavior still occurs. Hence mirror-symmetry breaking appears to be rather resistant to a possible loss of stereoselectivity once the system has been established in the appropriate parameter space that gives rise to symmetry breaking under stereospecific conditions.

Beyond the qualitative reproduction of the main striking properties of the Soai reaction, model 1 has been proved to reproduce well the shape of experimentally obtained kinetic curves (19, 21) showing the formation of the chiral product with characteristic induction periods that depend on the initial catalyst concentrations and that are followed by a steep increase in product formation.

Properties of Model 2. Model 2 has been found to behave almost identically to model 1 in reproducing mirror-symmetry breaking and amplification of ee. Because it has been attributed to more chemical realism, several specific features deserve to be illustrated. Table 3 shows the influence of the heterodimerization rate constant k₂ (R + S → RS) and homodimerization rate constant k₄ (R + R → RR or S + S → SS) on the occurrence of mirror-symmetry breaking. It appears that k₂ must be sufficiently high while k₄ has to be adequately small to display the effect.

Table 3. Final enantiomeric ratio generated from achiral starting conditions in model 2 as a function of the rate constants k₂ and k₄.

	log k4
log k2	0	1	2	3	4	5
7	2,221	2,107	1,999	1,537	1,428	499
6	311	293	240	199	104	1
5	26.6	25.7	22.8	13.3	1	1
4	2.18	2.07	1.08	1	1	1
3	1	1	1	1	1	1

k₂ is for (R + S → RS) and k₄ is for (R + R → RR or S + S → SS). [A]₀ = [Z]₀ = 1 M, k₀′ = 10^-6 M^-1·s^-1, k₁′ = 1 M^-2·s^-1, and k₃ = k₅ = 10 s^-1.

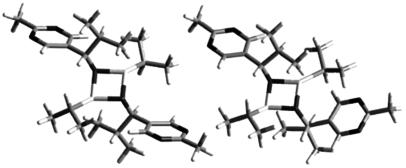
A comparable situation occurs with the rate constants for the dimer splitting in which k₃ (RS → R + S) has to be sufficiently small whereas k₅ (RR → R + R or SS → S + S) must be high enough. By defining the two equilibrium constants K_HETERO = k₂/k₃ and K_HOMO = k₄/k₅, it is expected that the heterochiral dimer needs to be more stable than the homochiral dimers. This result is of interest because preliminary semiempirical PM-3 calculations that we have performed to estimate the heat of formation of the heterochiral and homochiral dimers indicate that the heterochiral dimer could be indeed slightly more stable than its homochiral stereoisomer by around 2 kcal·mol^–1 (Fig. 3), i.e., K_HETERO/K_HOMO ≈ 20 at 300 K. However, on the basis of the same [ZnO]₂ ring structures as predicted by our approach, Gridnev et al. (30) reported the relative stabilities of the RR and RS dimers as being “comparable” in enthalpy. This observation reinforces our results for the structures proposed but also indicates that a definite determination of their relative stabilities is still pending. Nevertheless, our kinetic simulations show that the difference in the relative thermodynamic stabilities of the dimers is a necessary but not sufficient condition to ensure mirror-symmetry breaking: the rate of heterodimer formation has to be faster than that of its homodimer counterpart.

Fig. 3.

Predicted molecular structures of the heterochiral dimer RS (Left), 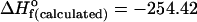kcal·mol^–1 and of the homochiral dimer SS or RR (Right), 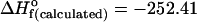kcal·mol^–1.

The most comprehensive kinetic record so far of a Soai reaction that counts with a high number of data points and information directly given in concentration has been reported by Gridnev et al. (16). As shown in Fig. 4, we were able to achieve an excellent fitting of this data that demonstrates the capacity of model 2 to respond to well defined experimental data. Note that this fitting has been realized for a kinetic curve exhibiting a nontrivial shape for reactant consumption and that the set of parameters that have been established by the data fitting gives rise to a mirror-symmetry breaking (ee_final ≈ 57%) of the same order of magnitude as has been observed by the authors of ref. 16.

Fig. 4.

Aldehyde consumption vs. time in an NMR-monitored Soai reaction (○) (ref. 16) fitted by model 2 (continuous line) and by model 3 (broken line). Initial concentrations (M): [A] = 1.92 × 10^–2 and [Z] = 0.04; rate parameters model 2 {model 3}: k₀′ = 5.2 × 10^–3 {3.7 × 10^–3} M^–1·s^–1; k₁′ = 69 M^–2·s^–1 {k₆ = 154 M^–2·s^–1, k₇ = 2.1 × 10^–4 M^–2·s^–1}; k₂ = 4.5 × 10⁵ {9.2 × 10⁵} M^–1·s^–1; k₃ = 5.2 × 10^–2 {6.4 × 10^–4} s^–1; k₄ = 4.8 × 10³ {1.1 × 10⁴} M^–1·s^–1; and k₅ = 21 {6.4 × 10^–4} s^–1. The first seven data points have not been taken into account.

The adjusted parameter values lead to a ratio of K_HETERO/K_HOMO ≈ 3.8 × 10⁴ (ΔG^o ≈ 6 kcal·mol^–1). This value is higher than expected from the PM-3 calculations. However, the pyrimidine aldehyde used in the studies of Gridnev et al. (16) contains a more bulky substituent than the molecule used for our calculations, –CC–Si(CH₃)₃ vs. –CH₃, and possible solvent effects have not been taken into account. Nevertheless, the trend that the heterochiral dimer is more stable than the homochiral one is respected. Furthermore, the established value of k₃ = 5.2 × 10^–2 s^–1 (RS → R + S) can be favorably compared to the experimental value of k_diss = 2.5 × 10^–2 s^–1 obtained from NMR shape analysis of the dimers (16). These results show that model 2, when supplied with proper parameters, is sufficient to describe quantitatively the dynamics of the Soai reaction. However, in contrast to the supposed chemically realistic description of the dimerization equilibria, the autocatalytic steps (3′ and 4′) remain entirely formal because of the lack of experimental information about the detailed mechanism of the stereoselective replication.

Properties of Model 3. The consideration that the autocatalyst is not monomeric but dimeric does not show significant differences between models 1 and 2 in reproducing huge amplification of ee, extreme catalytic sensitivity, and mirror-symmetry breaking. From the parameter values obtained by the fitting of the kinetic data of Gridnev et al. (16) with model 3 it results that K_HETERO/K_HOMO = 80, ΔG^o ≈ 2.6 kcal·mol^–1, whereas the relative catalytic efficiency of the homochiral over the heterochiral dimers, k₆/k₇, has to be about 10⁵, i.e., ΔΔG^‡ ≈ 7 kcal·mol^–1. Model 3 gives rise also to the experimentally observed mirror-symmetry breaking with the obtained parameters resulting in ee_final = 51%.

Taking into account the available kinetic data, it is still not possible to discriminate accurately between model 2 and model 3. However, slight preference for a monomeric catalytic scenario is indicated. This preference is due to the better capacity of model 2 over model 3 to reproduce the detailed experimental data of Gridnev et al. (16), as is demonstrated in Fig. 4. Notably, a monomeric catalytic network for chiral amplification has been recently proposed by Asakura et al. (34) for a very similar reaction system, the amino alcohol-catalyzed alkylzinc addition to benzaldehydes as pioneered by Noyori and coworkers (25, 26).

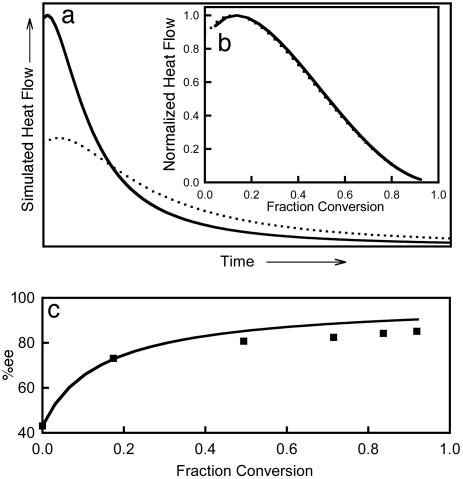
Blackmond and coworkers (20) conducted a series of calorimetrically monitored kinetic studies from which it was first concluded that the catalyst is dimeric, and then later that it is tetrameric (23) or even multimeric. In these experiments no mirror-symmetry breaking has been mentioned. An important result of these experiments is the effect of the catalyst enantiomeric purity on the measured reaction heat flows. It was shown that an enantiomerically pure catalyst is twice as active as its racemic counterpart, whereas the overall rate profile vs. extent of reaction remains independent of the catalyst ee. As shown in Fig. 5, by using model 2 and tentatively assuming that the heat flows were proportional to the rate of the aldehyde consumption, it was simple to reproduce these effects even by employing a monomeric approach. Blackmond and coworkers (20) also reported an amplification of ee_initial = 43% to ee_final ≈ 87% during the same study. Under our conditions, the ee increases similarly from 43% to ≈90% during the course of the reaction (Fig. 5).

Fig. 5.

Effect of catalyst enantiomeric purity. (a) Simulated reaction heat flows vs. time by model 2. Continuous line, enantiopure catalyst; dotted line, racemic catalyst. The relation between the heat flow maxima is around 50%. (b) Normalized heat flows vs. fraction conversion. The enantiopure and racemic catalyst curves are nearly superimposed. (c) Percent ee vs. fraction conversion for the case ee(cat) = 43%; ▪, experimental results from ref. 20. For all simulations, the rate constants were the same as in Fig. 4 except k₃ = 1.0 × 10² s^–1; [A]₀ = [Z]₀ = 0.2 M; and [R}₀ + [S]₀ = 2.0 × 10^–2 M.

The simulations have been realized with the fitted rate parameters of the experiment of Gridnev et al. (16) (model 2). For the present case, k₃ (RS → R + S) has been increased from 5.2 × 10^–2 to 1.0 × 10² s^–1, corresponding to a decrease in the stability of the hetero- vs. homochiral dimer to K_HETERO/K_HOMO ≈ 20 (similar to our PM-3 calculations) while all other parameters remained unchanged. This result shows that the effects of catalyst enantiomeric purity and amplification are not specific to dimer catalysis.

Conclusion

We have shown that essentially simple kinetic models that were derived from the pioneering Frank model (8) can reproduce the whole variety of striking phenomena that were observed in the autocatalytic Soai reaction until now.

The most prominent effect of the Soai reaction is the spontaneous generation of ee from achiral starting conditions that has been shown sensitive especially regarding the relative thermodynamic stabilities of the dimers and the rate of their formation. In particular, it has been established that the heterochiral dimers have to be more stable but also have to be formed faster than the homochiral isomers. Because of the relation between mirror-symmetry breaking and dimer formation rates and stabilities, it is likely that the structure of the aromatic part of the pyrimidine carbaldehydes is of essential importance not only for the amplification of ee but also for the occurrence of spontaneous symmetry breaking. For instance, there was no chiral amplification observed with ferrocenyl or 3-pyridyl carbaldehydes (35, 36), whereas the amplification effects increased from 3-quinolyl to 5-pyrimidinyl and 2-methylpyrimidinyl to 2-alkynyl-5-pyrimidinyl carbaldehydes (12, 24, 37, 38). Mirror-symmetry breaking has been observed only with the bulkiest alkynyl aldehydes.

We were able to fit model 2 to the most complete kinetic data of the Soai reaction available. The extracted rate parameters again confirm the higher stability of the heterochiral dimers and simultaneously gave rise to mirror-symmetry breaking that has been also observed experimentally in this specific system. A variation in only one of the fitted parameters in the monomeric mechanism (model 2) leads to a qualitative reproduction of the kinetic results of Blackmond et al. (20). Hence arguments that have been previously promoted to exclude monomer catalysis (18, 20, 22, 23) have to be reassessed. In fact, our simulations give slight indication for a monomeric instead of a dimeric catalytic pathway because of the better agreement of model 2 with the experimental kinetic data reported by Gridnev et al. (16). We have verified that this observation remains consistent also for the case in which to both models additional equilibria between the dimer species and a further diisopropylzinc molecule have been added, yielding RR–Z, SS–Z, and RS–Z association complexes as were suggested by NMR studies (30).