Abstract
Microarray analysis of gene expression patterns for thousands of human genes has led to the proposal that a large number of genes are expressed in a cell-cycle-specific manner. The identification of cyclically expressed genes was based on Affymetrix microarray analysis of gene expression after double-thymidine block synchronization. A statistical reanalysis of the original data leads to three principal findings. (i) Randomized data exhibit periodic patterns of similar or greater strength than the experimental data. This finding suggests that all apparent cyclicities in the expression measurements may arise from chance fluctuations. (ii) The presence of cyclicity and the timing of peak cyclicity in a given gene are not reproduced in two replicate experiments. This fact suggests there is an uncontrolled source of experimental variation that is stronger than the innate variation of gene expression in cells over time. (iii) The amplitude of peak expression in the second cycle is not consistently smaller than the corresponding amplitude in the first cycle. This finding places doubt on the assumption that the cells are actually synchronized. We propose that the microarray results do not support the proposal that there are numerous cell-cycle-specifically expressed genes in human cells.
Keywords: Affymetrix‖G1 phase
Microarray technology has led to the proposal that there are a large number of mammalian genes (≈700) that have cell-cycle-specific expression patterns (1). The original microarray data presented to support the existence of cyclic gene expression in human cells is now reexamined with a statistical approach. We find there is internal evidence implying that the original microarray data do not support the proposed patterns of gene expression.
Analysis of human gene expression during the division cycle (1) was performed by synchronizing primary human foreskin cells with a double-thymidine block. The mRNA was isolated from cells at different times after synchronization (i.e., at what are presumed to be different times during two successive division cycles). mRNA samples were isolated from cells every 2 h for 24 h, covering two cell cycles. The isolated mRNA was labeled with a fluorescent marker and hybridized to microarrays containing probes for 7,129 genes.
The primary result of the original authors was the identification of 387 cell-cycle-regulated genes (1). From a larger set of 40,000 transcripts, it was noted that 731 transcripts were assigned to cell-cycle-regulated expression clusters (1); the smaller number relates to those that were assigned to different cell-cycle phases with a smaller Affymetrix (Santa Clara, CA) chip. The putatively cyclic genes were identified by searching among the expression patterns for those that fit, according to a particular threshold, a sine wave pattern over the presumed two cell cycles. The computer pattern search (1) classified as cell-cycle-specific those genes that exhibited a Pearson correlation coefficient of at least 0.7 relative to at least one member of a family of shifted sine waves with a 12-h period. That is, a search was made for those patterns that approximated a sine wave, with the peaks of the sine wave occurring at any pair of points separated by 12 h.
Based on two replicate experiments, 53 genes were labeled as being G1-phase specific, 107 as S-phase specific, 108 as G2-phase specific, and 119 as M-phase specific. The designation of phase specificity was based on the time during the experiment that a peak in mRNA expression was observed. A plot of all proposed cell-cycle-specific genes revealed that the times of peak expression varied continuously and smoothly during the division cycle (figure 1b in ref. 1), making the assignment of peak expression to a particular phase slightly arbitrary. Nevertheless, the primary conclusion from the microarray analysis (1) is that there exist genes that are expressed specifically in each phase of the cell cycle.
We now present a reanalysis of the original data on gene expression during the division cycle of human cells. We find that within a particular experiment the level of cyclic expression is not sufficiently large to eliminate the possibility that all apparent cyclicities arise by chance. Moreover, the cyclicities that do occur are not reproduced between two replicate experiments. Furthermore, an analysis of the peak expression values in the two cycles suggests that the cells were not actually synchronized by the double-thymidine block.
Methods
Data.
Data are available (1) for two duplicate experiments (denoted N2 and N3). In each experiment, gene expression was measured over 24 h with mRNA collected at 13 points occurring at 2-h intervals. It was assumed [as in the original analysis (1)] that there were two cell cycles present of approximately 12 h each. Therefore, time point 24 is an isolated observation from the third cycle after synchronization, and was eliminated from consideration. Time point 12 was missing from experiment N2, and time point 0 was missing from experiment N3, so we eliminated both of these time points from consideration. The remaining 11 time points are measured in both experiments.
Gene Selection.
The data were obtained from the web site http://www.salk.edu/docs/labs/chipdata/data/hu6800_raw_wt_bothCellCycle.txt. Although the data are available for 7,129 genes, we first removed from consideration those genes that had positive expression measurements for fewer than two points in either experiment. These transcripts presumably have such a low level of expression that the background level is as high or higher than the experimental value. This removal left 6,133 genes for our reanalysis.
Normalization of Data.
The data were normalized to enable direct comparison across experiments and across genes. We began by applying the transform log(max(x + 200, 200)) to each expression measurement. This transformation symmetrizes the expression distribution, which has the effect of balancing the influence of high- and low-abundance transcripts on derived quantities such as correlation coefficients. From this point, the normalization is identical to that used by previous groups (1, 2). The transformed values for each chip were centered, then the measurements for each gene were centered across the chips. The first normalization corrects for variations in hybridization across chips, the second eliminates the influence of differing baseline abundances for different genes.
Numerical Characterization of Sinusoidal Expression.
For each gene, the measured time points were fit with least squares to two basis curves. The first basis curve has the form S(t) = sin(2πt/T), and the second basis curve has the form C(t) = cos(2πt/T), where T = 12 h is the nominal interdivision time. Suppose Yi(t) denotes the measured expression for transcript i at time t. The vector Yi(t) was regressed against S(t) and C(t), leading to the decomposition Yi(t) = aiS(t) + biC(t) + Ri(t), where Zi(t) = aiS(t) + biC(t) represents the periodic component of expression with T-minute period, and Ri(t) represents the component of expression that is either aperiodic or that has a period substantially different from T minutes. The proportion of variance explained by the Fourier basis [Fourier-proportion of variance explained (PVE)] is the ratio mi = var(Zi(t))/var(Yi(t)), which lies between 0 and 1. Values closer to 1 indicate greater sinusoidal expression with a T-minute period, whereas values closer to 0 indicate a lack of periodicity, or periodicity with a period that is substantially different from T minutes.
The fitted waveform Zi(t) is proportional to a shifted sine wave of the form sin(πU + 2πt/T), where −1 < U < 1 is the phase. Phases close to 0, 1, or −1 are sine-like in that at time t = 0 they take on an intermediate value, whereas phases close to 1/2 or −1/2 are cosine-like in that at time t = 0 they are close to their maximum or minimum value.
Randomization of Data.
It was important to determine whether the level of cyclic expression in the different experiments could be explained as arising from chance arrangements of random fluctuations in the measurements (i.e., variation arising from biological or technical sources that have an equal influence on all time points). Therefore, an artificial data set was constructed that was compatible with the observed data in terms of the overall variation at each time point, but which lacked any special tendency to exhibit periodic or sinusoidal expression patterns. To construct this data set, a random permutation of the observed values for a given gene across the time points was generated in such a way that any permutation was as likely to appear as any other. In other words, an artificial experiment was constructed by sampling uniformly and without replacement from the measured values for each gene in an actual experiment.
Results
Comparison of Experimental Data to Randomized Data.
We asked whether the observed cyclical expression in human cells identified with microarrays could be explained as arising from chance fluctuations that are not related to the cell cycle. Given the existence of measurement error as well as biological variation in expression that is not the result of the cell cycle, it is possible that even if none of the genes were truly expressed in synchrony with the cell cycle, a certain number of genes with apparently cyclic expression might be found because of chance fluctuations and noncyclic biological variation. Put another way, it is generally agreed that a substantial number of genes present on the microarray do not possess cell-cycle-specific expression. In any given experiment, many of these genes will exhibit cyclic expression because of the chance arrangement of noncyclic random fluctuations. We were interested in determining whether all cyclic variation in expression could be explained as arising from these random fluctuations.
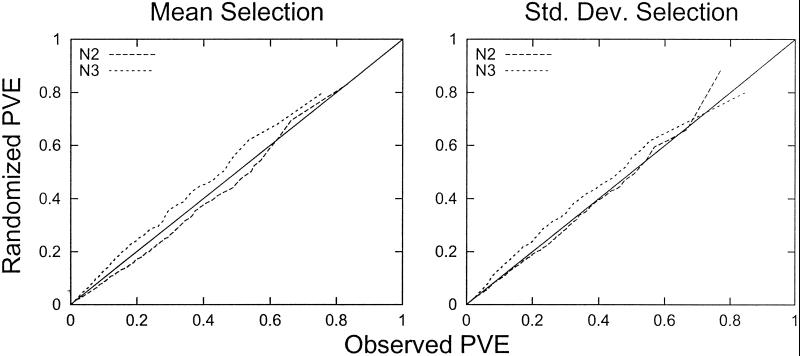
An analysis of the human cell data are presented in Fig. 1. For each rank r = 1, 2, … , the cyclicity (quantified as Fourier-PVE) of the rth most cyclic gene in the randomized data is plotted against the cyclicity of the rth most cyclic gene in the observed data. The data used in Fig. 1 are from the 1,000 genes that in the original data have the highest mean expression (Left) or the highest SD in expression (Right). This selection process eliminates from consideration a large number of genes with either low baseline expression or negligible variation. We have previously found that such selection increases the statistical evidence for cyclic expression. Results similar to Fig. 1 are obtained with all 6,133 genes.
Figure 1.
Comparison of overall cyclicity between observed and randomized data. In this figure, the 1,000 genes with the highest average expression (Left) or the 1,000 genes with the highest SD in expression (Right) are compared to randomized gene expression values. For each experiment (N2 and N3), the Fourier PVE was calculated for the 1,000 selected genes. The PVE was also determined for 1,000 randomized genes (constructed as described in Methods). The lists of observed and randomized numbers were sorted from least to greatest. The sorted randomized values are plotted against the sorted values from the actual experimental data. The cyclicity in each experiment is therefore compared with the cyclicity in its randomized counterpart. Points below the line indicate that there is more cyclicity in the experimental genes than in the randomized genes. Points above the line indicate that there is more cyclicity in the randomized genes than in the experimental genes. Similar results are obtained for the entire gene set.
In Fig. 1, the points (seen as a line) below the diagonal line indicate a level of cyclicity in the observed data that is greater than the corresponding level in the randomized data. Points above the line indicate that the observed cyclicity is not as great as that in the randomized data. This analysis indicates that the expression values in experiment N3 are completely explainable by random experimental error and noncyclic biological variation. In fact, the randomized data from experiment N3 exhibit a slightly greater cyclicity than the experimental data from experiment N3. The values for experiment N2 are just barely below the diagonal, indicating that at most a small fraction of genes may have genuinely cyclic expression. Another implication of these results is that even if one were to accept that a few genes are cyclically expressed in experiment N2, any attempt to identify these genes would be contaminated with a large number of false-positives.
Fig. 1 indicates that the periodicities observed in gene expression for human cells can be explained as arising from chance arrangements of fluctuation in the measurements that are not driven by the cell cycle. The patterns cannot be attributed to genuine periodicities in gene expression in the synchrony experiments.
Reproducibility of the Cyclicity Values.
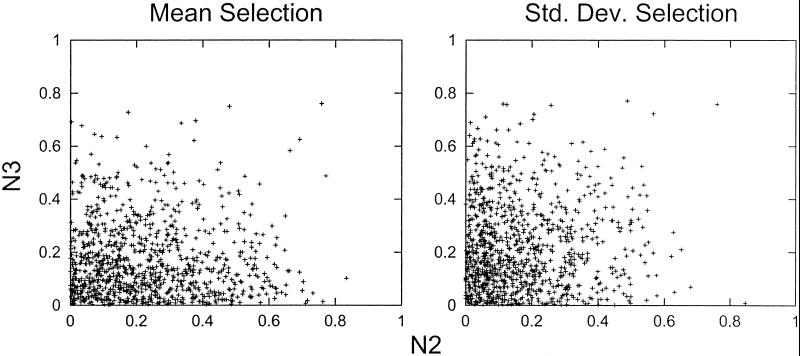
To determine whether genes that have apparent cyclic expression in one experiment also tend to have cyclic expression in the other experiment, we looked at the reproducibility of the Fourier-PVE between the two experiments. In Fig. 2, the cyclicities (quantified as Fourier-PVE) of the two experiments are compared in a scatter plot. As in Fig. 1, either the 1,000 genes with highest mean expression (Fig. 2 Left) or the greatest SD (Fig. 2 Right) are analyzed. Similar results are obtained with all 6,133 genes. Visual inspection of Fig. 2 Left and Right indicates that there is no apparent correlation of cyclicity between the two published experiments.
Figure 2.
Reproducibility of cyclicity between different experiments. For each experiment (N2 and N3), the cyclicity levels (quantified as Fourier-PVE) for the 1,000 genes with the highest mean expression (Left) and the 1,000 genes with the highest SD in expression (Right) were calculated. For each set of 1,000 genes, experiments N2 and N3 are compared in a scatter plot. If cyclicity was reproducible between the two experiments, the points would cluster along the diagonal.
Reproducibility of Time of Peak Expression.
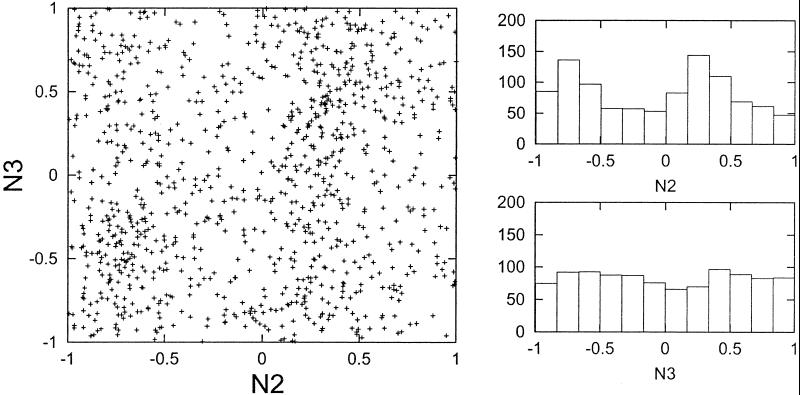
The time of peak expression for each gene was determined with Fourier analysis as described in Methods. For the 1,000 genes identified as having the greatest average cyclicity across the two experiments, the timing of peak expression was determined in both experiments N2 and N3. A scatter plot of the results for experiment N3 against the results for experiment N2 is shown in Fig. 3 Left. There is no apparent reproducibility in the timing of peak expression between the two experiments, as there is no evidence of points clustering along the diagonal. The clustering of points along two vertical bands is related to the nonrandom tendency of genes to begin experiment N2 at an extreme value rather than an intermediate value (Fig. 3 Right Upper). This property is not reproduced in experiment N3 (Fig. 3 Right Lower).
Figure 3.
Reproducibility of peak expression timing between different experiments. For each experiment (N2 and N3), the timing of peak expression was determined (as described in Methods) for the 1,000 genes with greatest cyclicity. The timing values were compared between the two experiments in a scatter plot (Left). If there was strong reproducibility in the timing, the points would cluster along the diagonal. Two histograms, showing the frequencies of different peak timing values in experiments N2 and N3, are shown (Right). The nonuniformity evident in experiment N2 is not repeated in experiment N3.
Peak Decay.
If the double-thymidine block succeeded in synchronizing the cells, one would expect that over two cell cycles a tendency toward decay in the peak amplitude would be observed; a defined peak in the first cycle would be moderated in the second cycle. This expected peak decay results from the tendency of synchrony curves to decay and lose sharpness with each passing cycle.
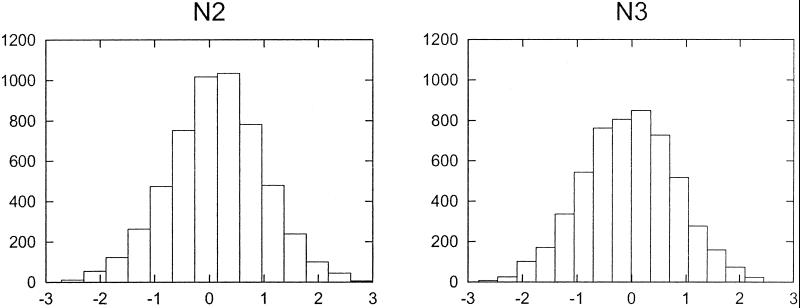
The peak amplitudes for the first and second cycles in both experiments N2 and N3 were computed for the 1,000 genes with greatest cyclicity (as determined by Fourier-PVE). The peak amplitude differences (the maximum experimental value among observations at 2, 4, 6, 8, and 10 h minus the maximum among observations at 14, 16, 18, 20, and 22 h), presented as histograms, are shown in Fig. 4 for experiments N2 and N3. The peak amplitude difference has a distribution that is symmetric about zero. If the synchrony in the first cycle was better or sharper than the synchrony in the second cycle, the mode of this distribution of peak amplitude differences would be distinctly positive. The results in Fig. 4 may be interpreted as suggesting that the cells were not actually synchronized, and that peaks found in either the first or second cycles are likely the result of random experimental variation.
Figure 4.
Comparison of peak amplitudes in the first and second cycles. The highest point in the first cycle minus the highest point in the second cycle was calculated for each gene in experiments N2 and N3. The distributions of these values are presented as histograms. The symmetry of the histograms around zero indicates that there is no tendency for the peak in the second cycle to be smaller than the peak in the first cycle.
Discussion
Our statistical analysis was framed above as a response to four questions. We first asked whether the cyclicity present in a randomization of the experimental data are at least as strong as the cyclicity present in the actual data. To this question we answered yes, suggesting that most, and possibly all, of the apparent cyclicity in gene expression arises from coincidental arrangements of measurement error and biological variation unrelated to the cell cycle. Then we asked whether genes that exhibit a cyclical gene expression pattern in one of the two replicate experiments also tend to exhibit a cyclical pattern in the other experiment. To this question we answered no, indicating that the microarray data cannot be used to reliably support cell-cycle-specific expression in human cells. We then asked whether the timing of peak expression during the division cycle is reproducible between two experiments. Again we answered no. Finally, we asked whether the overall cyclicity in the second cycle is weaker than the overall cyclicity in the first cycle. To this question we answered no, indicating that there is internal evidence suggesting that the primary human fibroblasts may not have been synchronized by the double-thymidine block.
Have Genes Expressed at Particular Phases of the Division Cycle Been Identified with Microarray Data?
Our reanalysis indicates that the microarray data do not unequivocally support the identification of numerous cell-cycle-specifically expressed genes in human cells (1).
Nevertheless, at least for experiment N2, there appears to be a slight excess of cyclical expression patterns relative to what would be expected to arise by chance. What might be the source of these cyclic patterns? One possibility that should be considered is that the procedures used to induce synchronization could bring about an oscillating response that is not present in unperturbed cells. The slight excess of cyclical expression patterns in a single experiment could be explained as a response to the perturbation in growth conditions resulting from the experimental synchronization procedure.
Definition of a Synchronized Culture.
The central experimental problem faced when analyzing data proposing cell-cycle-specific expression using synchronized cultures is the question: “Are the cells actually synchronized?” It is important to have criteria for analyzing cells as a function of cell age during the division cycle. An important criterion—and perhaps the single most important criterion—is that the cells should exhibit synchronized cell divisions. Without synchronized cell divisions it is difficult to know how to evaluate a synchrony experiment. No cell counts or frequency of mitosis data are provided along with the microarray data to allow one to know whether the mammalian cells studied with the microarray technology exhibited synchronized divisions (1).
It has been proposed that no synchronization method where all cells are treated identically can synchronize cells (3–5). This stricture applies to the double-thymidine block of Rao and Johnson (6) that was used to synchronize mammalian cells for cell cycle analysis (1). A truly synchronized culture is one that displays synchronized cell divisions and a synchronized passage through the cell cycle. We are unaware of reproducible evidence that cells subjected to this double-thymidine block are actually synchronized. No evidence related to synchronization is presented in the microarray article (1). If the cells were not synchronized, then of course the results under examination would not be valid. In addition, we have pointed out that the lack of peak decay (Fig. 4) supports the proposal that the cells are not actually synchronized.
For the statistical analysis presented here, however, we have given the data the benefit of the doubt and have assumed that the cells were actually synchronized. We have also assumed that the proposal (1) that the interdivision times were 12 h, and that over 24 h of analysis two complete cell cycles were studied. As it turns out, even if the cellular interdivision time was different (e.g., as short as 10 h or as long as 14 h), our results (data not shown) would not be any different. The proposal that there is periodic cell-cycle-specific variation in the expression of a large number of genes should therefore be viewed with caution.
Problems with Artifacts.
In addition to the question whether the cells were synchronized, the additional critique of whether the synchronizing treatment itself caused artifacts can be raised. Direct experiments indicating that thymidine blocks alter gene expression have been published (7).
Criteria for Identifying Cell-Cycle-Specific Genes.
How might one identify a gene as having cell-cycle-specific expression using microarrays? We propose that for a gene to be identified as presumptively being expressed in a cell-cycle-specific manner, the following criteria should be met. (i) If synchronization is to be used, the method should not involve inhibition or starvation methods, but only selection methods. (ii) The results should be reproducible over several experiments. (iii) If it is too expensive or difficult to do replicate microarray experiments, a presumptive cell-cycle-specifically expressed gene should be examined in several experiments with alternative methods such as Northern blots or RNase protection assays. (iv) The patterns should be confirmed on fixed, unsynchronized cells that are separated by size (e.g., elutriation) or DNA content (e.g., flow cytometric sorting) so that no synchronization artifacts are introduced. (v) The results should be shown to be statistically robust and not the result of random fluctuations; specifically, the number of time points, the number of genes under consideration, and the numerical threshold used to ascertain cyclicity should be chosen so that only a small fraction of randomized genes are expected to exceed the threshold. (For a further analysis of such criteria, see chapter 3 in ref. 4.)
Gene Expression During the Yeast Cell Cycle.
Wide-ranging cell-cycle-specific gene expression during the division cycle of Saccharomyces cerevisiae has been proposed (2, 8). A reanalysis of this data (K.S. and S.C., unpublished data) revealed, in contrast to the analysis of human cells, that cyclicities were present that could not be attributed to random fluctuations. A large excess of cyclic expression patterns in the observed relative to the randomized data were found in four distinct experiments, and a high level of agreement in peak expression timing was found in three of the experiments. The analysis of S. cerevisiae was carried out with the same statistical procedures that are applied to the human data in this article. This analysis demonstrates that the criteria to which we hold the human data are not so strict as to be impossible to meet in practice.
The history of the yeast data also points out the relevance of this analysis. At the time of this writing, the data on gene expression during the S. cerevisiae cell cycle (2) has been referenced by over 293 published papers and has spawned a large body of analytical work on gene expression during the cell cycle of yeast. This citation record indicates the strong level of interest in the cell biology community in the question of cell-cycle-specific gene expression.
It is very likely that the data on human cells will also generate a great deal of interest and further analysis. Because of the enormous interest in understanding which (or whether) specific genes are expressed at particular times during the human cell cycle, it is important that any uncharacterized sources of experimental variation or reasonable alternative explanations for the patterns in the experimental data be brought to light. That is what we have endeavored to present in this analysis.
G1 Phase and the Cell Cycle.
Although the analysis presented here is independent of particular models of cell cycle control, it is of interest to point out that the impetus for this study is the proposal that there are no G1-phase-specific controls. That a significant number of patterns was attributed to the G1 phase of the human cell cycle led to this reexamination of the microarray data. This view of the G1 phase has been extensively reviewed and applied to a number of experimental results (3, 5, 9–16).
Although the analysis presented here is only circumstantially related to the problem of whether or not there are a number of G1-phase events, previous publications have dealt with such matters as the existence of G1-less cells (14), the statistical variation of interdivision times and the transition-probability model (12), the existence of G(0) (10, 17, 18), the nature of G1-phase arrest (3, 5, 18), the problem of synchronization (5), the expression of c-myc protein during the division cycle (13), the proposed G1-phase-specific phosphorylation of Rb protein (9, 15), the effect of cyclins on the length of the G1 phase (11), and the relationship of the G1 phase to cell differentiation (16). This alternative view has been the subject of two reviews (3, 15).
Acknowledgments
We thank Dr. Raymond Cho for his comments that improved this article. This work was supported by a grant from the University of Michigan Cancer Committee. Correspondence related to detailed mathematical and statistical methods should be addressed to K.S. (e-mail: kshedden@umich.edu). Correspondence related to general analysis of the mammalian division cycle should be addressed to S.C. (e-mail: cooper@umich.edu). Additional material on the cell cycle may be found at www.umich.edu/∼cooper.
Abbreviation
- PVE
proportion of variance explained
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Cho R J, Huang M, Dong H, Steinmetz L, Sapinoso L, Hampton G, Elledge S J, Davis R W, Lockhart D J, Campbell M J. Nat Genet. 2001;27:48–54. doi: 10.1038/83751. [DOI] [PubMed] [Google Scholar]
- 2.Spellman P T, Sherlock G, Zhang M Q, Iyer V R, Anders K, Eisen M B, Brown P O, Botstein D, Futcher B. Mol Biol Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cooper S. Prog Cell Cycle Res. 2000;4:27–39. doi: 10.1007/978-1-4615-4253-7_3. [DOI] [PubMed] [Google Scholar]
- 4.Cooper S. Bacterial Growth and Division. San Diego: Academic; 1991. [Google Scholar]
- 5.Cooper S. Cell Prolif. 1998;31:9–16. doi: 10.1046/j.1365-2184.1998.00110.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rao P N, Johnson R T. Nature (London) 1970;225:159–164. doi: 10.1038/225159a0. [DOI] [PubMed] [Google Scholar]
- 7.Gong J, Traganos F, Darzynkiewicz Z. Cell Growth Differ. 1995;6:1485–1493. [PubMed] [Google Scholar]
- 8.Cho R J, Campbell M J, Winzeler E A, Steinmetz L, Conway A, Wodicka L, Wolfsberg T G, Gabrielian A E, Landsman D, Lockhart D J, Davis R W. Mol Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
- 9.Cooper S, Yu C, Shayman J A. IUBMB Life. 1999;1:27–39. doi: 10.1080/713803488. [DOI] [PubMed] [Google Scholar]
- 10.Cooper S. FASEB J. 1998;12:367–373. doi: 10.1096/fasebj.12.3.367. [DOI] [PubMed] [Google Scholar]
- 11.Cooper S. Exp Cell Res. 1998;238:110–115. doi: 10.1006/excr.1997.3807. [DOI] [PubMed] [Google Scholar]
- 12.Cooper S. J Theor Biol. 1982;94:783–800. doi: 10.1016/0022-5193(82)90078-9. [DOI] [PubMed] [Google Scholar]
- 13.Cooper S. J Theor Biol. 1988;135:393–400. doi: 10.1016/s0022-5193(88)80253-4. [DOI] [PubMed] [Google Scholar]
- 14.Cooper S. Nature (London) 1979;280:17–19. doi: 10.1038/280017a0. [DOI] [PubMed] [Google Scholar]
- 15.Cooper S, Shayman J A. Cell Mol Life Sci. 2001;58:580–595. doi: 10.1007/PL00000883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cooper S. J Theor Biol. 2001;208:399–402. doi: 10.1006/jtbi.2000.2228. [DOI] [PubMed] [Google Scholar]
- 17.Cooper S. BioEssays. 1987;7:220–223. doi: 10.1002/bies.950070507. [DOI] [PubMed] [Google Scholar]
- 18.Cooper S. In: Cell Growth. Nicolini C, editor. New York: Plenum; 1981. pp. 315–336. [Google Scholar]