Abstract
Many efforts to date evolutionary divergences by using a molecular clock have yielded age estimates that are grossly inconsistent with the paleontological evidence. Such discrepancies often are attributed to the inadequacy of the fossil record, but many potential sources of error can affect molecular-based estimates. In this study, we minimize the potential error caused by inaccurate topology and uncertain calibration times by using a well-supported tree, multiple genes, and multiple well-substantiated dates to explore the correspondence between the fossil record and molecular-based age estimates for major clades of tracheophytes. Age estimates varied because of gene effects, codon position, lineage effects, method of inferring branch lengths, and whether or not rate constancy was assumed. However, even methods designed to ameliorate the effects of rate heterogeneity among lineages could not accommodate the substantially slower rates observed in Marattia + Angiopteris and in the tree ferns. Both of these clades of ferns have undergone dramatic decelerations in their rates of molecular evolution and are “molecular living fossils,” consistent with their relative morphological stasis for the past 165–200 million years. Similar discrepancies between the fossil record and molecular-based age estimates noted in other studies may also be explained in part by violations of rate constancy among lineages.
For nearly four decades, biologists have attempted to infer divergence dates from molecular data by using the concept of a molecular clock (1, 2). However, these efforts have met with only mixed success, as evidence for rate heterogeneity has accumulated (e.g., refs. 3–7), and as it has become clear that many estimated divergence times are grossly inconsistent with the fossil record (e.g., refs. 8–10). Although “the clock” has been known for some time to “tick” at different rates in different lineages and different genes, most studies that have used molecular data to estimate divergence times have neither considered potential sources of error or bias, nor provided confidence levels for the estimates reported. Furthermore, although the fossil record is typically regarded as sufficiently reliable to provide dates to calibrate the clock, when dates inferred from molecular data conflict with the fossil record, the latter is often dismissed as inadequate.
Many sources of error and bias can affect molecular-based estimates of divergence times. Obviously, an incorrect topology will yield erroneous estimates, although the magnitude of the problem depends on the extent of the topological error (11). Likewise, inaccurate calibration will bias the resulting estimates for other divergences. Equally seriously, however, heterogeneous rates of evolution among lineages are well known (3–7), and a failure to recognize such heterogeneity can compromise resulting estimates of divergence times. Inadequate sampling of taxa, coupled with rate heterogeneity, can compound the problem. For example, most molecular-based estimates of the age of the angiosperms greatly exceed the date inferred from the fossil record, 125–135 million years ago (mya). However, taxon sampling in these studies is skewed toward herbaceous species, especially grasses, which have elevated rates of molecular evolution relative to woody species (4). Estimates of divergence times may also vary among genes or other data partitions (e.g., 1st and 2nd vs. 3rd codon positions); such effects may be accommodated by different substitution models and should be evaluated in studies that combine multiple genes. A further key potential source of error or bias is the method used to estimate divergence dates. Although nearly any phylogram for any group of organisms clearly portrays violation of a molecular clock, with interspersed long and short branches, few studies that estimate divergence times test for clock-like behavior, and fewer still attempt to accommodate this violated assumption. Alternative methods, designed to accommodate rate inconstancy, have been proposed [e.g., nonparametric rate smoothing (NPRS; refs. 12 and 13); hidden-Markov methods (see ref. 13); likelihood methods (14, 15); Bayesian methods (16, 17); alternatives reviewed by Sanderson and Doyle (11)] but have rarely been tested, and their effectiveness is unknown.
Utilization of the fossil record also confronts many potential errors that could create problems in calibrating a molecular clock or for comparisons with molecular-based dates. Differing degrees of uncertainty in dating fossils is an inherent feature of the study of the geological record. The relevant fossils must also be accurately positioned on a cladogram of extant taxa based on synapomorphies. Further, it is also important that the date for the stem lineage of an extant group, which corresponds to the time a lineage diverged from its extant sister group, is not confused with the date for the crown group, which corresponds to the age of the extant group's most recent common ancestor. Molecular-based dates correspond to the ages of the crown groups, and thus it is critical that the fossils under consideration are also referable to the crown group. Finally, of course, fossils only provide minimum age estimates, and the fossil record inevitably incorporates many biases and real gaps.
Molecular-based estimates of divergence times in plants reveal a vast range of dates: for example, the age of the angiosperms has been estimated as 350–420 mya (18), >319 mya (8, 9), 200 mya (19, 20), 160 mya (7), to 140–190 mya (11). However, although some of these studies examined potential error caused by calibration time, lineage effects, or substitutional noise, only Sanderson and Doyle (11) thoroughly investigated multiple sources of error. Despite the uncertainties and the multiplicity of potential errors associated with molecular-based estimates of divergence times, the presence of large molecular data sets will continue to stimulate attempts to apply a molecular clock. Furthermore, even approximate age estimates for groups that lack a fossil record are better than none. Thus, it is imperative that such analyses are placed on the most secure foundation possible, consider potential sources of error, and determine the best methods to deal with realities such as rate heterogeneity among lineages or genes. The robustness of current methods to violations of their assumptions also needs careful examination.
In this article, we minimize errors of topology and calibration by using a well-supported tree that includes all major clades of tracheophytes and multiple strongly supported dates across a broad span of geologic time, to explore the correspondence between the fossil record and molecular-based age estimates. We also evaluate variation caused by method of estimation and calibration point. We estimate the ages, with confidence intervals, of major clades of tracheophytes, using (i) a tree based on four genes and morphology (21), (ii) data from four genes singly and combined, and (iii) multiple calibration points representing well-substantiated dates in the fossil record. We also test for rate constancy among lineages and heterogeneity of rates among genes and codon positions in protein-coding genes and evaluate sensitivity of age estimates to branch lengths inferred by maximum parsimony (MP) and maximum likelihood (ML), the effectiveness of NPRS relative to an assumption of rate constancy, and the correspondence of molecular-based estimates to the fossil record.
Materials and Methods
Topology and Calibration Points.
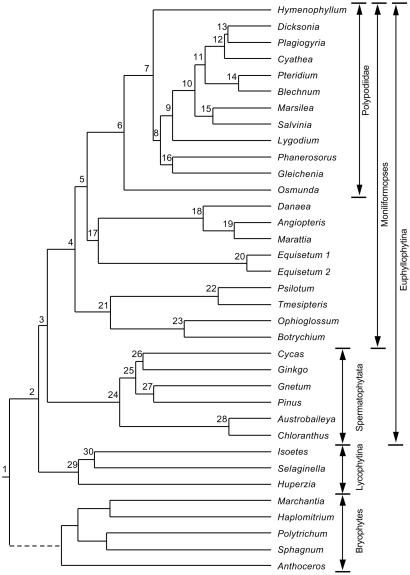
The phylogenetic tree of tracheophytes used in this study is the ML tree of Pryer et al. (21) inferred from analysis of the plastid genes rbcL, atpB, and rps4 and nuclear 18S ribosomal DNA (Fig. 1); a nearly identical tree was obtained in MP analyses of these four genes plus 136 morphological characters. This tree shows strong support for three major clades—lycophytes, seed plants, and horsetails + ferns (Moniliformopses)—with equally strong support for most relationships within each of these clades. Pryer et al.'s tree shows a basal polytomy with the interrelationships of hornworts, liverworts + mosses, and tracheophytes unresolved. Because dichotomous branching at the base of the tree is required for computation of likelihoods under the assumption of a molecular clock, we made the bryophyte outgroup monophyletic, with hornworts sister to liverworts + mosses, in some analyses. Using macclade version 3.05 (22), we tested the impact of relationships among outgroups on the estimates of divergence times in the ingroup by rearranging the outgroups to conform to the following topologies: hornworts, liverworts, mosses, tracheophytes [abbreviated HLM; consistent with analyses of land plant relationships based on 18S rDNA (e.g., refs. 23 and 24]); liverworts, hornworts, mosses, tracheophytes [abbreviated LHM; consistent with analyses of morphology (25, 26), the distribution of introns (27), and some DNA sequence data sets (e.g., ref. 28)]; basal polytomy, as reported by Pryer et al. (21).
Figure 1.
ML tree from Pryer et al. (21) with outgroup monophyletic and nodes numbered.
The dates for the calibration points used in this paper are based on the time scale of Harland et al. (29). Ages of clades are minimum ages estimated conservatively for the crown group by the first appearance of fossils clearly referable to one of the constituent lineages based on morphological synapomorphies. For example, although the time of origin of the angiosperms is unclear, the dates selected as calibration points correspond to fossils that are clearly angiosperms and are thus conservative. Further justification for the dates used is provided in the Appendix, which is published as supporting information on the PNAS web site, www.pnas.org. Four different calibration points were used, and in two cases a more conservative and less conservative calibration were used to explore the potential effects.
Tests of Rate Heterogeneity.
In all ML analyses, we used an HKY85 model of DNA evolution (30) in which we estimated base frequencies and the transition/transversion ratio from the data; to account for rate heterogeneity among sites, we used a gamma distribution (31) with the alpha shape parameter estimated from the data (Table 1). Although we did not test the HKY85 + Γ model against alternative models, this model represents a reasonable compromise between generality of the model and computational time required.
Table 1.
Parameter values for the HKY85 + Γ model on the tracheophyte tree, with outgroup monophyletic
| Gene | Frequency of adenine | Frequency of cytosine | Frequency of guanine | Frequency of thymine | Transit./ Transv. ratio | Alpha, shape parameter |
|---|---|---|---|---|---|---|
| rbcL | 0.283 | 0.219 | 0.182 | 0.317 | 3.946 | 0.233 |
| atpB | 0.305 | 0.198 | 0.156 | 0.341 | 5.303 | 0.288 |
| rps4 | 0.345 | 0.192 | 0.201 | 0.261 | 3.354 | 0.779 |
| 18S rDNA | 0.209 | 0.251 | 0.255 | 0.285 | 2.586 | 0.182 |
| Combined | 0.277 | 0.221 | 0.206 | 0.296 | 3.948 | 0.233 |
For each gene taken separately and all genes combined, rate heterogeneity across lineages was tested by using a likelihood ratio (LR) test (32). Significance was assessed by comparing Λ = −2 log LR, where LR is the difference between the -ln likelihood of the tree, with and without enforcing a molecular clock, with a χ2 distribution (with n − 2 degrees of freedom, where n is the number of taxa).
Rate heterogeneity between pairs of data partitions (genes or codon positions) was also tested by using a LR test: LR = [ln L − (ln L1 + ln L2)], where L1 is the likelihood of the tree with one partition, L2 is the likelihood of the tree with the second partition, and L is the likelihood of the tree with both partitions combined. The test statistic Λ was compared with a χ2 distribution, with degrees of freedom computed following Sanderson and Doyle (11). Rate heterogeneity among partitions was assessed with and without enforcing a molecular clock. In the tests without a molecular clock enforced, likelihoods were computed on the tree of Pryer et al. (21); however, the basal polytomy of this tree precluded the computation of likelihood values on this tree under the assumption of a molecular clock. Therefore, tests of rate heterogeneity among genes with a molecular clock enforced used the tree with outgroups monophyletic (see above).
Estimation of Ages.
Because all tests of rate heterogeneity among lineages were highly significant (Table 2), we dated the nodes by using the NPRS method of Sanderson (12). Using PAUP* 4.0 (33), we calculated MP and ML branch lengths when single genes, or all combined, were optimized onto the tree of Pryer et al. (21). These trees with branch lengths were then transformed into ultrametric trees by using the NPRS method implemented in the software treeedit (version 1.0 alpha 4–61, August 2000, written by Andrew Rambaut and Mike Charleston and available at http://evolve.zoo.ox.ac.uk/software/TreeEdit/main.html). To transform relative time to absolute ages we calibrated the trees by using dates from the fossil record. To compute error estimates for the ages inferred from single genes or all combined, we reapplied the NPRS procedure to 100 bootstrapped matrices obtained by resampling the data irrespective of codon position by using PHYLIP 3.573c (34).
Table 2.
LR tests of lineage effects, based on a χ2 distribution and 33 df
| Genes | -ln likelihood without molecular clock enforced | -ln likelihood with molecular clock enforced | Λ | P |
|---|---|---|---|---|
| rbcL | 14,619.9 | 15,773.2 | 2,307 | <0.0001 |
| atpB | 13,533.5 | 13,826.0 | 585 | <0.0001 |
| rps4 | 10,775.2 | 11,045.8 | 541 | <0.0001 |
| 18S rDNA | 9,053.2 | 9,249.4 | 392 | <0.0001 |
| Combined | 43,136.6 | 43,752.5 | 1,232 | <0.0001 |
Results and Discussion
Tests of Rate Heterogeneity.
All genes, separate and combined, show significant rate heterogeneity among lineages (Table 2). Furthermore, all pairs of genes evolve at significantly different rates across this tree (Table 3), whether or not a molecular clock is enforced. The relative rates of evolution of the four genes are rps4 > atpB ≈ rbcL > 18S rDNA. With the exception of 1st versus 2nd codon positions in rps4, computed with a molecular clock, all codon positions evolve at significantly different rates in the three protein-coding genes, whether or not a molecular clock is enforced (Table 7, which is published as supporting information on the PNAS web site).
Table 3.
LR tests of gene effects, computed without (−cl) and with (+cl) enforcing a molecular clock, based on a χ2 distribution and 36 df
| Genes | Λ (−cl) | Λ (+cl) |
|---|---|---|
| rbcL vs. atpB | 152 | 89 |
| rbcL vs. rps4 | 297 | 203 |
| rbcL vs. 18S rDNA | 38,006 | 38,643 |
| atpB vs. rps4 | 3,756 | 3,830 |
| atpB vs. 18S rDNA | 1,064 | 846 |
| rps4 vs. 18S rDNA | 1,042 | 840 |
All values are significant at P < 0.0001.
Comparison of Estimates from Different Partitions.
Age estimates varied considerably among genes (Table 4). For example, considering estimates only for node 2 (tracheophytes), when 125 mya was used as a conservative calibration point for node 28 (angiosperms), values for node 2 using MP ranged from 414.3 mya (rps4) to 513.2 mya (18S rDNA), and using ML ranged from 490.5 mya (rps4) to 680.3 mya (18S rDNA). The plastid gene rps4 typically yielded the youngest age estimates for a given node, followed in order of increasing age by atpB and rbcL, with the oldest age estimates consistently provided by the only nuclear gene, 18S rDNA. However, deviations from this general pattern were observed for some nodes (e.g., nodes 22, 24, 25, and 26) for which rbcL or atpB provided the oldest age estimates (Table 4). The standard deviations for all estimates are also high (Table 4), for individual genes and for the combined matrix. Thus, considerable variance surrounds each age estimate.
Table 4.
Ages of nodes with standard deviations from bootstrapped matrices inferred from the optimization of single genes or the combined data set using MP (upper values) or ML (lower values), an estimated age for node 28 of 125 mya as a calibration point, and the tracheophyte tree of Pryer et al. (21) with the outgroup specified as monophyletic (see Fig. 1 for node numbers and text for details)
| Node | rbcL | atpB | rps4 | 18S rDNA | Combined | Direct |
|---|---|---|---|---|---|---|
| 1 | 541.6 ± 75.7 | 506.0 ± 93.4 | 459.6 ± 92.2 | 599.4 ± 89.3 | 546.8 ± 44.0 | 545.0 |
| 651.0 ± 114.2 | 662.5 ± 170.4 | 496.8 ± 165.7 | 683.3 ± 167.9 | 716.8 ± 72.0 | 696.0 | |
| 2 | 497.2 ± 69.6 | 462.0 ± 84.0 | 414.3 ± 83.5 | 513.2 ± 80.4 | 495.9 ± 39.3 | 493.7 |
| 646.3 ± 114.0 | 654.8 ± 168.3 | 490.5 ± 163.2 | 680.3 ± 167.5 | 710.1 ± 71.5 | 688.7 | |
| 3 | 460.4 ± 63.0 | 430.6 ± 79.2 | 388.6 ± 77.2 | 481.9 ± 74.9 | 460.9 ± 36.0 | 458.0 |
| 612.0 ± 106.3 | 645.6 ± 165.6 | 474.8 ± 159.1 | 621.0 ± 151.5 | 683.4 ± 67.5 | 661.6 | |
| 4 | 401.9 ± 56.2 | 379.3 ± 71.5 | 329.4 ± 66.7 | 428.9 ± 72.2 | 398.4 ± 32.9 | 395.3 |
| 535.1 ± 91.3 | 568.1 ± 148.6 | 409.9 ± 140.9 | 616.9 ± 150.2 | 600.0 ± 59.9 | 579.7 | |
| 5 | 357.1 ± 50.8 | 336.9 ± 65.8 | 297.5 ± 60.6 | 398.7 ± 66.6 | 354.4 ± 29.9 | 350.9 |
| 514.7 ± 91.0 | 542.1 ± 144.1 | 374.2 ± 129.0 | 616.5 ± 150.3 | 567.8 ± 58.4 | 543.7 | |
| 6 | 321.2 ± 45.6 | 272.0 ± 54.3 | 245.6 ± 49.1 | 340.4 ± 59.7 | 297.1 ± 26.6 | 293.6 |
| 442.3 ± 77.6 | 432.3 ± 118.0 | 301.3 ± 104.7 | 568.1 ± 149.0 | 453.8 ± 49.3 | 435.0 | |
| 7 | 265.2 ± 37.7 | 217.9 ± 43.7 | 192.4 ± 38.2 | 311.5 ± 54.3 | 238.8 ± 21.5 | 235.6 |
| 370.5 ± 65.9 | 329.2 ± 87.1 | 253.6 ± 91.9 | 568.1 ± 149.0 | 366.3 ± 39.7 | 350.8 | |
| 8 | 215.6 ± 30.7 | 189.4 ± 37.9 | 157.3 ± 32.9 | 271.9 ± 50.6 | 198.2 ± 18.3 | 195.2 |
| 343.1 ± 59.0 | 311.2 ± 90.0 | 240.9 ± 91.3 | 563.6 ± 150.0 | 347.1 ± 36.8 | 328.0 | |
| 9 | 172.6 ± 24.2 | 160.7 ± 32.5 | 132.4 ± 28.5 | 247.1 ± 51.4 | 163.7 ± 15.1 | 161.4 |
| 298.0 ± 55.2 | 280.6 ± 73.0 | 228.0 ± 86.9 | 523.4 ± 144.6 | 313.0 ± 35.0 | 292.1 | |
| 10 | 131.3 ± 18.8 | 122.0 ± 24.5 | 97.0 ± 22.2 | 224.6 ± 48.2 | 123.3 ± 11.8 | 121.5 |
| 240.3 ± 41.7 | 214.0 ± 55.7 | 169.2 ± 66.5 | 505.0 ± 138.7 | 240.1 ± 27.3 | 225.9 | |
| 11 | 98.5 ± 15.5 | 100.0 ± 20.0 | 82.4 ± 19.5 | 197.1 ± 46.8 | 97.6 ± 9.4 | 95.9 |
| 208.0 ± 38.1 | 195.3 ± 49.2 | 147.8 ± 58.0 | 465.7 ± 123.6 | 210.5 ± 23.2 | 195.2 | |
| 12 | 63.7 ± 10.1 | 61.3 ± 13.4 | 54.2 ± 14.6 | 155.8 ± 49.3 | 61.8 ± 6.8 | 60.8 |
| 150.9 ± 31.6 | 138.7 ± 42.0 | 124.3 ± 47.4 | 465.7 ± 123.6 | 155.4 ± 21.4 | 139.9 | |
| 13 | 51.0 ± 8.6 | 54.9 ± 11.4 | 42.5 ± 11.9 | 155.8 ± 49.3 | 51.0 ± 6.3 | 50.2 |
| 129.4 ± 30.0 | 134.6 ± 40.7 | 115.2 ± 43.5 | 465.7 ± 123.6 | 142.5 ± 21.2 | 127.7 | |
| 14 | 57.6 ± 9.9 | 48.9 ± 10.4 | 43.5 ± 12.0 | 197.1 ± 46.8 | 52.6 ± 5.4 | 51.6 |
| 116.0 ± 26.4 | 84.2 ± 24.1 | 70.7 ± 32.7 | 465.7 ± 123.6 | 105.4 ± 13.9 | 98.1 | |
| 15 | 96.7 ± 13.8 | 90.7 ± 20.2 | 71.4 ± 17.6 | 175.9 ± 38.3 | 91.1 ± 9.7 | 89.4 |
| 169.2 ± 33.6 | 160.4 ± 46.7 | 157.3 ± 65.5 | 435.4 ± 127.8 | 185.3 ± 24.2 | 173.2 | |
| 16 | 174.3 ± 24.9 | 151.2 ± 32.0 | 129.6 ± 27.9 | 256.9 ± 49.9 | 160.8 ± 15.0 | 158.3 |
| 305.3 ± 54.3 | 289.0 ± 80.1 | 217.7 ± 85.9 | 556.5 ± 144.1 | 312.5 ± 35.2 | 293.2 | |
| 17 | 297.3 ± 43.1 | 293.8 ± 57.6 | 248.9 ± 53.2 | 381.2 ± 62.4 | 299.8 ± 26.0 | 297.5 |
| 487.7 ± 91.7 | 487.0 ± 133.8 | 368.7 ± 127.9 | 615.6 ± 150.5 | 539.0 ± 54.5 | 511.8 | |
| 18 | 128.3 ± 21.0 | 135.1 ± 34.1 | 116.7 ± 29.4 | 269.9 ± 55.8 | 135.4 ± 15.4 | 132.4 |
| 181.4 ± 37.6 | 221.1 ± 65.6 | 141.0 ± 59.4 | 425.1 ± 122.2 | 214.1 ± 30.7 | 202.1 | |
| 19 | 59.3 ± 13.1 | 81.1 ± 24.0 | 48.2 ± 16.4 | 102.8 ± 36.5 | 64.2 ± 9.2 | 62.2 |
| 113.9 ± 33.0 | 216.5 ± 65.7 | 62.6 ± 40.2 | 133.5 ± 51.0 | 122.7 ± 25.7 | 111.4 | |
| 20 | 64.8 ± 12.7 | 62.1 ± 14.5 | 48.9 ± 14.3 | 114.5 ± 67.9 | 61.5 ± 6.7 | 60.3 |
| 70.7 ± 18.2 | 56.3 ± 17.8 | 49.8 ± 23.7 | 127.6 ± 80.0 | 71.9 ± 9.3 | 73.0 | |
| 21 | 334.2 ± 50.6 | 312.8 ± 58.5 | 252.5 ± 52.5 | 369.5 ± 67.6 | 324.0 ± 27.8 | 320.6 |
| 444.5 ± 81.3 | 450.9 ± 120.3 | 352.8 ± 126.5 | 509.3 ± 132.1 | 494.4 ± 53.8 | 475.2 | |
| 22 | 155.7 ± 35.6 | 122.1 ± 28.6 | 106.9 ± 29.6 | 133.7 ± 52.6 | 131.8 ± 15.3 | 131.5 |
| 180.0 ± 52.5 | 132.4 ± 42.0 | 107.8 ± 47.1 | 148.1 ± 67.1 | 158.9 ± 22.2 | 157.6 | |
| 23 | 175.1 ± 27.1 | 194.2 ± 37.3 | 146.7 ± 33.2 | 236.0 ± 58.2 | 183.6 ± 18.3 | 182.0 |
| 209.8 ± 40.4 | 256.5 ± 71.7 | 239.9 ± 94.8 | 359.4 ± 113.5 | 269.2 ± 33.5 | 258.5 | |
| 24 | 352.0 ± 47.6 | 322.8 ± 58.8 | 338.2 ± 67.6 | 304.2 ± 46.1 | 343.7 ± 25.3 | 340.2 |
| 459.3 ± 76.0 | 457.0 ± 117.6 | 409.8 ± 129.7 | 386.0 ± 93.3 | 465.4 ± 44.8 | 447.8 | |
| 25 | 282.8 ± 40.7 | 259.4 ± 49.1 | 265.2 ± 53.4 | 261.5 ± 41.4 | 277.5 ± 21.2 | 274.0 |
| 402.1 ± 74.6 | 418.6 ± 107.1 | 372.9 ± 122.4 | 376.8 ± 91.6 | 424.5 ± 41.3 | 402.2 | |
| 26 | 247.3 ± 38.2 | 234.4 ± 46.7 | 229.4 ± 50.4 | 234.9 ± 37.1 | 246.9 ± 19.7 | 242.8 |
| 387.3 ± 72.0 | 387.6 ± 93.0 | 360.2 ± 120.3 | 350.8 ± 82.6 | 401.7 ± 40.0 | 378.8 | |
| 27 | 227.0 ± 32.3 | 205.5 ± 40.1 | 239.2 ± 50.7 | 190.3 ± 34.3 | 222.9 ± 18.1 | 219.7 |
| 323.7 ± 59.2 | 376.0 ± 99.1 | 372.9 ± 122.4 | 298.0 ± 76.6 | 373.0 ± 36.8 | 346.8 | |
| 28 | 125, 125 | 125, 125 | 125, 125 | 125, 125 | 125, 125 | 125, 125 |
| 29 | 365.7 ± 52.0 | 364.5 ± 70.4 | 289.1 ± 61.2 | 422.2 ± 73.3 | 374.7 ± 32.2 | 372.7 |
| 563.1 ± 108.3 | 564.0 ± 150.0 | 385.1 ± 133.4 | 605.4 ± 151.7 | 599.1 ± 67.3 | 568.0 | |
| 30 | 277.4 ± 42.6 | 310.3 ± 59.9 | 227.4 ± 50.5 | 291.2 ± 55.1 | 294.3 ± 26.3 | 292.7 |
| 496.5 ± 103.1 | 538.7 ± 147.9 | 373.2 ± 134.0 | 508.7 ± 127.5 | 557.0 ± 64.0 | 522.1 |
“Direct” age estimates are NPRS estimates computed directly from the tree by using the original combined data set rather than the bootstrapped matrices.
Age estimates also varied dramatically by codon position (Table 8, which is published as supporting information on the PNAS web site). For example, when 125 mya was used for node 28 (angiosperms), values for node 2 (age of tracheophytes) using MP ranged from 403.8 (3rd position) to 814.9 (1st) for atpB, from 193.6 (2nd) to 506.8 (3rd) for rbcL, and from 361.4 (3rd) to 517.5 (2nd) for rps4. ML values for 3rd positions were generally older than MP estimates, often nearly twice as old (Table 8), suggesting that multiple substitutions may have occurred at some 3rd positions. Age estimates obtained by using a calibration of 377.4 mya for node 29 (lycophytes) showed similar patterns among codon positions but different ages (data not shown).
Comparison of Estimates from Different Methods.
ML and MP age estimates differed greatly (Table 4), with the ML estimates considerably older than those obtained with MP for all data partitions; the MP estimates agree more closely with the fossil record (Table 4). Because ML corrects for multiple substitutions, ML estimates may be expected to be older than MP estimates, but the ML estimates for most nodes are clearly inconsistent with the fossil record.
Because significant lineage effects were detected, we used Sanderson's (12) NPRS method to ameliorate rate differences among clades. This method estimates rates and divergence times by using a criterion that maximizes the autocorrelation of rates within clades. However, the effectiveness of this approach for accommodating rate inconstancy has not been tested, and Sanderson and Doyle's (11) preliminary analyses with angiosperms suggest that NPRS may actually aggravate rather than ameliorate the problem, at least when rates of molecular evolution change abruptly.
To examine the effects of using NPRS, we compared the results obtained with NPRS to those obtained with the widely used approach of defining the relative age of a node in a nonultrametric tree as the maximum branch length from that node to any of the tips descended from it (see e.g., refs. 13, 35, and 36). This approach was repeated with both MP and ML branch lengths for all genes combined. With all six calibrations examined, the estimated ages were clearly anomalously old, with all but one estimate for the age of tracheophytes ranging from 1.0 billion to 4.0 billion years and all but one estimate for the age of land plants ranging from 1.1 billion to 4.3 billion years (data not shown). The earliest fossil record of probable embryophytes (a more inclusive clade that comprises tracheophytes plus bryophytes) is from the Middle Ordovician (Llanvirn 476.1–472.7 mya). The more “reasonable” estimates, of 740 mya for tracheophytes and 794 mya for land plants, both of which are approximately 350 million years older than the fossil record, came from the calibration of lycophytes at 400 mya. However, use of this calibration point resulted in estimates for other lineages, such as the angiosperms (56 mya), Marattia + Angiopteris (38 mya), and tree ferns (127 mya), much younger than the fossil record (conservatively 125, 166.1, and 166.1 mya, respectively). Estimates obtained by using the ML branch lengths were even more problematic: the older dates were far older, and the younger dates were far younger. The use of NPRS, although not sufficient to account for all rate heterogeneity among lineages, certainly brought at least some estimated ages into line with the fossil record.
Effects of Outgroup Topology on Estimates.
The effects of outgroup topology were ascertained through comparisons of divergence estimates by using MP branch lengths and the calibration point of 125 mya for the angiosperms. The most severe effects were at the basal tracheophyte nodes, although the differences were no more than 3 mya or 4 mya, except for the lycophyte dates, which differed by 12 mya (Table 5). Effects at more internal and terminal nodes were minimal, with differences of 1–2 mya (data not shown). Thus, as Sanderson and Doyle (11) found in their analysis of the age of the angiosperms, relationships among the outgroups have surprisingly little effect, even on basal nodes of the ingroup.
Table 5.
Effect of outgroup topology on ages (in mya) inferred for selected nodes, using MP, the combined data set, and the angiosperm (node 28) calibration point of 125 mya
| Outgroup topol. | Node 2 | Node 29 | Node 3 | Node 4 | Node 24 |
|---|---|---|---|---|---|
| Basal polytomy | 497 | 372 | 460 | 397 | 341 |
| Monophyletic | 494 | 373 | 456 | 395 | 340 |
| HLM | 496 | 384 | 458 | 398 | 338 |
| LHM | 493 | 378 | 458 | 398 | 338 |
Node 2, tracheophytes, Node 29, lycophytes, Node 3, euphyllophytes, Node 4, moniliforms, Node 24, seed plants. See text for details on topologies.
Comparison of Estimates from Different Calibration Points.
The use of different calibration points had a major impact on the age estimates for nodes (Table 6). For example, when node 28 (angiosperms) was used and a conservative age estimate of 125 mya used, estimates for the ages of node 15 (Marsileales + Salviniales), node 25 (gymnosperms), and node 29 (lycophytes) agree reasonably closely with estimates from the fossil record (89.8 mya vs. 90 mya; 274.5 mya vs. 290 mya; 371.6 mya vs. 400 or 377.4 mya, respectively). However, the estimate for node 6 (Osmunda + all other leptosporangiate ferns) is 294.7 mya, which is somewhat older than the first appearance of the crown group Polypodiidae in the Late Permian (255–230 mya), and the estimate for node 2 (tracheophytes) extends back to the Cambrian whereas there is no reliable fossil evidence for the group until the Late Silurian (Ludlovian, ca. 415 mya). In contrast, the estimates for node 12 (tree ferns) and node 19 (Marattia + Angiopteris) are considerably younger than the fossil record indicates (61.0 mya vs. 166.1 mya; 62.4 mya vs. 166.1 mya, respectively). Even under the most conservative interpretation, there is no doubt that Dicksoniaceae, Angiopteris, and Marattia are all present in the Middle Jurassic flora of Yorkshire, northern England (37, 38).
Table 6.
Ages of nodes inferred from the optimization of the combined data set using MP, the tracheophyte tree of Pryer et al. (21) with a basal polytomy, and various nodes as calibration points (see Fig. 1 for node numbers and text for details)
| Node | Node 28, 125 mya | Node 28, 131.8 mya | Node 12, 166.1 mya | Node 19, 166.1 mya | Node 25, 290 mya | Node 29, 377.4 mya | Node 29, 400 mya |
|---|---|---|---|---|---|---|---|
| 1 | 581.3, 545.0 | 612.9 | 1,581.3 | 1,546.5 | 614.2 | 590.2 | 625.6 |
| 2 | 497.3, 493.7 | 524.3 | 1,352.8 | 1,323.0 | 525.4 | 505.0 | 535.2 |
| 3 | 460.4, 458.0 | 485.4 | 1,252.5 | 1,225.0 | 486.5 | 467.5 | 495.5 |
| 4 | 397.0, 395.3 | 418.6 | 1,080.2 | 1,064.4 | 419.5 | 403.2 | 427.4 |
| 5 | 352.3, 350.9 | 371.6 | 958.6 | 937.4 | 372.3 | 357.8 | 379.2 |
| 6 | 294.7, 293.6 | 310.8 | 801.8 | 784.1 | 311.4 | 299.3 | 317.2 |
| 7 | 236.5, 235.6 | 249.3 | 643.3 | 629.2 | 249.9 | 240.1 | 254.5 |
| 8 | 196.0, 195.2 | 206.8 | 533.2 | 521.5 | 207.1 | 199.1 | 211.0 |
| 9 | 162.0, 161.4 | 170.8 | 440.9 | 431.1 | 171.2 | 164.5 | 174.4 |
| 10 | 121.9, 121.5 | 128.6 | 331.7 | 324.4 | 128.8 | 123.8 | 131.2 |
| 11 | 96.3, 95.9 | 101.5 | 262.0 | 256.3 | 101.8 | 97.8 | 103.7 |
| 12 | 61.0, 60.8 | 64.3 | 165.3 | 162.4 | 64.5 | 62.0 | 65.7 |
| 13 | 50.4, 50.2 | 53.1 | 137.1 | 134.1 | 53.2 | 51.1 | 54.2 |
| 14 | 51.8, 51.6 | 54.7 | 141.1 | 138.0 | 54.8 | 52.6 | 55.8 |
| 15 | 89.8, 89.4 | 94.7 | 244.3 | 238.9 | 94.9 | 91.1 | 96.6 |
| 16 | 159.0, 158.3 | 167.6 | 432.4 | 422.9 | 168.0 | 161.4 | 171.1 |
| 17 | 298.6, 297.5 | 314.8 | 812.5 | 794.6 | 315.5 | 303.2 | 321.4 |
| 18 | 132.9, 132.4 | 140.1 | 361.6 | 353.6 | 140.4 | 134.9 | 143.0 |
| 19 | 62.4, 62.2 | 65.8 | 169.8 | 166.1 | 66.0 | 63.4 | 67.2 |
| 20 | 60.5, 60.3 | 63.8 | 164.6 | 160.9 | 63.9 | 61.4 | 65.1 |
| 21 | 321.8, 320.6 | 339.3 | 875.4 | 856.0 | 340.0 | 326.7 | 346.3 |
| 22 | 131.9, 131.5 | 139.0 | 358.8 | 350.9 | 139.3 | 133.9 | 141.9 |
| 23 | 182.6, 182.0 | 192.5 | 496.8 | 485.8 | 192.9 | 185.4 | 196.5 |
| 24 | 341.0, 340.2 | 359.6 | 927.8 | 907.4 | 360.4 | 346.4 | 367.1 |
| 25 | 274.5, 274.0 | 289.4 | 746.7 | 730.2 | 290 | 278.7 | 295.4 |
| 26 | 243.1, 242.8 | 256.4 | 661.4 | 646.8 | 256.9 | 246.9 | 261.7 |
| 27 | 220.0, 219.7 | 232.0 | 598.4 | 585.3 | 232.4 | 223.4 | 236.8 |
| 28 | 125, 125 | 131.8 | 330.7 | 332.6 | 132.1 | 126.9 | 134.5 |
| 29 | 371.6, 372.7 | 391.9 | 1,011.1 | 988.8 | 392.7 | 377.4 | 400 |
| 30 | 291.2, 292.7 | 307.0 | 792.3 | 774.8 | 307.7 | 295.7 | 313.4 |
Node 28, angiosperms; node 12, Dicksonia/Plagiogyria/Cyathea; node 19, Angiopteris/Marattia; node 25, gymnosperms; node 29 lycopsids. For the angiosperm calibration at 125 mya, values computed with the outgroup specified as monophyletic are in italics.
We obtained very similar results when dates for either node 29 (lycophytes) or node 25 (gymnosperms) were used as calibration points. The estimates for the age of seed plants, gymnosperms, and angiosperms (in the former) and estimates for the age of lycophytes and angiosperms (in the latter) agreed closely with the fossil record, whereas the estimates for the ages of both node 12 (tree ferns) and node 19 (Marattia + Angiopteris) were again very low compared with the fossil record. In contrast, however, when fossil dates for nodes 12 (tree ferns) and 19 (Marattia + Angiopteris) were used as calibration points, the estimates for all other nodes became anomalously old (Table 6).
Conclusions
We detected significant rate heterogeneity among lineages of land plants and among genes, even those from the plastid genome. Age estimates based on techniques that assume rate constancy among lineages are highly skewed, with most basal nodes being several hundred million years too old and some internal and terminal nodes being much too young, based on interpretations of the fossil record. NPRS provides estimates that are much more in line with the known history of life on earth. However, NPRS cannot accommodate all of the lineage effects, and age estimates vary substantially depending on the calibration point used.
Estimates of ages for clades of seed plants and lycophytes are reasonably consistent with each other, and with the fossil record, when other seed plant or lycophyte nodes are used for calibration. However, ages for several fern groups inferred from calibrations using seed plants or lycophytes are much too young compared with their unequivocal fossil record. Even when very conservative fern fossil dates are used to estimate the ages of seed plants and lycophytes, the results are strongly at odds not just with paleobotanical data but the whole corpus of geochronological knowledge. Our interpretation is that some clades, notably Marattia + Angiopteris and the tree ferns, have apparently experienced a dramatic slowdown in their rates of molecular evolution. This pattern cannot be an artifact of insufficient sampling of ferns: all extant members of the (Marattia + Angiopteris) + Danaea clade were included in the Pryer et al. (21) tree. Likewise, the tree fern clade is also well sampled, and the overall backbone of the clade of leptosporangiate ferns (Polypodiidae) is also well represented.
Marattia, Angiopteris, and the tree ferns are “molecular living fossils,” consistent with their relatively stable morphologies through time. Two clades of angiosperms with good fossil records have also been considered molecular living fossils: Nelumbo + Platanus and Fagus + Carya (11). The correspondence between relative stasis in morphological features and relative stasis in gene sequences indicates that, in some cases and in broad terms, the genome may evolve as a unit over long periods. At least in angiosperm families, the rate of morphological evolution correlates with the rate of neutral molecular substitutions (39). This pattern stands in stark contrast to that observed for many angiosperm groups that have radiated recently on oceanic islands and exhibit extensive morphological divergence with minimal molecular evolution (40).
Supplementary Material
Acknowledgments
We thank Kathleen Pryer and collaborators for sharing their phylogenetic tree and data sets with us before the publication of their paper, Mike Sanderson and Jim Doyle for sharing their unpublished work and for valuable discussion and advice, and Mike Sanderson for helpful comments on the manuscript. This work was supported in part by a U.S.-U.K. Fulbright Distinguished Professorship (to P.S.S. and D.E.S.), National Science Foundation Grant DEB-0090283 (to D.E.S., P.S.S., D. L. Dilcher, and P. S. Herendeen), a Swiss National Science Foundation grant (to V.S.), and a Royal Society University Research Fellowship (to T.G.B.).
Abbreviations
- mya
million years ago
- NPRS
nonparametric rate smoothing
- MP
maximum parsimony
- ML
maximum likelihood
- LR
likelihood ratio
References
- 1.Zuckerkandl E, Pauling L. In: Horizons in Biochemistry. Kasha M, Pullman B, editors. New York: Academic; 1962. pp. 189–225. [Google Scholar]
- 2.Zuckerkandl E, Pauling L. In: Evolving Genes and Proteins. Bryson V, Vogel H J, editors. New York: Academic; 1965. pp. 97–166. [DOI] [PubMed] [Google Scholar]
- 3.Britten R J. Science. 1986;231:1393–1398. doi: 10.1126/science.3082006. [DOI] [PubMed] [Google Scholar]
- 4.Gaut B S, Muse S V, Clark W D, Clegg M T. J Mol Evol. 1992;35:292–303. doi: 10.1007/BF00161167. [DOI] [PubMed] [Google Scholar]
- 5.Clegg M T, Gaut B S, Learn G H, Jr, Morton B R. Proc Natl Acad Sci USA. 1994;91:6795–6801. doi: 10.1073/pnas.91.15.6795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li W-H. Molecular Evolution. Sunderland, MA: Sinauer; 1997. [Google Scholar]
- 7.Goremykin V, Hansmann S, Martin W. Plant Syst Evol. 1997;206:337–351. [Google Scholar]
- 8.Martin W, Gierl A, Saedler H. Nature (London) 1989;339:46–48. [Google Scholar]
- 9.Martin W, Lydiate D, Brinkmann H, Forkmann G, Saedler H, Cerff R. Mol Biol Evol. 1993;10:140–162. doi: 10.1093/oxfordjournals.molbev.a039989. [DOI] [PubMed] [Google Scholar]
- 10.Heckman D S, Geiser D M, Eidell B R, Stauffer R L, Kardos N L, Hedges S B. Science. 2001;293:1129–1133. doi: 10.1126/science.1061457. [DOI] [PubMed] [Google Scholar]
- 11.Sanderson M J, Doyle J A. Am J Bot. 2001;88:1499–1516. [PubMed] [Google Scholar]
- 12.Sanderson M J. Mol Biol Evol. 1997;14:1218–1231. [Google Scholar]
- 13.Sanderson M J. In: Molecular Systematics of Plants II. Soltis D E, Soltis P S, Doyle J J, editors. Boston: Kluwer; 1998. pp. 242–264. [Google Scholar]
- 14.Rambaut A E, Bromham L D. Mol Biol Evol. 1998;15:442–448. doi: 10.1093/oxfordjournals.molbev.a025940. [DOI] [PubMed] [Google Scholar]
- 15.Yoder A D, Yang Z. Mol Biol Evol. 2000;17:1081–1090. doi: 10.1093/oxfordjournals.molbev.a026389. [DOI] [PubMed] [Google Scholar]
- 16.Thorne J L, Kishino H, Painter I S. Mol Biol Evol. 1998;15:1647–1657. doi: 10.1093/oxfordjournals.molbev.a025892. [DOI] [PubMed] [Google Scholar]
- 17.Huelsenbeck J P, Larget B, Swofford D L. Genetics. 2000;154:1879–1892. doi: 10.1093/genetics/154.4.1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ramshaw J A M, Richardson D L, Meatyard B T, Brown R H, Richardson M, Thompson E W, Boulter D. New Phytol. 1972;71:773–779. [Google Scholar]
- 19.Wolfe K H, Gouy M, Yang Y-W, Sharp P M, Li W-H. Proc Natl Acad Sci USA. 1989;86:6201–6205. doi: 10.1073/pnas.86.16.6201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Larouche J, Li P, Bousquet J. Mol Biol Evol. 1995;12:1151–1156. [Google Scholar]
- 21.Pryer K M, Schneider H, Smith A M, Cranfill R, Wolf P G, Hunt J S, Sipes S D. Nature (London) 2001;409:545–648. doi: 10.1038/35054555. [DOI] [PubMed] [Google Scholar]
- 22.Maddison W P, Maddison D R. macclade. Sunderland, MA: Sinauer; 1992. , version 3.05. [Google Scholar]
- 23.Nickrent D L, Parkinson C L, Palmer J D, Duff R J. Mol Biol Evol. 2000;17:1885–1895. doi: 10.1093/oxfordjournals.molbev.a026290. [DOI] [PubMed] [Google Scholar]
- 24.Soltis P S, Soltis D E, Wolf P G, Nickrent D L, Chaw S-M, Chapman R L. Mol Biol Evol. 1999;16:1774–1784. doi: 10.1093/oxfordjournals.molbev.a026089. [DOI] [PubMed] [Google Scholar]
- 25.Mishler B D, Churchill S P. Brittonia. 1984;36:406–424. [Google Scholar]
- 26.Kenrick P, Crane P R. The Origin and Diversification of Land Plants: A Cladistic Study. Washington, DC: Smithsonian; 1997. [Google Scholar]
- 27.Qiu Y-L, Cho Y, Cox J C, Palmer J D. Nature (London) 1998;394:671–674. doi: 10.1038/29286. [DOI] [PubMed] [Google Scholar]
- 28.Lewis L A, Mishler B D, Vilgalys R. Mol Phylogenet Evol. 1997;7:377–393. doi: 10.1006/mpev.1996.0395. [DOI] [PubMed] [Google Scholar]
- 29.Harland W B, Armstrong R L, Cox A V, Craig L E, Smith A G, Smith D G. A Geologic Timescale. Cambridge, U.K.: Cambridge Univ. Press; 1989. [Google Scholar]
- 30.Hasegawa M, Kishino H, Yano T. J Mol Evol. 1985;21:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- 31.Yang Z. Mol Biol Evol. 1993;10:1396–1401. doi: 10.1093/oxfordjournals.molbev.a040082. [DOI] [PubMed] [Google Scholar]
- 32.Felsenstein J. Annu Rev Genet. 1988;22:521–565. doi: 10.1146/annurev.ge.22.120188.002513. [DOI] [PubMed] [Google Scholar]
- 33.Swofford D L. paup* 4.0: Phylogenetic Analysis using Parsimony (* and Other Methods) Sunderland, MA: Sinauer; 1998. [Google Scholar]
- 34.Felsenstein J. phylip: Phylogeny Inference Package. Seattle: Univ. of Washington; 1993. [Google Scholar]
- 35.Hillis D M, Mable B K, Moritz C. In: Molecular Systematics. 2nd Ed. Hillis D M, Moritz C, Mable B K, editors. Sunderland, MA: Sinauer; 1996. pp. 515–544. [Google Scholar]
- 36.Bremer K. Proc Natl Acad Sci USA. 2000;97:4707–4711. doi: 10.1073/pnas.080421597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Harris T M. The Yorkshire Jurassic Flora: I. Thallophyta-Pteridophyta. London: British Museum Natural History; 1961. [Google Scholar]
- 38.Hill C R. Rev Paleobot Palynol. 1987;51:65–93. [Google Scholar]
- 39.Barraclough T G, Savolainen V. Evolution. 2001;55:677–683. doi: 10.1554/0014-3820(2001)055[0677:erasdi]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 40.Baldwin B G, Crawford D J, Francisco-Ortega J, Kim S-C, Sang T, Stuessy T. In: Molecular Systematics of Plants II. Soltis D E, Soltis P S, Doyle J J, editors. Boston: Kluwer; 1998. pp. 410–441. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.