Stochastic and mesoscopic models for tropical convection

Abstract

A new way to parametrize certain aspects of tropical convection through stochastic and mesoscopic models is developed here. The technical idea is to adapt tools from statistical physics and materials science to model important unresolved features of tropical convection. This new strategy consists of modeling the unresolved effects of convective inhibition in a coarse mesh mesoscopic parametrization through a “heat bath” model involving a stochastic spin flip model with very natural interaction rules for convective inhibition combined with a suitable external potential defined by the coarse mesh values. In turn, the values of the order parameter from this heat bath alter the vertical mass flux in regions of deep convection. Both stochastic and systematic deterministic mesoscopic parametrizations are developed here. The deterministic mesoscopic models derived in this fashion exhibit new phenomena such as multiple radiative equilibria in suitable parameter regimes. The simplest first numerical experiments reported here with the mesoscopic deterministic parametrization qualitatively reproduce several key features of the observational record regarding convectively coupled tropical waves. The systematic stochastic modeling strategy proposed here could also be very useful for capturing other features of tropical convection such as those involving cloud radiation feedbacks.

Convection in the tropics has a profound impact on short-term climate. Tropical convection is roughly organized into two types of cloud structures. The first type is ubiquitous and involves shallow cumulus convection over heights of roughly 1 km above the surface, and the second type involves deep penetrative convection to heights of 5–10 km with associated anvil towers of clouds. Observational data indicate that tropical deep convection is organized on a hierarchy of scales ranging from hundreds of kilometers due to mesoscale organized squall lines to intraseasonal oscillations over planetary scales of order 40,000 km (1–3). The present practical models for prediction of both weather and climate involve general circulation models (GCM) where the physical equations for these extremely complex flows are discretized in space and time and the effects of unresolved processes are parametrized according to various recipes (4, 5). With the current generation of supercomputers, the smallest possible mesh spacings are roughly 50–100 km for short-term tropical weather simulations and of 200–300 km for short-term climate simulations. With such coarse mesh spacing, despite much progress in the parametrization of tropical convection, the current generation of GCMs (4, 5) still fails to reproduce most of the significant features of the observational record (1–3) regarding tropical convection (4, 5). Thus, given the importance of the tropics for short-term climate, new strategies for parametrizing the unresolved effects of tropical convection are very important.

The main topic of this paper is to introduce a different approach for parametrizing certain features of tropical convection. The climate mean vertical profile over the western Pacific warm pool gives a large convectively available potential energy (CAPE) highly favorable for deep convection, yet paradoxically the area fractions where such deep convection occurs are extremely small, on the order of 1% or less (4, 5). One of the reasons for this much smaller area fraction is the fact that in the climatological mean state, there is usually a small negative potential energy for vertical motion over the boundary layer roughly 1 km in vertical extent and this leads to convective inhibition (CIN).

Here, a new stochastic modeling strategy is introduced for parametrizing the unresolved effect of the CIN in the boundary layer on the dynamics of deep tropical convection on coarse discrete spatial meshes. The main idea is to consciously mimic ideas from nonequilibrium statistical mechanics with firm mathematical underpinnings that have been developed recently for applications in materials science involving adsorption processes of molecules from surfaces (6–11). Such an approach is used here to develop both microscopic stochastic models and mesoscopic mean field models for tropical convection. The plan of the remainder of the paper is as follows. First, the stochastic models are developed and then these models are coarse-grained to mesoscopic scales to yield a new convective parametrization for CIN. In the remainder of the paper, the implications and new phenomena in this parametrization strategy are developed briefly for a model tropical convective parametrization that mimics other important features of a basic parametrization strategy for GCMs.

The Stochastic Model for CIN

In a typical GCM, the fluid dynamical and thermodynamical variables, denoted here by the generic vector u⃗, are regarded as known only over a discrete horizontal mesh with u⃗_j = u⃗(jΔx, t) denoting these discrete values. Throughout the discussion in this paper, one horizontal spatial dimension along the equator in the east–west direction is assumed for simplicity in notation and explanation. As mentioned above, the typical mesh spacing in a GCM is coarse with Δx ranging from 50 km to 250 km depending on the time duration of the simulation. However, observationally, CIN is known to have significant fluctuations on a horizontal spatial scale on the order of 1 km, the microscopic scale here, with changes in CIN attributed to different mechanisms in the turbulent boundary layer such as gust fronts, gravity waves, and turbulent fluctuations in equivalent potential temperature (12). Here the view is adopted that all of these different microscopic physical mechanisms and their interactions which increase and decrease CIN are too complex to model in detail in a coarse mesh GCM parametrization and instead, as in statistical mechanics (6–11), they will be modeled by a simple order parameter, σ_I, taking only two discrete values,

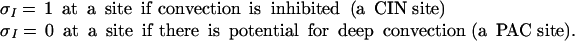1

As depicted in Fig. 1, the value of CIN at a given coarse mesh point is determined by the averaging of CIN over the microscopic states in the vicinity of the given mesh point, i.e.,

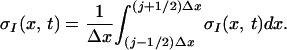2

Note that the mesh size, Δx, is mesoscopic, i.e., between the microscale, O(1 km), and the macroscale, O(10,000 km), and that σ_I can have any value in the range 0 ≤ σ_I ≤ 1. Here in 2 and elsewhere in the paper, discrete sums over microscopic mesh values (of order 1 km) and continuous integrals are used interchangeably for notational convenience. How should microscopic CIN sites interact? The observation of the turbulent fluctuation of CIN (12) suggests the following plausible interaction rules which are adopted here:

[3]

Figure 1.

CIN at a given coarse mesh point determined by the averaging over the microscopic states in the vicinity of the given mesh point.

To satisfy the requirements in 3, the microscopic energy content in the boundary layer for CIN is assumed to be given by

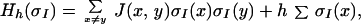4

where J(x, y) is a nonnegative interaction potential, J ≥ 0 satisfying

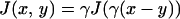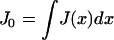5

with γ a parameter defining the range of microscopic interaction. Note that for external potentials h₁, h₂

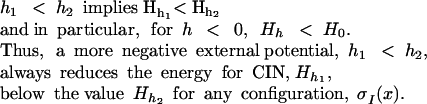6

In the approach presented here, the boundary layer states measuring CIN are regarded as a “heat bath” coupled to the mesoscopic fluid variables u⃗_j via the external potential h(u⃗_j) so that the equilibrium statistics of CIN in the boundary layer are given through the Gibbs measure (13)

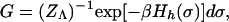7

where Z_Λ is a normalizing constant for the probability measure and the “inverse temperature β” is chosen to determine the average mean energy for CIN. Next, the approach in refs. 8 and 11 is followed: a microscopic stochastic time-dependent dynamics is defined which allows for flipping back and forth locally between sites with CIN and PAC with probabilities reflecting the intuitive rules in A and B from 3. A local spin flip takes a configuration, σ_I(x), at some random discrete site, x, and flips it to a new configuration

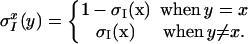8

Assume that such a spin flip occurs at a rate c(x, σ_I)Δt for Δt ≪ 1 given by the Arrhenius adsorption/desorption model (8, 11),

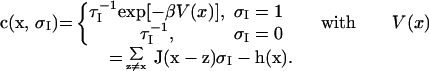9

Here τ_I is a characteristic time of interaction. According to the rate in 9, if a CIN site is mostly surrounded by CIN sites, it needs to overcome a larger energy barrier statistically to become a PAC site; however, no such extra energy barrier exists to convert a PAC site to a CIN site. In mathematical terms, these stochastic dynamical models are continuous Markov jump models (14) which keep the Gibbs measure in 7 invariant under the dynamics. In physical terms, the energy barrier in 9 corresponds to the local CIN energy that needs to be overcome to convert a CIN site into a PAC site which favors deep convection and corresponds to the intuitive reasoning in ref. 12 with a different quantitative modeling perspective.

Convective mass flux parametrizations for deep convection are among the most common ways to parametrize deep tropical convection in GCMs (4, 5). Theoretical efforts in understanding parametrization of deep tropical convection have focused on parametrizations that mimic those in the vastly more complex GCMs in simpler models with crude vertical resolution (see refs. 15 and 16, and the references therein). Here the stochastic and mesoscopic models for CIN are presented in the context of the simplified models from ref. 16, which are prototype mass parametrizations to illustrate both the stochastic model and to analyze its implications briefly in a simplified context.

A Stochastic Model for Parametrizing Convection with CIN

Here the prototype mass flux parametrization with crude vertical resolution developed in section 2 of ref. 16 is used to illustrate the fashion in which the stochastic model for CIN developed in 2–9 above can be coupled to a nonstochastic convection mass flux parametrization. For simplicity in exposition, the parameters α₂, b in ref. 16 are set identically to zero so that explicit coupling to the second baroclinic mode is ignored. Under these circumstances with a single horizontal x-variable, the prognostic variables u⃗ = (u, θ, θ_eb, q₂) are the x-component of the fluid velocity, u, the potential temperature in the middle troposphere, θ, the equivalent potential temperature, θ_eb, measuring the potential temperature plus moisture content of the boundary layer, and q₂, the stratiform heating rate for the second baroclinic mode. The dynamic equations for these variables in the parametrization (16) are given by

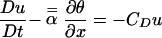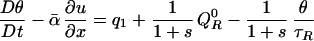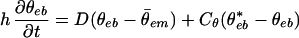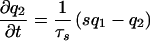10

with D/Dt = ∂/∂t + u∂/∂x, while the constants Q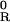, θ^*_eb are externally imposed and represent the radiative cooling in the upper troposphere and saturation equivalent moist potential temperature in the boundary layer. The crucial quantities in the prototype mass flux parametrization are the terms q₁ and D, where q₁ represents the middle troposphere heating due to deep convection and D represents the downward mass flux on the boundary layer. The heating term q₁ is given by

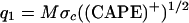11

with M a fixed constant and

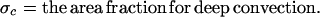12

The quantity σ_c controls the vertical mass flux from the deep convection. The downward mass flux on the boundary layer, D, is a sum of three contributions including the environmental downdrafts, m_e, and both the deep convective and stratiform mass fluxes, m_c, m_s, so that

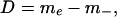13

where the downward mass flux due to convection m₋ is given by

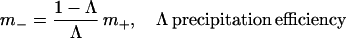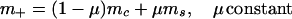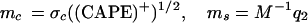[14]

and that due to the environment, m_e, by

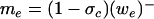15

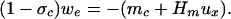See ref. 16 for extended discussion. In 11, 14, and 15, the notation (X)^± denotes, respectively, the positive or negative part of the number X. For the discussion in this paper, the values of the remaining constants in 10–15 are given in table 1 of ref. 16 and are not repeated here unless noted below. The equations in 10–15 define the prototype convective mass flux parametrization used here. It is established in refs. 12 and 16 that this parametrization reproduces key features of convectively coupled tropical waves on scales of order 1,500 km in the observational record (3) that are not captured in other prototype parametrizations of tropical convection.

The equations in 10–15 are regarded as the prototype GCM parametrization when discretized in a standard fashion using central differences on a coarse mesh Δx with Δx ranging from 50 km to 250 km. How is the stochastic CIN model defined in 2–9 coupled to this basic parametrization? First, the area fraction for deep convection, σ_c, governing the upward mass flux strength, is allowed to vary on the coarse mesh and is given by

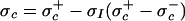16

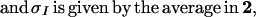where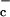 σ < σ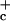 are threshold constant values. When the order parameter σ_I signifies strong CIN locally so that σ_I = 1, the flux of deep convection is diminished to the fraction σ 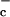while with PAC locally this flux increases to the value σ.

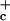To complete the coupling of the stochastic CIN model into the parametrization, the coarse mesh external potential, h(u⃗_j), from 3 and 4 needs to be specified from the coarse mesh values, u⃗_j. There is no unique choice of the external potential but its form can be dictated by simple physical reasoning. Here, the plausible physical assumptions are made that

17

With the properties in 6, the conditions in 17 are satisfied with the choice

18

and the constant value α̃ = 0.75 is used below. The stratiform mass flux is used in h here because it is known observationally that the stratiform wake of tropical squall lines often preconditions the CIN to allow for additional deep convection through gust fronts and gravity waves (12). There are other plausible choices for the external potential that will be compared and contrasted elsewhere by the authors. The equations in 8–16 and 18 complete the description of the stochastic model for parametrizing convection with CIN.

The Mesoscopic Deterministic Parametrization with CIN

The stochastic parametrization model derived above converges to a completely deterministic parametrization with CIN provided that the interaction potential for the boundary layer, J, from 5 has sufficiently long-range interaction so that γ = O(Δx) is sufficiently large compared to the microscale. Under these circumstances it is known with full mathematical rigor in somewhat simpler circumstances (6, 8, 9, 11) that the mesoscale averages, σ_I(jΔx, t), solve the integro-differential equation,

[19]

with the external potential, h, given from 18 and βJ ∗ σ_I the discrete average given by

20

with some constant value of a, 0 < a ≤ 1. Recall the constant J₀ from 5. In this limiting regime of the stochastic model, the equations in 10–16 together with 18–20 describe a completely deterministic prototype mass flux parametrization of convection with CIN that retains some features of the physical basis of the underlying stochastic model. The remainder of the paper briefly describes some of the new features of this parametrization.

Regimes with Multiple Radiative Convective Equilibria (RCE)

RCE are simple basic states that are homogeneous in x where radiative cooling through Q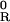 in 10 exactly balances the warming of the boundary layer driven by θ^*_eb and define the simplest climatological mean state for theory (4, 5, 15, 16).

Next it is shown below that multiple regimes for RCE can exist in the convective parametrization with CIN defined by 10–16 and 18–20. It is interesting that there is recent evidence for the existence of multiple RCE in cloud resolving numerical simulations with interactive radiation (17).

The mass flux parameter is given by

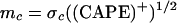21

with σ_c determined from σ_I through 16. Following ref. 16, the RCE is given through the mass flux parameter m̄_c via

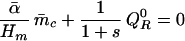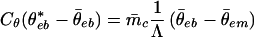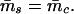[22]

Given the external parameters Q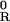, θ^*_eb, θ̄_em, the equations in 22 imply that

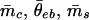are determined as functions of the external parameters

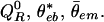Following ref. 11, the steady states σ̄_I at RCE are determined through the mass flux, m̄_s, and θ̄_eb by the equation

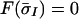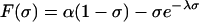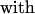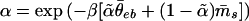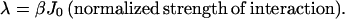[23]

According to ref. 11, the equation

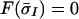has either a unique solution or three roots as solutions depending on the values of α and λ; obviously, only a single root occurs for λ = 0 given explicitly by

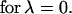24

Below, σ_* is used as a parameter to illustrate various values of J₀ and β where the multiple RCE can occur.

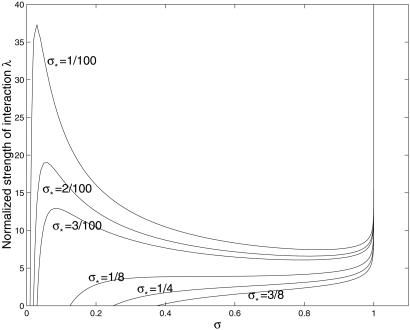
In Fig. 2, the zero level set of this function is plotted for different values of the parameter σ_*. The intersection of each curve with the straight line defined by a fixed normalized interaction strength, λ, defines the number of equilibria for that strength of interaction. Clearly, either one or three multiple RCE equilibria exist depending on the parameter values.

Figure 2.

Multiple equilibria. Here we plot the zero level set of the function F(σ) = F(σ, λ) in 23 for different fixed values of σ_*. The intersection of each curve with the straight line defined by a fixed normalized interaction strength, λ, defines the number of equilibria.

Numerical Experiments with the Mesoscopic CIN Parametrization

Here the results of some simple preliminary numerical experiments that illustrate several facets of the parametrization are described briefly. In the numerical experiments reported below, the large scale domain is 4,000 km and Δx = 80 km. Perturbation of the standard RCE from refs. 15 and 16 will be used to demonstrate the additional role of the CIN parametrization. A critical parameter in the behavior that we find in the parametrization is τ_I, the convective inhibition time, in 19.

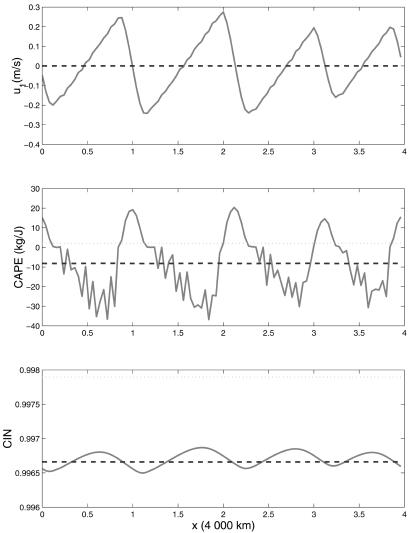
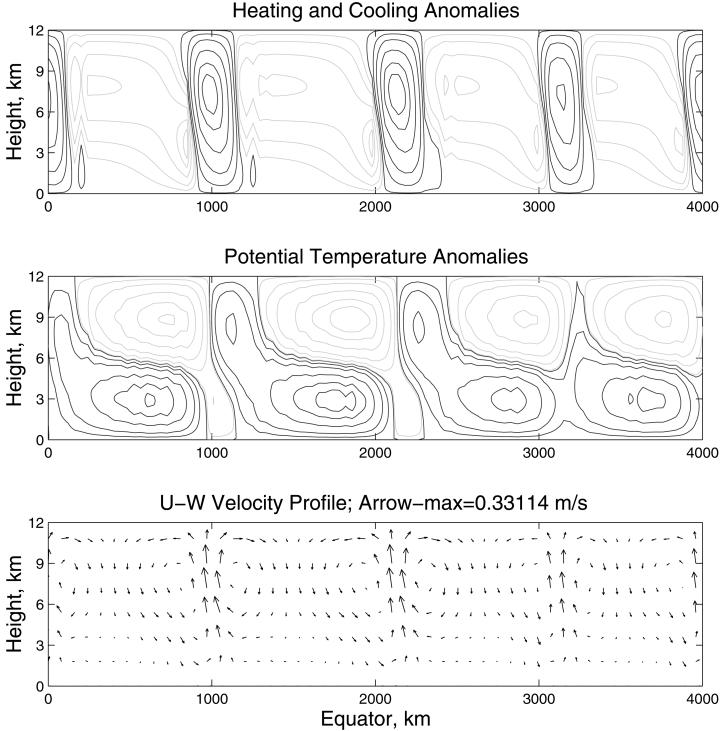
In the first experiment, the larger value τ_I = 72 h is used with mean state given by an RCE with σ_c = 0.002. Without the dynamic CIN parametrization, this RCE is unstable to linear theory (16). This RCE is perturbed by a small amplitude unstable wave train according to linear theory and the simulation is run until a new statistical mean state is developed; this takes about 100 days. As shown in Fig. 3, this new mean state has less mean CIN with a 75% larger area fraction, σ_c = 0.0035. The structure of the solution over days 100 ≤ t ≤ 200 consists of a nonlinear wave train with four parametrized supercloud clusters of scale roughly 1,000 km propagating as a wave group with eastward speed (to the right) of 13 m/s. These are the parametrizations in the model of the super-cluster convectively coupled tropical waves in the observational record (3, 18). The key structural feature to note in these waves as depicted in Figs. 3 and 4 are that the depletion of CIN leads the increase in CAPE which in turn leads the strong vertical updraft region and the region of heating. These are all key features in the observational record of such waves (3, 18). Another way to study tropical convection is through detailed numerical cloud resolving modeling using bulk microphysics and roughly 1 km resolution in two dimensions (17). In figures 13 and 14 of ref. 17, a supercluster wave train moving eastward at 18 m/s was produced through post-processing the numerical output of a cloud resolving modeling simulation. The qualitative resemblance between Figs. 3 and 4 of the present paper and figures 13 and 14 of ref. 17 is striking and gives further evidence supporting two different approaches to understanding tropical convection and its parametrization.

Figure 3.

Nonlinear wave train after 100 days for τ_I = 72 h and initial RCE with σ_c = 0.002. Solid, solution at t = 100 days; dashed, time average during days 100 < t < 200; dotted, initial RCE.

Figure 4.

Vertical-zonal physical picture of the flow associated with the wave train in Fig. 3. Dark contours correspond to positive anomalies and light contours correspond to negative anomalies.

To test the behavior of the mesoscopic CIN parametrization in parameter regimes with multiple equilibria, the mean initial data for the domain was divided into two regions with one RCE with less CIN occupying 0 < x < 2,000 km and an other RCE with the largest CIN occupying 2,000 < x < 4,000 km with random perturbations added suitably. 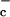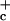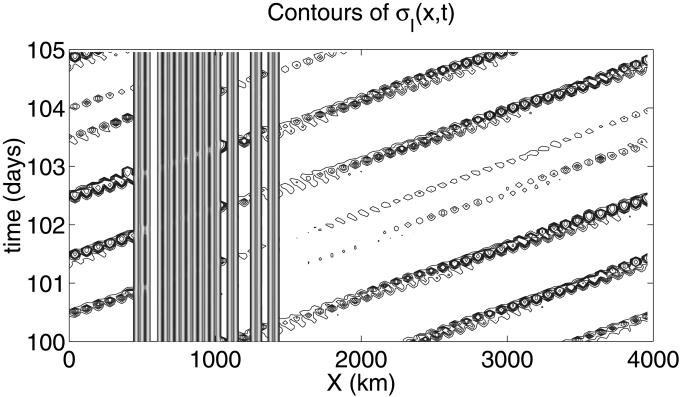In these experiments, the threshold values, σ = 0.01 and σ = 0.001 were used in 15, the values σ, σ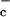 correspond to unstable and stable RCE, respectively, without the effects of CIN (16). The results of the parametrizations depend on τ_I in an interesting fashion. For τ_I = 72 h, the results are similar to those discussed in the first case where the changes in CIN move with the wave. At the other extreme, a small value of τ_I = 3 h results in a steady pattern of large spikes and plateaus of CIN with propagating waves that do not carry changes in CIN. In the intermediate regime τ_I = 12 h, the very interesting situation emerges with competition of both effects with propagating waves which carry CIN like those in Figs. 3 and 4 and also quasi-steady convectively coupled large spikes and plateaus of CIN. The pattern of CIN depicting this mixed behavior for several days of the statistical equilibrium is depicted in Fig. 5. Notice from Fig. 5 that the strength of the propagating waves decreases as the waves sweep through the standing spikes and plateaus of larger CIN.

Figure 5.

Pattern of CIN depicting a situation of a mixed behavior of propagating waves that carry CIN and quasi-steady convectively coupled large spikes and plateaus of CIN. τ_I = 12 h.

Concluding Discussion

In this paper, a new way to parametrize features of tropical convection through stochastic and mesoscopic models has been proposed. The main approach was to use and adapt ideas from statistical physics that have been successful in other contexts from materials science. New features for tropical convection emerge such as the possibility of multiple RCE; the new mesoscopic parametrizations exhibit several novel features of pattern formation that agree qualitatively with both key aspects of the observational record (3, 18) and recent results from cloud resolving numerical modeling (17). Despite these encouraging first results, many further tests of the approach are needed. The sensitivity of this mesoscopic parametrization to key parameters such as τ_I and the external potential, h(u⃗_j), are central issues and will be explored in the future. Other interesting future research directions include the direct simulation of the full stochastic model for parametrization developed here as well as the possibility of deriving coarse grained stochastic corrections to the mesoscopic model in a systematic fashion.

Abbreviations

CIN

convective inhibition

GCM

general circulation models

CAPE

convectively available potential energy

PAC

potential for deep convection

RCE

radiative convective equilibrium