Population Dynamics of Active and Total Ciliate Populations in Arable Soil Amended with Wheat

Abstract

Soil protozoa are characterized by their ability to produce cysts, which allows them to survive unfavorable conditions (e.g., desiccation) for extended periods. Under favorable conditions, they may rapidly excyst and begin feeding, but even under optimal conditions, a large proportion of the population may be encysted. The factors governing the dynamics of active and encysted cells in the soil are not well understood. Our objective was to determine the dynamics of active and encysted populations of ciliates during the decomposition of freshly added organic material. We monitored, in soil microcosms, the active and total populations of ciliates, their potential prey (bacteria and small protozoa), their potential competitors (amoebae, flagellates, and nematodes), and their potential predators (nematodes). We sampled with short time intervals (2 to 6 days) and generated a data set, suitable for mathematical modeling. Following the addition of fresh organic material, bacterial numbers increased more than 1,400-fold. There was a temporary increase in the number of active ciliates, followed by a rapid decline, although the size of the bacterial prey populations remained high. During this initial burst of ciliate growth, the population of cystic ciliates increased 100-fold. We suggest that internal population regulation is the major factor governing ciliate encystment and that the rate of encystment depends on ciliate density. This model provides a quantitative explanation of ciliatostasis and can explain why protozoan growth in soil is less than that in aquatic systems. Internally governed encystment may be an essential adaptation to an unpredictable environment in which individual protozoa cannot predict when the soil will dry out and will survive desiccation only if they have encysted in time.

Processes that lead to the degradation and mineralization of organic matter play a crucial role in terrestrial ecosystems. These processes are performed by soil inhabitants and governed by interactions within the soil food webs (30). Thus, to understand soil changes it is necessary to understand the nature of the population interactions. Protozoa occupy a critical niche in soil food webs, as they are direct predators of bacteria and fungi (16, 17, 23) and food sources for nematodes (19, 38), astigmatic mites (41), and earthworms (29, 33).

Soil is a heterogeneous environment in both time and space, and microbial and microfaunal activity usually is concentrated at localized sites on and around organic residues. The decomposer communities undergo a succession as these organic residues are degraded (26, 35). When fresh organic material enters the soil, microbial activity and production are greatly stimulated (7, 35). Due to their ubiquitous occurrence and short generation times, protozoan populations track changes in bacterial populations with minimal delays (17, 35).

The protozoa are an extremely diverse group, both taxonomically and ecologically (20, 32). Four types of protozoa occur commonly in soil, namely, heterotrophic flagellates, ciliates, naked amoebae, and testate amoebae (17). In agricultural soils heterotrophic flagellates and naked amoebae are by far the most abundant protozoa, with ciliates and testate amoebae occurring in lower numbers. A common feature of soil protozoa is their ability to produce cysts (17) that allow the organisms to survive unfavorable conditions (e.g., low soil moisture) for many years. However, even under conditions suitable for growth, a large proportion of the population may be encysted, a phenomenon that has been termed ciliatostasis (23).

Factors regulating ex- and encystment of protozoa in the soil are not well understood (17), and due to methodological difficulties, there is little knowledge about the dynamics of active and encysted populations in soil. The most-probable-number (MPN) method, which is commonly used to enumerate heterotrophic flagellates and naked amoebae (12, 34), gives an estimate of total numbers but does not provide any information about the number of active and encysted individuals (17, 23). The so-called hydrochloric acid method (10) has repeatedly been proven inefficient (4, 6, 17). Hence, there are no available methods to make direct estimates of the number of active flagellates and amoebae in soil.

In contrast, the number of active ciliates can be estimated by direct microscopic examination of diluted soil suspensions (24, 28). The standard version of the MPN method (12, 34) is not suitable for estimating ciliate abundance (3; H. B. Frederiksen, F. Ekelund, and R. Rønn, unpublished data), but we have found that a modification of the method provides reliable estimates of total (active and encysted) ciliates (H. B. Frederiksen et al., unpublished). Thus, ciliates can be used as model organisms to study the dynamics of active and encysted protozoa in soil. The most-abundant soil ciliates also resemble amoebae and flagellates in having short generation times and in their ability to increase rapidly in number in response to increased bacterial production (39).

Our objective in this study was to determine the dynamics of active and encysted protozoa in soil enriched with decomposing organic material. We used ciliates as model organisms because there are methods available for enumeration of active ciliates and of total (active and encysted) ciliates. Using soil microcosms, we tested the hypothesis that ciliate excystment and growth are stimulated upon addition of fresh organic material. By mathematical modeling, we gained evidence for the hypothesis that encystment is governed by density dependence rather than by food depletion, as we sampled with short time intervals in order to obtain a data set with sufficient detail to allow modeling of the dynamics of active and encysted cells.

MATERIALS AND METHODS

Microcosm setup and sampling.

Spring wheat (cv. Dragon) was grown for 9 weeks, and the shoots were harvested, oven dried (24 h, 60°C), and ground (2-mm mesh size). Soil (clay, 16%; silt, 32%; sand, 50%) collected at the experimental fields in Tåstrup, Denmark, at the Royal Veterinary and Agricultural University Farm, was sieved (2 mm), air dried, and mixed 3:1 with quartz sand (particle diameter, 0.3 to 1 mm).

Microcosms were prepared in 150-ml cylindrical glass containers (4 cm in diameter). Each microcosm contained 15 g of soil-sand mixture, 0.5 g of dried wheat material, and 5.2 ml of distilled water. Additional control microcosms were prepared the same way, without wheat. The microcosms were kept in three sealed buckets (10 liters) with wet filter paper at the bottom. Every second day the atmospheric air in the buckets was renewed, and the filter papers were rewetted. Incubation took place at 15°C in darkness. Three replicate microcosms (one from each bucket) were destructively sampled at each sampling. We sampled the amended microcosms (n = 3) at day 0 (immediately after preparation) and at days 2, 4, 6, 8, 10, 12, 15, 18, and 24. The unamended microcosms (n = 3) were sampled at days 0, 6, and 24.

Bacterial CFU.

From each sampled microcosm a 1.0-g sample was transferred to a Waring blender (38BL41; Waring Products Division, New Hartford, Conn.), mixed with 100 ml of modified Neff's amoebae saline (31), and blended for 1 min at speed 2. From the homogenized suspension (10⁻²), a successive 10-fold dilution series was prepared (10⁻⁴ to 10⁻⁸). From each suspension 0.1 ml was spread on three replicate TSA plates, prepared from 15 g of agar (Merck Eurolab, Albertslund, Denmark) and 0.3 g of tryptic soy broth (Difco, Detroit, Mich.) suspended in 1 liter of modified Neff's amoebae saline (31). Bacterial CFU were counted after 1 and 3 weeks of incubation at 15°C, and an average for each microcosm was calculated.

Heterotrophic flagellates and naked amoebae.

The numbers of heterotrophic flagellates and naked amoebae were estimated by the MPN method (12) as modified by Rønn et al. (34). For each microcosm, we prepared a 96-well sterile microtiter plate (catalog no. 3598; Costar, Corning, N.Y.) with 100 μl of sterile TSB solution (0.3 g liter⁻¹; Difco) in each well. Subsequently we added 50 μl of the homogenized suspension prepared for plate counts (10⁻² suspension) to the eight wells in the first column and made threefold dilutions by successively transferring 50 μl to the next 11 columns in the plate. We used the 10⁻² suspension on days 0 and 2 and the 10⁻³ suspension on the remaining sampling dates. Microtiter plates were incubated at 10°C in the dark and were inspected for the presence of naked amoebae and heterotrophic flagellates after 1 and 3 weeks using a microscope with an inverted lens at a magnification of ×300.

Total ciliate abundance estimated by MPN method.

The total number of ciliates (active plus encysted) was estimated by a modified MPN method. For each microcosm, we prepared six successive 10-fold dilutions (10⁻³ to 10⁻⁸) in sterile modified Neff's amoebae saline (31) from the original homogenized suspension (10⁻²). We transferred 5 ml of diluted suspension to a well of a six-well cluster plate (catalog no. 3506; Costar). Dilutions of 10⁻² to 10⁻⁷ were used on days 0, 2, 4, and 6, and dilutions of 10⁻³ to 10⁻⁸ were used on days 10, 18, and 24. A sterile wheat grain was added to each well as the food source. The plates were incubated at 15°C in the dark; the wells were inspected for ciliates using an inverted microscope at a magnification of ×40 after 1 and 3 weeks.

Active ciliates.

The number of active ciliates was estimated by a direct counting technique (1, 24, 28). Subsamples of 0.1 g were weighed into 5-ml test tubes and suspended in 1 ml of soil extract (22), and the soil slurries were inspected in a counting chamber (Sedgewick-Rafter cell) at a magnification of ×40 with a microscope. The washing and counting procedure was repeated three times for each subsample, ensuring that all ciliates were extracted from the sample. Three subsamples were examined from each microcosm, and the average number per gram in each microcosm was then calculated.

Nematodes.

Nematodes from a 5-g sample from each microcosm were extracted by a modified Baerman method for 24 h (42) and counted using a dissection microscope (14).

Statistics.

All counts were log transformed, and the effect of time on population development was analyzed with a one-way analysis of variance. Significant differences between sampling days were detected by Tukey's multiple comparison test. SigmaStat (version 2.03 for Windows; SPSS Inc., Chicago, Ill.) was used for these analyses.

Mathematical considerations. (i) Model assumptions.

An aquatic population of ciliates (C) without an encysted stage can simply be described by the differential equation dC/dt = rC − mC, where r is the cell reproduction rate, and m is the rate of mortality, usually caused by grazing. In an experimental setup where no grazers are present and mortality can be considered zero, the population reproduction rate and the reproduction rate of the individual cell will be identical, and the value can simply be determined as r = (dC/dt)/C. If the bacterial density is sufficiently high, r will assume a constant maximum value determined by the physiological capabilities of the ciliate cell (21, 39).

In soil, however, the situation is more complex, because the total ciliate population (C_T) consists of subpopulations of actively dividing cells (C_A) and inactive encysted cells (C_C) and because we also have to consider encystment and excystment. In the following paragraphs, we derive a differential equation that describes the growth dynamics of this more complex system and solve this equation. Our model is based on two fundamental assumptions: (i) the total population can be expressed as the sum of the active and encysted cells:

(1)

and (ii) the change in the total population can be expressed as the difference between the production (r_AC_A) and the mortality (mC_T) of the population:

(2)

as only the actively dividing cells contribute to the production. We use r_A to denote the reproduction rate of an individual actively dividing cell. In equation 2, we need not be concerned about encystment and excystment as the total population C_T neither gains nor loses cells by these processes. Equations 1 and 2 will be valid for any population that consists of an active and a resting (encysted) subpopulation. Until now, we have made no assumptions about the nature of the rates r_A and m.

In order to simplify the problem, we now make three further assumptions, which are not universal, but which are useful approximations in a system similar to the one we describe. (i) We assume zero mortality (m = 0) during the experiment. This assumption is supported by our empirical data (Fig. 1c), which suggest that no ciliate death takes place during the experiment, and by the absence of significant amounts of potential ciliate predators in our systems. (ii) We further assume that all excystment takes place in an initial burst. Even if this is not absolutely correct—i.e., some excystment takes place during the experiment—it will have only a small impact since the exponential growth of the previously excysted cells will far exceed the growth of newly excysted cells. Furthermore, our empirical data (Fig. 1c) support the assumption that the excystment rate is low after the initial burst, since, after day 2, the absolute increase in encysted cells is higher than the increase in active cells, even during the period of maximal exponential growth of the active population. In the absence of death, equation 2 simply takes the form

(3)

and the change in the encysted population during the experiment can simply be expressed as

(4)

where k_en denotes the rate at which active cells are converted into cysts. (iii) Our third additional assumption is that the bacterial density remains so high throughout the experiment that the reproduction rate of the individual active ciliate cell (r_A) is not decreased due to lack of food; this assumption is clearly justified by our results (Fig. 1a). We claim that r_A in equations 2 and 3 has the same constant maximum value only determined by the intrinsic capabilities of the cell machinery as it would have in some hypothetical mutant without the ability to form cysts. It appears counterintuitive that the encystment does not have any impact on the reproduction rate. We, however, argue that the situation can be compared to a strain of laboratory rats living under optimal conditions. Encystment can be compared to an experimental situation in which a fraction of the animals are removed per unit of time, sterilized, and then put back. This action will affect the absolute population growth but not the fertility of the fertile part of the population, which is equivalent to our r_A. In a population where encystment occurs, the population growth rate, r_T = (dC_T/dt)/C_T, will always be smaller than r_A; e.g., if only a very small active subpopulation is present, this subpopulation may have a very high growth rate even though r_T may be close to zero.

FIG. 1.

Bacterial CFU (a), protozoa (naked amoebae and heterotrophic flagellates) (b), total ciliates (circles) and active ciliates (trian-gles) (c), and nematodes (d) in microcosms amended with wheat straw material (filled symbols) and in unamended control systems (open symbols). Points represent the average value from three independent destructively sampled microcosms; error bars represent 2 standard errors. Points not sharing any similar letters differ significantly for the particular treatment (P < 0.05 [Tukey's multiple comparison]).

Finally, in the absence of external factors, e.g., water stress and prey depletion, that may trigger encystment, we hypothesize that the rate of encystation is density dependent. The simplest solution to this problem is to assume a linear relationship:

(5)

where a and b are constants. Here b is a measure of the encystment at very low cell densities and a is a measure of the degree of density dependence.

(ii) The differential equation.

By differentiation of equation 1 we get dC_T/dt = dC_A/dt + dC_C/dt or dC_A/dt = dC_T/dt − dC_C/dt. Now by substituting from equations 3 and 4, we get

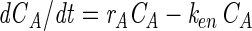(6)

Now differentiation of equation 3 yields d²C_T/dt² = r_A(dC_A/dt) and, by substituting from equation 6, d²C_T/dt² = r_A(r_AC_A − k_enC_A); equation 3, d²C_T/dt² = (r_A − k_en)dC_T/dt; and equation 5

(7)

This second-order differential equation describes the development in the total ciliate population.

(iii) Solving the differential equation.

By integration of equation 7 we get

where K is an arbitrary constant. By inserting C_T = 0, we deduce that K must be 0, since dC_T/dt = 0 when C_T = 0; hence,

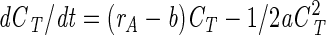(8)

Since growth cannot continue forever, dC_T/dt → 0 for t → ∞; hence, we get the following from equation 8:

(9)

where C_max is the total ciliate number at infinite time (the horizontal asymptote to the growth curve). Substituting from equation 9 into equation 8 yields

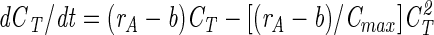(10)

which can be solved directly as follows: C_T/(C_T − C_max) = e^K exp[(r_A − b)t], where K is an arbitrary constant. By insertion of t = 0, we get e^K = C₀/(C₀ − C_max), where C₀ denotes the number of organisms at time zero; hence, we get C_T/(C_T − C_max) = C₀/(C₀ − C_max) exp[(r_A − b)t], or the following:

(11)

which describes the development in the total ciliate population.

Equation 11 is formally identical to the solution of the logistic equation, but the premises are quite different, and the constants on the right-hand side have other meanings.

By inserting equation 3, dC_T/dt = r_AC_A, in equation 10 we get the following:

(12)

This equation describes the relationship between the total and the active part of the population, where all the factors can be assumed to be constant. We do not claim that equation 12 describes a general relationship between active and encysted cells, and it is valid only when systems similar to our system are described.

Finally, by dividing both sides of equation 10 by C_T, we get a formula for the relationship between the growth rate of the total population, r_T = [dC_T/dt]/C_T, and r_A: r_T = (r_A − b) − [(r_A − b)/C_max]C_T. From this we derive that during the whole experiment r_T is less than r_A and at the start of the experiment when C_T is small relative to C_max, r_T is equal to r_A − b.

RESULTS

Bacterial CFU.

The number of bacterial CFU per gram of dry soil increased from 10⁷ at day 0 to 1.4 × 10⁹ at day 2, after which the number of CFU decreased to 4.6 × 10⁸ at day 10. CFU then remained relatively constant (∼8 × 10⁹ to 9 × 10⁹ CFU g of dry soil⁻¹). In the unamended microcosms CFU remained constant at about 1 × 10⁷ to 2 × 10⁷ CFU g of dry soil⁻¹ during the incubation period (Fig. 1a).

Heterotrophic flagellates and naked amoebae.

The number of heterotrophic flagellates and naked amoebae (estimated by an MPN method) increased exponentially from 5 × 10⁴ organisms g of dry soil⁻¹ on day 0 to 3 × 10⁶ organisms g of dry soil⁻¹ at day 6. By day 8 the population had decreased to about 10⁶ organisms g of dry soil⁻¹. Throughout the rest of the experiment, the population remained at about this level. In the unamended systems the heterotrophic flagellates and naked amoebae remained at about 5 × 10⁴ organisms g of dry soil⁻¹ for the entire experiment (Fig. 1b).

Total ciliate abundance estimated by MPN method.

The total ciliate population initially decreased from 300 to 100 organisms g of dry soil⁻¹ and then increased exponentially to 8,000 organisms g of dry soil⁻¹ at day 10, after which the population remained at a relatively constant level of about 10⁴ organisms g of dry soil⁻¹. In the unamended systems, the total ciliate number remained between 150 and 250 organisms g of dry soil⁻¹ (Fig. 1c).

Active ciliates.

Virtually no active ciliates were observed by the direct counting procedure at the beginning of the experiment, but active ciliates increased rapidly to a maximum number of 850 organisms g of dry soil⁻¹ at day 8. They subsequently decreased to 17 organisms g of dry soil⁻¹ at day 25. Active ciliates in the unamended systems were below the detection level of about 3 organisms g of dry soil⁻¹ throughout the experiment (Fig. 1c).

Nematodes.

The number of nematodes increased from about 1 to about 30 organisms g of dry soil⁻¹ in the amended systems, but they remained below 5 organisms g of dry soil⁻¹ in the unamended systems (Fig. 1d).

Statistics.

In the amended systems, time had a highly significant effect (P < 0.001 [one-way analysis of variance on log-transformed data]) on the number of bacterial CFU, total numbers of naked amoebae and heterotrophic flagellates, total (obtained by an MPN method) and active (obtained by direct counting) numbers of ciliates, and number of nematodes. There were significantly more nematodes in the unamended treatments on day 24 than on day 6 (P < 0.005) but no significant effect of time in the numbers of bacterial CFU and protozoa.

DISCUSSION

The soil community responded quickly to the addition of the dead wheat material. The changes in population sizes of the different organism groups probably reflected differences in substrate demand, initial population size, and turnover rates.

Ciliate prey and predators.

The rapid 1,400-fold increase in bacterial abundance from day 0 to day 2 was followed by a decline until day 10. We attribute this decline to the grazing by increasing populations of heterotrophic flagellates, naked amoebae, and ciliates (Fig. 1). The numbers of flagellates and amoebae peaked between days 6 and 8, and the number of active ciliates declined after day 10. Hence, the increase in bacterial number after day 10 is probably due to the lower grazing rate. Still, the bacterial population remained high, and depletion of prey is not the reason for the decline of the protozoa. The number of bacteria in the microcosms should be sufficient to ensure maximal protozoan growth. Thus, we hypothesize that internal feedback regulation is a key to understanding protozoan dynamics in soil.

The only potential predators on ciliates in our systems would be predatory nematodes, but the total number of nematodes in the microcosms (Fig. 1d) remained low throughout the experiment. The ln of the number of nematodes (ln N) showed a clear linear relationship with time (t): ln N = −1.7945 + 0.1291 × t (r² = 0.8814).

Thus, the nematode population grew exponentially throughout the experiment with an intrinsic growth rate, r = 0.1291, which corresponds to a doubling time of 130 h, which is five to six times longer than that of the protozoa. Generally, populations of nematodes around decomposing organic material increase more slowly than protozoa unless the nematodes can immigrate from the surrounding soil (25). Since insufficient soil volume was available in the microcosms, the nematodes never became abundant enough to significantly reduce the ciliate population.

Methods for enumeration of ciliates.

We monitored active ciliates by direct counting and the total ciliate population by an MPN method concomitantly during the initial decomposition of freshly added organic material. Total (MPN) and active ciliate numbers from the same soil samples have been compared previously, but only for single dates and not in a time series. Berthold and Palzenberger (4) reported very low numbers of active ciliates (0.06 to 5.5%). We observed that 10 to 25% of the population was active during the burst (the model predicts about 17%). This difference probably reflects the fact that the earlier results were obtained in field studies where the soil sampled included both active and less-active microsites, whereas our results were obtained in microcosms with high microbial activity and ample soil moisture.

Ciliate population dynamics in the soil microcosms.

We fitted data on total and active ciliates (Fig. 1c) to the model equations 11 and 12 by simple nonlinear regression (Fig. 2 and 3). The fits were rather good, as we obtained r² values of 0.988 and 0.843 for equations 11 and 12, respectively. In this manner we obtained a C_max of 12,900 and a C₀ of 37. This exercise also generated a value for r_T = (r_A − b) of 0.6238 day⁻¹, the initial intrinsic growth rate of the total ciliate population, equivalent to an initial doubling time of 26.7 h. Likewise, we find that (r_A − b)/r_A is 0.174 and (r_A − b)/(r_AC_max) is 1.29 × 10⁻⁵.

FIG. 2.

Data for total number of ciliates (MPN) from microcosms amended with wheat straw material (points) fitted to a theoretically derived equation (solid line): C_T = [C₀C_max exp(r_A − b)t]/[C_max − C₀ + C₀ exp(r_A − b)t] and r² = 0.9884. For further details, see the text.

FIG. 3.

Data for direct counts of active versus total MPN-derived ciliate numbers (points) fitted to a theoretically derived equation (solid line): C_A = [(r_A − b)/r]C_T − [(r_A − b)/(r_AC_max)]C_T² and r² = 0.8426. For further details, see the text.

From these values we deduce that at the very beginning of the experiment C_A is proportional to C_T since the coefficient to the second-order term in equation 12, (r_A − b)/(r_AC_max), is very small. Finally by dividing the value obtained for r_A − b with the value of (r_A − b)/r_A, we get an estimate of the intrinsic growth rate of the single actively dividing cell: r_A = 3.585 day⁻¹, corresponding to a doubling time of 4.6 h.

The low doubling time of the single actively dividing cell of 4.6 h seems incongruent with the 26.7-h doubling time of the entire population. Taylor (39), however, observed doubling times for ciliates in liquid culture of about 4 h, and the common soil ciliate Colpoda steinii had a doubling time of approximately 5 h when grown at 15°C (value derived from reference 11) during a period of growth when cyst formation was negligible. The parameter b in equation 5 can be interpreted as the initial encystation rate; by subtracting the values obtained for r_A and r_A − b, we find a value for b of 2.757 day⁻¹ and that b/r_A is 0.7690. Thus, during the period of vigorous growth about 75% of the ciliate production is converted to cysts.

Active ciliates in soil.

We do not generally detect significant numbers of active ciliates in arable soil (5; H. B. Frederiksen, unpublished data), but the total numbers may be relatively high (several hundreds per gram) (18). Although this phenomenon is probably common, it has not attracted much attention (23). We think that ciliate growth (Fig. 1c) occurs in a short, sudden burst induced by appropriate environmental conditions. The addition of water, without wheat material, did not stimulate ciliate production (Fig 1c); hence, ciliate excystment is probably triggered by some substance produced by growing bacteria, e.g., carbon dioxide or an organic bacterial waste product (2, 9, 13, 37, 40).

The factor that triggers ciliate encystment after the initial activity burst also is unknown. Decreasing soil water content has been suggested as a major factor regulating protozoan encystment in soil (17). However, it is unlikely that this effect is direct, since there is no known mechanism by which an individual protozoan could sense if the soil it inhabits is drying out. Instead, the strategy employed is probably to begin the forming of drought-resistant cysts before severe drying occurs. In the model, we have assumed that encystment is density dependent and could perhaps be triggered by a signaling substance excreted by the ciliates. This process is conceptually similar to quorum sensing, which has been documented in many bacteria (36) and in yeast (27). A quorum sensing mechanism has also been suggested to be involved in the regulation of cell survival of the ciliate Tetrahymena thermophila (8). The phenomenon to describe the fact that the number of active ciliates is lower than expected has been termed ciliatostasis by Foissner (23). Our model offers a quantitative description of this phenomenon.

Population dynamics of naked amoebae and heterotrophic flagellates.

The population dynamics of naked amoebae and heterotrophic flagellates in our microcosms cannot be modeled in the same manner as the ciliates, because we do not have access to data on the active population and we cannot assume zero mortality, as death occurs between days 6 and 8 (Fig. 1b). Death kinetics are generally much more difficult to model than growth, as the underlying mechanisms are not as well defined. Linear regression of the first four points in Fig. 1b yields the following: ln P = 0.7021 t + 10.777 (r² = 0.9992), where P is protozoa g of dry soil⁻¹ and t is time (in days). Thus, there is exponential growth between days 0 and 6 with an intrinsic growth rate of 0.7021 day⁻¹, and the doubling time is 24 h. As with the ciliates, comparison of this population's doubling time with the often-reported doubling time of about 4 to 5 h for small heterotrophic flagellates (15, 20) leads to the conclusion that about 75% of the amoebal and flagellate production is converted to cysts during the period of vigorous growth.

We do not know why the population of amoebae and flagellates declines between days 6 and 8. Depletion of the bacterial food supply is not the explanation, since the bacterial number remains high after day 6 and ciliate growth continues. Similarly, we exclude environmental deterioration, e.g., accumulation of bacterial waste products or depletion of oxygen, since ciliate population growth continues until day 10. Nematode predation also is an insufficient explanation, since nematode numbers remained very low until day 15 (Fig. 1d). We suggest that the population dynamics of the amoebae and flagellates can be best modeled by assuming a density-dependent encystment rate, as for the ciliates, combined with grazing by the ciliates and by large predatory amoebae, parameters that we did not quantify.

In conclusion, we find that even under optimal conditions, a large proportion of active ciliate cells is converted into cysts and that encystment is likely to be controlled by a density-dependent mechanism. Hence, we suggest that energetic considerations alone cannot explain bacterial protozoan interactions. Whether our model predictions can be confirmed in other soil types, under different humidity conditions, etc., needs to be tested. Furthermore, it would lend strong support to our theory if the actual chemical compound responsible for the density dependence could be identified. A preliminary step in this direction would be to examine whether a cell extract from a dense ciliate culture would have any impact on growth of ciliates or other protozoa in soil.