A percolating path to green iron

Summary

About 1.9 gigatons of steel is produced every year, emitting 8% (3.6 gigatons) of global CO₂ in the process. More than 50% of the CO₂ emissions come from a single step of steel production, known as ironmaking. Hydrogen-based direct reduction (HyDR) of iron oxide to iron has emerged as an emission-free ironmaking alternative. However, multiple physical and chemical phenomena ranging from nanometers to meters inside HyDR reactors alter the microstructure and pore networks in iron oxide pellets, in ways that resist gaseous transport of H₂/H₂O, slow reaction rates, and disrupt continuous reactor operation. Using synchrotron nano X-ray computed tomography and percolation theory, we quantify the evolution of pores in iron oxide pellets and demonstrate how nanoscale pore connectivity influences micro- and macroscale flow properties such as permeability, diffusivity, and tortuosity. Our modeling framework connects disparate scales and offers opportunities to accelerate HyDR.

Graphical abstract

Highlights

• •Mapped pore connectivity in iron oxide pellets during reduction using in situ nano-XCT
• •Developed a percolation framework linking pore connectivity to mass transport
• •Identified transitions in mass transport regimes using this framework
• •Observed significant increase in gas permeability due to improved state of pore percolation

S. Paul et al. present a study on pore network evolution during hydrogen-based reduction of iron ore pellets using in situ nano-XCT. Their work quantifies the effects of pore connectivity on gas transport properties like permeability, providing critical insights for enhancing efficiency in low-emission ironmaking.

Introduction

Steel is a pillar of modern society. With 1.89 gigatons produced in 2023,¹ steel is irreplaceable for engineering, construction, and other high-value applications. Steel production, however, accounts for 8% of global CO₂ emissions (3.6 gigatons/year).^2,3,4 For an emission-free future, the steel industry must undergo a historic transformation, shifting its $2.6 trillion infrastructure from fossil-fuel processes to zero-emissions approaches.⁵ Leading steel manufacturers are exploring nontraditional processes to reduce or remove emissions, but risk mitigation is urgently needed to reach today’s climate goals.⁶

Over half the CO₂ emissions from steel production come from one step—reducing iron ores into iron metal, ironmaking.⁷ Perfected for >2,000 years, the coal-based reduction of hematite (Fe₂O₃) to magnetite (Fe₃O₄) to wüstite (FeO) to iron (Fe) generates >3.5 molecules of CO₂ per atom of iron, including the impurity separations intrinsic to the process.⁸ Blast furnaces refined since the Industrial Revolution have scaled this chemistry, making up 71% of ironmaking’s current market share.⁹ No emission-free ironmaking processes are available today at commercial scales. Use of hydrogen instead of coal could decarbonize ironmaking, but the associated hydrogen-based direct reduction (HyDR) of iron ores has yet to progress beyond the pilot-scale plants first operated in the 1950s.¹⁰

Profitably scaling the multistep iron ore reduction reactions in HyDR to the >10-m-wide reactors presents long-standing challenges in retaining continuous operation. Active studies seek to reduce the high cost of green hydrogen for cost parity with today’s fossil-fuel alternatives.⁶ Often overlooked, however, are the immense multiscale challenges of scaling HyDR from the milligram-gram laboratory scales to the kilogram-kiloton scales relevant to reactor design. The gas-liquid exothermic chemistry in blast furnaces (T > 1,700°C) drives self-sustaining reduction chemistry, but the endothermic HyDR reactions use solid-gas chemistry at 700°C–1,100°C that relies on efficient transport of reactive gases through pores and solid species in the evolving material microstructure. The mechanisms required to describe gas transport can alter the HyDR process efficiency by orders of magnitude via subtle changes to feedstocks, making them difficult to reconcile effective reactor models.^11,12

Efficient inflow of H₂ and outflow of H₂O are required to drive HyDR’s multiscale, multistep reactions to completion. The pellets fed into reactors are 1–2 cm in size and produced by pelletization, which involves agglomeration and sintering of crushed iron ores and natural clays. As a result of pelletization, the pellets are naturally porous and have highly variable structure and composition.¹³ HyDR kinetics are often modeled as surface reactions, but the intricate micrometer scale pore networks cause gases to navigate a tortuous path to reduce each pellet. Beyond the native inherited pore structures, reduction from hematite to iron causes a 42% atomic-scale volume shrinkage as oxygen is removed from the lattice.¹⁴ The volume shrinkage during reduction chemistry causes inherited pores to grow as vast populations of new pores emerge at tens-of-nanometer sizes.^15,16,17 Diffusion of hydrogen and water vapor through the intricate nanoscale pore networks is known to compete with surface chemistry to become the rate-limiting step. These rate-limiting steps dictate the overall kinetics and set the reactor design needs (e.g., length, temperature, etc.).^17,18,19,20 Increased porosity can enhance mass transport and reactivity, but in the final reaction step causes pellets to swell or crack.^21,22,23 The swelling and mechanical effects change the intricate pore networks that alter the macroscopic reactor-bed permeability that is a crucial metric for reactor yield.^11,21

Given the complex nature of mass transport in HyDR, efficient reactors must be designed in tandem with pellet fabrication. Subtle changes to the additives (called “fluxes”) and sintering conditions used to fabricate pellets can change the pellet porosity by 5%–63%, depending on the conditions.²⁴ The tortuosity, pellet porosity, and pore characteristics are also affected by the reduction reaction and local conditions (e.g., temperature, pressure).²⁵ As pellet porosity increases from 0.27 to 0.46 during HyDR,²⁶ the permeability and diffusivity undergo drastic changes that are not well quantified. These drastic changes in permeability and diffusivity are caused by the evolution of an increasingly complex pore network during HyDR. This porous network alters the transport of gases to and from the reactive sites. At the nanoscale, the complex network of isolated and interconnected pores alters the atomic-scale diffusion rates,¹⁷ in addition to the bulk effects on tortuosity. Since HyDR is a hierarchical process, these atomistic and nanoscale phenomena that have been studied in single crystalline iron oxide^19,27 have not been integrated into prediction of gas transport typically studied for millimeter-sized samples.¹²

At large scales, the significance of interconnected pore networks on reactor performance has still not been quantified. Dating back to the 1970s, the Brunauer-Emmett-Teller (BET) method and mercury porosimetry have been used together to track changes in pore volume and surface area in mm-sized samples during reduction.^12,15,28 However, these techniques are unable to resolve pore characteristics like shape and connectivity and can be destructive in nature when used together. Hence, to visualize the pore morphology, several studies used 2D electron microscopy.^12,15,27,28 However, these studies primarily focused on HyDR kinetics and discussed pore network characteristics qualitatively. 3D micro X-ray computed tomography (XCT) was used to accurately characterize pore morphology and identify open and closed pores in iron ore sinters.²⁹ A recent study also performed micro-XCT on full 1-cm-sized pellets and were able to connect porosity to tortuosity and gas permeability.²¹ This study demonstrates the importance of interconnectedness of pore networks in defining gas-flow dynamics in HyDR. Their framework, however, is not transferable across scales. Hence, deployment of commercial scale HyDR reactors requires different methods to connect reduction and gas flow within nanoscale porosity to macroscopic reactor scales.¹¹

Percolation theory is a scale-invariant geometrical model that describes how the connectedness of a random network defines a macroscopic property that “turns on” when the network becomes fully connected, a.k.a., percolated. Convenient low-dimensional models from percolation theory have enabled widespread advances in predicting diverse phenomena, including computer network security in the internet of things,³⁰ earthquake likelihood for different fault lines,³¹ and even fracture probability for engineering materials.³² Percolation theory upscales the connectivity of a network through scale-invariant critical exponents. In geophysics, percolation theory is often used to develop analytical expressions of transport properties following the governing equations relevant to a given scale. In fluid dynamics, percolation theory is used to predict surface reaction rates in porous reactive flow systems analogous to HyDR.³³ To date, percolation theory has not been used to reconcile the porosity and gas flow physics required to achieve scalable HyDR reactors.

In this work, we develop a computationally efficient percolation theory model to compute key fluid-dynamics parameters by upscaling nanoscale porosity caused by reduction. We use operando nano X-ray computed tomography (nano-XCT) to quantify how pore networks evolve during HyDR with unprecedented 3D resolution in an internal region of a commercial iron ore pellet. We then define a “percolation threshold” that describes a 50× increase in gas permeability due to pore-network connectedness. We show how the percolation threshold signifies a change in the regime of flow physics required to describe mass transport. Using analytical fluid-dynamics models, we predict permeability, diffusivity, and tortuosity to compare our percolation-based modeling approach to conventional methods. Our findings demonstrate the significant macroscopic changes resulting from the subtle shift in network connectivity at the nanoscale. We conclude by discussing how our modeling framework offers a solution to reconcile interlinked HyDR phenomena that occur at vastly different scales. Future implementations of this model will offer opportunities to overcome key challenges to realize emission-free ironmaking.

Results and discussion

Measuring pore evolution in iron ore pellets

To accurately define the attributes of our pore network, we began our study by performing in situ nano-XCT to resolve how the internal 3D structure of pores evolve in a hematite pellet lamella as it reacts in a bed of H₂ at 700°C. We measure at three representative times—100 s, 200 s, and 600 s—as the initial chemistry progresses then halts. Our nano-XCT scan probes a selected 68 × 60 × 27 μm³ volume inside a conical specimen of 300 μm diameter and 1 mm height, extracted from a commercial direct reduction (DR) pellet. The internal region of interest (ROI) enables our scans to achieve a 30 × 30 × 30 nm³ voxel size of a representative region inside the pellet—i.e., not describing boundary condition effects of the gas transport.

The reconstructed 3D images are segmented into regions representing material and pores, as shown for 100 s in Figure 1A. Experimental and segmentation details are included in methods. The temporal progression of pores is shown for 2D slices extracted from the 3D measured volumes in Figure 1B. Those slices reveal that as the initial pores expand, another growing population of isolated pores emerge in the pellet as the reduction progresses. We convert the volume of pores vs. total sample into measurements of the porosity fraction (p), as plotted in Figure 1C. The p vs. time plot shows an increase in p from 0.32 to 0.55 with progress of HyDR chemistry. We observe a 40% increase in p as the variance in p decreases by 78%, as calculated based on 2D porosity distribution over the reaction time.

Figure 1.

Pore morphology and evolution with reduction

(A) Reconstructed volumes from nano-XCT scans of iron oxide pellets after 100 s of reduction (material, gray; pores, brown).

(B) Pore (white) evolution as observed in 2D image slices for 100 s, 200 s, and 600 s.

(C) Porosity fraction from the reconstructed nano-XCT and 2D porosity slices.

(D) Heterogeneous pore networks in iron oxide represented as throats and pores.

Using the pore-modeling framework OpenPNM,³⁴ we sort all pores into two distributions: connected and isolated, as shown in Figure 1D. We observe a population of emergent isolated pores with mean diameter of 297.5 ± 90.1 nm that are orders of magnitude smaller than the typical size of a connected cluster of pores (∼10 μm). These results are consistent with a dual-porosity system in which there are two important distributions of pores, each with their own distinct morphological properties.³⁵ Our nano-XCT measurements of the pore network reveal a heterogeneous structure similar to those encountered in geological datasets.^36,37 Pore-scale heterogeneity often leads to anisotropy in effective parameters like permeability, diffusivity, and tortuosity at the pellet scale, as outlined in supplemental note S2. This is because heterogeneities in scale and connectedness of the pores determine flow pathways for the gases and influence mass transport necessary to drive HyDR chemistry to completion. At the scale of percolation theory, the connectedness of the network is invariant to flow direction; however, interpretation of flow properties has a directional component. Therefore, our percolation theory model is complete as constructed; however, its extension to gas-flow dynamics was only considered along one direction. As this work focuses on developing the modeling framework for percolation theory to address hierarchical pore evolution in HyDR pellets, we leave consideration of the gas flow anisotropy arising from a percolated network to a future study.

Defining a percolation model for HyDR permeability

Using the segmented pore networks defined by our experiments, we show how percolation theory can model nanoscale porosity that alters bulk transport as the iron oxide pellet reduces. Our plots of the histogram of cluster sizes present in our nano-XCT sampled volumes (Figure 2B) reveal a single fully connectled cluster at each time step that makes up 90% of the sample porosity (see Figure 1C above). The presence of the fully connected cluster indicates that the pore network measured by nano-XCT is already percolated after 100 s of reaction within our measured ROI. This internal measured ROI does not include the surface of the pellet that defines the boundary condition relevant to mass transport in HyDR. We therefore upscale our analysis to explore how the intricate pore networks in unreacted pellets translate over the entire network.

Figure 2.

Determining state of percolation

(A) Micro-XCT reconstructed volume of an entire direct reduction pellet along with a 2D slice and extracted pore network model (for full pellet) computed using OpenPNM.

(B) Cluster size distribution of pores extracted from the nano-XCT volumes. Cluster size is computed as the number of pores constituting a particular cluster and is dimensionless.

(C) Tracking reduction in porosity fraction using the erosion operator to simulate nonpercolated pore networks from percolated pore networks. Orange network images display the porosity fraction measured at 100 s (p = 0.32), the network after 32 isotropic erosion steps for p = p_c, and finally the subpercolated network at p = 0.09. Data at p_c are represented as mean ± SD.

We use micro-XCT to measure the initial inherited pore network describing the starting connectedness of the full pellet structure. The pore network geometries of the full pellet include the boundary conditions for mass transport at the 11 μm pixel size, scanned over the 1-cm-diameter pellet, as shown in Figure 2A. The largest connected cluster, plotted in pink in Figure 2A, is located in the core of the pellet and does not connect to the outermost surface of pellet for pores >11 μm. As reduction progresses, the core network is expected to increase in connectivity and turn on flow once the largest connected network reaches the surface.

We thus computationally upscale the trends in connectedness of the pore network observed in nano-XCT to include the boundary conditions relevant to the full pellet. We simulate the transition from a nonpercolated to a percolated pore network using an erosion-dilation algorithm, as has been demonstrated for percolation models elsewhere.³⁸ Erosion and dilation are morphological operations used in image processing that recursively shrink (erode) or expand (dilate) image features computationally. In our work, we use only the erode operator to simulate the structure of the pore network at earlier porosity levels. Full details of our erosion and dilation methods are described in the methods section under “erosion and dilation algorithm.” In this work, we evaluate the significant statistics of pore connectivity and combine it with scale-dependent gas flow dynamics to describe transport phenomena at the nanoscale. The model proposed in this work can be combined with appropriate gas-flow dynamics to describe transport at larger length scales. We identify critical percolation parameters below and leave the evaluation of critical exponents for a future study.

As we erode the largest connected cluster from our 100 s measurement, the cluster size reduces until it forms disconnected segments. We interpret the porosity fraction, p, necessary to form the smallest fully connected cluster in our sampled ROI as the percolation threshold, p_c. Figure 2C includes representative images of the largest cluster measured by nano-XCT at 100 s (right), eroded to p = p_c (middle), and eroded beyond p_c (left). Figure 2C shows the pore network at p = p_c and p < p_c. We note that the value of p_c in percolation theory corresponds to the lowest connectedness required to achieve a nonzero probability that a connected cluster is present. To add statistics to our p_c value, we thus compute p_c starting from each of the three measured datasets in this work to define our uncertainty in the value. We quantify the percolation threshold as 0.1 ± 0.007 and observe that it is significantly lower than the porosity fraction of 0.32 observed at 100 s.

Nano- to microscale permeability and its relationship to percolation

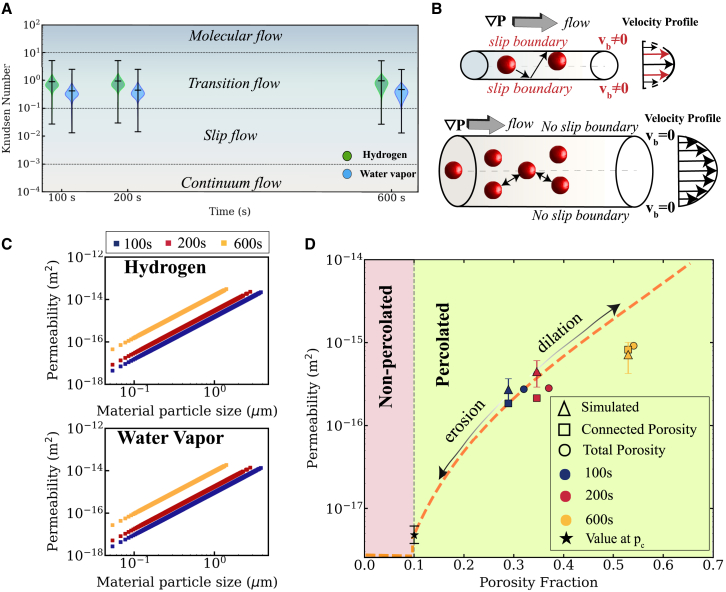
In HyDR, gas permeability takes the form of macroscopic gas flow, but at the smallest scales it promotes reduction chemistry by enabling hydrogen to reach reaction sites and water vapor to move away from reaction sites. These different scales of permeability have different governing equations and thus must be treated differently. To identify the appropriate expression to evaluate permeability in our model, we thus begin by exploring which governing flow physics define our nano-XCT networks. Fluid dynamics describes the physics required to define the flow of a fluid through a channel using the Knudsen number (K_n).³⁹ The macroscopic flow of the fluid (a.k.a. the “flow streams”) are defined at the largest scales as continuum flow—in which the behavior of the fluid does not depend on interactions with the pipe boundary. In HyDR reactors, the continuum scale is typically appropriate to describe the macroscopic flow of gas through the entire 50-m-wide reactor vessel.⁴⁰ By contrast, as the channel size decreases, for K_n > 10⁻³ the boundary plays a nonnegligible role in determining the flow physics, requiring that the governing flow equations include contributions from fluid-boundary interactions. In HyDR reactors, the gas-boundary effects in channels at widths of ∼0.1–100 μm, inside or between pellets, and the mixing between H₂ and H₂O are most important to drive chemistry by shifting the local equilibrium constant.⁴¹ As the size of the flow channels we measure in this work (∼100 nm) becomes commensurate with the mean free path of the fluid molecules, even the molecular structure of the fluid particles becomes critical to define the flow stream velocities. Using kinetic theory equations,⁴² we estimate that at 700°C, 1 atm, the mean free path of the gas molecules is 350–400 nm. At these K_n > 10 values, the molecular flow regime is required to define the much more limited flows accessible to nanoscale pores like those seen inside HyDR’s reacting pellets. We note that in the molecular regime of HyDR gas transport, atomic diffusion of gas atoms, like O and H, through solid media can compete with fluid dynamics for the dominant transport behaviors.²⁶

In Figure 3A, we evaluate the K_n for both hydrogen and water vapor as the ratio of the mean free path of gas molecules to pore diameter at 700°C, 1 atm. We find K_n ranging between 0.01 and 5 due to the wide size distribution of the pores. Further analysis of pore size distribution (see Figure S4) reveals that ∼70% of pores (0.3–10 μm) result in K_n ranging from 0.01 to 1.0 and are therefore governed by the slip and transition flow regimes. These regimes define that both gas-gas and gas-solid interactions control the velocity, momentum, and other properties of the flow field at the pore scale. At the 10-μm scale relevant to the percolated cluster, we find that the interactions most important to defining the flow-field properties follow the equations governing the slip-flow regime. Since our pores correspond to K_n values at the boundary between slip and transition flow regimes, a complete model describing gas flow through a pellet should account for the permeabilities representative of both regimes. To establish our percolation theory framework, however, we construct our model using only slip flow to describe the percolated system as those contributions are valid at larger scales—especially after percolation. The gas slip at the iron oxide interface imparts a higher overall velocity to the gas molecules that results in higher permeability when compared with continuous flow of a liquid through the same geometry. Figure 3B illustrates the slip vs. no slip effects⁴³ experienced by gas molecules flowing through cylindrical channels of pores.

Figure 3.

Evaluating flow properties

(A) Violin plot displays the distribution of Knudsen number for hydrogen (green) and water vapor (blue) for each time point. The width of the violin indicates data density; central line shows mean, and the extrema lines represent minimum and maximum values.

(B) Slip and no-slip effects from the perspective of gas collisions.

(C) Variation in permeability of hydrogen and water vapor with iron oxide particles that constitute the pellets.

(D) Permeability evaluation to capture the effect of pore connectivity. At p_c, mean permeability is shown with corresponding maximum and minimum values, while simulated permeability values are shown as mean ± SD.

We apply the Klinkenberg factor to account for slip effects beyond continuum flow to predict gas permeability in our measured nano-XCT pore volumes. We include the full details of our theoretical expressions and computations of permeability in supplemental note S3. We compute gas permeability from Darcy’s Law and the Carman-Kozeny equation. These equations depend on computable parameters including the gas mean free path, the porosity of the solid material, and the size of the subpellet particles of the material— similar to how grains of sand might make up a porous rock. We quantify the material particle sizes using an OpenPNM segmentation method that is similar to the one we used above for our pore-size measurements.

Figure 3C shows the wide range of gas permeability values (10⁻¹⁸ to 10⁻¹⁵ m²) through the iron oxide pellet for hydrogen and water vapor, plotted as a function of the subpellet particle size. We validate the gas permeability values derived in this study with a Stokes flow simulation through the pore network extracted from the nano-XCTs. The simulated permeability values are in the same order of magnitude as the values derived previously in this study and are reported in Figure 3D under the label “simulated”. More details on the simulation performed can be found in supplemental note S3.

We observe that as the subpellet particle size decreases, porosity increases. From a packing density consideration, this is counterintuitive as one might expect the porosity to decrease as smaller particles pack tighter together. By contrast, in this system, the chemical reactions cause material loss over the course of the experiment. As this implies that mass is not conserved, our resulting particle size reduction gives rise to a porosity increase. Permeability values are directly correlated with the size of particles and pellet porosity. As such, the increase in permeability we observe over the duration of our reduction implies that the increase in porosity plays a stronger role in gas transport than the subpellet particle size.

Given the scales of porosity in this work, we now explore the role of molecular size in determining the slip effects of gas permeability. The Klinkenberg factor accounts for the difference in slip effect based on the gas molecule’s mean free path, which depends on the molecular weight and radius of the gas species. The different permeabilities as calculated for hydrogen and water vapor are shown in Figure 3C. We observe that hydrogen has ∼1.6× higher permeability than water vapor under the same thermodynamic conditions. The higher permeability of hydrogen is because of its smaller molecular size and lower molecular weight, which imparts ∼3× greater mobility compared to water vapor.

Permeability values predicted in this work (10⁻¹⁵ to 10⁻¹⁸ m²) overlap with the range of permeability values reported in literature (10⁻¹⁸ to 10⁻²² m²) for industrial pellets, thereby validating our approach. By combining 4D nano-XCT and percolation theory, we account for nanoscale pore connectivity, which is a critical factor often oversimplified in conventional models. Our consideration of slip effects in permeability calculations accounts for important gas-solid interactions at the pore boundary relevant to HyDR and is, therefore, more accurate than classical Carman-Kozeny permeability models. Overall, our permeability analysis integrates multiscale insights and addresses the challenge of connecting nanoscale porosity to macroscale flow.

We note that our nano-XCT analysis is limited to the imaged ROI and does not capture the role of the boundary pores in determining flow properties. We quantify the boundary effects on permeability in our nano-XCT sample through a separate set of computations using the erosion algorithm. As demonstrated in the micro-XCT images of an entire iron oxide pellet, the microscale connectivity of a random network of pores is not confirmed. To replicate similar boundary conditions in our nano-XCT sample, we erode the percolated pore network until the pore network shrinks and forms nonpercolated pore networks. We calculate gas permeability during the entire span of the erosion operation to quantify the impact of pore connectivity on permeability.

Figure 3D shows how permeability is “turned on” inside the iron oxide pellet and the pellet transitions from being impermeable at p < p_c, to permeable (10⁻¹⁸ m²) at p = p_c. The permeability increases to 10⁻¹⁵ m² at p > p_c as the volume fraction of connected pores increases. Our simulated permeability values at 200 s and 600 s are higher than the values calculated from the experimental data because the simulation does not account for chemical reactions and hence does not capture the subpellet particle-size effects. In Figure 3D, we also distinguish connected and total porosity and observe that the permeability is lowered when only the connected network of pores is considered. Overall, the permeability values attest to intricacies in the pore space geometry that resists the forward progress of flowing gas. We note that our permeability analysis using the erosion algorithm is creating an artificial set of boundary conditions. Future work is required to characterize what the appropriate boundary pores are.

Influence of percolation on reactor-model inputs

To quantify the flow resistance afforded by percolation in the context of reactor-scale insights, we now evaluate how our p_c determination translates to significant changes to inputs for reactor models. These model inputs can be chosen from a wide variety of reactor design variables like gas flow rate, desired thermal efficiency, pellet characteristics, etc. These inputs will dictate reactor geometry and operating conditions for more efficient HyDR reactors. In this work, we devise a modeling framework to demonstrate how sub-micron-scale pore evolution manifests in macroscale flow properties. We now connect this to the reactor model input, tortuosity. We first identify the dominant mode of mass transport while accounting for gas dynamic effects and then use these values to compute tortuosity of the pore networks with progress of reduction. Then we compare how tortuosity and mass transport properties change at and beyond the percolation threshold.

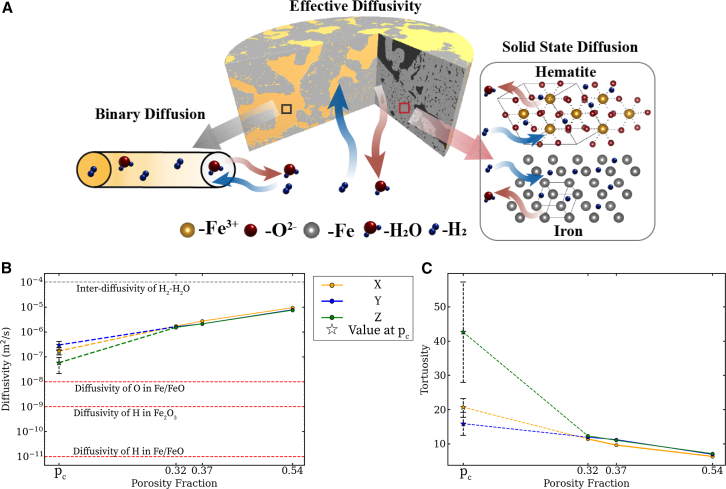
At the microscale, molecular and Knudsen diffusion are the two different processes that describe the dynamics of gases through iron oxide pellets. Nano- to microscale mass transport is governed by the diffusion of hydrogen and water vapor through cracks and the convoluted network of pores (a.k.a. “effective diffusion”), as shown in Figure 4A. Based on the K_n associated with isolated and smaller clusters of pores (100–500 nm), we consider molecular diffusion to model the diffusion of hydrogen and water vapor through the nano-XCT structures of the pellet ROIs scanned in this work. Our choice of molecular diffusion is consistent for the given reaction conditions (700°C, 1 atm) with the study by Turkdogan et al.¹²

Figure 4.

Evaluating diffusion and tortuosity

(A) Microscale-nanoscale flow mechanism.

(B) Comparing effective diffusion of gas through the pellet with interdiffusivity and solid-state diffusion.

(C) Tortuosity calculated based on effective diffusivity from t_pc to 600 s. All data are plotted with mean (marker), maximum, and minimum values.

In Figure 4B, we simulate the effective diffusivity of an equimolar mixture of hydrogen and water vapor through the pore network at 700°C using Fick’s second law at steady state. We describe the equations for our full computation of diffusivity in supplemental note S3. The effective H₂-H₂O diffusivity increases from 1.5×10⁻⁶ m²/s at 100 s to 8×10⁻⁶ m²/s at 600 s. We observe that effective gas diffusivity through the pellet is faster than solid-state diffusivity (10⁻¹¹ to 10⁻⁸ m²/s)^44,45,46 and slower than interdiffusivity of a binary gas mixture of H₂-H₂O (10⁻⁴ m²/s). For reference, we also plot the effective gas diffusivity through the pore network at the percolation threshold, which is 10× lower than the values at p > p_c. Comparing our results with solid-state diffusion of H and O in Figure 4B, we find that atomic lattices of iron or iron oxide offer higher resistance to flow of gases compared with the network of pores. Hence, a percolated network of pores offers a 5× increase in the rate of mass transport of the gases to and from reaction sites inside pellets.

A percolated network, though, may still exhibit flow resistance. The tortuous and twisted pathways required for gases to move through a percolated pore may still hinder the flow of gases—making it slower than gas diffusion through a straight channel.²¹ To quantify how the convoluted nature of the pore networks influences mass transport, we use the tortuosity factor. Geometrically, the tortuosity factor is defined as the ratio of the convoluted diffusive path length of the pore network to the straight-line path length in the direction of flow.⁴⁷ Morphological models define the tortuosity factor based on effective diffusivity, interdiffusivity of H₂-H₂O, and porosity,⁴⁸ which we use to compute the results in Figure 4C based on our nano-XCT results. We observe the tortuosity factor to decrease from 12 at p = 0.32 to 5 at p = 0.54 when computed based on our measured pore structures. The tortuosity values of the partially reduced nano-XCT sample are of the same order of magnitude as those reported recently for a reduced cm-sized pellet.²⁵ Minor deviations in the tortuosity values reported in the present and previous work arise due to different experimental conditions and sample specifications. Tortuosity of the nano-XCT sample decreases with increase in porosity, and this trend is consistent with the previous work.²⁵ The increase in porosity creates more pathways for gases to move from one side of the ROI to the other—resulting in a more direct “path of least resistance” for the gases to diffuse through. At the percolation threshold, the tortuosity factor is up to 3.5× higher, indicating that at p = p_c the pore network lacks paths of least resistance. The heterogeneous structure of pores leads to anisotropy in tortuosity and, as such, tortuosity factors in x, y, and z directions show 42%–66% variation at p_c. Thus, a well-percolated network is necessary to lower the tortuosity factor and accelerate HyDR.

Connecting the nanoscale to reactor scale

Parameters discussed in this work, like permeability, gas diffusivity, and tortuosity, impact the continuous operation of HyDR reactors. Hence, to deploy HyDR reactors at the commercial scale, it is critical to ensure that these parameters are maintained within a suitable range. As HyDR is a multiscale process, all the aforementioned parameters also have multiscale dependence. For example, although permeability describes the flow of hydrogen gas through the bed of iron ore inside reactors, permeability itself depends on micro- to nanoscale properties such as size of the ore, porosity of the ore, etc. By identifying p and p_c at the scale of nanoporosity, we lay the groundwork to develop analytical formulations of percolation properties like permeability as function of scale for ironmaking.

Our results provide quantitative evidence of the dependence of transport properties on pore connectivity. Permeability increases by 50×, diffusivity increases by 10×, and tortuosity decreases by a factor of 1.4–3.5 depending on direction of flow as the pore networks transition from p_c to p > p_c. By using percolation theory, we offer a framework to devise a scale-invariant approach to capture the pore-connectivity effects on flow properties and reconcile the hierarchical nature of HyDR process. One aspect to explore further is how change in pellet composition may alter flow properties. While in this work we do not consider composition, previous studies have demonstrated that the impurities in the pellets can alter porosity.^49,50,51 Percolation theory offers a way to quantify how pellet composition alters the porous networks and changes reactor attributes, as described in previous studies.

It is worth mentioning that this work focuses on the hydrogen-based direct reduction process of iron ore pellets, and additional reactions (including carburization) that may take place in HyDR reactors are beyond the scope of this study.^52,53 In future work, this model could be extended to explore how carburization also changes the pore characteristics and transport phenomena. Future work may also explore creating higher dimensional versions of the current model to account for the range of operating conditions relevant to HyDR. We acknowledge that upscaling our work to HyDR reactors requires energy, mass, and momentum transfer considerations as is done in traditional computational fluid dynamics (CFD) models.^54,55 We envision the present model acting as an input to reactor-scale CFD models to capture the multiscale effects that are often not considered due to computational limitations. Our work thus presents a modeling framework that can bridge the gap between fundamental studies done at the smallest scale to pellet-⁵⁶ and reactor-scale models for deployment of HyDR.

Methods

X-ray nano- and micro-computed tomography

For synchrotron X-ray nano-tomography experiments, a cone-shaped specimen with a diameter of 300 μm and height of 1 mm was prepared from a commercial direct-reduction pellet as in a preceding study.⁵⁷ The pellet is composed of mainly Fe₂O₃, 0.36 wt % FeO, 1.06 wt % SiO₂, 0.40 wt % Al₂O₃, 0.73 wt % CaO, 0.57 wt % MgO, 0.19 wt % TiO₂, 0.23 wt % V, 0.10 wt % Mn, as well as traces of P, S, Na, and K. The nano-XCT measurements were done in situ, and the specimen was encapsulated in a hydrogen-filled quartz capillary with alumina rod as a support.

The in situ nano-XCT experiments were carried out at the beamline ID16B of the European Synchrotron Radiation Facility (ESRF) in Grenoble, France,⁵⁸ and were performed with an X-ray beam with a fixed energy of 29.4 keV. The beamline setup was configurated to ensure a high spatial resolution, with a voxel size of 30 × 30 × 30 nm³. The capillary sample was heated up rapidly to 700°C with the furnace available at the beamline⁵⁹ during the in situ nano-XCT measurements. The sample was rotated 360° with a speed of ∼3.75°/s. The exposure time for each projection image was 0.03 s, and 3,203 projections were captured. Because the imaging technique is based on phase contrast, the volume reconstruction is a two-step process. The phase is retrieved from the 2D projections using an in-house phase-retrieval calculation, executed through a custom in-house octave script based on a Paganin-like approach using a delta/beta ratio of 83. The tomographic reconstruction was then performed using the standard filtered back-projection algorithm implemented at ESRF.⁶⁰ The reconstructed virtual slices were integrated into image stacks, and the Affine registration among in situ datasets was conducted using the software Fiji (ImageJ).

For the micro computed tomography (micro-CT) experiment, we used an entire commercial direct-reduction pellet that is roughly spherical with a diameter of 1 cm. The pellet was imaged in air at room temperature at 140 kV with tungsten source using the ZEISS Xradia 520 Versa X-ray microscope (XRM) at Stanford University. The sample was rotated 180° with an exposure time for 4 s, and 1,601 projections were captured with a voxel size of 11 × 11 × 11 μm³. The tomographic reconstruction was performed using the Scout and Scan Control System Reconstructor software. The reconstructed slices were integrated into image stacks, and the pores were distinguished from material based on their different attenuation to X-ray in Dragonfly software.

Extraction of the pore network

This study analyzed 4-dimensional (x, y, z, and t) nanotomography images of a section of iron oxide pellets in TIFF format. The first three dimensions (x, y, and z) represent the volume of the pellet, while the last dimension is time (t), i.e., 100 s, 200 s, and 600 s. Each dataset (3D dataset of 3 time intervals) consists of 901 binary images, each with a resolution of 30 × 30 nm² pixel size, capturing the particular section of the pellet at different time intervals. The binary images distinguish between voids (corresponding to pores) and solids (iron oxide). The 3D datasets for each time point are processed separately using the identical workflow described in this section. We used the snow2 algorithm from Porespy⁶¹ for segmenting pores, which are represented by the value “0” in this binary dataset. Using this algorithm is particularly suitable for our dataset, given its high porosity (i.e., the ratio of pore volume to the total material volume), which are 0.32, 0.37, and 0.55 for the 100, 200, and 600 s time points, respectively. For further details on the snow2 algorithm and its implementation, the readers are referred to supplemental note S1.

Erosion and dilation algorithm

Understanding the evolution of pore structures over time is essential for determining permeability and the percolation threshold in our work. Dilation and erosion are two key morphological operations that help analyze these critical parameters. Dilation adds pixels to the boundaries of pores in 3D space (x, y, and z directions), promoting pore growth. In contrast, erosion removes pixels from the pore boundaries, causing the pores to shrink in 3D space. By expanding or shrinking the pores, these operations allow us to assess different pore states based on the number of iterations applied. This is particularly important because our scans are in situ and limited to three time points. By applying dilation and erosion, we can access different time points for which we do not have real data and estimate the percolation threshold (the sample is already percolated at 100 s).

The amount of dilation and erosion is determined by the shape of the structuring element used and the number of iterations. Increasing the number of dilation iterations moves the sample pores forward in time, while increasing the number of erosion iterations reverses the pores’ progression, which is crucial for determining the percolation threshold. We used a structuring element with a 1:1:1 ratio for the x, y, and z scales, assuming that dilation and erosion occur uniformly in 3D space (see Figure S3). Although this assumption of uniformity does not perfectly represent the natural progression of pore sizes (as found in rocks), determining the exact structuring element is beyond the scope of this study. Therefore, we treat pore size progression as an isotropic process in each iteration.

Resource availability

Lead contact

Requests for further information and resources should be directed to and will be fulfilled by the lead contact, Leora Dresselhaus-Marais (leoradm@stanford.edu).

Materials availability

This study did not generate new unique materials.

Data and code availability

• •All the data and original code have been deposited at Zenodo and are publicly available as of the date of publication at Zenodo: https://doi.org/10.5281/zenodo.15751094.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Acknowledgments

The main work for this project (S.P., B.K., and L.D.-M.) is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Separation Science, under award DE-SC0024326. D.R. acknowledges funding by the European Union through the project ROC, sponsored by the European Research Council (ERC; grant number 101054368). Y.M. and G.R. acknowledge the European Synchrotron Radiation Facility for provision of synchrotron radiation facilities under proposal number MA-4880. Y.M. is grateful for the financial support through the Walter Benjamin Programme of the Deutsche Forschungsgemeinschaft (project no. 468209039). D.R. is grateful for the financial support through the ERC Advanced grant ROC (grant agreement no. 101054368). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the ERC. Neither the European Union nor the granting authority can be held responsible for them.

Author contributions

Writing – original draft, S.P.; data curation, S.P., J.V., G.R., and S.C.A.; formal analysis, S.P. and S.C.A.; writing – supplemental information, B.K.; data analysis, B.K.; data curation, Y.M., J.V., G.R., and S.C.A.; writing – review & editing, Y.M., J.V., G.R., D.R., I.B., and L.D.-M.; conceptualization, D.R., I.B., and L.D.-M.; and supervision, L.D.-M.

Declaration of interests

The authors declare no competing interests.

Published: August 5, 2025