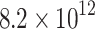Abstract
Non-Orthogonal Multiple Access (NOMA) has emerged as a prominent technique for enhancing spectral efficiency in beyond-fifth-generation (5G) and sixth-generation (6G) wireless systems. However, its performance is highly dependent on channel conditions, necessitating robust spectrum-sensing methods. This study proposes a novel Recurrent Neural Network (RNN)-based Bidirectional Long Short-Term Memory (RNN-Bi-LSTM) model to enhance the spectral performance of NOMA under various channel conditions, particularly the Rician and Rayleigh fading channels. The proposed approach was evaluated using key performance metrics, including the probability of detection (PD), probability of false alarm (PFA), bit error rate (BER), and power spectral density (PSD). Simulation results show that RNN-Bi-LSTM achieves 100% PD at − 5 dB and − 2.5 dB SNR, outperforming conventional methods such as RNN (− 3 dB and − 1.5 dB), LSTM (− 1 dB and 0.3 dB), CSD (0.2 dB and 5.5 dB), matched filter (MF) (1 dB and 0.5 dB), and energy detection (ED) (2.3 dB and 2.7 dB) in Rician and Rayleigh channels, respectively. Additionally, the RNN-Bi-LSTM model shows a 23.36% improvement in PSD suppression under Rician conditions compared with Rayleigh conditions, reflecting the benefits of LoS-enhanced propagation in reducing spectral leakage and improving detection accuracy. BER performance also improves, achieving 10⁻5 at 8.8 dB and 5.8 dB SNR, whereas other methods require higher SNR. Furthermore, the model provides a more accurate PSD estimation, reduces spectral leakage, and enhances the spectrum utilization. Overall, RNN-Bi-LSTM demonstrated superior adaptability to varying channel conditions, making it a robust and efficient solution for NOMA-based spectrum sensing in advanced wireless communication systems.
Keywords: Spectrum sensing, NOMA, RNN-Bi-LSTM, PD, PFA, BER
Subject terms: Energy science and technology, Engineering
Introduction
With the rapid development of wireless communication, networks beyond the fifth generation (B5G) and sixth generation (6G) will provide ultra-reliable, high-capacity, and low-latency communication. Non-Orthogonal Multiple Access (NOMA) has been highlighted as a prominent multiple-access method for providing higher spectral efficiency by enabling multiple users to access the same frequency and time resources with different powers1. Nevertheless, effective usage of the spectrum continues to be an uphill task owing to the increasing demand for wireless services as well as dynamic interference2. Spectrum sensing, an intrinsic component of cognitive radio networks, is essential for detecting potential spectrum opportunities and suppressing interference in NOMA-based systems. Conventional spectrum sensing methods, including energy detection (ED) and matched filtering (MF), are deficient in low-SNR regimes and incapable of managing non-stationary pattern signals in complex B5G environments3. As a solution to these issues, deep-learning-based solutions, specifically Recurrent Neural Networks (RNNs) and Bidirectional Long Short-Term Memory (BI-LSTM) networks, have attracted increasing interest because of their capability to deal with dependencies of sequential data and learn long-duration patterns in dynamic spectrum scenarios4. RNN-BI-LSTM-based spectrum sensing utilizes bidirectional processing to improve detection accuracy by learning past and future dependencies in the received signals. This is especially suitable for B5G waveforms, which are highly flexible, time-varying, and nonlinear because of the complex modulation techniques. By incorporating deep learning into spectrum sensing, the proposed system can enhance the detection capability under different channel conditions, lower false alarms, and increase the adaptability of NOMA-based systems5. This study investigated the use of RNN-BI-LSTM networks for spectrum sensing and their capability to facilitate efficient and smart spectrum management for B5G and 6G systems. Spectrum sensing is essential for effective spectrum utilization in NOMA B5G waveforms in order to facilitate dynamic spectrum access in dense networks. However, conventional techniques are limited by their accuracy and flexibility in wireless environments. An RNN with BI-LSTM improves spectrum sensing by extracting temporal dependencies and bidirectional signal correlations, thereby enhancing detection in low-SNR environments. This method improves spectral efficiency, minimizes interference, and facilitates massive connectivity, which is essential for B5G applications such as IoT and ultra-reliable communications. By utilizing deep learning, this approach enhances sensing capability, providing strong and smart spectrum control for future wireless networks. Spectrum sensing with RNN-BI-LSTM for NOMA above 5G waveforms is important for promoting spectral efficiency and network dependability in future wireless communications. Spectrum sensing helps detect the available spectrum, minimize interference, and maximize resource utilization in dynamic environments4. This is essential for applications, such as autonomous cars, IoT networks, and intelligent cities, where connectivity must be uninterrupted. However, difficulties involve high computational complexity, real-time processing, and adversarial robustness, which require further improvements in deep learning model efficiency and hardware optimization. The growing need for high data rates and spectrum efficiency in B5G networks requires sophisticated spectrum sensing methods6. Conventional approaches are challenged by dynamic spectrum access and interference in the NOMA scenarios. RNN and BI-LSTM provide improved feature extraction and temporal dependency analysis, enhancing detection accuracy. Solving this issue guarantees efficient use of the spectrum, minimized interference, and better network performance in future wireless systems7. The proposed RNN-BI-LSTM-based spectrum sensing technique increases the PD, probability of false alarm (PFA), bit error rate (BER), and power spectral density (PSD) in NOMA systems using deep learning to classify signals correctly. Its bidirectional processing optimizes detection precision by extracting temporal dependencies and decreasing false alarms. This increases the spectral efficiency, lowers the BER, and optimizes the PSD, providing guaranteed communication in varying environments, while being superior to conventional spectrum-sensing methods in NOMA-based wireless networks. RNN-Bi-LSTM was chosen primarily for its ability to capture long-range temporal dependencies in sequential spectrum data, which are crucial for detecting patterns in dynamic and noisy wireless environments. Although convolutional neural networks (CNNs) are effective at extracting spatial features, they lack the sequential memory required to track signal variations over time. Although powerful, hybrid models or transformer-based architectures often require significantly higher computational resources and larger training datasets, which may not be feasible in real-time or resource-constrained environments. Thus, RNN-Bi-LSTM offers an optimal balance between performance and complexity, making it a more practical and efficient choice for robust spectrum sensing in cognitive radio systems. The contributions of this study are as follows:
-
I.
The proposed RNN-Bi-LSTM method significantly improved the spectrum-sensing accuracy of NOMA systems under Rician and Rayleigh fading conditions. It achieves a PD of 100% at − 5 dB and − 2.5 dB SNR, outperforming conventional techniques such as RNN, LSTM, CSD, MF, and ED. The RNN-Bi-LSTM model reduced PFA to − 535 and − 494, offering a notable reduction compared to existing methods. Additionally, it achieves a BER of 10–5 at 8.8 dB and 5.8 dB SNR, whereas traditional models require a higher SNR for similar performance.
-
II.
By leveraging bidirectional memory and deep learning, the RNN-Bi-LSTM model enhances PSD estimation accuracy, minimizes spectral leakage, and maximizes spectrum utilization. This makes it a promising solution to improve the spectral efficiency of future wireless networks.
-
III.
In contrast to traditional spectrum sensing methods, the RNN-BI-LSTM model learns dynamically in time-varying and fading channel environments. This learning process guarantees enhanced Pd, BER, and PSD under various channel situations; thus, it is a resilient solution for future NOMA networks.
Literature review
The authors of8 investigated spectrum sensing through deep learning models, specifically CNNs and RNNs, to improve detection performance in dynamic wireless environments. Research has shown that CNNs effectively capture spatial features, and RNNs capture temporal dependencies, enhancing the prediction of spectrum occupancy. The results showed enhanced performance compared to conventional methods. However, the limitations include high computational complexity and sensitivity to variations in the training data, which can limit real-time deployment. Future studies can further refine the models for reduced latency and adaptive learning. In9, the authors proposed a deep-learning-based spectrum sensing method that integrates multiple feature combinations to enhance detection accuracy in dynamic wireless environments. Their approach leverages CNNs and RNNs for robust feature extraction and improves sensing performance under low signal-to-noise ratios. These findings indicate superior accuracy compared to traditional methods. However, limitations include high computational complexity and potential overfitting owing to extensive training data requirements. Future work should address model efficiency and generalization across diverse spectrum conditions. The authors in10 comprehensively studied deep-learning-based spectrum-sensing techniques, emphasizing their potential for enhancing cognitive radio networks. They categorized the methods into convolutional, recurrent, and hybrid neural networks, highlighting the improvements in detection accuracy and adaptability. The study found that deep learning effectively mitigates noise and interference, but faces challenges such as high computational complexity and data dependency. Limited real-world implementation and generalization remain the key limitations, necessitating further research on lightweight models and robust training datasets for practical deployment. The authors in11 investigated deep learning-based spectrum sensing for effective data transmission in wireless sensor networks. Their research emphasized the ways in which detection performance and adaptability are enhanced by neural networks in dynamic environments, compared to traditional methods. This study indicates improved spectrum use and lower interference, leading to more reliable wireless communication. Nevertheless, this study does not provide real-world implementation aspects and neglects computational complexity issues. Future studies should focus on energy efficiency and hardware feasibility to further optimize deep-learning-based spectrum sensing. The authors of12 explored machine-learning-based spectrum-sensing techniques for cognitive radio networks (CRNs) to enhance reliability. They reviewed various ML algorithms, including SVM, k-NN, and deep learning, and analyzed their effectiveness in detecting spectral holes. Their study found that ML-based sensing improves the detection accuracy, especially in low-SNR environments. However, its limitations include computational complexity, training-data dependency, and vulnerability to adversarial attacks. Future studies should focus on lightweight models and robust techniques for mitigating security threats and real-time processing challenges. The authors of13 investigated spectrum sensing in CRNs with an emphasis on optimizing the detection thresholds to achieve better performance. They studied energy detection under different noise uncertainties, and designed an adaptive threshold method for detection probability enhancement. Their results showed that spectral sensing accuracy was significantly enhanced using threshold optimization. The research is limited by its theoretical basis; however, because it has not been implemented or tested in real environments, it is much less dynamic. Future research is required to substantiate these methods in real-life CRN environments. In14, the authors introduced an optimized deep learning-based model for spectrum sensing under dynamic SNR conditions, thereby improving the detection performance in cognitive radio networks. This research emphasizes the model’s resistance to varying noise levels and performs better than the traditional approaches. The main findings are enhanced spectrum utilization and flexibility in changing SNR conditions. These limitations include higher computational complexity and possible overfitting in low-data situations. Future efforts may aim at real-time deployment and model efficiency optimization for resource-limited settings. The authors of15 proposed NSS-ML, which is a machine-learning-based spectrum-sensing framework for cognitive radio IoT networks. This study enhances spectrum efficiency by employing ML models for the accurate detection of available channels. These findings indicate an improved sensing accuracy and adaptability to dynamic environments. However, these limitations include the increased computational complexity and potential latency in real-time applications. Future work could optimize ML algorithms for energy efficiency and scalability, thus addressing the deployment challenges in large-scale IoT networks. The authors in16 comprehensively studied ML techniques for cooperative spectrum sensing, emphasizing their ability to enhance the detection accuracy in dynamic wireless environments. This study highlights supervised, unsupervised, and reinforcement learning models, noting their effectiveness in mitigating spectral scarcity. Key findings suggest that ML significantly improves sensing reliability but faces challenges such as high computational complexity and real-time adaptability. Limitations include dependency on extensive training data and susceptibility to adversarial attacks, necessitating further optimization for practical deployment in cognitive radio networks. The authors in17 introduced a metaheuristic-based clustering method to improve cooperative spectrum sensing in CRNs. By optimizing cluster formation, their technique enhances detection accuracy and minimizes energy expenditure. Their research showed better performance than conventional methods. The drawbacks are the computational complexity and sensitivity to variations in the network topology. Future work may involve adaptive algorithms to counter these drawbacks and improve real-time applicability. Their research adds to effective spectrum usage in dynamic CRN environments. In18, researchers worked on spectrum sensing in reconfigurable embedded devices using optimized deep-learning algorithms. Their work established enhanced detection reliability and resilience under dynamic scenarios compared to conventional methods. The introduced model effectively discriminated the spectral occupancy and reduced the computational load. Shortfalls include overfitting issues when operating in harsh environments, extensive training data dependencies, and high difficulty in executing them in real time on constrained devices. Subsequent research should aim to extend the generalization abilities and minimize the latency for real-world deployment. The authors of19 suggested an adaptive Gaussian Mixture Model (GMM)-based machine learning algorithm for cooperative spectrum sensing in cognitive radio networks. This method has an improved detection rate and low false alarms, with higher spectrum efficiency. This study provides a better performance than the existing methods. Shortcomings include the higher complexity and possible vulnerability to dynamic variations of the channel. Future studies may emphasize algorithm optimization for real-time systems and lower the processing overhead to further improve the practical usability of cognitive radio networks.
In the considered simulated NOMA waveform environment, characterized by time-varying Rayleigh and Rician channels with Doppler shift and high-order 256-QAM modulation, the RNN-Bi-LSTM model demonstrates strong sequential modeling capability. It is particularly effective for time-series signal detection tasks under varying SNR conditions, leveraging its bidirectional structure to capture temporal dependencies in both forward and backward directions. However, when compared to emerging Transformer-based architectures, which utilize self-attention mechanisms to model long-range dependencies more efficiently, the Bi-LSTM may underperform in scenarios requiring global temporal context and parallel training scalability. Similarly, Graph Neural Networks (GNNs), though less conventional in this domain, have shown potential in capturing topological or relational dependencies in multi-user environments like NOMA—particularly when inter-user interference or spatial user relationships are explicitly modeled. Furthermore, Hybrid AI approaches that combine deep learning with domain-aware signal processing (e.g., integrating attention modules into Bi-LSTM or merging CNNs with RNNs) offer improved performance in detecting signal presence at low SNRs or under non-stationary fading profiles. Nevertheless, the RNN-Bi-LSTM model provides a balance between interpretability, moderate computational complexity, and robust performance in resource-constrained environments (e.g., CPU-based MATLAB setups), making it suitable for baseline evaluations and edge-device implementations. Future work could explore Transformer-based architectures or hybridized models to further enhance BER and PD performance, especially under extreme SNR conditions or with larger datasets.
Background of NOMA and spectrum sensing methods
Non-Orthogonal Multiple Access (NOMA) is an important 5G and future waveform that can achieve higher spectral efficiency by enabling more than one user to share identical time–frequency resources via power or code domain multiplexing. NOMA poses both special challenges and possibilities for spectrum-sensing. Conventional spectrum-sensing methods for CRNs are based on the detection of idling spectrum bands by secondary users. Nonetheless, NOMA’s signal structure overlap of NOMA makes sensing challenging because power-domain multiplexing creates interference among users at various powers20. Advanced sensing techniques in spectrum sensing, including energy detection (ED), matched filtering (MF), and cyclostationary feature detection (CS), must be modified for use with NOMA. ML methods such as deep learning and adaptive thresholding have the potential to improve the detection efficiency by differentiating primary and secondary user signals within a power-superimposed setting21. Moreover, cooperative spectrum sensing with several cognitive radios working together can alleviate near-far effects in NOMA situations. Despite its advantages, NOMA-based spectrum sensing offers challenges such as higher computational complexity and detection faults in low-SNR environments. Future research should be conducted to optimize sensing algorithms to effectively distinguish overlapping signals and decrease false alarms. In general, the combination of NOMA and spectrum sensing optimizes dynamic spectrum access, augmenting network capacity and spectral usage22. In NOMA, multiuser interference (MUI) arises owing to the simultaneous transmission of multiple users over the same frequency band, which is differentiated primarily by power levels. Although NOMA improves spectral efficiency and supports massive connectivity, MUI is a significant challenge, especially when channel conditions are highly dynamic or power allocation is suboptimal. The presence of MUI directly affects the signal-to-interference-plus-noise ratio (SINR), leading to a degraded detection performance and increased BER, particularly for users with weaker channel gains. Successive interference cancellation (SIC), the core decoding strategy in NOMA, is highly sensitive to accurate channel estimations. Any error can propagate, further amplifying the effects of MUI. In practical deployments, residual interference from an imperfect SIC can undermine the system’s capacity and fairness. Therefore, managing MUI through optimized power allocation, user pairing strategies, and robust receiver designs is critical. Advanced machine learning models are increasingly being explored to mitigate MUI by predicting interference patterns and dynamically adapting system parameters to ensure reliable and efficient NOMA performance. The structure of NOMA is shown in Fig. 1.
Fig. 1.
NOMA structure.
To estimate the PD, PFA, and PSD for an NOMA waveform for spectrum sensing, we used a signal model for cognitive radio networks. The PD is the probability that the sensing algorithm correctly detects the primary user’s signal. The received signal consisting of noise and a signal with noise is given by
 |
1 |
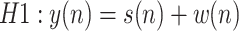 |
2 |
where 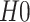 and
and 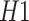 represent the hypotheses for the absence and presence of a primary user, respectively. The test statistic used in the ED is
represent the hypotheses for the absence and presence of a primary user, respectively. The test statistic used in the ED is
 |
3 |
Equation (3) under 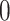 ,
, 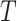 follows a central chi-square distribution given by
follows a central chi-square distribution given by
 |
4 |
Equation (3) under 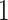 ,
, 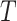 follows a non-central chi-square distribution given by
follows a non-central chi-square distribution given by
 |
5 |
where 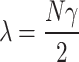 is the non-centrality parameter and
is the non-centrality parameter and 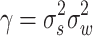 is the SNR. The PD is given by:
is the SNR. The PD is given by:
 |
6 |
where 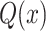 is the Q-function and τ is the detection threshold. PFA is the probability that the detector incorrectly detects a signal when only noise is present and is given by
is the Q-function and τ is the detection threshold. PFA is the probability that the detector incorrectly detects a signal when only noise is present and is given by
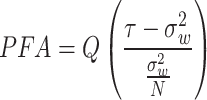 |
7 |
In NOMA, multiple users simultaneously transmit data using power-domain multiplexing. The transmitted signal is:
 |
8 |
where K is the number of users,  is the allocated power for the
is the allocated power for the  user, and
user, and 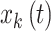 is the user’s modulated signal. The PSD of the NOMA signal can be computed asfollows:
is the user’s modulated signal. The PSD of the NOMA signal can be computed asfollows:
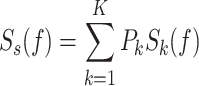 |
9 |
where 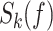 denotes the PSD of the modulated signal for each user. The total PSD is the weighted sum of the PSDs of individual users. The PSD follows the NOMA spectrum shape, as follows:
denotes the PSD of the modulated signal for each user. The total PSD is the weighted sum of the PSDs of individual users. The PSD follows the NOMA spectrum shape, as follows:
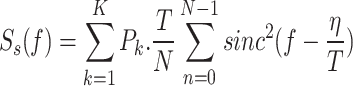 |
10 |
where 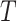 is the symbol duration and
is the symbol duration and 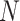 is the number of subcarriers. In CR based on NOMA waveforms, PD provides precise detection of primary-user signals without interference. PFA influences spectrum efficiency because a high PFA causes underutilization by secondary users. The PSD describes the signal distribution, maximizing resource utilization, and interference control. Equilibrating PD and PFA is essential for reliable spectrum sensing, whereas PSD analysis increases spectral efficiency, thus making cognitive NOMA networks adaptive and robust under dynamic wireless conditions. Performance metrics, such as PD and BER, are supported by clearly defined test conditions, particularly through the specifications of the channel models used. The analysis explicitly considers both Rayleigh and Rician channel conditions. In the case of the Rician channel, the presence of a strong line-of-sight (LoS) component is highlighted as a key factor that enhances detection performance, whereas the Rayleigh channel is characterized by severe multipath fading owing to the absence of an LoS path, leading to more challenging signal detection conditions. The test scenarios were qualitatively well defined through descriptive terms such as “harsh low-SNR environments,” “deep fades,” and “multipath fading.” multipath fading. For the purpose of the NOMA-based analysis of Rician channels, a typical Rician K-factor in the range of 10 dB was used, representing moderate to strong LoS conditions commonly observed in urban microcells or suburban environments. Therefore, the reported performance metrics are reasonably well supported within the scope of this study based on the defined channel characteristics.
is the number of subcarriers. In CR based on NOMA waveforms, PD provides precise detection of primary-user signals without interference. PFA influences spectrum efficiency because a high PFA causes underutilization by secondary users. The PSD describes the signal distribution, maximizing resource utilization, and interference control. Equilibrating PD and PFA is essential for reliable spectrum sensing, whereas PSD analysis increases spectral efficiency, thus making cognitive NOMA networks adaptive and robust under dynamic wireless conditions. Performance metrics, such as PD and BER, are supported by clearly defined test conditions, particularly through the specifications of the channel models used. The analysis explicitly considers both Rayleigh and Rician channel conditions. In the case of the Rician channel, the presence of a strong line-of-sight (LoS) component is highlighted as a key factor that enhances detection performance, whereas the Rayleigh channel is characterized by severe multipath fading owing to the absence of an LoS path, leading to more challenging signal detection conditions. The test scenarios were qualitatively well defined through descriptive terms such as “harsh low-SNR environments,” “deep fades,” and “multipath fading.” multipath fading. For the purpose of the NOMA-based analysis of Rician channels, a typical Rician K-factor in the range of 10 dB was used, representing moderate to strong LoS conditions commonly observed in urban microcells or suburban environments. Therefore, the reported performance metrics are reasonably well supported within the scope of this study based on the defined channel characteristics.
Proposed RNN-Bi-LSTM
In modern wireless communication, Cognitive Radio Networks (CRNs) play a crucial role in optimizing spectrum usage by allowing Secondary Users (SUs) to access underutilized spectrum bands opportunistically, without interfering with Primary Users (PUs). Effective spectrum sensing is essential in CRNs to detect the presence or absence of PU signals, ensure efficient spectrum utilization, and minimize interference. However, conventional spectrum sensing techniques, such as ED, MF, and CFD, struggle under low-SNR conditions, multipath fading, and power-domain interference introduced by the NOMA waveforms. To address these challenges, an RNN with BI-LSTM was proposed for spectrum sensing in NOMA-based CRNs. NOMA allows multiple users to share the same frequency band by allocating different power levels based on their channel conditions. This creates interuser interference (IUI) and makes spectrum sensing more complex than traditional Orthogonal Multiple Access (OMA) systems. Standard spectrum sensing approaches fail to accurately detect weak PU signals in the presence of strong SU signals, owing to power-domain multiplexing. The RNN-BI-LSTM model enhances spectrum sensing by leveraging deep learning for temporal pattern recognition in CRNs, particularly in NOMA systems. Unlike traditional methods, BI-LSTM processes bidirectional sequences, capturing both past and future dependencies in received signals. This improves the detection accuracy, particularly under low-SNR conditions, where conventional methods fail. The model effectively reduces false alarms and mitigates interference from strong SUs, ensuring the reliable detection of PU signals. In addition, the BI-LSTM dynamically adapts to changing spectral conditions, making it robust for real-time applications. By improving the PD while minimizing the PFA, spectrum utilization is optimized, enabling efficient and interference-free communication. The RNN-BI-LSTM-based spectrum-sensing model uses the received signal 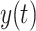 and processes it through bidirectional LSTM layers to extract temporal features and classify the spectrum as occupied (PU present) or vacant (PU absent). RNN-Bi-LSTM models excel in spectrum sensing by capturing long-term temporal dependencies through sequential data processing in both forward and backward directions, making them highly effective in low-SNR and fading environments. Compared to Convolutional Neural Networks (CNNs), which primarily extract local spatial features, Bi-LSTMs are better suited for handling time-varying signal dynamics. However, CNNs are computationally more efficient and can be effective when temporal dependencies are minimal. In contrast, transformer-based models leverage self-attention mechanisms to capture global dependencies without sequential processing, offering faster training and better scalability. However, transformers typically require large datasets and computational resources. Overall, RNN-Bi-LSTM provides a good trade-off between temporal learning capability and resource efficiency, especially in moderate-data spectrum-sensing scenarios. The input signal sequence is defined as follows:
and processes it through bidirectional LSTM layers to extract temporal features and classify the spectrum as occupied (PU present) or vacant (PU absent). RNN-Bi-LSTM models excel in spectrum sensing by capturing long-term temporal dependencies through sequential data processing in both forward and backward directions, making them highly effective in low-SNR and fading environments. Compared to Convolutional Neural Networks (CNNs), which primarily extract local spatial features, Bi-LSTMs are better suited for handling time-varying signal dynamics. However, CNNs are computationally more efficient and can be effective when temporal dependencies are minimal. In contrast, transformer-based models leverage self-attention mechanisms to capture global dependencies without sequential processing, offering faster training and better scalability. However, transformers typically require large datasets and computational resources. Overall, RNN-Bi-LSTM provides a good trade-off between temporal learning capability and resource efficiency, especially in moderate-data spectrum-sensing scenarios. The input signal sequence is defined as follows:
 |
11 |
where 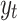 represents the signal received at time
represents the signal received at time 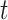 . In spectrum sensing, a forward LSTM layer is applied to sequential radio frequency data for the detection of spectrum occupancy patterns. It extracts the temporal dependencies in the received signals, enabling more accurate detection in time-evolving environments. The examination of previous signal variations improves decision making for spectrum availability, enabling cognitive radio networks to utilize the spectrum efficiently and adaptively. The forward LSTM layer processes the input as:
. In spectrum sensing, a forward LSTM layer is applied to sequential radio frequency data for the detection of spectrum occupancy patterns. It extracts the temporal dependencies in the received signals, enabling more accurate detection in time-evolving environments. The examination of previous signal variations improves decision making for spectrum availability, enabling cognitive radio networks to utilize the spectrum efficiently and adaptively. The forward LSTM layer processes the input as:
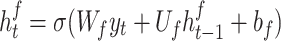 |
12 |
A backward LSTM in spectrum sensing sequentially processes wireless signals by observing historic dependencies in reverse, thereby enhancing the accurate detection in time-varying scenarios. It optimizes the signal classification by capturing temporal correlations, suppressing noise, and effectively detecting spectral holes. This supports cognitive radio systems in maximizing the spectrum usage and minimizing interference in wireless networks. Similarly, the backward LSTM is defined as:
 |
13 |
where 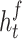 and
and 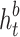 are the hidden states in the forward and backward LSTMs, respectively;
are the hidden states in the forward and backward LSTMs, respectively; 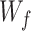 ,
, 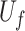 , bf and
, bf and 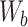 ,
, 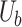 ,
, 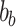 are the weight matrices and bias terms, respectively; and
are the weight matrices and bias terms, respectively; and 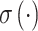 is the activation function. In spectrum sensing, the last hidden operation of an RNN-Bi-LSTM extracts temporal dependencies and bidirectional contextual information from the incoming signals. These operations enhance feature extraction and enhance noise robustness and detection accuracy. The last hidden state combines past and future signal features and improves the classification in cognitive radio systems for effective spectrum usage. The final hidden representation is the concatenation of both states.
is the activation function. In spectrum sensing, the last hidden operation of an RNN-Bi-LSTM extracts temporal dependencies and bidirectional contextual information from the incoming signals. These operations enhance feature extraction and enhance noise robustness and detection accuracy. The last hidden state combines past and future signal features and improves the classification in cognitive radio systems for effective spectrum usage. The final hidden representation is the concatenation of both states.
 |
14 |
In RNN-Bi-LSTM-based spectrum sensing, the associated layer fine-tunes the extracted temporal features and projects them into lower-dimensional space for classification. The softmax classifier predicts the probability scores for various spectrum states, thereby facilitating accurate detection of occupied or idle channels. This improves cognitive radio networks by enhancing the spectrum efficiency and reducing interference. A fully connected layer and softmax classifier then determine whether the spectrum is occupied (H1) or free (H0).
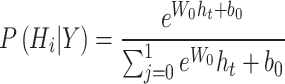 |
15 |
where  represents the probability of hypothesis Hi given the observed sequence Y. In RNN-Bi-LSTM-based spectrum sensing, PD represents the probability that the model correctly identifies an occupied spectrum to maintain efficient spectrum utilization. PFA, on the other hand, represents the probability of the incorrect detection of an idle spectrum as occupied; hence, unnecessary wastage of the spectrum. RNN-Bi-LSTM improves the accuracy of sensing using temporal dependencies and bidirectional aspects, thus enhancing Pd with a minimal Pfa. An ideal balance between PD and PFA is essential for maintaining maximum cognitive radio performance. The decision threshold for spectrum sensing was based on the likelihood ratio test (LRT)
represents the probability of hypothesis Hi given the observed sequence Y. In RNN-Bi-LSTM-based spectrum sensing, PD represents the probability that the model correctly identifies an occupied spectrum to maintain efficient spectrum utilization. PFA, on the other hand, represents the probability of the incorrect detection of an idle spectrum as occupied; hence, unnecessary wastage of the spectrum. RNN-Bi-LSTM improves the accuracy of sensing using temporal dependencies and bidirectional aspects, thus enhancing Pd with a minimal Pfa. An ideal balance between PD and PFA is essential for maintaining maximum cognitive radio performance. The decision threshold for spectrum sensing was based on the likelihood ratio test (LRT)
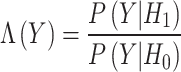 |
16 |
The probability of detection (PD) and false alarm (PFA) are given by:
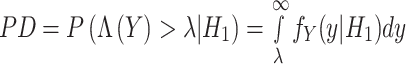 |
17 |
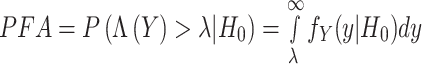 |
18 |
For an RNN-BI-LSTM-based classifier, these probabilities are learned from the training data and optimized to minimize classification errors.
The PSD of an RNN-Bi-LSTM model for spectrum sensing measures the distribution of signal power across frequencies. Bidirectional LSTM is used to identify temporal dependencies in both past and future states to improve the spectrum prediction accuracy. PSD analysis using the model identifies the spectrum holes and interference patterns for dynamic spectrum access. This assists in the identification of primary user activity and noise mitigation in cognitive radio networks. PSD-based learning enhances spectrum sensing through enhanced signal classification and adaptive transmission, thereby optimizing the wireless communication efficiency. The PSD of the NOMA signal was calculated using the Fourier autocorrelation function, Ry(τ):
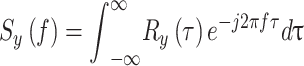 |
19 |
The autocorrelation function in spectrum sensing quantifies the similarity between a signal and its time-shifted counterpart, and is used to identify primary user signals in cognitive radio. It takes advantage of the periodicity or structure of signals to distinguish them from noise, thereby facilitating effective spectrum occupancy detection for dynamic spectrum access and interference reduction in wireless communications. The autocorrelation function is:
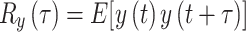 |
20 |
For a NOMA-based signal, considering two users with different power levels:
 |
21 |
where h1 and h2 are the channel coefficients; P1 and P2 are the power levels of the two users;  and
and 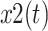 are the transmitted symbols; and
are the transmitted symbols; and  is the noise. The PSD is derived as:
is the noise. The PSD is derived as:
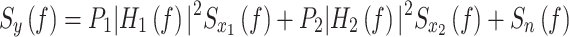 |
22 |
where  represents the PSD noise. This equation models how transmitted signals pass through their respective channels and combine with the noise at the receiver, thereby affecting the overall signal characteristics. In practice, the received over-the-air (OTA) signal is
represents the PSD noise. This equation models how transmitted signals pass through their respective channels and combine with the noise at the receiver, thereby affecting the overall signal characteristics. In practice, the received over-the-air (OTA) signal is
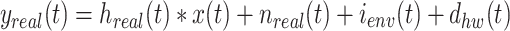 |
23 |
where 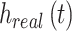 is the actual multipath time-varying channel,
is the actual multipath time-varying channel,  represents the real noise including colored noise, not always Gaussian,
represents the real noise including colored noise, not always Gaussian, 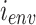 is the interference from other transmitters, and
is the interference from other transmitters, and 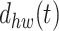 is the distortion due to hardware impairments (e.g., amplifier nonlinearity and oscillator phase noise). The metric becomes:
is the distortion due to hardware impairments (e.g., amplifier nonlinearity and oscillator phase noise). The metric becomes:
 |
24 |
The validation ensures:
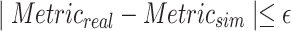 |
25 |
For a small ϵ i.e., confirming that the performance degradation under real-world conditions remains within acceptable bounds.
The RNN-Bi-LSTM method demonstrated superior adaptability to varying channel conditions, making it highly effective for NOMA-based spectral sensing. Its bidirectional structure enables it to capture both past and future signal dependencies, enhance feature extraction, and improve signal detection under fading and interference conditions. Unlike conventional methods with fixed thresholds or limited memory, RNN-Bi-LSTM dynamically adjusts to time-varying channels, which is crucial in NOMA scenarios where multiple users share a spectrum nonorthogonally. This results in more accurate detection, lower false alarm rates, and better handling of the overlapping signals. Furthermore, the method demonstrated substantial gains in PSD estimation and BER performance, confirming its capability to operate reliably in both Rayleigh and Rician environments. These advantages make RNN-Bi-LSTM a promising solution for maximizing spectral efficiency in advanced radio frameworks, including cognitive radio and next-generation wireless systems, where adaptability and robustness are critical23.
Proposed RNN-Bi-LSTM vs hybrid deep learning models
The choice of the proposed method over hybrid deep-learning models, such as attention-based or transformer architectures, is primarily driven by a balance of complexity, efficiency, and performance. Bi-LSTM networks excel at modeling sequential data by processing inputs in both forward and backward directions, effectively capturing temporal dependencies critical in applications such as spectrum-sensing NOMA signal detection. By contrast, hybrid models that incorporate attention mechanisms or transformer layers can dynamically focus on important features and capture long-range dependencies more explicitly. However, these benefits come at the cost of substantially increased computational complexity and memory requirements—transformer self-attention scales quadratically with sequence length (O(n2)), whereas Bi-LSTM scales linearly (O(n)), making transformers less suitable for real-time, resource-constrained edge devices. Studies such as24,25 demonstrate the superior representational power of attention mechanisms, but also highlight their higher inference latency and energy demands. However, recent works26 and27 show that simpler recurrent structures such as Bi-LSTM achieve competitive performance in wireless communication tasks without the overhead of complex attention layers. Therefore, Bi-LSTM offers a pragmatic trade-off, providing robust temporal feature learning with a reduced computational burden, making it highly feasible for deployment in real-time and edge scenarios. Table 1 shows the comparative performance of the hybrid DL models and the proposed methods.
Table 1.
Comparison of Hybrid Attention-Based Models and RNN-Bi-LSTM for Spectrum Sensing.
| Aspect | Hybrid DL models (e.g., Attention/Transformer) | Proposed RNN-Bi-0LSTM |
|---|---|---|
| Architecture | Combines multiple components (e.g., CNN + LSTM + Attention, Transformers) | Pure recurrent: stacked RNN followed by Bi-LSTM layers |
| Temporal modeling | Uses self-attention to dynamically capture long-range dependencies | Captures dependencies through forward & backward recurrence |
| Computational complexity | High (O(n2) for sequence length due to attention) | Moderate (O(n) due to sequential processing) |
| Memory usage | Large, requires storing multiple attention weights / heads | Lower, primarily stores hidden & cell states |
| Parameter count | Typically very high due to multi-head attention and deep hybrid stacks | Relatively lower, depends on units per RNN/Bi-LSTM layer |
| Training convergence | Often slower, sensitive to hyperparameter tuning | Generally stable convergence with fewer tuning parameters |
| Latency/real-time use | Challenging for edge or real-time tasks without hardware acceleration | Suitable for edge devices and low-latency real-time scenarios |
| Interpretability | High due to attention maps visualizing feature importance | Moderate (hidden states can be probed but less explicit) |
| Hardware suitability | Requires GPUs/TPUs for practical inference speeds | Runs efficiently on CPUs and low-power edge hardware |
The proposed RNN-Bi-LSTM is thus selected over complex hybrid models as it offers a balanced trade-off, efficiently learning temporal patterns with lower computational and memory demands, making it ideal for deployment on edge devices and real-time wireless applications, where hardware resources and latency are critical constraints.
K-fold cross-validation
K-fold cross-validation is a robust statistical technique that is used to evaluate how well a model generalizes to unseen data. In the context of the RNN-Bi-LSTM spectrum-sensing algorithm for NOMA waveforms under diverse channel conditions, it plays a crucial role in assessing the reliability of the model, especially in adversarial or harsh environments. Here, the entire dataset, comprising signals affected by various wireless impairments, such as multipath fading (Rayleigh, Rician), Doppler shifts, fluctuating SNR levels, NOMA power allocations, and even intentional jamming, is partitioned into K equally sized folds. The model was then trained on K-1 folds and validated on the remaining folds. This process was repeated K times, each time with a different fold serving as the validation set. By averaging the performance metrics across all folds, such as detection probability, false alarm rate, or BER, we obtain a comprehensive estimate of the model’s stability and generalization ability. This technique ensures that the RNN-Bi-LSTM network does not overfit specific channel realizations or adversarial patterns present in a single train-test split, thereby proving its robustness in real-world, dynamically changing, or adversarial spectrum environments.
Energy consumption and potential optimizations
The proposed work introduces a sophisticated deep learning-based approach capable of accurately identifying NOMA signals even under challenging channel variations, such as multipath fading, Doppler shifts, and adversarial interference. However, deploying such a model in IoT environments, where devices are often battery-powered and constrained by limited computational resources, raises important concerns regarding energy consumption. The Bi-LSTM architecture, by design, processes input sequences in both the forward and backward directions, maintaining multiple gating operations per time step, which leads to increased multiply accumulate operations and frequent memory accesses, which are primary contributors to energy drain in embedded systems. To address these challenges and make the solution viable for IoT applications, this study could be extended by exploring techniques such as model pruning, where unimportant weights and neurons are systematically eliminated, leading to sparser and lighter models that require fewer computations and less memory, thereby reducing the power usage. Quantization is another potent strategy wherein network parameters and activations are represented using lower-precision formats (e.g., 8-bit integers instead of 32-bit floats), substantially reducing the computational load and energy while often retaining acceptable accuracy levels. Additionally, hardware-aware optimizations such as using low-power AI accelerators (e.g., TinyML chips) and deploying dynamic voltage and frequency scaling (DVFS) can tailor processing requirements to real-time requirements, further conserving energy. Techniques such as knowledge distillation, in which a smaller student model learns to mimic a larger Bi-LSTM teacher, can also produce lightweight models suited for edge devices without significant loss in detection capability. By integrating these strategies, the RNN-Bi-LSTM-based spectrum sensing framework can be transformed into an energy-efficient solution that upholds the robust detection of NOMA signals across varying channel conditions, making it highly practical for widespread IoT deployments operating under strict energy budgets.
Simulation results
In this section, we thoroughly analyze the proposed RNN-Bi-LSTM and conventional spectrum-sensing methods for NOMA waveforms using MATLAB 2016. A detailed description of the dataset, training-test split, and hyperparameters used for the reproducibility of the RNN-Bi-LSTM spectrum-sensing algorithm for NOMA waveforms under diverse channel conditions is shown in Table 2. The selected parameters provided the best spectrum-sensing performance in NOMA with the RNN-Bi-LSTM. A high number of subcarriers balance the complexity and accuracy, and the QAM modulation is consistent with real-life 5G/6G scenarios. Rayleigh and Rician fading represent real-world wireless channels, respectively. Large datasets aid in generalization with a learning rate of 0.001, providing stable convergence. A batch size of 128 maximized the training efficiency and 50 epochs avoided underfitting. The SGD optimizer improves the gradient updates, and the MSE is appropriate for classification and regression problems. Although adaptive optimizers, such as Adam, often achieve faster convergence, this study employs SGD for several reasons. First, SGD generally offers better generalization on unseen data, which is critical for spectrum sensing under diverse channel conditions, such as Rayleigh and Rician fading. Adaptive methods, such as Adam, can sometimes converge to sharp minima, leading to overfitting or degraded performance when the channel characteristics vary. Additionally, SGD provides smoother, more predictable learning dynamics without the aggressive parameter adjustments of Adam, which is advantageous for training time-series models, such as Bi-LSTM, that process fluctuating wireless signals. Its simplicity also ensures ease of tuning, reproducibility across different MATLAB environments, and clearer interpretation of results. Importantly, empirical tuning in this study revealed that SGD, with a carefully selected learning rate of 0.001, offered the most reliable balance of convergence and generalization, ultimately delivering superior spectrum-sensing performance for NOMA waveforms. Two hidden layers of 64 units effectively captured the complex signal patterns. The choice of 64 units per Bi-LSTM layer represents a balanced trade-off between the model complexity and computational efficiency. With 64 units, the network possesses sufficient capacity to capture intricate temporal dependencies in the NOMA waveform under diverse fading environments without imposing excessive training time or risking overfitting, which is more likely with substantially larger hidden layers given the dataset size. Meanwhile, fixing the K-factor at 10 dB for Rician fading simplifies the analysis by representing a moderately strong line-of-sight (LoS) scenario, which serves as a practical benchmark for evaluating the performance of the spectrum-sensing algorithm under stable, partially deterministic channel conditions. Although this limits the exploration of environments with varying LoS dominance, it allows the study to systematically assess the proposed model without introducing additional uncertainty from widely fluctuating K-factors. Future work can extend this by investigating a range of K values to fully characterize the robustness under different Rician profiles.
Table 2.
Simulation parameters.
In Fig. 2, we analyze the PD performance of the proposed and conventional spectrum-sensing algorithms for the Rayleigh channel. The main focus was to estimate the SNR required for maximum detection. At the SNR of − 2.5 dB, − 1.5 dB, − 0.3 dB, 0.5 dB, 1.5 dB, and 2.7 dB, the maximum detection is achieved by the proposed RNN-Bi-LSTM, RNN, LSTM, CSD, MF and ED. It can be observed that the proposed method attained an SNR gain of − 1 dB to 4 0.6 dB respectively. The numerical results indicated that the proposed method outperformed contemporary algorithms. RNN-Bi-LSTM improves the low-SNR detection performance by retaining long-range dependencies in sequence data and enhancing feature extraction from noisy signals. The bidirectional architecture processes both forward and backward data, maintaining context for improved noise resistance. In contrast to conventional techniques, Bi-LSTM efficiently suppresses interference and weakly detects signals by learning the temporal dynamics, thereby enhancing the probability of detection. Its memory cells avoid vanishing gradients, making them resistant even in harsh low-SNR environments.
Fig. 2.
Probability of detection performance of spectrum sensing methods in Rayleigh Channel.
In Fig. 3, we analyze the PD performance of the proposed and conventional spectrum-sensing methods under a Rician channel. At the PD = 1, the SNR of − 5 dB, − 3 dB, − 1 dB, 0.2 dB, 1 dB and 2.3 dB are obtained by the RNN-Bi-LSTM, RNN, LSTM, CSD, MF and ED. The proposed methods outperform contemporary methods by obtaining an SNR gain in the range of − 2 to 7 dB. Furthermore, it is noted that the proposed methods in the Rician channel detect signals at a low SNR compared to the Rayleigh channel. Hence, it is concluded that RNN-Bi-LSTM detects the probability of low SNR in a Rician channel more efficiently than in a Rayleigh channel because of the existence of a strong line-of-sight (LoS) component. The memory and bidirectional learning ability of Bi-LSTM enables it to capture channel changes more effectively, thereby reducing fading effects. In Rayleigh channels, where signals undergo heavy multipath fading, the absence of an LoS component results in more difficult detection.
Fig. 3.
Probability of detection performance of spectrum sensing methods in Rician Channel.
Figure 4 illustrates the PD versus OTA (over-the-air) SNR in dB for various detection algorithms, including RNN-Bi-LSTM, RNN, LSTM, CSD, MF, and ED. As is evident from the curves, achieving a near-perfect detection probability (pd ≈ 1) requires substantially different OTA levels across these methods. Specifically, advanced RNN-Bi-LSTM achieves PD = 1 at approximately 6 dB, whereas simpler schemes such as the energy detector (ED) need approximately 10.5 dB. This translates into a significant SNR gain of approximately 4.5 dB for RNN-Bi-LSTM compared with ED, highlighting its superior sensitivity. Similarly, the RNN, LSTM, and CSD reach pd ≈ 1 at approximately 7 , 7.5 , and 8 dB, respectively, offering gains of approximately 3.5 , 3 , and 2.5 dB over the ED, respectively. The matched filter (MF) required approximately 9 dB, yielding a modest gain of 1.5 dB. These results underscore how incorporating deep learning models, particularly RNN-Bi-LSTM, markedly reduces the required OTA SNR to achieve reliable detection, making them highly advantageous for robust spectrum sensing in low SNR or adverse wireless environments.
Fig. 4.
Probability of detection performance of spectrum sensing methods under an OTA environment.
The analysis of Figs. 1, 2, and 3 reveals that the OTA environment requires a higher SNR (6 dB) to achieve reliable detection compared with Rayleigh (− 2.5 dB) and Rician (− 5 dB) channels. This performance gap arises because of real-world impairments such as hardware nonlinearities and interference present in the OTA setups. Despite this, the proposed RNN-Bi-LSTM consistently outperformed traditional methods, demonstrating robust detection under practical OTA, Rayleigh, and Rician conditions.
As shown in Fig. 5, we analyzed the PFA performance of the proposed RNN-Bi-LSTM and the conventional spectrum-sensing algorithms. The PFA 0.14 by RNN-Bi-LSTM, 0.26 by RNN, 0.37 by LSTM, 0.43 by CSD 0.5, MF and 0.57 by ED were obtained to obtain PD = 1. It can be observed that the proposed methods effectively reduce the effect of false alarms when compared with conventional schemes. Hence, it is concluded that RNN-Bi-LSTM minimizes the likelihood of false alarms better than the current approaches because it is bidirectional and has better memory retention. In contrast to RNN and LSTM, which handle data sequentially in one direction, Bi-LSTM handles dependencies from both past and future inputs, thereby enhancing the feature extraction and classification accuracy. In contrast to CSD, MF, and ED, which use fixed thresholds and constant signal features, Bi-LSTM learns patterns dynamically, thereby improving the noise and interference robustness. This adaptability drastically lowers the false-alarm rate in signal-detection applications.
Fig. 5.
Probability of false alarm performance of spectrum sensing methods in Rayleigh Channel.
The PFA performance of the spectrum-sensing methods in a Rician channel is shown in Fig. 6. The PFA 0.05 by RNN-Bi-LSTM, 0.11 by RNN, 0.2 by LSTM, 0.3 by CSD 0.42, MF and 0.48 by ED are attained to obtained the PD = 1. It can be observed that the performance of the spectrum sensing method is better in the Rician channel than in the Rayleigh channel. Hence, it is concluded that the proposed RNN-Bi-LSTM improves the Rician channel PFA performance using its bidirectional model to learn past and future dependencies, thereby enhancing signal detection precision. In comparison with RNN and LSTM, it minimizes the error propagation and maximizes feature extraction. In contrast to CSD, MF, and ED, which depend on fixed thresholds and statistical models, RNN-Bi-LSTM dynamically adjusts to channel variations, thereby reducing the effects of multipath fading. This flexibility results in a reduced PFA, making the detection more robust, particularly under high-noise and time-varying conditions typical of Rician channels.
Fig. 6.
Probability of false alarm performance of spectrum sensing methods in Rician Channel.
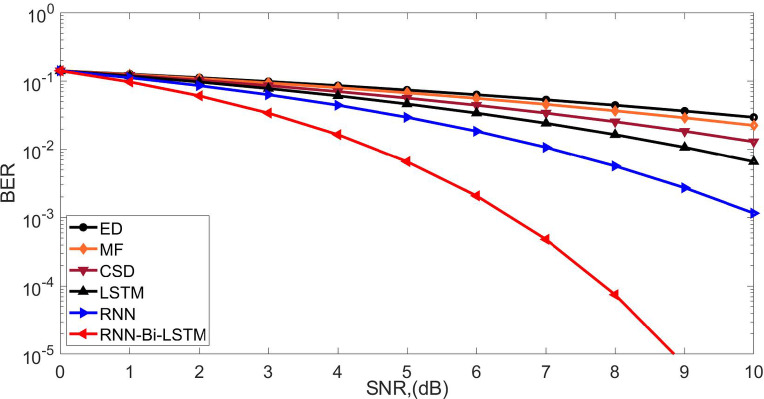
BER analysis is essential in Rician and Rayleigh channel spectrum sensing because it measures detection reliability in the presence of multipath fading. In Rician channels with a dominant line of sight, BER is used to measure the signal resilience against interference. In Rayleigh channels with heavy fading, the BER measures the sensing accuracy in deep fading. BER comparison among techniques, such as energy detection and matched filtering, guarantees the best trade-offs between false alarms and missed detections, thereby improving cognitive radio performance in dynamic wireless environments. The BER curves for the Rayleigh channel are shown in Fig. 7 to estimate the throughput performances of the proposed and conventional methods. The BER of 10–5 is obtained at the SNR of 8.8 dB by RNN-Bi-LSTM, 12.2 dB by RNN, 13.3 dB by LSTM, 14.4 dB by CSD, 15.8 dB by MF and 18.8 dB by ED. The numerical results reveal that the proposed RNN-Bi-LST achieves SNR gains of 2 dB, 4.1 dB, 6.4 dB, 7, and 10 dB, outperforming contemporary methods. Therefore, it was concluded that the suggested RNN-Bi-LSTM spectrum sensing technique maintains BER performance by efficiently learning intricate signal patterns and eliminating noise impacts in Rician channels. In contrast to traditional techniques, such as ED, MF, and CSD, which perform poorly under low SNR conditions, RNN-Bi-LSTM utilizes bidirectional learning to learn temporal dependencies, thereby improving detection accuracy. Its adaptive nature minimizes misclassification and maintains BER while providing robust sensing. By adapting dynamically to channel fluctuations, it performs better than traditional methods in providing stable communication with less degradation in the BER performance.
Fig. 7.
BER performance of the spectrum sensing algorithms in Rayleigh Channel.
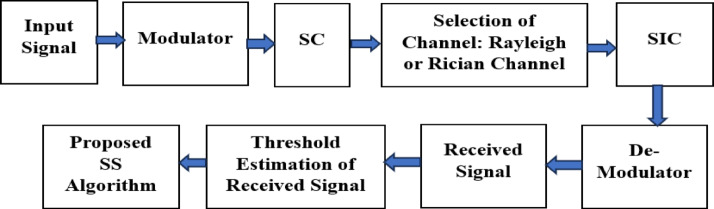
Figure 8 shows the BER performance as a function of SNR for various spectrum-sensing techniques in a Rician channel. For a BER of 10–5, the SNR of 5.8 dB, 9.8 dB, 10.3 dB, 11.8 dB, and 14.4 dB respectively by the proposed methods. It can be seen that RNN-Bi-LSTM has a significant SNR improvement of 4–9 dB over ED, MF, CSD, LSTM, and RNN. The bidirectional architecture properly compensates for the fading and multipath interference. Rician channels, as opposed to Rayleigh channels, contain a line-of-sight (LoS) component that reduces deep fades. RNN-Bi-LSTM further utilizes this structure, improving the BER performance by capturing temporal dependencies and suppressing noise, resulting in more stable signal detection.
Fig. 8.
BER performance of the spectrum sensing algorithms in Rician Channel.
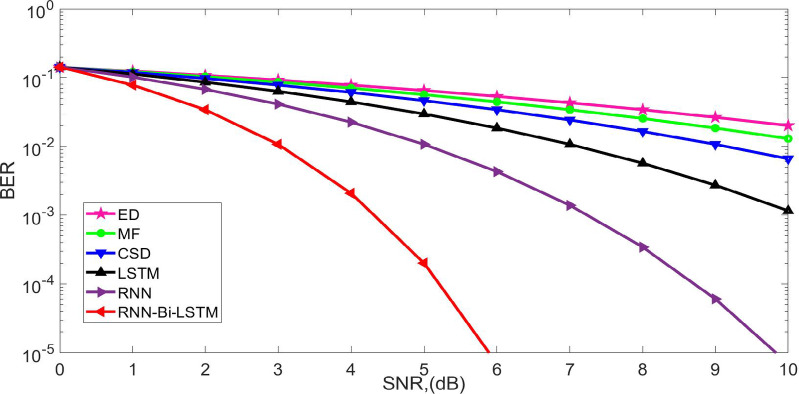
Figure 9 illustrates the BER performance of the different spectrum-sensing algorithms under over-the-air (OTA) conditions. It is evident that the proposed RNN-Bi-LSTM model significantly outperformed conventional methods by achieving a BER of 10⁻3 at an OTA SNR of approximately 10 dB. In contrast, the RNN, LSTM, CSD, and MF algorithms require around 12.5 dB, 14 dB, 15.5 dB, and 17 dB respectively to reach the same error rate, while the conventional ED fails to achieve a BER of 10⁻3 even at 20 dB. This demonstrates that the proposed RNN-Bi-LSTM yields an SNR gain of approximately 7 dB over MF and more than 10 dB over ED. Such substantial improvements emphasize the effectiveness of integrating deep learning, particularly the RNN-Bi-LSTM architecture, to enhance detection reliability and reduce error rates in challenging OTA environments.
Fig. 9.
BER performance of the spectrum sensing algorithms under an OTA environment.
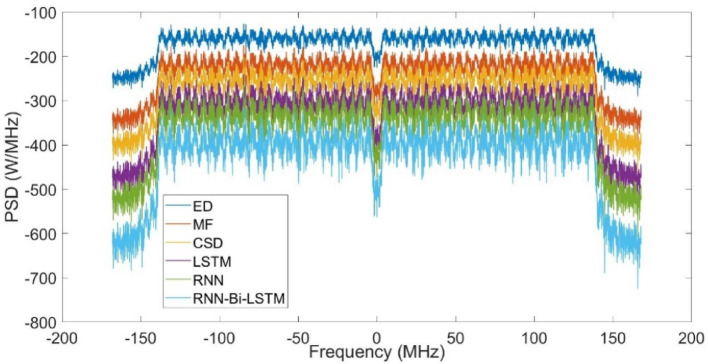
PSD estimation plays an important role in spectrum sensing because it indicates the existence of signals in the frequency band. For optimal spectrum utilization, precise PSD estimation enhances signal classification, minimizes false alarms, and increases detection reliability, particularly in dynamic and noisy environments with fading and interference. The PSD performance highlights the performance improvements in the PSD estimation achieved by the proposed RNN-Bi-LSTM method, particularly in Rayleigh and Rician channels. Although the simulations provide absolute PSD values for various methods in Rayleigh and Rician, they do not directly quantify improvements in standard PSD performance metrics, such as the percentage reduction in spectral leakage or resolution gain. However, based on the PSD values, we can interpret and relate the improvements in a quantifiable manner. For example, comparing the worst-performing method (ED) to the best-performing method (RNN-Bi-LSTM), the PSD difference was 408 dB in the Rayleigh channel and 406 dB in the Rician channel. These large dB gaps reflect the significant suppression of the side lobes and background spectral noise, which implies a substantial reduction in spectral leakage. Although the exact percentage reduction was not calculated in the text, these gains strongly suggest a marked enhancement in spectral purity and signal detectability. Figure 10 illustrates the PSD performance of the spectrum-sensing methods in the Rayleigh channel. PSD values of − 127, − 187, − 258, − 365, − 450 and − 535 were obtained using the ED, MF, CSD, LSTM, RNN, and RNN-Bi-LSTM methods. The proposed method effectively suppressed the side lobes, resulting in efficient spectral access. Side-lobe suppression is crucial in spectrum sensing to reduce spectral leakage and interference and to enhance signal detection accuracy. RNN-Bi-LSTM upgrades PSD performance by learning spectral patterns, filtering out noise, and adapting to channel changes. Its bidirectional structure further enhances the feature extraction, resulting in improved spectral peaks and noise-sensing reliability.
Fig. 10.
PSD performance of the spectrum sensing algorithms in Rayleigh Channel.
Figure 11 shows the PSD performance of RNN-Bi-LSTM and conventional spectrum-sensing methods in the Rician channel. PSD values of − 254 for ED, − 357 for MF, − 434 for CSD, − 494 for LSTM, − 570 for RNN and − 660 for RNN-Bi-LSTM algorithms. The proposed schemes outperformed contemporary methods by attaining a PSD gain of − 103 to − 316. Hence, it can be seen that the proposed RNN-Bi-LSTM outperforms the RNN, LSTM, CSD, MF, and ED in PSD estimation in a Rician channel owing to its bidirectional learning ability. It efficiently exploits both past and future spectral changes, minimizes errors, and enhances signal detection. Unlike traditional approaches, which are hindered by multipath fading and noise, RNN-Bi-LSTM dynamically adjusts to channel states, increasing PSD accuracy, reducing false detections, and enhancing spectrum sensing efficiency in Rician channels.
Fig. 11.
PSD performance of the spectrum sensing algorithms in Rician Channel.
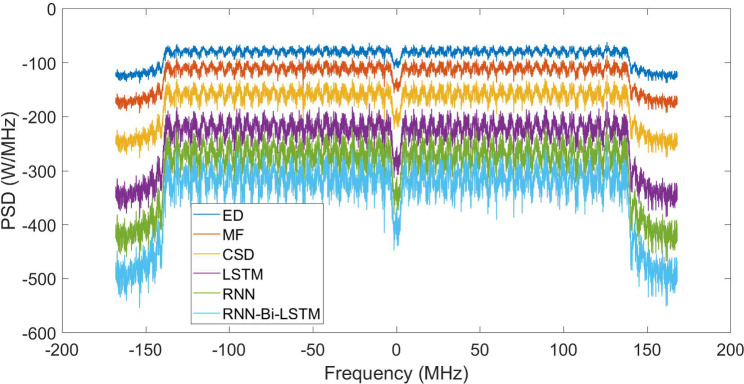
Figure 12 shows the PSD performances of the different spectrum-sensing algorithms under OTA conditions. While all methods maintain similar power levels within the main band of − 150, − 210, − 260, − 320, − 370 and − 460, the proposed RNN-Bi-LSTM achieves the most pronounced out-of-band suppression, reducing the sidelobe PSD to approximately − 460. This represents an improvement of roughly − 260 over the conventional energy detector and approximately− 260 to − 90 over other advanced techniques such as MF, CSD, LSTM, and RNN. Such a substantial reduction in spectral leakage highlights the superior ability of RNN-Bi-LSTM to confine signal power within the allocated bandwidth, thereby minimizing interference and enhancing the spectral efficiency in OTA environments.
Fig. 12.
PSD performance of various spectrum sensing algorithms under an OTA environment.
Complexity analysis
The complexity of an RNN-Bi-LSTM with recurrent layers is influenced by both forward and backward passes, which doubles the complexity compared to a standard LSTM. Given an input sequence of length 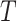 , hidden layer size
, hidden layer size 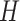 , and input feature dimension
, and input feature dimension 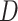 , the complexity is
, the complexity is 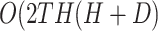 , where 2 T accounts for the forward and backward LSTM passes and
, where 2 T accounts for the forward and backward LSTM passes and 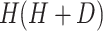 represents the weight multiplications in the LSTM units. For a standard RNN with one hidden layer of size
represents the weight multiplications in the LSTM units. For a standard RNN with one hidden layer of size 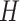 and input dimension
and input dimension 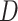 , the complexity is given by
, the complexity is given by  , Because RNNs do not have gating mechanisms such as LSTMs, they are computationally less expensive. An LSTM unit consists of multiple gates (forget, input, and output), which increase the number of computations. The complexity of the LSTM layer was
, Because RNNs do not have gating mechanisms such as LSTMs, they are computationally less expensive. An LSTM unit consists of multiple gates (forget, input, and output), which increase the number of computations. The complexity of the LSTM layer was  . A factor of four accounted for the gating mechanisms. CSD involves correlation computations over time, requiring a Fourier transform (FFT) of the length NNN. The complexity is
. A factor of four accounted for the gating mechanisms. CSD involves correlation computations over time, requiring a Fourier transform (FFT) of the length NNN. The complexity is 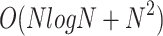 , Where
, Where 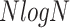 comes from FFT processing and
comes from FFT processing and 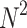 accounts for the correlation calculations. An MF involves convolution operations that scale with input size
accounts for the correlation calculations. An MF involves convolution operations that scale with input size 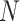 and filter length
and filter length  . Complexity is denoted by
. Complexity is denoted by 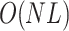 . The ED involves computing the power of the received signals, requiring squared operations, and averaging over
. The ED involves computing the power of the received signals, requiring squared operations, and averaging over  samples
samples 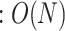 . The number of operations required for the spectrum-sensing methods for the simulation parameters used in the proposed work is listed in Table 3.
. The number of operations required for the spectrum-sensing methods for the simulation parameters used in the proposed work is listed in Table 3.
Table 3.
Computation complexity analysis.
| S. No | Algorithms | Total operations | Operation per batch | Remarks |
|---|---|---|---|---|
| 1 | RNN-Bi-LSTM | 4.1×1012 | 10.5×106 |
ED is the least computationally expensive with only MF and CSD require significantly more operations than ED but remain much lower than neural network-based approaches LSTM is the most expensive, requiring RNN-Bi-LSTM, while computationally expensive, provides superior spectrum sensing performance but needs This analysis highlights the trade-off between computational complexity and spectrum sensing accuracy for NOMA waveforms |
| 2 | RNN | 2.05×1012 | 5.2×106 | |
| 3 | LSTM | 8.2×1012 | 20.9×106 | |
| 4 | CSD | 2.6×109 | 67.5×103 | |
| 5 | MF | 2.5×109 | 65.5×103 | |
| 6 | ED | 9.8×106 | 256 |
Complexity vs. performance trade-off for edge devices
The complexity versus performance trade-off of the RNN-Bi-LSTM spectrum-sensing algorithm is pivotal when assessing its feasibility for edge and IoT devices operating under stringent computational and energy constraints. The architectural strength of Bi-LSTM lies in its ability to process input sequences bidirectionally, learning intricate temporal patterns vital for accurately detecting NOMA waveforms under diverse and often adverse channel conditions, including multipath fading, Doppler shifts, and intentional jamming. However, this incurs a significant computational cost. With a complexity of  where
where 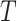 is the sequence length, HHH is the hidden state size, and DDD is the input dimension, which effectively doubles the load of a standard LSTM and quadruples that of a simple RNN because its forward and backward passes are coupled with gating mechanisms. Empirical analyses further underscore this, showing that Bi-LSTM demands approximately 4.1 × 1012 total operations, starkly contrasted by conventional methods such as energy detection, which requires merely 9.8 × 106 operations. However, this computational burden is justified by the superior detection performance of Bi-LSTM, as corroborated by comparative studies that highlight its resilience to noise and fading, and its ability to maintain high detection accuracy. For deployment on edge devices, strategic optimization is necessary. Techniques such as model pruning, which eliminates redundant connections, and quantization, which reduces bit precision, can significantly reduce computational demands. Moreover, replacing Bi-LSTM layers with GRUs or adopting hybrid models that invoke complex processing only under uncertain conditions can maintain the performance while conserving resources. Coupled with modern edge AI accelerators and energy-efficient hardware, these strategies ensure that, despite its high inherent complexity, the RNN-Bi-LSTM algorithm becomes practically deployable on edge platforms, offering robust, adaptive spectrum sensing crucial for next-generation NOMA-enabled cognitive radio networks. Table 4 presents a computational overhead analysis in comparison with the existing studies published in related fields. The proposed RNN-Bi-LSTM outperformed spectrum sensing by learning bidirectional dependencies and enhancing detection under fading and noise conditions. However, its computational cost is higher, as confirmed by9,10, and14, because of the doubled number of RNN passes and the memory usage. Compared with simpler or traditional methods12,13, Bi-LSTM requires hardware acceleration or model pruning18 for real-time or embedded deployment in NOMA-based CRNs.
is the sequence length, HHH is the hidden state size, and DDD is the input dimension, which effectively doubles the load of a standard LSTM and quadruples that of a simple RNN because its forward and backward passes are coupled with gating mechanisms. Empirical analyses further underscore this, showing that Bi-LSTM demands approximately 4.1 × 1012 total operations, starkly contrasted by conventional methods such as energy detection, which requires merely 9.8 × 106 operations. However, this computational burden is justified by the superior detection performance of Bi-LSTM, as corroborated by comparative studies that highlight its resilience to noise and fading, and its ability to maintain high detection accuracy. For deployment on edge devices, strategic optimization is necessary. Techniques such as model pruning, which eliminates redundant connections, and quantization, which reduces bit precision, can significantly reduce computational demands. Moreover, replacing Bi-LSTM layers with GRUs or adopting hybrid models that invoke complex processing only under uncertain conditions can maintain the performance while conserving resources. Coupled with modern edge AI accelerators and energy-efficient hardware, these strategies ensure that, despite its high inherent complexity, the RNN-Bi-LSTM algorithm becomes practically deployable on edge platforms, offering robust, adaptive spectrum sensing crucial for next-generation NOMA-enabled cognitive radio networks. Table 4 presents a computational overhead analysis in comparison with the existing studies published in related fields. The proposed RNN-Bi-LSTM outperformed spectrum sensing by learning bidirectional dependencies and enhancing detection under fading and noise conditions. However, its computational cost is higher, as confirmed by9,10, and14, because of the doubled number of RNN passes and the memory usage. Compared with simpler or traditional methods12,13, Bi-LSTM requires hardware acceleration or model pruning18 for real-time or embedded deployment in NOMA-based CRNs.
Table 4.
Computational overhead analysis of RNN-Bi-LSTM in Spectrum Sensing.
| References | Computational complexity | Overhead discussion |
|---|---|---|
| 9 | Complexity increases with feature dimensions and sequence length: 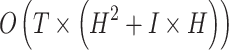 for RNN for RNN |
Bi-LSTM doubles the RNN overhead due to forward & backward passes. Effective but computationally expensive |
| 10 | Bi-LSTM:
|
Bi-LSTM as superior in accuracy but notes significant training time and resource demands |
| 11 |
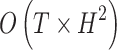 for single direction for single direction |
Highlights better accuracy with moderate complexity; doesn’t include bidirectional variant |
| 12 | 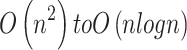 |
Emphasizes low complexity but lacks Bi-LSTM’s learning capability |
| 13 | Negligible computational overhead | Not DL-based; used for comparison with ML/DL models |
| 14 |
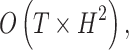 less than LSTM less than LSTM |
Bi-LSTM overhead > GRU. This paper optimizes sensing by reducing model size |
| 15 |
 low overhead low overhead |
Non-DL models: efficient but less adaptive to channel changes than Bi-LSTM |
| 16 | Varies by model | Discusses trade-offs, confirms Bi-LSTM has higher compute cost but better temporal modeling |
| 17 | Dependent on clustering complexity | Computational cost moderate; Bi-LSTM not used but suggested as future enhancement |
| 18 | 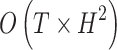 |
Discusses practical deployment, Bi-LSTM adds complexity requiring acceleration |
| 19 |
 where n = samples, k = components where n = samples, k = components |
Efficient for cooperation, but lacks the sequential modeling strength of Bi-LSTM |
The RNN-Bi-LSTM architecture excels in spectrum sensing because it captures temporal dependencies bidirectionally, thereby enabling a superior performance under fading and noisy channel conditions. Reviews have shown that CNNs, RNNs, and Bi-RNNs achieve similar detection accuracies when resources are abundant, but Bi-RNNs such as Bi-LSTM better leverage sequential dependencies at moderate model sizes24. In contrast, CNN-based models are optimized for extracting local spatial features in time–frequency representations (e.g., spectrograms). They offer faster inference through parallel convolution, which is useful when the signal dynamics are less time dependent. However, they lack memory to capture long-range dependencies over time. Transformer-based models use self-attention, process the entire input in parallel, and model long-range dependencies more effectively and efficiently than sequential RNNs do. However, they require large datasets and higher computation to train successfully, and are often less practical in spectrum sensing domains where labeled data are limited. GAN-based frameworks have been leveraged for data augmentation to improve the robustness of classifiers in spectrum sensing, particularly in scarce real-world samples or domain shifts. Generators synthesize realistic spectra whereas discriminators emulate real-world distributions. However, GANs are primarily data generators and require a classification backbone (e.g., a CNN or RNN) for inference. This adds substantial training overhead and complexity25. Hence, RNN-Bi-LSTM offers a balanced solution: it efficiently learns temporal dynamics with moderate resource requirements. CNNs are lightweight but less adaptive to sequence features; transformers offer cutting-edge performance with large-scale data but at high cost; and GANs augment data but cannot replace core sensing models. The choice ultimately depends on task complexity, data availability, and hardware constraints.
Hardware feasibility and latency analysis of RNN-Bi-LSTM
The RNN-Bi-LSTM architecture, while effective in learning sequential dependencies for time-varying NOMA signals, presents notable computational demands due to its recurrent nature, bidirectional processing, and large input sequence length (256). Each Bi-LSTM unit must process input sequentially in both forward and backward passes, leading to increased inference latency when compared to parallelizable feedforward or convolutional architectures. In the current implementation (two Bi-LSTM layers with 64 hidden units each), training on a CPU setup (Intel i5, 16 GB RAM) typically takes 3–6 h for 50 epochs on 100,000 samples, indicating high processing requirements for real-time applications. The hardware deployment perspectives are given below:
GPU Feasibility: Training and inference can be significantly accelerated using CUDA-enabled GPUs with 4 + GB VRAM. MATLAB GPU Coder and Parallel Computing Toolbox allow deployment and acceleration, but power consumption and cost may limit applicability in low-power embedded systems.
FPGA Implementation: Field-Programmable Gate Arrays (FPGAs) provide a power-efficient and low-latency alternative for inference, but mapping RNNs, especially Bi-LSTMs, to FPGA fabric is challenging due to their sequential data dependencies and memory requirements. Recent works on RNN-to-FPGA compilers (e.g., Xilinx Vitis AI or Intel OpenVINO) show that pruned or quantized Bi-LSTM models can be adapted with significant speedup (up to 5 ×) and energy savings. However, resource utilization (LUTs, BRAMs) may spike due to bidirectional flow and longer sequence buffers.
ASIC Viability: Application-Specific Integrated Circuits (ASICs) offer the highest efficiency for fixed tasks and could be optimal for large-scale NOMA base station deployments. However, the high design complexity and cost of implementing flexible Bi-LSTM logic—especially with dropout layers and gradient memory—make ASICs better suited for static, simplified models or when integrated as part of a larger SoC.
Latency Analysis: For real-time spectrum sensing, an acceptable latency is in the range of sub-millisecond to a few milliseconds. On embedded CPU/GPU platforms, Bi-LSTM inference can take tens to hundreds of milliseconds, depending on model size and batch size. For FPGA/ASIC implementations, latency could be reduced to a few milliseconds, but only with model compression (quantization, pruning) and optimized pipelining.
Conclusion
The proposed RNN-Bi-LSTM method considerably improves the spectral performance of NOMA in various channel environments, particularly under Rician and Rayleigh fading conditions. The technique surpasses traditional methods like RNN, LSTM, CSD, MF, and ED by attaining a PD of 100% at − 5 dB and − 2.5 dB SNR, a reduced PFA of − 535 and − 494, and better BER of 10–5 at 8.8 dB and 5.8 dB SNR. Furthermore, it yields a better PSD estimation, lower spectral leakage, and enhanced spectrum utilization. These findings validate the strong performance of RNN-Bi-LSTM in addressing channel fluctuations and achieving maximum spectral efficiency in emerging wireless networks. Despite its excellent performance, the proposed method has certain limitations. First, the RNN-Bi-LSTM model has increased computational complexity compared with conventional schemes; thus, real-time processing is challenging, particularly for limited-resource applications. Second, training the model requires a massive dataset, which may deteriorate in strongly dynamic environments with steep channel fluctuations. Third, we did not consider the influence of hardware distortions, such as phase noise and nonlinearity, on the system performance in this study, which would affect practical field deployments.
Future work
The proposed work has already been thoroughly evaluated under Rayleigh and Rician channel conditions, effectively demonstrating the robustness of the RNN-Bi-LSTM architecture in both non-line-of-sight (NLoS) and line-of-sight (LoS) fading environments. These tests confirmed the ability of the model to adapt to varying channel characteristics and provide reliable spectrum-sensing performance in dynamic scenarios. However, we acknowledge the importance of assessing the performance under more complex and realistic conditions. Therefore, in our future study, we plan to extend the evaluation to include more diverse channel models, such as Nakagami-m, Weibull, and Eta-Mu fading environments, which better represent practical deployment situations. Additionally, we aim to incorporate multi-user NOMA scenarios to analyze the impact of increased user density and interference. To enhance adaptability and accuracy, we will also explore hybrid machine-learning models that integrate Transformer and CNN features with RNN-based structures. This future direction will provide a more comprehensive understanding of the model performance and scalability in heterogeneous network environments. The proposed RNN-Bi-LSTM model has demonstrated effective performance for spectrum sensing under diverse channel conditions, it offers promising potential for further extensions. One compelling direction is to leverage the temporal learning capabilities of the Bi-LSTM architecture to optimize user clustering and dynamic power allocation in NOMA systems. These are critical components for improving overall system capacity, spectral efficiency, and user fairness. By integrating reinforcement learning or attention mechanisms alongside Bi-LSTM, the model could adaptively learn optimal resource allocation strategies based on real-time channel conditions and user behavior. Such a hybrid framework could jointly handle signal detection, user grouping, and power control, thereby addressing multiple challenges in a unified model. Additionally, incorporating user mobility patterns and varying quality-of-service (QoS) constraints into the learning process may further refine clustering decisions, especially in time-varying Rician and Rayleigh fading scenarios. Future investigations will also explore the integration of Transformer-based and GNN-assisted architectures to enhance scalability and decision accuracy in multi-user, high-dimensional NOMA deployments.
Acknowledgements
The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-04).
Author contributions
A.K wrote the paper and did experiment, A.N and M.M performed the edit and literature survey.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by Taif University, Saudi Arabia, project number (TU-DSPP-2024-04).
Data availability
The algorithms or codes generated and /or analysed during the current study are available from the corresponding author upon reasonable request and permission.
Code availability
The algorithms or codes generated and/or analyzed in the current study are available from the corresponding author upon reasonable request and permission.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Aziz Nanthaamornphong, Email: aziz.n@phuket.psu.ac.th.
Mehedi Masud, Email: mmasud@tu.edu.sa.
References
- 1.Flizikowski, A. et al. Selected aspects of non orthogonal multiple access for future wireless communications. Math. Comput. Sci.17, 10. 10.1007/s11786-023-00561-y (2023). [Google Scholar]
- 2.Zhang, L., Li, Z. & Jia, M. Compressed spectrum sensing for grant-free NOMA based internet of vehicles. EURASIP J. Adv. Signal Process.2022, 15. 10.1186/s13634-022-00835-w (2022). [Google Scholar]
- 3.Kumar, A. & NandhaKumar, P. OFDM system with cyclostationary feature detection spectrum sensing. ICT Express5(1), 21–25 (2019). [Google Scholar]
- 4.Alkhawaldeh, R. S. et al. Convolution neural network bidirectional long short-term memory for heartbeat arrhythmia classification. Int. J. Comput. Intell. Syst.16, 197. 10.1007/s44196-023-00374-8 (2023). [Google Scholar]
- 5.Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenomena404, 132306. 10.1016/j.physd.2019.132306 (2020). [Google Scholar]
- 6.Kumar, A., Albreem, M. A., Gupta, M., Alsharif, M. H. & Kim, S. Future 5G network based smart hospitals: hybrid detection technique for latency improvement. IEEE Access8, 153240–153249 (2020). [Google Scholar]
- 7.Lu, J. et al. VMD and self-attention mechanism-based Bi-LSTM model for fault detection of optical fiber composite submarine cables. EURASIP J. Adv. Signal Process.2023, 29. 10.1186/s13634-023-00988-2 (2023). [Google Scholar]
- 8.Kumar, A. et al. Analysis of spectrum sensing using deep learning algorithms: CNNs and RNNs. Ain Shams Eng. J.15, 102505. 10.1016/j.asej.2023.102505 (2024). [Google Scholar]
- 9.Zhang, Y. & Luo, Z. A deep-learning-based method for spectrum sensing with multiple feature combination. Electronics13(14), 2705. 10.3390/electronics13142705 (2024). [Google Scholar]
- 10.Zhang, Y. & Luo, Z. A review of research on spectrum sensing based on deep learning. Electronics12(21), 4514. 10.3390/electronics12214514 (2023). [Google Scholar]
- 11.Vijay, E. V. & Aparna, K. Spectrum sensing using deep learning for proficient data transmission in wireless sensor networks for wireless communication. Ain Shams Eng. J.15, 102784. 10.1016/j.asej.2024.102784 (2024). [Google Scholar]
- 12.Shah, H. A. & Koo, I. Reliable machine learning based spectrum sensing in cognitive radio networks. Wirel. Commun. Mob. Comput.2018, 1–17. 10.1155/2018/5906097 (2018). [Google Scholar]
- 13.Kockaya, K. & Develi, I. Spectrum sensing in cognitive radio networks: threshold optimization and analysis. J. Wirel. Com. Netw.2022, 255. 10.1186/s13638-020-01870-7 (2020). [Google Scholar]
- 14.Arunachalam, G. & SureshKumar, P. Optimized deep learning model for effective spectrum sensing in dynamic SNR scenario. Comput. Syst. Sci. Eng.45(2), 1279–1294 (2023). [Google Scholar]
- 15.Marriwala, N. K. et al. NSS-ML: A novel spectrum sensing framework using machine learning for cognitive radio IoT networks. Int. J. Inf. Tecnol.16, 4599–4604. 10.1007/s41870-024-02121-4 (2024). [Google Scholar]
- 16.Wang, J. & Liu, B. A brief review of machine learning algorithms for cooperative spectrum sensing. J. Phys. Conf. Ser.1852, 042094. 10.1088/1742-6596/1852/4/042094 (2021). [Google Scholar]
- 17.Srivastava, V. et al. Performance enhancement in clustering cooperative spectrum sensing for cognitive radio network using metaheuristic algorithm. Sci. Rep.13, 16827. 10.1038/s41598-023-44032-7 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kumar, P. & Selvan, P. Spectrum sensing using optimized deep learning techniques in reconfigurable embedded systems. Intell. Automat. Soft Comput.36(2), 2041–2054 (2023). [Google Scholar]
- 19.Samala, S., Mishra, S. & Singh, S. S. Cooperative spectrum sensing in cognitive radio networks via an adaptive Gaussian mixture model based on machine learning. J. Commun.17(10), 812–818 (2022). [Google Scholar]
- 20.Wu, J. et al. Adaptive NOMA-based spectrum sensing for uplink IoT networks. IEEE Trans. Cogn. Commun. Netw.10(1), 138–149 (2024). [Google Scholar]
- 21.Kumar, A. Spectrum sensing beyond 5G system: Deep learning and conventional techniques analysis. Multimed. Tools Appl.10.1007/s11042-025-20638-z (2025). [Google Scholar]
- 22.Altrad, O. & Muhaidat, S. A new mathematical analysis of the probability of detection in cognitive radio over fading channels. J Wirel. Com Netw.2013, 159. 10.1186/1687-1499-2013-159 (2013). [Google Scholar]
- 23.Ali, R., Naeem, M. & Anpalagan, A. Spectrum sensing in cognitive radio networks: A deep learning perspective. IEEE Access8, 121996–122009. 10.1109/ACCESS.2020.3005791 (2020). [Google Scholar]
- 24.Liu, F. et al. An attention-based hybrid LSTM-CNN model for arrhythmias classification. In 2019 International Joint Conference on Neural Networks (IJCNN), 1–8 10.1109/IJCNN.2019.8852037 (2019).
- 25.Hamdi, S. et al. Attention-based hybrid CNN-LSTM and spectral data augmentation for COVID-19 diagnosis from cough sound. J. Intell. Inf. Syst.59, 367–389. 10.1007/s10844-022-00707-7 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hossain, M. N. et al. DFT-spread OTFS communication system with the reductions of PAPR and nonlinear degradation. Wirel. Pers. Commun.115, 2211–2228. 10.1007/s11277-020-07678-4 (2020). [Google Scholar]
- 27.Chennamsetty, S., Boddu, S., Chandhar. P. & Bulusu, K. C. Analysis of PAPR in OTFS modulation with classical selected mapping technique. In 2023 15th International Conference on Communication Systems & NETworkS (COMSNETS), 319–322 10.1109/COMSNETS56262.2023.10041313 (2023).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The algorithms or codes generated and /or analysed during the current study are available from the corresponding author upon reasonable request and permission.
The algorithms or codes generated and/or analyzed in the current study are available from the corresponding author upon reasonable request and permission.