Abstract
A thermodynamic analysis of the magnetic, caloric and magnetocaloric properties of the ferromagnets undergoing the structural phase transitions (SPTs) near the Curie temperature has been carried out taking into account the effect of SPT on the energy of magnetic subsystem of ferromagnet. A special emphasis has been placed on the account of minimum conditions for Gibbs free energy and the modification of magnetic Maxwell relations with consideration of the effect of SPT on the magnetic energy. The computations, based on the commonly used equations for the energy and entropy of the magnetic subsystem of ferromagnet, discovered and estimated quantitatively a drastic dependence of magnetic heat capacity and magnetic-field-induced temperature change on the difference between the SPT temperature and Curie point. The performed theoretical analysis is aimed to motivate the systematic experimental research of magnetic and magnetocaloric materials undergoing the SPT at temperatures intentionally tuned close to the Curie point.
Keywords: Magnetic energy, Modified Maxwell relation, Magnetization, Heat capacity, Magnetocaloric effect, Temperature change
Subject terms: Materials science, Physics
Introduction
Some solid-state compounds and alloys exhibit a magnetocaloric effect (MCE), i.e. a noticeable temperature change caused by application or removal of a magnetic field (see1 and references therein). These solids are referred to as magnetocaloric materials. Magnetocaloric materials are considered promising for solid-state refrigeration technologies1–3. The purposeful search for materials usable for solid-state refrigeration is an actual task.
Ferromagnets that exhibit the magnetostructural phase transitions form a special type of magnetocaloric materials. The MCE observed in such ferromagnets is conventionally referred to as a “giant MCE”4. Consistent experimental research of giant MCE requires significant efforts and expenditures, which can be minimized by preliminary theoretical evaluation of the magnetic-field-induced temperature change observable in such materials. However, such evaluation encounters problems arising during theoretical analysis of magnetostructural transitions (see e.g.5).
Two research trends of giant MCE are noticeable among others. First, the research of magnetocaloric properties of quasistoichiometric Heusler alloys, which undergo the structural phase transitions (SPTs) in the temperature range adjusted to Curie temperature 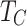 by the purposeful change of their chemical composition6–8. Second, the research of intermetallic rear-earth alloys, which undergo the magnetostructural phase transitions from paramagnetic (PM) to ferromagnetic (FM) state at the temperatures, which are rather close to the boiling point of natural gas,
by the purposeful change of their chemical composition6–8. Second, the research of intermetallic rear-earth alloys, which undergo the magnetostructural phase transitions from paramagnetic (PM) to ferromagnetic (FM) state at the temperatures, which are rather close to the boiling point of natural gas,  . (Among them the intermetallics TbAl2 (with
. (Among them the intermetallics TbAl2 (with 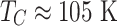 )9, TbFeSi10, Nd2In (both with
)9, TbFeSi10, Nd2In (both with 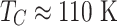 )11 and Dy0.7Er0.3Co2 (with
)11 and Dy0.7Er0.3Co2 (with 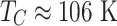 ) can be mentioned12. To unite these trends under a common interest in the thermodynamic (particularly magnetocaloric) properties of multiferroic materials, the results of thermodynamic analysis of the magnetic, caloric, and magnetocaloric properties of a representative ferromagnet undergoing a SPT near the Curie temperature are presented below. A special emphasis is placed on:
) can be mentioned12. To unite these trends under a common interest in the thermodynamic (particularly magnetocaloric) properties of multiferroic materials, the results of thermodynamic analysis of the magnetic, caloric, and magnetocaloric properties of a representative ferromagnet undergoing a SPT near the Curie temperature are presented below. A special emphasis is placed on:
-
i)
the theoretical analysis of thermodynamic properties of the representative ferromagnet, accounting for the effect of SPTs on the energy of the magnetic subsystem;
-
ii)
the elucidation of the drastic effect of SPTs and external magnetic field on the temperature dependences of magnetization and heat capacity of the equilibrium magnetic subsystem of ferromagnet;
-
iii)
the modification of the commonly known (orthodox) magnetic Maxwell relations, to enable their applicability for the quantitative evaluation of the giant MCE in magnetic solids undergoing SPTs;
-
iv)
the computation of magnetic-field-induced temperature change with proper account of the temperature dependences of magnetic energy and heat capacity.
Thermodynamic equations and basic assumption
The Gibbs free energy of ferromagnet is the sum of internal energy of the magnetic subsystem of this ferromagnet, U, the entropy term,  where T is temperature, and Zeeman term,
where T is temperature, and Zeeman term,  , where
, where 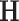 is external magnetic field,
is external magnetic field,  is magnetization vector. Therefore, Gibbs free energy is expressed as
is magnetization vector. Therefore, Gibbs free energy is expressed as
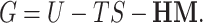 |
1 |
The internal energy of ferromagnet possessing the uniaxial magnetocrystalline anisotropy can be expressed as
 |
2 |
where, the first summand is a spin-exchange energy, the second one is a magnetic anisotropy energy, 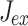 is spin-exchange constant,
is spin-exchange constant, 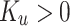 is the anisotropy constant,
is the anisotropy constant, 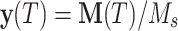 ,
, 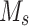 is saturation magnetization, z-axis is aligned with the easy magnetization direction.
is saturation magnetization, z-axis is aligned with the easy magnetization direction.
Let the ferromagnet undergo a SPT above or below the Curie temperature. Generally speaking, the structural changes influence the spin-exchange interaction between magnetic atoms and the magnetic anisotropy. If the magnetic field value exceeds the saturating value  , the magnetization vector is practically parallel to the magnetic field, and therefore,
, the magnetization vector is practically parallel to the magnetic field, and therefore, 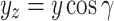 , where
, where 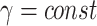 is the angle between the easy magnetization axis of the experimental sample and vector
is the angle between the easy magnetization axis of the experimental sample and vector 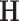 . In this case the internal energy and the Gibbs free energy of the ferromagnet undergoing the SPT are expressed as
. In this case the internal energy and the Gibbs free energy of the ferromagnet undergoing the SPT are expressed as
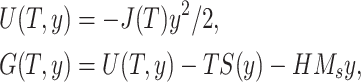 |
3 |
where
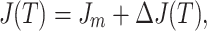 |
4 |
the constant coefficient  characterises the magnetic (spin-exchange and/or spin-orbit) energy density of the high-temperature phase (see Eq. (2)), the summand
characterises the magnetic (spin-exchange and/or spin-orbit) energy density of the high-temperature phase (see Eq. (2)), the summand  is introduced in Eq. (4) to take into account the energy change caused by SPT.
is introduced in Eq. (4) to take into account the energy change caused by SPT.
The thermodynamic phase corresponding to the minimum of Gibbs potential at  or
or 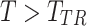 is referred to as the low-temperature or high-temperature phase, respectively. Equation (4) expresses the basic assumption, which simplifies theoretical analysis of thermodynamic properties of ferromagnet undergoing the SPT. In accordance with this assumption the SPT essentially is an external (with respect to magnetic subsystem) factor, which predetermines the difference between the magnetic energies of the low-temperature and the high-temperature phases. It should be emphasized, first, that the assumption is not true or is at least questionable if the Curie temperature lies in the temperature range of the SPT, because a consistent thermodynamic analysis of magnetostructural phase transitions must be based on the interrelated minimum conditions for Gibbs free energy with respect to the magnetic variable y and the structural order parameter (elastic strain, electric polarization, etc.); second, the difference between the magnetic energies,
is referred to as the low-temperature or high-temperature phase, respectively. Equation (4) expresses the basic assumption, which simplifies theoretical analysis of thermodynamic properties of ferromagnet undergoing the SPT. In accordance with this assumption the SPT essentially is an external (with respect to magnetic subsystem) factor, which predetermines the difference between the magnetic energies of the low-temperature and the high-temperature phases. It should be emphasized, first, that the assumption is not true or is at least questionable if the Curie temperature lies in the temperature range of the SPT, because a consistent thermodynamic analysis of magnetostructural phase transitions must be based on the interrelated minimum conditions for Gibbs free energy with respect to the magnetic variable y and the structural order parameter (elastic strain, electric polarization, etc.); second, the difference between the magnetic energies, 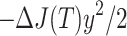 , may be caused by the impact of structural changes on the spin-exchange energy and/or the magnetic anisotropy energy (see Eq. (4) and definition of parameter
, may be caused by the impact of structural changes on the spin-exchange energy and/or the magnetic anisotropy energy (see Eq. (4) and definition of parameter  ).
).
The entropy function of the magnetic subsystem of ferromagnet can be expressed as
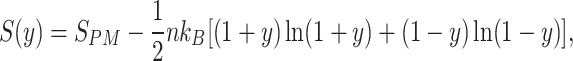 |
5 |
where 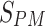 is the entropy of ferromagnet in paramagnetic state,
is the entropy of ferromagnet in paramagnetic state,  , N and V are the number of magnetic atoms and volume of magnetic solid, respectively,
, N and V are the number of magnetic atoms and volume of magnetic solid, respectively,  is Boltzmann constant. Equation (5) is derived for the statistical ensemble of atoms with spin
is Boltzmann constant. Equation (5) is derived for the statistical ensemble of atoms with spin  but is widely used for the general description of the magnetic properties of ferromagnets13,14.
but is widely used for the general description of the magnetic properties of ferromagnets13,14.
The temperature dependence of magnetization in the equilibrium state of ferromagnet and the appropriate function  should be found from the minimum principle for Gibbs free energy. The minimum conditions are formulated as
should be found from the minimum principle for Gibbs free energy. The minimum conditions are formulated as
 |
6 |
 |
7 |
The Eqs. (5), (6) and the mathematical identity  result in the following equation:
result in the following equation:
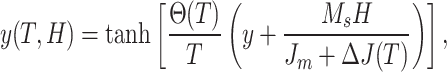 |
8 |
where
 |
9 |
The Eqs. (8), (9) enable the quantitative description of the equilibrium magnetization values 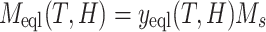 inherent to ferromagnets undergoing SPTs in the constant magnetic field (for more details and the relevant examples, see15,16). Curie temperature
inherent to ferromagnets undergoing SPTs in the constant magnetic field (for more details and the relevant examples, see15,16). Curie temperature  is the PM ‒ FM phase transition temperature, corresponding to the high-temperature phase, i.e. the temperature which satisfies the condition
is the PM ‒ FM phase transition temperature, corresponding to the high-temperature phase, i.e. the temperature which satisfies the condition  at
at 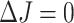 ; the function
; the function  varies from
varies from  to the value
to the value  , which is interpreted as the Curie temperature of the low-temperature phase15,17.
, which is interpreted as the Curie temperature of the low-temperature phase15,17.
The heat capacity of ferromagnet can be computed from the Eq.
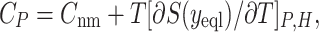 |
10 |
where P is pressure,  is non-magnetic part of heat capacity. Outside the temperature range of SPT, the volume V can be considered constant due to the smallness of thermal expansion coefficient. Therefore, the approximate equality
is non-magnetic part of heat capacity. Outside the temperature range of SPT, the volume V can be considered constant due to the smallness of thermal expansion coefficient. Therefore, the approximate equality  and the Eq.
and the Eq.
 |
11 |
can be used for computations18.
Let the magnetic field applied to ferromagnetic solid increase from value 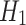 to value
to value  . If
. If  , a mechanical work performed by the experimental sample due to the magnetic field application can be disregarded, and the first law of thermodynamics results in the approximate equality
, a mechanical work performed by the experimental sample due to the magnetic field application can be disregarded, and the first law of thermodynamics results in the approximate equality  .
.
Equations describing the magnetic-field-induced temperature change
Let the magnetic field applied to ferromagnetic solid vary from value 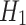 to value
to value  . If
. If  denotes the infinitesimal heat evolved/absorbed by unit volume of the solid in the increasing/decreasing magnetic field, the commonly known relationships
denotes the infinitesimal heat evolved/absorbed by unit volume of the solid in the increasing/decreasing magnetic field, the commonly known relationships  ,
, 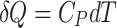 and
and  lead to the following equation for the adiabatic temperature change:
lead to the following equation for the adiabatic temperature change:
 |
12 |
The orthodox Maxwell relation (OMR),
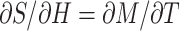 |
13 |
is commonly used to replace the entropy with the directly measurable magnetization value, 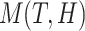 . But the basic assumption leads to an explicit dependence of the internal energy on temperature, and therefore, the equations
. But the basic assumption leads to an explicit dependence of the internal energy on temperature, and therefore, the equations
 |
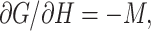 |
14 |
 |
result in the modified Maxwell relation,
 |
15 |
and Eqs.
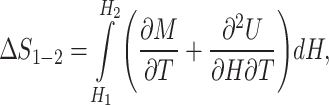 |
16 |
 |
17 |
If 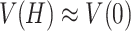 , the mechanical work performed by the experimental sample due to the magnetic field application can be disregarded, and the first law of thermodynamics results in the approximate Eq.
, the mechanical work performed by the experimental sample due to the magnetic field application can be disregarded, and the first law of thermodynamics results in the approximate Eq.
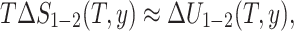 |
18 |
which relates the heat absorbed/evolved by the sample to its internal energy. The internal energy density expressed by Eqs. (3, 4) is independent on volume. In this case, Eq. (18) is an exact equality, and the temperature change is expressed as
 |
19 |
Equation (19) may be more convenient for theoretical analysis of MCE, because characteristics of ferromagnet (such as the spin-exchange energy, magnetocrystalline anisotropy energy, the energy of magnetostatic interaction, etc.) can be evaluated theoretically from first principles or estimated from experimental data.
Impact of structural phase transition on heat capacity and giant magnetocaloric effect
The SPTs of intermetallics and Heusler alloys typically go through the mixed two-phase states, and therefore, the energy parameter  , which describes the effect of SPT on the magnetic energy, is expressed as
, which describes the effect of SPT on the magnetic energy, is expressed as
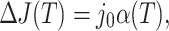 |
20 |
where 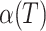 is the volume fraction of low-temperature phase,
is the volume fraction of low-temperature phase,  . The volume fraction of the low-temperature phase increases from zero to unit on cooling of ferromagnet and can be modelled by the function
. The volume fraction of the low-temperature phase increases from zero to unit on cooling of ferromagnet and can be modelled by the function
 |
21 |
where the temperature of SPT,  , corresponds to the value
, corresponds to the value 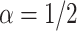 , the parameter
, the parameter 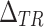 is the half-width of the temperature range of the mixed two-phase state. The temperature evolution of the volume fractions of phases coexisting in the temperature interval of magnetostructural transitions can be obtained from X-ray powder diffraction measurements and shows a similar dependence to that of the model function (21) (see, e.g7,19). The temperatures of SPTs observed in intermetallic compounds and Heusler alloys can be expressed as
is the half-width of the temperature range of the mixed two-phase state. The temperature evolution of the volume fractions of phases coexisting in the temperature interval of magnetostructural transitions can be obtained from X-ray powder diffraction measurements and shows a similar dependence to that of the model function (21) (see, e.g7,19). The temperatures of SPTs observed in intermetallic compounds and Heusler alloys can be expressed as 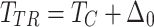 , where the difference between the temperatures of magnetic and SPTs,
, where the difference between the temperatures of magnetic and SPTs,  , can be purposefully changed by the variation of chemical composition of the compound/alloy6–8. The abrupt change of the magnetization value is commonly recognized as the factor promoting giant MCE. Such change is observed in the case if
, can be purposefully changed by the variation of chemical composition of the compound/alloy6–8. The abrupt change of the magnetization value is commonly recognized as the factor promoting giant MCE. Such change is observed in the case if 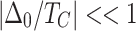 (see solid line in Fig. 1). Therefore, this case deserves a detailed consideration.
(see solid line in Fig. 1). Therefore, this case deserves a detailed consideration.
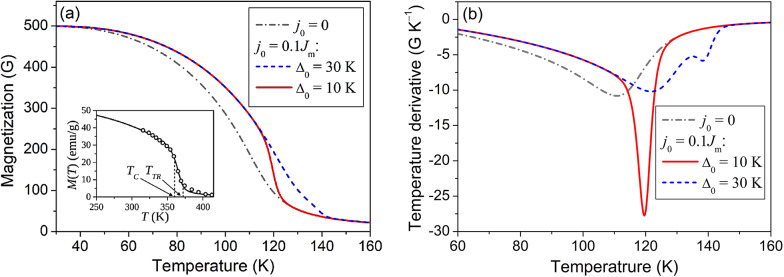
Fig. 1.
Magnetization functions M(T) (a), and their temperature derivatives dM(T)/dT (b), computed using Eq. (8) for ferromagnets undergoing SPTs at 120 K (solid lines) and 140 K (dashed lines), TC = 110 K. The values computed for the ferromagnet, which does not undergo structural phase transition, are shown by the dash-dotted lines. Inset: Temperature dependence of magnetization of Ni53.1Mn26.6Ga20.3 alloy, measured (circles) and computed using Eq. (8) (line).
Figure 1 (a) illustrates the 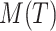 functions computed from Eqs. (8), (9), (20) and (21); the values used for computations are shown in Table 1; inset illustrates the applicability of Eq. (8) for the quantitative calculation of the temperature dependence of magnetization of real alloys (for the details of the measurements and the calculations see Refs.17 and 16, respectively).
functions computed from Eqs. (8), (9), (20) and (21); the values used for computations are shown in Table 1; inset illustrates the applicability of Eq. (8) for the quantitative calculation of the temperature dependence of magnetization of real alloys (for the details of the measurements and the calculations see Refs.17 and 16, respectively).
Table 1.
Parameters used for computation of the temperature dependences of magnetization.
| MS(0) (G) |
TC (K) |
Jm (erg/cm3) |
j0/Jm | ΔTR (K) |
H (kOe) |
|---|---|---|---|---|---|
| 500 | 110 | 5⋅108* | 0.1 | 3** | 20*** |
* Corresponds to the Weiss field Jm/MS (0) = 103 kOe, typical for ferromagnets with Curie temperature of about 100 K.
** Typical for the SPTs observed in intermetallic rear-earth alloys and shape memory alloys.
*** Achievable in the experiments with permanent magnets.
The 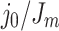 value shown in Table 1 results in the relationship
value shown in Table 1 results in the relationship
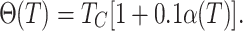 |
22 |
The volume fraction of the high-temperature phase decreases from 0.999 to 0.013 on cooling of ferromagnet from the temperature  to the temperature
to the temperature  . Therefore, if the SPT temperature satisfies equality
. Therefore, if the SPT temperature satisfies equality  , the function
, the function 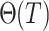 decreases from the value
decreases from the value 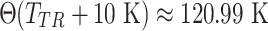 to the value
to the value  . In this case the cooling of ferromagnet induces the SPT from the high-temperature phase in its paramagnetic state to the low-temperature phase in its ferromagnetic state. Due to this, the
. In this case the cooling of ferromagnet induces the SPT from the high-temperature phase in its paramagnetic state to the low-temperature phase in its ferromagnetic state. Due to this, the 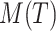 function computed for
function computed for 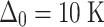 exhibits a sharp decrease in the temperature range of SPT (see solid line in Fig. 1 (a)). The
exhibits a sharp decrease in the temperature range of SPT (see solid line in Fig. 1 (a)). The 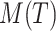 function computed for
function computed for 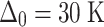 , by contrast, smoothly depends on the temperature, because SPT starts and finishes in the almost pure high-temperature state with Curie temperature
, by contrast, smoothly depends on the temperature, because SPT starts and finishes in the almost pure high-temperature state with Curie temperature  (see dashed line in Fig. 1 (a)). The dash-dotted line in Fig. 1 (a) presents the magnetization function computed the ferromagnet with
(see dashed line in Fig. 1 (a)). The dash-dotted line in Fig. 1 (a) presents the magnetization function computed the ferromagnet with  , which does not exhibit SPT.
, which does not exhibit SPT.
It should be mentioned, first, that the minimum point of the temperature derivative of 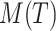 function is traditionally used for evaluation of Curie temperature. Figure 1 (b) obviously shows that such evaluation is approximately valid for the ferromagnet which does not exhibit SPT (see dash-dotted line in Fig. 1 (b)). If the ferromagnet undergoes SPT, the derivative of
function is traditionally used for evaluation of Curie temperature. Figure 1 (b) obviously shows that such evaluation is approximately valid for the ferromagnet which does not exhibit SPT (see dash-dotted line in Fig. 1 (b)). If the ferromagnet undergoes SPT, the derivative of 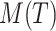 has minimum near the SPT temperature (see solid line in Fig. 1 (b)), or two minimums, first, near the
has minimum near the SPT temperature (see solid line in Fig. 1 (b)), or two minimums, first, near the  , and second, between
, and second, between  and
and  (see dashed line).
(see dashed line).
It should be stressed, second, that according to the phase transition theory the external magnetic field “abolishes” a second-order phase transition from ferromagnetic to paramagnetic phase, because the magnetization value is not equal to zero above the Curie temperature. Therefore, the determination of the magnetic-field-induced shift of Curie temperature is either meaningless procedure or the determination of magnetic-field-induced shift of the SPT temperature.
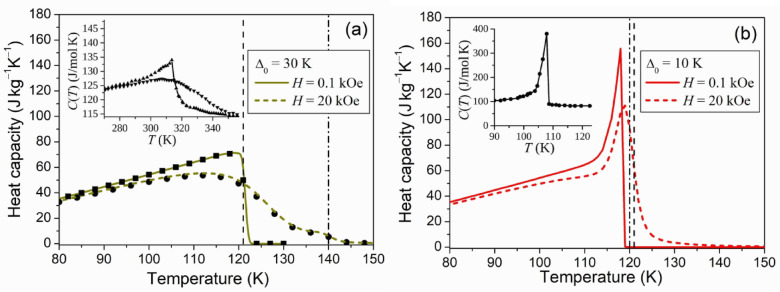
A substitution of computed magnetization values in Eqs. (10), (11) enables the computation of temperature dependence of heat capacity observed in the equilibrium thermodynamic processes. Figure 2 shows the contribution of magnetic subsystem of ferromagnet to the heat capacities  and
and 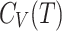 , computed from Eqs. (10), (11), respectively. The insets illustrate the resemblance between the typical temperature dependencies of heat capacities, observed in the experiments, and the theoretical ones. The Eqs. (10), (11) yielded the same results, because the Gibbs free energy expressed by Eqs. (1), (2) does not involve elastic energy, and therefore, the mechanical work performed by elastic forces is disregarded. Figure 2 (a) shows the orthodox temperature dependencies of heat capacity, reported elsewhere (see e.g.20). The only feature caused by the SPT is a faintly visible plateau in the graph plotted for the external magnetic field of 20 kOe. In contrast, Fig. 2 (b) shows the sharp peak of heat capacity in the temperature range of SPT. When the SPT temperature appeared to be close to Curie temperature of the high-temperature phase, theoretical curves clearly reflect the peculiarities of experimental ones obtained in Refs.21–23 for the ferromagnets exhibiting magnetostructural phase transitions.
, computed from Eqs. (10), (11), respectively. The insets illustrate the resemblance between the typical temperature dependencies of heat capacities, observed in the experiments, and the theoretical ones. The Eqs. (10), (11) yielded the same results, because the Gibbs free energy expressed by Eqs. (1), (2) does not involve elastic energy, and therefore, the mechanical work performed by elastic forces is disregarded. Figure 2 (a) shows the orthodox temperature dependencies of heat capacity, reported elsewhere (see e.g.20). The only feature caused by the SPT is a faintly visible plateau in the graph plotted for the external magnetic field of 20 kOe. In contrast, Fig. 2 (b) shows the sharp peak of heat capacity in the temperature range of SPT. When the SPT temperature appeared to be close to Curie temperature of the high-temperature phase, theoretical curves clearly reflect the peculiarities of experimental ones obtained in Refs.21–23 for the ferromagnets exhibiting magnetostructural phase transitions.
In the external field of 0.1 kOe the heat capacity shown in Fig. 2 (a) by the solid line decreases almost to zero at the temperature 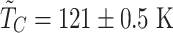 , i.e., at the Curie temperature of low-temperature phase. The heat capacity shown by the solid line in Fig. 2 (b) reaches maximum at the temperature of
, i.e., at the Curie temperature of low-temperature phase. The heat capacity shown by the solid line in Fig. 2 (b) reaches maximum at the temperature of 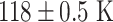 . The temperature derivative of magnetization shown by the solid line in Fig. 1 (b) reaches maximum at the temperature of
. The temperature derivative of magnetization shown by the solid line in Fig. 1 (b) reaches maximum at the temperature of  . All temperatures mentioned here are noticeably higher than the Curie temperature of high-temperature phase, that is the temperature
. All temperatures mentioned here are noticeably higher than the Curie temperature of high-temperature phase, that is the temperature 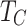 , involved into Eq. (9).
, involved into Eq. (9).
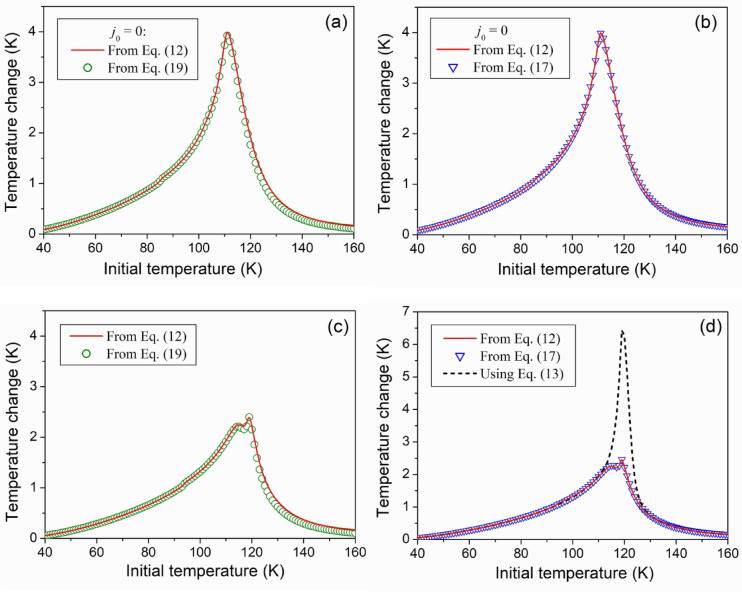
A substitution of the computed values of heat capacity into Eqs. (12), (17) or (19) enables three different ways of calculating the magnetic-field-induced temperature change. Figure 3 shows that these ways lead to the same result, which is strongly different from the result obtained using the OMR, Eq. (13). Therefore, this figure obviously demonstrates an internal consistency of the equation system (2)–(5), (8), (9), which describes the magnetic properties of ferromagnet, with commonly known thermodynamic relationships and modified Maxwell relation Eq. (15). Moreover, comparing the graphs shown in Figs. 3 (a), (b) with those presented in Figs. 3 (c), (d), one can see that the theory discovers a possibility of suppression of MCE by SPT, if this SPT results in the increase of the internal energy of magnetic subsystem of ferromagnet in the low-temperature phase. It should be stressed, that such SPTs are observed in the widely studied ferromagnetic shape memory alloys (see17 and review article16).
Fig. 2.
Computed temperature dependencies of the heat capacities, CP (lines), CV (symbols), of the magnetic subsystem of ferromagnets, undergoing the temperature-induced structural transitions in the stationary magnetic field. Vertical dashed and dash-dotted lines mark the values TC and TTR, respectively. Insets: Temperature dependences of the heat capacity of Ni2Mn1.4Sn0.6 measured in the magnetic fields of 0 kOe and 20 kOe24(a); the heat capacity of Nd2In11(b).
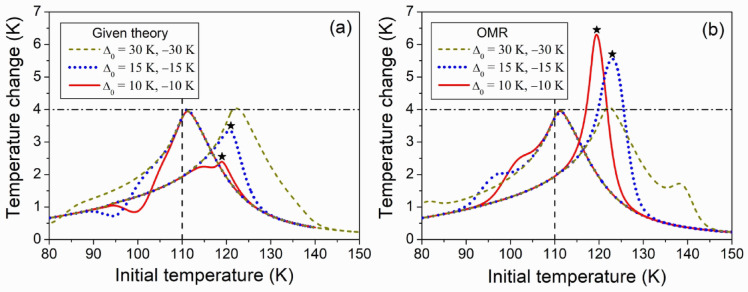
The coupling between magnetic and structural transitions is considered a key strategy for achieving a giant MCE. Such coupling has been successfully realized in many magnetic systems through chemical substitutions6–8. Therefore, it is of practical interest to theoretically analyze how the adiabatic temperature change depends on the temperature interval  , which is the difference between the Curie point and SPT temperature. To this end, the
, which is the difference between the Curie point and SPT temperature. To this end, the  functions were computed for different values of
functions were computed for different values of  . Figure 4 shows the results obtained for the representative ferromagnet described above. As far as Eqs. (12), (17) and (19) lead to the same results, these results are referred to as the results of given theory.
. Figure 4 shows the results obtained for the representative ferromagnet described above. As far as Eqs. (12), (17) and (19) lead to the same results, these results are referred to as the results of given theory.
Fig. 4.
Adiabatic temperature change caused by the magnetic field change from 100 Oe to 20 kOe as a function of initial temperature of ferromagnet; the computations were carried out using Eq. (12) (panel (a)), and orthodox Maxwell relations (panel (b)). The curves with maxima near TC = 110 K correspond to negative values Δ0, the curves with maxima near 120, 125, and 140 K correspond to positive Δ0 values. The horizontal dash-dotted line shows the maximum temperature change computed for the alloy, which does not undergo the structural transition (i.e., for j0 = 0), the vertical dashed line shows the Curie temperature, the stars indicate the points discovering the maximum difference between the results of given theory and orthodox one.
Figure 4 (a) shows the results of computations carried out in the framework of given theory. Comparing the lines presented in the same format and colour one can see the drastic dependence of MCE on the sign of  value. It is seen, moreover, that the maximum values of
value. It is seen, moreover, that the maximum values of  computed for the ferromagnets undergoing the SPTs do not exceed the maximum value of 4.0 K computed for
computed for the ferromagnets undergoing the SPTs do not exceed the maximum value of 4.0 K computed for  , i.e., for the ferromagnet, which does not undergo SPT. If
, i.e., for the ferromagnet, which does not undergo SPT. If 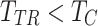 the SPT does not noticeable influence the maximum value of
the SPT does not noticeable influence the maximum value of  , but noticeably lowers this value in the opposite case (by factors of about 1.6 or 1.2, if
, but noticeably lowers this value in the opposite case (by factors of about 1.6 or 1.2, if  is equal to 10–15 K, respectively). The maximum value computed for
is equal to 10–15 K, respectively). The maximum value computed for 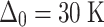 is close to 4.0 K, because SPT occurs far from PM – FM phase transition.
is close to 4.0 K, because SPT occurs far from PM – FM phase transition.
Figure 4 (b) shows the results of computations carried out using OMR. This figure shows that the  graphs resulting from OMR demonstrate resemblance to those shown in Fig. 4 (a) if
graphs resulting from OMR demonstrate resemblance to those shown in Fig. 4 (a) if 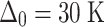 . However, the use of OMR leads to considerable overestimation of
. However, the use of OMR leads to considerable overestimation of  resulting from the given theory if
resulting from the given theory if 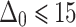 . A disagreement of two ways of estimation of MCE can be explained formally with help of modified Maxwell relation. This relation was used to obtain Eq. (17), which expresses the temperature change through the sum of derivatives
. A disagreement of two ways of estimation of MCE can be explained formally with help of modified Maxwell relation. This relation was used to obtain Eq. (17), which expresses the temperature change through the sum of derivatives 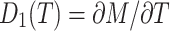 and
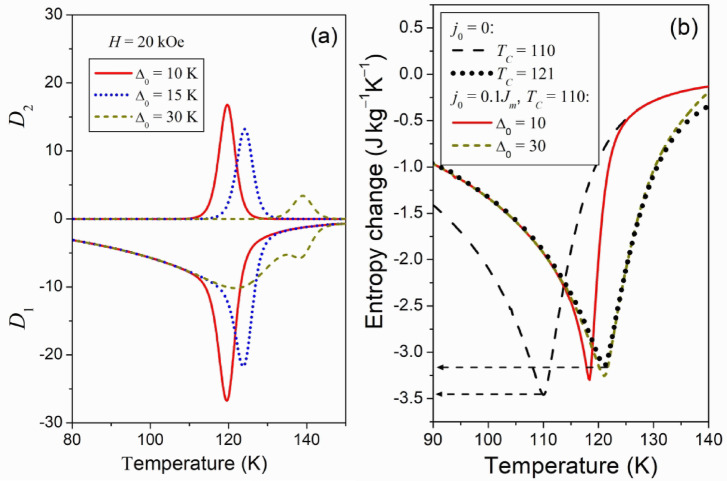
and  . The derivatives have different signs (see Fig. 5 (a)) and therefore
. The derivatives have different signs (see Fig. 5 (a)) and therefore  . In the equation resulting from OMR, the derivative
. In the equation resulting from OMR, the derivative  is absent, and due to this, the use of OMR leads to the overestimation of the temperature change.
is absent, and due to this, the use of OMR leads to the overestimation of the temperature change.
Fig. 3.
Adiabatic temperature change caused by the magnetic field change from 100 Oe to 20 kOe, computed for the ferromagnet, which does not undergo structural transition, (a), (b), and ferromagnet undergoing structural phase transition at TTR = 120 K (c), (d).
Fig. 5.
Derivatives D1 and D2 included in the modified Maxwell relation (Eq.(17)), computed for various Δ0 values (a). Magnetic-field-induced entropy change computed for different TC and Δ0 values (b).
As mentioned above, the magnetic-field-induced entropy change is considered the main characteristic of MCE. This characteristic is shown in Fig. 5 (b). It is seen that the SPT reduces the entropy change if the temperature of SPT is close to Curie temperature of the high-temperature phase, 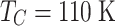 . (Compare the curve plotted for
. (Compare the curve plotted for  with the curve corresponding to
with the curve corresponding to  ). If the temperature of SPT is much higher than
). If the temperature of SPT is much higher than 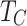 , the entropy change is approximately equal to the entropy change computed for the high temperature phase, that is for the ferromagnet with
, the entropy change is approximately equal to the entropy change computed for the high temperature phase, that is for the ferromagnet with 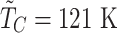 . (Compare the curve plotted for
. (Compare the curve plotted for  ,
,  with the curve corresponding to
with the curve corresponding to  ,
,  ). The horizontal arrows show that the relative difference between the maximum absolute values of the entropy changes computed for two phases is close to 0.09. This value is close to the relative difference of Curie temperatures
). The horizontal arrows show that the relative difference between the maximum absolute values of the entropy changes computed for two phases is close to 0.09. This value is close to the relative difference of Curie temperatures  . The computations carried out for
. The computations carried out for  , 100 K and 80 K, without changing the other parameters, show that in the absence of magnetostructural phase transitions, the increase of the maximum absolute value of the entropy change is strictly proportional to the lowering of Curie temperature. This preliminary conclusion deserves a special theoretical analysis and experimental verification.
, 100 K and 80 K, without changing the other parameters, show that in the absence of magnetostructural phase transitions, the increase of the maximum absolute value of the entropy change is strictly proportional to the lowering of Curie temperature. This preliminary conclusion deserves a special theoretical analysis and experimental verification.
Summary and discussion
Commonly known magnetic Maxwell relations, called above the orthodox Maxwell relations, are widely used for evaluation of giant magnetocaloric effect. It is important, however, that OMR are derived for thermodynamic processes, which go through the subsequent equilibrium states of thermodynamic system, while the giant MCE is the MCE preconditioned by magnetostructural phase transition. The evaluation of magnetic-field-induced temperature change on the base of OMR ignores the phase transition process between two equilibrium thermodynamic states. As far as the general self-consistent theory of magnetostructural phase transitions is not created until now, the thermodynamic properties of “representative ferromagnet” whose Curie point lies outside the temperature range of SPT have been analyzed and the modified Maxwell relations were derived, assuming that the SPT results in the explicit temperature dependence of the energy density of the magnetic subsystem of ferromagnet. The given approach to theoretical analysis of magnetic and magnetocaloric properties of ferromagnets is based on this assumption and on the fundamental thermodynamic relationships. This analysis resulted in:
-
i)
the theoretical temperature dependencies of magnetization (Fig. 1), which are in agreement with dependencies inherent to the real ferromagnets undergoing the SPTs (see inset in Fig. 1 and Ref.16);
-
ii)
the theoretical curves of heat capacity
 (Fig. 2), which reproduce the sharp narrow peaks on the experimental curves taken for the ferromagnets undergoing SPTs on cooling in the constant magnetic field (see insets in Fig. 2 and Ref.11);
(Fig. 2), which reproduce the sharp narrow peaks on the experimental curves taken for the ferromagnets undergoing SPTs on cooling in the constant magnetic field (see insets in Fig. 2 and Ref.11); -
iii)
theoretical values of the magnetic-field-induced temperature change
 computed for the different intervals
computed for the different intervals  between the temperature of SPT and Curie temperature.
between the temperature of SPT and Curie temperature.
It has been stressed, that computed  values are rather close to those resulting from the OMR, if the temperature interval
values are rather close to those resulting from the OMR, if the temperature interval 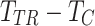 is much wider than the temperature interval of SPT. However, a drastic contradiction between the results of given theory and the theory based on OMR arises if
is much wider than the temperature interval of SPT. However, a drastic contradiction between the results of given theory and the theory based on OMR arises if  approaches
approaches 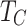 : the given theory predicts the suppression of MCE by the SPT that increases the energy of magnetic subsystem of ferromagnet, while the orthodox theory predicts the enhancement of MCE.
: the given theory predicts the suppression of MCE by the SPT that increases the energy of magnetic subsystem of ferromagnet, while the orthodox theory predicts the enhancement of MCE.
It should be noted that the given approach to the theoretical analysis of MCE is promising for the elucidation of the interrelation between MCE and the basic properties of ferromagnets exhibiting SPT. The properties, related to the Curie temperature through the spin-exchange process and magnetic anisotropy (large magnetostriction, spontaneous or forced straining of crystal lattice, the displacements of the magnetic atoms inside the unit cells of the crystal lattice, etc.) can be taken into account. These properties can be related to multicaloric effects25.
It should be emphasised that the inverse MCE related to the SPTs of ferroelastic type in the metamagnetic alloys is widely studied26–28. It is argued that the spontaneous deformation of the crystal lattice weakens the inverse MCE observed in these alloys29. The results obtained in this article suggest the possibility of similar magnetocaloric property of the materials exhibiting normal magnetocaloric effect. However, the application of given theoretical approach to ferromagnets exhibiting the phase transitions from high-temperature ferromagnetic to the low-temperature paramagnetic27,30, ferrimagnetic31 or antiferromagnetic32–34 phases needs the detailed experimental data about the magnetic structure of the high-temperature and low-temperature states of ferromagnets with the competing spin-exchange interactions.
Finally, the magnetic solids exhibiting giant MCE at the liquid helium and sub-liquid helium temperatures worth mentioning (see Refs.35–37 and references therein). Such solids are promising for the solid-state helium temperature refrigeration. An applicability of the given theoretical approach to the description of MCE in such solids is questionable and needs special consideration.
Conclusion
A thermodynamic analysis based on the commonly used equations for the energy and entropy of the magnetic subsystem of ferromagnet showed how the structural phase transition occurring near the Curie point impacts the magnetic, caloric and magnetocaloric properties of the ferromagnet. The analysis discovered a sharp dependence of these properties on the difference between the SPT temperature and Curie point. The obtained results can motivate the systematic experimental research of magnetic and magnetocaloric materials undergoing the SPT at the temperature, which can be purposefully approached to Curie point (see e.g., the experiments presented in Refs.6–8).
Acknowledgements
Financial support from the National Academy of Science of Ukraine (Project 0124U000392 and Project 0125U001287) and the Austrian Science Fund (FWF) [10.55776/RIC5537124] is acknowledged. For open access purposes, the author has applied a CC BY public copyright license to any author accepted manuscript version arising from this submission.
Author contributions
V.A.L: Conceptualization, Formal analysis, Investigation, Writing - review & editing. A.K.: Formal analysis, Investigation, Writing - review & editing. O.S.: Investigation, Validation. All authors contributed to the development of the initial idea and wrote the final manuscript.
Data availability
The datasets used and/or analyzed during the current study available from the corresponding author and Victor L’vov on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Franco, V. et al. Magnetocaloric effect: from materials research to refrigeration devices. Prog Mater. Sci.93, 112–232. 10.1016/j.pmatsci.2017.10.005 (2018). [Google Scholar]
- 2.Gutfleisch, O. et al. Magnetic materials and devices for the 21st century: stronger, lighter, and more energy efficient. Adv. Mater.23, 821–842. 10.1002/adma.201002180 (2011). [DOI] [PubMed] [Google Scholar]
- 3.Gottschall, T. et al. Making a cool choice: the materials library of magnetic refrigeration. Adv. Energy Mater.9, 1901322. 10.1002/aenm.201901322 (2019). [Google Scholar]
- 4.Chernenko, V. A., L’vov, V. A., Cesari, E. & Barandiaran, J. M. Fundamentals of magnetocaloric effect in magnetic shape memory alloys. in Handbook Magn. Materials28 1–45 (Elsevier, 2019). 10.1016/bs.hmm.2019.03.001
- 5.Kato, T., Nagai, K. & Aisaka, T. A model of magneto-structural phase transition in MnAs. J. Phys. C Solid State Phys.16, 3183. 10.1088/0022-3719/16/16/020 (1983). [Google Scholar]
- 6.Liu, J. et al. Realization of magnetostructural coupling by modifying structural transitions in MnNiSi-CoNiGe system with a wide Curie-temperature window. Sci. Rep. 6, 23386 (2016). 10.1038/srep23386 (2016). [DOI] [PMC free article] [PubMed]
- 7.Biswas, A. et al. Designed materials with the giant magnetocaloric effect near room temperature. Acta Mater.180, 341–348. 10.1016/j.actamat.2019.09.023 (2019). [Google Scholar]
- 8.Pal, S. K. et al. Enhancing giant magnetocaloric effect near room temperature by inducing magnetostructural coupling in Cu-doped MnCoGe. Mater. Des.195, 109036. 10.1016/j.matdes.2020.109036 (2020). [Google Scholar]
- 9.Wang, F. W., Zhang, X. X. & Hu, F. X. Large magnetic entropy change in TbAl2 and (Tb0.4Gd0.6)Al2. Appl. Phys. Lett.77, 1360–1362. 10.1063/1.1290389 (2000). [Google Scholar]
- 10.Zhang, H. et al. Large magnetocaloric effects of RFeSi (R = Tb and Dy) compounds for magnetic refrigeration in nitrogen and natural gas liquefaction. Appl. Phys. Lett.103, 202412. 10.1063/1.4832218 (2013). [Google Scholar]
- 11.Biswas, A. et al. Unusual first-order magnetic phase transition and large magnetocaloric effect in Nd2In. Phys. Rev. Mater.6, 114406. 10.1103/PhysRevMaterials.6.114406 (2022). [Google Scholar]
- 12.Ćwik, J., Palewski, T., Nenkov, K., Gutfleisch, O. & Klamut, J. The influence of Er substitution on magnetic and magnetocaloric properties of Dy1 – xErxCo2 solid solutions. Intermetallics19, 1656–1660. 10.1016/j.intermet.2011.07.012 (2011). [Google Scholar]
- 13.Isihara, A. Statistical Physics (Academic, 2013).
- 14.Ziman, J. M. Principles of the Theory of Solids (Cambridge University Press, 1972).
- 15.L’vov, V. A. & Salyuk, O. Thermodynamic model of quasi-first-order paramagnetic–ferromagnetic phase transition and giant magnetocaloric effect. Low Temp. Phys.51, 300–305. 10.1063/10.0035811 (2025). [Google Scholar]
- 16.L’vov, V. Effects of magnetoelastic coupling in ferromagnetic shape memory alloys and piezopolymer/fsma composite material. Low. Temp. Phys.51, 1030–1039 10.1063/10.0037097 (2025). [Google Scholar]
- 17.Chernenko, V., L’vov, V., Zagorodnyuk, S. & Takagi, T. Ferromagnetism of thermoelastic martensites: theory and experiment. Phys. Rev. B. 67, 064407. 10.1103/PhysRevB.67.064407 (2003). [Google Scholar]
- 18.Landau, L. D. & Lifshitz, E. M. Course of Theoretical Physics (Elsevier, 2013).
- 19.Ghorai, S. et al. Giant magnetocaloric effect in the (Mn,Fe)NiSi-system. Phys. Rev. Mater.8, 124401. 10.1103/PhysRevMaterials.8.124401 (2024). [Google Scholar]
- 20.Dan’kov, S. Y., Tishin, A. M., Pecharsky, V. K. & Gschneidner, K. A. Magnetic phase transitions and the magnetothermal properties of gadolinium. Phys. Rev. B. 57, 3478–3490. 10.1103/PhysRevB.57.3478 (1998). [Google Scholar]
- 21.Pecharsky, V. K. & Gschneidner, K. A. Giant magnetocaloric effect in Gd5Si2Ge2. Phys. Rev. Lett.7810.1103/PhysRevLett.78.4494 (1997).
- 22.Gràcia-Condal, A. et al. Magnetic and structural entropy contributions to the multicaloric effects in Ni-Mn-Ga-Cu. Phys. Rev. Mater.6, 084403. 10.1103/PhysRevMaterials.6.084403 (2022). [Google Scholar]
- 23.Tang, X. et al. Magnetic refrigeration material operating at a full temperature range required for hydrogen liquefaction. Nat. Commun.13, 1817. 10.1038/s41467-022-29340-2 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kosogor, A., Barandiaran, J. M., L’vov, V. A., Fernandez, J. R. & Chernenko, V. A. Magnetic and nonmagnetic contributions to the heat capacity of metamagnetic shape memory alloy. J. Appl. Phys.121, 183901. 10.1063/1.4983025 (2017). [Google Scholar]
- 25.Stern-Taulats, E. et al. Multicaloric materials and effects. MRS Bull.43, 295–299. 10.1557/mrs.2018.72 (2018). [Google Scholar]
- 26.Krenke, T. et al. Inverse magnetocaloric effect in ferromagnetic Ni–Mn–Sn alloys. Nat. Mater.4, 450–454. 10.1038/nmat1395 (2005). [DOI] [PubMed] [Google Scholar]
- 27.Kihara, T., Xu, X., Ito, W., Kainuma, R. & Tokunaga, M. Direct measurements of inverse magnetocaloric effects in metamagnetic shape-memory alloy NiCoMnIn. Phys. Rev. B. 90, 214409. 10.1103/PhysRevB.90.214409 (2014). [Google Scholar]
- 28.Mejía, C. S. et al. On the high-field characterization of magnetocaloric materials using pulsed magnetic fields. J. Phys. Energy. 5, 034006. 10.1088/2515–7655/acd47d (2023).
- 29.Gottschall, T., Skokov, K. P., Benke, D., Gruner, M. E. & Gutfleisch, O. Contradictory role of the magnetic contribution in inverse magnetocaloric heusler materials. Phys. Rev. B. 93, 184431. 10.1103/PhysRevB.93.184431 (2016). [Google Scholar]
- 30.Sannigrahi, J. et al. Magnetic States of Ni-Mn-Sn based shape memory alloy: A combined Muon spin relaxation and neutron diffraction study. Phys. Rev. B. 99, 224401. 10.1103/PhysRevB.99.224401 (2019). [Google Scholar]
- 31.Semboshi, S., Umetsu, R. Y., Kawahito, Y. & Akai, H. A new type of half-metallic fully compensated ferrimagnet. Sci. Rep.12, 10687. 10.1038/s41598-022-14561-8 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nikitin, S. et al. The magnetocaloric effect in Fe49Rh51 compound. Phys. Lett. A. 148, 363–366. 10.1016/0375-9601(90)90819-A (1990). [Google Scholar]
- 33.Aksoy, S., Acet, M., Deen, P., Mañosa, L. & Planes, A. Magnetic correlations in martensitic Ni-Mn-based heusler shape-memory alloys: neutron polarization analysis. Phys. Rev. B—Condensed Matter Mater. Phys.79, 212401. 10.1103/PhysRevB.79.212401 (2009). [Google Scholar]
- 34.Kosogor, A., Umetsu, R. Y., Golub, V., Xu, X. & Kainuma, R. Magnetic properties, phase diagram and low-temperature specific heat of Ni50Mn50-xSbx alloys. J. Alloys Compd.988, 174130. 10.1016/j.jallcom.2024.174130 (2024). [Google Scholar]
- 35.Zhang, Y., Na, Y., Xie, Y. & Zhao, X. Unveiling the structural and magnetic properties of RENaGeO4 (RE = Gd, dy, and Ho) oxides and remarkable low-temperature magnetocaloric responses in GdNaGeO4 oxide. J. Mater. Chem. A. 10.1039/D5TA00892A (2025). [Google Scholar]
- 36.Zhang, Y., Li, A., Hao, W., Li, H. F. & Li, L. Apatite-type gadolinium-based dense MGd4Si3O13 (M = Mg, ca, and Sr) ceramics: an emerging class of sub-liquid helium temperature magnetic refrigerant. Acta Mater.292, 121033. 10.1016/j.actamat.2025.121033 (2025). [Google Scholar]
- 37.Chen, F., Xu, J., Zhao, X., Na, Y. & Zhang, Y. Structural and magnetic characterization of weberite-type RE3NbO7 (RE = Gd, dy, ho, and Er) ceramics with notable cryogenic magnetocaloric responses. Sci. China Mater. 1–13. 10.1007/s40843-025-3468-4 (2025).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study available from the corresponding author and Victor L’vov on reasonable request.