Reversal of Flagellar Rotation Is Important in Initial Attachment of Escherichia coli to Glass in a Dynamic System with High- and Low-Ionic-Strength Buffers

Abstract

The attachment rates of wild-type, smooth-swimming, tumbly, and paralyzed Escherichia coli to glass was measured at fluid velocities of 0.0044 and 0.044 cms⁻¹ (corresponding to shear rates of 0.34 and 3.4 s⁻¹, respectively), in 0.02 and 0.2 M buffer solutions. At the highest ionic strength, we did not observe a significant difference in the attachment rate of wild-type and paralyzed cells at either fluid velocity. However, when the ionic strength was reduced, paralyzed bacteria attached at rates 4 and 10 times lower than that of the wild type under fluid velocities of 0.0044 and 0.044 cms⁻¹, respectively. This suggested that the rotation of the flagella assisted in attachment. We then compared the attachment rates of smooth-swimming (counterclockwise rotation only) and tumbly (clockwise rotation only) cells to the wild type to determine whether the direction of rotation was important to cell attachment. At 0.0044 cms⁻¹, the smooth-swimming cells attached at rates similar to that of the wild type in both buffer solutions but significantly less at the higher fluid velocity. Tumbly cells attached at much lower rates under all conditions. Thus, the combination of clockwise and counterclockwise flagellar rotation and their coupling appeared to be important in cell attachment. We considered a number of hypotheses to interpret these observations, including a residence time analysis and a comparison of traditional Derjaguin-Landau-Verwey-Overbeek (DLVO) theory to soft-particle theory.

The attachment of bacteria to surfaces and the subsequent formation of biofilms is important in many medical, industrial, and environmental processes. For example, in the medical field, biofilm formation on the surfaces of medical implants (17) and lungs (12) can lead to critical infections. Biofilms also reduce the efficiency of heat exchangers and foul membranes in water filtration (10). In the environment, the development of biofilms on the surfaces of soil particles is essential to the success of bioremediation strategies (42, 43).

In a typical bioaugmentation scheme, a portion of injected bacteria is transported through the subsurface environment with groundwater flow, while the remaining cells attach to soil particles and grow to develop biofilms. The formation of biofilms on mineral surfaces is necessary for the continuous removal of contaminants from in-flowing groundwater, as well as for the degradation of contaminants partitioned into organic matter associated with mineral surfaces (11). Thus, an understanding of the factors that govern bacterial attachment in a dynamic system is important in optimizing bioremediation systems.

The swimming behavior of motile bacteria may also be important in bioremediation, in that motility has been shown to facilitate transport through porous media in stagnant (19, 34) and flowing (43) systems and also enhances attachment to surfaces in smaller-scale systems under dynamic conditions (9, 21, 23, 29, 30). We were interested in comparing the attachment and detachment rates of wild-type and paralyzed bacterial strains to glass in the presence of fluid flow to determine the conditions (fluid velocity and ionic strength) under which motility becomes important. Previous studies in the literature have investigated the attachment of motile and nonmotile bacterial strains to surfaces by varying either fluid velocity (8, 9, 22) or ionic strength (2, 20, 27, 35); however, few studies have been performed to evaluate the coupled effects of ionic strength and fluid velocity on bacterial attachment.

We were also interested in understanding how the swimming mechanism of motile bacteria facilitates their attachment to a glass surface. In an isotropic environment, motile Escherichia coli organisms swim in a series of runs (relatively straight paths) and tumbles (periodic changes in direction) (1). During a run, most of the flagella assume a normal conformation associated with counterclockwise rotation to form a bundle at the base of the cell body which propels the cell forward (1, 24, 37). Flagellar filaments undergo several conformational changes while in transition from a run to a tumble, usually from normal to semicoiled (when reorientation occurs), then to curly 1, and finally back to normal (37). A tumble begins when the bundle loosens and then subsequently one or more flagella switch their rotational direction and leave the bundle (37). This causes the cell body to reorient in a new direction (1, 24, 37). A cell begins moving in a new direction after the cell body has reoriented, while filaments participating in the tumble are still in a semicoiled orientation (37). The flagella gradually transition back to a normal conformation, consolidating the bundle, at which point the cell regains full run speed. The trajectories of motile bacteria therefore resemble the random walk of a gas molecule, and the swimming behavior is modeled by analogy to molecular diffusion. To determine how runs and tumbles affect attachment, we tested two mutant strains: a tumbly strain (in which the flagella rotate in the clockwise direction only) and a smooth-swimming strain (in which the flagella rotate only counterclockwise). Thus, our objectives were to determine the fluid conditions under which motility facilitates bacterial attachment and to gain a better understanding of how flagellar motion aids in attachment and detachment of cells to surfaces.

The initial attachment of cells to a glass surface generally occurs in two steps: transport to the surface and adsorption on the surface. We further separate mass transfer into macroscopic and microscopic transport, such that macroscopic transport implies movement from the bulk fluid to a distance of several microns above the surface, and microscopic transport occurs from the micron separation distance to a distance of ca. 100 nm above the surface, where long-range van der Waals forces become important as predicted by DLVO (Derjaguin-Landau-Verwey-Overbeek) theory [31]). We distinguish between the two transport mechanisms because, at micron separation distances, the settling or swimming velocity of a bacterium decreases as a result of the proximity of the solid surface (5, 33); however, the degree of reduction may differ for motile and nonmotile bacteria.

The effective attachment rate we measure in our experimental system (a parallel-plate flow chamber) includes all three aspects of cell attachment, and thus differences between strains could reflect differences in mass transfer (both macroscopic and microscopic) or adsorption. By comparing wild-type and paralyzed bacteria, we were able to determine how the general movement of the flagella affects their attachment and detachment in a dynamic system. We hypothesize that the rotation of the flagella influences both transport and adsorption. Motile cells (wild type and smooth swimmers) could have a larger contribution to attachment rate than nonmotile cells (paralyzed and tumbly cells) from the macroscopic cell transport component because their diffusion coefficient is 3 orders of magnitude higher (1). However, at low fluid velocities, the flux of nonmotile cells to the surface as a result of settling is similar in magnitude to the diffusive flux of motile cells (26). For the low flow rates tested in this study, we do not expect to see a difference in the attachment of motile and nonmotile cells as a result of macroscopic transport.

On a microscopic scale, the presence of a solid boundary decreases the swimming speed of a motile bacterium and settling velocity of a nonmotile bacterium (5). However, the angle at which a bacterium approaches the surface is critical to how much the cell velocity is decreased (15, 33). Using the boundary element method, Ramia et al. (33) and Frymier (14) determined that bacteria moving perpendicular to a surface experienced the greatest amount of velocity reduction at separation distances of less than several microns. Cells approaching the surface at angles between perpendicular and parallel to the surface experienced less of a velocity decrease. In fact, cells moving parallel to the surface actually had a propulsive advantage and moved slightly faster than those in the bulk (15). The magnitude of the settling velocity is also much smaller than the swimming speed of a motile bacterium. For paralyzed bacteria, we measured a settling velocity of 0.07 μm s⁻¹ (26) compared with typical E. coli swimming speeds of 10 to 40 μm s⁻¹ (26). Thus, since motile bacteria have a larger velocity and could approach the surface from any angle, it is reasonable to assume that the microscopic transport of a population of motile bacteria to the surface would be greater than that of nonmotile population.

Flagellar rotation could also be important to cell adsorption. For example, the movement of flagella on a bacterium close to the surface could cause one or more flagella to adsorb and thus act as an anchor to initially adsorb cells to the surface (tethering). We also expect that the motion of the flagella could aid in detaching cells from the surface or strengthen adsorption once the cell body has adsorbed.

MATERIALS AND METHODS

Bacterial strains and buffer solutions.

E. coli K-12 AW405 (motile), E. coli K-12 HCB136 (nonmotile with paralyzed flagella), E. coli K-12 HCB437 (smooth swimming), and E. coli K-12 HCB359 (tumbly) were generously provided by Howard Berg, Harvard University, Cambridge, Mass. Bacteria were grown from frozen stock on a rotary shaker (Orbit Environ-Shaker; Lab-Line Instruments, Inc.) in 100 ml of tryptone broth to optical densities at 590 nm of 1.0 (values corresponded to the late exponential phase). Tryptone broth was composed of 5 g of NaCl and 10 g of tryptone (Difco 0123-17-3) per liter of filtered, deionized water.

All bacterial strains were suspended in phosphate buffer for experiments. The 0.2 M buffer solution consisted of 11.2 g of KH₂PO₄, 4.8 g of K₂HPO₄, and 0.029 g of EDTA per liter of filtered, deionized water. The 0.02 M solution was a 10-fold dilution of the 0.2 M stock.

Parallel-plate flow chamber and data analysis.

The attachment of E. coli strains to glass was studied by using the parallel-plate flow chamber as described elsewhere (26). The inner dimensions of the chamber are 1 cm (width) by 3 cm (length) by 0.0762 cm (height). Briefly, 200 to 300 μl of bacteria suspended in growth medium was transferred to 50 ml of buffer solution and allowed to sit for ca. 1 h (roughly the doubling time). This yielded a bulk concentration of (5 ± 2) × 10⁶ cells ml⁻¹. Once the flow chamber system was equilibrated with buffer, bacteria were pumped through the chamber at the desired flow rate (0.02 or 0.2 ml min⁻¹, corresponding to fluid velocities of 0.0044 or 0.044 cm s⁻¹ and shear rates of 0.34 or 3.4 s⁻¹, respectively) by using a syringe pump (Harvard Apparatus PHD 2000). The corresponding Reynolds numbers were 0.03 and 0.3 for fluid velocities of 0.0044 and 0.044 cm s⁻¹, respectively, where Re is defined as ρ_fQ/[μ(w + 2 h)] (4) and where ρ_f is the fluid density, Q is the flow rate, w is the width of the chamber, and μ is the fluid viscosity. The flow within the chamber is therefore laminar. Cells were observed attaching and detaching to the bottom glass surface of the flow chamber, which sat directly on the stage of an inverted microscope (Nikon TMS). Two images of the surface (obtained 4 s apart) were captured every 2 to 3 min for ca. 1.5 h by using Global Village VideoImpression and then analyzed in NIH Image. We defined attached cells as those that were immobilized on the surface at the same location for the pair of snapshots, i.e., for at least 4 s (26).

We calculated the effective attachment rate, k_eff, from experimental data according to the following:

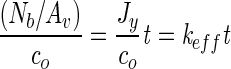(1)

where N_b/A_v is the number of attached bacteria per viewing area, c_o is the initial, bulk concentration of cells, J_y is the flux of bacteria to the surface, and t is time. Thus, the effective attachment rate is the slope of experimental data (cells per area measured as a function of time).

The fraction of bacteria retained on the surface is defined as the ratio of the net effective attachment rate to the total effective attachment rate, where the two rates are determined from the net and total (net plus detached) number of cells that attached to the surface as a function of time, respectively. Thus, the fraction retained is a measure of cell detachment.

We report our attachment rates in a nondimensional form, k_eff x/(uh), to eliminate the artificial increase in attachment at higher flow rates due to a greater number of cells flowing over the surface in a given period of time, where x is the viewpoint in the chamber, u is the average fluid velocity, and h is the chamber half-height. We also note that time zero is defined as the time at which cells traveling with the average fluid velocity reach the viewpoint in the flow chamber where the microscope is focused (x = 1.5 cm).

Figure 1 is an example of typical experimental data, shown for a fluid velocity of 0.044 cm s⁻¹ and an ionic strength of 0.2 M. The experimental results are plotted as nondimensional concentration, (N_b/A_v)/(c_o h), as a function of time, ut/x. Three experiments were performed for each bacterial strain and condition tested, provided we observed a significant interaction. Specifically, if little or no attachment occurred, then experiments were performed only twice. The reported error represents one standard deviation of the measured slopes. The statistical significance of attachment rates and fractions retained for each strain (compared to the wild type for the various ionic strength solutions) was determined from single-factor analysis of variance (with α = 0.05).

FIG. 1.

Total number of wild-type (○), paralyzed (▵), smooth-swimming (⋄), and tumbly (×) bacteria attaching in a viewing area as a function of dimensionless time at a fluid velocity of 0.044 cm s⁻¹ and an ionic strength of 0.02 M. Data points are an average of two or three experiments; error bars represent one standard deviation of the slope. For clarity, error bars are only shown on every fourth datum point. The data for wild-type and paralyzed cells will be reported elsewhere (26).

RESULTS

Total effective attachment rates.

Table 1 shows the total effective attachment rates measured for each bacterial strain at the two fluid velocities and ionic strengths tested in this study. For all strains, an increase in fluid velocity significantly decreased the attachment rate for both ionic strength solutions. For the wild type, a decrease in ionic strength did not significantly affect the rate at which cells attached to the surface at either fluid velocity. Paralyzed cells attached at a rate similar to that of the wild type in the 0.2 M buffer solution at both 0.0044 and 0.044 cm s⁻¹ (no significant difference). However, the attachment rate was significantly reduced when the ionic strength was decreased: the attachment rate was roughly half as much as that of the wild type at a fluid velocity of 0.0044 cm s⁻¹ and an order of magnitude lower at 0.044 cm s⁻¹.

TABLE 1.

Total effective attachment rates measured for wild-type, tumbly, smooth-swimming, and paralyzed E. coli to glass in the parallel-plate flow chamber

E. coli cell type	Mean total effective attachment rates ± SD (103)a at:
	0.0044 cm s−1 at:		0.044 cm s−1 at:
	I = 0.2 M	I = 0.02 M	I = 0.2 M	I = 0.02 M
Wild type	32 ± 2b	32 ± 8	4.8 ± 1b	5.6 ± 2
Paralyzed	63 ± 26b	14 ± 5∗	6.0 ± 2b	0.61 ± 0.15c∗
Smooth swimming	50 ± 8∗	33 ± 5	1.9 ± 0.6∗	-∗
Tumblyc	12 ± 5∗	-∗	0.48 ± 0.1∗	-∗

^aThe rates presented are nondimensional to illustrate the effect of fluid velocity; dimensional rates can be obtained by multiplying the slope (nondimensional rate) by uh/x. Three experiments were performed for wild-type and paralyzed bacteria for all conditions; three experiments were also performed for smooth-swimming bacteria for all conditions except 0.044 cm s⁻¹ and 0.2 M, for which only two experiments were performed because there was no interaction. Two experiments were performed for tumbly bacteria for all conditions tested. The reported error is one standard deviation of the slope. I, ionic strength. -, No attached cells were observed on the glass surface during the experiment (∼1.5 hr). ∗, Statistically different than the wild-type (for the same conditions).

^bData for wild-type and paralyzed E. coli strains in 0.2 M buffer are from McClaine and Ford (26).

^cWe report an attachment rate, but note that the number of cells that attached during experiments ranged between 8 and 15 cells per field.

Smooth-swimming cells attached at a slightly higher rate than that of the wild type at the lower fluid velocity in 0.2 M buffer (more similar to the attachment rate of paralyzed cells) and about half as fast at a fluid velocity of 0.044 cm s⁻¹. A decrease in ionic strength slightly decreased the attachment rate at 0.0044 cm s⁻¹ (but not significantly) and significantly reduced attachment at the higher fluid velocity (no cells were observed to attach within the 1.5-h time period of experiments). Tumbly cells attached at a significantly slower rate than the other three strains at both fluid velocities, with the more significant decrease observed at the higher fluid velocity. No tumbly cells attached in the lower-ionic-strength medium for either fluid velocity.

Fraction of cells retained on the surface.

The fraction of bacteria retained on the surface was measured from experimental data by using both the net rate of cells accumulated on the surface and the total rate of cells that had interacted with the surface (net accumulated plus those that had previously detached) (Table 2). For wild-type cells, the fraction retained was not significantly influenced by ionic strength. However, an increase in the fluid velocity significantly increased the fraction of cells that remained attached to the surface. The fraction of paralyzed cells retained on the surface was much higher than that of the wild type at the lowest fluid velocity and decreased when the fluid velocity increased (in the 0.2 M solution). In the lower-ionic-strength buffer, the fractions of paralyzed cells retained at 0.044 and 0.0044 cm s⁻¹ were similar, but this result is not statistically significant because a much lower number of cells attached and detached during experiments in low-ionic-strength buffer. The percentage of smooth swimmers that remained on the surface was lower than the other strains for all cases, and there was no significant difference between the various ionic-strength solutions or the fluid velocities tested. The fraction of tumbly cells also did not appear to be influenced by fluid velocity, although again we note that the number of attached tumbly cells was small (in terms of statistical significance).

TABLE 2.

Fractions retained measured for wild-type, tumbly, smooth-swimming, and paralyzed E. coli strains to a glass surface in the parallel-plate flow chamber

E. coli cell type	Mean fraction retained ± SDa at:
	0.0044 cm s−1 at:		0.044 cm s−1 at:
	I = 0.2 M	I = 0.02 M	I = 0.2 M	I = 0.02 M
Wild-type	0.47 ± 0.09b	0.43 ± 0.18	0.70 ± 0.08b	0.82 ± 0.09
Paralyzed	0.75 ± 0.02b	0.78 ± 0.1∗	0.45 ± 0.07b∗	0.74 ± 0.08c
Smooth swimming	0.21 ± 0.04∗	0.14 ± 0.007	0.15 ± 0.04∗	-∗
Tumbly	0.62 ± 0.04c	-∗	0.65 ± 0.12c	-∗

^a-, No attached cells were observed on the glass surface during the experiment (∼1.5 h), and therefore a fraction retained could not be determined. ∗, Statistically different than the wild type (for the same conditions). I, ionic strength.

^bData for wild-type and paralyzed E. coli strains in 0.2 M buffer are from McClaine and Ford (26).

^cWe report a fraction retained, but note that the number of cells that attached during experiments ranged between 8 and 15 cells per field (and thus the number of detached cells was small). In typical experiments, the number of cells per field is between 60 and 80.

Qualitative observations.

In the flow chamber, we were able to observe bacteria attached to the glass surface, as well as cells swimming or moving with the fluid several microns above the glass surface. Wild-type and smooth-swimming bacteria were able to swim in all directions near the surface at both fluid velocities, presumably because the fluid velocity approaches zero close to the surface. The smooth swimmers, however, had a much greater tendency to swim in circular trajectories in the plane of the surface compared to the wild-type bacteria and remaining in the viewing area for a longer period of time. Paralyzed and tumbly cells moved only in the direction of flow, but the motion of tumbly cells along a fluid streamline was much more erratic than the Brownian motion of paralyzed cells.

The numbers of wild-type, smooth-swimming, and paralyzed strains moving near the surface seemed to be similar and independent of ionic strength and fluid velocity. Tumbly bacteria did not seem to be able to get as close to the surface as the other three strains, as judged by the majority of cells near the surface being slightly out of focus in comparison to the attached cells.

The length of time a bacterium remained attached to the surface was also different for the various strains. Although the duration of attachment varied within a single strain, for the most part, wild-type, paralyzed, and tumbly bacteria continued to stay attached considerably longer than the smooth-swimmers. Smooth-swimming cells typically attached and detached in less than a minute, while the other three strains remained on the surface for average times on the order of several minutes to tens of minutes.

We also observed an occasional wild-type bacterium that appeared to be tethered to the surface in the lower ionic strength medium. In most cases (both in 0.2 M and in 0.02 M concentrations), bacteria attached at some point on the cell body and spun on the surface about that point due to the rotation of the flagella. For tethered cells, the point about which a bacterium rotated was a small distance away from the cell body, on the order of a micron. This motion is different from the circular swimming patterns observed in the tracking microscope with smooth-swimming bacteria (15, 23, 41) because the movement was more irregular and the area of revolution was smaller for a given ionic strength. We did count cells that were tethered to the surface as attached, provided the cell remained in the same vicinity for ca. 4 s. We did not observe any tumbly, smooth-swimming, or paralyzed cells tethered to the surface for the fluid conditions tested.

DISCUSSION

We first performed experiments with wild-type and paralyzed bacteria in 0.2 M buffer to determine how the rate of mass transport to the surface would affect their attachment rate. Since the diffusion coefficient was 3 orders of magnitude smaller for the paralyzed strain, we expected to see a large difference in the attachment rate. However, because gravitational settling was dominant at the fluid velocities tested, there was no difference in attachment rate with the 0.2 M solution as we had anticipated. We then decreased the ionic strength by an order of magnitude, expecting that the attachment rate would also decrease for both strains. We found that the paralyzed strain followed our predictions, but the attachment of motile bacteria seemed to be unaffected by ionic strength for the two solutions tested. We thought that this could be for two reasons: (i) swimming would enable the wild-type to get closer to the surface or (ii) tumbling may cause one or more flagella to attach to the surface and act as an anchor. We therefore measured the attachment rates of smooth-swimming and tumbly strains to help explain our experimental results. We consider several hypotheses, both transport related (residence time analysis) and adsorption related (soft-particle theory and the role of the flagella), to explain why wild-type bacteria have greater attachment rates.

Residence time analysis.

To better understand the differences in the observed attachment behavior of motile and nonmotile bacteria, we compared the residence time within the flow chamber to the time it takes a bacterium to settle or swim to the surface and adsorb. We calculate the residence time (τ_r) within a specific viewing area as L_v/v(d), where L_v is the length of the viewing area (0.029 cm) and v is the fluid velocity, given by:

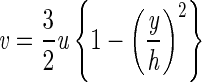(2)

where u is the average fluid velocity, h is the chamber half-height, and y is the direction perpendicular to fluid flow. Equation 2 was derived from a momentum balance, assuming a Newtonian fluid with constant density and no-slip boundary conditions. The separation distance (d) is equal to h − (y + r_b), where r_b is the radius of a bacterium (in this case, we assumed a radius of 0.6 μm).

In the macroscopic environment (bulk to ∼10 μm), the transport time is given by d/v_s and d²/D_b for nonmotile and motile bacteria, respectively, where D_b is the diffusion coefficient of a motile bacterium (equal to 2.9 × 10⁻⁶ cm² s⁻¹ for wild-type E. coli [25]). The time needed to settle or swim to the surface within the microenvironment (∼10 μm to ∼100 nm) is equal to d/v_s,r and d/v_b,r for nonmotile and motile bacteria, respectively, where v_s,r is the reduced settling velocity of a nonmotile bacterium and v_b,r is the reduced swimming speed of a motile bacterium, both of which are a function of separation distance near the surface. We have assumed for this analysis that the decrease in both velocities as a result of the presence of the solid surface is as given by Brenner (5), although we note that the swimming speed of a motile bacterium is not reduced in the same manner as the settling velocity close to the solid surface (14, 33). Bulk values for the settling and swimming velocities are 0.07 and 25 μm s⁻¹, respectively.

We can also characterize the time needed to adsorb on the surface, equal to d/k_a, where k_a is the adsorption rate constant. We note that we have assumed the adsorption rate is constant for this illustration, although according to DLVO theory the force of attraction varies with separation distance (and therefore k_a will also vary). In effect, we assume an average adsorption rate constant between the secondary minimum and 100 nm.

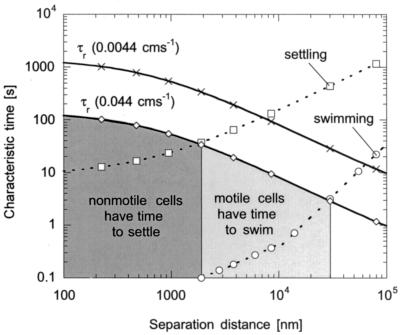
Figure 2 shows the residence and transport times as a function of separation distance for fluid velocities of 0.0044 and 0.044 cms⁻¹. We assume cells are transported to a distance of ca. 100 nm above the surface by diffusion, swimming, or settling and then begin to adsorb to the surface (adsorption kinetics dominate below 100 nm). We chose 100 nm because DLVO theory predicts bacteria begin to experience a net attraction toward the glass surface at this location; however, we note that microscopic transport and adsorption most likely overlap to some extent at nanometer separation distances. In Fig. 2, the location at which residence time and transport curves cross indicates the separation distance at which cells are able to transport within 100 nm of the surface. For fluid velocities of 0.044 and 0.0044 cm s⁻¹, nonmotile bacteria closer than 1.9 and 7 μm, respectively, from the surface have time to settle to a distance of 100 nm above the surface. Since the swimming speed of motile bacteria is much greater than the settling velocity of nonmotile bacteria, motile cells at distances farther away from the surface have time to swim to 100 nm above the surface. At 0.044 cm s⁻¹, motile bacteria 30 μm away from the surface have time to reach nanometer separation distances (provided they are swimming toward the surface) and, at 0.0044 cm s⁻¹, this distance is increased to ca. 60 μm.

FIG. 2.

Residence time and times to settle (□) and swim (○) to the surface as a function of separation distance (d) for fluid velocities of 0.0044 cm s⁻¹ (×) and 0.044 cm s⁻¹ (⋄). The shaded regions show the areas in which motile and nonmotile bacteria have time to reach the surface at the higher fluid velocity.

Since we did measure a decrease in the attachment rate with increased fluid velocity for all bacterial strains (Table 1), this suggested a transport or kinetic limitation at the higher fluid velocity for both ionic-strength solutions. According to DLVO theory, a bacterium will be “pulled” closer to the surface by attractive forces until it reaches the secondary minimum. To attach in a dynamic system, the rate at which bacteria are pulled to the surface must be higher than the rate at which they travel along the surface with the fluid or through swimming. Because this effect was observed in both 0.2 and 0.02 M solutions, this suggested the movement of the fluid prevented both motile and nonmotile cells from reaching separation distances on the order of nanometers. This agrees with our residence time analysis, in that both motile and nonmotile cells had less time to reach distances close to the surface at the higher fluid velocity. This is also consistent with research performed by Lawrence and coworkers, who studied the initial attachment and colonization of Pseudomonas fluorescens CC-840406-E to glass surfaces by continuous-flow slide culture (7, 22, 23). They found that the number of attached motile and nonmotile bacteria was significantly reduced when the fluid velocity was increased from 0.14 to 7 cm s⁻¹ by using a suspending solution of 10% tryptic soy broth (22).

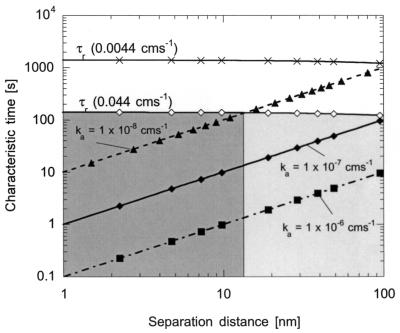
For high adsorption rate constants (on the order of 10⁻⁶ and 10⁻⁷ cm s⁻¹), both motile and nonmotile bacteria have time to adsorb to the surface. However, for rates lower than 10⁻⁷ cm s⁻¹, the effective attachment rate will be reduced at the higher fluid velocity because bacteria that reach 100 nm will not have enough time to attach (Fig. 3). The adsorption rate constants chosen for this analysis were based on experimental values, which are on the order of 10⁻⁶ cm s⁻¹ for wild-type and paralyzed cells in a 0.2 M solution (26). We then decreased the adsorption rate constant to 10⁻⁸ cm s⁻¹ (as would be expected in a lower-ionic-strength solution) to determine when fluid velocity and adsorption kinetics were competing.

FIG. 3.

Residence time and times needed to adsorb to the surface for k_a = 10⁻⁶ cm s⁻¹ (▪), k_a = 10⁻⁷ cm s⁻¹ (⧫), and k_a = 10⁻⁸ cm s⁻¹ (▴) as a function of separation distance for fluid velocities of 0.0044 cm s⁻¹ (×) and 0.044 cm s⁻¹ (⋄). The shaded regions show the areas in which bacteria (both motile and nonmotile) have time to adsorb to the surface at the higher fluid velocity. The light and dark regions refer to cells with adsorption rates constant of 10⁻⁸ and 10⁻⁷ cm s⁻¹, respectively. Cells within 100 nm of the surface have time to adsorb if their adsorption rate constant is 10⁻⁷ cm s⁻¹; cells with a k_a of 10⁻⁸ cm s⁻¹ must be within ∼15 nm to have enough time to adsorb.

In comparing characteristic times from this analysis, it is obvious that residence time will only play a significant role in cell attachment with a carrier fluid of 0.02 M ionic strength (because the adsorption rate constant should be lower). We would expect the effective attachment rate to decrease with ionic strength for a given fluid velocity, because the residence time within the chamber becomes more comparable to the time needed to adsorb to the surface. Further, we would anticipate the reduction in the attachment rate to be more significant at the higher fluid velocity because fewer cells have time to reach the surface and adsorb. It therefore makes sense that the attachment rate of paralyzed cells decreased by a factor of 4 at the lower fluid velocity and by a factor of 10 at the higher fluid velocity.

Conversely, wild-type cells did not appear to be influenced by the decrease in ionic strength at either fluid velocity. One possible explanation is that a larger number of motile cells are able to reach nanometer separation distances in comparison to paralyzed cells (motility aids in microscopic transport). Although we did observe a large number of paralyzed cells “near” the surface, the resolution of our microscope allows us to see several microns into the fluid. Thus, the fact that we see paralyzed cells above the surface means that they are not transport limited to within several microns of the surface. From the residence time analysis (Fig. 2), it is clear that more motile bacteria have time to reach the surface at both flow rates, because their swimming speed is higher than the settling velocity of nonmotile cells. Further, since the swimming behavior of motile bacteria is mechanistically different than the downward settling of nonmotile bacteria, their velocity is not reduced in the same manner near a solid surface (15, 33). An increase in the drag force will certainly slow their swimming speed, but because motile cells swim in all directions, their velocity is less hindered (and therefore their microscopic transport is not limited). Thus, in our analysis, our estimate of the maximum distance above the surface from which a motile bacterium has time to reach 100 nm is conservative (because we assumed swimming and settling velocities were reduced in the same manner).

The adsorption kinetics may also be different for wild-type and paralyzed cells. In a high-ionic-strength solution, a slight difference in rate constants for the two strains may not be observed experimentally, because both are high enough not to be limiting. However, when the ionic strength is lowered, this difference may become more apparent. We hypothesize a difference in the adsorption rate constant could be a result of flagellar rotation (which could cause flagella to adsorb and anchor cells to the surface) or reflect slight variations in surface charge between strains.

Mechanisms of detachment.

For paralyzed cells, the two possible mechanisms of detachment are through fluid shear or Brownian motion. In 0.2 M buffer, the fraction of bacteria retained on the surface decreased with fluid velocity. This suggested shear was the primary mechanism for detachment. We can calculate the shear force (F_s) acting on a bacterium attached to the surface according to the following equation (16):

(3)

where μ is the viscosity of the fluid and S is the shear rate (the derivative of the velocity with respect to the y direction). The bracketed expression is a correction factor to account for the proximity of the solid surface (16). For a fluid velocity of 0.0044 cm s⁻¹, the shear force at a distance of 100 nm from the surface is 0.024 pN and decreases linearly to 0.023 pN when r_b/(d + r_b) ≈ 1. The shear force at 0.044 cm s⁻¹ ranges between 0.24 and 0.23 pN for separation distances between 100 nm from the surface and the surface, respectively. Thus, when the force of shear is greater than the strength of interaction, cells will detach from the surface.

In the lower-ionic-strength media, the fraction of paralyzed bacteria retained on the surface was similar for the two flow rates. We believe this reflects the small number of cells that attached at the higher fluid velocity. A possible explanation for this is that, because it was difficult for paralyzed cells to attach in a low ionic strength solution, those that were able to attach were tightly held and consequently less likely to detach. Wild-type cells had the opposite trend: at the lower fluid velocity, the fraction retained was significantly smaller than that at the higher fluid velocity. This suggested the movement of the flagella gave bacteria enough energy to detach from the surface at the lower fluid velocity but was not advantageous to cell detachment at the higher fluid velocity. Camesano and Logan found a similar trend for motile and nonmotile (killed) P. fluorescens P17 using columns packed with soil (8). In that study, the fraction of motile bacteria remaining in the column increased with fluid velocity (for a range of 6.5 × 10⁻⁴ to 0.7 cm s⁻¹) and decreased for killed cells in 0.00414 M artificial groundwater. The fraction of motile and killed bacteria remaining in soil columns was similar in magnitude at higher fluid velocities, but at lower fluid velocities the fraction of motile cells retained on the soil grains was significantly less (8). This is consistent with our results with the lower-ionic-strength media. We note that Camesano and Logan defined their fraction retained as the total amount of bacteria remaining in the column at the end of an experiment divided by the total amount of bacteria introduced into the column, which is slightly different from our definition.

DLVO and soft-particle theory.

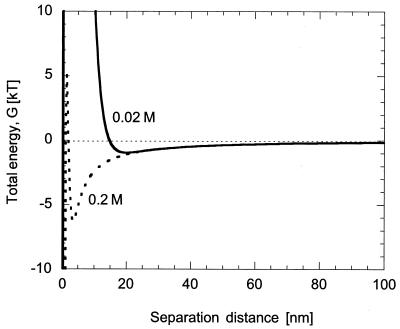
The DLVO theory is one approach we considered for explaining the effect of electrolyte concentration on the initial attachment of bacteria to charged surfaces (31, 39). DLVO theory describes the total interaction Gibbs energy between bacteria and solid surfaces as the sum of van der Waals and electrostatic interactions (31). At a separation distance of several nanometers, DLVO theory predicts a net attraction (in the secondary energy minimum) between a bacterium and surfaces in a fluid of moderate ionic strength (Fig. 4). As the bacterium and solid surface get closer, there is a net repulsion, followed by an even greater attraction (in the primary minimum). A decrease in ionic strength changes the position and depth of the secondary minimum; i.e., the separation distance between a bacterium and surface is extended and the depth of the energy well is reduced. This is a result of an increase in double layer thickness on both the bacteria and the surface. As a consequence, fewer bacteria are expected to adhere to a surface when the ionic strength of the solution is decreased because of the greater degree of repulsion.

FIG. 4.

Total Gibbs energy (G) as a function of separation distance between wild-type E. coli and a glass surface for ionic strengths of 0.2 M (dashed line) and 0.02 M (solid line). We calculated the total energy as the sum of van der Waals and electrostatic interactions given by equations 4 and 5 in the text. For ionic strengths of 0.2 and 0.02 M, the secondary minima were at 3.5 nm (−6.3 kT) and 20 nm (−0.98 kT), respectively.

According to DLVO theory, the van der Waals interactions (G_A) and the electrostatic interactions (G_E) for a spherical colloidal particle interacting with a flat surface are given as follows (31):

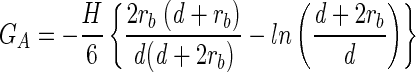(4)

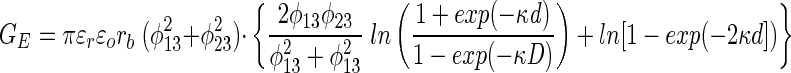(5)

The van der Waals interaction energy is a function of the Hamaker constant (H), the radius of the bacterium (r_b), and the separation distance (d) measured from the cell surface to the planar surface. The repulsion resulting from an overlap in electrical double layers is a function of glass (φ₁₃) and bacterium (φ₂₃) surface potentials, the reciprocal Debye length (κ), the dielectric permittivity of the medium (ɛ_rɛ_o), the radius of the bacterium, and the separation distance. The total interaction energy (G) is the sum of van der Waals and electrostatic interactions.

From Fig. 4, we can see that, at a separation distance of ca. 100 nm, bacteria begin to experience a slight attraction toward the surface. The strength of this attraction increases as the cell moves closer until it reaches the secondary energy minimum, at which the net attractive force is zero (the force of attraction is equal to the derivative of the Gibbs energy with respect to separation distance). In the 0.02 M solution, the strength of attraction is lower and, consequently, the adsorption rate constant is expected to be smaller. For wild-type bacteria, the location of the secondary minimum is 3.5 nm in 0.2 M buffer and 20 nm for a 0.02 M solution. We note that we have assumed a Hamaker constant of 10⁻²¹ J (40) and an (equivalent) bacterial radius of 0.6 μm, and we used zeta potentials measured by Vigeant and Ford (41).

Since the ionic strength of the suspending medium did not seem to influence the attachment rate of wild-type bacteria or fractions retained at both fluid velocities, this suggested that the depth and location of the secondary energy minimum did not influence attachment. We speculated that this could be because wild-type bacteria may be attaching at distances >20 nm from the surface, where the attractive force is the same for both ionic-strength solutions (and therefore cells do not attach in the secondary minimum). We also considered the possibility that wild-type bacteria may have enough kinetic energy to overcome the energy barrier at the surface and attach in the primary minimum.

We can calculate the kinetic energy of a wild-type bacterium by multiplying the cell mass by the square of the swimming speed and dividing by two. For an E. coli cell with a mass of 3 × 10⁻¹² g (6) and velocity of 25 μm s⁻¹ (25), the kinetic energy is on the order of 10⁻⁴ kT. The thermal energy of a bacterium is estimated to be ca. 0.5 kT (1). Thus, according to DLVO theory, motile cells should not have enough energy to overcome the energy barrier (ca. 10 to 1,000 kT) for either 0.02 or 0.2 M solutions.

We assumed for this analysis that the total interaction energy as calculated with DLVO theory is accurate for a bacterium interacting with a solid surface. However, the interaction energy was determined for a rigid, spherical particle interacting with planar surface. Since the outer cell membrane of a bacterium generally consists of phospholipids, polysaccharides, and proteins (13), the surface is far from rigid and smooth. The distribution of charge around a cell is also not uniform. To account for this, several articles in the literature have recently suggested a soft-particle theory in which the complex nature of the cell surface is considered as a soft, polyelectrolyte layer (3, 18, 28, 32, 37). This changes the relationship between electrophoretic mobility and surface potential, which is needed to calculate the interaction energy, as in Fig. 4. According to this theory, the zeta (surface) potential typically calculated by using the Smoluchowski equation is an overestimate for bacteria and other soft particles and should be calculated according to Ohshima's theory for soft particles (32). Morisaki et al. (28) reported a soft-particle surface potential that was a factor of 40 less than that determined from the Smoluchowski expression (using an ionic strength of 0.05 M). This effectively eliminated the secondary minimum and lowered the energy barrier to allow cells to attach in the primary minimum (28).

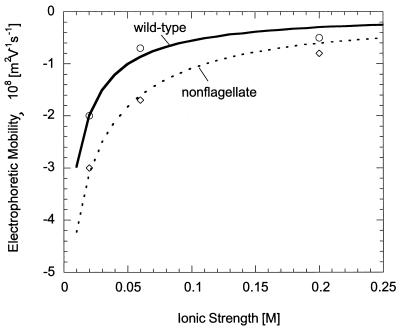
Vigeant and Ford (41) measured the electrophoretic mobility of wild-type and nonflagellate E. coli for ionic strengths of 0.02, 0.06, and 0.2 M. We can estimate the surface potential according to the soft-particle theory by fitting these data to the following equation (32):

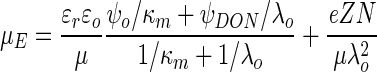(6)

where ɛ_r is the relative permittivity of the liquid, ɛ_o is the permittivity in a vacuum, μ is the fluid viscosity, ψ_o is the surface (zeta) potential, κ_m is the Debye-Huckel parameter for the polymer layer, ψ_DON is the Donnan potential, Z is the valence of the charged groups in the polymers, e is the unit charge of an electron, N is the density of the charged groups, and λ_o is the softness parameter (usually reported as the reciprocal with units of length). In equation 6, κ_m, ψ_o, and ψ_DON are all functions of ionic strength; the expressions for these parameters are given by Ohshima (32).

Using equation 6, we are able to fit the data of Vigeant and Ford to determine the unknown parameters, ZN and λ_o, for wild-type and nonflagellate E. coli (Fig. 5). For wild-type bacteria, we obtained 1/λ_o and ZN values of 0.62 nm and −0.092 M, respectively. We calculated 1/λ_o and ZN values of 0.28 nm and −0.22 M, respectively, for nonflagellate E. coli. The values obtained for the wild-type are similar to those measured by others (3, 28, 36, 37); however, the 1/λ_o value for the nonflagellate strain is slightly lower than those reported in the literature for E. coli strains, and the ZN value is greater. We note that the use of ZN and 1/λ_o values closer to those reported in the literature did not yield a reasonable fit to experimental data for nonflagellate E. coli. Thus, even though our parameters for nonmotile bacteria were inconsistent with other literature values, they best represented the experimental data of Vigeant and Ford (41) and were consequently used in our analysis. We note that, in using Equation 6 to fit experimental data, we have assumed that the valence of the ionic species is equal to 1, even though other species were present in the potassium phosphate buffer at low concentrations.

FIG. 5.

Electrophoretic mobility of wild-type (○) and nonflagellate (⋄) E. coli as a function of ionic strength as measured by Vigeant and Ford (41). The lines correspond to the best fit (as measured by the sum of squared errors) of equation 6 to the experimental data.

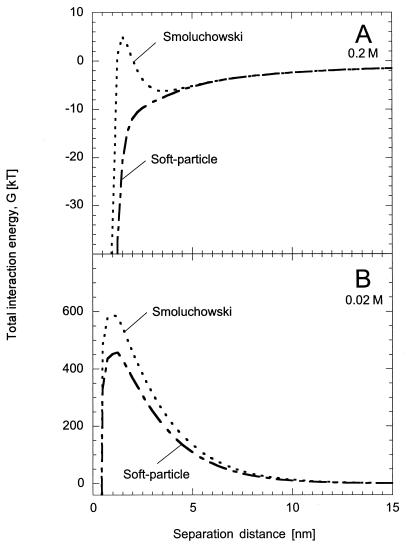
For both ionic-strength solutions, values of the bacterial surface potential as calculated from equation 6 were slightly lower than those determined from the Smoluchowski equation. For wild-type bacteria, we calculated surface potentials of −3 and −24 mV for the 0.2 and 0.02 M buffer solutions, respectively, compared with −7 and −29.5 mV with the Smoluchowski equation. We obtained values of −7 and −40 mV for the nonflagellate strain in 0.2 and 0.02 M solutions, respectively, and −11 and −43 mV with the Smoluchowski equation. At the lower ionic strength, we saw little effect on the interaction energy diagram for wild-type bacteria (Fig. 6B). The height of the energy barrier is slightly reduced but not reduced enough to allow cells to reach the primary minimum. This is in contrast to the higher-ionic-strength solution (Fig. 6A), in which the secondary minimum and energy barrier were both eliminated. We saw similar results for nonflagellate cells in the lower-ionic-strength media; at 0.2 M, the energy barrier was reduced to ca. 0.5 kT. Thus, even with a correction to DLVO theory to account for the properties of the bacterial surface, it still seems unlikely that the wild-type E. coli cells used in this study are able to attach in the primary minimum in the low-ionic-strength solution.

FIG. 6.

Total interaction energy as a function of separation distance between wild-type E. coli and a glass surface as determined by using the Smoluchowski equation and soft-particle theory for bacterial surface potentials. (A) 0.2 M solution: Smoluchowski (dotted line) and soft particle (dashed line). (B) 0.02 M solution: Smoluchowski (dotted line) and soft particle (dashed line).

This therefore suggested that bacteria could attach at distances greater than 20 nm from the surface (where differences in attraction strength for the two ionic-strength solutions is small). If wild-type cells attached closer to the secondary minimum, we would anticipate the strength of the attractive force to influence the attachment rate. Further, if cells attached in the secondary minimum, the net attractive force acting on a cell would be zero. Thus, fluid shear would become important to cell detachment. However, we did not measure a decrease in the fraction of bacteria retained on the surface with fluid velocity (in fact, we saw the opposite), which suggests shear was not an important detachment mechanism.

Role of the flagella.

We hypothesized that motility enabled more wild-type cells to get closer to the surface than paralyzed cells. If this were true, we would expect the attachment rate of smooth swimmers to be similar to that of the wild type. At the lowest fluid velocity, the rate of attachment of smooth-swimming cells is approximately the same as that of the wild type (in fact, it was slightly larger in the 0.2 M solution). However, at the higher fluid velocity, the attachment rate is half as fast with a 0.2 M solution and could not be measured in the 0.02 M solution because no bacteria attached. This suggested the residence time within the flow chamber was competing with adsorption kinetics for smooth-swimming cells, which in turn meant that they were not attaching by the same mechanism as did the wild type. The length of time smooth-swimming bacteria remained attached to the surface was also observed to be relatively short, and therefore the fraction of bacteria retained on the surface was low for all fluid conditions. Thus, smooth swimmers seem to be able to get to the surface and attach, but only for a brief time.

For all strains tested in this study, the possible ways a cell can attach to the surface is by some point on the cell body, one or more flagella, or both. For a smooth-swimming cell, the flagella form a bundle behind the cell body and rotate together in a counterclockwise motion. Thus, it seems likely that if a smooth swimmer attached at some point on the cell body, the continuous movement of the flagella as a unit would detach the cell more quickly than would a wild-type bacterium. An attached wild-type cell may switch the direction of rotation for one or more flagella, which in turn would cause it to change conformation and escape from the bundle. The rotational force of the flagellar bundle on the cell body would then be reduced, and a flagellum outside the bundle could also attach to initiate or strengthen adsorption. This is one possible reason wild-type cells may be able to attach at a faster rate than smooth swimmers at the higher fluid velocity. Further, the uninterrupted run of a smooth swimmer may make it difficult for these cells to have enough time to attach to the surface, especially in lower-ionic-strength solutions where the rate of adsorption is less. It also seems unlikely for a smooth swimmer to attach by one or more flagella because the helical diameter of the flagellar bundle is about half the size of the diameter of the cell body (25).

Flagella on tumbly bacteria constantly rotate in a clockwise direction, which means the cell is in a continual state of reorientation. Since flagella emerge at various points on the cell body, it seems reasonable to assume the attachment of tumbly cells occurs (at least first) by some point on the flagellar filament. However, the rate of attachment is significantly lower than the three other strains for all conditions, which suggests that the cell has difficulty attaching by the cell body, possibly as a result of steric hindrance (i.e., flagella may get in the way). We observed many cells moving erratically near the surface but not remaining in the same location for more than a second or two. We hypothesize that during this time the cell is attached by one or more flagella but that this type of attachment is not as strong as the cell body (unless possibly a significant number of flagella are all attached). Thus, cells attached by their flagella are easily sheared from the surface (and therefore attach and detach too quickly to be measured in our system).

Since smooth swimmers and tumbly bacteria did not have similar attachment kinetics in comparison to the wild type, this suggests that the switching of flagellar rotation is optimal for adsorption. We believe motility allows a greater number of cells to get closer to the surface, but a pause near the surface is required to allow a cell to attach for a significant amount of time. During a tumble, one or more flagella leave the bundle in a rapid, erratic movement, which causes the cell to reorient. This change in direction may be less chaotic in wild-type cells than in tumbly bacteria because fewer flagella may be involved in the tumble (and therefore fewer rotate in the clockwise direction). The fraction of a second in which the cell is changing direction may be when it attaches, because the cell slows down (1, 15, 25). Further, the cell does not return to its original speed until ca. 0.4 s later when all flagella have returned to the bundle (38). This would give bacteria additional time to interact with the surface. The ability to reverse direction of flagellar rotation could allow flagella to attach to the surface (and stabilize adsorption) or, if several are able to form a bundle, the cell may detach.

For motile bacteria, the variation of fraction retained with fluid velocity suggests that the movement of their flagella can both enable and prevent cells from leaving the surface, depending on the magnitude of the shear force. At the lower fluid velocity, fewer than half of the attached bacteria remained on the surface compared to 70% of the nonmotile bacteria. This suggests that the rotation of the flagella is enabling cells to detach from the surface. The observation that the smooth-swimming bacteria had such a low number of cells remaining on the surface (at both fluid velocities) suggests that the counterclockwise rotation of flagella (bundle formation) is important in cell detachment. However, at the higher fluid velocity, the movement of the flagella seemed to prevent wild-type cells from leaving the surface, because the fraction retained on the surface was much higher than that measured for nonmotile cells. Thus, motile cells appear to be influenced by shear in a different manner than nonmotile bacteria. Further, since a large number of smooth-swimming cells were still able to detach at the higher fluid velocity, this suggests that the clockwise rotation of one or more flagella (as in a tumble) may anchor cells to the surface.