Staphylococcus aureus Growth Boundaries: Moving towards Mechanistic Predictive Models Based on Solute-Specific Effects

Abstract

The formulation of shelf-stable intermediate-moisture products is a critical food safety issue. Therefore, knowing the precise boundary for the growth-no-growth interface of Staphylococcus aureus is necessary for food safety risk assessment. This study was designed to examine the effects of various humectants and to produce growth boundary models as tools for risk assessment. The molecular mobility and the effects of various physical properties of humectants, such as their glass transition temperatures, their membrane permeability, and their ionic and nonionic properties, on S. aureus growth were investigated. The effects of relative humidity (RH; 84 to 95%, adjusted by sucrose plus fructose, glycerol, or NaCl), initial pH (4.5 to 7.0, adjusted by HCl), and potassium sorbate concentration (0 or 1,000 ppm) on the growth of S. aureus were determined. Growth was monitored by turbidity over a 24-week period. Toxin production was determined by enterotoxin assay. The 1,792 data points generated were analyzed by LIFEREG procedures (SAS Institute, Inc., Cary, N.C.), which showed that all parameters studied significantly affected the growth responses of S. aureus. Differences were observed in the growth-no-growth boundary when different humectants were used to achieve the desired RH values in both the absence and the presence of potassium sorbate. Sucrose plus fructose was most inhibitory at neutral pH values, while NaCl was most inhibitory at low pH values. The addition of potassium sorbate greatly increased the no-growth regions, particularly when pH was <6.0. Published kinetic growth and survival models were compared with boundary models developed in this work. The effects of solutes and differences in modeling approaches are discussed.

Olsen et al. (28) reported that Staphylococcus aureus was involved in 42 documented outbreaks of food-borne poisoning in the United States, with 1,413 cases and 1 death occurring from 1993 to 1997. S. aureus has been estimated to cause approximately 185,000 illnesses, 1,750 hospitalizations, and 2 deaths per year in the United States, all from consumption of contaminated foods (24). Food-borne staphylococcal poisoning, caused by the ingestion of one or more preformed toxins in food contaminated with S. aureus, is one of the most prevalent causes of gastroenteritis worldwide (16). Recently, powdered milk produced in Taiki, Hokkaido, Japan, was linked to contaminated dairy products that made more than 14,700 people in Japan ill in June and July of 2000. Health authorities determined that dry skim milk powder was contaminated with staphylococcal enterotoxin A (11).

Scott (32) related the relative vapor pressures (rvp's) of foods to the thermodynamic activity of water, using the definition a_w = p/p_o, where a_w is the water activity as derived from the laws of equilibrium thermodynamics, p is the vapor pressure of the sample, and p_o is the vapor pressure of pure water. He showed a clear correlation between the rvp of the growth medium and the rate of S. aureus growth. In the field of food science, the general acceptance and application of this concept relating the rvp's of foods to a minimum a_w for microbial growth began with the review by Scott (33). The important point is that the equality of a_w with p/p_o is based on the assumption of the existence of thermodynamic equilibrium and that the value is true only for specified conditions of temperature and pressure. Although dilute solutions obey the laws of equilibrium thermodynamics, the same is not necessarily true for intermediate-moisture systems and is even less likely for low-moisture systems, the properties of which are determined mainly by slow reaction rates. The concept of a_w then becomes meaningless, because the measured rvp of water is no longer the same as the equilibrium vapor pressure (13). The equation a_w = p/p_o therefore applies only in the range 0.95 <a_w <1.0, where equilibrium is established rapidly (13). With many foods, this assumption of thermodynamic equilibrium is violated, so the appropriate term is rvp or relative humidity (RH) rather than a_w.

For the past several decades, in the food science literature, the phenomenon denoted by the term “a_w” has been widely used to predict microbial growth as well as the relationship between many common food deterioration reactions and a_w. Although RH is a better indicator of food stability and safety than the water content of a system, it is not always a reliable predictor. For example, several authors have reported that the growth boundaries for various genera of microorganisms differ depending on the type of humectant used to depress RH rather than the absolute value of RH (6, 8, 22, 33). The literature on microbial osmoregulation via compatible solutes has also shown that the type of humectant, rather than the absolute value of RH, is critical (14). In recent years, increasing evidence based on glass transition theory has shown that molecular mobility (Mm) may be an attribute that deserves further attention, as it is related to many important diffusion-limiting properties of foods (5, 36, 37, 43). This is because the temperature at which a viscous liquid changes to a “glass” (glass transition temperature [T_g]), which governs Mm, is a solute-specific property that is inversely linearly related to the measured RH of a system. Although the use of RH has served the food industry well for the past several decades since Scott introduced the concept of a_w in 1953, further study to understand these solute-specific effects on microbial growth should continue.

Microbial growth models are typically developed when the objective is to understand the responses of microorganisms when part of the range of conditions studied permits growth to occur. Such models can describe the increase in numbers with time (kinetic models), the conditions allowing growth or no growth (boundary models), or the chance of growth (probabilistic models). Kinetic growth models are typically based on growth curves over a range of conditions and can allow growth rates to be predicted. In the 1980s, the United Kingdom Ministry of Agriculture, Fisheries, and Food and the U.S. Department of Agriculture (USDA) funded programs to develop kinetic models for the growth, survival, and death of food-borne pathogens, including S. aureus. This work resulted in suites of models which are currently available. NaCl was the humectant chosen to control the RH in these models, and the resulting kinetic models do not allow the growth-no-growth boundary to be estimated (4, 23, 41, 47).

The statistical effects and interactions of RH, initial pH, and potassium sorbate concentration on the boundary for S. aureus growth were modeled in this study by using the approach described previously (30, 40). Additionally, the concepts of Mm and the effects of various physical properties of humectants, such as the T_g, membrane permeability, and ionic and nonionic properties of solutes, on S. aureus growth were investigated by controlling the RH with sucrose-fructose (50:50, wt/wt), glycerol, or NaCl.

MATERIALS AND METHODS

Preparation of bacteria and media.

Five S. aureus strains were used as a cocktail in this study: ATCC 13565, ATCC 14458, and ATCC 27664, from the American Type Culture Collection, Manassas, Va.; D-2, from Toxin Technology, Inc., Sarasota, Fla.; and A-100, from the U.S. Army Natick Laboratories, Natick, Mass. A cocktail of strains was chosen for use because it helps to overcome the variability between strains and increase the chance of detecting the fastest growth at different points in the experimental matrix. These benefits of using a cocktail help to create a fail-safe model without repeating the experiment many times with different strains (19). All strains showed typical growth on Baird-Parker agar (Difco, Detroit, Mich.) plates and were coagulase positive. Their identification as S. aureus was confirmed by the use of a Riboprinter (Qualicon, Wilmington, Del.). Stock cultures were grown overnight at 37°C in brain heart infusion (BHI) broth (Difco), suspended in solution containing a 2:1 BHI broth-glycerol solution, and stored at −80°C until needed.

For this study, BHI broth was reconstituted with the appropriate ratio of water to sucrose-fructose (50:50, wt/wt) or to NaCl to achieve the desired RHs for the study (84, 88, 92, or 95%). Appropriate amounts of 10% stock solutions of potassium sorbate (Hoechst, Frankfurt, Germany) were added to achieve a final concentration of 1,000 ppm. The pH was adjusted to 4.5, 5.0, 6.0, or 7.0 by using 0.1 or 1.0 N HCl (J. T. Baker, Inc., Phillipsburg, N.J.). The final RH was determined by using an Aqualab CX-2 a_w meter (Decagon Devices, Inc., Pullman, Wash.). The RHs of the media measured at ambient temperature differed by no more than ±0.003% relative to those measured at 37°C. Each of the 64 broths was filter sterilized and stored in screw-cap tubes at 4°C until needed.

Bioscreen microtiter plate preparation, incubation, and measurement.

The five stock cultures were removed from −80°C storage, and one loopful of each was transferred separately into 9 ml of BHI broth. The inoculated broths were incubated for 18 h at 37°C. The five cultures were individually adjusted to optical densities (ODs) at 530 nm of 0.750 to 0.780 (measured with a Perkin-Elmer model 35 spectrophotometer) with 0.1% sterile peptone to achieve a concentration of approximately 10⁸ CFU/ml. Diluted cultures (10 ml) were transferred into a single sterile test tube and vortexed to create the S. aureus cocktail used in our experiments. Three 1/10 dilutions with sterile 0.1% peptone water were used to make a final working cocktail with a concentration of approximately 10⁵ CFU/ml. This working cocktail was kept on ice until it was used to inoculate the various media used in the experiments. Samples (1 ml) of the working cocktail were taken, serially diluted, spread plated onto Baird-Parker agar plates, and incubated at 37°C for 48 h, and cells were counted to determine their initial concentrations.

Each of the 64 broths (10 ml) was aseptically transferred to a sterile tube, and the S. aureus cocktail (100 μl) was added to the broth to achieve an initial concentration of approximately 10³ CFU/ml. The inoculated broths (400 μl) were aseptically transferred into sterile 100-well microtiter plates, with eight replicate wells per medium. The outer wells of the microtiter plates were filled with uninoculated medium to act both as a partial moisture barrier and as uninoculated controls. Each plate contained media at only one RH level. A piece of sterile thermaseal film was placed on top of the open wells under the lid during incubation. The plates were placed on a rack in a sealed plastic container that contained the appropriate saturated salt slurries needed to maintain the environmental RH and thereby ensure the stability of the RHs of the media. The saturated salt solutions used were as follows: ZnSO₄ · H₂O (83% RH at 37°C), KNO (89% RH at 37°C), KPO₄ (93% RH at 37°C), and K₂Cr₂O₇ (96% RH at 37°C). The containers were closed and incubated at 37°C. Plates were periodically removed and shaken for 60 s, and the ODs of the 1,024 individual wells were measured for up to 24 weeks by using the wideband filter on the Bioscreen C system (Labsystems Oy, Helsinki, Finland). The experiments were repeated on separate dates. A total of 1,024 wells were monitored.

Data collection.

The S. aureus population was considered to have grown when the Bioscreen OD measured with a wideband filter (OD_wb) increased from an initial reading between 0.200 and 0.220 to an OD_wb of 0.350 or higher. The time to growth (TTG) was determined by calculating the geometric mean of the time of the last measurement that showed no growth (OD_wb < 0.350) and the first time point that showed growth (OD_wb > 0.350). In instances of no growth, TTG was censored at the final measurement time of 168 days.

A threshold OD_wb value of 0.350 was used to score wells with S. aureus growth (OD_wb ≥ 0.350) and wells with no growth (OD_wb < 0.350). This threshold value was determined as discussed in detail by Stewart et al. (40). In brief, OD_wb measurements were compared with plate counts, and an OD_wb of 0.350 was identified as the lowest OD_wb value at which an increase in turbidity regularly correlated to an increase in plate counts.

OD measurements were transferred from the Bioscreen C ASCII file to a DOS text editor and then imported into Statistica software (StatSoft, Tulsa, Okla.) for initial analysis. Data were transferred to a Microsoft Excel spreadsheet to determine TTG and then to SAS software for modeling by the LIFEREG procedure (SAS Institute, Inc., Cary, N.C.).

An additional data set (40) was also included in the development of the model. This data set included information on TTG for the same S. aureus cocktail obtained by an identical experimental procedure, with the exception that the humectant used to achieve the desired RH of the BHI broth was glycerol, a glass-forming membrane-permeable solute. The experimental design of Stewart et al. (40) included three levels of potassium sorbate (0, 500, and 1,000 ppm). A total of 768 data points from the glycerol data set were included in the data analysis.

Statistical analysis.

The TTG data along with a censoring indicator, the percent RH, the pH, the potassium sorbate level, and the humectant type (sucrose-fructose, glycerol, or NaCl) were input data for the construction of the growth boundary model. RH, pH, and potassium sorbate values were normalized [(RH − 89.75)/4.15], [(pH − 5.625)/0.96], [(sorbate − 500)/500] prior to model development. The TTG results from replicate test wells were averaged before modeling to minimize the effect of measurement error. The SAS LIFEREG procedure was used to develop predictive models of the natural logarithm of TTG (ln TTG) as a function of the factors percent RH, pH, preservative level, and humectant type. The resulting model can easily be transformed into a regular time scale. It should be noted that the type of humectant is considered a categorical variable (i.e., nonnumeric) in the SAS procedure. In growth modeling, there are often conditions under which no growth occurs; therefore, TTG may be missing or censored. Under these conditions, ordinary least-squares regression is not applicable and special procedures are required (19). The LIFEREG procedure can accommodate such censored data and uses maximum-likelihood estimation methods to find regression coefficients. Further details of this method of analysis are given by Allison (1). The LIFEREG procedure works best with many replicates in which the intervals between growth parameters are equally spaced, with approximately 50% of conditions limiting growth. The ranges of the parameters studied (RH, pH, and preservative levels) were chosen to satisfy these requirements.

Toxin production.

Toxin production for experimental conditions close to the growth-no-growth boundary was measured by the VIDAS staph enterotoxin assay (VSEA; bioMerieux, Inc., Hazelwood, Mo.). The VSEA is a qualitative enzyme-linked fluorescent immunoassay performed in an automated mini-VIDAS instrument (bioMerieux, Inc.). The media from the microtiter plates were removed for assay after the final OD_wb measurements were taken (24 weeks). The broth from each of the eight replicate wells was removed via pipette, combined into two microcentrifuge tubes, and centrifuged for 10 min. The supernatants were combined, and the pH values were adjusted with 1 N NaOH to 6.0 to 8.0. Samples (0.5 ml) were placed into the appropriate wells in a test strip, and the assays were run in the mini-Vidas. Positive and negative controls were run with each set of test strips. The VSEA is sensitive to 1 ng of toxin/ml of sample.

RESULTS

Model development and diagnostics.

Models were developed from the 1,792 data points generated. The models included all three main effects: percent RH, pH, and potassium sorbate concentration (“sorb” in the equations); their quadratic effects (RH × RH = RH²; pH × pH = pH²; and sorb × sorb = sorb²); and the three two-factor interactions (RH × pH, RH × sorb, and pH × sorb). The impact of the humectant type on the main effects and interactions was assessed by including indicator variables in the model. These main effects, quadratic effects, and two-factor interactions are collectively referred to as the factors. SAS LIFEREG allows the user to specify the error distribution to account for the variation in TTG not explained by the regression model. For model development purposes, Weibull, lognormal, and loglogistic distributions were considered. All three distributions gave very similar models (the regression coefficients were similar in sign and magnitude), and we selected the loglogistic distribution model, which has been used in previous work (40).

Model development is an iterative process. The first analysis of the data created models which were all-inclusive; this allowed for the determination of those factors which had a significant effect on the growth of S. aureus. All of the main effects, quadratic effects, and two-factor interactions were significant (P < 0.005), except for the potassium sorbate concentration quadratic term and the interaction between RH and potassium sorbate concentration. The insignificant factors were dropped, and the data were reanalyzed to develop the final models. SAS LIFEREG outputs a table of regression coefficient estimates and approximate chi-square distribution P values for each factor in the model. The relative importance of each factor can be judged by its P value: factors with low P values have the greatest influence on and are most predictive of the TTG (Tables 1 to 3 ).

TABLE 1.

Parameters of the sucrose-fructose model to predict ln TTG based on RH, pH, and the presence of potassium sorbate

Variable	Degree of freedom	Estimated ln TTG	SE	Chi-square value	P valueb
Intercept	1	4.4629	0.4600	94.1353	<0.0001
RH	1	−5.8959	0.5322	122.7110	<0.0001
pH	1	−2.6200	0.3498	56.0835	<0.0001
Sorba	1	1.4174	0.2340	36.6897	<0.0001
RH2	1	1.7768	0.3048	33.9823	<0.0001
pH2	1	1.0572	0.1584	44.5164	<0.0001
RH × pH	1	0.4806	0.2075	5.3649	0.0205
pH × sorb	1	−0.9453	0.1369	47.6565	<0.0001

^aSorb, potassium sorbate.

^bP as determined by the chi-square test.

TABLE 3.

Parameters of the NaCl model to predict ln TTG based on RH, pH, and the presence of potassium sorbate

Variable	Degree of freedom	Estimated ln TTG	SE	Chi-square value	P valueb
Intercept	1	3.1553	0.5154	6.4375	0.0112
RH	1	−3.5814	0.4680	24.4595	<0.0001
pH	1	−3.8094	0.3561	11.1547	0.0008
Sorba	1	1.6400	0.2986	0.0056	0.9403
RH2	1	1.7768	0.3048	33.9823	<0.0001
pH2	1	1.0572	0.1584	44.5164	<0.0001
RH × pH	1	0.4806	0.2075	5.3649	0.0205
pH × sorb	1	−0.9453	0.1369	47.6565	<0.0001

^aSorb, potassium sorbate.

^bP as determined by the chi-square test.

The resulting model equation for the use of sucrose-fructose as the humectant was as follows (where TTG is measured in days, RH is a percentage, and the potassium sorbate concentration is measured in parts per million): ln TTG = 4.46 − (5.90 × RH) − (2.62 × pH) + (1.42 × sorb) + (1.78 × RH²) + (1.06 × pH²) + (0.48 × RH × pH) − (0.94 × pH × sorb).

The resulting model equation for the use of glycerol as the humectant was ln TTG = 2.24 − (3.86 × RH) − (2.29 × pH) + (1.00 × sorb) + (1.78 × RH²) + (1.06 × pH²) + (0.48 × RH × pH) − (0.94 × pH × sorb).

The resulting model equation for the use of NaCl as the humectant was ln TTG = 3.15 − (3.59 × RH) − (3.81 × pH) + (1.64 × sorb) + (1.78 × RH²) + (1.06 × pH²) + (0.48 × RH × pH) − (0.94 × pH × sorb).

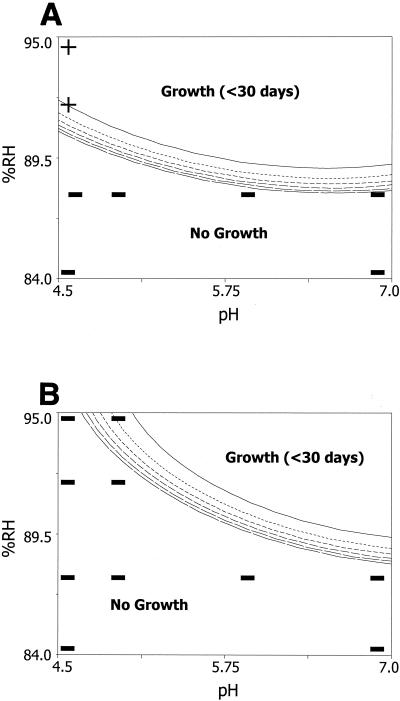
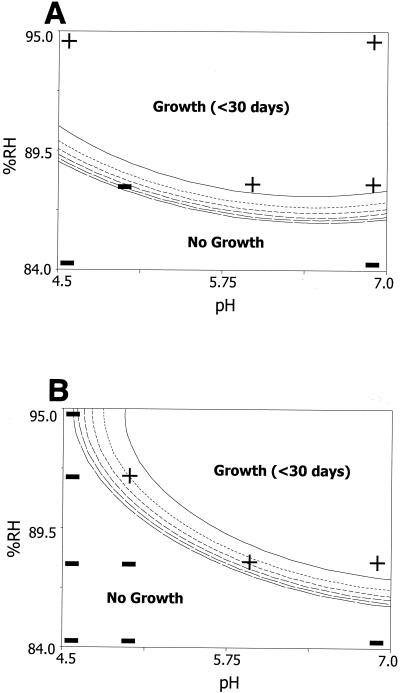
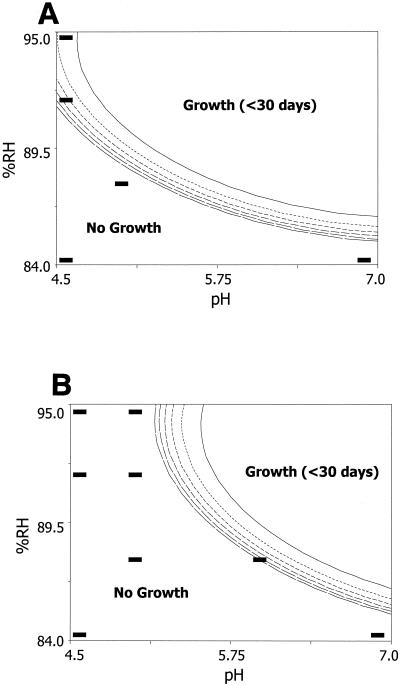
From the model equations, the TTG contour plots for sucrose-fructose (Fig. 1), glycerol (Fig. 2), and NaCl (Fig. 3) were created. The contour plots were created by generating a grid of evenly spaced points in the experimental design space of pH, RH, and potassium sorbate concentration. With a grid of 2,268 points, a predicted TTG was calculated for each point and humectant by using the appropriate model shown above. The grid of points and predicted TTG values was input into the SAS procedure “proc gcontour” to create Fig. 1 to 3. Diagnostic methods to check for departures from model assumptions can be used in a manner that is similar to their use in ordinary regression analysis. However, when nonnormal distributions are being fitted, an appropriate standardization of residuals must be used (25). The SAS reliability procedure (SAS Institute, Inc.) was used for residual analysis. A probability plot of standardized residuals was examined, and no unusual patterns or anomalies were detected (data not shown).

FIG. 1.

Predicted TTG of S. aureus based on the combined effects of RH adjusted with sucrose-fructose (%RH), pH, and potassium sorbate. The contours are scaled in intervals of 30 days, with the upper- and rightmost contours being the 30-day lines and the lower- and leftmost contours being the 180-day lines. The region above the 180-day contour lines is not a plateau but a series of ever-increasing contours or longer TTGs. Potassium sorbate was either absent (A) or present at 1,000 ppm (B). Selected data points are identified as positive (+) or negative (−) for enterotoxin.

FIG. 2.

Predicted TTG of S. aureus based on the combined effects of RH adjusted with glycerol (%RH), pH, and potassium sorbate. The contours are scaled in intervals of 30 days, with the upper- and rightmost contours being the 30-day lines and the lower- and leftmost contours being the 180-day lines. The region above the 180-day contour lines is not a plateau but a series of ever-increasing contours or longer TTGs. Potassium sorbate was either absent (A) or present at 1,000 ppm (B). Selected data points are identified as positive (+) or negative (−) for enterotoxin.

FIG. 3.

Predicted TTG of S. aureus based on the combined effects of RH adjusted with NaCl (%RH), pH, and potassium sorbate. The contours are scaled in intervals of 30 days, with the upper- and rightmost contours being the 30-day lines and the lower- and leftmost contours being the 180-day lines. The region above the 180-day contour line is not a plateau but a series of ever-increasing contours or longer TTGs. Potassium sorbate was either absent (A) or present at 1,000 ppm (B). Selected data points are identified as positive (+) or negative (−) for enterotoxin.

Model predictions and comparison with published work.

As conditions became increasingly unfavorable for growth, the contour lines drew closer together, indicating that conditions were approaching those that do not allow growth (Fig. 1 to 3). As the RH or pH of the system decreased, a corresponding increase in TTG was seen and the no-growth area of the contour plot increased in size. The addition of potassium sorbate at low pH values (4.5 to 5.5) dramatically changed the contour plots in the low-pH area of the plot (Fig. 1 to 3). The effect of potassium sorbate decreased as the pH value approached 7.0.

Differences were observed in the growth-no-growth boundary when different humectants were used to achieve the desired RH values in both the absence and the presence of potassium sorbate. The use of sucrose-fructose as the humectant resulted in the greatest delay of S. aureus growth under the highest pH and RH combination (i.e., pH 7.0 and 88% RH) either with or without potassium sorbate (Fig. 1). Even with the addition of potassium sorbate at 1,000 ppm at pH 7.0, glycerol and NaCl were less effective in delaying S. aureus growth than sucrose-fructose with no added preservative (Fig. 1 to 3). At pH values above ca. 5.3 and in the absence of potassium sorbate, a rank order was observed, with NaCl being the least inhibitory, followed by glycerol, and with sucrose-fructose being the most inhibitory; by contrast, at pH values below ca. 5.3, NaCl showed dramatically increased inhibition. With the addition of potassium sorbate at 1,000 ppm, the same rank order occurred at pH values above ca. 6.1. It has generally been accepted that the limits for the growth of S. aureus are 85% RH when NaCl is used as the humectant and 89% when glycerol is used (15). Our models showed the limiting RH for growth to be approximately 88% (pH 7.0) when sucrose-fructose was used, 86% when glycerol was used, and 85% when NaCl was used. The limiting RH with glycerol as the humectant was markedly different from that reported by Marshall et al. (22), who found that the growth limits were 89 and 86% RH when glycerol and NaCl were used as the humectants, respectively. This disagreement may be due to strain variation or to the fact that only quarter-strength BHI broth was used in the work by Marshall et al. (22) while full-strength BHI broth was used in our model system. Whatever the reason, this result suggests that if glycerol makes a large contribution to the humectant content of a food product, it would be wise to consider the target RH carefully. Additionally, there is published literature that describes the ability of S. aureus to grow in various food systems, mainly meats and cheeses (3, 17, 18, 21, 29, 38, 45). Unfortunately, these data cannot be used for model validation, as RH was not reported and/or other parameters not included in our models (such as oxygen concentration or temperature) were varied. Additionally, the pH and/or ingredient lists of the products used in these studies were not reported.

NaCl was most inhibitory at pH values below ca. 5.3 in the absence of potassium sorbate and at pH values below ca. 6.1 in the presence of potassium sorbate at 1,000 ppm. For example, no growth was seen even at conditions of 95% RH (Fig. 3). This finding disagrees with predictions made by the USDA's pathogen modeling program (PMP) version 5.1, which indicates that at 95% RH and pH 4.5, S. aureus will grow from 10³ to 10⁷ CFU/ml in 1.65 days (Table 4). Comparison of the sucrose-fructose and glycerol models developed in this study with other published work is difficult, as the majority of previously published studies have used NaCl to control the RH of the system. As discussed previously, differences in the physical properties of humectants can lead to various responses, even when RH is constant (Table 4). The differences in modeling approaches also make comparisons difficult. Neither the Food Micro Model of the United Kingdom Ministry of Agriculture, Fisheries, and Food nor PMP was created from data sets containing many replicated experiments where the bacteria were subjected to stressed conditions. There is also the danger of extrapolation beyond the conditions under which data were actually collected. The PMP gives a prediction for growth under the conditions of pH 4.5 and 95% RH (with NaCl as the humectant), although data were not collected for this combination of parameters (4, 47). A full factorial design was utilized for the boundary models presented in this paper, and the models were constructed by using interpolation only.

TABLE 4.

Comparison of USDA PMP S. aureus growth and survival kinetic models with this work's growth boundary models

% RH	pH	TTG (days) as determined by PMP growth model (NaCl)a	TTD (days) as determined by PMP survival model (NaCl)b	TTG (days) as determined by boundary model with indicated humectant
				NaCl		Glycerol		Sucrose-fructose
				Measured	Predicted	Measured	Predicted	Measured	Predicted
95.0	7.0	0.50		1.0	0.29c	1.0c	1.37c	1.0	0.39
95.0	6.0	0.54		1.5	0.40	1.0c	0.40	1.0	0.16c
95.0	5.0	0.95		1.5	5.69c	1.5c	1.15	1.0	0.65c
95.0	4.5	1.65		>168	50.63c	2.0	4.63c	4.16	3.12c
92.0	7.0	0.83	41.59	1.5	0.23c	1.0	1.33c	1.5	1.66c
92.0	6.0	0.84	24.21	1.5	0.46c	1.0	0.55c	1.5	0.97
92.0	5.0	1.37	8.65	4.16	9.35c	2.0	2.29c	1.5	5.69c
92.0	4.5	2.23	4.30	>168	99.57c	4.16c	11.06c	4.16	32.59c
91.1	7.0	0.98	35.25		0.31c		1.89c		3.67c
91.1	6.0	0.97	20.90		0.69		0.88		2.40c
91.1	5.0	1.54	7.60		15.59c		4.05c		15.65c
91.1	4.5	2.46	3.82		175c		20.64c		94.68c
88.0	7.0		20.11	4.16	3.05	8.74	22.99	>168	205
88.0	6.0		12.63	4.16	9.99	17.10	15.48	>168	195
88.0	5.0		4.87	>168	327	>168	104	>168	1,843
88.0	4.5		2.52	>168	4,432	>168	639	>168	13,442
84.0	7.0		9.70	>168	1,110	>168	10,869	>168	692,144
84.0	6.0		6.52	>168	5,896	>168	11,848	>168	1,063,969
84.0	5.0		2.69	>168	312,378	>168	128,860	>168	16,318,851
84.0	4.5		1.40	>168	5,387,262	>168	1,006,907	>168	151,427,721

^aTime to cell count increase from 10³ to 10⁷ CFU/ml.

^bTTD, time to 1-log decrease in CFU per milliliter.

^cValue is outside the confidence limits of the PMP kinetic growth model.

Enterotoxin assays.

When the final OD_wb was close to 0.350, the samples were tested for enterotoxin. Assays were also conducted for all samples with combinations of 84% RH and pH 7.0 or 84% RH and pH 4.5. A total of 94 assays were run, and in every case where the data were scored as “no growth,” the toxin assay results were negative for the presence of toxin, while in every case where the data were scored as “growth,” the toxin assay results were positive for the presence of toxin. This further supports the choice of an OD_wb of 0.350 as an appropriate cutoff value for TTG in the individual wells and greatly increases confidence in the practical value of the models.

DISCUSSION

Using RH without considering the effect of the type of humectant has often led to difficulties in predicting the stability and microbial safety of intermediate-moisture foods. For example, S. aureus is highly salt tolerant and has been reported to grow at RHs as low as 85% in NaCl concentrations up to 25% (wt/wt); however, RH values limiting growth are typically higher when humectants other than NaCl are used to control RH (15). Notermans and Heuvelman (27) showed that the RH limiting S. aureus growth varied depending on whether sucrose (with which it was reported that an a_w of 0.90 limited growth) or NaCl (with which it was reported that an a_w of 0.87 limited growth) was used as the humectant. Marshall et al. (22) reported that the level of inhibition of the growth of S. aureus by glycerol at neutral pH was about 10% greater than that caused by NaCl in the rvp range (reported as a_w) from 0.96 to 0.90. Clearly, the choice of humectant used to depress the RH in a food system is critical and its effects on microbial survival and/or growth depend not only on the RH but also on the chemical and physical properties of the humectant, as well as the biological effects of the humectants on the microorganisms.

As stated previously, although RH is a better indicator for food stability and safety than water content, it is not always a reliable predictor of stability. As described by Fennema (9), increasing evidence has shown that the T_g and Mm may be important means to explain many diffusion-limiting properties of food. Interest in Mm was first generated by Luyet (20) and associates in the United States as well as by Rey in France, who showed relationships between Mm and biological materials (31), while basic concepts relating nonequilibrium Mm in synthetic amorphous polymer systems were formulated by Ferry (10). The importance of the role of glassy states in various sugar-containing foods was described by White and Cakebread (46), who suggested that these states played an important role in the stability and processability of many food systems (9, 36). The basic principles that apply to synthetic amorphous polymers, as described by Ferry and others, also apply to the behavior of glass-forming foods (12, 36). Foods of this type include starch-containing products like pasta and bread, boiled confections, protein-based foods, intermediate-moisture foods, and dried, frozen, or freeze-dried foods. The RH and Mm approaches to food stability are complementary, not contradictory. RH, referred to as a_w, focuses on the availability of water in a food matrix, while Mm defines this availability in terms of microviscosity and diffusibility, with the latter being dependent on the properties of water as a plasticizer to depress the T_g of the food matrix.

Humectants with various characteristics were employed in this study specifically to begin to explore the influence of various physical properties of humectants, such as their T_gs, on microbial growth under osmotically stressed conditions. When glass-forming solutes are used to achieve desired RH values in systems, the underlying T_g and the relaxation behavior of the glasses become the controlling parameters of the system (36). Within each glass-forming system, T_g is inversely linearly related to the measured RH of the system. However, across different glass-forming solute systems, T_g increases as the weight-average molecular weight of the solutes increases. As T_g increases, the viscosity of the system increases, which in turn decreases the mobility of molecules in the system (including the mobility of water molecules). This relative decrease in mobility between glass-forming systems may partially explain the varied responses of microorganisms in systems with matching RH values but in which different humectants were utilized to achieve the targeted RH. The humectants used in this study included sucrose-fructose (non-membrane-permeable glass-forming solutes with a reference T_g of approximately −32°C), glycerol (a membrane-permeable glass-forming solute with a reference T_g of approximately −65°C), and NaCl (a non-glass-forming ionic solute which may affect various ion channels in the cell) (35).

The limits of microbial growth cannot be predicted by the RH of the system alone, as seen by comparison of the growth boundaries developed with the three types of humectants used in this study. Instead, the RH of the system should be considered in conjunction with the physical properties of the solutes and their effects on the biological systems. Ionic solutes, such as NaCl, may place both ionic and osmotic stresses on the cell. Of the three humectants studied, NaCl was the most inhibitory below pH values of ca. 5.3 in the absence of potassium sorbate. The no-growth region of NaCl was expanded to pH values below ca. 6.1 with the addition of potassium sorbate at 1,000 ppm. This exaggerated interaction between NaCl, low pH, and potassium sorbate may suggest that the Na⁺ proton antiport (26, 39) may be the critical ion channel involved. These data suggest that growth inhibition may be due to overwhelming ionic stress. The membrane permeability of solutes such as glycerol may influence the degree of osmotic stress experienced by the cell. Additionally, the influence of the T_g of the solute on Mm directly affects the degree of osmotic stress a specific solute (e.g., sucrose-fructose or glycerol) places on the cell. Sucrose-fructose with a higher T_g than that of glycerol (and, therefore, a larger constraint on Mm than that of glycerol) was most inhibitory at pH values above ca. 5.3 or 6.1 in the absence or presence of potassium sorbate, respectively. Glycerol is also membrane permeable, and therefore, the cell may experience less osmotic stress than when sucrose-fructose (membrane impermeable) is utilized. Physiological effects on S. aureus cells have been shown to differ when various solutes are used to cause osmotic stress. Cellular transport systems responsible for the uptake of compatible solutes by S. aureus during osmotic stress have been shown to respond differently to the stresses caused by NaCl, sucrose, and glycerol (2). Additionally, the effects of osmotic stress on S. aureus cell size also differ depending on whether NaCl, sucrose, or glycerol is used as the humectant (44). Although these models are empirical in nature, they demonstrate that the limits of growth based on RH would be different when various humectants were used to control RH, so comparing studies based on RH alone may lead to false conclusions (33, 35). These results also allow us to begin to explore the possibility of moving towards a mechanistic approach to creating predictive models. Further work in this laboratory to study solute-specific effects on cellular energy (ATP levels) is ongoing in an effort to continue to work towards a better understanding of the mechanism(s) of bacterial inactivation.

Three statistical models describing the growth boundaries for S. aureus with respect to RH controlled by three types of humectants, pH, and preservative were developed, and results were confirmed by toxin assays. Building on previous work (42) that has established regions of growth and no growth, these mathematical models predict actual TTG as a function of the humectant type, RH, pH, and preservative level. These predictions can be used to develop much more detailed and informative boundary surfaces. Good agreement between all three of these growth boundary surfaces and PMP growth kinetic models was found in the relatively unstressed regions. Growth boundary predictions were outside the confidence limits of the PMP growth kinetic model under more stressful conditions, even when NaCl was used as the humectant. Kinetic models and growth boundary models can be used as complementary tools for the development of microbially safe products with short and long shelf lives. These models will allow product developers to visualize the “safe space” for the formulation of shelf-stable intermediate-moisture foods by employing these preservation factors, will allow microbiologists to assess risks more effectively over a wide range of products, and will ultimately allow the consumer to have greater assurance of food safety.

The use of sucrose-fructose as the humectant results in the greatest delay of S. aureus growth when the highest pH and RH (i.e., pH 7.0 and 88% RH) are used either with or without potassium sorbate. NaCl is the most inhibitory humectant at pH values below ca. 5.3 in the absence of potassium sorbate and at pH values below ca. 6.1 in the presence of potassium sorbate at 1,000 ppm. Solute-specific effects on bacterial growth were evident, as growth boundaries differed at the same RH values when different humectants were used. Over the almost 50 years since Scott first published his work on the water relations of S. aureus, measurement techniques and the fields of physical chemistry, microbial physiology, and microbial modeling have progressed significantly. Scott was well aware that a_w would not necessarily be adequate to describe all of the properties of solutions that influence microbial growth, metabolism, and survival (7). He suggested that, with further work to fill some of the obvious gaps in our knowledge, we would discover whether a_w could be replaced by something more meaningful (reference 34, as cited in reference 7). With careful experimentation and understanding, we will continue to fill the gaps and allow the food industry to produce the highest-quality products while ensuring food safety.

TABLE 2.

Parameters of the glycerol model to predict ln TTG based on RH, pH, and the presence of potassium sorbate

Variable	Degree of freedom	Estimated ln TTG	SE	Chi-square value	P valueb
Intercept	1	2.2408	0.4701	22.3009	<0.0001
RH	1	−3.8604	0.4311	22.2903	<0.0001
pH	1	−2.2948	0.2885	1.2707	0.2596
Sorba	1	0.9988	0.2752	2.3144	0.1282
RH2	1	1.7768	0.3048	33.9823	<0.0001
pH2	1	1.0572	0.1584	44.5164	<0.0001
RH × pH	1	0.4806	0.2075	5.3649	0.0205
pH × sorb	1	−0.9453	0.1369	47.6565	<0.0001

^aSorb, potassium sorbate.

^bP as determined by the chi-square test.