Computation of the Face Index of Certain Polycyclic Aromatic Hydrocarbons

Abstract

The face index is a topological descriptor that sheds light on the molecular makeup of polycyclic aromatic hydrocarbons (PAHs), which is important because of their potential health effects and environmental persistence. We determine mathematical expressions for these compounds’ face indices by examining their graphical representations, emphasizing the connections between their structural characteristics and chemical characteristics. Our results open the door for additional study in the fields of theoretical and applied chemistry by providing a better understanding of how the molecular structure affects PAH behavior. This work not only improves the characterization of intricate PAH structures but also lays the groundwork for further research into the toxicological and environmental effects of these compounds. We obtain analytical expressions for the faces of supercoronene, cove-type coronene, and triangle-shaped discotic graphene.

1. Introduction

Graph-theoretical notions have witnessed rapid progress in the past few years and have become a central part of mathematical chemistry, where atoms are represented as vertices and bonds are represented as edges. This field explores the intricate relationships between the structural properties of chemical compounds and their mathematical representations. The interaction of graph theory with chemistry has opened the way to many novel ideas and techniques. In particular, mathematical features related to bond adjacency matrices have been important in the investigation of molecular structures. Increased focus on molecular structures has brought forward new perspectives regarding how chemical compounds can be analyzed from a topological standpoint. Thus, the field has gained significant momentum in research, providing deeper insights into the properties of materials and compounds. Readers can refer to − for a detailed description of chemical structures and the process of conversion of compounds.

The key tool developed in this area is topological indices (TIs), which are crucial for the analysis of molecular graphs. These are numerical values derived from the structure of a molecular graph that represent the compound’s topological properties. TIs are vital parameters in the prediction of chemical, physical, and biological properties of compounds. Some can be applied in predicting biological activity, toxicity, and physicochemical properties and thus become useful for fields such as medicinal chemistry, toxicology, and environmental science. ,

TIs are very well classified under two general terms: global and local indices. The former categories include indices more frequently applied, such as the Wiener index, Hosoya index, Randic index, and Zagreb indices. The Wiener index, developed by Wiener in 1947, was the first TI used to predict the boiling point of paraffin. Next, the Hosoya index, introduced in 1971 by Haruo Hosoya, is based on the matching polynomial and independent edge sets and is used to analyze molecular complexity and has numerous applications in chemical graph theory in predicting the properties of chemical compounds.

After the Hosoya index, the Zagreb index was introduced in 1972 by Gutman and Trinajstić. This index is based on the topological basis of the π-electron energy and describes the branching degree of molecular carbon atom skeletons. The Zagreb index is considered a robust molecular structure index and has been extensively applied in studies related to chemical properties. Another important TI is the Randic index, which was described by Randić in 1975. It has shown effectiveness in structure–property and structure–activity relationship studies. This index is used to measure connectivity and branching in molecular structures, making it a very important tool in cheminformatics and drug design. These indices have greatly contributed to the field of molecular chemistry. They give valuable insights into the structure and properties of molecules, especially in applications related to predicting chemical behaviors and properties like boiling points, stability, and reactivity.

On the other hand, local indices focus more on the properties of individual atoms and specific bonds within the molecule rather than looking at the entire molecule. While computing these indices is sometimes simple, they may not be detailed enough to predict how a molecule behaves in different environments. Therefore, research is ongoing to develop advanced indices that provide better precision and deeper insight into how molecules behave. Yasin et al. discussed the M-polynomial and MN-polynomial methods for TIs for polymers. Lal et al. studied degree-based topological indices of boron nanotubes. Koam et al. gave a comparative study of valency-based topological descriptors for the hexagon star network. Govardhan and Santiago examined degree-sum-based topological indices of supercoronene and triangle-shaped discotic graphene using the NM-polynomial. Additionally, Govardhan et al. computed neighborhood degree-based TIs of supercoronene and triangle-shaped discotic graphene through NM-polynomial. For a deeper understanding of TIs, readers can refer − .

Jamil et al. achieved a correlation coefficient exceeding 0.99 in multiple linear regression analyses by introducing the face index, a topological descriptor that simplifies computations and improves models for benzenoid hydrocarbons. While their work focused on organic systems, later studies by Ye et al., Luo et al., Negi et al., etc. extended the face index to inorganic nanomaterialsincluding carbon nanotubes (e.g., TUC ₄, TUHC ₆), boron nanotubes, silicon carbide structures, certain polycyclic chemical networks and carbon nanoconesdemonstrating its adaptability to diverse molecular topologies.

The face index has proven particularly valuable for predicting physical properties (e.g., boiling points, energy levels) without computationally expensive simulations, offering researchers an efficient alternative for molecular analysis. , Additionally, it provides enhanced structural insights, improving the accuracy of topology–property relationships across chemical, physical, and biological applications. −

1.1. Polycyclic Aromatic Hydrocarbons (PAHs)

PAHs are an important class of compounds to be studied because they are widely found in nature and have significant environmental, toxicological, and material implications. PAHs can be formed through both natural processes, such as volcanic eruptions and forest fires, as well as human activities, including the combustion of fossil fuels and industrial emissions. The continued presence of PAHs in the environment, along with their potential carcinogenic effects, raises serious concerns about human health. Stading et al. conducted a study on the molecular mechanisms of pulmonary carcinogenesis caused by PAHs. Therefore, understanding their molecular properties and behavior is critical for assessing their impact on the environment and human health.

PAHs vary in structural complexity, ranging from simple compounds such as naphthalene to more complex structures like pyrene, coronene, and hexabenzocoronene. The simplest member, naphthalene, consists of just two fused benzene rings, providing a basic yet important example of aromaticity. In contrast, Pyrene is composed of four fused benzene rings, which form a structure more complex with greater conjugation. Moving to more sophisticated structures, coronene consists of six fused benzene rings arranged in a central hexagonal shape, which increases its stability and conjugation. Hexabenzocoronene is one of the most complex PAHs. It comprises a larger network of fused benzene rings that help to form an extremely conjugated and robust structure. The diversity in their structures directly influences their physical properties like solubility, volatility, and stability under different environmental conditions, which are often governed by π–π stacking interactions and aromatic ring arrangements. , This variability requires that the structural characteristics of PAHs be understood in detail, since these features have a great impact on their behavior in the environment. Hussain et al. focused on monitoring and risk analysis of PAHs in the environment, and Zhang et al. investigated the biological impact of environmental PAHs, specifically focusing on their role as endocrine disruptors.

By using graph-theoretical methods, especially those based on the face index, researchers can penetrate more deeply into the behavior and properties of PAHs. This allows the creation of more precise QSAR/QSPR models that predict the biological activity of chemical compounds.

In addition, a deep understanding of the topological properties of PAHs would have wide material science implications regarding their physical attributes. This might be helpful for designing novel materials for nanotechnology, organic electronics, and other applications such as environmental remediation. , Recent studies have also demonstrated the effective use of PAH-based materials as chemosensors for nitroaromatic pollutants, showcasing their potential in environmental monitoring and sensing technologies. , The discovery of new PAH materials with desired features can open pathways to innovative solutions for some of the most challenging and pressing global issues that humanity faces.

The article includes the following sections: Section covers some key definitions, Section explores coronene and its variants, as well as triangular discotic graphene, Section includes the results on the face index of supercoronene, cove-type coronene, and triangle-shaped discotic graphene, and last, Section provides the conclusion of the study.

2. Preliminaries

This section gives the definitions and formulas necessary for computing a newly introduced parameter measuring information obtained from the faces of a graph, especially in the case of planar graphs. This parameter is termed the face index of PAHs. Let G = (V(G), E(G), F(G)) be a graph with vertex set V(G), edge set E(G), and face set F(G). It is essential that the graph is connected, simple, and planar for calculating the face index. If an edge e ∈ E(G) is one of the edges that form the boundary of a face, then the face f ∈ F(G) is incident to the edge e. Similarly, if a vertex α ∈ V(G) is an endpoint of edges incident to the face, then the face f is considered incident to that vertex.

Definition 1. The vertex degree is a fundamental concept that quantifies the number of edges incident to a particular vertex in a graph. For any vertex, v, the degree is denoted as deg­(v).

Definition 2. The face degree of a face f is defined as the number of edges that are incident to it. Mathematically, if E(f) represents the set of edges that enclose the face, then the face degree can be expressed as

$$\mathrm{deg}(f)=|E(f)|$$

Definition 3. The face-vertex degree of a face f ∈ F(G) is the sum of the degrees of the vertices incident to the edges that form the boundary of the face. Mathematically, if α ∈ V(G) is a vertex incident to the edges that surround the face f, then the face-vertex degree d(f) is defined as

$$d(f)=\sum _{\alpha \sim f}d(\alpha )$$

where α ∈ V(G) represents a vertex of G, α ∼ f denotes that α is incident to the boundary edges of face f, and d(α) is the degree of vertex α, i.e., the number of edges incident to α.

Definition 4. The face index of a graph G is defined as the sum of the face-vertex degrees of all faces in the graph. Mathematically, the face index ζ­(G) of a graph G is defined as

$$\zeta (G)=\sum _{f\in F(G)}d(f)=\sum _{\alpha \sim f,f\in F(G)}d(\alpha )$$

where F(G) denotes the set of faces in the graph G. The face index provides insights into the structural complexity of molecular graphs by accounting for how faces interact with the vertices and edges.

3. Coronene and Its Variants

Coronene (C ₂₄ H ₁₂) is a PAH characterized by a central benzene ring symmetrically fused to six peripheral benzene rings, forming a planar structure with D _6h symmetry, as shown in Figure . Its face index is 156, a topological index defined by Jamil et al. in 2020, quantifies the connectivity and π-conjugation of its 7-ring system, correlating strongly with its physicochemical properties. According to the study, coronene’s π-electron energy (34.572β) and boiling point (590.0 °C) were analyzed, and they also studied linear mathematical models of the face index for the π-electron energy and the boiling point. The study shows that the face index is strongly correlated to the π-electron energy and boiling point. This highlights the face index’s utility as a rapid computational tool for estimating molecular stability and optoelectronic behavior in applications like organic semiconductors.

1.

Coronene.

3.1. Hexabenzocoronene (HBC)

HBC, also known as hexa-peri-hexabenzocoronene, is a larger PAH with the molecular formula C₄₂H₁₈. It consists of a central coronene structure with additional benzene rings fused between each adjacent pair of rings around the periphery. The molecular graph of HBC is shown in Figure .

2.

HBC.

From the analysis of the HBC graph, we observe that there are a total of 14 faces, with seven faces having a face-vertex degree of 18, six faces having a face-vertex degree of 15, and one external face with a face-vertex degree of 72. Let f ₁₈ and f ₁₅ represent the faces with face-vertex degrees of 18 and 15, respectively, and f _∞ denote the external face, as shown in Figure . Additionally, let |f ₁₈| = 7 and |f ₁₅| = 6 represent the number of faces with face-vertex degrees of 18 and 15, respectively.

Now, applying the face-index definition to the graph in Figure , we have

$$\begin{array}{l}\zeta (\mathit{HBC})=\sum _{\alpha \sim f\in F(\mathit{HBC})}d(\alpha )\\ =\sum _{\alpha \sim f_{15}\in F(\mathit{HBC})}d(\alpha )+\sum _{\alpha \sim f_{18}\in F(\mathit{HBC})}d(\alpha )+\sum _{\alpha \sim f_{\infty }\in F(\mathit{HBC})}d(\alpha )\\ =15\times |f_{15}|+18\times |f_{18}|+|f_{\infty }|\times 72\\ =15\times 6+18\times 7+1\times 72\\ =90+126+72=288\end{array}$$

3.1.1. Supercoronene (SC(n))

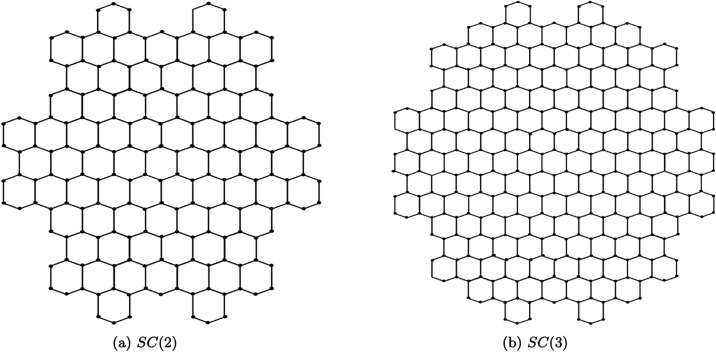
SC(n) is a large PAH constructed by extending the hexagonal ring system of HBC. The structure of SC(n) is formed by circumscribing the HBC molecule with additional benzene rings, resulting in a more complex arrangement that enhances its aromatic character and stability. The edges of SC(n) are both armchair and cove type, which confer specific electronic properties, making it an interesting topic for investigation in materials science and organic electronics.

The modification of the HBC structure to form SC(n) allows the molecules to exhibit distinctive chemical behaviors. These behaviors make SC(n) a fascinating material for applications in organic electronics such as organic semiconductors, light-emitting diodes (OLEDs), and sensors. The unique combination of aromaticity and structural complexity in SC(n) sets it apart from other PAHs, offering opportunities for novel chemical reactions and physical properties.

The structure of SC(n) for n = 2, 3 is shown in Figure (a,b). Here, n is the number of hexagons forming along the six sides of the boundary, resulting in a highly symmetric and extended molecular structure. For example, SC(2) involves the addition of a second layer of hexagons around the core, while SC(3) extends the structure further with an additional layer, leading to even greater complexity.

3.

SC(n); n = 2, 3.

This extended structure of SC(n) increases the size of the molecule while enhancing its π-conjugation, thus improving the stability and electronic properties of the molecule. The specific arrangement of these hexagonal rings optimizes the electronic characteristics, making them applicable in advanced organic materials and devices.

3.2. Cove-Type Coronene (coveHBC(n))

This compound is known as cove-type coronene or, more accurately, coveHBC(n), in which the base structure is an HBC. The periphery has cove-type edges rather than armchair or zigzag edges, so the designation is appropriate for a member of this distinct class of PAHs. In general, coveHBC(n) describes how many hexagons are located along the six sides of the HBC core. The value n denotes the number of structural extensions of the degree.

For n = 2,3, as shown in Figure (a,b), the structure of coveHBC(n) shows that more layers of hexagonal rings are wrapped around the HBC base to give a more complicated molecular structure. This extension leads to different types of cove-type edges, which are reported to influence the optical and electronic properties of the compound, thus potentially making it a candidate for applications in advanced molecular devices.

4.

coveHBC(n); n = 2, 3.

The structure of coveHBC(n) exhibits an irregular distribution of π-electrons, which makes its electronic properties distinct from those of other molecules. These edge effects make cove-type coronene an important material in nanotechnology and organic electronics, as its unique properties are being explored for use in organic semiconductors. The addition of cove-shaped edges introduces significant curvature to the molecule, affecting its chemical reactivity and stability.

3.3. Triangle-Shaped Discotic Graphene (TDG(n))

TDG(n) is studied for two different conditions about n, either being odd or even, such that n is the number of hexagons along each side of the triangular boundary.

The structures for n = 3, 4 are displayed in Figure (a,b). These are those arrangements that exhibit different levels of complexity. TDG(n) contains an arrangement of carbon atoms, where the atomic arrangement is triangular in shape. The structure resembles that of benzenoid; however, due to its triangular arrangement, it shares a close similarity in carbon number with fullerene C ₆₀. The core of TDG(n) is a large D _3h symmetric disk shape, which provides not only considerable symmetry but also a stable structure compared to other PAHs. The D _3h symmetry imparts unique electronic properties and chemical reactivity, which makes TDG(n) a promising candidate for advanced applications.

5.

TDG(n); n = 3, 4.

TDG(n) geometry serves as the cornerstone of its physical properties. The difference in the π-conjugation influences the electronic structure. Due to the unique arrangement of these molecules, various stacking interactions significantly influence electronic conductivity, optical properties, and mechanical strength in solid-state materials. TDG(n) is particularly relevant for graphene-based systems, especially in organic electronics, energy storage devices, and nanotechnology.

As the number of hexagons (n) increases in TDG(n), the evolution of its properties introduces new possibilities, particularly for use in novel organic semiconductors, molecular electronics, and high-performance energy storage systems such as supercapacitors and batteries. The value of n determines the shape and size of the core discotic component, setting new directions for designing tailored optical and electronic properties in graphene-based materials. This makes TDG(n) an exciting material for future applications in materials science, potentially contributing to a wide variety of high-tech applications, including flexible electronics, solar cells, and more.

4. Results and Discussion

This section examines the molecular structures of SC(n), coveHBC(n), and TDG(n). Additionally, the face indices of these structures are calculated.

Theorem 1. Let SC(n) represent the supercoronene structure, where n ≥ 2. Then, the face index of SC(n) is 162n ² + 426n – 36.

Proof. Consider the graph SC(n), which represents the structure of the supercoronene for n ≥ 2. To calculate its face index, we need to examine the graph’s vertices, edges, and faces. Denote the sets of vertices, edges, and faces of the graph as V(SC(n)), E(SC(n)), and F(SC(n)), respectively.

Each face of the graph is represented by f _k , where k is the degree of the face, defined as the sum of the degrees of all vertices incident to that face. The graph of SC(n) contains several internal faces and one external face. The external face, which is represented by f _∞, is bounded by vertices of degree 2 and some vertices of degree 3, and the set of all faces in the graph is given as F(SC(n)) = {f ₁₅, f ₁₆, f ₁₇, f ₁₈, f _∞}.

We now compute the degree of the external face, f _∞. By analyzing the graph, it is evident that all vertices of degree 2 are incident to the external face, and some vertices of degree 3 are also connected to it. Let |V ₃ | denote the number of degree-3 vertices that are incident to the external face. Thus, the degree of the external face is the sum of the degrees of all vertices that lie on it. To compute this, let x denote the degree of the external face f _∞. Using Table , we compute the degree of the external face:

1. Vertex Sets |V ₂|and |V ₃ | of (SC(n)).

n	|V 2|	|V 3 |
2	42	36
3	54	48
4	66	60
⋮	⋮	⋮
n	12n + 18	12n + 12

By substituting the values from Table , the degree of the external face can be calculated as

$$\sum _{\alpha \sim f_{\infty }\in F(\mathrm{SC}(n))}d(\alpha )=x=2|V_2|+3|V_3^{\ast }|=2(12n+18)+3(12n+12)=24n+36+36n+36=60n+72$$

Now, we analyze the internal faces of SC(n). It is observed that only four types of internal faces exit from n ≥ 2, namely, {f ₁₅, f ₁₆, f ₁₇, f ₁₈}. The exact number of these faces is given in Table based on the graph’s structure.

2. Distribution of Internal Faces by Degrees in the Graph of SC(n).

n	|f 15|	|f 16|	|f 17|	|f 18|
2	12	0	6	55
3	12	6	6	115
4	12	12	6	193
⋮	⋮	⋮	⋮	⋮
n	12	6n – 12	6	9n 2 + 15n – 11

Finally, by applying the definition of the face index ζ, we have

$$\begin{array}{l}\zeta (\mathit{SC}(n))=\sum _{\alpha \sim f\in F(\mathit{SC}(n))}d(\alpha )\\ =\sum _{\alpha \sim f_{15}\in F(\mathit{SC}(n))}d(\alpha )+\sum _{\alpha \sim f_{16}\in F(\mathit{SC}(n))}d(\alpha )+\sum _{\alpha \sim f_{17}\in F(\mathit{SC}(n))}d(\alpha )+\sum _{\alpha \sim f_{18}\in F(\mathit{SC}(n))}d(\alpha )+\sum _{\alpha \sim f_{\infty }\in F(\mathit{SC}(n))}d(\alpha )\\ =15\times |f_{15}|+16\times |f_{16}|+17\times |f_{17}|+18\times |f_{18}|+|f_{\infty }|\times x\\ =15\times 12+16\times 6(n-2)+17\times 6+18\times (9n^2+15n-11)+1\times (6\mathrm{on}+72)\\ =180+96n-192+102+162n^2+270n-198+60n+72\\ =162n^2+426n-36\end{array}$$

Theorem 2. Let coveHBC(n) represent the cove-type coronene structure, where n ≥ 2. Then, the face index of coveHBC(n) is 486 n ² – 930 n + 468.

Proof. Consider the graph coveHBC(n), which represents the structure of the cove-type coronene for n ≥ 2. To calculate its face index, we need to examine the graph’s vertices, edges, and faces. Denote the sets of vertices, edges, and faces of the graph as V(coveHBC(n)), E(coveHBC(n)), and F(coveHBC(n)), respectively.

Each face of the graph is represented by f _k , where k is the degree of the face, defined as the sum of the degrees of all vertices incident to that face. The graph of coveHBC(n) contains several internal faces and one external face. The external face, which is represented by f _∞, is bounded by vertices of degree 2 and some vertices of degree 3, and the set of all faces in the graph is given as F(coveHBC(n)) = {f ₁₅, f ₁₆, f ₁₇, f ₁₈, f _∞}.

We now compute the degree of the external face f _∞. By analyzing the graph, it is evident that all vertices of degree 2 are incident to the external face, and some vertices of degree 3 are also connected to it. Let |V ₃ | denote the number of degree-3 vertices that are incident to the external face. Thus, the degree of the external face is the sum of the degrees of all vertices that lie on it. To compute this, let x denote the degree of the external face f _∞. Using Table , we compute the degree of the external face:

3. Vertex Sets |V ₂|and |V ₃ | of the coveHBC(n).

n	|V 2|	|V 3 |
2	30	24
3	54	48
4	78	72
5	102	96
⋮	⋮	⋮
n	24n – 18	24n – 24

By substituting the values from Table , the degree of the external face can be calculated as

$$\sum _{\alpha \sim f_{\infty }\in F(\mathit{coveHBC}(n))}d(\alpha )=x=2|V_2|+3|V_3^{\ast }|=2(24n-18)+3(24n-24)=48n-36+3(24n-24)=120n-108$$

Now, we analyze the internal faces of coveHBC(n). It is observed that only four types of internal faces exit from n ≥ 2, namely, f ₁₄, f ₁₅, f ₁₇, and f ₁₈. The exact number of these faces is given in Table based on the graph’s structure.

4. Distribution of Internal Faces with Degree 14,15,17, and 18 in the Graph of coveHBC(n).

n	|f 14|	|f 15|	|f 17|	|f 18|
2	6	0	6	13
3	6	6	12	79
4	6	12	18	199
5	6	18	24	373
⋮	⋮	⋮	⋮	⋮
n	6	6n – 12	6n – 6	27n 2 – 69n + 43

Finally, by applying the definition of the face index ζ, we have

$$\begin{array}{l}\zeta (\mathit{coveHBC}(n))=\sum _{\alpha \sim f\in F(\mathit{coveHBC}(n))}d(\alpha )\\ =\sum _{\alpha \sim f_{14}\in F(\mathit{coveHBC}(n))}d(\alpha )+\sum _{\alpha \sim f_{15}\in F(\mathit{coveHBC}(n))}d(\alpha )+\sum _{\alpha \sim f_{17}\in F(\mathit{coveHBC}(n))}d(\alpha )+\sum _{\alpha \sim f_{18}\in F(\mathit{coveHBC}(n))}d(\alpha )+\sum _{\alpha \sim f_{\infty }\in F(\mathit{coveHBC}(n))}d(\alpha )\\ =14\times |f_{14}|+15\times |f_{15}|+17\times |f_{17}|+18\times |f_{18}|+|f_{\infty }|\times x\\ =14\times 6+15\times 6(n-2)+17(6n-6)+18(27n^2-69n+43)+1(120n-108)\\ =84+90(n-2)+102n-102+486n^2-1242n+774+120n-108\\ =486n^2-930n+468\end{array}$$

Theorem 3. Let TDG(n) represent the triangle-shaped discotic graphine, where n ≥ 3. Then, the face index is 27n ² – 3n.

Proof. Consider the graph TDG(n), which represents the structure of the TDG(n) for n ≥ 3. To calculate its face index, we need to examine the graph’s vertices, edges, and faces. Denote the sets of vertices, edges, and faces of the graph as V(TDG(n)), E(TDG(n)), and F(TDG(n)), respectively.

Each face of the graph is represented by f _k , where k is the degree of the face, defined as the sum of the degrees of all vertices incident to that face. The graph of TDG(n) contains several internal faces and one external face. The external face, which is represented by f _∞, is bounded by vertices of degree 2 and some vertices of degree 3, and the set of all faces in the graph is given as

$$F(\mathit{TDG}(n))=\{f_{14},f_{16},f_{18},f_{\infty }\}$$

We now compute the degree of the external face f _∞. By analyzing the graph, it is evident that all vertices of degree 2 are incident to the external face, and some vertices of degree 3 are also connected to it. Let |V ₃ | denote the number of degree-3 vertices that are incident to the external face. Thus, the degree of the external face is the sum of the degrees of all vertices that lie on it. To compute this, let x denote the degree of the external face f _∞. Using Table , we compute the degree of the external face:

5. Vertex Sets |V ₂|and |V ₃ | of TDG(n).

n	|V 2|	|V 3 |
3	18	12
4	24	18
5	30	24
6	36	30
⋮	⋮	⋮
n	6n	6n – 6

By substituting the values from Table , the degree of the external face can be calculated as

$$\begin{array}{l}\sum _{\alpha \sim f_{\infty }\in F(\mathit{TDG}(n))}d(\alpha )=x=2|V_2|+3|V_3^{\ast }|\end{array}=2\times (6n)+3\times (6n-6)=12n+18n-18=30n-18$$

Now, we determine the number of internal faces of each degree in TDG(n). Table shows the number of internal faces in TDG(n). Also, by graphical study of TDG(n), we observe that only f ₁₄, f ₁₆, and f ₁₈ exist for n ≥ 3.

6. Distribution of Internal Faces with Degree 14, 16, and 18 in the Graph of TDG(n).

n	|f 14|	|f 16|	|f 18|
3	3	3	4
4	3	6	10
5	3	9	19
6	3	12	31
⋮	⋮	⋮	⋮
n	3	3n – 6	$\frac{3n^2-9n+8}{2}$

By applying the definition of the face index ζ, we have

$$\begin{array}{l}\zeta (TDG(n))=\sum _{\alpha \sim f\in F(\mathit{TDG}(n))}d(\alpha )\\ =\sum _{\alpha \sim f_{14}\in F(\mathit{TDG}(n))}d(\alpha )+\sum _{\alpha \sim f_{16}\in F(\mathit{TDG}(n))}d(\alpha )+\sum _{\alpha \sim f_{18}\in F(\mathit{TDG}(n))}d(\alpha )+\sum _{\alpha \sim f_{\infty }\in F(\mathit{TDG}(n))}d(\alpha )\\ =14\times |f_{14}|+16\times |f_{16}|+18\times |f_{18}|+|f_{\infty }|\times x\\ =14\times 3+16\times 3(n-2)+18\times \frac{3n^2-9n+8}{2}+1\times (30n-18)\\ =42+48n-96+27n^2-81n+72+30n-18\\ =27n^2-3n\end{array}$$

5. Conclusions

Due to a lack of knowledge about their properties, many chemical compounds are still underutilized. The combination of graph theory and chemistry facilitates the application of graphical parameters to molecular compounds, since chemical structures are represented as graphs. It is possible to predict various physicochemical features using parameters such as topological indices. The face index is a fairly accessible metric for predicting the chemical properties of molecular structures because of its simplicity of computation. This study aims to fill in the knowledge gap regarding the compound and its potential applications by calculating the face index of SC(n), coveHBC(n), and TDG(n).

Regardless of whether chemical structures are two-dimensional (2D) or three-dimensional (3D), shell theory offers an additional theoretical framework to be considered in converting chemical structures into 2D graphical formats. The fundamental objective of shell theory is to represent three-dimensional phenomena using two-dimensional models. The Carrera unified formulation (CUF) , is a computational method specifically designed to analyze complex structures such as shells and plates. In future work, we aim to extend this approach by analyzing the face-based topological features of 2D representations to compute face indices for a broader range of chemical structures. Furthermore, we plan to study the electronic properties, such as band gaps, of these structures using density functional theory (DFT) or tight-binding theory, as these methods are highly relevant and valuable for understanding the electronic behavior of nanostructures.

The authors affirm that the data substantiating the conclusion of this study have been incorporated within the article.

The concept was initially proposed by J.P., who also conducted a detailed validation of the results. The findings were further verified by V.K.B. and S.N. J.P. and S.N. conducted an extensive review of the existing literature. The preparation of figures, tables, alignment, data adjustments, and all calculations was carried out by J.P. and S.N. under the supervision of V.K.B. The final draft underwent a thorough review and editing process with the active participation of all of the authors.

The authors declare no competing financial interest.