Abstract
In HRMS-based nontargeted analysis (NTA), spectral matching is crucial for chemical identification, particularly in the absence of retention information. This study introduces class probability of true positives (P(TP)) as an innovative approach, leveraging data from MS/MS spectra and calibrant-free predicted retention time indices (RTIs) through 3 machine learning (ML) models to enhance identification probability (IP). The first model is a molecular fingerprint (MF)-to-RTI model trained on 4713 calibrants. The second model, a cumulative neutral loss (CNL)-to-RTI model, utilized 485,577 experimental spectra. The final model, a binary classification model, was trained using 1,686,319 TP and semisynthetic true negative (TN) spectral matches. High correlations between MF-derived and CNL-derived RTI values (R 2 = 0.96 for training; 0.88 for testing) suggest reduced RTI errors in TP spectral matches. Incorporating reference spectral library searches and RTI errors, the k-nearest neighbors algorithm achieved a weighted F1 score of 0.65 and a Matthews correlation coefficient of 0.30 for pesticides at concentrations of 1 to 1000 ppb in blank samples, with a recall of 0.60 in black tea matrices. Compared to solely library matching, the average IPs for pesticides increased by 54.5, 52.1, and 46.7% when spiked in blank, 10× diluted, and 100× diluted tea matrices, respectively. This work demonstrates the effectiveness of ML in enhancing the chemical IPs of annotated compounds within complex matrices.


Introduction
Mass spectrometry (MS)-based nontargeted analysis (NTA) is a high-throughput technique that profiles sample analytes, distinguishing itself from targeted analysis through its discovery-oriented approach. The integration of reversed-phase liquid chromatography (RPLC) with high-resolution MS (HRMS) has emerged as a prominent methodology for analyzing the chemical exposome, , including toxic contaminants such as pesticides and per- and polyfluoroalkyl substances (PFAS). These contaminants are detected in surface and groundwater, potentially affecting drinking water supplies. , Consequently, RPLC/HRMS-based NTA is increasingly employed for screening analyses.
Chemical identification confidence (IC) is necessary for compound annotation in LC/MS-based NTA. The Chemical Analysis Working Group at the Metabolomics Standards Initiative proposed minimum metadata requirements for non-novel metabolite identification in 2007. For an annotated two-dimensional (2D) LC/MS tensor, IC is considered putative if its mass-to-charge ratio (m/z) and tandem MS (MS/MS) spectrum match references from external libraries when verification by chemical standards is lacking. Since 2014, similar criteria have been introduced in environmental analysis, − emphasizing the necessity for further experimental efforts, such as matching the retention behavior of reference standards under identical instrumental conditions to enhance confidence.
While in-house databases of standard retention times (RTs) and MS/MS spectra efficiently provide high IC, their establishment requires significant resources. In silico analyses can assist in screening annotated compounds needing further validation, typically involving spectral matching against m/z values of molecular ions and their fragment ions, , followed by ranking candidate hits based on spectral entropy or similarity. , False discovery rate (FDR) is commonly used to adjust the matching scores thresholds, allowing more annotations with lower confidence levels. , However, as multiple reference spectra and hits for each incident MS/MS spectrum complicate library searches, a method to assess the overall quality of chemical annotations (considering confidence and ambiguity) is lacking.
Class probability assessments can evaluate the probability of individual true positive (P(TP)) spectral matches. − Recently, the concept of “identification probability” (IP) was introduced by Metz et al., advocates for transferable annotation results across analytical platforms, allowing for multiple hits to be considered after calculating the average P(TP) for each hit. Model transferabilitythe ability to predict accurately beyond the original training datais crucial for forecasting chemical retention behavior. This requires diverse data sources and substantial volumes for statistical modeling. Previous studies have reported machine learning (ML) models for RT prediction of the chemical exposome, − but their transferability is often limited by varying chromatographic conditions. − Although there are different schemes of RT index (RTI), a harmonized RTI scale is necessary to provide a method-independent alternative for the integration with spectral information to enhance IC. −
This study presents a computational approach for calibrant-free, transferable RTI prediction on a harmonized scale, integrating it with spectral matching for P(TP) determination and chemical IP enhancement. Our approach employs 3 ML models, including 2 built on quantitative structure-retention relationship (QSRR), to compute expected RTI values for chemicals beyond calibrant data. A binary classification model that incorporates information from both retention and m/z domains is used to determine P(TP) for each matched reference spectrum. The average P(TP) is then calculated for chemical IP determination. We demonstrate our framework using RPLC/HRMS NTA data from pesticides-spiked blanks and black tea samples, aiming to improve nontargeted screening for compounds requiring further validation.
Materials and Methods
Overall Roadmap
This study employed 3 ML models alongside the MS/MS spectral matching algorithm, ULSA. As illustrated in Figures and S01, Model 1 is a random forest (RF) regression model correlating molecular fingerprints (MFs) to true RTI values of calibrants across 3 comparable scales. Model 2 is another RF regression model predicting expected RTI values on a harmonized scale, using experimental MS/MS spectra from various external databases without knowledge of the extract structure. Model 3 is a k-nearest neighbors (KNN) binary classification model calculating P(TP) for each matched reference spectrum with a matching score of ≥50%. This model integrates features from both RTI and m/z domains and was validated using independent data sets, including RPLC/HRMS data from pesticide analyses in blank spike and tea extracts.
1.
A diagram of the roadmap in this study. (A) Three models were developed in this study. Model 1, a random forest (RF) regression (reg.) model predicting molecular fingerprint (MF)-derived retention time index (RTI). Model 2, a RF reg. model for predicting cumulative neutral loss (CNL)-derived RTI. Semisynthetic MS/MS data were prepared, and Models 1 and 2 predicted expected RTI values for these data, which were processed by library search to output spectral matching scores for training Model 3. Model 3 was a k-Nearest neighbors (KNN) binary classification (class.) model with features from retention and m/z domains to predict true positive (TP) and true negative (TN) reference spectral matches. (B) The 3 models were applied to analyze RPLC/HRMS-based nontargeted analysis (NTA) data, enhancing chemical identification probability. Abbreviations: APC2D, AtomPairs2DFingerprintCount; PubChem, PubChem Fingerprinter.
Model 1: Molecular Fingerprint-Based Regression Model
A previously reported RF model for predicting a vector of molecular RTIs (3 scales) was retrained to predict a single RTI on a harmonized scale, correlating 790 preselected MFs to a RTI (Figure A). Unlike previous studies, stratification was based on MFs rather than RTIs to ensure training by structural diversity. This model was trained on 4713 calibrants with simplified molecular-input line-entry system (SMILES) identities across 3 comparable scales in RPLC: the C3–14 n-alkylamide system, the RTI system developed by Aalizadeh et al., and the C0–23 cocamide diethanolamine homologous series. Details on modeling are discussed in Supporting Information. The accuracy of predicted RTI values was assessed using 1237 untrained calibrants, focusing on mean absolute error (MAE) and mean relative error (MRE). The list of compounds used for modeling is available online (see file 1 at 10.5281/zenodo.16402775).
Model 2: Cumulative Neutral Loss-Based Regression Model
In addition to predicting expected RTI values from 2D chemical descriptors, a second RF regression model was established to correlate empirical positive electrospray ionization (ESI+) MS/MS data to RTI values predicted by Model 1 using a similar strategy as a prior study (Figure S01). This model employs cumulative neutral loss (CNL) masses as features, which have proven effective for matching analogous molecules ,, and chemical componentization. , Based on the previous results, , a total of 15,961 high probability masses-of-interest (MOIs) were preselected (the list is available online, see file 2 at 10.5281/zenodo.16402775), along with monoisotopic mass as an additional feature due to its discriminative power.
The training data set comprised MS/MS reference data from known compounds with InChIKeys and SMILES IDs, totaling 27,211 distinct molecules and 693,685 MS/MS spectra (the list is available online, see file 3 at 10.5281/zenodo.16402775). Each spectrum contained at least 2 MOIs. Model 2 was trained on 485,577 query MS/MS spectra. Train/test split were based on CNL leverage. Details on modeling are discussed in Supporting Information. Exploratory data analysis (EDA) and quartile analysis were performed to assess the distributions and the closeness of predicted and true RTI values. Predictive power was evaluated on 208,104 query spectra using root-mean-square error (RMSE, calculated according to eq ), MRE, and R 2 value as performance metrics.
Spectral Reference Library and Universal Library Search Algorithm
ULSA, a previously developed algorithm, was employed to annotate compounds by matching MS/MS spectra from various reference spectral databases. During ULSA execution, 7 matching parameters were summed to derive a final matching score, as discussed in Supporting Information. These parameters, derived from statistical calculations, can be generated independently of ULSA. Publicly available spectral libraries are integrated with ULSA, allowing for new reference data to be uploaded and matched, which is particularly valuable for annotating emerging chemicals of concern.
Model 3: Computing P(TP) for Individual Reference Spectral Match
Model 3 determines whether a spectrum match is a TP (labeled “1” as shown in Figure A) or true negative (TN) (labeled “0”). Features for this model include RTI error (as defined by eq ) between RTI values derived from Models 1 (RTI MF ) and 2 (RTI CNL ), monoisotopic mass and 4 parameters obtained from ULSA. A larger RTI error indicates a TN spectral match while a smaller error correlates with a TP match. Pearson correlation was used to eliminate redundant features with r values >0.80 and less importance. Various ML algorithms, including logistic regression (LR), decision tree (DT), RF, and KNN, were evaluated, with a focus on the model’s sensitivity to excluded features. Details on modeling and semisynthetic data preparation are discussed in Supporting Information. A set of TP and semisynthetic TN MS/MS spectra was analyzed by ULSA, yielding 4,368,902 spectral matches. Matches with scores <50% were classified as TN, making ML unnecessary for distinguishing TP from TN. Ultimately, 1,686,319 spectra were used for training and 421,381 for testing. Among the training samples, 1,535,009 spectra were TN (labeled “0”), while 151,310 instances represented TP (label “1”). Nine additional replicates of TP spectra were included to balance the data set. The optimal model was assessed primarily based on the Matthews correlation coefficient (MCC) score (eq ) and secondarily by weighted F1 score (eq ) using an external independent data set of pesticides spiked into blank samples at varying concentrations (1, 2.5, 5, 10, 25, 50, 100, and 1000 ppb). For real sample analyses, pesticides were spiked into 10× diluted and 100× diluted black tea matrices. Recall (as defined by eq ) was chosen as the primary performance metric since TN and FP rates are unknown in real samples.
Model Applicability Domain (AD)
Leverage (h ii ) was used to assess whether a matched compound fell within the ADs of Model 1 (h ii < 0.275) and Model 2 (h ii < 0.146). A leverage threshold was set at the 95% leverage of the model training data, calculated by eq (where X represents the matrix of training data, and x i is the vector for an individual data query).
Identification Probability Calculation
Multiple compound hits and reference spectra can be matched, yet each spectral match gives a P(TP). To measure ambiguity in a candidate RPLC/HRMS tensor, an average P(TP) was calculated for each compound hit (Figures B and S01). A decision threshold of 0.50 was applied to determine whether to retain or exclude a hit. IP was then calculated by eq based on the number of shortlisted hits.
Computations and Code Availability
All scripts for ML modeling and data visualization were written in Julia v.1.6 using Visual Studio Code (Microsoft), with additional visualizations done in Python v.3.10 on Jupyter Notebook (Anaconda3). Details on computational resources and packages are available in Table S1. Updates will be published with the final DOI citation.
Results and Discussion
Performance of Model 1 (Molecular Fingerprint-to-Retention Time Index Model)
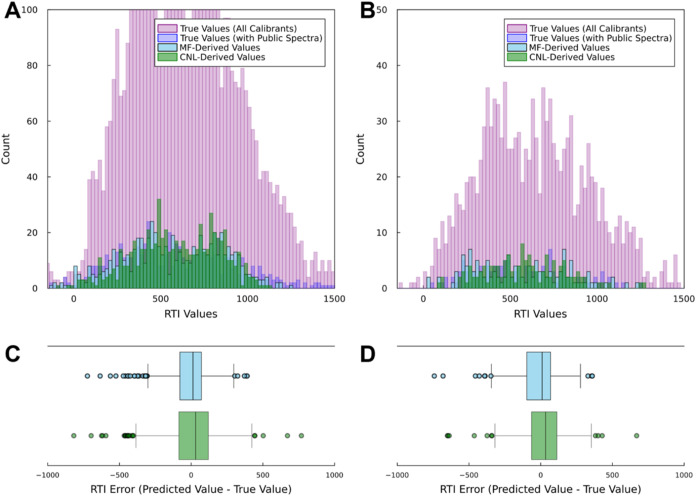
The first model developed in this study predicted RTI MF (measured RTI for each suggested match) on a harmonized scale. It was trained using 4713 compound calibrants with 5048 true RTI values across 3 similar RTI scale systems. MAE and MRE of the predicted values for the trained calibrants were 89.52 and 16.23%, respectively. In contrast, the mean absolute difference and the mean relative difference for the calibrants with their true RTI values from 2 different scales were 78.23 and 11.50% (see file 4 at 10.5281/zenodo.16402775), indicating similar uncertainty for the predicted values from Model 1. When tested against 1263 true values from 1237 calibrants, the uncertainty increased slightly, with a MAE of 111.15 and a MRE of 27.53%. The true RTI values and CNL MF values exhibited similar distributions in both training (Figure A) and testing (Figure B) data sets, validating the retrained MF-to-RTI model’s transferability.
2.
Performance assessment of the quantitative structure-retention relationship (QSRR)-based models. Histograms illustrate the distributions of true retention time indices (RTIs) of calibrants used to (A) train and (B) test Model 1, along with predicted values from Models 1 and 2. Boxplots present the variances of predicted values against true values of calibrants used to (C) train and (D) test Model 1.
Performance of Model 2 (Cumulative Neutral Loss-to-Retention Time Index Model)
The distribution of RTI CNL were similar to RTI MF and the true RTI values of chemical calibrants used to train (Figure A) and test (Figure B) Model 1. Variances in RTI error from Model 1 was smaller than those from Model 2 (Figure C) for the data originally used to train Model 1. However, both models showed similar RTI error variances for extended data not used in Model 1’s training (see Figure D). These patterns indicate the exchangeability of RTI values computed from Models 1 and 2.
For the model trained with a 7:3 train/test split, RTI MF values correlated well with RTI CNL values in training (Figure S02A) and testing (Figure S02B) data sets. The RMSEs were 51.8 and 92.8, equivalent to MREs of 6.90% and 9.92% with R 2 values of 0.96 and 0.88 for the training and testing data sets, respectively (Table ). These results were comparable to the predictive power of the CatBoost model trained on the NORMAN data set using different descriptors by Boelrijk et al. Our retrained RF model demonstrated better correlation with MF-derived RTIs (train: R 2 = 0.94; test: 0.85 in Boelrijk et al.’s work). Larger RMSEs were observed in our study (train: 44.0; test: 67.0 in Boelrijk et al.’s work) could be due to the RTI scale adopted across 3 systems. The comparable predictive performance confirms that Model 2 is transferable and effectively predicts expected RTI values based on QSRR.
1. Summary of the Machine Learning Models’ Predictive Power.
| ML model |
model 1 |
model
2 |
model
3 |
||||
|---|---|---|---|---|---|---|---|
| function | to predict RTI from MF | to predict RTI from CNL | to predict acceptance/rejection decision of an individual reference spectral match | ||||
| performance metric | RMSE | MRE | R 2 | weighted F1 score | MCC | recall | |
| training | 51.8 | 6.90% | 0.9634 | 0.89 | 0.77 | 0.99 | |
| testing | 92.8 | 9.92% | 0.8824 | 0.89 | 0.77 | 0.99 | |
| validation | 0.65 | 0.30 | 0.66 | ||||
| real Sample | 0.60 | ||||||
Machine learning.
Retention time index.
Molecular fingerprint.
Cumulative neutral loss.
Root mean square error.
Mean relative error.
Matthews correlation coefficient.
Performance of Model 3 (TP/TN Individual Reference Spectral Match Determination)
Model 3, a KNN model incorporated 6 features: “RefMatchFragRatio”, “MS1Error”, “MS2ErrorStd”, “FinalScoreRatio”, monoisotopic mass, and RTI error. It was applied only to individual spectral matches with scores ≥50% for TP/TN match determination. The model achieved a weighted F1 score of 0.65 and a MCC score of 0.30 in bulk analyses of NTA data from pesticides-spiked blank samples at concentrations from 1 to 1000 ppb (Table ). Notably, the inclusion of RTI error improved recall (0.60) for individual reference spectral matches in 10× and 100× diluted black tea matrices compared to the RTI error-exclusive model (recall = 0.54). This demonstrates that Model 3 achieved acceptable transferability to real samples Figure .
3.

Recalls of pesticide-spiked solutions at different P(TP) cutoff thresholds. Pesticide standards from the LC/MS Pesticide Comprehensive Mix Kit (PestMix) were spiked into solvent blank and 10× and 100× diluted black tea matrices to create 1 ppm final solutions for analysis. Various final solution concentrations (1, 2.5, 5, 10, 25, 50, 100, and 1000 ppb) were tested for blank spikes (No Tea).
By setting the default probability threshold for accepting a spectral match as TP at 0.50 (i.e., P(TP) ≥ 0.5), we achieved TP and FP rates of 98.8 and 23.4%, respectively (Figure S03A), resulting in an acceptable FDR of 19.1% for omics studies. More rigorous FDR-controlled cut-offs for 5 and 10% FDRs corresponded to P(TP) values of 0.89 and 0.78, respectively (Figure S03B). These decision thresholds were used to calculate recalls for samples in different IC levels. To balance recall and FDR, we selected 0.50 as the P(TP) cutoff. For 1 ppm samples, recalls increased as the matrix effect decreased. Our results indicated no predictive power for 1 ppb solutions, while stable analysis of chemical contaminants was achieved at concentrations of 2.5 ppb or higher. Since the recall for the 1 ppm sample was significantly below 50%, we estimated the limit of identification by Model 3 to be between 1 and 2.5 ppb.
Identification Probability Enhancement Comparison
Taking the measurement of ambiguity in candidate compounds into account, we assessed the improvement achieved through the incorporation of ML by evaluating IP using 2 definitions of “hit”. The first definition referred to a compound whose measured spectrum matches a collection of reference spectra. The fungicide Pencycuron (InChIKey: OGYFATSSENRIKG-UHFFFAOYSA-N) was selected as a successful case for discussion due to its structural complexity, which includes a phenylurea moiety, a cyclopentyl ring, and a chlorobenzyl group. For Pencycuron, identification yielded 5 compound hits through conventional matching (Table ), resulting in an accuracy of 20% (Figure ). Deploying Models 1, 2, and 3 alongside spectral library searches allowed us to compute P(TP) for individual matches. Detailed data of all individual matches for Pencycuron can be found in file 5 at 10.5281/zenodo.16402775. Averaging P(TP) from 12 spectral matches resulted in values of 0.73, 0.78, and 0.71 for pesticide samples with no tea, 100× diluted matrix, and 10× diluted matrix, respectively (Table ), indicating a TP hit. If the average P(TP) values of other compound hits were below 0.50, the IP of Pencycuron was considered 100%. However, compound hit B exhibited a moderate average P(TP) from 16 matches in the samples with no tea and the 10× diluted matrix (Table ). Although these IPs decreased from 100 to 50%, their values remained higher than the IPs obtained from the ULSA approach (i.e., 20%, Figure ).
2. Summary of the Predictions for 1000 ppb Pencycuron in Various Degrees of Black Tea Matrix.
| blank
spike |
100
times diluted |
10
times diluted |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| compound | matches | label | prediction | avg. P(0) | avg. P(1) | prediction | avg. P(0) | avg. P(1) | prediction | Avg. P(0) | Avg. P(1) |
| Hit A (Pencycuron) | 12 | 1 | 1 | 0.27 | 0.73 | 1 | 0.22 | 0.78 | 1 | 0.29 | 0.71 |
| Hit B | 16 | 0 | 1 | 0.43 | 0.57 | 0 | 0.54 | 0.46 | 1 | 0.40 | 0.60 |
| Hit C | 14 | 0 | 0 | 0.60 | 0.40 | 0 | 0.57 | 0.43 | 0 | 0.56 | 0.44 |
| Hit D | 12 | 0 | 0 | 1.00 | 0.00 | 0 | 1.00 | 0.00 | 0 | 1.00 | 0.00 |
| Hit E | 1 | 0 | 0 | 1.00 | 0.00 | 0 | 1.00 | 0.00 | 0 | 1.00 | 0.00 |
InChIKey: OGYFATSSENRIKG-UHFFFAOYSA-N.
InChIKey: JTVPZMFULRWINT-UHFFFAOYSA-N.
InChIKey: VCKAUONIDRWIGP-UHFFFAOYSA-N.
InChIKey: SGUAFYQXFOLMHL-UHFFFAOYSA-N.
InChIKey: ZDVGWHJBNGTLKF-UHFFFAOYSA-N.
4.

Identification probability (IP) assessment by average P(TP). Integration of machine learning (ML) with Universal Library Search Algorithm (ULSA) enhanced average IP by 24 and 25% for blank spikes and 100× diluted tea matrix samples, representing increments of 54.5 and 52.1%, respectively. The presence of a 10× diluted matrix reduced this improvement to 21%, equivalent to a 46.7% increase. Abbreviations: nd, not detected.
We averaged the IPs of all positive results from our pesticide panel for overall performance comparison. For 1 ppm sample solutions, integrating our KNN model (Model 3) enhanced average IPs from 44 to 68% for blank spikes and from 48 to 73% in the 100× diluted tea matrix samples (Figure ), representing increments of 54.5 and 52.1%, respectively. The presence of a more concentrated matrix (10× diluted) slightly affected the improvement from ML incorporation, yielding a 21% higher IP than using ULSA alone (from 45 to 66%), which corresponds to a 46.7% increase.
Standard library searches typically rely on ranking individual matches by score. , This can mislead the structural assignment results, as only 1 match from multiple reference spectra with the highest score (as known as Top-1 search) is considered, while results from remaining matches with lower scores are neglected. To illustrate this issue, we compared performance by defining a hit as a compound whose measured spectrum matches an individual reference spectrum with high rank that sorted by matching score “FinalScoreRatio” in the ULSA approach, or by individual P(TP) in the ML-aided approach. An alternative IP, defined in eq especially for ranking analysis, represented the occurrence frequency of TP spectral matches among the top-ranked hits. The incorporation of ML for our pesticide panel improved slightly (1–3%) on average for samples with tea matrices, while remaining comparable for spiked blanks (Figure S4). This finding underscores the importance of including as many reference spectra as possible rather than relying on a single reference to account for the identification ambiguity of a candidate compound.
Conclusions
Integrating ML with reference spectral library searches improved recall in real samples with and without tea matrices and increased annotation confidence compared to single library searches. The application of Model 3 resulted in acceptable weighted F1 and MCC scores for the blank spikes, alongside notable IP increases in diluted tea matrices. Greater IP improvements were observed as the number of reference spectra increased. For both tea matrix-containing and matrix-free samples, computing chemical IP from collection of all available reference MS/MS spectra significantly improved annotation confidence, providing a higher confidence in silico analysis solution for early stage data analytics. However, a primary limitation of our approach is the reliance on the quality and diversity of the spectral reference libraries. Incomplete or biased libraries may hinder the identification of highly structurally diverse compounds or those with limited accessible reference data. To address this challenge, continuous updates the reference spectral libraries with denoised spectra and computational spectra are essential. Additionally, ongoing validation with various real-world samples of TN MS/MS spectra will be crucial to fine-tuning Model 3.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
Supplementary Material
Acknowledgments
H.-L.N. acknowledges the sponsorship from the Graduate School of Hong Kong Baptist University for overseas research attachment, the Environmental Monitoring and Computational Mass Spectrometry (EMCMS, www.emcms.info) group for their insights and feedback, and Prof. S.S. for his host of overseas research experience program. S.S. and V.T. thank the ChemistryNL for financial support. H.Y thanks the Start-up Grant for New Academics–YAN Hong (165520).
Three preprocessed experimental data sets are provided for demonstration at https://github.com/TommyNHL/exposomeIDProba/tree/main/demo_data (CSV). List of compounds used for modeling (files 1 and 3), their predicted RTI values (file 4), the selected MOIs (file 2), and the spectral matching data for Pencycuron (file 5) are available at 10.5281/zenodo.16402775 (XLSX).
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.5c01873.
Experimental methods for ULSA, semisynthetic and experimental data preparation, and the identification workflow; code availability for model development and application; technical details presented by a roadmap (Figure S01); scatter plots of correlation between RTI MF and RTI CNL values (Figure S02); line plots representing the performance of Model 3 (Figure S03); heatmap representing the IPs by ranking (Figure S04); histograms showing the distribution of TP and TN spectral matches (Figures S05–S13); and plots indicating the performance of Model 3 during feature and model selection (Figures S14–S16) (PDF)
Conceptualization: H.-L.N., V.T., and S.S.; resources: H.-L.N., V.T., D.v.H., Z.C., and S.S.; data curation: H.-L.N., V.T., and D.v.H.; writingoriginal draft preparation: H.-L.N.; writingreview and editing: H.-L.N., V.T., H.Y., and S.S.; visualization: H.-L.N. and H.Y.; supervision: H.Y., Z.C., and S.S.; project administration: Z.C. and S.S.; funding acquisition: Z.C. and S.S. All authors have read and agreed to the published version of the manuscript.
The authors declare no competing financial interest.
References
- Manz K. E., Feerick A., Braun J. M., Feng Y. L., Hall A., Koelmel J., Manzano C., Newton S. R., Pennell K. D., Place B. J., Godri Pollitt K. J., Prasse C., Young J. A.. Non-Targeted Analysis (NTA) and Suspect Screening Analysis (SSA): A Review of Examining the Chemical Exposome. J. Exposure Sci. Environ. Epidemiol. 2023;33:524–536. doi: 10.1038/s41370-023-00574-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samanipour S., Barron L. P., van Herwerden D., Praetorius A., Thomas K. V., O’Brien J. W.. Exploring the Chemical Space of the Exposome: How Far Have We Gone? JACS Au. 2024;4(7):2412–2425. doi: 10.1021/jacsau.4c00220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Z., Zhu Z., Huang S., Wang J.. Non-Targeted Screening of Pesticides for Food Analysis Using Liquid Chromatography High-Resolution Mass Spectrometry-a Review. Food Addit. Contam.,:Part A. 2020;37(7):1180–1201. doi: 10.1080/19440049.2020.1753890. [DOI] [PubMed] [Google Scholar]
- Zweigle J., Bugsel B., Zwiener C.. FindPFΔS: Non-Target Screening for PFAS-Comprehensive Data Mining for MS2 Fragment Mass Differences. Anal. Chem. 2022;94(30):10788–10796. doi: 10.1021/acs.analchem.2c01521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grunfeld D. A., Gilbert D., Hou J., Jones A. M., Lee M. J., Kibbey T. C. G., O’Carroll D. M.. Underestimated Burden of Per- and Polyfluoroalkyl Substances in Global Surface Waters and Groundwaters. Nat. Geosci. 2024;17:340–346. doi: 10.1038/s41561-024-01402-8. [DOI] [Google Scholar]
- De Souza R. M., Seibert D., Quesada H. B., de Jesus Bassetti F., Fagundes-Klen M. R., Bergamasco R.. Occurrence, Impacts and General Aspects of Pesticides in Surface Water: A Review. Process Saf. Environ. Prot. 2020;135:22–37. doi: 10.1016/j.psep.2019.12.035. [DOI] [Google Scholar]
- Sumner L. W., Amberg A., Barrett D., Beale M. H., Beger R., Daykin C. A., Fan T. W. M., Fiehn O., Goodacre R., Griffin J. L., Hankemeier T., Hardy N., Harnly J., Higashi R., Kopka J., Lane A. N., Lindon J. C., Marriott P., Nicholls A. W., Reily M. D., Thaden J. J., Viant M. R.. Proposed Minimum Reporting Standards for Chemical Analysis: Chemical Analysis Working Group (CAWG) Metabolomics Standards Initiative (MSI) Metabolomics. 2007;3(3):211–221. doi: 10.1007/s11306-007-0082-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schymanski E. L., Jeon J., Gulde R., Fenner K., Ruff M., Singer H. P., Hollender J.. Identifying Small Molecules via High Resolution Mass Spectrometry: Communicating Confidence. Environ. Sci. Technol. 2014;48(4):2097–2098. doi: 10.1021/es5002105. [DOI] [PubMed] [Google Scholar]
- Hollender J., Schymanski E. L., Ahrens L., Alygizakis N., Béen F., Bijlsma L., Brunner A. M., Celma A., Fildier A., Fu Q., Gago-Ferrero P., Gil-Solsona R., Haglund P., Hansen M., Kaserzon S., Kruve A., Lamoree M., Margoum C., Meijer J., Merel S., Rauert C., Rostkowski P., Samanipour S., Schulze B., Schulze T., Singh R. R., Slobodnik J., Steininger-Mairinger T., Thomaidis N. S., Togola A., Vorkamp K., Vulliet E., Zhu L., Krauss M.. NORMAN Guidance on Suspect and Non-Target Screening in Environmental Monitoring. Environ. Sci. Eur. 2023;35:75. doi: 10.1186/s12302-023-00779-4. [DOI] [Google Scholar]
- Alygizakis N., Lestremau F., Gago-Ferrero P., Gil-Solsona R., Arturi K., Hollender J., Schymanski E. L., Dulio V., Slobodnik J., Thomaidis N. S.. Towards a Harmonized Identification Scoring System in LC-HRMS/MS Based Non-Target Screening (NTS) of Emerging Contaminants. TrAC, Trends Anal. Chem. 2023;159:116944. doi: 10.1016/j.trac.2023.116944. [DOI] [Google Scholar]
- Ciccarelli D., Samanipour S., Rapp-Wright H., Bieber S., Letzel T., O’Brien J. W., Marczylo T., Gant T. W., Vineis P., Barron L. P.. Bridging Knowledge Gaps in Human Chemical Exposure via Drinking Water with Non-Target Screening. Crit. Rev. Environ. Sci. Technol. 2025;55(3):190–214. doi: 10.1080/10643389.2024.2396690. [DOI] [Google Scholar]
- Hulleman T., Turkina V., O’Brien J. W., Chojnacka A., Thomas K. V., Samanipour S.. Critical Assessment of the Chemical Space Covered by LC-HRMS Non-Targeted Analysis. Environ. Sci. Technol. 2023;57(38):14101–14112. doi: 10.1021/acs.est.3c03606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittremieux W., Schmid R., Huber F., van der Hooft J. J. J., Wang M., Dorrestein P. C.. Comparison of Cosine, Modified Cosine, and Neutral Loss Based Spectrum Alignment for Discovery of Structurally Related Molecules. J. Am. Soc. Mass Spectrom. 2022;33(9):1733–1744. doi: 10.1021/jasms.2c00153. [DOI] [PubMed] [Google Scholar]
- Li Y., Kind T., Folz J., Vaniya A., Mehta S. S., Fiehn O.. Spectral Entropy Outperforms MS/MS Dot Product Similarity for Small-Molecule Compound Identification. Nat. Methods. 2021;18:1524–1531. doi: 10.1038/s41592-021-01331-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baygi S. F., Banerjee S. K., Chakraborty P., Kumar Y., Barupal D. K.. IDSL.UFA Assigns High-Confidence Molecular Formula Annotations for Untargeted LC/HRMS Data Sets in Metabolomics and Exposomics. Anal. Chem. 2022;94(39):13315–13322. doi: 10.1021/acs.analchem.2c00563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samanipour S., Reid M. J., Bæk K., Thomas K. V.. Combining a Deconvolution and a Universal Library Search Algorithm for the Nontarget Analysis of Data-Independent Acquisition Mode Liquid Chromatography-High-Resolution Mass Spectrometry Results. Environ. Sci. Technol. 2018;52(8):4694–4701. doi: 10.1021/acs.est.8b00259. [DOI] [PubMed] [Google Scholar]
- Scheubert K., Hufsky F., Petras D., Wang M., Nothias L. F., Dührkop K., Bandeira N., Dorrestein P. C., Böcker S.. Significance Estimation for Large Scale Metabolomics Annotations by Spectral Matching. Nat. Commun. 2017;8:1494. doi: 10.1038/s41467-017-01318-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svensson F., Afzal A. M., Norinder U., Bender A.. Maximizing Gain in High-Throughput Screening Using Conformal Prediction. J. Cheminf. 2018;10(1):7. doi: 10.1186/s13321-018-0260-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Wang B., Zhao Y., Shao X., Wang M., Ma F., Yang L., Nie M., Jin P., Yao K., Song H., Lou S., Wang H., Yang T., Tian Y., Han P., Hu Z.. Metabolomic Machine Learning Predictor for Diagnosis and Prognosis of Gastric Cancer. Nat. Commun. 2024;15(1):1657. doi: 10.1038/s41467-024-46043-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gloaguen Y., Kirwan J. A., Beule D.. Deep Learning-Assisted Peak Curation for Large-Scale LC-MS Metabolomics. Anal. Chem. 2022;94(12):4930–4937. doi: 10.1021/acs.analchem.1c02220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Appel I. J., Gronwald W., Spang R.. Estimating Classification Probabilities in High-Dimensional Diagnostic Studies. Bioinformatics. 2011;27(18):2563–2570. doi: 10.1093/bioinformatics/btr434. [DOI] [PubMed] [Google Scholar]
- Metz T. O., Chang C. H., Gautam V., Anjum A., Tian S., Wang F., Colby S. M., Nunez J. R., Blumer M. R., Edison A. S., Fiehn O., Jones D. P., Li S., Morgan E. T., Patti G. J., Ross D. H., Shapiro M. R., Williams A. J., Wishart D. S.. Introducing “Identification Probability” for Automated and Transferable Assessment of Metabolite Identification Confidence in Metabolomics and Related Studies. Anal. Chem. 2025;97:1–11. doi: 10.1021/acs.analchem.4c04060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assis J., Serrão E. A., Fragkopoulou E., Legrand T., Gouvêa L., Araújo M. B.. Misconception of Model Transferability Precludes Estimates of Seagrass Community Reorganization in a Changing Climate. Nat. Plants. 2024;10:1071–1074. doi: 10.1038/s41477-024-01735-7. [DOI] [PubMed] [Google Scholar]
- Munro K., Miller T. H., Martins C. P. B., Edge A. M., Cowan D. A., Barron L. P.. Artificial Neural Network Modelling of Pharmaceutical Residue Retention Times in Wastewater Extracts Using Gradient Liquid Chromatography-High Resolution Mass Spectrometry Data. J. Chromatogr. A. 2015;1396:34–44. doi: 10.1016/j.chroma.2015.03.063. [DOI] [PubMed] [Google Scholar]
- McEachran A. D., Mansouri K., Newton S. R., Beverly B. E. J., Sobus J. R., Williams A. J.. A Comparison of Three Liquid Chromatography (LC) Retention Time Prediction Models. Talanta. 2018;182:371–379. doi: 10.1016/j.talanta.2018.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aalizadeh R., Nika M. C., Thomaidis N. S.. Development and Application of Retention Time Prediction Models in the Suspect and Non-Target Screening of Emerging Contaminants. J. Hazard. Mater. 2019;363:277–285. doi: 10.1016/j.jhazmat.2018.09.047. [DOI] [PubMed] [Google Scholar]
- Feng C., Xu Q., Qiu X., Jin Y., Ji J., Lin Y., Le S., She J., Lu D., Wang G.. Evaluation and Application of Machine Learning-Based Retention Time Prediction for Suspect Screening of Pesticides and Pesticide Transformation Products in LC-HRMS. Chemosphere. 2021;271:129447. doi: 10.1016/j.chemosphere.2020.129447. [DOI] [PubMed] [Google Scholar]
- Song D., Tang T., Wang R., Liu H., Xie D., Zhao B., Dang Z., Lu G.. Enhancing Compound Confidence in Suspect and Non-Target Screening through Machine Learning-Based Retention Time Prediction. Environ. Pollut. 2024;347:123763. doi: 10.1016/j.envpol.2024.123763. [DOI] [PubMed] [Google Scholar]
- Bonini P., Kind T., Tsugawa H., Barupal D. K., Fiehn O.. Retip: Retention Time Prediction for Compound Annotation in Untargeted Metabolomics. Anal. Chem. 2020;92(11):7515–7522. doi: 10.1021/acs.analchem.9b05765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanstrup J., Neumann S., Vrhovšek U.. PredRet: Prediction of Retention Time by Direct Mapping between Multiple Chromatographic Systems. Anal. Chem. 2015;87(18):9421–9428. doi: 10.1021/acs.analchem.5b02287. [DOI] [PubMed] [Google Scholar]
- Ruttkies C., Schymanski E. L., Wolf S., Hollender J., Neumann S.. MetFrag Relaunched: Incorporating Strategies beyond in Silico Fragmentation. J. Cheminf. 2016;8:3. doi: 10.1186/s13321-016-0115-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bach E., Szedmak S., Brouard C., Böcker S., Rousu J.. Liquid-Chromatography Retention Order Prediction for Metabolite Identification. Bioinformatics. 2018;34(17):i875–i883. doi: 10.1093/bioinformatics/bty590. [DOI] [PubMed] [Google Scholar]
- Kretschmer F., Harrieder E. M., Hoffmann M. A., Böcker S., Witting M.. RepoRT: A Comprehensive Repository for Small Molecule Retention Times. Nat. Methods. 2024;21:153–155. doi: 10.1038/s41592-023-02143-z. [DOI] [PubMed] [Google Scholar]
- Rigano F., Arigò A., Oteri M., La Tella R., Dugo P., Mondello L.. The Retention Index Approach in Liquid Chromatography: An Historical Review and Recent Advances. J. Chromatogr. A. 2021;1640:461963. doi: 10.1016/j.chroma.2021.461963. [DOI] [PubMed] [Google Scholar]
- Aalizadeh R., Alygizakis N. A., Schymanski E. L., Krauss M., Schulze T., Ibáñez M., McEachran A. D., Chao A., Williams A. J., Gago-Ferrero P., Covaci A., Moschet C., Young T. M., Hollender J., Slobodnik J., Thomaidis N. S.. Development and Application of Liquid Chromatographic Retention Time Indices in HRMS-Based Suspect and Nontarget Screening. Anal. Chem. 2021;93(33):11601–11611. doi: 10.1021/acs.analchem.1c02348. [DOI] [PubMed] [Google Scholar]
- Boelrijk J., van Herwerden D., Ensing B., Forré P., Samanipour S.. Predicting RP-LC Retention Indices of Structurally Unknown Chemicals from Mass Spectrometry Data. J. Cheminf. 2023;15:28. doi: 10.1186/s13321-023-00699-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Herwerden D., Nikolopoulos A., Barron L. P., O’Brien J. W., Pirok B. W. J., Thomas K. V., Samanipour S.. Exploring the Chemical Subspace of RPLC: A Data Driven Approach. Anal. Chim. Acta. 2024;1317:342869. doi: 10.1016/j.aca.2024.342869. [DOI] [PubMed] [Google Scholar]
- Hall L. M., Hill D. W., Menikarachchi L. C., Chen M. H., Hall L. H., Grant D. F.. Optimizing Artificial Neural Network Models for Metabolomics and Systems Biology: An Example Using HPLC Retention Index Data. Bioanalysis. 2015;7(8):939–955. doi: 10.4155/bio.15.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aalizadeh R., Nikolopoulou V., Thomaidis N. S.. Development of Liquid Chromatographic Retention Index Based on Cocamide Diethanolamine Homologous Series (C(n)-DEA) Anal. Chem. 2022;94(46):15987–15996. doi: 10.1021/acs.analchem.2c02893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue J., Guijas C., Benton H. P., Warth B., Siuzdak G.. METLIN MS2Molecular Standards Database: A Broad Chemical and Biological Resource. Nat. Methods. 2020;17:953–954. doi: 10.1038/s41592-020-0942-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aisporna A., Benton H. P., Chen A., Derks R. J. E., Galano J. M., Giera M., Siuzdak G.. Neutral Loss Mass Spectral Data Enhances Molecular Similarity Analysis in METLIN. J. Am. Soc. Mass Spectrom. 2022;33(3):530–534. doi: 10.1021/jasms.1c00343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohanty I., Mannochio-Russo H., Schweer J. V., El Abiead Y., Bittremieux W., Xing S., Schmid R., Zuffa S., Vasquez F., Muti V. B., Zemlin J., Tovar-Herrera O. E., Moraïs S., Desai D., Amin S., Koo I., Turck C. W., Mizrahi I., Kris-Etherton P. M., Petersen K. S., Fleming J. A., Huan T., Patterson A. D., Siegel D., Hagey L. R., Wang M., Aron A. T., Dorrestein P. C.. The Underappreciated Diversity of Bile Acid Modifications. Cell. 2024;187(7):1801–1818. doi: 10.1016/j.cell.2024.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Herwerden D., O’Brien J. W., Lege S., Pirok B. W. J., Thomas K. V., Samanipour S.. Cumulative Neutral Loss Model for Fragment Deconvolution in Electrospray Ionization High-Resolution Mass Spectrometry Data. Anal. Chem. 2023;95(33):12247–12255. doi: 10.1021/acs.analchem.3c00896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H., Wang C., Wu Z.. PROPER: Comprehensive Power Evaluation for Differential Expression Using RNA-Seq. Bioinformatics. 2015;31(2):233–241. doi: 10.1093/bioinformatics/btu640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zulfiqar M., Gadelha L., Steinbeck C., Sorokina M., Peters K.. MAW: The Reproducible Metabolome Annotation Workflow for Untargeted Tandem Mass Spectrometry. J. Cheminform. 2023;15:32. doi: 10.1186/s13321-023-00695-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Three preprocessed experimental data sets are provided for demonstration at https://github.com/TommyNHL/exposomeIDProba/tree/main/demo_data (CSV). List of compounds used for modeling (files 1 and 3), their predicted RTI values (file 4), the selected MOIs (file 2), and the spectral matching data for Pencycuron (file 5) are available at 10.5281/zenodo.16402775 (XLSX).