High-power lithium-ion battery characterization dataset for stochastic battery modeling

Abstract

High-power lithium-ion battery (LIB) applications, such as electric racing cars and electric vertical take-off and landing (eVTOL) aircrafts, are growing rapidly. Degradation in LIBs such as lithium plating, particle cracking, and SEI breakdown is accelerated at high C-rate at different temperatures and depth-of-discharges (DOD); however, high-power cells are designed to better withstand these operating conditions as compared to high-energy cells. Despite this, publicly available datasets of high-power batteries are limited. In this work, we present a characterization dataset of 12 high-power NMC cells which includes capacity tests, high C-rate pulse tests, and impedance tests, all of which are conducted at temperature set points of 5 °C, 25 °C, and 40 °C. Additionally, the dataset captures cell-to-cell variations, enabling the development of stochastic battery models that account for parameter uncertainty and its impact on the cell terminal voltage.

Background & Summary

The lithium-ion battery (LIB) has become the most widely used technology for energy storage systems, since its introduction commercially in 1991, primarily due to its high energy density and long lifespan¹. These batteries are commonly used in a range of applications spanning consumer electronics, electric vehicles (EVs), long-haul heavy duty trucks², and power grid³. Nowadays, there is also an increasing interest in high-power applications such as electric vertical take-off and landing (eVTOL) planes^4,5, electric racing cars, and DC fast charging for EVs^6,7. The inception of high rate charge/discharge started with spinel LiMn₂O₄ electrodes which improved lithium-ion diffusion and electronic conductivity⁸. Further improvements for high-power cells with LiFeO₄ electrodes were achieved by increasing electronic conductivity through controlled changes in the cation ratio and by adding metals with a charge higher than Li⁺⁹. Typically, high-power battery cells have low areal cathode capacity (mAh/cm²), high cathode porosity, high electrolyte mass, smaller particle size, and thicker current collectors^10,11 as compared to high-energy cells. From an operational standpoint, these design trade offs enable faster intercalation/de-intercalation of lithium-ions and reduce the resistance of high-power cells. Cell manufacturers provide the maximum charge/discharge C-rate, where C-rate is the ratio of the current in Amperes (A) and the nominal capacity in Ampere-hour throughput (Ah) of the cell expressed in the units of per hour (h⁻¹), that a cell can safely support, and the operational C-rate is determined by the application for which it is used.

Performance of lithium-ion batteries is directly dependent upon factors such as temperature, C-rate, and depth-of-discharge (DOD) in terms of the energy and power that the cell can provide¹². High C-rate operation at low temperatures promotes lithium plating on the negative electrode due to slower reaction kinetics and amalgamation of lithium-ions at the surface of the electrode^13,14. Similarly, at low temperatures, cycling and/or high DOD can also lead to lithium plating¹⁵. Conversely, high C-rate usage at high temperatures promotes the breakdown and decomposition of the solid-electrolyte interphase (SEI) layer on the negative electrode leading to the formation of gases inside the cell¹⁴. The heat generation from the gases leads to a further increase in temperature of the cell, eventually resulting in a positive feedback loop that can lead to thermal runaway^16,17. Mechanical stress at high C-rates can lead to particle cracking in the negative electrode due to high rate of expansion and contraction of the electrode during charging and discharging, respectively¹⁴. On the positive electrode, high C-rates at high temperature and charging to high voltages can lead to the dissolution of the transition metal resulting in cathode-electrolyte interphase (CEI) formation¹⁸, electrolyte decomposition¹⁹, and site exchanges between lithium-ions and transition metals^14,20. These degradation mechanisms are prevalent for all types of LIBs, but their occurrence is accelerated for high-energy batteries since they are not designed for high C-rate operation. For similar operating conditions, high-power batteries, by design, are able to push the limits of operation without degrading at the same rate, making them a viable option for newer high-power applications.

The number of publicly available battery datasets have grown significantly over the last decade, but majority of these datasets cater to C-rates below 3C²¹. Even though the literature lacks a standard definition of high C-rate, in this work, we classify high C-rate to be 3C or above. Table 1 summarizes the existing datasets and it also highlights the gaps filled by the present work. Severson et al. published a battery dataset where high-power APR18650M1A LFP cells were fast-charged with varying C-rates between 3.6C and 6C at a constant temperature of 30 °C²². Similarly, Attia et al. provides a fast-charging battery dataset for the same LFP cells where the charging C-rate varied between 3.6C and 5.6C determined by a closed-loop bayesian optimization framework to maximize battery cycle life²³. Another fast-charging dataset using Sanyo 18650 LCO cells by Gun et al. shows the use of alternative charging profiles at high C-rate to minimize degradation of LIBs²⁴. The Sanyo cells are designed to have a balance between power and energy. Other datasets^25–31 are also based on either high-power or high-energy cells, and experience varying charging C-rates above 3C. All of these datasets are useful for developing SoH estimation models for high-power applications; however, these datasets do not contain other types of characterization tests, such as Hybrid pulse power characterization (HPPC) or Electrochemical Impedance Spectroscopy (EIS), which can provide critical intrinsic information about internal battery dynamics for accurate state estimation. Only the dataset by Pozzato et al.³² cycles high-energy INR21700-M50T NMC cells at varying charging C-rates while discharging using a UDDS profile, and also performs comprehensive characterization tests including EIS.

Table 1.

Comparison of publicly available high C–rate datasets and the dataset in this work.

High C-rate Datasets
Dataset	# Cells	Chemistry	Type	C–rates	Notes
Severson et al.22 [URL]	124	LFP	High-power	3.6C – 6C	No HPPC or EIS
Attia et al.23 [URL]	40	LFP	High-power	3.6C – 5.6C	No HPPC or EIS
Gun et al.24 [URL]	24	LCO	Balanced	Up to 10C	No HPPC or EIS
Trad et al.25 [URL] and Govindrajan et al.26 [URL]	27	NMC	—	C/2 -- 3C drive cycles	No HPPC or EIS
Preger et al.27 [URL]	86	NCA, NMC, LFP	High-energy High-power	C/5 - 2C, C/5 - 3C (LFP)	No HPPC or EIS
Catenaro et al.28 [URL]	12	NCA, NMC, LFP	High-energy High-power	C/20 - 5C, C/20 - 20C (LFP)	No HPPC or EIS
Pozzato et al.32 [URL]	10	NMC	High-energy	C/4 - 3C	Only 2 cells at 3C
Che et al.29 [URL]	8	LFP	High-power	1C - 10C	No HPPC or EIS
He et al.30 [URL]	12	LCO	—	C/2 – 3C	No HPPC or EIS, Only 1 cell at 3C
This work [URL]	12	NMC	High-power	C/5 - 8C	Pulses up to 8C, Full cell characterization

In this work, we introduce an open-source battery dataset of 12 high-power lithium-ion cells. The complete experimental campaign occurs in two phases. Phase 1 consists of screening 45 cells to select 12 cells using a capacity and resistance-based selection criteria. Phase 2 consists of comprehensive characterization tests of the 12 selected cells, including capacity tests, HPPC-inspired pulse tests at various C-rates in charge and discharge, and EIS tests, all performed at three different temperature set points of 5 °C, 25 °C, and 40 °C. The high C-rate pulses represent short periods of high-power demands in-line with battery usage in high-power applications. The dataset enables an initial evaluation of inter–cell variability to be impacted in the future. The remainder of the paper is organized as follows: the Methods section discusses the experimental setup and the design of experiments for Phase 1 and Phase 2, the Data Records section describes the data repository, and the structure and format of the dataset, and the Technical Validation section provides analysis of the capacity, pulse resistance, and EIS resistance data along with a discussion on the cell-to-cell variability in the dataset.

Methods

Experimental setup

In this work, the dataset is based on the Molicel INR-21700-P42A cells with LiNiMnCoO₂ (NMC) cathode and Silicon-graphite anode. Technical specifications of the cells are summarized in Table 2.

Table 2.

Technical specifications of the Molicel INR-21700-P42A cell.

	Label	Specification
	Manufacturer	Molicel
	Model	INR-21700-P42A
	Positive electrode	LiNiMnCoO2 (NMC)
	Negative electrode	Graphite and Silicon
	Nominal capacity	4.2 Ah
	Nominal voltage	3.6 V
	Maximum voltage	4.2 V
	Minimum voltage	2.5 V
	Maximum discharge C-rate / current	11C / 45 A
	Maximum temperature	60 °C

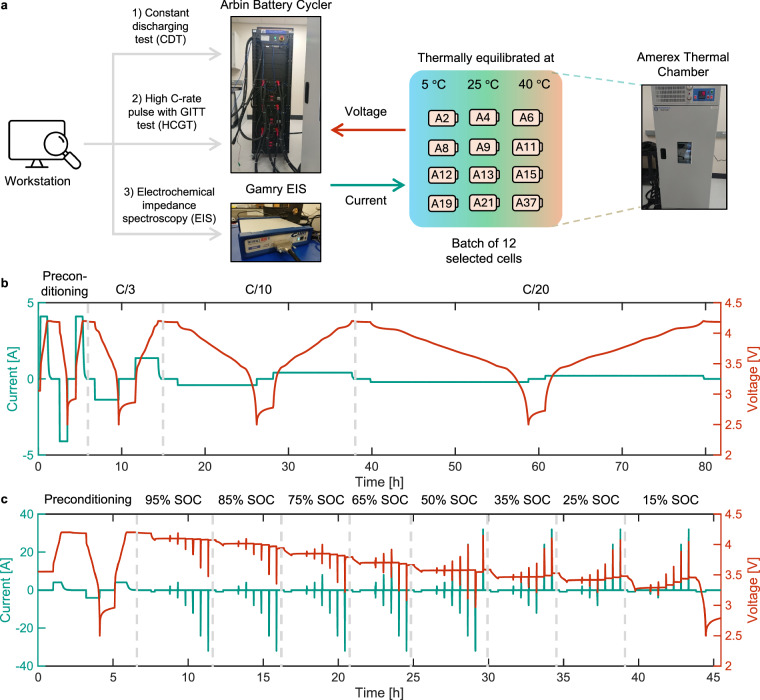
In Phase 1, screening of the initial batch of 45 cells is carried out at Stanford Linear Accelerator Laboratory (SLAC) using a BioLogic battery cycler with a voltage range of 0-9 V and a maximum current of  ± 15 A, and an Associated Environmental Systems (AES) thermal chamber for temperature control. Figure 1a illustrates the experimental procedure in which 45 cells are thermally equilibrated at 25 °C inside the AES thermal chamber. The battery cycler executes the screening protocol shown in Fig. 1b, and the collected current and voltage data are processed to extract C/3 capacity, Q_C/3, and three pulse resistances, $R_{puls{e}_k}$, which are defined as follows:

$$Q_{C/3}=\frac{1}{3600}·|I_{C/3}|·T$$ 1

$$R_{puls{e}_k}:={|\frac{\mathrm{\Delta }V}{\mathrm{\Delta }I}|}_k={|\frac{V_{i+1}-V_i}{I_{i+1}-I_i}|}_k$$ 2

where I_C/3 is the C/3 discharge current in Amperes (A), T = 5 s is the length of time in seconds for which I_C/3 is applied, k ∈ {3.4, 3.7, 4.0} V denotes the voltage value corresponding to 20%, 50%, and 80% SoC, respectively, and i is the index of time at which the 1C pulse is applied. For $R_{puls{e}_k}$, I_i = 1.3 A is the C/3 current, and I_i+1 = 5.3 A is the C/3 plus 1C current since the pulse is applied during C/3 discharge. The sampling time Δt between time index i+1 and i is 0.01 s. The current convention is positive for charge and negative for discharge. In this phase, a subset of 12 cells is selected from the original batch of 45 cells.

Fig. 1.

Phase 1: Experimental setup and screening protocol. (a) Batch of 45 cells is tested at 25 °C at Stanford Linear Accelerator Laboratory (SLAC) using a BioLogic Battery Cycler and an AES Thermal Chamber for temperature control. 12 out of 45 cells are chosen based on the statistical distribution of resistance and capacity. (b) Screening protocol consisting of preconditioning followed by a C/3 discharge with 1C discharge pulses at three different voltages corresponding to 80%, 50%, and 20% SoC. Capacity, Q_C/3, from C/3 discharge and three resistances, $R_{puls{e}_k}$, where k denotes the voltage at which the pulse is applied, from 1C discharge pulses are used to obtain the statistical distribution, and select 12 cells to be tested in Phase 2.

In Phase 2, characterization of the 12 selected cells is conducted at Stanford Energy Control Lab (SECL) using an Arbin battery cycler with a voltage range of 0-5 V and a maximum current of  ± 250 A for both charge and discharge. An Amerex IC500R thermal chamber, with a temperature range of -5 °C to 65 °C, is used with the Arbin cycler for thermal control. Figure 2a illustrates the characterization procedure along with the testing equipment. For characterization, three tests are performed namely Constant discharging test (CDT), High C-rate pulse with GITT test (HCGT) and Electrochemical Impedance Spectroscopy (EIS). The first two tests are conducted using the Arbin battery cycler while the EIS test is conducted using a Gamry EIS 1010E interfaced through the Arbin battery cycling software. The thermal chamber equilibrates the cells at three temperatures of 5 °C, 25 °C, and 40 °C, and each of the three tests is performed at all three temperatures.

Fig. 2.

Phase 2: Experimental setup and testing protocols. (a) Characterization testing procedure conducted in Stanford Energy Control Lab (SECL) on 12 selected cells from Phase 1. CDT and HCGT are performed using an Arbin battery cycler, and EIS is conducted through a Gamry EIS. The Amerex thermal chamber is used to control the temperature at 5 °C, 25 °C, and 40 °C during Phase 2. (b) Constant discharging test (CDT) protocol with preconditioning followed by discharging and charging at C/3, C/10, and C/20 C-rates. (c) High C-rate pulse with GITT test (HCGT) used to test the cells at various SoC values using pulses at C/2, 1C, 2C, 3C, 6C, and 8C. The pulses are designed to avoid crossing maximum and minimum cell voltage limits at high and low SoC, respectively.

Design of experiments

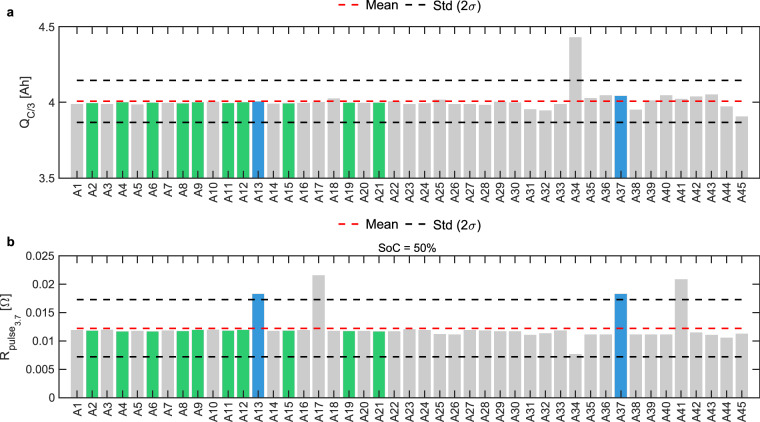
The screening protocol for Phase 1, as shown in Fig. 1b, consists of a preconditioning step followed by a constant-current (CC) C/3 discharge with three 1C pulses at 20%, 50%, and 80% SoC. Table 3 lists the steps of the screening protocol along with the exit conditions at each step. The capacity, Q_C/3, and pulse resistance, $R_{puls{e}_k}$, data obtained from the screening protocol is used to select 12 cells. Two selection criteria are applied in which the first criterion is used to select 10 out of 12 cells based on the proximity of cell capacity and cell resistance to their mean capacity, $\stackrel{\circledR }{Q}$, and mean pulse resistance, ${\stackrel{\circledR }{R}}_{pulse}$, of the batch of 45 cells. These cells were chosen to represent the pack’s average behavior and to exclude units affected by manufacturing defects. The second selection criterion selects the remaining 2 cells, deemed as outliers, based on the maximum distance from the mean capacity, $\stackrel{\circledR }{Q}$, and the mean pulse resistance, ${\stackrel{\circledR }{R}}_{pulse}$. With these two additional cells, it is possible to evaluate how compromised or atypical cells would perform within a module. Figure 3 shows Q_C/3 and $R_{puls{e}_k}$ for all 45 cells along with the mean and standard deviations. 10 cells, shown in green, are the minimum variation cells, and 2 cells, shown in blue, are the maximum variation cells. We limited the detailed characterization to 12 cells to keep in-line with the testing capability available and the testing time required to perform all the tests in the next phase.

Table 3.

Screening protocol at 25 °C.

Phase 1: Cell Screening
Step	Action	Exit Condition	Notes
1	1C CC charge	Vcell ≥ 4.2 V
2	CV hold at 4.2 V	Icell ≤ 50 mA
3	Rest	30 mins
4	1C CC discharge	Vcell ≤ 2.5 V
5	Rest	30 mins
6	1C CC charge	Vcell ≥ 4.2 V
7	CV hold at 4.2 V	Icell ≤ 50 mA
8	Rest	1 h
9	C/3 CC discharge	Vcell ≤ 4 V	Corresponds to an SoC of 80%
10	1C CC discharge	5 s
11	C/3 CC discharge	Vcell ≤ 3.7 V	Corresponds to an SoC of 50%
12	1C CC discharge	5 s
13	C/3 CC discharge	Vcell ≤ 3.4 V	Corresponds to an SoC of 20%
14	1C CC discharge	5 s
15	C/3 CC discharge	Vcell ≤ 2.5 V
16	Rest	1 h

Steps 1-8 are used for preconditioning the cell, and Steps 9-15 are used to perform a C/3 CC discharge on the cell while inducing 1C CC discharge pulses at 80%, 50%, and 20% SoC values.

Fig. 3.

Bar plots of C/3 capacity, Q_C/3, and pulse resistance, $R_{puls{e}_k}$, from cell screening protocol. (a) Q_C/3 for all cells with a $\stackrel{\circledR }{Q}$ of approximately 4 Ah. (b) $R_{puls{e}_k}$ for all cells at 50% SoC with a ${\stackrel{\circledR }{R}}_{pulse}$ of approximately 0.0125 Ω . Ten cells are selected that have minimum variation (green) from the mean capacity and mean resistance, and two cells are selected that have the maximum variation (blue) from the mean capacity and mean resistance. Due to minimal variation in resistance across SoC, $R_{puls{e}_k}$ values are only shown for 50% SoC.

In Phase 2, all tests are conducted at three different temperature set points of 5 °C, 25 °C, and 40 °C. The cells undergo CDT, HCGT, and EIS characterization tests as shown in Fig. 2a. The CDT protocol takes approximately 3.5 days to run, and it consists of CC discharge-CCCV charge at C/3, C/10, and C/20 C-rates as shown in Fig. 2b. Table 4 outlines the steps of the CDT protocol. The HCGT protocol, as shown in Fig. 2c, takes approximately 2 days to run and it consists of pulses at 0.5C, 1C, 2C, 3C, 6C, and 8C in both charge and discharge. To minimize accelerated cell degradation, the protocol is carefully designed to maintain the cell voltage between 2.5 V and 4.2 V by applying high C-rate pulses during discharge at high SoC and during charge at low SoC. The value of maximum C-rate pulse in HCGT is determined by conducting an analysis on a real battery pack, with representative specifications shown in Table 5, used in a high-performance racing car with N_parallel modules each containing N_series cells in series. The current request at the pack level is taken as I_pack = 2 ⋅ I_EM,peak, where I_EM,peak is the peak electric motor current, since there are two electric motors in the car. A high-performance racing vehicle frequently operates at peak power during rapid acceleration and braking events³³. The cell current and the maximum operating C-rate, based on the nominal cell capacity Q_cell is as follows:

$$I_{cell}=\frac{I_{pack}}{N_{parallel}}$$ 3

$$C_{rate}=\frac{I_{cell}}{Q_{cell}}=\frac{I_{pack}}{N_{parallel}\cdot Q_{cell}}$$ 4

Given the architecture of the battery pack, the electric motor specifications, and the cell characteristics, the resulting maximum operating cell C-rate is approximated to be 10C. To ensure safe cell operation in our experiments, we limit the maximum C-rate to be 8C in the HCGT protocol, in line with the manufacturer’s specifications. The pulses are executed at 95%, 85%, 75%, 65%, 50%, 35%, 25%, and 15% SoC values. At the start of each SoC, a C/5 GITT pulse is also induced. Details about the steps in the HCGT protocol are given in Table 6. Lastly, EIS is conducted at 20%, 50%, and 80% SoC within a frequency range of 10 mHz to 10 kHz at all three temperatures, and impedance data is collected at seven frequency points per decade totaling 42 points per EIS test. Due to issues with voltage limits at 5 °C and 25 °C set points, Galvanostatic EIS was performed at these two temperatures while Potentiostatic EIS was performed at 40 °C.

Table 4.

Constant discharging test (CDT) protocol.

Phase 2: CDT
Step	Action	Exit Condition	Notes
1	1C CC charge	Vcell ≥ 4.2 V
2	CV hold at 4.2 V	Icell ≤ 50 mA
3	Rest	1 h
4	1C CC discharge	Vcell ≤ 2.5 V
5	Rest	1 h
6	1C CC charge	Vcell ≥ 4.2 V
7	CV hold at 4.2 V	Icell ≤ 50 mA
8	Rest	1 h
9	C/3 CC discharge	Vcell ≤ 2.5 V
10	Rest	1 h
11	C/3 CC charge	Vcell ≥ 4.2 V
12	CV hold at 4.2 V	Icell ≤ 50 mA
13	Rest	1 h
14	C/10 CC discharge	Vcell ≤ 2.5 V
15	Rest	1 h
16	C/10 CC charge	Vcell ≥ 4.2 V
17	CV hold at 4.2 V	Icell ≤ 50 mA
18	Rest	1 h
19	C/20 CC discharge	Vcell ≤ 2.5 V
20	Rest	1 h
21	C/20 CC charge	Vcell ≥ 4.2 V
22	CV hold at 4.2 V	Icell ≤ 50 mA
23	Rest	1 h

Steps 1-8 are used for preconditioning the cell followed by CC discharge-CCCV charge at C/3, C/10, and C/20 rates.

Table 5.

Electric motor specifications³⁵.

Specification	Value
Peak power	230 kW
Continuous power	122 kW
Peak torque	450 Nm
Continuous torque	209 Nm
Peak current	550 Arms

Table 6.

High C-rate pulse with GITT (HCGT) protocol.

Phase 2: HCGT
Step	Action	Exit Condition	Notes
1	1C CC charge	Vcell ≥ 4.2 V
2	CV hold at 4.2 V	Icell ≤ 50 mA
3	Rest	1 h
4	1C CC discharge	Vcell ≤ 2.5 V
5	Rest	1 h
6	1C CC charge	Vcell ≥ 4.2 V
7	CV hold at 4.2 V	Icell ≤ 50 mA
8	Rest	1 h
9	C/5 CC discharge	15 mins / 30 mins	Performed for 15 mins only once to get to 95% SoC
10	Rest	1 h
11	C/2 CC discharge	12 s	Performed at all SoC values
12	Rest	40 s
13	C/2 CC charge	12 s	Performed at all SoC values
14	Rest	30 mins
15	1C CC discharge	12 s	Performed at all SoC values
16	Rest	40 s
17	1C CC charge	12 s	Performed at all SoC values
18	Rest	30 mins
19	2C CC discharge	12 s	Performed at all SoC values except at 15% SoC
20	Rest	40 s
21	2C CC charge	12 s	Performed at all SoC values except at 95% and 85% SoC
22	Rest	30 mins
23	3C CC discharge	12 s	Performed at all SoC values except at 25% and 15% SoC
24	Rest	40 s
25	3C CC charge	12 s	Performed at all SoC values except at 95%, 85% and 75% SoC
26	Rest	30 mins
27	6C CC discharge	12 s	Performed at all SoC values except at 35%, 25% and 15% SoC
28	Rest	40 s
29	6C CC charge	12 s	Performed at all SoC  < 50%
30	Rest	30 mins
31	8C CC discharge	12 s	Performed at all SoC ≥ 50%
32	Rest	40 s
33	8C CC charge	12 s	Performed at all SoC ≤ 50%
34	Go to Step 8	counter ≥ 7
35	Rest	30 mins
36	C/5 CC discharge	Vcell ≤ 2.5 V
37	Rest	1 h

Steps 1-8 are for preconditioning the cell followed by C/5 CC discharges for GITT at all SoC values. Pulses are induced at C/2, 1C, 2C, 3C, 6C, and 8C in both charge and discharge. Details about the SoC at which the pulse is performed are given under Notes. The sequence of pulses are repeated 7 times to go through the complete SoC range (as indicated in Step 34).

Data Records

The dataset is available on the Open Science Framework (OSF) at 10.17605/OSF.IO/9CEAV³⁴ consisting of a combination of comma-separated values (CSV) and Microsoft Excel Spreadsheet (XLSX) files. Phase 1 data at 25 °C consists of 45 CSV files corresponding to 45 cells in which the ‘time/s’, ‘Ecell/V’, and ‘I/mA’ columns represent test time, voltage, and current, respectively. Phase 2 data is divided into CDT, HCGT, and EIS folders, and each folder consists of three subfolders corresponding to 5 °C, 25 °C, and 40 °C temperatures set points. For the CDT and HCGT data files, the XLSX files consist of ‘Test_time(s)’, ‘Voltage(V)’, ‘Current(A)’ and ’Aux_Temperature(°C)’ columns representing the test time, voltage, current, and cell surface temperature, respectively. The difference in column names stems from the use of BioLogic cycler in Phase 1 and Arbin cycler in Phase 2. In the EIS folder, the XLSX files have impedance data in ‘Freq’, ‘Zmod’, and ‘Zphz’ columns representing the frequency, amplitude, and phase of the impedance, respectively. At each temperature, EIS data is also collected at 20%, 50%, and 80% SoC, which is indicated in the XLSX filename. For example, ’20240427_A9_EIS_SOC50_5degC_Channel_1.xlsx’ is an XLSX file with EIS data for cell A9 collected at 5 °C temperature set point and 50% SoC. The current convention in the provided data files is negative current for discharge and positive current for charge. The dataset folder structure is shown in Fig. 4.

Fig. 4.

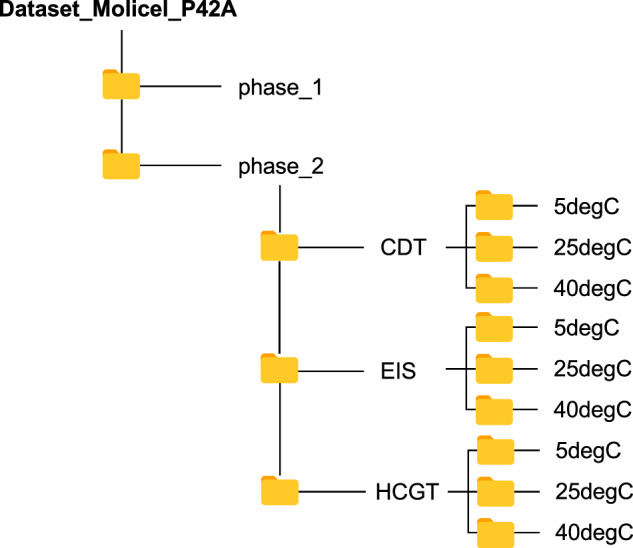
Dataset folder structure.

Technical Validation

Capacity, pulse resistance, and EIS resistance

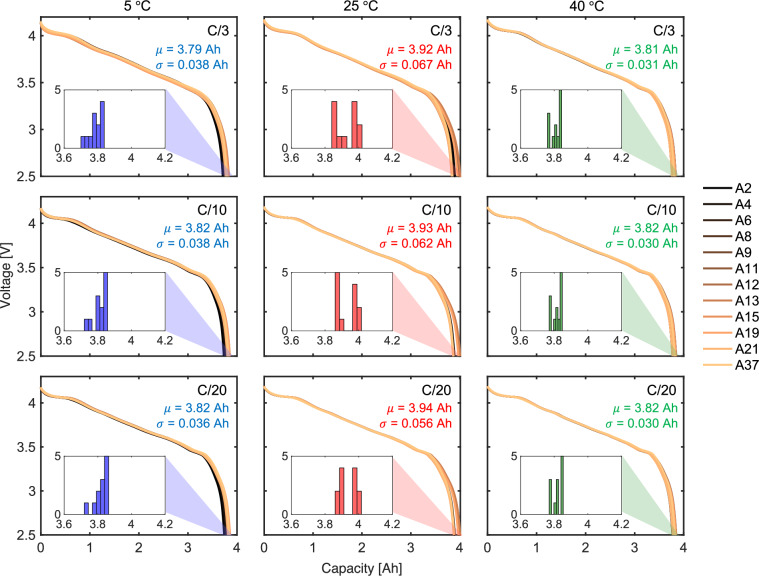
The CC discharge portions of the CDT protocol at different C-rates are used to extract the discharge capacity of the cells. Figure 5 shows the variation in capacity with temperature (increasing to the right) and C-rates (decreasing downwards). The variation of capacity across different C-rates for all three temperatures is linear until approximately 3.4 V (or 20% SoC). The variation below 3.4 V shows a divergence across cells as shown in the histogram in the inset. Cells at 25 °C, at all C-rates, show a relatively higher average capacity μ (μ and σ are used as generic notation in this figure to represent mean and standard deviation of capacity in each subplot) of approximately 3.9 Ah compared to the average capacity of the cells at 5 °C and 40 °C, which is around 3.8 Ah. Furthermore, the standard deviation σ is approximately 0.06 Ah for cells at 25 °C, which is larger than the σ of cells at the other two temperatures. Across all three temperatures, decrease in C-rate does not have a significant impact on the discharge capacity. This suggests that, for fresh cells, the influence of temperature is stronger on cell capacity than the C-rate.

Fig. 5.

Cell voltage as a function of capacity at different C-rates and temperatures. Discharge voltage from CDT protocol is plotted against capacity with histograms of the final cell capacity shown in the inset. Cells at 25 °C show a higher average capacity than cells at the other two temperatures with final cell capacities reaching 4 Ah. Cells discharged at 5 °C and 40 °C show a capacity of less than 3.9 Ah. At all operating conditions, the cell voltage shows a linear trend until approximately 3.4 V followed by a knee-point. Based on the standard deviation σ, the capacity deviation is the largest for cells at 25 °C at all C-rates.

For data collected using EIS, the respective plots in Fig. 6a show the impedance curves with respect to both temperature and SoC. The impedance curves at 5 °C set point at all SoCs show large semicircles and long tails that correspond to charge transfer and diffusion resistances, respectively. The impedance curves at 40 °C set point are the smallest with minimal variation due to SoC. Across different cells, the EIS plots show different impedances owing to the cell-to-cell variation present in this dataset. Figure 6b shows the distribution of the high-frequency resistance R₀ (which is obtained from the intersection of the EIS curve with the real impedance axis) at 20% SoC. The R₀ of all the cells is well distributed around the average with one outlier close to 0.012 Ω. Similarly, in Fig. 6c,d at 50% and 80% SoC, majority of the values are still around the average; however, for 80% SOC, the distribution is skewed towards the right. Additionally, during the 5 °C EIS experiments, the ambient temperature inside the Amerex thermal chamber did not consistently stay at the 5 °C set point. For approximately 20% of the tests, inadequate regulation led to recorded temperatures in the range of 8-10 °C. After the issue was addressed, temperature control was significantly improved, and the remaining EIS experiments were carried out with chamber temperatures stabilized between 5-7 °C.

Fig. 6.

EIS data at different temperatures and SoCs, and the distribution of high-frequency resistance R₀. (a) The EIS curves shrink as temperature increases. Across SOC, there is little variation except for EIS of cells at 5 °C which show significant variation. EIS data for A13 and A37 are shown in red boxes to indicate that they are the two outlier cells. (b) Histogram of R₀ at 20% SoC shows a large spread around the average R₀ for all temperatures. (c) Histogram of R₀ at 50% SoC with a high frequency of R₀ concentrated near the average. (d) Histogram of R₀ at 80% SoC with a right-skewed distribution.

For the HCGT protocol, the pulses at varying C-rates are used to calculate resistance values using Ohm’s law given by

$$R_{HCG{T}_{c,j,q}}:={|\frac{\mathrm{\Delta }V}{\mathrm{\Delta }I}|}_{c,j,q}={|\frac{V_{i+1}-V_i}{I_{i+1}-I_i}|}_{c,j,q}$$ 5

where c ∈ {C/2, 1C, 2C, 3C, 6C, 8C} denotes the C-rate of the pulse, j ∈ {ch, dis} denotes charge or discharge, q ∈ {15, 25, 35, 50, 65, 75, 85, 95}% is the SoC, and i is the index of time at which the pulse is applied. For all pulses, I_i = 0 since the pulse is applied from rest, and I_i+1 = Q_cell × c is dependent on the C-rate. Hence, $R_{HCG{T}_{c,j,q}}$ is the pulse resistance from HCGT at a C-rate c, applied in j at an SoC of q. The sampling time Δt between time index i+1 and i is 0.01 s. The comparison of $R_{HCG{T}_{c,j,q}}$ at different temperatures across SoC is shown in Fig. 7a,f for different C-rates. The box plots show the spread of $R_{HCG{T}_{c,j,q}}$ for all cells at different temperatures in charge and discharge as a function of SoC. It should be noted that for most of the cases, the charge and discharge box plots at one SoC value overlap. As the C-rate increases, the resistance decreases as indicated by the downward shift of the box plots. At 5 °C, there is a large spread in the resistance; however, as the temperature increases, the box plots become smaller indicating less variation in resistances across cells. It should be noted that the values of pulse resistances is sensitive to the inherent measurement accuracy of the testing equipment. Due to this, it is important to ensure that the same equipment or hardware should be used during such experiments to have comparable results for resistance.

Fig. 7.

Comparison of pulse resistance $R_{HCG{T}_{c,j,q}}$ at different temperatures and C-rates. (a–f), Box plots of $R_{HCG{T}_{c,j,q}}$ in charge and discharge at (a) C/2, (b) 1C, (c) 2C, (d) 3C, (e) 6C, and (f) 8C at 5 °C, 25 °C, and 40 °C as a function of SoC. 5 °C resistance box plots are consistently higher than at other two temperatures, but the spread and resistance value decreases as C-rate increases. For high and low SoC, the resistance box plots at all three temperatures are higher than the ones at middle SoC.

 Cell-to-cell variations

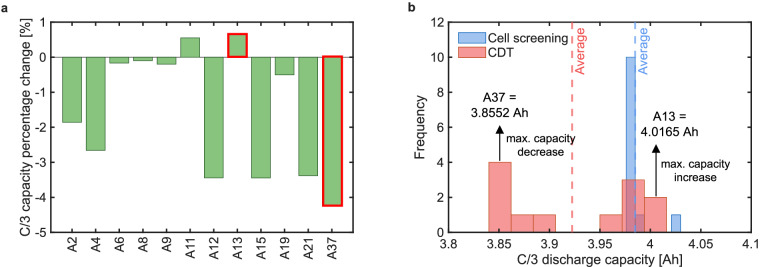
In this dataset, cells are only tested to collect characterization data and no cycling is conducted to age the cells. Nevertheless, in Fig. 8a, by comparing the C/3 capacity percentage change between CDT protocol compared to the cell screening protocol, we observe differences in capacity for various cells. As shown previously in Fig. 3a, all the 12 cells in Phase 2 had a C/3 capacity close to 4 Ah. Furthermore, during the selection of 12 cells, 10 cells were selected with minimum variation in both capacity and resistance as compared to $\stackrel{\circledR }{Q}$ and ${\stackrel{\circledR }{R}}_{pulse}$. From Fig. 8a, 6 out of 12 cells had a drop in capacity between 1.85–4.25% while cells A11 and A13 experienced an increase in capacity of 0.55–0.66%. Only cells A6, A8, and A9 had an infinitesimal change in capacity. The outlier cells A13 and A37 experienced the largest increase and decrease in capacity, respectively. The distribution of C/3 capacity from cell screening and CDT is shown in Fig. 8b. The capacity distribution for cell screening protocol shows cells to be concentrated around 3.98 Ah with two outliers on the right (A13 and A37).However, capacity collected from CDT shows a bimodal distribution even though the cells were initially selected to be similar based on Q_C/3 and R_pulse. The ends of the histogram contain the outlier cells. These observations highlight that despite ensuring similarity among cells in terms of capacity and resistance, and testing them using the same design of experiments, the cell capacities change stochastically without any consistent trend among them. These observations highlight the importance of accounting for parameter variations in battery models, and this dataset is useful for developing models that are stochastic and capture the parameter uncertainties, and their impact on the model output.

Fig. 8.

Comparison of C/3 capacity from cell screening protocol with C/3 capacity from CDT protocol. (a) Percentage change in CDT C/3 capacity with reference to the cell screening C/3 capacity shows 6 out of 12 cells had a capacity loss of up to 4.25% and 2 cells had a capacity gain of up to 0.66%. Notably, the maximum increase in capacity is observed for the outlier cell A13 and the maximum decrease in capacity is observed for the outlier cell A37, both of which are highlighted in red. (b) Histogram of C/3 capacity from cell screening shows a large peak around 3.98 Ah, but it transforms into a bimodal distribution for the CDT protocol. The bars on the ends of the CDT histogram consist of the outlier cells A13 (showing maximum capacity increase), and A37 (showing maximum capacity decrease). The C/3 percentage change in a and distribution transformation in b reflects the increase in cell-to-cell variations among the cells compared to their fresh cell state despite similar testing conditions.

Usage Notes

This dataset can be used with any programming language of choice e.g., Python, MATLAB, Julia, etc. All data files are provided in their raw format of CSV and XLSX as outputted by the battery cyclers to ensure that users can utilize the original data according to their desired applications. This dataset can be employed to perform stochastic modeling (e.g., empirical, physics-based, hybrid) of fresh lithium-ion batteries. The presence of cell-to-cell variation can also be leveraged to develop module-level battery models.

Author contributions

M.A.K., S.T., and L.X. collected the data. M.A.K., S.T., and L.T. processed the data and performed the analysis. M.A.K. and S.O. wrote the manuscript. M.A.K., S.T., and S.O. reviewed the manuscript. A.T. provided resources, and funding. S.O. conceived the experiments, and provided resources, funding and supervision.

Code availability

The custom scripts used to generate the plots in the paper are provided in the data repository along with the dataset.

Competing interests

L.T. is affiliated with Politecnico di Torino. He was affiliated with Stanford University at the time this research was conducted.