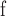Abstract
The exploration of brain networks has reached an important milestone as relatively large and reliable information has been gathered for connectomes of different species1,2. Analyses of connectome data sets reveal that the structural length follows the exponential rule3, the distributions of in- and out-node strengths4,5 follow heavy-tailed lognormal statistics, while the functional network properties exhibit powerlaw tails6, suggesting that the brain operates close to a critical point where computational capabilities7 and sensitivity to stimulus is optimal8. Because these universal network features emerge from bottom-up (self-)organization, one can pose the question of whether they can be modeled via a common framework, particularly through the lens of criticality of statistical physical systems. Here, we simultaneously reproduce the powerlaw statistics of connectome edge weights and the lognormal distributions of node strengths from an avalanche-type model with learning that operates on baseline networks that mimic the neuronal circuitry. We observe that the avalanches created by a sandpile-like model9 on simulated neurons connected by a hierarchical modular network (HMN)10,11 produce robust powerlaw avalanche size distributions with critical exponents of 3/2 characteristic of neuronal systems12. Introducing Hebbian learning, wherein neurons that ‘fire together, wire together,’ recovers the powerlaw distribution of edge weights and the lognormal distributions of node degrees, comparable to those obtained from connectome data5. Our results strengthen the notion of a critical brain, one whose local interactions drive connectivity and learning without a need for external intervention and precise tuning13.
Subject terms: Biophysics, Physics
Introduction
The association between form and function in the complex neuronal circuitry continues to be an open and exciting problem, one that is now being pursued with the aid of empirical data on actual connectome networks1–13. It has been well-established that many aspects of neural dynamics produce heavy-tailed statistical distributions. Previous works report log-normal (LN) distributions in the firing rates as well as in the structural connection strengths and propose generative mechanisms for their occurrence14–16. On the other hand, other works observe power law (PL) distributions in brain activity, oftentimes viewed as a consequence of brain criticality12,17,18. Recently, these heavy-tailed statistics have also been reported for the physical structure of the connectome19–21. These works do not assume the backward relation of function to structure, involving the brain criticality hypothesis, but rely on optimization arguments. For example, heavy-tailed regimes in the edge weight and degree distributions of various animal connectomes have been fitted by PL at the tails; their occurrence is explained using a simple growth model based on mean-field approximations with preferential mechanisms of synaptic rearrangements21. Other works report global weight distributions of the human white matter22 and neuronal-level fruit fly brain23 that are found to exhibit PL tails. A more detailed network analysis, involving more full or partial brain networks5 has strengthened this PL tail observation for global weights, but provided a distinction with node strength (degree) distributions, which are found to be best fitted by LN functions.
The heavy-tailed statistical distribution of the global weights and strength (degree) is deemed to be the consequence of the neuron dynamics via the Hebbian learning of long-term synaptic (LTS) mechanism14,16,21. In a previous work5, a possible scaling argument has been proposed to describe the observed connectome weight PL distribution via the “firing together and wiring together” mechanism. In this work, however, we note that the existence of robust PL statistics raises the possibility of analyzing these systems from the lens of statistical physics, particularly through a criticality framework. In particular, the universally observed exponent 3 decay can be derived by a relation to the mean-field criticality of simple models of statistical physics. Viewing the connectome as a consequence of critical behavior is consistent with the brain criticality hypothesis, which is deemed to be at work in the dynamical processes in the brain12.
Therefore, as a plausible framework for modeling the observed universal statistics, we provide here a critical system, a self-organized one, which has extensively been used as a toy model to support brain criticality. The brain criticality hypothesis6,24 has been observed in experiments12,25 and is supported by many theoretical models26. From a discrete modeling perspective, critical behavior is often associated with the avalanche-like dynamics characteristic of self-organized criticality (SOC)9,27,28, the paradigm model of which is the sandpile. In a sandpile model, local relaxations lead to cascades of nearest-neighbor redistributions. Previous models replicated empirical time signatures of neuronal activity using nearest-neighbor avalanches similar to the sandpile operating in lattice and small-world networks29.
Many of the previous approaches, however, operate on lattice geometries that are too simplified to mimic the aforementioned complexity of neural circuitry30. For one, neural connections are inherently directed and weighted, precluding the use of undirected regular networks commonly used in sandpile model implementations. More importantly, brain networks are known to exhibit hierarchical structures with modular effective functioning units31. Kaiser and Hilgetag10 utilized this fact to create hierarchical modular networks (HMNs) with small-world characteristics embedded in two-dimensional substrates that represent brain connectivity on a large/mesoscopic scale, where the nodes represent cortical columns rather than individual neurons. They used this model to investigate topological effects on limited-sustained activity. Ódor et. al.11 used a variant of this and showed that Griffiths Phases (GP)32 may emerge by a simple threshold model dynamics. The fact that pure topological inhomogeneity may result in GP in finite-dimensional networks33, or in Griffiths effects34 in infinite dimensions, was confirmed by brain experiments25. GP is suggested to be a good candidate mechanism for explaining working memory in the brain35. Additionally, GP provides an alternative mechanistic explanation for dynamical critical-like behavior observed without fine-tuning, consistent with the criticality hypothesis11,22,36,37.
In addition to the use of more realistic network architectures, the models should still incorporate learning, the strengthening of network links through correlated neuronal activity and the corresponding weakening of unused pathways. Learning in critical state brain models was patterned after neuroscience modeling of empirical connectomes38. However, in these early approaches, the role of random weakening mechanisms in learning and system criticality has not yet been studied in detail. Recent results on connectome database analysis5 and magnetoencephalography and tractography suggest that this is the driving mechanism for the complexity of real connectomes39.
To address these research gaps, we revisit here the avalanche perspective on cortical dynamics and introduce refinements to the sandpile-based model of neural criticality. First, we use graph-dimension-controllable HMN structures for implementation, which are denser than the commonly used random networks in literature and are deemed to be more representative of the actual structure and dynamics of the brain11. Secondly, while keeping the avalanche dynamics similar to the sandpile rules, we introduce different rates of activation and inhibition mechanisms in the Hebbian learning. In particular, the rate of new link creation is deemed to be instantaneous for all sites reaching criticality over a single avalanche cycle; on the other hand, random weakenings of unused pathways are gradual, following an exponential decay over time. By modifying the proposed model’s update rules to incorporate Hebbian learning, we show by extensive simulations that it can generate global PL weight distributions and LN ones for the degrees and node strengths. We provide finite-size scaling collapses and provide numerical evidence for this. We also investigate the effect of initial conditions by running simulations on HMN networks with different graph dimensions. Finally, to test the validity of the model, we provide comparisons with the actual edge weight distributions found in empirical connectome data. Our work provides a very important step towards understanding SOC in complex-adaptive systems40.
Results
In the following, we present the results of extensive simulations that run the locally conservative sandpile model with Hebbian learning on hierarchical modular networks (HMNs) where each node represents a neuron. For the baseline HMNs used, the number of nodes  , are varied, with
, are varied, with  . The edges are weighted and directed, simulating synaptic connectivity. The average edge count per node,
. The edges are weighted and directed, simulating synaptic connectivity. The average edge count per node,  , is the total number of edges
, is the total number of edges  of the initial HMN divided by the number of nodes N. We tested for
of the initial HMN divided by the number of nodes N. We tested for 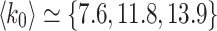 , and most of the results presented are for
, and most of the results presented are for  [see Figs. S2 and S3 in Supplementary Information for details]. Finally, we also looked at the effect of long-range connectivity: Starting from a single connected two-dimensional base lattice, long-range links are added among levels of the HMN whose probabilities of connectivity decay with Euclidean distance via
[see Figs. S2 and S3 in Supplementary Information for details]. Finally, we also looked at the effect of long-range connectivity: Starting from a single connected two-dimensional base lattice, long-range links are added among levels of the HMN whose probabilities of connectivity decay with Euclidean distance via  ; here, we considered cases where
; here, we considered cases where  and
and  [see “Hierarchical modular networks (HMNs)”]. Dynamical activity is then introduced into the baseline HMN through a locally conservative sandpile model (“Sandpile model implementation”), while network evolution is imposed through correlated link creation and random link weakening/removal (“Hebbian learning”). The state of the system is analyzed at the instant when the network achieves maximal connectivity [see Fig. S1, Supplementary Information]. Analysis of the resulting avalanches and the network connectivity reveal strong indications of critical behavior, reminiscent of those found in actual connectomes.
[see “Hierarchical modular networks (HMNs)”]. Dynamical activity is then introduced into the baseline HMN through a locally conservative sandpile model (“Sandpile model implementation”), while network evolution is imposed through correlated link creation and random link weakening/removal (“Hebbian learning”). The state of the system is analyzed at the instant when the network achieves maximal connectivity [see Fig. S1, Supplementary Information]. Analysis of the resulting avalanches and the network connectivity reveal strong indications of critical behavior, reminiscent of those found in actual connectomes.
Avalanche size distributions
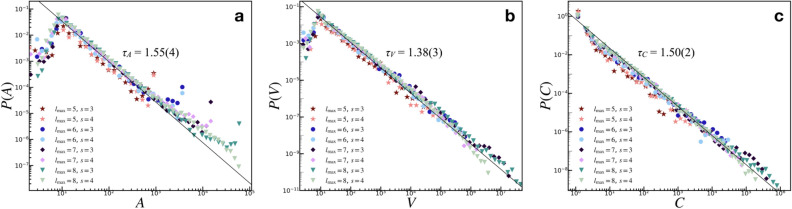
The first indication of critical behavior is the emergence of PL distributions of characteristic avalanche sizes similar to those obtained for the non-adaptive SOC models like the original sandpile model9 and other models with static rules in undirected lattice geometries41,42. For the specific case of neuronal criticality, the PL exponents of 3/2 obtained from experiments13 are recovered “for the high-dimensional, directed mean-field conserved sandpile universality class”43,44 with the upper critical dimension 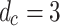 . Here, we report robust PL distributions that span several orders of magnitude for various measures of avalanche sizes, one of which manifests the 3/2 exponent of neuronal criticality [see also Fig. S2, Supplementary Information for comparable results for smaller initial HMN].
. Here, we report robust PL distributions that span several orders of magnitude for various measures of avalanche sizes, one of which manifests the 3/2 exponent of neuronal criticality [see also Fig. S2, Supplementary Information for comparable results for smaller initial HMN].
In the implementation used here, individual sites contain continuous-valued “grains”, which, for simplicity, reach a threshold value at unity. Continuous driving of the grid at random node sites results in avalanches when the threshold value is reached or exceeded at random node locations. We measure the extent of the avalanche in the network of nodes using three metrics. One is the simple count of the nodes that changed state during an avalanche event; in keeping with the literature on grid implementations, we call it the area, A. Another is the count of the actual number of individual toppling and receiving events, in which nodes can be counted more than once based on their repeated participation in the entire avalanche; we call this the activation, V, consistent with other previous works45. Finally, we also investigate the toppled sites count C, which is the number of sites that exceeded their threshold states and toppled, redistributing the “grains” to their direct outward connections. This metric is inspired by the actual measurements done in neural connections, which only account for the total number of active nodes within an avalanche including multiple activations of the same nodes46,47. The A, V, and C measures of avalanche magnitudes exhibit PL tails, indicating that they are just different characterizations of the same critical behavior operating within the network [see Fig. S4, Supplementary Information for details].
Interestingly, despite the highly dynamic nature of the rules, specifically those that govern the network evolution, we found very robust PL tails for areas, P(A), activations, P(V), and toppled sites, P(C). Figure 1a shows the tails of the area distributions that follow a linear trend on a double logarithmic scale: starting from the modal value  , the tails obey a PL distribution
, the tails obey a PL distribution 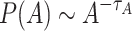 , where
, where 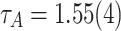 . It should be noted that the tails of P(A) show spikes due to the repeated occurrences of avalanches of size
. It should be noted that the tails of P(A) show spikes due to the repeated occurrences of avalanches of size  (i.e. spreading to all nodes), especially for many iterations (an iteration refers to one instance of dropping a grain of sand), when the network becomes very densely connected. This highlights the limitations of the measure A in capturing the extent of the activity in the network: the network of nodes can manifest spatiotemporal activities several orders of magnitude greater than the node count N, which A cannot measure.
(i.e. spreading to all nodes), especially for many iterations (an iteration refers to one instance of dropping a grain of sand), when the network becomes very densely connected. This highlights the limitations of the measure A in capturing the extent of the activity in the network: the network of nodes can manifest spatiotemporal activities several orders of magnitude greater than the node count N, which A cannot measure.
Figure 1.
Avalanche size distributions. (a) The area distributions show powerlaw tails that follow  , where
, where 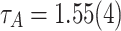 . The tails of the distribution show increased occurrences of
. The tails of the distribution show increased occurrences of 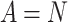 , making the tails significantly deviate from the initial decaying trend. (b) The activation distributions follow
, making the tails significantly deviate from the initial decaying trend. (b) The activation distributions follow 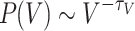 , where
, where 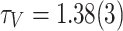 . (c) The toppled sites count distributions follow
. (c) The toppled sites count distributions follow 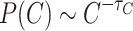 , where
, where  consistent with the mean field universality scaling and electrode experimental results of the human brain12. Initial HMN graph parameters are displayed by the legends.
consistent with the mean field universality scaling and electrode experimental results of the human brain12. Initial HMN graph parameters are displayed by the legends.
As such, the dynamical features of the network are better captured by the activation V, which is the spatiotemporal measure of each node’s participation (both as a receiving or a toppling site) in the avalanche. The distribution of site activations, Fig. 1b, follows PL tails  , with
, with 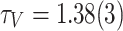 , starting from the mode
, starting from the mode  . Unlike the area A, the activation V extends beyond the physical limit of the number of nodes in the network, capturing individual toppling and redistribution of “grains” within the network. It is worth noting that the tails of the P(V) distributions show a tapering at the tails, indicating the expected finite-size limitations on the activity of the network. The decrease in the powerlaw slope for P(V) can be explained by the increased incidence of larger avalanches caused by the reactivations of ancestor nodes12.
. Unlike the area A, the activation V extends beyond the physical limit of the number of nodes in the network, capturing individual toppling and redistribution of “grains” within the network. It is worth noting that the tails of the P(V) distributions show a tapering at the tails, indicating the expected finite-size limitations on the activity of the network. The decrease in the powerlaw slope for P(V) can be explained by the increased incidence of larger avalanches caused by the reactivations of ancestor nodes12.
Finally, the distribution of toppled site counts, Fig. 1c, shows PL tails that obey  , with
, with  . By counting only the sites that toppled during an avalanche event, regardless of whether they are initially directly connected or not, the model recovers similar statistics as those obtained from the local field potential measurements of electrodes on brain slices, replicating the well-known critical PL exponents of 3/2 for the neuronal avalanches as reported by Beggs and Plenz12 and in other brain experiments48. Also, this avalanche universality occurs in directed models of firms44 among others.
. By counting only the sites that toppled during an avalanche event, regardless of whether they are initially directly connected or not, the model recovers similar statistics as those obtained from the local field potential measurements of electrodes on brain slices, replicating the well-known critical PL exponents of 3/2 for the neuronal avalanches as reported by Beggs and Plenz12 and in other brain experiments48. Also, this avalanche universality occurs in directed models of firms44 among others.
It is important to note that the obtained PL distributions are not sensitive to the sizes of the original HMN,  , for the broad range of
, for the broad range of  considered. Furthermore, there is very little effect of the other control parameters of the HMN. This suggests a mean-field-type of critical behavior, despite the variability of the network architecture. An explanation for this could be related to the rapid long-range interactions generated by the avalanches. We will show further evidence of scaling behavior via finite-size scaling.
considered. Furthermore, there is very little effect of the other control parameters of the HMN. This suggests a mean-field-type of critical behavior, despite the variability of the network architecture. An explanation for this could be related to the rapid long-range interactions generated by the avalanches. We will show further evidence of scaling behavior via finite-size scaling.
Edge weight distributions
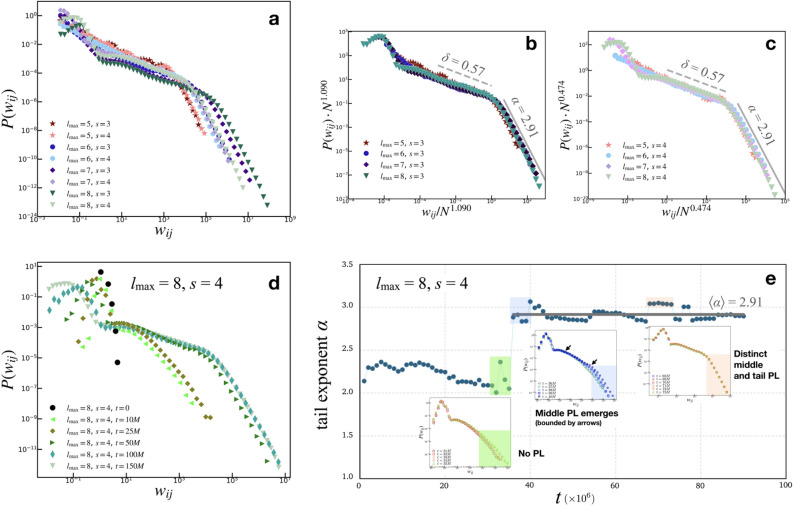
Unlike previous sandpile-based implementations that preserve the structure of the grid, the instantaneous link creation during avalanche events and the gradual decay of randomly selected links during stasis times (i.e. time instances with no avalanche events) produces a dynamic network that is deemed to better represent the interacting functional brain units. The state of the network at its peak connectivity, that is, when it has reached the maximum number of links, can be described by the distribution of edge weights  , displayed in Fig. 2.
, displayed in Fig. 2.
Figure 2.
Global edge weight distributions. [Top panels: Results for various  and s values for
and s values for  ; Bottom panels: Time evolution of the representative case
; Bottom panels: Time evolution of the representative case 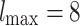 ,
, 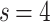 ,
,  .] (a) The
.] (a) The 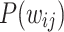 show two PL regimes that are better observed upon finite-size scaling: (b) the
show two PL regimes that are better observed upon finite-size scaling: (b) the 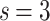 distributions collapse into a universal curve upon rescaling by
distributions collapse into a universal curve upon rescaling by 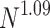 ; and (c) for the
; and (c) for the 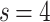 distributions,
distributions, 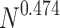 . For both (b) and (c), the rescaled curves show an intermediate regime with a gentle PL trend
. For both (b) and (c), the rescaled curves show an intermediate regime with a gentle PL trend 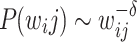 , where
, where  , and a tail with steeper PL,
, and a tail with steeper PL,  , where
, where 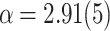 . (d) For the case of
. (d) For the case of 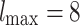 ,
, 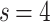 , representative snapshots of the network for various instances of time show the gradual evolution of the
, representative snapshots of the network for various instances of time show the gradual evolution of the 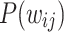 , particularly the evolution of the PL regimes. (e) A detailed examination of the first 90 million iterations show the strong approach towards steeper tails
, particularly the evolution of the PL regimes. (e) A detailed examination of the first 90 million iterations show the strong approach towards steeper tails  , with
, with 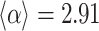 ; the PL trend with this exponent is shown by the gray guides to the eye in (b) and (c).
; the PL trend with this exponent is shown by the gray guides to the eye in (b) and (c).
For a sufficiently large number of iterations and before the network becomes fragmented, Fig. 2a shows the general trends in the distribution of  for
for 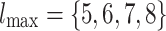 and
and  , of the original HMNs with an average edge count per node
, of the original HMNs with an average edge count per node  . The regime of the smallest edge weights, appearing as unimodal bumps for the smallest
. The regime of the smallest edge weights, appearing as unimodal bumps for the smallest 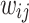 , is deemed to be an artifact of the original HMN construction. In particular, it is worth noting that these peaks are close to the tolerance value
, is deemed to be an artifact of the original HMN construction. In particular, it is worth noting that these peaks are close to the tolerance value 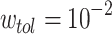 , which is the threshold for pruning links out of the network. These features of the distributions are changed, if not completely lost, upon the temporal evolution of the network. What follows is a “middle” region, which, especially for the largest baseline HMNs, shows a slow PL decay. Above a certain knee value of
, which is the threshold for pruning links out of the network. These features of the distributions are changed, if not completely lost, upon the temporal evolution of the network. What follows is a “middle” region, which, especially for the largest baseline HMNs, shows a slow PL decay. Above a certain knee value of  , the distributions cross over to steep PL tails, with a common decay trend. This regime, unlike those for smaller
, the distributions cross over to steep PL tails, with a common decay trend. This regime, unlike those for smaller  , is robust and continue to manifest for longer iteration times.
, is robust and continue to manifest for longer iteration times.
In Fig. 2b,c, the results for 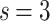 and
and 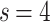 , respectively, show data collapses upon finite-size scaling (FSS). In Fig. 2b, the
, respectively, show data collapses upon finite-size scaling (FSS). In Fig. 2b, the 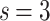 data shows data collapse upon rescaling by
data shows data collapse upon rescaling by 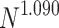 ; on the other hand, in Fig. 2c, the
; on the other hand, in Fig. 2c, the 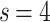 data shows the same collapse upon rescaling by
data shows the same collapse upon rescaling by  . The different FSS exponents suggest that the
. The different FSS exponents suggest that the  and
and 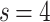 weight distributions belong to different finite-size scalings. Note, that there is no indication for different avalanche size scaling behaviors in these cases. The case of
weight distributions belong to different finite-size scalings. Note, that there is no indication for different avalanche size scaling behaviors in these cases. The case of 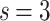 in Fig. 2b shows FSS with
in Fig. 2b shows FSS with 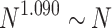 , corresponding to
, corresponding to 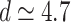 [see dimensions in Fig. 7b under “Hierarchical modular networks (HMNs)”]; on the other hand, in Fig. 2c, the
[see dimensions in Fig. 7b under “Hierarchical modular networks (HMNs)”]; on the other hand, in Fig. 2c, the 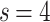 case with FSS factor of
case with FSS factor of  is related to
is related to  topological dimension version of the graph.
topological dimension version of the graph.
Figure 7.
HMN construction and characterization. (a) Illustrating a two-dimensional HMN (HMN2d) with  . Nodes at the bottom level
. Nodes at the bottom level  are fully connected. Four bottom modules are grouped on the next hierarchical level to form one upper-level module and so on.
are fully connected. Four bottom modules are grouped on the next hierarchical level to form one upper-level module and so on. 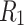 (solid lines) denotes the randomly chosen connections among the bottom level;
(solid lines) denotes the randomly chosen connections among the bottom level; 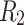 (dashed lines) and
(dashed lines) and 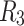 (dotted lines) denote the connection to the second level, and third level respectively. (b) Characterizing HMN: Average number of shortest path, chemical distances between nodes of
(dotted lines) denote the connection to the second level, and third level respectively. (b) Characterizing HMN: Average number of shortest path, chemical distances between nodes of 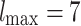 level HMNs, for
level HMNs, for  ,
,  and
and 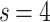 ,
,  before [hollow symbols] and after [crosses, plus signs] the learning. Lines show powerlaw fits before saturation of the curves, describing the topological (graph) dimensions, defined by Eq. (3), similarly as in11.
before [hollow symbols] and after [crosses, plus signs] the learning. Lines show powerlaw fits before saturation of the curves, describing the topological (graph) dimensions, defined by Eq. (3), similarly as in11.
In both cases, however, the strong data collapse further highlight the gentle middle PL and the sharp tail PL. Figure 2b,c shows the best-fit PL exponents for the middle regime [dashed gray lines] and the tails [thick gray lines]. The gentle PL decay in the middle regions follows  , with
, with  . The tails collapse to a PL
. The tails collapse to a PL  , characterized by
, characterized by  . To further illustrate the emergence of these regimes, Fig. 2d shows the representative case for one of the largest baseline HMNs considered, for
. To further illustrate the emergence of these regimes, Fig. 2d shows the representative case for one of the largest baseline HMNs considered, for  ,
, 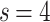 , and
, and  , tracked for various time snapshots. From the original HMN with an exponential distribution of edge weights, the
, tracked for various time snapshots. From the original HMN with an exponential distribution of edge weights, the 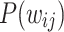 gradually evolve to produce the clear distinction between the two PL regimes. In particular, from around
gradually evolve to produce the clear distinction between the two PL regimes. In particular, from around  iterations, the middle and tail PL regions of
iterations, the middle and tail PL regions of 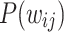 begin to overlap, until the point of maximum connectivity at around
begin to overlap, until the point of maximum connectivity at around 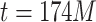 ; in Fig. 2d, the case of
; in Fig. 2d, the case of 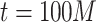 and
and 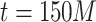 are shown.
are shown.
The distinction between the middle and tail regimes of 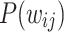 is further investigated by statistical tests for PL behavior. Using the largest network
is further investigated by statistical tests for PL behavior. Using the largest network  for
for  , the snapshots of the network are obtained for every 1 million iterations and their corresponding
, the snapshots of the network are obtained for every 1 million iterations and their corresponding 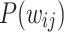 are obtained. For each of these time snapshots, the last two orders of magnitude of the set of
are obtained. For each of these time snapshots, the last two orders of magnitude of the set of 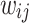 are taken and tested for PL trends using the powerlaw Python package49 that is based on the Kolmogorov-Smirnoff statistics50. The use of the last two orders of magnitude of the data makes it a good approximation for the tail regions. The algorithm tests for
are taken and tested for PL trends using the powerlaw Python package49 that is based on the Kolmogorov-Smirnoff statistics50. The use of the last two orders of magnitude of the data makes it a good approximation for the tail regions. The algorithm tests for 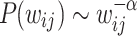 , where
, where 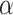 is computed along with the minimum value of
is computed along with the minimum value of 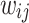 that best recovers the PL fit. In Fig. 2e, the computed
that best recovers the PL fit. In Fig. 2e, the computed  of the tails are plotted with the time snapshot t, showing a sharp transition at around 35 million iterations. The insets of Fig. 2e show the actual
of the tails are plotted with the time snapshot t, showing a sharp transition at around 35 million iterations. The insets of Fig. 2e show the actual  plots, along with the chosen regions of PL from the algorithm.
plots, along with the chosen regions of PL from the algorithm.
For iteration times  , the distributions
, the distributions  exhibit tails showing no distinction between the two PL regimes and are thus qualitatively not best represented by PL. In the green shaded region of Fig. 2e, the insets show the relative range of values chosen by the powerlaw algorithm to be the best approximation of the PL regimes. The lack of “true” PL regimes results in low computed
exhibit tails showing no distinction between the two PL regimes and are thus qualitatively not best represented by PL. In the green shaded region of Fig. 2e, the insets show the relative range of values chosen by the powerlaw algorithm to be the best approximation of the PL regimes. The lack of “true” PL regimes results in low computed 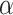 values for these runs [see also Fig. S3, Supplementary Information, showing no PL regimes for lower edge density initial HMNs]. However, shortly after the
values for these runs [see also Fig. S3, Supplementary Information, showing no PL regimes for lower edge density initial HMNs]. However, shortly after the 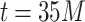 iterations, the middle region with a gentle PL slope begins to emerge. At this point in the learning, the short ranged correlations of the base lattice build up, resulting in the middle PL and a crossover to the tail PL scaling behavior. As such, the powerlaw algorithm determined the “true” tails, resulting in the jump to the larger
iterations, the middle region with a gentle PL slope begins to emerge. At this point in the learning, the short ranged correlations of the base lattice build up, resulting in the middle PL and a crossover to the tail PL scaling behavior. As such, the powerlaw algorithm determined the “true” tails, resulting in the jump to the larger 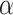 values from this point onwards. The blue shaded region and the corresponding insets show the range of PL considered by the algorithm, which corresponds to the region beyond the knee. Finally, for the orange shaded region in Fig. 2e, the tails (and, in turn, the middle region) are now well-defined, resulting in the continuous recovery of large
values from this point onwards. The blue shaded region and the corresponding insets show the range of PL considered by the algorithm, which corresponds to the region beyond the knee. Finally, for the orange shaded region in Fig. 2e, the tails (and, in turn, the middle region) are now well-defined, resulting in the continuous recovery of large  . These regimes are the result of the gradual emergence of long-range correlated weight structured networks via learning. From this point onwards, the tail PLs show
. These regimes are the result of the gradual emergence of long-range correlated weight structured networks via learning. From this point onwards, the tail PLs show 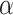 values close to 3; the average of the runs from
values close to 3; the average of the runs from 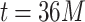 to
to 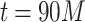 is
is 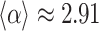 , which is also shown as the guides to the eye for Fig. 2b,c.
, which is also shown as the guides to the eye for Fig. 2b,c.
Extensive and long-time simulations point to the strong convergence towards the 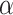 PLs at the tails, a fact that is not observed for similar approaches that utilized non-HMN initial network configurations [see Fig. S5, Supplementary Information]. Interestingly, the values of
PLs at the tails, a fact that is not observed for similar approaches that utilized non-HMN initial network configurations [see Fig. S5, Supplementary Information]. Interestingly, the values of 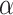 obtained by the model are close to the PL tails of the empirical connectome data. The top panels of Fig. 3 present comparisons of the PL tails edge weight distributions of the model (normalized with their corresponding mean values) with those measured from connectome datasets of fruit fly [larva, Fig. 3a; and adult, Fig. 3b] and humans [H01 1 mm
obtained by the model are close to the PL tails of the empirical connectome data. The top panels of Fig. 3 present comparisons of the PL tails edge weight distributions of the model (normalized with their corresponding mean values) with those measured from connectome datasets of fruit fly [larva, Fig. 3a; and adult, Fig. 3b] and humans [H01 1 mm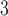 , Fig. 3c; KKI-18, Fig. 3d; and KKI-113, Fig. 3e], also rescaled with their respective average values (see “Connectome datasets” for details). The model-generated distributions, regardless of network size and long-range connectivity, show remarkable correspondence with the empirical data, regardless of brain complexity.
, Fig. 3c; KKI-18, Fig. 3d; and KKI-113, Fig. 3e], also rescaled with their respective average values (see “Connectome datasets” for details). The model-generated distributions, regardless of network size and long-range connectivity, show remarkable correspondence with the empirical data, regardless of brain complexity.
Figure 3.
Edge weight distributions: Model comparisons with data. The model captures the distribution of edge weights from connectome data (arranged here in increasing levels of complexity): (a) fruit fly (larva) (b) fruit fly (adult) (c) H01 Human 1 mm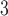 (d) human KKI-18 and (e) human KKI-113.
(d) human KKI-18 and (e) human KKI-113.
Node degree and strength distributions
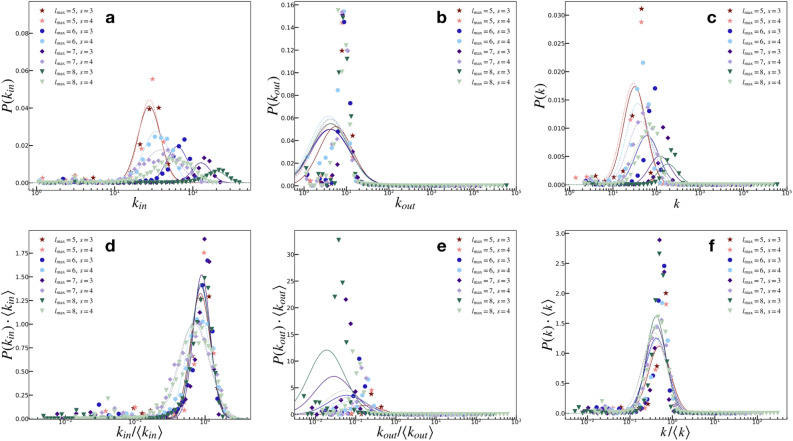
Figure 4 shows the distribution of the in-degree 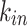 , out-degree
, out-degree 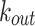 , and total
, and total  degree for the case of maximum network connectivity [see Supplementary Information: Network Evolution for details]. In Fig. 4a–c, the node strength values are best fitted with lognormal (LN) distributions, here shown by the lines corresponding to the mean and standard deviation of the simulation results, with different shape and scale parameters resulting from different network sizes. A simple rescaling by the mean, however, shows a strong data collapse into a common lognormal trend, as shown in Fig. 4d–f.
degree for the case of maximum network connectivity [see Supplementary Information: Network Evolution for details]. In Fig. 4a–c, the node strength values are best fitted with lognormal (LN) distributions, here shown by the lines corresponding to the mean and standard deviation of the simulation results, with different shape and scale parameters resulting from different network sizes. A simple rescaling by the mean, however, shows a strong data collapse into a common lognormal trend, as shown in Fig. 4d–f.
Figure 4.
Node degree distributions [colored symbols are model results; LN fits are lines: solid lines for 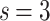 , dashed lines for
, dashed lines for  ]. The (a)
]. The (a)  , (b)
, (b)  , and (c) P(k) are best fitted with lognormals, with characteristic (modal) values related to the original network size. (d–f) Rescaling with the mean results in a collapse into a common lognormal trend.
, and (c) P(k) are best fitted with lognormals, with characteristic (modal) values related to the original network size. (d–f) Rescaling with the mean results in a collapse into a common lognormal trend.
The recovery of LN node strength distributions strongly agrees with recent empirical observations on actual connectome data5. While other authors empirically describe only the tails of the node strength distributions, approximating them as decaying PLs21, there are good reasons to believe that the LN distributions obtained by the model is also the one manifested by real neuronal networks. In particular, the intrinsic restrictions imposed by basic spatial and metabolic constraints31 on the density and number of connections that may be maintained at any given node may make it seem difficult for geographically embedded networks to demonstrate a pure scale-free activity, resulting in LN distributions with a characteristic mode and decaying trends at the upper tail.
Additionally, the local nature of the node degree that results in LN distributions stands in sharp contrast with the global distributions of edge weights, which follow PL trends. For this model, these statistical manifestations are the result of Hebbian learning that is strongly predicated upon the critical avalanche mechanisms. Larger avalanches produce more unstable sites over broader swaths of the network, producing more new outward directed links from the origin of the avalanche event. Furthermore, the strength of these new connections is proportional to the avalanche size (specifically, the activation), making these new connections less prone to the random pruning mechanisms. These aggressive mechanisms of strong link creations produce the broad tails of the strength distributions, particularly the  . It is therefore unsurprising that the presence of a characteristic modal values followed by heavy tails in the distributions of node strengths strongly aligns with previous works that show lognormal distributions in connectome data5.
. It is therefore unsurprising that the presence of a characteristic modal values followed by heavy tails in the distributions of node strengths strongly aligns with previous works that show lognormal distributions in connectome data5.
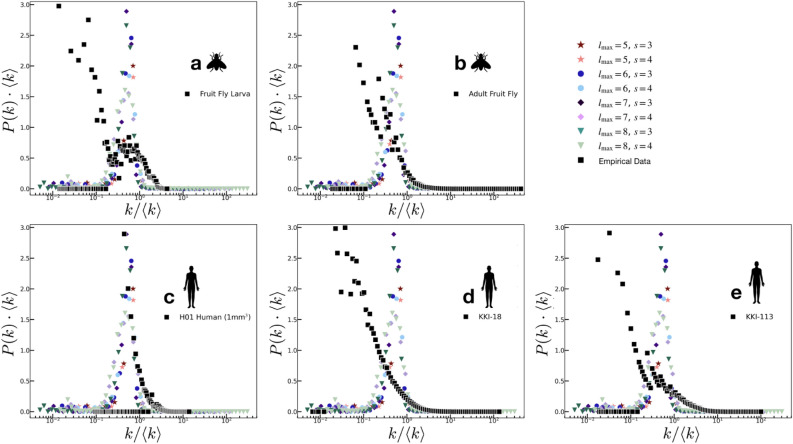
In Fig. 5, we present a comparison among the normalized model results with the same empirical connectome data sets presented in Fig. 3. The distributions of the data [black squares] used smaller bin widths (in logarithmic scale) to highlight some features that are otherwise lost (smoothened) with larger bin widths. The strict unimodal distributions of the model replicates some features of the simpler connectome strength distributions, particularly those of the fruit fly larva (Fig. 5a), adult fruit fly (Fig. 5b), and the H01 human 1 mm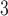 (Fig. 5c). However, one clearly sees that the empirical data has a preponderance of smaller degree values; in fact, for more complex connectomes such as in the KKI-18 (Fig. 5d) and KKI-113 (Fig. 5e), these small
(Fig. 5c). However, one clearly sees that the empirical data has a preponderance of smaller degree values; in fact, for more complex connectomes such as in the KKI-18 (Fig. 5d) and KKI-113 (Fig. 5e), these small  values dominate, such that the modes of the degree distributions are shifted left. The mismatch between the degree distributions of the complex connectomes is deemed to be a result of the lengthening of the tails of the empirical data: real neurons are more dynamic at creating new connections. The lengthening of the P(k) tails of the data result in the mean being shifted rightward from the mode, which then shifts the mode of the data leftward from that of the model.
values dominate, such that the modes of the degree distributions are shifted left. The mismatch between the degree distributions of the complex connectomes is deemed to be a result of the lengthening of the tails of the empirical data: real neurons are more dynamic at creating new connections. The lengthening of the P(k) tails of the data result in the mean being shifted rightward from the mode, which then shifts the mode of the data leftward from that of the model.
Figure 5.
Node degree distributions: Model comparisons with data. (a) Fruit fly larva (b) Adult fruit fly (c) H01 Human (1 mm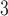 ) (d) KKI-18 (e) KKI-113. The unimodal behavior of the model recovers some features of the simpler and smaller connectomes: (a) fruit fly larva (b) adult fruit fly (c) H01 Human (1 mm
) (d) KKI-18 (e) KKI-113. The unimodal behavior of the model recovers some features of the simpler and smaller connectomes: (a) fruit fly larva (b) adult fruit fly (c) H01 Human (1 mm ). All empirical results show a preponderance of small
). All empirical results show a preponderance of small  values.
values.
In Fig. 6, we present the comparison for the 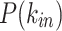 (Fig. 6a–e) and
(Fig. 6a–e) and  (Fig. 6f–j) between our model and the same set of empirical data as in Fig. 5. Similar to the observed behavior in Fig. 5, the model shows comparable
(Fig. 6f–j) between our model and the same set of empirical data as in Fig. 5. Similar to the observed behavior in Fig. 5, the model shows comparable  distributions as the smaller and simpler connectomes, particularly those of the fruit fly larva (Fig. 6a), adult fruit fly (Fig. 6b), and the human H01 1 mm
distributions as the smaller and simpler connectomes, particularly those of the fruit fly larva (Fig. 6a), adult fruit fly (Fig. 6b), and the human H01 1 mm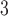 (Fig. 6c). The more complex connectomes KKI-18 (Fig. 6d) and KKI-113 (Fig. 6e) show higher probabilities of small
(Fig. 6c). The more complex connectomes KKI-18 (Fig. 6d) and KKI-113 (Fig. 6e) show higher probabilities of small  values that is not captured by the unimodal trends of the model. On the other hand, we observe that the
values that is not captured by the unimodal trends of the model. On the other hand, we observe that the  distributions from both empirical data and the model follow matching decay trends with tails that span several orders of magnitude as the mean. The mechanism of instantaneous link creation among firing nodes allows the model to recover the heavy-tailed distributions
distributions from both empirical data and the model follow matching decay trends with tails that span several orders of magnitude as the mean. The mechanism of instantaneous link creation among firing nodes allows the model to recover the heavy-tailed distributions 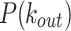 .
.
Figure 6.
Comparison of the in- and out- node strength distributions between data and model. Top panels: The 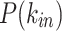 of the model fails to capture the high occurrences of smaller
of the model fails to capture the high occurrences of smaller 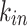 values of the data. Bottom panels: The tails of the
values of the data. Bottom panels: The tails of the 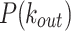 of the model and the data follow comparable decay trends.
of the model and the data follow comparable decay trends.
Discussion
In summary, we have presented here an implementation of a continuous sandpile model on a highly dynamic network topology. In previous works, sandpiles have been implemented on various network architectures51–53, some of which are based on real-world44,54. The novelty of the model presented here lies on the use of a baseline network that is inspired by the complex neural connectivity11, and the introduction of a network edge weight recalibrations, also inspired by the presumed dynamics of functional brain connectomes.
One of the most striking results is the recovery of robust broad-tailed distributions of avalanche sizes (Fig. 1), a key signature of critical behavior. By probing the area, activation, and toppled-site measures for a wide range of parameter values and network reconfigurations, we have shown robust PL tails across all network sizes and initial HMN wiring probabilities tested. In particular, the number of toppled sites during a single avalanche event shows PL distributions best-fitted with the 3/2 decaying exponent characteristic of local field potential electrode experiment neuronal avalanches12. This result is deemed to be remarkable, given the highly dynamic nature of reconnections among the individual nodes in the network, which strongly affect the avalanching behavior of the system. The robustness of the avalanche-size distributions can be considered to be the manifestation of SOC mean-field universality, which occurs for 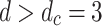 for this model.
for this model.
Apart from the recovery of the dynamical properties of the brain, the model also recovers the statistics of the structural properties of the connectomes. It should be noted that the results obtained from the different connectome data sets, which have different granularities and processes, already reflect a self-organization towards nearly universal heavy-tailed statistics [see “Connectome datasets” for details]. It is therefore unsurprising that a model that hinges on self-organized criticality recovers the macro-level statistics despite the micro-level differences.
On the structural side, the model reproduces the observed statistics of global edge weight distributions, whose tails can be fitted with decaying PLs with scaling exponents close to 3 in empirical data5,22,23. The tails of the edge weight distributions are found to be robust across all the parameter sets tested (Fig. 2), and manifest remarkable comparisons with those obtained from actual connectomes (Fig. 3). An explanation for this can be given by the instantaneous avalanche propagation in mature networks close to maximal connectivity, which creates effective long-range interactions and smoothens out the spatio-temporal fluctuation effects. Under such conditions, a mean-field-like behavior emerges, explaining the emergence of the exponent 3 that closely matches that of the heuristic derivation for mean-field models in a previous work5. Furthermore, this scaling, with some exponent variations within error margins, can also be the related to the heterogeneous HMN structure, which enhances rare-region effects in the modules. This means that even when the system is slightly super- (or sub-) critical, there can be arbitrarily large domains persisting in the opposite phase for long times, causing Griffiths effects, i.e. dynamical scale-free behavior in an extended parameter space. Our preliminary simulation results on homogeneous 4D lattices do not provide clear PLs as we see here for HMNs, strengthening the view that the network modularity plays an important role [see Robustness of Edge Weight Tail Distributions for details].
Another network-structure statistics captured by the model is that of the node strengths. Remarkably, the model shows robust LN statistics for the node degree (Fig. 4), which is also in agreement with the simpler connectome structures from empirical data (Fig. 5). The recovery of LN statistics is unsurprising considering the previously reported LN distributions in neural activity15–17; however, it is noteworthy that this result has been obtained using a model based on (self-organized) criticality, which is traditionally associated with PL statistics9.
The model therefore simultaneously replicates the critical behavior of the brain from two distinct but related perspectives: (i) through the dynamic measures of brain activity12,28, and (ii) through the static physical networks of neurons obtained from the connectome data5,22,23. The latter is of particular importance; other discrete models only capture the criticality of neuronal avalanches, but not the statistics of the actual neuronal network structure. Here, the model we presented captures both the PL distributions of global edge weights and the LN distributions of local node degrees and sheds light on the adaptive structure-function relation in the brain39. The model does so by incorporating key details that are not considered in other works, namely, (i) the baseline HMN, and (ii) the adaptive strengthening [weakening] of nodal connections through correlated activity [inactivity].
In our view, the approach presented here provides a balanced modeling perspective. On one hand, critical behavior has been traditionally captured by the simplest models that self-organize and require no fine-tuning and specificity9; but directly applying these approaches without proper context may lead to misleading or incorrect description of neuronal dynamics. On the other hand, the brain is perhaps one of the most complex and adaptive systems, whose associated functions are not yet completely attributed to structure and form; it is impossible to provide a complete description of the brain, as we are just starting to probe deeper into its physical intricacies. Our approach therefore has used the straightforward rules of discrete self-organizing models, while also incorporating the realistic conditions learned from recent physical investigations of the brain. The success of the model in recovering the signatures of neuronal activity and the physical network structure of the brain itself is predicated on two crucial components: (i) the retention of the criticality from the sandpile model; and (ii) the realistic depiction of learning on a hierarchical and modular network baseline that is inspired by the actual brain structure and dynamics.
The model may benefit from further details that mimic the realistic conditions in cortical dynamics. On the modeling side, additional factors such as local dissipation via ohmic losses, random fluctuations, and oscillatory mechanisms, among others, are not incorporated in the continuous sandpile used here. Moreover, subsequent implementations may benefit from incorporating some other features of neuronal dynamics; in particular, there could be reciprocity in link creation, which, when added to the model, could address the recovery of heavier tails of the degree distributions of more complex connectome empirical data (Fig. 5). We believe that these attributes can easily be implemented for a more nuanced description. The rich dynamics and these hints of similarities with real systems further signify the emergence of complex behavior from simple rules, resulting in robust statistical regularities.
Methods
Connectome datasets
In Table 1 below, we provide a tabulation of the different datasets with the methods of acquisition, network roles defined, and relevant references. The KKI-18 and KKI-113 (large human connectomes from Kennedy Krieger Institute) are connectomes that show the structural connectivity of white matter bundles. It is obtained via Diffusion Tensor Imaging (DTI) where the diffusion of water molecules in the brain is used to infer the orientation and density of white matter fiber tracts. We dowloaded the data from the Open Connectome Project. Here, the nodes represent brain regions, while the edges represent the connections or pathways between these regions. On the other hand, the remaining datasets: H01 human 1 mm , fruit fly, and fruit fly larva are obtained via serial section electron microscopy (ssEM) and all are in neuronal scale.
, fruit fly, and fruit fly larva are obtained via serial section electron microscopy (ssEM) and all are in neuronal scale.
Table 1.
Connectome data description and sources.
| Data set | Acquisition | Node | Edge | Edge weight |
|---|---|---|---|---|
KKI-113 ,4 ,4
|
Diffusion Tensor Imaging (1 mm voxel resolution) voxel resolution) |
Brain regions | White matter fiber tracts | No. connections |
KKI-18 4 4
|
||||
H01 Human 1 mm 
|
Serial section EM | Neurons | Synapses | No. synaptic connections |
Adult Fruit Fly 1 1
|
Serial section EM ( nm nm voxel) voxel) |
Neurons | Synapses | No. synaptic connections |
Fruit Fly Larva 2 2
|
Serial section EM | Neurons | Synapses | No. Tbar 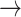 PSD synapses PSD synapses |
 Open Connectome Project, https://neurodata.io.
Open Connectome Project, https://neurodata.io.
 https://public.ek-cer.hu/~odor/pub/KKI2009_113_1_bg.edg.gz.
https://public.ek-cer.hu/~odor/pub/KKI2009_113_1_bg.edg.gz.
 https://public.ek-cer.hu/~odor/pub/KKI-21_KKI2009-18_big_graph_w_inv.graphml.zip.
https://public.ek-cer.hu/~odor/pub/KKI-21_KKI2009-18_big_graph_w_inv.graphml.zip.
 https://zenodo.org/records/13376416.
https://zenodo.org/records/13376416.
 Flywire Connectome Data, https://codex.flywire.ai/api/download.
Flywire Connectome Data, https://codex.flywire.ai/api/download.
For the large-scale connectomes, mechanisms such as axonal growth and pruning55, activity-dependent myelination56, or long-range synchrony57 are responsible for the differences in edge weights. On the other hand, in the neuronal-level connectome datasets, the edge weight variations can be attributed to spike-timing dependent plasticity (STDP), long-term potentiation/depression (LTP/LTD)58, dendritic integration59, and spike timing15. Despite the differences in scale (the physical size of the nodes) and underlying biology (the generation and growth of links), all data sets show comparable statistical distributions of edge counts and weights5 (see also Figs. 3 and 5).
Hierarchical modular networks (HMNs)
To mimic the complex network connectivity of the brain in the modeling, we utilized a variant of HMNs, introduced by Kaiser and Hilgetag10 and modified by Ódor et.al11 to guarantee simple connectedness of nodes on the base level. This is constructed from nodes embedded on a square lattice with additional long links between randomly selected pairs, by an iterative rewiring algorithm of the following steps.
To generate the HMN we define 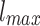 levels in the same set of
levels in the same set of  nodes. At every level, 4l modules are defined. Each module is split into four equal-sized modules on the next level, as if they were embedded in a regular, two-dimensional (2d) lattice. This is done because HMNs in 2d base lattices are closer to the real topology of cortical networks11. The probability
nodes. At every level, 4l modules are defined. Each module is split into four equal-sized modules on the next level, as if they were embedded in a regular, two-dimensional (2d) lattice. This is done because HMNs in 2d base lattices are closer to the real topology of cortical networks11. The probability  that an edge connects two nodes follows
that an edge connects two nodes follows  where l is the greatest integer such that the two nodes are in the same module on level l and b is related to the average node degree via
where l is the greatest integer such that the two nodes are in the same module on level l and b is related to the average node degree via 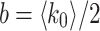 . To illustrate, Fig. 7a shows a representative 3-level HMN2d hierarchical network construction. Here, the network is expanded to show how modules are defined on every level.
. To illustrate, Fig. 7a shows a representative 3-level HMN2d hierarchical network construction. Here, the network is expanded to show how modules are defined on every level.
The addition of long-range graph links provides connections beyond the nearest-neighbor ones of the 2d substrate to mimic brain. Taking these into account, the HMN2d being utilized contains short links connecting nearest neighbors and long links, whose probability decays algebraically with Euclidean distance R,
 |
1 |
which makes it an instance of a Benjamini-Berger (BB) networks60. In this work, we consider a modified BB network in which the long links are added level by level, from top to bottom10. The levels: 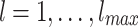 are numbered from bottom to top. The size of domains, i.e., the number of nodes in a level, grows as
are numbered from bottom to top. The size of domains, i.e., the number of nodes in a level, grows as 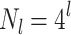 in the 4-module construction, related to a tiling of the two-dimensional base lattice. Due to the approximate distance-level relation,
in the 4-module construction, related to a tiling of the two-dimensional base lattice. Due to the approximate distance-level relation,  , the long-link connection probability on level l is:
, the long-link connection probability on level l is:
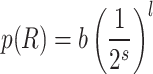 |
2 |
where b is related to the average degree of the node. Here, we consider two-dimensional HMNs of different sizes  , where, again,
, where, again, 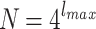 . We also used with different s values,
. We also used with different s values,  by providing single-connectedness on the base lattice.
by providing single-connectedness on the base lattice.
We define r as the shortest path (chemical) distance and the average number of nodes within this distance 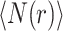 is measured by the Breadth First Search algorithm61 emanating from all nodes of the graph. The topological (graph) dimension (d), can be defined as
is measured by the Breadth First Search algorithm61 emanating from all nodes of the graph. The topological (graph) dimension (d), can be defined as
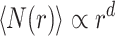 |
3 |
This is infinite for 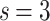 as
as 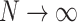 , which appears to be
, which appears to be  in Fig. 7b, in case of a finite graph with
in Fig. 7b, in case of a finite graph with  levels (By increasing the size this effective dimension estimate would diverge.). In case of
levels (By increasing the size this effective dimension estimate would diverge.). In case of 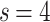 (for
(for 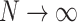 ) one can obtain finite dimensions with
) one can obtain finite dimensions with 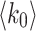 initial degree dependent values. In Fig. 7b one can fit
initial degree dependent values. In Fig. 7b one can fit 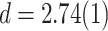 for
for 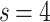 ,
, 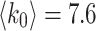 , which is below the upper critical dimension of this directed sandpile model (
, which is below the upper critical dimension of this directed sandpile model ( ).
).
We can observe that the learning does not seem to change the graph dimension (the shortest path lengths between nodes); instead, it only increases the average degree and the in/out strengths of nodes. This also means the lack of synaptogenesis in our model, which really happens in adult animals, only the synaptic weights increase.
One possible explanation for why the topological dimension of the HMNs does not change after imposing the model is the modular structure of the HMNs. Modularity aids in maintaining the overall structure of the network. During an avalanche, the span of the cascade may occur only within a module unless the avalanche is too big. As such, only the local connectivity is improved but does not dramatically change the topological properties of a modular network resulting to an unchanged dimension. In addition to this, the edge weight reinforcement rule includes a factor of 1/r which accounts for the realistic setting where the creation and maintenance of synapses in neural connectomes is accompanied by wiring cost5,62,63 [see “Hebbian learning” for details]; this appears to suppress the creation of very long links within the network.
Sandpile model implementation
The cellular automata (CA) model of the sandpile is composed of a network of nodes, each representing a functional unit in the neural circuitry. Each node i is characterized by its state  , a measure of its activity; in actual neurons, this can represent the action potential that spikes during firing. Because neuronal sections can only accommodate a finite potential, we set
, a measure of its activity; in actual neurons, this can represent the action potential that spikes during firing. Because neuronal sections can only accommodate a finite potential, we set 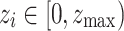 , where
, where  is set to unity. The threshold state
is set to unity. The threshold state  , when reached or exceeded by the node, triggers the relaxation of the site through the redistribution of stress to its direct neighbors. Finally, to also mimic the physical structure of the brain, the nodes are given physical site locations
, when reached or exceeded by the node, triggers the relaxation of the site through the redistribution of stress to its direct neighbors. Finally, to also mimic the physical structure of the brain, the nodes are given physical site locations  in a two-dimensional square-lattice grid.
in a two-dimensional square-lattice grid.
The network structure is introduced through a hierarchical modular network (HMN) [see previous section “Hierarchical modular networks (HMNs)”]. The directed connections between nodes i (origin) and j (destination) are represented by the edges  , which is characterized by its weight
, which is characterized by its weight  , a proxy for the relative strength of synaptic connectivity between two brain sections. Mathematically, the HMN2d can now be represented as a graph
, a proxy for the relative strength of synaptic connectivity between two brain sections. Mathematically, the HMN2d can now be represented as a graph  }, where the set of nodes
}, where the set of nodes 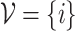 has N elements, while
has N elements, while 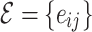 contains E number of connections; here, majority of the results are
contains E number of connections; here, majority of the results are 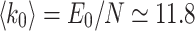 for the original HMN2d. Upon defining the network structure, the individual nodes i now have a set of neighbors
for the original HMN2d. Upon defining the network structure, the individual nodes i now have a set of neighbors  , where j are the out-degree connections or downlines of i. Whereas in simple grid implementations, the edges are bidirectional, uniformly weighted, and fixed to the discrete (usually, von Neumann) nearest neighbors in a grid, the HMN construction results in connections that are asymmetric
, where j are the out-degree connections or downlines of i. Whereas in simple grid implementations, the edges are bidirectional, uniformly weighted, and fixed to the discrete (usually, von Neumann) nearest neighbors in a grid, the HMN construction results in connections that are asymmetric 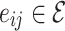 does not guarantee that
does not guarantee that 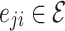 , i.e.
, i.e.  .
.
In this context, it is also instructive to define the peripheral nodes of the network  . These nodes form the topological “margins” for “overflow” during avalanche events. In an actual grid setting, the periphery is the literal margins of the grid, whose states are zeroed out every iteration. Upon using HMNs as baseline networks, however, the notion of physical extremity is lost because of the structure of the network. Therefore, to be able to assign the nodes of egress, we used the betweenness centrality as a measure of periphery64. The states of the nodes with zero betweenness centrality are designated to be
. These nodes form the topological “margins” for “overflow” during avalanche events. In an actual grid setting, the periphery is the literal margins of the grid, whose states are zeroed out every iteration. Upon using HMNs as baseline networks, however, the notion of physical extremity is lost because of the structure of the network. Therefore, to be able to assign the nodes of egress, we used the betweenness centrality as a measure of periphery64. The states of the nodes with zero betweenness centrality are designated to be  and zeroed out
and zeroed out 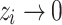 at every instant when they receive grains from the external driving or from the redistributions from their connections in the network. The egress of “grains” at the
at every instant when they receive grains from the external driving or from the redistributions from their connections in the network. The egress of “grains” at the 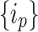 nodes ensure that, every time step, all the nodes in the network will “relax” to have finite and below-threshold values of the states.
nodes ensure that, every time step, all the nodes in the network will “relax” to have finite and below-threshold values of the states.
During initialization, the nodes are given random states 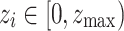 drawn from a uniform distribution. Dynamic activity is represented by the introduction of a trigger to random nodes every time step, akin to the continuous reception of a background stimulus in actual neural activity. Here, the trigger strength
drawn from a uniform distribution. Dynamic activity is represented by the introduction of a trigger to random nodes every time step, akin to the continuous reception of a background stimulus in actual neural activity. Here, the trigger strength 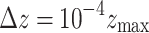 increases the state
increases the state 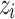 of the randomly chosen node i at an iteration time t,
of the randomly chosen node i at an iteration time t,
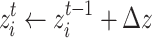 |
4 |
where the temporal index is placed at the superscript. Needless to say, repeated triggerings may result in the approach to the marginally stable state; such a site i will be driven to  . When such an event occurs, time is frozen (i.e. no new
. When such an event occurs, time is frozen (i.e. no new 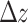 is added to the system) while this above-threshold state is “toppling,” i.e. its above-threshold state
is added to the system) while this above-threshold state is “toppling,” i.e. its above-threshold state 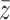 is being redistributed to its downline neighborhood in the network,
is being redistributed to its downline neighborhood in the network, 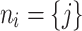 . Each downline neighbor receives a fraction of
. Each downline neighbor receives a fraction of 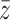 that is proportional to the ratio of the individual edge weight
that is proportional to the ratio of the individual edge weight  it receives from i over the total out-degree edge weight of the neighborhood,
it receives from i over the total out-degree edge weight of the neighborhood, 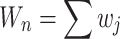 :
:
 |
5 |
 |
6 |
The redistribution and relaxation rules, Eqs. (5) and (6) are repeated until all the nodes in the HMN have states below  . Repeated redistributions affect portions of the network, resulting in one distinct avalanche event for the same instance of the initial triggering at t. Here, we consider two measures of avalanches used in traditional sandpile studies: the raw count of all the unique affected sites is called the area
. Repeated redistributions affect portions of the network, resulting in one distinct avalanche event for the same instance of the initial triggering at t. Here, we consider two measures of avalanches used in traditional sandpile studies: the raw count of all the unique affected sites is called the area 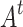 (the name being inspired by the extent of the avalanche in the usual 2D grid implementations); the number of multiple activations, counting multiple relaxations and/or receiving of redistributed states for all affected sites, is denoted by
(the name being inspired by the extent of the avalanche in the usual 2D grid implementations); the number of multiple activations, counting multiple relaxations and/or receiving of redistributed states for all affected sites, is denoted by 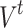 . Furthermore, the individual toppled sites during a single triggering event is counted and labeled as C, corresponding to the measures of activated sites in actual experimental protocols12. A representative example of an avalanche event and the corresponding avalanche measures is shown in Fig. 8.
. Furthermore, the individual toppled sites during a single triggering event is counted and labeled as C, corresponding to the measures of activated sites in actual experimental protocols12. A representative example of an avalanche event and the corresponding avalanche measures is shown in Fig. 8.
Figure 8.
Avalanches and Hebbian learning. The participation of the nodes in the original toppling event is measured as A, V, or C. During avalanche events, sites that toppled as a result of the original toppling event (at the avalanche origin) receives reinforced (or entirely new) connections based on Eq. (7). When there is no avalanche event, a random link is weakened (or entirely pruned) based on Eq. (8).
Hebbian learning
During initialization, the starting HMN has discrete-valued i.e. 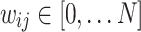 edge weights corresponding to the number of links between two nodes. To dynamically alter the network architecture, we added rules that strengthen and weaken the existing links based on measures of correlated activity and inactivity, respectively. These two mechanisms are guided by different mechanisms, and thus have different characteristic rates. On one hand, firing neurons tend to form stronger links within shorter time frames; on the other hand, less favored pathways tend to progressively decay in strength over extended periods of time. These foundational principles of Hebbian learning in the brain are simulated in the model through separate mechanisms of link creations and weakenings during avalanche and stasis periods, respectively.
edge weights corresponding to the number of links between two nodes. To dynamically alter the network architecture, we added rules that strengthen and weaken the existing links based on measures of correlated activity and inactivity, respectively. These two mechanisms are guided by different mechanisms, and thus have different characteristic rates. On one hand, firing neurons tend to form stronger links within shorter time frames; on the other hand, less favored pathways tend to progressively decay in strength over extended periods of time. These foundational principles of Hebbian learning in the brain are simulated in the model through separate mechanisms of link creations and weakenings during avalanche and stasis periods, respectively.
After an avalanche event originating from i at time t, all the other sites k that reached 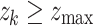 are tracked as candidate sites that will receive new connections
are tracked as candidate sites that will receive new connections  from i. The weight
from i. The weight 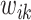 of this new synaptic connection should reflect the mechanisms that enhance and hinder the connectivity of these functional units. Here, we impose that this weight be proportional to the avalanche measure, particularly the activation V; stronger connections are expected for multiple repetitions of correlated firings. Meanwhile, in a realistic setting, the connectivity is hindered by physical distance; here we use the simple distance
of this new synaptic connection should reflect the mechanisms that enhance and hinder the connectivity of these functional units. Here, we impose that this weight be proportional to the avalanche measure, particularly the activation V; stronger connections are expected for multiple repetitions of correlated firings. Meanwhile, in a realistic setting, the connectivity is hindered by physical distance; here we use the simple distance  based on their locations on the square grid. With these assumptions, new links are created from i to all k nodes, with weights computed as
based on their locations on the square grid. With these assumptions, new links are created from i to all k nodes, with weights computed as
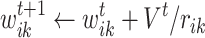 |
7 |
This rule instantaneously updates the neighborhood (downlines) of i for the next time step  , with the nodes k now joining the neighborhood
, with the nodes k now joining the neighborhood 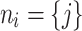 and new connections
and new connections  are added to
are added to 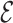 . The ratio
. The ratio 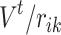 is deemed to be the simplest representation of the effect of the avalanche and the separation distance on connection strength; increasing powers of
is deemed to be the simplest representation of the effect of the avalanche and the separation distance on connection strength; increasing powers of 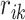 (say,
(say, 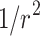 ) significantly decreases the strength and spatial extent of new connectivity, especially for larger networks.
) significantly decreases the strength and spatial extent of new connectivity, especially for larger networks.
What happens to the grid during periods of stasis? Here, we impose weakenings of random edges, albeit at a significantly slower rate; in reality, we don’t expect neural connections to be severed instantaneously. The simplest assumption for the decay in edge weight is an exponential decay, wherein the subsequent (weakened) value is proportional to the current value. Therefore, for every time step with no avalanche event, a randomly chosen node m and one of its neighbors n, originally connected by an edge  with weight
with weight 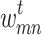 at time t, will have an updated connection weight,
at time t, will have an updated connection weight,
 |
8 |
where, here,  is the decay rate. The repeated reinforcement [weakening] of the edges results in the edge weights being continuous valued. Additionally, when weakened down to a tolerance value
is the decay rate. The repeated reinforcement [weakening] of the edges results in the edge weights being continuous valued. Additionally, when weakened down to a tolerance value 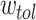 , the edge
, the edge  is completely severed,
is completely severed, 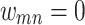 . In some cases, for very long iteration times, this can lead to some nodes being isolated when all of their edges are removed. Here, we consider
. In some cases, for very long iteration times, this can lead to some nodes being isolated when all of their edges are removed. Here, we consider  , i.e.
, i.e. 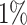 of a unit connectivity. For this
of a unit connectivity. For this 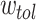 and all the starting HMN considered, we used
and all the starting HMN considered, we used  ; rapid deterioration of the network is observed for
; rapid deterioration of the network is observed for 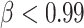 .
.
Supplementary Information
Acknowledgements
We are thankful for the financial support from the Hungarian National Research, Development and Innovation Office NKFIH (Grant No. K146736 and the KIFU access to the Hungarian supercomputer Komondor.).
Author contributions
G. Ó conceptualized the work, did the theoretical analysis, and created the HMN; R.C.B. designed the model and ran the simulations; M.T.C. did the fitting with empirical data and tested the PL fits. All authors analyzed the results and reviewed the manuscript.
Data availability
Data is provided within the manuscript and is available upon request from G. Ódor via email at odor.geza@ek.hun-ren.hu.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-025-16377-8.
References
- 1.Dorkenwald, S. et al. Neuronal wiring diagram of an adult brain. Nature634, 124–138. 10.1038/s41586-024-07558-y (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Winding, M. et al. The connectome of an insect brain. Science 379, eadd9330. 10.1126/science.add9330 (2023). [DOI] [PMC free article] [PubMed]
- 3.Ercsey-Ravasz, M. et al. A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron80, 184–197. 10.1016/j.neuron.2013.07.036 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gastner, M. T. & Ódor, G. The topology of large Open Connectome networks for the human brain. Sci. Rep.6, 27249. 10.1038/srep27249 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cirunay, M., Ódor, G., Papp, I. & Deco, G. Scale-free behavior of weight distributions of connectomes. Phys. Rev. Res.7, 013134. 10.1103/PhysRevResearch.7.013134 (2025). [Google Scholar]
- 6.Chialvo, D. & Bak, P. Learning from mistakes. Neuroscience90, 1137–1148. 10.1016/S0306-4522(98)00472-2 (1999). [DOI] [PubMed] [Google Scholar]
- 7.Legenstein, R. & Maass, W. Edge of chaos and prediction of computational performance for neural circuit models. Neural Netw. 20, 323–334. 10.1016/j.neunet.2007.04.017 (2007). [DOI] [PubMed]
- 8.Kinouchi, O. & Copelli, M. Optimal dynamical range of excitable networks at criticality. Nat. Phys.2, 348–351. 10.1038/nphys289 (2006). [Google Scholar]
- 9.Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett.59, 381. 10.1103/PhysRevLett.59.381 (1987). [DOI] [PubMed] [Google Scholar]
- 10.Kaiser, M. & Hilgetag, C. C. Optimal hierarchical modular topologies for producing limited sustained activation of neural networks. Front. Neuroinform.4, 713. 10.3389/fninf.2010.00008 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ódor, G., Dickman, R. & Ódor, G. Griffiths phases and localization in hierarchical modular networks. Sci. Rep.5, 14451. 10.1038/srep14451 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci.23, 11167–11177. 10.1523/JNEUROSCI.23-35-11167.2003 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Beggs, J. M. The cortex and the critical point: understanding the power of emergence ( MIT Press, 2022).
- 14.Koulakov, A. A., Hromádka, T. & Zador, A. M. Correlated connectivity and the distribution of firing rates in the neocortex. J. Neurosci.29, 3685–3694. 10.1523/JNEUROSCI.4500-08.2009 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Buzsáki, G. & Mizuseki, K. The log-dynamic brain: how skewed distributions affect network operations. Nat. Rev. Neurosci.15, 264–278. 10.1038/nrn3687 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Scheler, G. Logarithmic distributions prove that intrinsic learning is Hebbian. F1000Research6, 1222. 10.12688/f1000research.12130.2 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Friedman, N. et al. Universal critical dynamics in high resolution neuronal avalanche data. Phys. Rev. Lett.108, 208102. 10.1103/PhysRevLett.108.208102 (2012). [DOI] [PubMed] [Google Scholar]
- 18.Zhang, X.-Y., Moore, J. M., Ru, X. & Yan, G. Geometric scaling law in real neuronal networks. Phys. Rev. Lett.133, 138401. 10.1103/PhysRevLett.133.138401 (2024). [DOI] [PubMed] [Google Scholar]
- 19.Ansell, H. S. & Kovács, I. A. Unveiling universal aspects of the cellular anatomy of the brain. Commun. Phys.7, 184. 10.1038/s42005-024-01665-y (2024). [Google Scholar]
- 20.Salova, A. & Kovács, I. A. Combined topological and spatial constraints are required to capture the structure of neural connectomes. Netw. Neurosci.9, 181–206. 10.1162/netn_a_00428 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lynn, C. W., Holmes, C. M. & Palmer, S. E. Heavy-tailed neuronal connectivity arises from Hebbian self-organization. Nat. Phys.20, 484–491. 10.1038/s41567-023-02332-9 (2024). [Google Scholar]
- 22.Ódor, G. Critical dynamics on a large human open connectome network. Phys. Rev. E94, 062411. 10.1103/PhysRevE.94.062411 (2016). [DOI] [PubMed] [Google Scholar]
- 23.Ódor, G., Deco, G. & Kelling, J. Differences in the critical dynamics underlying the human and fruit-fly connectome. Phys. Rev. Res.4, 023057. 10.1103/PhysRevResearch.4.023057 (2022). [Google Scholar]
- 24.Chialvo, D. R. Emergent complex neural dynamics. Nat. Phys.6, 744–750. 10.1038/nphys1803 (2010). [Google Scholar]
- 25.Palva, J. et al. Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws. Proc. Natl. Acad. Sci. U.S.A.110, 3585–3590. 10.1073/pnas.1216855110 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Munoz, M. A. Colloquium: Criticality and dynamical scaling in living systems. Rev. Mod. Phys.90, 031001. 10.1103/RevModPhys.90.031001 (2018). [Google Scholar]
- 27.Haimovici, A., Tagliazucchi, E., Balenzuela, P. & Chialvo, D. R. Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett.110, 178101. 10.1103/PhysRevLett.110.178101 (2013). [DOI] [PubMed] [Google Scholar]
- 28.Hesse, J. & Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci.8, 166. 10.3389/fnsys.2014.00166 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.De Arcangelis, L., Perrone-Capano, C. & Herrmann, H. J. Self-organized criticality model for brain plasticity. Phys. Rev. Lett.96, 028107. 10.1103/PhysRevLett.96.028107 (2006). [DOI] [PubMed] [Google Scholar]
- 30.Nowrouzi-Nezhad, H., Mahdisoltani, S. & Moghimi-Araghi, S. Self-organized criticality and structural dynamics in evolving neuronal networks: A modified sandpile model. Phys. A Stat. Mech. Appl. 130535. 10.1016/j.physa.2025.130535 (2025).
- 31.Sporns, O. Networks of the Brain ( MIT press, 2016).
- 32.Griffiths, R. B. Nonanalytic Behavior Above the Critical Point in a Random Ising Ferromagnet. Phys. Rev. Lett.23, 17–19. 10.1103/PhysRevLett.23.17 (1969). [Google Scholar]
- 33.Muñoz, M. A., Juhász, R., Castellano, C. & Ódor, G. Griffiths Phases on Complex Networks. Phys. Rev. Lett.105, 128701. 10.1103/PhysRevLett.105.128701 (2010). [DOI] [PubMed] [Google Scholar]
- 34.Cota, W., Ferreira, S. C. & Ódor, G. Griffiths effects of the susceptible-infected-susceptible epidemic model on random power-law networks. Phys. Rev. E93, 032322. 10.1103/PhysRevE.93.032322 (2016). [DOI] [PubMed] [Google Scholar]
- 35.Johnson, S., Marro, J. & Torres, J. J. Robust short-term memory without synaptic learning. PLoS ONE8, e50276. 10.1371/journal.pone.0050276 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Moretti, P. & Muñoz, M. A. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun.4, 2521. 10.1038/ncomms3521 (2013). [DOI] [PubMed] [Google Scholar]
- 37.Ódor, G. Robustness of griffiths effects in homeostatic connectome models. Phys. Rev. E99, 012113. 10.1103/PhysRevE.99.012113 (2019). [DOI] [PubMed] [Google Scholar]
- 38.de Arcangelis, L. & Herrmann, H. J. Learning as a phenomenon occurring in a critical state. Proc. Natl. Acad. Sci.107, 3977–3981. 10.1073/pnas.0912289107 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Angiolelli, M. et al. Criticality explains structure-function relationships in the human brain. bioRxiv10.1101/2024.07.15.603226 (2024).
- 40.Berner, R., Gross, T., Kuehn, C., Kurths, J. & Yanchuk, S. Adaptive dynamical networks. Phys. Rep.1031, 1–59. 10.1016/j.physrep.2023.08.001 (2023). [Google Scholar]
- 41.Zhang, Y.-C. Scaling theory of self-organized criticality. Phys. Rev. Lett.63, 470. 10.1103/PhysRevLett.63.470 (1989). [DOI] [PubMed] [Google Scholar]
- 42.Dhar, D. Self-organized critical state of sandpile automaton models. Phys. Rev. Lett.64, 1613. 10.1103/PhysRevLett.64.1613 (1990). [DOI] [PubMed] [Google Scholar]
- 43.Dhar, D. & Ramaswamy, R. Exactly solved model of self-organized critical phenomena. Phys. Rev. Lett.63, 1659–1662. 10.1103/PhysRevLett.63.1659 (1989). [DOI] [PubMed] [Google Scholar]
- 44.Zachariou, N., Expert, P., Takayasu, M. & Christensen, K. Generalised sandpile dynamics on artificial and real-world directed networks. PLoS ONE10, e0142685. 10.1371/journal.pone.0142685 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Batac, R. C., Paguirigan, A. A. Jr., Tarun, A. B. & Longjas, A. G. Sandpile-based model for capturing magnitude distributions and spatiotemporal clustering and separation in regional earthquakes. Nonlinear Process. Geophys.24, 179–187. 10.5194/npg-24-179-2017 (2017). [Google Scholar]
- 46.Heiney, K. et al. Neuronal avalanche dynamics and functional connectivity elucidate information propagation in vitro. Front. Neural Circ.16, 980631. 10.3389/fncir.2022.980631 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pasquale, V., Massobrio, P., Bologna, L., Chiappalone, M. & Martinoia, S. Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience153, 1354–1369. 10.1016/j.neuroscience.2008.03.050 (2008). [DOI] [PubMed] [Google Scholar]
- 48.Plenz, D. et al. Self-organized criticality in the brain. Front. Phys. 9. 10.3389/fphy.2021.639389 ( 2021).
- 49.Alstott, J., Bullmore, E. & Plenz, D. powerlaw: a Python package for analysis of heavy-tailed distributions. PLoS ONE9, e85777. 10.1371/journal.pone.0085777 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Clauset, A., Shalizi, C. R. & Newman, M. E. Power-law distributions in empirical data. SIAM Rev.51, 661–703. 10.1137/070710111 (2009). [Google Scholar]
- 51.Chen, C.-C., Lee, Y.-T. & Chiao, L.-Y. Intermittent criticality in the long-range connective sandpile (LRCS) model. Phys. Lett. A372, 4340–4343. 10.1016/j.physleta.2008.04.043 (2008). [Google Scholar]
- 52.Goh, K.-I., Lee, D.-S., Kahng, B. & Kim, D. Sandpile on scale-free networks. Phys. Rev. Lett.91, 148701. 10.1103/PhysRevLett.91.148701 (2003). [DOI] [PubMed] [Google Scholar]
- 53.Pan, G.-J., Zhang, D.-M., Yin, Y.-P. & He, M.-H. Sandpile on directed small-world networks. XXPhys. A383, 435–442. 10.1016/j.physa.2007.04.113 (2007). [Google Scholar]
- 54.Wu, T., Xia, Y. & Liang, Y. Load cascades in spatial networks: A sandpile model approach. XXPhys. A644, 129833. 10.1016/j.physa.2024.129833 (2024). [Google Scholar]
- 55.Innocenti, G. M. & Price, D. J. Exuberance in the development of cortical networks. Nat. Rev. Neurosci.6, 955–965. 10.1038/nrn1790 (2005). [DOI] [PubMed] [Google Scholar]
- 56.Fields, R. D. A new mechanism of nervous system plasticity: activity-dependent myelination. Nat. Rev. Neurosci.16, 756–767. 10.1038/nrn4023 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fries, P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci.9, 474–480. 10.1016/j.tics.2005.08.011 (2005). [DOI] [PubMed] [Google Scholar]
- 58.Bi, G.-Q. & Poo, M.-M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci.18, 10464–10472. 10.1523/JNEUROSCI.18-24-10464.1998 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.London, M. & Häusser, M. Dendritic computation. Annual Reviews of. Neuroscience28, 503–532. 10.1146/annurev.neuro.28.061604.135703 (2005). [DOI] [PubMed] [Google Scholar]
- 60.Benjamini, I. & Berger, N. The diameter of long-range percolation clusters on finite cycles. Random Struct. Algorithms19, 102–111. 10.1002/rsa.1022 (2001). [Google Scholar]
- 61.Hart, P. E., Nilsson, N. J. & Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern.4, 100–107. 10.1109/TSSC.1968.300136 (1968). [Google Scholar]
- 62.Ahn, Y.-Y., Jeong, H. & Kim, B. J. Wiring cost in the organization of a biological neuronal network. XXPhys. A367, 531–537. 10.1016/j.physa.2005.12.013 (2006). [Google Scholar]
- 63.Bullmore, E. & Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci.13, 336–349. 10.1038/nrn3214 (2012). [DOI] [PubMed] [Google Scholar]
- 64.Batac, R. C. & Cirunay, M. T. Shortest paths along urban road network peripheries. XXPhys. A597, 127255. 10.1016/j.physa.2022.127255 (2022). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data is provided within the manuscript and is available upon request from G. Ódor via email at odor.geza@ek.hun-ren.hu.