Reversible and Irreversible Adhesion of Motile Escherichia coli Cells Analyzed by Total Internal Reflection Aqueous Fluorescence Microscopy

Abstract

The initial events in bacterial adhesion are often explained as resulting from electrostatic and van der Waals forces between the cell and the surface, as described by DLVO theory (developed by Derjaguin, Landau, Verwey, and Overbeek). Such a theory predicts that negatively charged bacteria will experience greater attraction toward a negatively charged surface as the ionic strength of the medium is increased. In the present study we observed both smooth-swimming and nonmotile Escherichia coli bacteria close to plain, positively, and hydrophobically coated quartz surfaces in high- and low-ionic-strength media by using total internal reflection aqueous fluorescence microscopy. We found that reversibly adhering cells (cells which continue to swim along the surface for extended periods) are too distant from the surface for this behavior to be explained by DLVO-type forces. However, cells which had become immobilized on the surface did seem to be affected by electrostatic interactions. We propose that the “force” holding swimming cells near the surface is actually the result of a hydrodynamic effect, causing the cells to swim at an angle along the glass, and that DLVO-type forces are responsible only for the observed immobilization of irreversibly adhering cells. We explain our observations within the context of a conceptual model in which bacteria that are interacting with the surface may be thought of as occupying one of three compartments: bulk fluid, near-surface bulk, and near-surface constrained. A cell in these compartments feels either no effect of the surface, only the hydrodynamic effect of the surface, or both the hydrodynamic and the physicochemical effects of the surface, respectively.

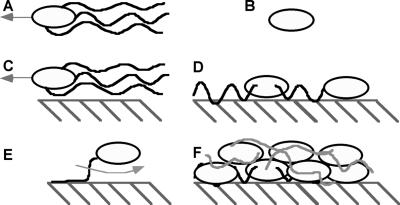
The goal of this work was to determine the force or forces controlling reversible adhesion of motile bacterial cells to surfaces. Reversible bacterial adhesion is operationally defined here as a situation in which a bacterium remains very close (within the same plane of focus for a light microscope) to a surface for a period of several minutes. Reversibly adhering bacteria are presumed to retain their ability to move laterally along the surface (37), by swimming or Brownian motion, and these cells may also eventually leave the vicinity of the surface. Cells behaving in this manner have been observed in numerous experiments and will often spend long times (>1 min) swimming near the surface (5, 12, 22, 25, 41). In irreversible adhesion, by contrast, bacteria adhering to the surface do not move, either by swimming or Brownian motion, for the duration of observation (36). In general, bacteria that have become immobilized on the surface are described as irreversibly adhered to the surface, while cells that can still swim along the surface are described as reversibly adhered. Cells may also become tethered to the surface, when a flagellum adheres to the surface but the cell body still rotates freely. Figure 1 illustrates the definitions of these terms.

FIG. 1.

Representations of different bacterium-surface interactions. (A) Motile bacterium swimming in bulk fluid; (B) nonmotile bacterium; (C) reversibly adhering bacterium, translating along a surface; (D) irreversibly adhered bacterium (note cells may or may not have flagella); (E) tethered bacterium; (F) biofilm. Note that the drawing is not to scale. Cells are ca. 1 μm thick by ca. 5 μm long; the separation distances are ca. 30 nm for swimming cells (C) and ca. 10 nm for irreversibly adhering cells (D). Tethered cells (E) are found in between the two distances.

Adhesion of individual cells to a surface is the first step in the formation of biofilms (37). Bacteria within biofilms are much harder to kill than are planktonic bacteria (33); therefore, it would be advantageous to control cellular adhesion and prevent formation of harmful biofilms before they start. This is especially important for motile bacteria, which make up 80% of known bacteria (28) and have been observed in some cases to seek out surfaces and colonize them more rapidly than nonmotile bacteria (see, for example, reference 30). Biofilms have been implicated in the clogging of industrial pipes and reduction of heat transfer coefficients (7), aiding in the attachment of larger, more-damaging organisms to ship hulls (26), and the plugging of soil pores near injection wells (35).

The standard model for bacterial adhesion implies that bacteria proceed from a loosely attached, reversible state to a more strongly attached, irreversible state (26); this transition is thought to be related to movement from the secondary to the primary energy minima as described by DLVO theory of Derjaguin, Landau, Verwey, and Overbeek (26). In brief, DLVO theory combines van der Waals and electrostatic forces to predict the overall interaction between two particles or a particle and a surface (17). Numerous researchers have found a link between increasing bacterial adhesion and increasing ionic strength, which is consistent with DLVO theory (6, 8, 9, 13, 20, 21, 23, 32, 36, 42). However, in our previous work, we found bacteria adhering reversibly to, that is, swimming along, the surface at both high and low ionic strength, when DLVO theory predicted that no reversible adhesion should have occurred at low ionic strength (41). Cells are clearly being held to the surface by some force when they are reversibly adhering; they remain near the surface for periods of >1 min, even though gravity and Brownian motion would tend to move them away over this time (12).

By measuring the separation distance between cells and the surface, conclusions can be drawn about the forces responsible for holding the bacteria there. DLVO-type forces tend to be relatively short range, on the order of ∼50 nm or less. On the other hand, hydrodynamic interactions can take place over several microns. Varying the conditions which affect the DLVO predicted adhesion distance and observing the effect on the actual bacterium-surface separation should enable us to distinguish between the forces responsible. In this work, we sought to uncover the force or forces responsible for reversible adhesion of cells to surfaces by exploring the relationship between bacterial adhesion and the properties of the surface to which the cell is adhering and the medium which separates them. Using a total internal reflection aqueous fluorescence (TIRAF) microscope, we measured the distances between Escherichia coli bacteria and clean quartz, hydrophobic, and positively charged surfaces. We examined the interaction between E. coli and clean quartz at both high and low ionic strengths. The charge characteristics of the cells and surfaces were measured and used in DLVO equations to generate free-energy versus distance curves for the adhesion of cells to surfaces. The measured separations were then compared to those predicted by using DLVO theory, and the ability of the theory to explain reversible adhesion of motile cells was assessed.

MATERIALS AND METHODS

Bacterial preparation.

E. coli strains HCB437, which is a smooth-swimming mutant, and HCB137, which is a nonmotile strain that lacks flagella, were generously provided by the laboratory of H. C. Berg (Harvard University). Stock cultures were stored in 400-μl aliquots at −70°C. An aliquot was thawed and used to inoculate 50 ml of autoclaved tryptone broth (10 g of tryptone, 5 g of NaCl, 1 liter of water), which was agitated on a shaker table (Labline Orbit Environ-Shaker; Labline, Melrose Park, Ill.) at 30°C and 150 rpm until the mid-exponential phase of growth was reached (generally after 6 h). Bacteria were harvested in mid-exponential phase, when the optical density of the culture was ca. 1.0, as measured at a wavelength of 590 nm by using a spectrophotometer (DU-7; Beckman, Fullerton, Calif.). Then, 1 ml of a bacterial solution was filtered with a 0.45-μm (pore-size) filter (Millipore, Bedford, Mass.) and rinsed three times with the appropriate buffer as described by Berg and Turner (5). The filtered bacteria were then resuspended in 25 ml of phosphate motility buffer (2) at a concentration of ca. 10⁷ cells/ml. Bacteria were suspended in either high (I = 0.202 M)- or low (I = 0.006 M)-ionic-strength buffer. Unless otherwise specified, high-ionic-strength buffer was used. A stock solution of 5 mg of fluorescein-dextran (molecular weight, 3,000; Molecular Probes, Eugene, Oreg.) in 1 ml of filtered distilled water was premixed and stored in an amber glass bottle at 4°C. Just prior to examination with the TIRAF microscope, 100 μl of fluorophore solution was added to 10 ml of bacterial suspension, resulting in a final fluorescein-dextran concentration of 0.05 mg/ml. All TIRAF experiments were conducted at a room temperature of 22 to 25°C.

Surface preparation.

For experiments with TIRAF microscopy, fused quartz slides (Quartz Scientific, Fairport Harbor, Ohio) were used as coverslides. The quartz was first sonicated in a 5% (vol/vol) solution of Contrad 70 (Fisher Scientific) and water for 15 min. This was followed by a thorough rinse in filtered distilled water and a final rinse in methanol, and then the slide was air dried. Slides were stored in covered dishes. Just prior to an experiment, the slides were exposed for 10 min in an argon-ion plasma chamber to remove any remaining impurities.

Two different silanized quartz surfaces were used in TIRAF experiments: one with a positive charge, and one which was hydrophobic. The positively charged surface was prepared by following the method detailed by Arnoldi et al. (3). In brief, the quartz was cleaned and allowed to dry in a 130°C oven for several days. A 1% (vol/vol) mixture of (3-aminopropyl)trimethoxysilane (Lancaster, Windham, N.H.) in 1 mM acidic acid was prepared and allowed to hydrolyze for 5 min before the clean slide was immersed in the mixture. The slide was exposed to the mixture for 2 min, rinsed thoroughly with distilled water, and then sonicated in distilled water for 15 min. After sonication, the slide was cured in the 130°C oven overnight.

For the hydrophobic surface coating, the method of Ulman was used (34). First, the quartz was thoroughly cleaned as detailed above. Because of the very reactive nature of the hydrophobic silane, all of the glassware used in the coating procedure, including the slide itself, was dried in the 130°C oven for at least 30 min. The slide was then immersed in a 0.5% (vol/vol) mixture of octadecyltrichlorosilane (OTS; Lancaster, Windham, N.H.) and isopropyl alcohol for 10 min. The slide was then rinsed in pure isopropyl alcohol and allowed to air dry.

Both coated slides were stored in covered dishes prior to use and rinsed with distilled water after use.

TIRAF microscopy.

Image data was collected and analyzed to produce measurements of the separation distance between the cells and the surface as described previously in Vigeant et al. (40), based on the work of Gingell et al. (14). Briefly, TIRAF microscopy is a method which can be used to measure the distances between bacteria and a glass surface. A laser beam is incident, at an angle greater than the critical angle, on the quartz slide covering the sample chamber, which generates an evanescent wave. This wave excites a fluorophore which is dissolved in the aqueous medium; cells near the surface appear as dark spots. By measuring the light level within these darker spots and applying Gingell's equations (14), the distance between the cells and the surface can be determined. With this illumination method, cells within ∼100 nm of the surface may be detected. An increasing uncertainty in the measurement encountered as the cells are farther from the surface was countered by using large numbers of replicate measurements.

Electrophoretic mobility measurements.

The surface charges of bacteria and quartz were quantified by electrophoretic mobility measurements. A Coulter Delsa 440 zeta meter was used to make these measurements (Beckman Coulter, Fullerton, Calif.). All measurements were made at 25°C. Before each set of experiments, the Delsa 440 was calibrated by using a standard mobility and conductivity calibration solution.

To obtain accurate mobilities, multiple measurements of mobility were made at regular intervals along the height of the sample chamber. A parabola was fit to the measured velocities at each point, and from this the velocity in the stationary layer, which is the true electrophoretic mobility, was determined (T. A. Camesano, unpublished data).

Because the Coulter 440 can only be used to measure charge on colloidal particles, the glass and quartz were crushed with an agate mortar and pestle and suspended in a liquid buffer prior to measurement (12, 16, 24, 41).

Zeta potentials, which were used as an approximation for the surface potential in DLVO calculations, were determined from the electrophoretic mobilities of particles by using the Smoluchowski equation (1).

The zeta potential of the coated glass was estimated because in order to measure charge, glass must be ground to fine powder, where the newly exposed surface area would be several orders of magnitude larger than the area of the original coated surface.

Calculated zeta potentials were used to compute the predicted interaction between E. coli cells and the quartz surfaces by using DLVO theory equations as developed by Norde and Lyklema (31). Values used in these equations were as follows: Hammaker constant, 10⁻²¹ J; temperature, 25°C; and equivalent cellular radius, 1.5 μm.

Calibration.

TIRAF measurements were calibrated by using hollow polystyrene microspheres (diameter, 1 μm; Polysciences, Warrington, Pa.). These were used as model bacteria in the calibration because they are very similar to bacteria optically while they are much more uniform physically.

The electrophoretic mobility for the microspheres was measured in the manner described above, in high-ionic-strength medium. The mobility was converted to a zeta potential (see Table 1), and DLVO theory was used to calculate a probable microsphere-quartz separation distance of 6 nm for secondary minimum adhesion. The interaction plot for the microspheres is very similar to that of the smooth-swimming bacteria in high-ionic-strength medium as shown in Fig. 2.

TABLE 1.

Zeta potentials for various bacteria and crushed quartz glass as calculated from measured electrophoretic mobilities

Particle or bacterium	Zeta potential (mV)a
Smooth-swimming E. coli in high-ionic-strength (I = 0.2 M) solution	−19.6
Smooth-swimming E. coli in low-ionic strength (I = 0.006 M) solution	−25.1
Hollow polystyrene microspheres	−20.1
Quartz in high-ionic-strength (I = 0.2 M) solution	−18.7
Quartz in low-ionic strength (I = 0.006 M) solution	−56.8
Positively coated quartzb	1.0
Hydrophobic quartzb	−0.5

^aValues have an error of ±2.5 mV.

^bEstimated zeta pontentials.

FIG. 2.

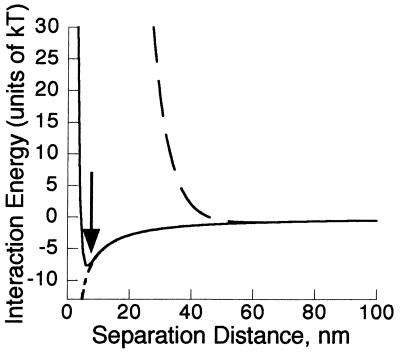
Interaction energy for smooth-swimming E. coli interacting with plain quartz in high-ionic-strength, I = 0.2 M medium (—) (the arrow indicates the location of the secondary minimum); plain quartz in low-ionic-strength, I = 0.006 M medium (- - -); hydrophobically coated quartz in high-ionic-strength medium (-----); and positively coated quartz in high-ionic-strength medium (- - - - -). Note that the last two lines overlay each other.

Microspheres were suspended in phosphate buffer and observed with the TIRAF microscope, and separation distances were calculated in the same manner as for bacterial cells (40), except that no binning was used on the data, and the analysis box was 1 by 162 pixels. The average measured distance was then calculated on the basis of 11 observations and set equal to the predicted 6-nm separation. All measurements of bacterium-surface separation were then corrected by subtraction of the apparent distance of the hollow polystyrene microspheres at the zero point. For further investigation of why TIRAF measurements yield non-zero distances at the zero point, please see the study by Smith and coworkers (32a).

RESULTS

Electrophoretic mobility measurements.

The electrophoretic mobility of both the smooth-swimming cells and the quartz slides used in the TIRAF experiments was measured, converted to zeta potentials, and used in DLVO equations as described in Materials and Methods. The zeta potentials are shown in Table 1, and they fall well within the range of those expected based on the literature (ζ = −31.3 mV at I = 0.001 M, and ζ = −13.7 mV at I = 0.15 M [21]; ζ < 0 mV [32] for E. coli).

Adhesion predictions based on DLVO theory.

Using the data from Table 1, interaction graphs were prepared for all experimental conditions as shown in Fig. 2. In all cases, there is a primary minimum, within ∼2 nm of the surface, which is not shown on the plot. The calculated interaction is shown for smooth-swimming E. coli; the interaction for nonmotile E. coli is essentially the same and is therefore omitted.

For smooth-swimming E. coli and clean quartz at the highest ionic strength, there is a significant barrier of 290 kT to primary minimum adhesion, which is truncated by the top of the graph. However, the secondary interaction minimum at 6 nm is both accessible and deep enough (−7.8 kT) to over come the thermal energy of the bacterium in the direction perpendicular to the glass (0.5 kT) and cause it to reversibly adhere to the surface. For low-ionic strength medium, the energy barrier is both higher (1,840 kT) and wider. The secondary minimum, while present, is smaller than the thermal energy of the bacterium. This means that bacteria are not expected to be significantly attracted to, or spend long times at, this distance from the surface.

Figure 2 also shows the predicted interaction between smooth-swimming E. coli and quartz surfaces coated with hydrophobic or positively charged compounds. Based on these calculations, it was expected that bacteria would irreversibly adhere to both surfaces and that no reversible adhesion would be observed. Note that adhesion due to van der Waals interactions is predicted for the hydrophobic surface. While a calculation incorporating hydrophobic interactions, such as DLVO-AB (38), was not attempted, the addition of hydrophobic interactions would be expected only to alter the attraction between the cells and the hydrophobic surface at very close range (less than ∼2 nm) (27). Since the experimentally observable result is the same with or without the inclusion of such forces, the calculation was omitted. This does not mean hydrophobic interactions are not present but rather that the predicted result (adhesion) will not be altered by their inclusion.

The estimated surface charges used in the DLVO equations are fairly conservative. In the case of OTS, the coating molecule is neutral, and the coating procedure eliminates the groups that otherwise lead to the negative surface charge. Therefore, the estimated surface charge was made very close to zero but slightly negative to account for unreacted surface groups. With a positive surface coating there will be no barrier to adhesion in the primary minimum, and varying the positive charge from 1 to 100 mV moves the expected descent to minimum outward only 3 nm. Therefore, the exact magnitude of the positive charge was not needed to predict the result.

Morisaki at al. (29) have proposed that the interactions of bacteria with surfaces may be better modeled by using zeta potentials obtained from soft particle theory rather than from the Smoluchowski equation. Recalculations based on this theory for similar E. coli bacteria (26a) show that the net effect is to increase the attractiveness of the surface for the cells but not so much so as to reverse any expected trend. Bacteria at high ionic strength would be expected to adhere in the primary energy minimum, as would cells interacting with positive and hydrophobic surfaces. Cells interacting with plain quartz at low ionic strength would still face a significant energy barrier to attachment which, although smaller than predicted with the Smoluchowski equation, would still be insurmountable.

Separation distances between bacteria and the surface resulting from different treatments.

By TIRAF microscopy, both smooth-swimming and nonmotile E. coli were observed and the distances between the cells and the surface were measured (40). Both types of cells interacted with the clean quartz surface at high ionic strength; at low ionic strength, immobilized cells were not seen for either cell type. These data are summarized in Table 2. The results of interaction measurements between smooth-swimming cells and positively charged and hydrophobic surfaces in high-ionic-strength buffer are shown in Table 3. The thickness of the coatings (∼5 nm) used to alter the surface properties of the quartz is most likely responsible for the larger separation distances observed for those immobilized cells. Each of the different categories of bacterial interaction shown in Fig. 1 was observed during TIRAF experiments, with the exception of bulk swimming (“A” and “B”), which occurs too far from the interface to be observed by TIRAF microscopy. The average distances were computed separately for each of these different types of interactions.

TABLE 2.

Summary of the behavior of nonmotile E. coli HCB 137 and smooth-swimming E. coli HCB437 near a clean quartz surface in solutions of different ionic strengths, corrected by calibration with hollow polystyrene particles^a

Cell type	High-ionic-strength medium (I = 0.2 M)		Low-ionic-strength medium (I = 0.006 M)
	n	Avg distance in nm ± SD (range)	n	Avg distance in nm ± SD (range)
Immobilized HCB137 (nonmotile)	162	8 ± 2 (−2-22)	0	NO
Immobilized HCB437	26	9 ± 3 (−2-31)	0	NO
Tethered HCB437	61	12 ± 2 (−2-36)	72	28 ± 2 (5-47)
Swimming (reversibly adhering) HCB437	152	32 ± 1 (13-47)	150	37 ± 1 (23-50)

^aUncertainties are expressed as 95% confidence limits; the ranges of observed values are given in parentheses. Negative distances do not reflect true distances but rather are within an experimental error of zero. Uncorrected distances for high ionic strengths were previously published (40). NO, none observed; n, number of observations.

TABLE 3.

Summary of TIRAF measurements on smooth-swimming E. coli HCB437 interacting with a positively charged or hydrophobically coated surface and corrected by calibration with hollow polystyrene particles^a

Cell type	Positive surface		Hydrophobic surface
	n	Avg distance in nm ± SD (range)	n	Avg distance in nm ± SD (range)
Immobilized	46	21 ± 3 (7-38)	65	18 ± 2 (4-39)
Tethered	30	31 ± 1 (25-39)	0	NO
Swimming (rever- sibly adhering)	61	34 ± 2 (23-48)	5	40 ± 3 (36-44)

^aUncertainties are expressed as 95% confidence limits; the range of observed values is given in parentheses. NO, none observed; n, number of observations.

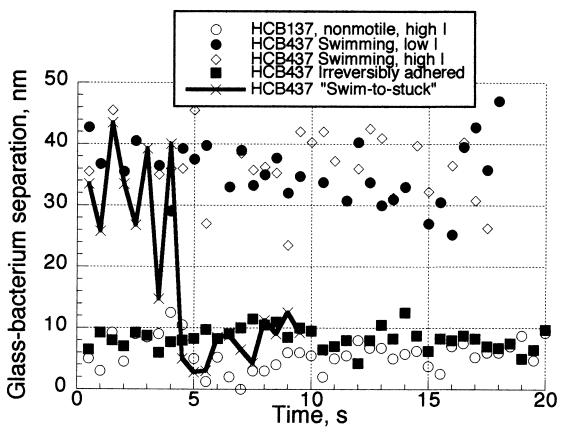
While the different modes of adhesion were distinct in terms of the behavior and separation distance for the cells, bacteria were capable of switching between modes. Figure 3 shows the separation distance over time for five individual E. coli interacting with clean quartz as a representative sampling of the behavior of the larger population which was studied. One of the swimming cells proceeded to become irreversibly adhered; this can be clearly seen in TIRAF images, where the cell is swimming for several movie frames before becoming immobilized. The difference in state was also confirmed by the change in distance; the switch from separation O(35 nm) to that of O(10 nm) exactly corresponded to the end of independent motility by the cell.

FIG. 3.

Separation distance of both smooth-swimming and nonmotile E. coli interacting with the clean quartz surface over time in both high- and low-ionic-strength solutions.

To complement the TIRAF measurements, observations were made of smooth-swimming bacteria interacting with the coated and clean quartz glass by using a phase-contrast microscope; the results are shown in Table 4. The purpose of these observations was to obtain an approximate percentage of the bacterial population engaging in each type of adhesion behavior. While cells were observed in all cases engaging in all behaviors, not all of these behaviors were equally probable. For example, while reversibly adhering (swimming) cells were observed in all cases, this behavior was most prevalent on clean quartz but was very rare on the coated quartz surfaces.

TABLE 4.

Summary of visual observations of the interaction of smooth-swimming E. coli HCB437 and variously treated glass surfaces^a

Cell type	% Content
	Clean quartz	Hydrophobic quartz	Positive quartz
Immobilized	8	85	75
Tethered	2	2	5
Swimming	90	13	20

^aCells in high-ionic-strength buffer were exposed to the surface for ca. 5 min and observed. Note that the percentages are approximate and that the observations were made with the coated slide on the bottom of the sample chamber.

DISCUSSION

DLVO theory is not consistent with all observations.

There are two possible interpretations of the distance data given in Tables 2 and 3 in terms of DLVO theory. The first hypothesis is that immobilized bacteria are adhering in the primary free-energy minimum, whereas swimming bacteria are found in the secondary free-energy minimum. This interpretation provides a workable model for the observed data on clean quartz; the adhesion barrier is relatively low at high ionic strength, and therefore immobilized bacteria are present, while at low ionic strength the barrier is much too high and broad to pass. The secondary minimum is closer to the surface at high ionic strength, which implies that swimming cells should be closer to the surface, and indeed they are.

However, this interpretation is not consistent with results from experiments varying both the ionic strength and the surface coating. In observations with TIRAF microscopy, a conventional microscope, as well as with a tracking microscope (41), bacteria were observed swimming near the surface in both high- and low-ionic-strength solutions. This finding was contrary to expectations based on DLVO theory: the predicted depth of the secondary minimum at low ionic strength is not sufficient to hold a cell near the surface, and yet cells are still found swimming near the surface for significant periods of time. Also, while the energy barrier is relatively small at high ionic strength, it is still sufficiently large to repel cells. In the case of both hydrophobic and positively charged surfaces, there was no barrier to primary minimum adhesion; this implies that all cells near the surface should become irreversibly adhered to it. However, the presence of bacteria swimming along the surface adds further evidence that DLVO-type interactions alone cannot explain the reversible adhesion of swimming bacteria to the surface. Finally, the separation distance between the swimming cells and the surface is greater than the expected range of electrostatic and van der Waals forces. Therefore, an alternate interpretation of the data was sought.

We propose that the immobilized bacteria are adhering in the secondary free-energy minimum or the primary minimum, when there is no secondary minimum, and that electrostatics, while important in cell immobilization, is not the driving force that keeps swimming cells near the surface. In this interpretation, the reason that immobilized cells are seen at high but not at low ionic strength is that the secondary minimum is sufficient to hold a cell at high but not at low ionic strength. This interpretation also addresses the issues raised in the previous paragraph. Cells do not need to overcome a large free-energy barrier to become immobilized on the surface. Also, the corrected separation distance observed for immobilized cells on clean quartz is within error of that predicted by theory (Fig. 2). However, the question that still remains is: what force is holding cells near the surface while swimming, if not DLVO-type forces? Our explanation for why bacteria spend long times swimming along the surface is that hydrodynamic forces are responsible, and these are discussed below.

Hydrodynamics of near-surface swimming.

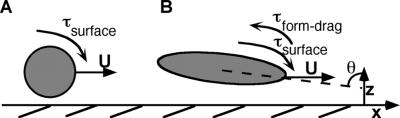
Objects translating in a viscous medium very close to a solid boundary are subject to a number of forces not felt by the object in bulk fluid. As shown in the classic work of Goldman et al., a sphere translating very close to a plane wall will experience a torque due to the increased drag on the side nearest the surface, which will cause it to “roll” forward along the surface (15). Cells swimming parallel to a wall experience not only the “wall” torque but additional torque resulting from their nonspherical shape. As approximate prolate spheroids (rather than spheres), cells experience drag created as the object turns downward (resulting from the first torque) and presents more cross-sectional area to the direction of flow. This is illustrated in Fig. 4.

FIG. 4.

Torques experienced by objects translating along a surface at constant velocity (U). (A) A sphere experiences increased drag on the side closest to the solid, creating a torque (“surface torque”), which causes it to roll forward. (B) A prolate spheroid experiences the surface torque, as well as an additional torque (“form-drag torque”) due to the increased cross-sectional area presented to flow as the cell rotates. These torques balance at an equilibrium angle (θ).

We believe it is this combination of torques which cause bacteria to spend such long times near the surface. While reversibly adhering cells are too far away to experience DLVO-type forces, they are close enough to feel a hydrodynamic effect from the surface (15, 19). In modeling the behavior of a prolate spheroid with aspect ratio of ɛ = 0.5 (similar to E. coli) moving parallel to a plane wall, Hsu and Ganatos (19) found that such an object would experience these two competing torques, resulting in the object settling in to an equilibrium angle with respect to the surface, at which the torques precisely balance. Bacteria moving along a surface will therefore tend to adopt a “nose down” orientation toward the surface. According to this model, cells swimming 100 nm (the closest separation for which Hsu and Ganatos show results) from the surface would be expected to adopt an equilibrium angle of ca. 60° to the surface normal (19). This equilibrium angle is a weak function of separation distance between the cell and the wall, as well as the aspect ratio of the cell (19).

This swimming position in turn leads to the observed “adhesion,” which may be better termed “hydrodynamic entrapment.” Because of their orientation, cells are constantly trying to swim into the surface. While there is some wobble about this equilibrium orientation (which allows cells to occasionally escape), cells swimming in this orientation are effectively trapped. An interesting note is that this sort of hydrodynamic entrapment would not be expected for spherical cells, because they do not experience the “form drag” as a prolate spheroid does. Observation of the spherical Rhodobacter sphaeroides supports this claim (M. A.-S. Vigeant, J. P. Armitage, and R. M. Ford, unpublished data); cells were observed to trace semicircular paths on the surface but only for very brief intervals (1 to 2 s) before leaving the surface.

The logical question which springs from this assertion is this: why then do not all of the cells become irreversibly adhered on the surface if they are always swimming toward it? In the case of low-ionic-strength solution, one could argue that the cells are running into the energy barrier. However, in all other cases, cells which continue to move toward the surface should eventually adhere. The key to this problem is that the drag force experienced by a cell swimming toward the surface is much greater than the drag force experienced by a cell moving along the surface (18). When a cell is approaching the surface at an angle, as is the case here, only part of its velocity is devoted to movement in the z-direction (U cosθ, where θ is the angle between the major axis of the cell and the surface normal, as shown in Fig. 4). At the relatively shallow equilibrium angle exhibited by swimming cells, this is the smaller portion of the cells' velocity and is insufficient to overcome the drag which opposes movement toward the surface. Therefore, it is possible for hydrodynamic entrapment to occur, without cells necessarily becoming irreversibly adhered.

However, cells swimming along the surface do occasionally adhere to the surface or may also occasionally leave the surface. This is because the cells are experiencing yet another torque, this one resulting from the rotation of their flagella. Flagellar rotation has the net effect of propelling the cells forward, but over the course of the rotation the cells will “wobble” (4); since the driving force of the flagella is relatively strong, this wobble may be sufficient to move the cells from their equilibrium angle. They will return to the angle if they “wobble” into an angle which allows them to continue to move along the surface. But if they wobble into an angle in which they are either facing away from the surface or directly toward it, they may leave the surface or become irreversibly attached, respectively. The same may be said for a tumble event; while the smooth-swimming cells studied here were not capable of tumbling, wild-type cells which do tumble would be expected to escape hydrodynamic entrapment more rapidly. Observations of wild-type E. coli have shown that they do indeed leave the surface more often than smooth-swimming cells (12) an observation which supports the hydrodynamic entrapment explanation. The kinetic energy of moving cells is too small to escape from a secondary minimum in a high-ionic-strength medium (12); however, if the cells are instead hydrodynamically trapped, there is no energy barrier and all that is needed is the change of swimming direction which a tumble provides.

Cells begin to swim along the surface due to the difference in drag forces that cells experience when moving parallel or perpendicular to the surface. Cells usually approach the surface at some angle other than parallel to the surface normal. There is a large drag force countering movement perpendicular to the surface; the drag force on parallel movement, while larger than that in the bulk, is not as large as that for perpendicular movement (19). Therefore, cells approaching the surface will tend to turn and swim along it, as long as the drag on perpendicular movement exceeds that for parallel movement. This was observed by P. D. Frymier et al. (12) with a tracking microscope. In the special case where the cell is approaching the surface at a very steep angle, that is, nearly perpendicular to the surface, the cell will not experience this force to turn and swim along the surface (19). Rather, the cell may proceed to swim directly into the secondary minimum (or the primary minimum) and adhere irreversibly to the surface, as has occasionally been observed (39). The exact approach angle at which direct adhesion occurs will depend on the speed at which the cell is swimming and the size of the cell and will be determined in future modeling work. Cells that are wobbling due to flagellar motion may also attain a configuration where one or more flagella strike the surface, which may result in tethered cells or the cells' irreversible adhesion.

Analysis by compartments.

Marshall et al. (26) proposed that cell adhesion to surfaces was a multiple-step process wherein cells first loosely associate with a surface reversibly before proceeding to a more firm, irreversible attachment. The data presented here quantitatively demonstrate a distance change associated with motile cells proceeding from a surface-associated state where they can swim relatively far from, but parallel to, the surface, to a more firmly attached state, closer to the surface, where they become immobilized. Other researchers have observed cells become attached to the surface (see, for example, reference 22) and have also observed, qualitatively, that immobilized cells are closer to the surface at high ionic strength than at low ionic strength (10, 11). In the present work, these results have been augmented with more quantitative measurement of distances, as well as the observation of motile cells.

Combining the theory of Marshall with our observations and DLVO theory, we propose that bacterial adhesion can be analyzed in terms of capture and repulsion distances. That is, the type of interaction (reversible adhesion or irreversible adhesion) observed between a cell and the surface is determined by the cells' distance from the surface, which in turn determines which forces are acting on the cell.

Bacteria encounter a surface because of diffusion, motility, or chemotaxis and start swimming parallel to it. These cells sample a range of surface separation distances and approach angles as they swim. The majority of cells will approach the surface at such an angle that they begin swimming parallel to it, maintaining an equilibrium angle relative to the surface. If there is a secondary minimum present, bacteria that deviate from the equilibrium angle sufficiently (due to flagellar wobble) may approach the surface closely enough to become entrapped by van der Waals and electrostatic interactions. Closer to the surface than the secondary minimum is the repulsive layer; cells cannot move this close to the surface because of the strong free-energy barrier. In cases where there is no energy barrier, such as the coated surfaces, cells wandering as close as the “capture distance” (the separation distance at which the primary minimum becomes sufficiently deep to overcome the thermal and kinetic energy of the bacterium) will become irreversibly adhered.

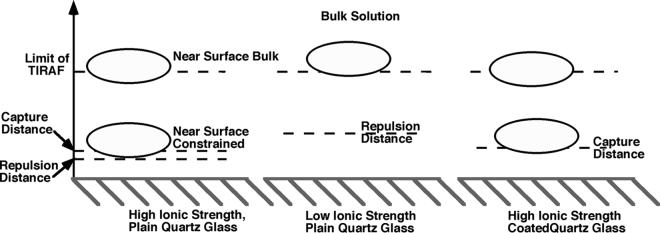
Viewed in the way detailed above, our analysis describes a three-compartment model of bacterium-surface interactions. The three compartments are bulk fluid, near-surface bulk, and near-surface constrained. The boundaries of these layers are formed by the hydrodynamic boundary layer, the secondary minimum, and the free-energy barrier (progressing from the bulk fluid to the surface). This is illustrated in Fig. 5. Bacteria may reside in any of three compartments in the fluid, determined by their distance from the surfaces, and the forces which are relevant at that point.

FIG. 5.

The three-compartment model, shown in application to the different cases encountered in bacterial adhesion experiments. Cells in the near-surface bulk compartment are capable of lateral motion, whereas cells in the near-surface constrained compartment are not.

The distance at which an approaching cell leaves bulk solution and enters the near-surface bulk compartment is the distance at which the cell must turn to swim along the surface, based on the hydrodynamic drag. Prolate spheroids such as E. coli moving parallel to surfaces will experience these hydrodynamic effects at a much greater separation distance than they experience electrostatic or van der Waals effects (<20 nm). According to the models of Hsu and Ganatos (19), average-sized E. coli (5 μm by 2 μm) would feel some effect of the wall as much as 10 μm away. The exact distance at which this occurs will depend on the size of the cell and the angle of its approach to the surface. Cells approaching the surface nearly parallel to the surface normal may skip the near-surface bulk compartment altogether and go into the near-surface constrained compartment.

The boundary of the near-surface constrained compartment is established by the secondary minimum of the surface interaction free energy or by the point at which the primary minimum becomes sufficiently deep to capture the cell, when no secondary minimum is present, as in the case of the coated surfaces. Once a cell is this distance from the surface, it may become held there more strongly through attachment of its flagella to the surface. However, this attachment will not necessarily draw the bacterium closer to the surface, because the cell body may be repelled by the free-energy barrier, which forms the lower boundary of the near-surface constrained compartment, when a secondary minimum is present.

This explains how DLVO forces can affect the average separation distance between a swimming cell and the surface without the cell necessarily ever entering the secondary minimum. In the low-ionic-strength experiments, the random movement of bacteria near the surface was constrained by the large free-energy barrier; cells were prohibited from sampling small surface separation distances. This can be seen in Fig. 3, where the distance over time curves show that the swimming cells at both high and low ionic strengths appear to sample the same distance ranges, save that periodically the high-ionic-strength bacterium approaches the surface more closely. In high-ionic-strength solution, cells are free to move much closer to the surface; however, when wandering into the secondary minimum, they might get trapped, as happens with the “swim-to-stuck” bacterium in Fig. 3.

In conclusion, we have developed a consistent conceptual model describing how E. coli cells interact with smooth surfaces. Cells may be thought of as residing in one of three compartments. The cells farther than ∼20 nm from the surface feel no additional forces, those within ∼10 μm to ∼20 nm of the surface feel the hydrodynamic effect of the surface, and those closer than ∼20 nm from the surface feel both the hydrodynamic and the electrostatic influences of the surface. This satisfactorily explains why cells are found swimming near the surface under conditions of varying ionic strengths along negative, positive, or hydrophobically coated surfaces; in order to control bacterium-surface interactions, manipulation of conditions affecting the hydrodynamics of the surface environment will need to be attempted.