Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles

Abstract

Although genomewide RNA expression analysis has become a routine tool in biomedical research, extracting biological insight from such information remains a major challenge. Here, we describe a powerful analytical method called Gene Set Enrichment Analysis (GSEA) for interpreting gene expression data. The method derives its power by focusing on gene sets, that is, groups of genes that share common biological function, chromosomal location, or regulation. We demonstrate how GSEA yields insights into several cancer-related data sets, including leukemia and lung cancer. Notably, where single-gene analysis finds little similarity between two independent studies of patient survival in lung cancer, GSEA reveals many biological pathways in common. The GSEA method is embodied in a freely available software package, together with an initial database of 1,325 biologically defined gene sets.

Genomewide expression analysis with DNA microarrays has become a mainstay of genomics research (1, 2). The challenge no longer lies in obtaining gene expression profiles, but rather in interpreting the results to gain insights into biological mechanisms.

In a typical experiment, mRNA expression profiles are generated for thousands of genes from a collection of samples belonging to one of two classes, for example, tumors that are sensitive vs. resistant to a drug. The genes can be ordered in a ranked list L, according to their differential expression between the classes. The challenge is to extract meaning from this list.

A common approach involves focusing on a handful of genes at the top and bottom of L (i.e., those showing the largest difference) to discern telltale biological clues. This approach has a few major limitations.

(i) After correcting for multiple hypotheses testing, no individual gene may meet the threshold for statistical significance, because the relevant biological differences are modest relative to the noise inherent to the microarray technology.

(ii) Alternatively, one may be left with a long list of statistically significant genes without any unifying biological theme. Interpretation can be daunting and ad hoc, being dependent on a biologist's area of expertise.

(iii) Single-gene analysis may miss important effects on pathways. Cellular processes often affect sets of genes acting in concert. An increase of 20% in all genes encoding members of a metabolic pathway may dramatically alter the flux through the pathway and may be more important than a 20-fold increase in a single gene.

(iv) When different groups study the same biological system, the list of statistically significant genes from the two studies may show distressingly little overlap (3).

To overcome these analytical challenges, we recently developed a method called Gene Set Enrichment Analysis (GSEA) that evaluates microarray data at the level of gene sets. The gene sets are defined based on prior biological knowledge, e.g., published information about biochemical pathways or coexpression in previous experiments. The goal of GSEA is to determine whether members of a gene set S tend to occur toward the top (or bottom) of the list L, in which case the gene set is correlated with the phenotypic class distinction.

We used a preliminary version of GSEA to analyze data from muscle biopsies from diabetics vs. healthy controls (4). The method revealed that genes involved in oxidative phosphorylation show reduced expression in diabetics, although the average decrease per gene is only 20%. The results from this study have been independently validated by other microarray studies (5) and by in vivo functional studies (6).

Given this success, we have developed GSEA into a robust technique for analyzing molecular profiling data. We studied its characteristics and performance and substantially revised and generalized the original method for broader applicability.

In this paper, we provide a full mathematical description of the GSEA methodology and illustrate its utility by applying it to several diverse biological problems. We have also created a software package, called gsea-p and an initial inventory of gene sets (Molecular Signature Database, MSigDB), both of which are freely available.

Methods

Overview of GSEA. GSEA considers experiments with genomewide expression profiles from samples belonging to two classes, labeled 1 or 2. Genes are ranked based on the correlation between their expression and the class distinction by using any suitable metric (Fig. 1A).

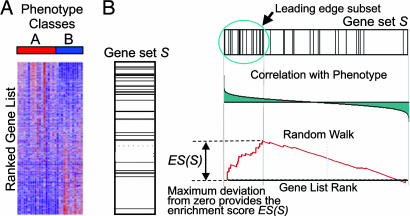
Fig. 1.

A GSEA overview illustrating the method. (A) An expression data set sorted by correlation with phenotype, the corresponding heat map, and the “gene tags,” i.e., location of genes from a set S within the sorted list. (B) Plot of the running sum for S in the data set, including the location of the maximum enrichment score (ES) and the leading-edge subset.

Given an a priori defined set of genes S (e.g., genes encoding products in a metabolic pathway, located in the same cytogenetic band, or sharing the same GO category), the goal of GSEA is to determine whether the members of S are randomly distributed throughout L or primarily found at the top or bottom. We expect that sets related to the phenotypic distinction will tend to show the latter distribution.

There are three key elements of the GSEA method:

• Step 1: Calculation of an Enrichment Score. We calculate an enrichment score (ES) that reflects the degree to which a set S is overrepresented at the extremes (top or bottom) of the entire ranked list L. The score is calculated by walking down the list L, increasing a running-sum statistic when we encounter a gene in S and decreasing it when we encounter genes not in S. The magnitude of the increment depends on the correlation of the gene with the phenotype. The enrichment score is the maximum deviation from zero encountered in the random walk; it corresponds to a weighted Kolmogorov–Smirnov-like statistic (ref. 7 and Fig. 1B).

• Step 2: Estimation of Significance Level of ES. We estimate the statistical significance (nominal P value) of the ES by using an empirical phenotype-based permutation test procedure that preserves the complex correlation structure of the gene expression data. Specifically, we permute the phenotype labels and recompute the ES of the gene set for the permuted data, which generates a null distribution for the ES. The empirical, nominal P value of the observed ES is then calculated relative to this null distribution. Importantly, the permutation of class labels preserves gene-gene correlations and, thus, provides a more biologically reasonable assessment of significance than would be obtained by permuting genes.

• Step 3: Adjustment for Multiple Hypothesis Testing. When an entire database of gene sets is evaluated, we adjust the estimated significance level to account for multiple hypothesis testing. We first normalize the ES for each gene set to account for the size of the set, yielding a normalized enrichment score (NES). We then control the proportion of false positives by calculating the false discovery rate (FDR) (8, 9) corresponding to each NES. The FDR is the estimated probability that a set with a given NES represents a false positive finding; it is computed by comparing the tails of the observed and null distributions for the NES.

The details of the implementation are described in the Appendix (see also Supporting Text, which is published as supporting information on the PNAS web site).

We note that the GSEA method differs in several important ways from the preliminary version (see Supporting Text). In the original implementation, the running-sum statistic used equal weights at every step, which yielded high scores for sets clustered near the middle of the ranked list (Fig. 2 and Table 1). These sets do not represent biologically relevant correlation with the phenotype. We addressed this issue by weighting the steps according to each gene's correlation with a phenotype. We noticed that the use of weighted steps could cause the distribution of observed ES scores to be asymmetric in cases where many more genes are correlated with one of the two phenotypes. We therefore estimate the significance levels by considering separately the positively and negatively scoring gene sets (Appendix; see also Fig. 4, which is published as supporting information on the PNAS web site).

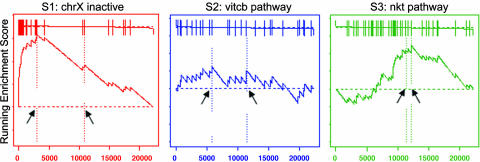
Fig. 2.

Original (4) enrichment score behavior. The distribution of three gene sets, from the C2 functional collection, in the list of genes in the male/female lymphoblastoid cell line example ranked by their correlation with gender: S1, a set of chromosome X inactivation genes; S2, a pathway describing vitamin c import into neurons; S3, related to chemokine receptors expressed by T helper cells. Shown are plots of the running sum for the three gene sets: S1 is significantly enriched in females as expected, S2 is randomly distributed and scores poorly, and S3 is not enriched at the top of the list but is nonrandom, so it scores well. Arrows show the location of the maximum enrichment score and the point where the correlation (signal-to-noise ratio) crosses zero. Table 1 compares the nominal P values for S1, S2, and S3 by using the original and new method. The new method reduces the significance of sets like S3.

Table 1. P value comparison of gene sets by using original and new methods.

Gene set	Original method nominal P value	New method nominal P value
S1: chrX inactive	0.007	<0.001
S2: vitcb pathway	0.51	0.38
S3: nkt pathway	0.023	0.54

Our preliminary implementation used a different approach, familywise-error rate (FWER), to correct for multiple hypotheses testing. The FWER is a conservative correction that seeks to ensure that the list of reported results does not include even a single false-positive gene set. This criterion turned out to be so conservative that many applications yielded no statistically significant results. Because our primary goal is to generate hypotheses, we chose to use the FDR to focus on controlling the probability that each reported result is a false positive.

Based on our statistical analysis and empirical evaluation, GSEA shows broad applicability. It can detect subtle enrichment signals and it preserves our original results in ref. 4, with the oxidative phosphorylation pathway significantly enriched in the normal samples (P = 0.008, FDR = 0.04). This methodology has been implemented in a software tool called gsea-p.

The Leading-Edge Subset. Gene sets can be defined by using a variety of methods, but not all of the members of a gene set will typically participate in a biological process. Often it is useful to extract the core members of high scoring gene sets that contribute to the ES. We define the leading-edge subset to be those genes in the gene set S that appear in the ranked list L at, or before, the point where the running sum reaches its maximum deviation from zero (Fig. 1B). The leading-edge subset can be interpreted as the core of a gene set that accounts for the enrichment signal.

Examination of the leading-edge subset can reveal a biologically important subset within a gene set as we show below in our analysis of P53 status in cancer cell lines. This approach is especially useful with manually curated gene sets, which may represent an amalgamation of interacting processes. We first observed this effect in our previous study (4) where we manually identified two high scoring sets, a curated pathway and a computationally derived cluster, which shared a large subset of genes later confirmed to be a key regulon altered in human diabetes.

High scoring gene sets can be grouped on the basis of leading-edge subsets of genes that they share. Such groupings can reveal which of those gene sets correspond to the same biological processes and which represent distinct processes.

The gsea-p software package includes tools for examining and clustering leading-edge subsets (Supporting Text).

Variations of the GSEA Method. We focus above and in Results on the use of GSEA to analyze a ranked gene list reflecting differential expression between two classes, each represented by a large number of samples. However, the method can be applied to ranked gene lists arising in other settings.

Genes may be ranked based on the differences seen in a small data set, with too few samples to allow rigorous evaluation of significance levels by permuting the class labels. In these cases, a P value can be estimated by permuting the genes, with the result that genes are randomly assigned to the sets while maintaining their size. This approach is not strictly accurate: because it ignores gene-gene correlations, it will overestimate the significance levels and may lead to false positives. Nonetheless, it can be useful for hypothesis generation. The gsea-p software supports this option.

Genes may also be ranked based on how well their expression correlates with a given target pattern (such as the expression pattern of a particular gene). In Lamb et al. (10), a GSEA-like procedure was used to demonstrate the enrichment of a set of targets of cyclin D1 list ranked by correlation with the profile of cyclin D1 in a compendium of tumor types. Again, approximate P values can be estimated by permutation of genes.

An Initial Catalog of Human Gene Sets. GSEA evaluates a query microarray data set by using a collection of gene sets. We therefore created an initial catalog of 1,325 gene sets, which we call MSigDB 1.0 (Supporting Text; see also Table 3, which is published as supporting information on the PNAS web site), consisting of four types of sets.

Cytogenetic sets (C₁, 319 gene sets). This catalog includes 24 sets, one for each of the 24 human chromosomes, and 295 sets corresponding to cytogenetic bands. These sets are helpful in identifying effects related to chromosomal deletions or amplifications, dosage compensation, epigenetic silencing, and other regional effects.

Functional sets (C₂, 522 gene sets). This catalog includes 472 sets containing genes whose products are involved in specific metabolic and signaling pathways, as reported in eight publicly available, manually curated databases, and 50 sets containing genes coregulated in response to genetic and chemical perturbations, as reported in various experimental papers.

Regulatory-motif sets (C₃, 57 gene sets). This catalog is based on our recent work reporting 57 commonly conserved regulatory motifs in the promoter regions of human genes (11) and makes it possible to link changes in a microarray experiment to a conserved, putative cis-regulatory element.

Neighborhood sets (C₄, 427 gene sets). These sets are defined by expression neighborhoods centered on cancer-related genes.

This database provides an initial collection of gene sets for use with GSEA and illustrates the types of gene sets that can be defined, including those based on prior knowledge or derived computationally.

gsea-p Software and MSigDB Gene Sets. To facilitate the use of GSEA, we have developed resources that are freely available from the Broad Institute upon request. These resources include the gsea-p software, MSigDB 1.0, and accompanying documentation.

The software is available as (i) a platform-independent desktop application with a graphical user interface; (ii) programs in r and in java that advanced users may incorporate into their own analyses or software environments; (iii) an analytic module in our genepat-tern microarray analysis package (available upon request) (iv) a future web-based GSEA server to allow users to run their own analysis directly on the web site. A detailed example of the output format of GSEA is available on the site, as well as in Supporting Text.

Results

We explored the ability of GSEA to provide biologically meaningful insights in six examples for which considerable background information is available. In each case, we searched for significantly associated gene sets from one or both of the subcatalogs C1 and C2 (see above). Table 2 lists all gene sets with an FDR ≤ 0.25.

Table 2. Summary of GSEA results with FDR ≤ 0.25.

Gene set	FDR
Data set: Lymphoblast cell lines
Enriched in males
chrY	<0.001
chrYp11	<0.001
chrYq11	<0.001
Testis expressed genes	0.012
Enriched in females
X inactivation genes	<0.001
Female reproductive tissue expressed genes	0.045
Data set: p53 status in NCl-60 cell lines
Enriched in p53 mutant
Ras signaling pathway	0.171
Enriched in p53 wild type
Hypoxia and p53 in the cardiovascular system	<0.001
Stress induction of HSP regulation	<0.001
p53 signaling pathway	<0.001
p53 up-regulated genes	0.013
Radiation sensitivity genes	0.078
Data set: Acute leukemias
Enriched in ALL
chr6q21	0.011
chr5q31	0.046
chr13q14	0.057
chr14q32	0.082
chr17q23	0.071
Data set: Lung cancer outcome, Boston study
Enriched in poor outcome
Hypoxia and p53 in the cardiovascular system	0.050
Aminoacyl tRNA biosynthesis	0.144
Insulin upregulated genes	0.118
tRNA synthetases	0.157
Leucine deprivation down-regulated genes	0.144
Telomerase up-regulated genes	0.128
Glutamine deprivation down-regulated genes	0.146
Cell cycle checkpoint	0.216
Data set: Lung cancer outcome, Michigan study
Enriched in poor outcome
Glycolysis gluconeogenesis	0.006
vegf pathway	0.028
Insulin up-regulated genes	0.147
Insulin signalling	0.170
Telomerase up-regulated genes	0.188
Glutamate metabolism	0.200
Ceramide pathway	0.204
p53 signalling	0.179
tRNA synthetases	0.225
Breast cancer estrogen signalling	0.250
Aminoacyl tRNA biosynthesis	0.229

For detailed results, see Table 4, which is published as supporting information on the PNAS web site.

Male vs. Female Lymphoblastoid Cells. As a simple test, we generated mRNA expression profiles from lymphoblastoid cell lines derived from 15 males and 17 females (unpublished data) and sought to identify gene sets correlated with the distinctions “male>female” and “female>male.”

We first tested enrichment of cytogenetic gene sets (C₁). For the male>female comparison, we would expect to find the gene sets on chromosome Y. Indeed, GSEA produced chromosome Y and the two Y bands with at least 15 genes (Yp11 and Yq11). For the female>male comparison, we would not expect to see enrichment for bands on chromosome X because most X linked genes are subject to dosage compensation and, thus, not more highly expressed in females (12).

We next considered enrichment of functional gene sets (C₂). The analysis yielded three biologically informative sets. One consists of genes escaping X inactivation [merged from two sources (13, 14) that largely overlap], discovering the expected enrichment in female cells. Two additional sets consist of genes enriched in reproductive tissues (testis and uterus), which is notable inasmuch as mRNA expression was measured in lymphoblastoid cells. This result is not simply due to differential expression of genes on chromosomes X and Y but remains significant when restricted to the autosomal genes within the sets (Table 5, which is published as supporting information on the PNAS web site).

p53 Status in Cancer Cell Lines. We next examined gene expression patterns from the NCI-60 collection of cancer cell lines. We sought to use these data to identify targets of the transcription factor p53, which regulates gene expression in response to various signals of cellular stress. The mutational status of the p53 gene has been reported for 50 of the NCI-60 cell lines, with 17 being classified as normal and 33 as carrying mutations in the gene (15).

We first applied GSEA to identify functional gene sets (C₂) correlated with p53 status. The p53⁺>p53^– analysis identified five sets whose expression is correlated with normal p53 function (Table 2). All are clearly related to p53 function. The sets are (i) a biologically annotated collection of genes encoding proteins in the p53-signaling pathway that causes cell-cycle arrest in response to DNA damage; (ii) a collection of downstream targets of p53 defined by experimental induction of a temperature-sensitive allele of p53 in a lung cancer cell line; (iii) an annotated collection of genes induced by radiation, whose response is known to involve p53; (iv) an annotated collection of genes induced by hypoxia, which is known to act through a p53-mediated pathway distinct from the response pathway to DNA damage; and (v) an annotated collection of genes encoding heat shock-protein signaling pathways that protect cells from death in response to various cellular stresses.

The complementary analysis (p53^–>p53⁺) identifies one significant gene set: genes involved in the Ras signaling pathway. Interestingly, two additional sets that fall just short of the significance threshold contain genes involved in the Ngf and Igf1 signaling pathways. To explore whether these three sets reflect a common biological function, we examined the leading-edge subset for each gene set (defined above). The leading-edge subsets consist of 16, 11, and 13 genes, respectively, with each containing four genes encoding products involved in the mitogen-activated protein kinase (MAPK) signaling subpathway (MAP2K1, RAF1, ELK1, and PIK3CA) (Fig. 3). This shared subset in the GSEA signal of the Ras, Ngf, and Igf1 signaling pathways points to up-regulation of this component of the MAPK pathway as a key distinction between the p53^– and p53⁺ tumors. (We note that a full MAPK pathway appears as the ninth set on the list.)

Fig. 3.

Leading edge overlap for p53 study. This plot shows the ras, ngf, and igf1 gene sets correlated with P53^– clustered by their leading-edge subsets indicated in dark blue. A common subgroup of genes, apparent as a dark vertical stripe, consists of MAP2K1, PIK3CA, ELK1, and RAF1 and represents a subsection of the MAPK pathway.

Acute Leukemias. We next sought to study acute lymphoid leukemia (ALL) and acute myeloid leukemia (AML) by comparing gene expression profiles that we had previously obtained from 24 ALL patients and 24 AML patients (16).

We applied GSEA to the cytogenetic gene sets (C₁), expecting that chromosomal bands showing enrichment in one class would likely represent regions of frequent cytogenetic alteration in one of the two leukemias. The ALL>AML comparison yielded five gene sets (Table 2), which could represent frequent amplification in ALL or deletion in AML. Indeed, all five regions are readily interpreted in terms of the current knowledge of leukemia.

The 5q31 band is consistent with the known cytogenetics of AML. Chromosome 5q deletions are present in most AML patients, with the critical region having been localized to 5q31 (17). The 17q23 band is a site of known genetic rearrangements in myeloid malignancies (18). The 13q14 band, containing the RB locus, is frequently deleted in AML but rarely in ALL (19). Finally, the 6q21 band contains a site of common chromosomal fragility and is commonly deleted in hematologic malignancies (20).

Interestingly, the remaining high scoring band is 14q32. This band contains the Ig heavy chain locus, which includes >100 genes expressed almost exclusively in the lymphoid lineage. The enrichment of 14q32 in ALL thus reflects tissue-specific expression in the lineage rather than a chromosomal abnormality.

The reciprocal analysis (AML>ALL) yielded no significantly enriched bands, which likely reflects the relative infrequency of deletions in ALL (21). The analyses with the cytogenetic gene sets thus show that GSEA is able to identify chromosomal aberrations common in particular cancer subtypes.

Comparing Two Studies of Lung Cancer. A goal of GSEA is to provide a more robust way to compare independently derived gene expression data sets (possibly obtained with different platforms) and obtain more consistent results than single gene analysis. To test robustness, we reanalyzed data from two recent studies of lung cancer reported by our own group in Boston (22) and another group in Michigan (23). Our goal was not to evaluate the results reported by the individual studies, but rather to examine whether common features between the data sets can be more effectively revealed by gene-set analysis rather than single-gene analysis.

Both studies determined gene-expression profiles in tumor samples from patients with lung adenocarcinomas (n = 62 for Boston; n = 86 for Michigan) and provided clinical outcomes (classified here as “good” or “poor” outcome). We found that no genes in either study were strongly associated with outcome at a significance level of 5% after correcting for multiple hypotheses testing.

From the perspective of individual genes, the data from the two studies show little in common. A traditional approach is to compare the genes most highly correlated with a phenotype. We defined the gene set S_Boston to be the top 100 genes correlated with poor outcome in the Boston study and similarly S_Michigan from the Michigan study. The overlap is distressingly small (12 genes in common) and is barely statistically significant with a permutation test (P = 0.012). When we added a Stanford study (24) involving 24 adenocarcinomas, the three data sets share only one gene in common among the top 100 genes correlated with poor outcome (Fig. 5 and Table 6, which are published as supporting information on the PNAS web site). Moreover, no clear common themes emerge from the genes in the overlaps to provide biological insight.

We then explored whether GSEA would reveal greater similarity between the Boston and Michigan lung cancer data sets. We compared the gene set from one data set, S_Boston, to the entire ranked gene list from the other. The set S_Boston shows a strong significant enrichment in the Michigan data (NES = 1.90, P < 0.001). Conversely, the poor outcome set S_Michigan is enriched in the Boston data (NES = 2.13, P < 0.001). GSEA is thus able to detect a strong common signal in the poor outcome data (Fig. 6, which is published as supporting information on the PNAS web site).

Having found that GSEA is able to detect similarities between independently derived data sets, we then went on to see whether GSEA could provide biological insight by identifying important functional sets correlated with poor outcome in lung cancer. For this purpose, we performed GSEA on the Boston and Michigan data with the C₂ catalog of functional gene sets. Given the relatively weak signals found by conventional single-gene analysis in each study, it was not clear whether any significant gene sets would be found by GSEA. Nonetheless, we identified a number of genes sets significantly correlated with poor outcome (FDR ≤ 0.25): 8 in the Boston data and 11 in the Michigan data (Table 2). (The Stanford data had no genes or gene sets significantly correlated with outcome, which is most likely due to the smaller number of samples and many missing values in the data.)

Moreover, there is a large overlap among the significantly enriched gene sets in the two studies. Approximately half of the significant gene sets were shared between the two studies and an additional few, although not identical, were clearly related to the same biological process. Specifically, we found a set up-regulated by telomerase (25), two different tRNA synthesis-related sets, two different insulin-related sets, and two different p53-related sets. Thus, a total of 5 of 8 of the significant sets in Boston are identical or related to 6 of 11 in Michigan.

To provide greater insight, we next extended the analysis to include sets beyond those that met the FDR ≤ 0.25 criterion. Specifically, we considered the top scoring 20 gene sets in each of the three studies (60 gene sets) and their corresponding leading-edge subsets to better understand the underlying biology in the poor outcome samples (Table 4). Already in the Boston/Michigan overlap, we saw evidence of telomerase and p-53 response as noted above. Telomerase activation is believed to be a key aspect of pathogenesis in lung adenocarcinoma and is well documented as prognostic of poor outcome in lung cancer.

In all three studies, two additional themes emerge around rapid cellular proliferation and amino acid biosynthesis (Table 7, which is published as supporting information on the PNAS web site):

1. We see striking evidence in all three studies of the effects of rapid cell proliferation, including sets related to Ras activation and the cell cycle as well as responses to hypoxia including angiogenesis, glycolysis, and carbohydrate metabolism. More than one-third of the gene sets (23 of 60) are related to such processes. These responses have been observed in malignant tumor microenvironments where enhanced proliferation of tumor cells leads to low oxygen and glucose levels (26). The leading-edge subsets of the associated significant gene sets include hypoxia-response genes such as HIF1A, VEGF, CRK, PXN, EIF2B1, EIF2B2, EIF2S2, FADD, NFKB1, RELA, GADD45A, and also Ras/MAPK activation genes (HRAS, RAF1, and MAP2K1).

2. We find strong evidence for the simultaneous presence of increased amino acid biosynthesis, mTor signaling, and up-regulation of a set of genes down-regulated by both amino acid deprivation and rapamycin treatment (27). Supporting this finding are 17 gene sets associated with amino acid and nucleotide metabolism, immune modulation, and mTor signaling. Based on these results, one might speculate that rapamycin treatment might have an effect on this specific component of the poor outcome signal. We note there is evidence of the efficacy of rapamycin in inhibiting growth and metastatic progression of non-small cell lung cancer in mice and human cell lines (28).

Our analysis shows that we find much greater consistency across the three lung data sets by using GSEA than by single-gene analysis. Moreover, we are better able to generate compelling hypotheses for further exploration. In particular, 40 of the 60 top scoring gene sets across these three studies give a consistent picture of underlying biological processes in poor outcome cases.

Discussion

Traditional strategies for gene expression analysis have focused on identifying individual genes that exhibit differences between two states of interest. Although useful, they fail to detect biological processes, such as metabolic pathways, transcriptional programs, and stress responses, that are distributed across an entire network of genes and subtle at the level of individual genes.

We previously introduced GSEA to analyze such data at the level of gene sets. The method was initially used to discover metabolic pathways altered in human diabetes and was subsequently applied to discover processes involved in diffuse large B cell lymphoma (29), nutrient-sensing pathways involved in prostate cancer (30), and in comparing the expression profiles of mouse to those of humans (31). In the current paper, we have refined the original approach into a sensitive, robust analytical method and tool with much broader applicability along with a large database of gene sets. GSEA can clearly be applied to other data sets such as serum proteomics data, genotyping information, or metabolite profiles.

GSEA features a number of advantages when compared with single-gene methods. First, it eases the interpretation of a large-scale experiment by identifying pathways and processes. Rather than focus on high scoring genes (which can be poorly annotated and may not be reproducible), researchers can focus on gene sets, which tend to be more reproducible and more interpretable. Second, when the members of a gene set exhibit strong cross-correlation, GSEA can boost the signal-to-noise ratio and make it possible to detect modest changes in individual genes. Third, the leading-edge analysis can help define gene subsets to elucidate the results.

Several other tools have recently been developed to analyze gene expression by using pathway or ontology information, e.g., (32–34). Most determine whether a group of differentially expressed genes is enriched for a pathway or ontology term by using overlap statistics such as the cumulative hypergeometric distribution. We note that this approach is not able to detect the oxidative phosphorylation results discussed above (P = 0.08, FDR = 0.50). GSEA differs in two important regards. First, GSEA considers all of the genes in an experiment, not only those above an arbitrary cutoff in terms of fold-change or significance. Second, GSEA assesses the significance by permuting the class labels, which preserves gene-gene correlations and, thus, provides a more accurate null model.

The real power of GSEA, however, lies in its flexibility. We have created an initial molecular signature database consisting of 1,325 gene sets, including ones based on biological pathways, chromosomal location, upstream cis motifs, responses to a drug treatment, or expression profiles in previously generated microarray data sets. Further sets can be created through genetic and chemical perturbation, computational analysis of genomic information, and additional biological annotation. In addition, GSEA itself could be used to refine manually curated pathways and sets by identifying the leading-edge sets that are shared across diverse experimental data sets. As such sets are added, tools such as GSEA will help link prior knowledge to newly generated data and thereby help uncover the collective behavior of genes in states of health and disease.

Appendix: Mathematical Description of Methods

Inputs to GSEA.

1. Expression data set D with N genes and k samples.

2. Ranking procedure to produce Gene List L. Includes a correlation (or other ranking metric) and a phenotype or profile of interest C. We use only one probe per gene to prevent overestimation of the enrichment statistic (Supporting Text; see also Table 8, which is published as supporting information on the PNAS web site).

3. An exponent p to control the weight of the step.

4. Independently derived Gene Set S of N_H genes (e.g., a pathway, a cytogenetic band, or a GO category). In the analyses above, we used only gene sets with at least 15 members to focus on robust signals (78% of MSigDB) (Table 3).

Enrichment Score ES(S).

1. Rank order the N genes in D to form L = {g₁,...,g_N} according to the correlation, r(g_j)= r_j, of their expression profiles with C.

2. Evaluate the fraction of genes in S (“hits”) weighted by their correlation and the fraction of genes not in S (“misses”) present up to a given position i in L.

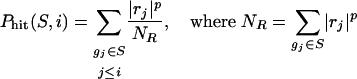[1]

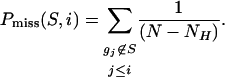The ES is the maximum deviation from zero of P_hit – P_miss. For a randomly distributed S, ES(S) will be relatively small, but if it is concentrated at the top or bottom of the list, or otherwise nonrandomly distributed, then ES(S) will be correspondingly high. When p = 0, ES(S) reduces to the standard Kolmogorov–Smirnov statistic; when p = 1, we are weighting the genes in S by their correlation with C normalized by the sum of the correlations over all of the genes in S. We set p = 1 for the examples in this paper. (See Fig. 7, which is published as supporting information on the PNAS web site.)

Estimating Significance. We assess the significance of an observed ES by comparing it with the set of scores ES_NULL computed with randomly assigned phenotypes.

1. Randomly assign the original phenotype labels to samples, reorder genes, and re-compute ES(S).

2. Repeat step 1 for 1,000 permutations, and create a histogram of the corresponding enrichment scores ES_NULL.

3. Estimate nominal P value for S from ES_NULL by using the positive or negative portion of the distribution corresponding to the sign of the observed ES(S).

Multiple Hypothesis Testing.

1. Determine ES(S) for each gene set in the collection or database.

2. For each S and 1000 fixed permutations π of the phenotype labels, reorder the genes in L and determine ES(S, π).

3. Adjust for variation in gene set size. Normalize the ES(S, π) and the observed ES(S), separately rescaling the positive and negative scores by dividing by the mean of the ES(S, π) to yield the normalized scores NES(S, π) and NES(S) (see Supporting Text).

4. Compute FDR. Control the ratio of false positives to the total number of gene sets attaining a fixed level of significance separately for positive (negative) NES(S) and NES(S, π).

Create a histogram of all NES(S, π) over all S and π. Use this null distribution to compute an FDR q value, for a given NES(S) = NES* ≥ 0. The FDR is the ratio of the percentage of all (S, π) with NES(S, π) ≥ 0, whose NES(S, π) ≥ NES*, divided by the percentage of observed S with NES(S) ≥ 0, whose NES(S) ≥ NES*, and similarly if NES(S) = NES* ≤ 0.