Metabolic Control Analysis of Glycerol Synthesis in Saccharomyces cerevisiae

Abstract

Glycerol, a major by-product of ethanol fermentation by Saccharomyces cerevisiae, is of significant importance to the wine, beer, and ethanol production industries. To gain a clearer understanding of and to quantify the extent to which parameters of the pathway affect glycerol flux in S. cerevisiae, a kinetic model of the glycerol synthesis pathway has been constructed. Kinetic parameters were collected from published values. Maximal enzyme activities and intracellular effector concentrations were determined experimentally. The model was validated by comparing experimental results on the rate of glycerol production to the rate calculated by the model. Values calculated by the model agreed well with those measured in independent experiments. The model also mimics the changes in the rate of glycerol synthesis at different phases of growth. Metabolic control analysis values calculated by the model indicate that the NAD⁺-dependent glycerol 3-phosphate dehydrogenase-catalyzed reaction has a flux control coefficient (Cv1J) of approximately 0.85 and exercises the majority of the control of flux through the pathway. Response coefficients of parameter metabolites indicate that flux through the pathway is most responsive to dihydroxyacetone phosphate concentration (RDHAPJ = 0.48 to 0.69), followed by ATP concentration (RATPJ = −0.21 to −0.50). Interestingly, the pathway responds weakly to NADH concentration (RNADHJ = 0.03 to 0.08). The model indicates that the best strategy to increase flux through the pathway is not to increase enzyme activity, substrate concentration, or coenzyme concentration alone but to increase all of these parameters in conjunction with each other.

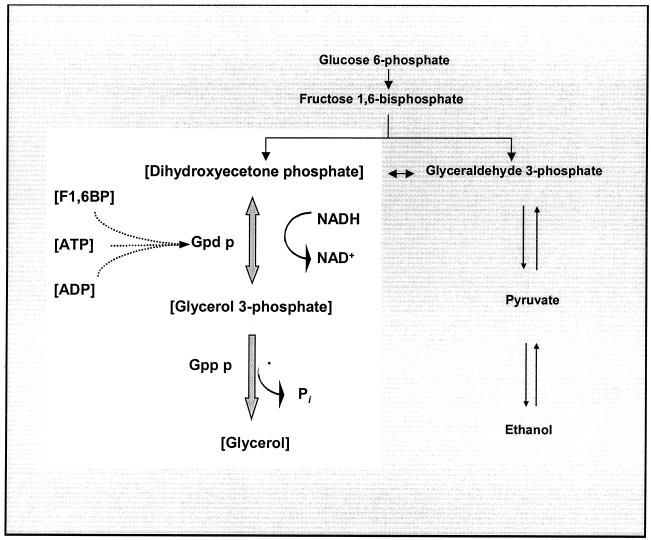
Glycerol is a major by-product of ethanol fermentation by Saccharomyces cerevisiae. Glycerol is formed by the reduction of dihydroxyacetone phosphate (DHAP) to glycerol 3-phosphate concomitant with NADH oxidation by NAD⁺-dependent glycerol 3-phosphate dehydrogenase (Gpd p) (EC 1.1.1.8) (2, 20, 30). Glycerol 3-phosphate is then dephosphorylated to glycerol by glycerol 3-phosphatase (Gpp p) (EC 3.1.3.21) (20, 34) (Fig. 1). Under anaerobic and glucose-repressing growth conditions, it is widely believed that yeast cells produce glycerol to help maintain a cytosolic redox state conducive to sustain glycolytic catabolism (1, 35, 55). The inability of a mutant defective in glycerol production to grow under anaerobic conditions bears out this observation (5, 10, 17, 33). Glycerol has another important physiological function, in that it is the primary compatible solute in S. cerevisiae and is accumulated intracellularly when cells are exposed to decreased extracellular water activity (3, 4, 12, 28, 41, 43).

FIG. 1.

The glycerol synthesis pathway in S. cerevisiae. The highlighted area indicates the metabolites and enzymes considered in the kinetic model.

The value of creating an industrial strain that produces larger-than-normal amounts of glycerol is illustrated by the number of recent studies undertaken to increase glycerol production in industrial and laboratory yeast strains (39, 44, 46). So far, three strategies have been employed to attain this objective: one approach has been to alter growth conditions (21), a second has been to improve wine-producing strains by classical breeding techniques involving spore-cell hybridization followed by repeated back-crossing (19, 39), and a third has been to improve strains through molecular manipulation by overexpressing either the GPD1 or the GPD2 gene, which encode isoenzymes of NAD-dependent glycerol-3-phosphate dehydrogenase, or by deleting either the acetaldehyde dehydrogenase or the pyruvate decarboxylase gene (44, 45, 46).

These strategies have proven to be successful as a result of the present understanding of the physiological conditions under which increased glycerol formation occurs. Concomitant with increased glycerol synthesis, decreased levels of ethanol occur, which is considered to be a positive attribute in the production of alcoholic beverages (40). However, increased quantities of other by-products such as acetaldehyde and acetate have also been observed, and in the case of wine production a number of these products are considered unfavorable. These induced alterations to the metabolism of yeast cells seem to be related to a redox imbalance created by the increased flux of carbon towards the formation of glycerol.

In light of an incomplete understanding of glycerol synthesis, we report here on the construction of a detailed kinetic model of the glycerol synthesis pathway, which has been used to evaluate and to quantify the parameters that control the rate of glycerol synthesis. Attention has been focused on glycerol synthesis and not on glycerol assimilation, since the enzymes involved in glycerol assimilation (glycerol kinase [Gut1p] and mitochondrial FAD⁺-dependant glycerol 3-phosphate dehydrogenase [Gut2p]) are repressed by glucose at the transcriptional level during fermentative growth (38, 48). The model provides insight into the roles of and extents to which the redox balance, substrate availability, modifier concentrations, and intrinsic enzyme capacities control the amount of glycerol produced. The data generated by the model may shed some light on the inherent capacities of the pathway and may provide a more insightful approach to controlled glycerol synthesis by S. cerevisiae.

MATERIALS AND METHODS

Strain.

An S. cerevisiae haploid laboratory strain, W303-1A (MATaleu2-3/112 ura3-1 trp1-1 his3-11/15 ade2-1 can1-100 GAL SUC2 mal0) (53), was used in this study.

Media and culture conditions.

In all experiments, yeast cells were cultured in a medium consisting of glucose (2 g/liter) and yeast nitrogen base (YNB) (6.7 g/liter) (United States Biological, Swampscott, Mass.) with amino acids (adenine [10 mg/liter]; Arg, His, Lys, Met, Trp, and Ura [20 mg/liter]; Ile, Leu, Ser, Thr, Tyr, and Val [30 mg/liter]; and Phe [50 mg/liter]) (Sigma-Aldrich, St. Louis, Mo.). All yeast cells were maintained on agar plates at 4°C for short-term storage and at −80°C in 15% (wt/vol) glycerol for extended storage. Ten-milliliter starter cultures were used to inoculate 100- and 250-ml batch cultures in 250- and 500-ml Erlenmeyer flasks, respectively. Cultures were incubated at 30°C and 140 rpm on an orbital shaker (New Brunswick Scientific Co., Edison, N.J.).

Sampling of yeast for metabolite extractions.

Volumes of culture containing at least 100 mg (dry weight) of biomass were harvested. The culture was rapidly filtered under vacuum through Millipore glass fiber prefilters (0.45-μm pore size, 47-mm diameter). While still on the filter, the cells were instantly frozen with liquid nitrogen. For determination of intracellular glycerol, cells were first rinsed with 5 ml of 60% methanol solution kept at −40°C (rinse step; complete within 5 s) before being frozen with liquid nitrogen and stored as described previously (49).

Determination of yeast dry weight.

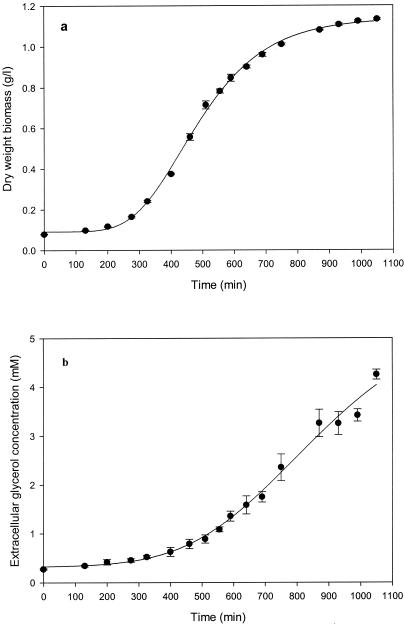
Volumes of 20 ml (from early exponential to mid-exponential phase [optical density at 600 nm {OD₆₀₀}, 0 to 0.7; approximately 0 to 450 min]) and 10 ml (late exponential to early stationary phase [OD₆₀₀, 0.7 to 1.2; approximately 450 to 1,100 min]) (Fig. 2) of culture were filtered under vacuum through Whatman glass microfiber filters (25-mm diameter; catalog no. 1822 025). The filters were dried at 80°C until a constant weight was obtained (usually 24 h).

FIG. 2.

Growth of S. cerevisiae (a) and extracellular glycerol production (b) during shake flask cultivation in glucose-YNB medium at 30°C. Each data point shows the mean of triplicate determinations, with error bars indicating the standard error. Values for the growth curve and change in extracellular glycerol concentration were fitted to a five-parameter sigmoidal function (correlation coefficients [r²] were above 0.989 for both curves).

Extraction of metabolites.

Intracellular metabolites were extracted at three different phases of growth: early exponential phase (OD₆₀₀, approximately 0.4; 400 to 430 min), mid-exponential phase (OD₆₀₀, approximately 0.7; 600 to 630 min), and early stationary phase (OD₆₀₀, approximately 1.1; 970 to 1,000 min). ATP and ADP were extracted in a 35% perchloric acid solution; DHAP, fructose 1,6-bisphosphate (F1,6BP), and NAD⁺ were extracted in a 6% perchloric acid solution; and NADH was extracted with boiling alkalized ethanol (9). Glycerol was extracted in boiling 0.1 M Tris-HCl buffer (pH 7.7) (56).

Assay of metabolites.

Intracellular metabolite concentrations were determined enzymatically by measuring the oxidation or reduction of NADH or NAD⁺, respectively, at 340 nm in a Beckman Coulter DU640 spectrophotometer (9). Extracellular glycerol was determined by high-performance liquid chromatography (Dionex). Anion-exchange chromatography followed by pulsed amperometric detection (gold electrode detector) was used with a CarboPac MA1 analytical column plus a CarboPac MA1 guard column, run at a flow rate of 0.25 ml/min, eluted with a 125 mM NaOH solution. Samples were diluted with double-distilled milli-Q water and filtered through 0.22-μm-pore-size filters (Millex). To calculate the intracellular concentrations of metabolites, a yeast cytosolic volume of 1.67 μl per mg of dry yeast biomass was assumed (18).

Preparation of cell extracts for enzyme activity assays.

Yeast cells were harvested at different growth phases as described above. Cells were washed twice in ice-cold TRED buffer (10 mM triethanolamine, 1 mM EDTA, 2 mM 2-mercaptoethanol, 1 mM dithiothreitol, pH 7.5) and resuspended in the same buffer with a 0.5 μl of protease inhibitor mix (70 mg of phenylmethylsulfonyl fluoride per ml, 1 mg of pepstatin per ml, and 12 mg of antipain per ml) (Sigma-Aldrich) per ml.

Extracts were prepared by disrupting cells with acid-washed glass beads (400 to 625 μm; Sigma-Aldrich) twice for 2 min, with a 1-min interval of cooling on ice. Cell debris was removed by centrifugation at 24,000 × g for 30 min, and the supernatant was removed and kept on ice until assayed for enzyme activity.

Enzyme assays.

Enzyme activity in cell extracts were assayed using a Beckman Coulter DU640 spectrophotometer. One unit of enzyme activity is defined as the rate of conversion of 1 μmol of substrate or product per min, and specific activities are given as units per milligram of protein. For modeling purposes the specific activities were converted to millimolar per minute, assuming a yeast cytosolic volume of 3.75 μl per mg of protein (18).

Gpd p activity was assayed by measuring the maximum rate of dl-glycerol 3-phosphate oxidation and NAD⁺ reduction (32). This assay measures the reverse V_max of the Gpd p-catalyzed reaction, which was subsequently converted to the forward V_max by use of a conversion factor of 33 (2). Determinations were started by the addition of 20 to 320 μl of a 10-fold-diluted cell extract to the cuvette, resulting in a total reaction mixture volume of 1.0 ml. This yielded linear reactions for 1 min under standard conditions with an absorption change of less than 0.1/min.

Gpp p activity was assayed as previously described (34) with minor modifications. Determinations were started by the addition of 20 to 320 μl of a 10-fold-diluted cell extract to a test tube, resulting in a total reaction mixture volume of 1.1 ml. After the reaction was started, five samples of 200 μl were removed from the reaction mixture at 15-s intervals and instantly quenched in a chilled 600-μl solution of 1% (vol/vol) sodium dodecyl sulfate, 100 mM zinc acetate, and 15 mM ammonium molybdate (pH 5.0) (8). Released inorganic phosphate was analyzed (7), and the reaction rate was calculated from the slope of the linear plot of released phosphate versus time.

Protein determination.

Protein concentrations were estimated by determining the absorbance of dilute samples at 280 nm in a 100-μl quartz microcuvette (50). OD₂₈₀ values were compared with those of a bovine serum albumin standard (Sigma-Aldrich). These values were verified by comparing them to values obtained by the Bradford method of protein analyses (13).

Calculation of the glycerol synthesis rate.

The changes in extracellular glycerol concentration and biomass versus time from three experiments were averaged and plotted. Because extracellular glycerol and biomass readings were taken approximately only every 60 min, a five-parameter sigmoidal function was fitted to each curve (Fig. 2) (correlation coefficients [r²] were above 0.989 for both curves), which enabled us to determine, with more accuracy, the rate at which glycerol was produced at very small time intervals. The glycerol production rate was calculated as the change in the amount of extracellular glycerol per gram (dry weight) of biomass per minute (moles per gram per minute). The change in intracellular glycerol was not taken into account, since intracellular glycerol never exceeded 0.2% of the total glycerol content of the flask. The model calculates the rate of glycerol production as flux (J) through the pathway and expresses it as the rate of change in intracellular glycerol concentration (millimolar per minute). To compare values calculated by the model with those determined experimentally, the measured glycerol synthesis rate (moles per gram per minute) was converted to the rate of change in intracellular glycerol concentration (millimolar per minute) by converting biomass to intracellular volume (1 g [dry weight] of biomass ≈ 1.67 ml of cytosolic volume [18]).

Kinetic model.

A kinetic model of glycerol synthesis via glycerol 3-phosphate (Fig. 1) was constructed by using the metabolic simulation program Gepasi (29). Three phases of growth, as described above, were modeled. The parameters for each phase of growth were derived from in vivo values measured at each of the growth phases. Steady-state calculations of the kinetic model were performed on an IBM-compatible personal computer.

Details on the kinetics of the enzyme-catalyzed reactions that form the core reaction sequence of the model and the aspects of metabolic control analysis (MCA) used in the presentation of results are provided in the appendix.

RESULTS

Construction of the kinetic model.

In S. cerevisiae, oxidation of NADH and reduction of DHAP by Gpd p results in the formation of glycerol 3-phosphate, which is then dephosphorylated to glycerol by Gpp p. To assess the importance of and to quantify the control that various pathway parameters have on flux, a kinetic model of the glycerol synthesis pathway was constructed (Fig. 1). The kinetic parameters of the pathway enzymes (Gpd p and Gpp p) were collected from reported values and are presented in Table 1. Maximal enzyme activities were determined at three phases of growth (Table 1). The intracellular concentrations of substrates, cofactors, products, and known effector metabolites were also determined at the above-mentioned phases of growth (Table 2). Except for the variable metabolite glycerol 3-phosphate, all metabolites were fixed and therefore were not modeled as system variables. In the model there are two types of pathway metabolites. The first type are source and sink (i.e., DHAP and glycerol), which must be fixed in order for a steady state to be achieved. The second type are cofactors (ATP, ADP, NADH, and NAD⁺). These were fixed because the model addresses only a small part of metabolism. If cofactors were set free to vary, it would be necessary to include virtually all reactions that require them to provide a realistic result.

TABLE 1.

Kinetic parameters of enzyme-catalyzed reactions

Reaction and parametera	Determined valueb	Published value	Reference(s)
Gpd p (reaction 1)
Vmax		36-61	2, 36
	47 ± 0.14c
	67 ± 0.09d
	46 ± 0.08e
Keq		104	9
KmNADH		0.023	2
KmDHAP		0.54	2
KmNAD+		0.93	2
KmG3P		1.2	32
KiF1,6BP		4.8	2
KiATP		0.73	31
KiADP		2.0	31
Gpp p (reaction 2)
Vmax		18	34
	53 ± 2.8c
	104 ± 6.6d
	68 ± 2.3e
KmG3P		3.5	34
KiPi	1.0f

^aAll maximal rates are in millimolar per minute. All K_m and K_i values are in millimolar.

^bValues are presented as the average from three independent experiments, with standard error of the mean.

^cEarly exponential growth phase (400 to 430 min).

^dMid-exponential growth phase (600 to 630 min).

^eEarly stationary growth phase (970 to 1,000 min).

^fEstimate.

TABLE 2.

Fixed metabolite concentrations of the kinetic model

Metabolite	Intracellular concn (mM) at the following growth phasea:			Published intracellular concn value (mM)	Reference(s)
	Early exponentialb	Mid-exponentialc	Early stationaryd
ATP	2.37 ± 0.12	2.25 ± 0.26	0.4 ± 0.03	0.04-4.8	18, 52
ADP	2.17 ± 0.20	1.31 ± 0.21	0.76 ± 0.07	0.4-4.2	23, 49
NADH	1.87 ± 0.24	0.62 ± 0.40	0.33 ± 0.02	0.23-1.2	23, 49
NAD+	1.45 ± 0.17	0.47 ± 0.09	0.48 ± 0.04	0.8-5.0	23, 49
F1,6BP	6.01 ± 0.35	3.12 ± 0.58	1.27 ± 0.06	0.5	18
DHAP	0.59 ± 0.07	0.31 ± 0.09	0.14 ± 0.02	0.4	18
Glycerol	15.10 ± 1.06	21.00 ± 0.99	6.72 ± 0.26	24	54

^aValues were derived from experiments performed in triplicate and are presented as the average with standard deviation.

^bOD₆₀₀, 0.4 [400 to 430 min].

^cOD₆₀₀, 0.7 [600 to 630 min].

^dOD₆₀₀, 1.1 [970 to 1,000 min].

Evaluation of the kinetic model.

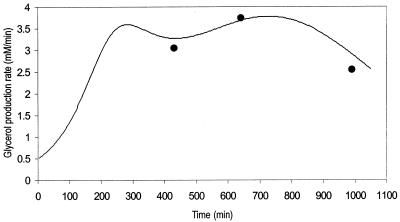
To evaluate the ability of the model to calculate correctly the flux through the pathway, experimental data on the rates of glycerol production at three phases of growth were compared to the rates of glycerol production calculated by the model with parameters determined at the corresponding phases of growth. The parameter values are presented in Tables 1 and 2 and Fig. 3. The results from experiments conducted to measure the rate of glycerol synthesis (Fig. 3) indicate that flux through the pathway steadily increases throughout the initial phase of growth (OD₆₀₀, 0 to 0.1; 0 to 200 min). Thereafter, during the exponential phase of growth (OD₆₀₀, 0.1 to 0.9; 200 to 700 min), flux fluctuates between 3.3 and 3.6 mM/min. Towards the onset of stationary phase (OD₆₀₀, 0.9 to 1.1; ⩾700 min), the rate of glycerol production decreases. This decline could possibly be the result of glucose exhaustion leading to glycerol reoxidation as a result of the derepression of GUT1 and GUT2, but this suggestion requires confirmation, as glucose levels were not analyzed.

FIG. 3.

Rate of glycerol production in S. cerevisiae during shake flask cultivation in glucose-YNB medium (—) compared to glycerol production rate calculated by the model (•). The glycerol production rate was calculated by plotting the change in extracellular glycerol concentration against time and the change in dry weight biomass against time. Both of these plots were fitted to a five-parameter sigmoidal function (correlation coefficients [r²] were above 0.989 for both curves), from which the glycerol production rate was derived. The three glycerol production rates calculated by the model were based on sets of parameters for each growth phase as defined in Tables 1 and 2.

Flux values calculated by the model estimate a rate of glycerol production very similar to the measured rate and closely mimic the change in the rate at which glycerol is synthesized at the corresponding phases of growth (Fig. 3). This suggests that (i) the parameters determined at each phase of growth are an accurate estimation of in vivo metabolite levels and enzyme activities, (ii) the kinetic parameters obtained from the literature are accurate and allow the model to calculate flux in accordance with results obtained experimentally, and (iii) the MCA values calculated by the model will provide a quantitatively accurate estimation of parameters that have a strong control of flux through the pathway.

Modeling results.

Since the flux values calculated by the model agreed well with those determined experimentally, the model has been used to provide insight into how the various known parameters affect the flux of carbon through the glycerol synthesis pathway. The model employs MCA to study the relative control exerted by each reaction on the flux of the system. To relate the effect of a change in a parameter to a change in the steady state of a system, the response coefficient was calculated. The response coefficient (27) allows one to relate the elasticity coefficient (which quantifies the effect of an effector on a reaction) to the flux control coefficient (which quantifies the control that a reaction has on flux) of a step. In this study, response coefficients have been used to provide insight into how various effectors (e.g., substrate or coenzyme) affect the rate of a reaction and in so doing affect flux through the system. Table 3 presents the flux control coefficients calculated by the model for the reactions catalyzed by Gpd p (reaction 1) and Gpp p (reaction 2), based on the requirement that the sum of all flux control coefficients (all reactions) of a pathway is equal to unity (22, 25, 27, 42): 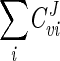= 1. This implies that all of the steps of a pathway exert a certain amount of control on flux through the pathway. 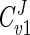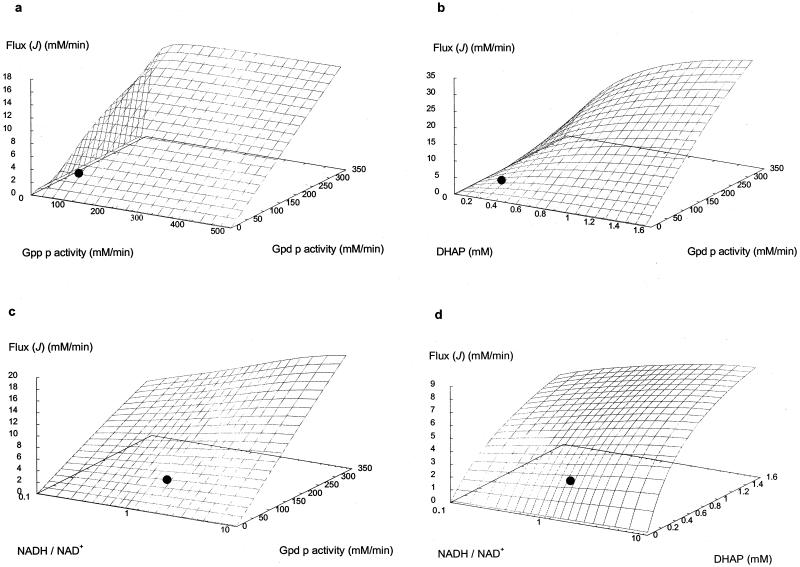The Gpd p reaction flux control coefficient () ranges from 0.83 to 0.88, while the Gpp p reaction flux control coefficient (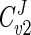) ranges from 0.12 to 0.17. These values were derived from the steady states calculated according to the parameters measured at each of the defined phases of growth. Thus, it is evident that flux through the glycerol synthesis pathway is regulated primarily by the Gpd p reaction. Figure 4a illustrates how flux through the pathway would be influenced by manipulation of the Gpd p and Gpp p activities. The measured activities of both enzymes were increased approximately fivefold at early exponential phase (Table 1). It is clear that increased Gpp p activity is futile unless it is combined with increased Gpd p activity. In contrast, when Gpd p activity is increased fivefold, the model predicts a marked increase in flux (approximately fourfold), which occurs while Gpp p activity remains unaltered from the activity measured.

TABLE 3.

MCA of the effects of various parameters on flux (J) through the glycerol synthesis pathway

Metabolic control coefficienta	Value at the following phase of growth:
	Early exponentialb	Mid-exponentialc	Early stationaryd
Response     coefficients
RNADHJ	0.03	0.05	0.08
RDHAPJ	0.48	0.60	0.69
RNADJ	−0.02	−0.02	−0.03
RF1,6BPJ	−0.16	−0.11	−0.10
RATPJ	−0.42	−0.50	−0.21
RADPJ	−0.14	−0.10	−0.14
Flux control     coefficients
Cv1J	0.85	0.88	0.83
Cv2J	0.15	0.12	0.17

^aMetabolic control coefficients were calculated by the Gepasi simulated model of the glycerol synthesis pathway. v₁, rate of Gpd p-catalyzed reaction; v₂, rate of Gpp p-catalyzed reaction.

^bOD₆₀₀, 0.4 [400 to 430 min].

^cOD₆₀₀, 0.7 [600 to 630 min].

^dOD₆₀₀, 1.1 [970 to 1,000 min].

FIG. 4.

Predictions by the model on the effects of manipulating different sets of parameters. (a) Gpd p and Gpp p activities increased fivefold from the measured activity. (b) Gpd p activity and DHAP concentration increased fivefold from the measured activity and concentration. (c) Gpd p activity and the NADH/NAD ratio increased 5-fold from the measured activity and approximately 10-fold for the ratio. (d) DHAP concentration and the NADH/NAD ratio increased 5-fold from the measured concentration and approximately 10-fold for the ratio, on flux through the glycerol synthesis pathway. (•), reference state, which refers to the flux value calculated by the model as defined by parameter values measured at mid-exponential growth phase (Tables 1 and 2).

Table 3 shows the response coefficients of various metabolites on flux through the pathway. According to MCA, flux through the pathway is controlled predominantly by substrate concentration (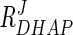= 0.48 to 0.69). By increasing the DHAP concentration fivefold, the system attains a twofold increase in flux (data not shown). This can drastically increase, however, when combined with as little as a twofold change in Gpd p activity (Fig. 4b). Note that by increasing the DHAP concentration in conjunction with Gpd p activity, flux is elevated higher than when Gpd p activity is increased alone.

It is interesting that the coenzyme of the reaction, NADH, does not have as much effect on flux as might be expected (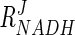= 0.03 to 0.08). Its effect does, however, increase slightly as fermentation progresses. The measured NADH/NAD⁺ ratio at early exponential phase is approximately 1.5, and when this ratio is increased to 5, the resultant increase in flux is less than 25% (data not shown). This may be improved drastically, however, by increasing the NADH/NAD⁺ ratio and Gpd p activity simultaneously (Fig. 4c). The difference in the response that the system has to DHAP and the NADH/NAD⁺ ratio is clearly illustrated in Fig. 4d. Figure 4d also illustrates how concomitant increases in DHAP concentration and the NADH/NAD⁺ ratio can increase the rate of glycerol synthesis to a larger extent than when either of these parameters is increased alone.

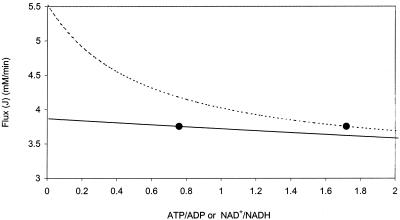
Response coefficients with a negative value indicate that these metabolites have a negative effect on the rate at which glycerol is synthesized. Three of the four metabolites presented, namely, ATP, ADP, and F1,6BP, are known inhibitors with published inhibition constants (Table 1) (2, 31). The other effector, NAD⁺, is a product of the reversible Gpd p reaction and will therefore have a negative effect on the rate of the forward reaction. Of the response coefficients presented, ATP has the strongest negative response on the system (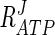= −0.21 to −0.50). An increase in the ATP/ADP ratio to fivefold its measured ratio results in a 10% decrease in flux through the pathway. When the ATP/ADP ratio is halved (reduced from 1.72 to 0.85), flux through the pathway is increased by approximately 10% (Fig. 5). It is noteworthy that a decrease in the NAD⁺/NADH ratio to the same extent results in only a 1% increase in flux through the pathway.

FIG. 5.

Effects of varying the ATP/ADP ratio (- - -) and the NAD⁺/NADH ratio (—) on flux through the glycerol synthesis pathway. The reference state (•) refers to the flux value calculated by the model for the enzyme activities and ATP, ADP, NAD⁺, and NADH levels measured at mid-exponential growth phase (see Tables 1 and 2).

If the moiety-conserved relationship of ATP, ADP, and AMP is ignored and the ATP concentration is increased fivefold, without affecting the concentrations of the other two metabolites, flux through the pathway decreases drastically, from 3.1 to 1.1 mM/min (data not shown). The inhibitory effect of ADP (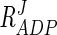= −0.10 to −0.14) is less than that of ATP. When the ADP concentration is increased fivefold, flux decreases by 35%. The response coefficient of F1,6BP (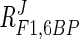= −0.10 to −0.16) is very close to that of ADP, and therefore a fivefold increase in F1,6BP concentration resulted in a 43% decrease in flux.

DISCUSSION

Accuracy of the model's calculations.

The ability of the model to predict flux through the glycerol synthesis pathway was evaluated by selecting three sets of parameters obtained from various stages of growth. In each case the model estimated the rate of glycerol synthesis accurately. The intrinsic activities of both enzymes, at each phase of growth measured, ranged from 46 to 104 mM/min (Table 1). This is well above the maximum steady-state flux of 3.75 mM/min (Fig. 3) calculated by the model. Therefore, the model was accurately defined by all of the parameters employed in its construction. This allowed flux values calculated by the model not only to be of the same magnitude as determined values but also to closely mimic the change in the rate at which glycerol is synthesized at different phases of growth (Fig. 3). In light of this, the model should be viewed as a quantitative tool with the ability to provide insight into the extent to which known parameters of the pathway affect the quantity of flux that passes through it.

Parameters affecting flux.

According to the model developed here, flux through the glycerol synthesis pathway is strongly controlled by the Gpd p reaction (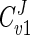= 0.83 to 0.87). This observation is in accordance with a previously determined flux control coefficient of 0.63 (11). The latter value was derived by plotting a double logarithmic plot of the glycerol production rate versus Gpd p activity, where the slope equaled the estimated flux control coefficient. In the study by Blomberg and Adler (11), increased Gpd p activity was the result of yeast cells being conditioned to medium with decreased water activity (0.35 to 0.7 M NaCl). In effect, their observations of increased glycerol productivity take into account not only increased Gpd p activity but also the concomitant alterations to metabolism that would occur under such conditions. The value derived by the model, however, is based on calculations where only perturbations in Gpd p activity occur, since all other parameters are fixed. This may explain the difference between flux control coefficient values calculated by the model and those arrived at experimentally.

An increase in Gpd p activity stimulates glycerol flux significantly (Fig. 4). Similarly, when GPD1 is overexpressed in industrial and laboratory S. cerevisiae strains, the increase in Gpd p activity results in a two- to threefold improvement in glycerol yields from fermentation (44, 46). However, the concomitant enhanced oxidation of NADH affects the redox state of these yeast cells, which results in sluggish growth and increased levels of various by-products, such as acetaldehyde and acetate. As mentioned, increased glycerol production occurs naturally when yeast cells are exposed to hyperosmotic or hypoxic conditions. This is achieved by the upregulation of GPD1, GPD2, GPP1, and GPP2 (3, 5, 10, 11, 17, 57). The model also indicates that maximal flux can be achieved with relatively little alteration in Gpp p activity (Fig. 4a). Recently this was confirmed, when it was shown that overexpression of GPP1 has very little effect on flux. Even when GPP1 is overexpressed in a GPD1-overexpressing strain, there is no enhancement in glycerol production compared to the strain overexpressing GPD1 alone (46).

The optimum rate of DHAP reduction by Gpd p occurs at pH 7.6, and activity declines only at pH values of less than 7 and greater than 8 (2). These pH values fall within the intracellular pH range (pH 6.8 to 7.2) observed in fermenting yeasts (26, 37), and therefore it appears unlikely that pH would affect the glycerol flux under the physiological conditions studied here.

From the response coefficients generated by the model, it is clear that of the two metabolites consumed in the Gpd p reaction, DHAP has more influence on flux through the pathway than NADH. This is most likely due to the fact that Gpd p has a far greater affinity for NADH than for DHAP (Table 1). The physiological NADH concentrations measured at each phase of growth (Table 2) are high enough to ensure that Gpd p is saturated, and therefore increasing the NADH concentration would in fact have very little effect on the forward reaction rate. However, as fermentation progresses, there is a slight increase in the response of the pathway to the NADH concentration, and this may be due to the progressive decrease in concentration of this metabolite (Tables 2 and 3). In contrast, physiological DHAP concentrations were never high enough to saturate Gpd p, and therefore an increase in DHAP concentration is likely to have more influence on flux through the pathway. Compagno et al. (15) have shown that an S. cerevisiae triose phosphate isomerase-deficient mutant with elevated levels of DHAP has a glycerol-producing ability two- to threefold that of a wild-type strain. This mutant, however, grows at a far lower rate due to an NADH-energy shortage (16).

Surprisingly, MCA has shown that glycerol flux is far more sensitive to the ATP/ADP ratio than it is to the NADH/NAD⁺ ratio (Fig. 5). This is due to ATP having a larger negative response coefficient (Table 3). A low ATP/ADP ratio, on the other hand, results in a decrease in the concentration of the metabolite with a stronger response coefficient and an increase in the concentration of the metabolite with a weaker response coefficient, which leads to an increase in flux. However, if the ADP concentration is increased without affecting the ATP concentration, flux decreases. Similarly, if the ATP concentration is increased alone, flux decreases, albeit, in this case, to a far greater extent. In reality, this would occur only to a limited extent, since ATP and ADP variation is constrained by the adenylate kinase equilibrium (51).

The strong response of the Gpd p reaction to ATP concentration has been confirmed experimentally. In extracts prepared from cells cultivated in carbon-limiting chemostats, Gpd p activity was decreased by at least 30% in the presence of 1 mM ATP (36). Similarly, Albertyn et al. (2) reported an 83% inhibition of purified Gpd p activity by 1 mM ATP. Furthermore, S. cerevisiae strains overexpressing GPD1 and/or GPD2 might have a reduced ATP concentration, as carbon is redirected away from the ATP-generating pathway towards glycerol. This could also have a major influence on the glycerol flux.

The effects presented by the model for increased F1,6BP concentration are very similar to those for ADP, in that we could expect a decrease in flux since F1,6BP is a known noncompetitive inhibitor of Gpd p (2). However, under glycolytic conditions, an increase in F1,6BP concentration might result in an increase in the DHAP concentration, since the F1,6BP/DHAP ratio appears to remain relatively constant at different phases of growth (Table 2). Therefore, even if the F1,6BP concentration increases, flux is also likely to increase, due to the response of the pathway to the increase in DHAP concentration, which holds a stronger response coefficient (Table 3).

Recently, Remize et al. (46) showed that glycerol production is enhanced in an FPS1 mutant with uncontrolled efflux of glycerol. This observation led them to suggest that glycerol efflux regulates glycerol production. However, the lack of appropriate kinetic data precluded us from including this component in the analysis of the model.

In conclusion, the model developed here for the glycerol synthesis pathway shows that the rate of glycerol production is controlled primarily by Gpd p activity. There are also a number of metabolites that affect glycerol formation, and at different phases of growth, the concentrations of these metabolites vary (Tables 1, 2, and 3). These alterations are not only in magnitude but also in relative proportions to each other. Thus, the effects of various parameters on the system do not remain constant. In essence, this means that as fermentation progresses, the extent to which the system responds to a parameter alters, and therefore, a parameter that affects flux early in fermentation might not affect flux to the same extent later. Similarly, in other studies, kinetic models have successfully been used to help researchers understand complex cellular systems. For example, a kinetic model of glycolysis in the bloodstream form of Trypanosoma brucei helped identify factors that affect glycolytic flux (6); similarly, the controlling factors of flux through the threonine synthesis pathway in Escherichia coli have been elucidated (14). Another kinetic model also helped identify targets for manipulation in an effort to maximize the efficiency of conversion of hexose to sucrose and to minimize futile cycling in sugar cane (47). The quantitative predictions provided by the model in this study have not only agreed with previous findings on the effects of various parameters on glycerol production but have also allowed us to quantify more accurately the extent to which different parameters affect glycerol flux.

APPENDIX

Kinetics of enzyme-catalyzed reactions.

Gpd p activity was simulated by using a reversible two-substrate, two-product rate equation with noncompetitive inhibition. At physiological concentrations, ATP, ADP, NAD⁺, and F1,6BP inhibit Gpd p activity (2), and these have been included as modifiers. The kinetic equation is

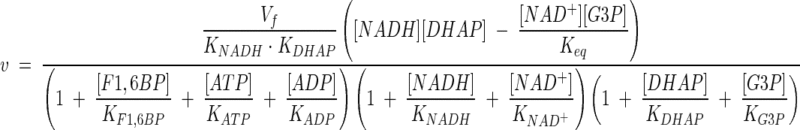(1)

Gpp p activity was simulated by using irreversible noncompetitive inhibition kinetics. The reaction has one substrate and two products, one of which is a modifier (inhibitor). The inhibitor is noncompetitive with the substrate; i.e., its effect is only to decrease the apparent limiting rate. The kinetic equation is

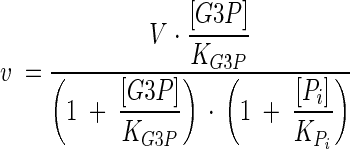(2)

Control analysis.

In this study, MCA has been used to quantify the control that the Gpd p and the Gpp p reactions each exert on the flux of carbon through the glycerol synthesis pathway. MCA provides a means to quantify the link between a system variable (e.g., flux through a pathway or the steady-state concentration of a metabolite) and a system parameter (e.g., activity of an enzyme) in terms of a flux or concentration control coefficient (24, 27). The flux or concentration control coefficient for step i of a system is defined as

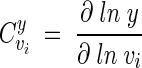(3)

where y is the variable, i is the step (enzyme), and v is the activity of the perturbed step (24, 27). In MCA the properties of an enzyme can be measured relative to a change in a parameter. The sensitivity of an enzyme to a metabolite is known as the elasticity coefficient (24, 27). An elasticity coefficient is defined as the ratio of relative change in local rate to relative change in one parameter (normally the concentration of an effector) and is written as

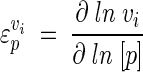(4)

where v is the rate of the enzyme in question and p is the parameter of the perturbation. Each enzyme has as many elasticity coefficients as the number of parameters that affect it. As parameters of the reaction, substrates, products, and modifiers will each have an elasticity coefficient. Unlike control coefficients, elasticity coefficients are not systemic properties. Therefore, to relate the effect of a change in a parameter to a change in the steady state of a system, we make use of a response coefficient. For example, the response coefficient of a modifier on a system will describe how the modifier affects the rate of a specific reaction, and this change in reaction rate will in turn increase or decrease the flux through a system. Thus, the effect of a parameter (p) on a pathway variable (y) is given by the so-called combined response property (27):

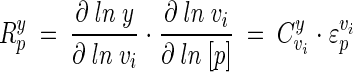(5)