Comparison of Kinematic Outputs and Reliability of Plug-in Gait versus Conventional Gait Model 2 During Cycling

Abstract

Motion analysis is used to measure proper bicycle fit, avoid injury, and improve cycling performance. Small changes in position can impact joint kinematics and risk for overuse injury. Concerns regarding the often-used biomechanical model Plug-in-Gait (PIG) resulted in the creation of Conventional Gait Model 2 (CGM2). This study aims to compare kinematic outputs of these two models for cycling biomechanics plus between-day reliability of each model. Thirty-five participants participated in two experimental sessions. PiG and CGM2 marker sets were applied, and data was collected while cycling between 80–90 rpm. Model outputs were compared using session one kinematic data. Reliability tests used session one and session two data. Differences in kinematics were found between models for hip flexion (CGM2 – PiG mean difference = −8.2° ± 5.2°, p < .001), hip frontal plane (mean = 5.4 ± 4.1°, p < .001), hip transverse plane (mean = −5.3° ± 11.6°, p = .011), knee extension (mean = 1.8° ± 4.2°, p = .015), knee frontal plane (mean = −10.8° ± 9.6°, p < .001), dorsiflexion (mean = −1.7° ± 3.6°, p = 0.005), and plantarflexion (mean = 3.3° ± 5.4°, p < 0.001). CGM2 ICCs were good-to-excellent (> 0.75) for all motions except frontal plane knee motion. PiG ICCs were > 0.75 only for ankle dorsiflexion and plantarflexion. If CGM2 is used to assess bicycle fit, reference values should be adjusted based on the difference between models to ensure an appropriate fit is obtained. CGM2 has better between-day reliability, therefore practitioners may consider using CGM2 for serial fit sessions.

Introduction

Cycling is a form of exercise that improves fitness and cardiovascular health.1 However, the repetitive nature of recreational and competitive cycling lends itself to overuse injuries.2,3 Studies have found that a majority of recreational cyclists have experienced a self-reported overuse injury, with prevalences as high as 85–88%,4,5 though a much lower 2.8% lifetime prevalence was found by du Toit et al.6 when an injury was restricted to incidents that required the cyclist to stop cycling and seek medical treatment. Regardless of population sampling method, the lower extremity is the most cited area of overuse injury, with the knee the most common joint affected in the lower extremity.2,4–6 A properly fitted bicycle reduces the potential for injury and improves cycling efficiency, decreasing the likelihood of overuse injuries.7 One major parameter of correct bicycle fit is the saddle height, typically determined by the angle of the knee at the bottom of the pedal stroke.8 Dynamic measurement of the knee angle at the bottom dead center (BDC) is the recommended method for setting saddle height.9,10 Correct saddle height impacts knee kinematics but also plays a role in the movement of the whole leg and trunk. Therefore, accurate and reliable measures of lower limb kinematics are critical for achieving proper bicycle fit.

Kinematic data have been collected on cyclists using multiple types of motion capture technology.11 For three-dimensional motion analysis (3DMA), Vicon or similar motion capture technology is considered gold standard.9,12,13 The use of motion capture technology and biomechanical models allows for the assessment of joint kinematics while riding to optimize bicycle fit. Much of the research in motion capture has used Vicon’s Plug-in-Gait (PiG) biomechanical model. However, problems have been identified with PiG that would result in potential errors in joint kinematics. For instance, the equations used to derive the hip joint axis of rotation are not as accurate as newer equations.14,15

Updates to PiG are currently available to fix several of these accuracy issues.16 The updated Conventional Gait Model 2 (CGM2) has been published as an open source model17 and has been integrated into Vicon’s Nexus software. Improvements in CGM2 include better hip joint estimation, the use of cluster marker sets and an inverse kinematic approach.16 As a result of CGM2 updates, significant differences in running kinetics and kinematics have been found between the two models.18 Additionally, studies examining between-day reliability have shown CGM2 has greater reliability in runners than PiG for hip flexion, abduction, and internal rotation (IR); knee flexion, abduction, and IR; and ankle dorsiflexion and IR.18 A similar analysis has not been performed for cycling.

The ability for 3DMA to reliably detect small changes in joint angles may allow for early detection of kinematics that can lead to overuse injuries. In runners, alterations in normal sagittal, frontal, and transverse plane motions at the hip and knee have been shown to be associated with running overuse injuries.19–21 In cyclists, sagittal plane knee angles are commonly examined as this angle is closely tied to saddle height and risk for knee pain. However, frontal and transverse hip and knee motions have been proposed to contribute to overuse injuries.12 Therefore, identification of a reliable method of analyzing three-dimensional lower extremity kinematics during cycling may provide a tool to reduce lower extremity overuse injury in cyclists.

An additional challenge of performing clinical kinematic analysis of a cyclist’s riding position is the between-day reliability of 3DMA. Often, changes to a cyclist’s position are performed in one session and subsequent adjustments are performed at a follow-up session based on the cyclist’s feedback. Therefore, reliability between sessions is crucial for this application. While PiG includes a relatively small number of markers and is therefore efficient to apply, numerous studies have found that PiG’s frontal and transverse plane kinematics have poor reliability.22–24 One cause of poor reliability is the location of the lateral thigh and lateral shank markers.

Because PiG uses a constrained three degrees of freedom joint, small differences in marker placement can have large effects on the kinematic outputs of the model.18 For instance, incorrect frontal plane measurement due to marker placement error could result in alterations to bicycle fit that cause an increase in unwanted frontal plane motions, potentially leading to injury.12 CGM2 models use clusters of markers at the thigh and shank, allowing for more accurate and repeatable determination of the frontal plane.16,18

Since there is a scarcity of data comparing these two biomechanical models, the purpose of this study is to compare the kinematic outputs of PiG and CGM2 in recreational cyclists. We hypothesize that there will be differences in output at the hip, knee, and ankle joints. A second purpose of this study is to investigate the between-day reliability of both models. Given what has been studied in other populations, we hypothesize that CGM2 will have better between-day reliability.

Methods

Participants

G*Power software (Heinrich-Heine-University Dusseldorf, Dusseldorf, Germany, version 3.1.9.7) was used to perform an a priori power analysis. A repeated-measures ANOVA from Holliday et al.9 was used to determine an effect size for knee extension angle as this angle is often cited as a clinically useful measure of bicycle fit and was therefore considered a clinically important measure for a power analysis. The Holliday et al. study examined changes in cycling kinematics across three intensities. The results of this study are a portion of a larger study that also examined the impact of three cadences on cycling kinematics; therefore, the power analysis was selected to power the parent study. Using an alpha level of .05 and desired power level of .80, a sample size of 34 was calculated. A drop-out rate of 10% was added for a final sample size of 37. Participants were recruited from the community and local cycling clubs. Participants were screened using the Physical Activity Readiness Questionnaire Plus and allowed to participate if they were deemed safe for exercise. Each participant was a cyclist over the age of 18 with their own bicycle and had a history of at least two hours of cycling per week. Exclusion criteria included participants with a lower extremity or spine injury in the past 6 months, women with a known pregnancy, failure to complete data collection, or inability to meet the power and/or cadence parameters. All participants who completed data collection with viable motion capture data were included in the final analysis. Thirty-seven participants provided documented informed consent (13 female, 24 male, 0 specified otherwise; mean ± standard deviation age 48.6 ±12.3 years; height 1.753 ±0.098m; body mass 76.3 ±14.7kg). The study was approved by the Institutional Review Board at Louisiana State University Health Sciences Center at Shreveport, and the research was carried out fully in accordance with the ethical standards of the International Journal of Exercise Science as described in Navalta, Stone, & Lyons.25

Protocol

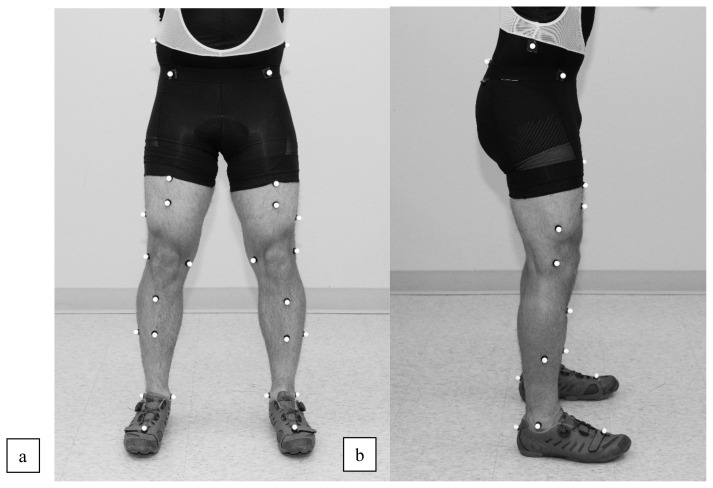
Study participation included two motion capture sessions spaced no more than two weeks apart. Participants used their own bicycle for each session and were instructed to avoid changes in bicycle fit or gear between the two sessions; verbal confirmation was provided by participants before the second session. Anthropometric measurements (height, weight, leg length, knee width, and ankle width) were taken in cycling attire and input into the motion capture software (Vicon Nexus 2.13). Next, PiG and CGM2 marker sets were placed on the participant’s body. Thirty 14mm retroreflective motion capture markers were placed to simultaneously capture CGM2 and PiG data, with two additional iliac crest markers added to the marker set (see Figure 1a, 1b).26 PiG reflective markers (16 total) are contained within CGM2’s marker set (28 total). Markers unique to CGM2 are the two anterior thigh, two anterior tibia, medial knee, and medial ankle markers. The iliac crest marker was added to both marker sets as a reference marker, bringing total number of markers used to 30. CGM2.6 was selected as the CGM2 biomechanical model, which consists of the marker set for CGM2.3 plus a functional knee calibration.17 Markers were added to the bicycle crank arm and pedal spindle to track pedal revolutions. All kinematic data were collected in the motion capture lab using 11 Vicon Vero cameras recording at 100 Hz (Vicon, Los Angeles, CA). Video data were collected using two Vicon Vue cameras. Static and knee joint functional calibrations were performed to begin each motion capture session.

Figure 1.

Marker Placement for the Combined PiG and CGM2 Marker Sets. Note: 1a shows the markers from the anterior view and 1b shows the markers from the lateral view.

Following a successful calibration, the participant began the cycling portion of the motion capture trial. As part of a larger study, data were collected as participants rode at three different cadences (60–70 rpm, 80–90 rpm, and 90–100 rpm). Cadence order was randomized for each participant, but the order was kept the same between motion capture sessions. Only the normal cadence (80–90 rpm) is analyzed here as this is representative of common cadences selected by recreational cyclists.27 Each session began with a five-minute light effort warm-up on the participant’s bicycle, which was mounted to a cycling ergometer (Road Machine Smart2, KurtKinetic). The participant had up to five minutes to practice cycling at three cadences while maintaining consistent power at self-selected light-to-moderate effort. Each cadence was maintained for two minutes. Data were recorded for the first 15 seconds of the second minute of each cadence interval. Ten pedal revolutions were processed, and data were extracted for each kinematic measurement. During the second motion capture session, the participant was given their average cadence and power from each cadence speed and asked to match these parameters.

Biomechanical data were processed in Vicon Nexus 2.13 software. Since the PiG and CGM2.6 data were collected synchronously by the 30-marker set, the same motion capture trial was gap-filled, smoothed, and then processed with each biomechanical model. Gaps in the pelvic markers were filled with rigid body gap filling. Gaps in other body regions were filled with cyclic or spline gap fill. The Woltring filter was used to smooth the trajectory data. Pedal revolutions were marked by the top of the pedal stroke at the 12 o’clock position using crank arm position.

Joint angle data were then exported to Microsoft Excel where the minimum and maximum joint angles for the sagittal, frontal, and transverse motions of the hip, knee, and ankle were identified. These angles were used to determine the peak hip flexion, peak knee extension, peak ankle dorsiflexion, peak ankle plantarflexion, total frontal plane motion of the hip and knee, and total transverse plane motion of the hip and knee for each revolution. The sum of peak abduction and adduction generated total frontal plane motion. The sum of peak internal rotation and external rotation generated total transverse plane motion. Ten revolutions were processed per participant, and the average of each of these angles was calculated and used in the analysis. The listed angles were selected based on their relevance to bicycle fit and cyclist biomechanical analysis, and to avoid inflating family-wise error during statistical assessment to analyze joint measurements that would not yield clinically relevant data. Total frontal and total transverse plane motion were used rather than the constituent components based on the work on Bini et al., who suggest larger ranges in these motions may contribute to lower extremity overuse injuries rather than only considering the individual angles.28

Statistical Analysis

Descriptive statistics (mean ± SD) were calculated for dependent variables as well as cyclist demographics of age, height, weight, body mass index, and years of cycling experience. Paired t-tests were used to examine the primary outcome of differences between PiG and CGM2 model outputs, using the mean of 10 revolutions from session one for each joint angle. Kinematics of the hip, knee, and ankle were compared, and Bonferroni corrections were used for each joint to control family-wise error. The significance level was set at p < 0.0167 at the hip because hip flexion, total frontal plane motion, and total transverse plane motion were compared between models. At the knee, significance was set to p < 0.0167 because knee extension, total frontal plane and total transverse plane motion were compared. At the ankle, only dorsiflexion and plantarflexion were compared so significance was set at p < 0.025. Effect sizes were calculated for the kinematic outcome data using Cohen’s d, and interpreted as 0.2 = small effect, 0.5 = moderate effect, and ≥ 0.8 = large effect. Additionally, Pearson’s r correlations between models were calculated for each kinematic measurement. SPSS statistical package software (version 28; SPSS, Chicago, IL, USA) was used for all statistical analyses.

Outliers were present in several of the joint motions using the SPSS extreme outlier analysis plus visual assessment of the histograms. These data points were retained after confirming they were true outliers and not data entry or data processing errors. Normality was tested using the Shapiro-Wilk test, with non-normal distributions (p < 0.05) found for hip flexion, hip transverse plane motion, knee frontal and transverse plan motion, and ankle plantarflexion. The paired samples t-test was used despite this violation of normality to preserve the meaning of the data. Data were also analyzed with the Wilcoxon Signed Rank test, and no differences in results were found compared to the parametric tests as described in the following sections. Therefore, the paired samples t-test results are reported in the following sections.

Paired t-tests were used to compare mean power and cadence values from session one and two, since alterations in power and cadence can change kinematics and therefore alter reliability testing.9,28 Additionally, paired t-tests were used to compare each model’s session one and session two kinematics (i.e. hip flexion in PiG session one compared to hip flexion in PiG session two). Significant differences between sessions could be caused by changes in pedaling style or differences in marker placement in addition to changes in cadence or power. Significance for these comparisons was set at p < 0.05.

Between-day reliability from session one and session two was assessed for each model using the mean values for each joint angle. Intraclass correlation coefficient (ICC) estimates with 95% confidence intervals were calculated for each kinematic measure, using a single-rater, absolute agreement, 2-way mixed-effects model. Levels of reliability were used from Koo and Li,28 with values less than 0.5 indicating poor reliability, 0.5–0.75 moderate reliability, 0.75–0.9 good reliability, and over 0.9 excellent reliability. The ICC estimates were used to calculate the standard error of measurement (SEM) and minimum detectable change (MDC).31 SEM was calculated by multiplying the standard deviation by √(1 - ICC). MDC was calculated as the product of the SEM × 1.96 × √2.

Results

Thirty-seven recreational cyclists participated in this study. Due to equipment errors during data collection, two participants were dropped for a total N = 35. Table 1 shows the final sample descriptive statistics. No significant differences in power (t(32) = −1.0, p = .312) or cadence (t(34) = 0.246, p = .807) were found between the two data collection sessions. No significant differences in kinematics between session one and session two were found with either model. Two participants’ power data was lost due to software error on one of the two data collection days, resulting in a sample size of 33 for the power data paired t-tests.

Table 1.

Participant Demographics of Participants Included in Data Analysis.

Demographic Measure	Mean	Standard Deviation
N = 35 (female = 12)
Age (years)	48.5	12.6
Years Cycling	18.6	13.0
Height (m)	1.75	0.10
Weight (kg)	75.2	14.4
Body Mass Index	24.3	3.2
Session 1 Power (W)	155.0	58.1
Session 2 Power (W)	157.8	56.8
Session 1 Cadence (rpm)	84.7	2.1
Session 2 Cadence (rpm)	84.7	2.1

Note: W, Watts; rpm, revolutions per minute

Impact of Model on Hip Joint Kinematics

Significant differences were found in all three planes of motion at the hip (Table 2). CGM2 calculated a less flexed maximum hip flexion angle than PiG (t(34) = −9.03, p < .001, ES = −1.573) by 8.2° (±5.2°). CGM2 found a greater range of motion in hip frontal plane motion (5.4° ±4.1°, t(34) = 7.8, p < .001, ES = 1.318) and a smaller range of motion in hip transverse plane motion (−5.3° ±11.6°, t(34) = −2.7, p = .011, ES = −0.456) during cycling. Correlation between model values was strong only for hip flexion (r = .864).

Table 2.

Comparison Between CGM2 and PiG Kinematics of the Lower Limb During Cycling.

		CGM 2 value, mean (SD)	PiG value, Mean (SD)	Difference (CGM2-PiG), mean (SD)	p-value	Effect size d [95% CI]	Correlation (r) between models [95% CI]
Hip Joint
Flexion		96.4° (10.3)	105.1° (8.7)	−8.2° (5.2)	<.001*	−1.573 [−2.006, −1.069]	.864 [.745, .929]
Total Plane	Frontal	11.7° (4.3°)	6.3° (2.5°)	5.4° (4.1)	<.001*	1.318 [0.858, 1.768]	.370 [.042, .626]
Total Plane	Transverse	10.0° (4.3°)	15.2° (11.2°)	−5.3° (11.6)	.011*	−0.456 [−0.802, −0.105]	.107 [−.235, .425]
Knee Joint
Extension		37.1° (5.8)	35.3° (5.9)	1.8° (4.2)	.015*	0.435 [0.085, 0.779]	.775 [.564, .870]
Total Plane	Frontal	7.7° (3.0)	18.5° (9.6)	−10.8° (9.6)	<.001*	−1.123 [−1.526, −0.686]	.131 [−.212, .444]
Total Plane	Transverse	18.8° (8.2°)	16.2° (9.9°)	2.6° (14.0)	.280	.186 [−0.150, 0.519]	−.181 [−.485, .162]
Ankle Joint
Dorsiflexion		6.7° (11.3)	8.4° (9.1)	−1.7° (3.6)	.005**	−0.454 [−0.810, −0.112]	.961 [.924, .980]
Plantarflexion		14.2° (12.2)	10.9° (9.5)	3.3° (5.4)	<.001**	0.609 [0.239, 0.945]	.896 [.803, .947]

Note: CGM2, Conventional Gait Model 2; PiG, Plug-in-Gait; SD, standard deviation; CI, Confidence Interval.

^*Statistical significance found at p < .0167 (Bonferroni adjustment)

^**Statistical significance found at p < .025 (Bonferroni adjustment)

Impact of Model on Knee Joint Kinematics

Significant differences were found in the sagittal and frontal planes of motion at the knee (Table 2). CGM2 calculated a less extended knee angle at the BDC of the pedal stroke than PiG (t(34) = 2.6, p = .015, ES = 0.435) by 1.8° (±4.1°). CGM2 found a smaller range of motion in knee frontal plane motion (−10.8° ±9.6°, t(34) = −6.6, p < .001, ES = −1.123). No significant differences existed in the total transverse plane motion at the knee. Strong correlations were found between models at knee extension (r = .755) but correlations in the frontal and transverse planes were weak.

Impact of Model on Ankle Joint Kinematics

Significant differences were found in both ankle dorsiflexion (t(34) = −2.7, p = .005, ES = −0.464) and ankle plantarflexion (t(34) = 3.6, p = <.001, ES = 0.609) (Table 2). CGM2 found less dorsiflexion (−1.7 ±3.6°) but more plantarflexion (3.3°±5.4°) than PiG. The model values for ankle motion were both strongly correlated at r = .954 for dorsiflexion and r = .867 for plantarflexion.

Reliability

ICC values for CGM2 between-day reliability were good to excellent (> 0.75) except for knee transverse motion (Table 3). ICC values for PiG were varied, with good to excellent reliability at the ankle; moderate for hip flexion, hip frontal plane motion, and knee extension; and poor for hip and knee transverse plane motion and knee frontal plane motion. MDCs were lower for CGM2 at the hip and knee except for hip frontal plane motion (Table 3). MDCs were lower for PiG for both ankle dorsiflexion and plantarflexion.

Table 3.

Between Day Reliability of CGM2 and PiG Models.

	ICC [95%CI]		MDC
	CGM2	PiG	CGM2	PiG
Hip Joint
Flexion	0.81* [.65, .90]	0.69 [.46, .83]	10.5°	13.4°
Total Frontal Plane	0.76* [.58, .88]	0.64 [.38, .80]	5.8°	4.2°
Total Transverse Plane	0.80* [.63, .89]	0.46 [.15, .69]	5.4°	22.9°
Knee Joint
Extension	0.85* [.72, .92]	0.74 [.55, .86]	6.2°	8.3°
Total Frontal Plane	0.59 [.32, .77]	0.43 [.11, .67]	5.3°	20.1°
Total Transverse Plane	0.76* [.56, .87]	0.41 [.08, .65]	11.2°	21.1°
Ankle
Dorsiflexion	0.91* [.82, .95]	0.95* [.91, .98]	9.3°	5.5°
Plantarflexion	0.81* [.66, .90]	0.87* [.76, .93]	14.1°	9.5°

Note: CGM2, Conventional Gait Model 2; PiG, Plug-in-Gait; ICC, intraclass correlation coefficient; MDC, minimal detectible change.

^*Indicates ICC value >.75, representing acceptable reliability metric

Discussion

No previous studies have compared the outputs of CGM2 and PiG for cycling kinematics despite known problems with the PiG modeling methodology. This study shows that there are differences between the two model outputs at all three major lower extremity joints. Additionally, this is the first study to examine between-day reliability of the two for cycling. The findings of this study indicate that CGM2 has higher reliability for most lower limb joint motions and suggest that CGM2 should be favored over PiG due to its higher reliability.

Small changes in angle measurements, especially at the knee, may result in alterations in bicycle fit that impact performance and injury risk. Knowing the translation between PiG and CGM2 joint angles allows researchers and bicycle fitters to understand how past data can integrate with data collected using CGM2. For instance, the ideal dynamic knee extension angle has been established at 33–43° using PiG.9 This may translate to 35–45° using CGM2 because the difference between the two models was found to be approximately 2° (Table 2) for knee extension. For clinicians accustomed to using PiG to determine bicycle fit, using CGM2 may require reassessing standard joint angles to avoid setting a cyclist’s saddle too high. Similarly, differences between the two models for hip and ankle joint kinematics may result in the clinician drawing incorrect conclusions about lower extremity biomechanics if PiG normal values are used to interpret CGM2 data.

Correlations between the two models’ outputs were strongest in the sagittal plane, with poorer correlations in the frontal and transverse planes (Table 2). One reason that CGM2 was developed was to improve the reliability and accuracy of the frontal plane orientation of the leg.15,16 This is accomplished by using clusters of markers on the anterior and lateral thigh and tibia, rather than only one lateral thigh and lateral shank marker as indicated by the PiG model. Therefore, differences in marker sets that lead to different joint angles and orientations could explain the poor correlation between the models in the non-sagittal planes. Additionally, CGM2 uses the Hara equations for the hip joint and therefore relies on leg length measurements rather than marker locations for predicting the hip joint center.14 As a result, small differences in marker placement are less likely to influence the limb kinematics when using CGM2.

The reliability of a model also plays a crucial role in model selection in sports where serial motion assessments are used to assess injury risk or performance. An ICC greater than 0.75 is considered to be highly reliable.29 Previous studies report PiG has poor reliability in the frontal and transverse plane.22–24,31 In this study, between-day ICC values exceeded 0.75 for all CGM2 kinematics except knee frontal motion, while only ankle dorsiflexion and plantarflexion exceeded it for PiG (Table 3). Other studies using PiG or CGM2 to analyze model reliability during cycling were not found. Fonda et al. used Vicon’s 3DMA system but did not use PiG; they found good reliability of their sagittal 3DMA data.32 Okahisa et al.18 analyzed runners but also compared PiG to CGM2. Their results agree with the results of this study, with greatest between-day reliability in the sagittal plane for lower extremity joints, and CGM2 reporting higher reliability than PiG. Therefore, CGM2’s higher reliability in the transverse and frontal planes may prove significant for sports that require repeated analysis of motion in these planes.

The MDC is a derivative of the ICC. In 3D motion capture studies, MDC’s less than 5° are considered acceptable and indicate that changes in joint angles over 5° are real changes not due to instrument error.22 In this study, MDCs are over 5° for both PiG and CGM2 (Table 3). One explanation for this could be that this study looks at total frontal plane motion (a sum of abduction and adduction) and total transverse plane motion (a sum of internal and external rotation), rather than the individual components as done in other studies. A second explanation could be a greater between-day difference in marker placement by the investigator. Overall, except for ankle motion and hip flexion, CGM2 has lower MDC’s than PiG. Therefore, the combination of higher ICC’s and smaller MDCs suggests that CGM2 could more reliably detect changes in cycling kinematics between sessions.

While this study is particular to cycling biomechanics, it suggests that similar studies should be performed for other sport motions to better understand the difference that biomechanical models have on kinematic analysis. As biomechanical models advance, switching between models clearly has an impact on the model outputs. For sporting motions, such as the knee angle during cycling, existing reference standards will also need to adapt to the new model to avoid errors in motion analysis. Lastly, this study reinforces the importance of clear reporting of data processing methodology since the biomechanical model impacts how joint angle calculations are completed, and therefore the final limb kinematics. Understanding the differences between model outputs on joint angles can provide the researcher or clinician with a better understanding how to interpret research findings.

One limitation of this study was that the participant’s position on the bike may have changed slightly between the two sessions, which would influence the between-day reliability for reasons outside the biomechanical model or marker set. For example, sitting slightly more forward on the bicycle saddle would result in a lower and more forward position, altering the lower limb kinematics. The authors did not find statistically significant differences in kinematics between the two data collection sessions, indicating minimal change in position between days. Future studies could standardize each participant’s position relative to their frame by using a reference marker on the frame to measure fore/aft position of the rider.

Differences in marker placement also introduces error in 3DMA. In this study, variability was reduced by having one researcher place all the markers for all participants. Errors in marker placement would impact kinematic outputs and between-day reliability of each model. However, since data for PiG and CGM2 were collected synchronously, inconsistencies in marker placement would affect both models. Therefore, this is not expected to alter the relationship between the models seen in the results.

One additional factor that limits applicability to other labs is that both the PiG and CGM2 marker sets were modified to add a marker to the most superior prominence of the iliac crest. The iliac crest marker was included to provide another reference point for gap filling of the anterior pelvic marker that tends to be occluded with more aggressive cycling positions. This allowed the researchers to consistently use a rigid body gap-fill (which requires three data points on the same rigid body) to calculate the anterior pelvic marker if the contralateral anterior pelvic marker was obscured due to cycling position. Other researchers looking to replicate our findings may not have the same results if this marker is not added to each marker set. A recent publication suggests the iliac crest marker modification is valid compared to the traditional pelvic marker set.33

This study found differences in lower extremity cycling kinematics when data are processed using CGM2 versus PiG. While the study design does not determine which biomechanical model should be used for accuracy, it does suggest that CGM2 is more reliable for between-day testing. Both models are more reliable in the sagittal plane than the frontal or transverse planes, which is consistent with the existing literature. CGM2’s higher reliability in multiple planes makes it a better choice for clinicians and scientists performing serial bicycle fitting sessions with cyclists.

Supplemental Materials: Correlation Scatterplots

The following scatterplots show the correlation between mean joint angles in degrees for CGM2 and PiG. The correlation with 95% confidence interval is shown for each graph.