Surface-mounted altitudinal molecular rotors in alternating electric field: Single-molecule parametric oscillator molecular dynamics

Abstract

Molecular dynamics simulations of the response to oscillating electric field elicited from an altitudinal dipolar molecular rotor mounted on the Au(111) surface and previously studied experimentally in static fields show unidirectional rotation in one of the three pairs of conformational enantiomers. The simulations are based on the universal force field and take into account electronic friction in the metal through its effect on the image charges. The rotor consists of two cobalt sandwich posts whose upper decks carry a biphenyl-like rotator with a dipole moment perpendicular to the rotation axle, mounted parallel to the surface. A phase diagram of rotor performance at 10 K as a function of field frequency and amplitude contains five unidirectional rotation regions: synchronous, half-synchronous (every other cycle skipped), quarter-synchronous (only indistinctly), asynchronous, and essentially no response. The nature of the subharmonic “single-molecule parametric oscillator” behavior is understood in mechanistic detail. Simulations at higher temperatures distinguish the thermal (“Brownian”) and driven regimes of rotation, elucidated in terms of time-dependent potential energy surfaces for the rotation.

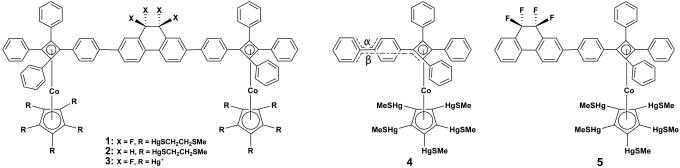
Biological systems contain functional nanoscopic machines. Modern nanotechnology has reached a level of sophistication where it seems possible to build artificial molecular machines, and rotors are among the essential parts needed (1-4). The “Molecular Tinkertoys” (5-8) concept has been used to prepare dipolar and nonpolar altitudinal (axle parallel to surface) molecular rotors mounted on a Au(111) surface, and barrier height imaging demonstrated that the dipolar 9,9,10,10-tetrafluoro-9,10-dihydrophenanthrene rotator in rotor 1 (Fig. 1) turns the direction of its dipole in response to a static electric field imposed by the tip of a scanning tunneling microscope (9). Under what conditions, if any, could an oscillating electric field normal to the surface be used to drive unidirectional rotation of surface-mounted 1? We use classical molecular dynamics to obtain an answer.

Fig. 1.

Chemical structures of altitudinal rotors and model systems.

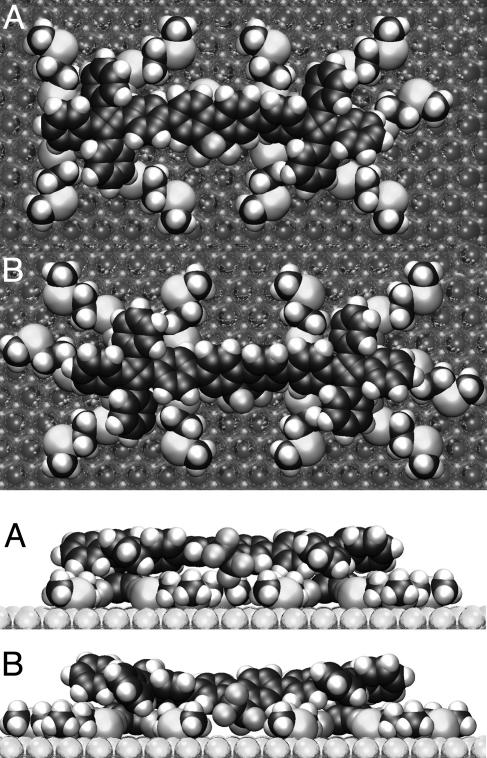
Scanning tunneling microscope measurements showed that the rotors are firmly attached to the surface and remain in place during hours-long scan periods, but changes in the conformational arrangement of the tentacles on the scale of tens of minutes are suggested by the observed slow “blinking” of the differential barrier height imaging images (9). In fresh samples, rotors with “tentacles,” 1 (polar) and 2 (nonpolar), are believed to be attached through Au-S bonds. Because of slow oxidative cleavage of the Hg-S bond (9), in samples of 1 aged in air the attachment is through Au-Hg⁺ bonds, which also may be true when tentacle-free rotors (3; Fig. 1) are used. In our simulations, all 20 S atoms (1, 2) or all 10 Hg atoms (3) are permanently attached to fixed lattice sites of the Au(111) surface for the few nanoseconds that are being simulated. We refer to rotors 1 and 2 unless otherwise noted and focus on the following two limiting conformations (Fig. 2): structure A, with one of the tentacles eclipsed with the rotator axle, and structure B, with the tentacles staggered with the axle.

Fig. 2.

Limiting conformations A and B of rotor 1 PMP on Au(111).

The rotors each have three pairs of conformational enantiomers, PPP/MMM, PMP/MPM, and MMP/PPM, where the first and third symbols mark the helicity of the nonplanar tetraarylcyclobutadienes at the two termini and the second symbol shows the sense of the approximately 15° twist of the dihydrophenanthrene rotator.

Computational Procedures

Isolated Molecule (Fig. 1). The dipole moment of the rotator in 1 and the rotation potential for the angle β in compounds 4 (model for 1) and 5 (model for 2) were calculated with the RI-BLYP (10-12) density functional theory method [turbomole (13)] and the SV(P) basis set (14) [ECP-60-MWB (15) pseudopotential and basis set for Hg]. It seems intuitive to use α rather than β to drive the rotation, but β more closely describes the rotation in a surface-mounted rotor.

Molecule Attached to Gold Surface. Potential energy profiles for rotational motion in 1-3 were calculated by molecular mechanics [tink (16)] using the universal force field (UFF) (17) and partial atomic charges determined by charge equilibration (18). The van der Waals forces due to the gold surface were described by a 3-12 Lennard-Jones term (19) with parameters (Table 1) derived from fits to UFF potential energy curves calculated for every required atom type interacting with a block of about 1,700 gold atoms. Inductive forces due to the gold surface were incorporated through image charges (20): the reaction field due to the surface charge induced by a charge distribution outside the metal is described by a mirrored charge distribution of opposite sign. The approach is valid if the surface distance is >2 Å (21).

Table 1. Parameters for the 3-12 Lennard-Jones surface potential.

Parameter	H	C	F	S	Co	Hg
A	2.26	3.43	2.68	4.22	1.86	3.05
B	2.46	2.98	2.69	3.18	2.33	2.59

Values of A are in Å(kcal/mol)^1/3, values of B are in Å(kcal/mol)^1/12, values of r are in Å, and those of V are in kcal/mol. The interaction between each atom and a gold surface is V = –(A/r)³ + (B/r)¹².

To generate a potential energy profile, a vector perpendicular to the axle of rotation z was rotated in steps of 10° in the xy plane, and the rotator dipole was constrained to be perpendicular to it.

Molecular Dynamics Simulations. The equations of motion were solved in a potential equal to the sum of the above-described extended UFF and a time-dependent electric field. The effect of the metal on the motion of adsorbates was approximated by image charges and by Langevin dynamics to account for friction acting on them. The approach is closely related to procedures described in refs. 22-24. The metal was assumed to have a constant temperature and no internal structure. Vibrational energy transfer from the adsorbed molecule to the motion of gold atoms was neglected.

The Langevin velocity Verlet algorithm (25) was used with a time step of 1.5 fs, at which the integration is still stable. Friction constants for the motion of a point image charge q inside gold parallel to the surface (η_∥) and perpendicular to the surface (η_∥) were (26) η_∥ = q²/16πσd³ and η_∥ = q²/8πσd³, where d is the distance from the charge to the surface and σ is the conductivity of gold. At nonzero metal temperatures T a random force R(T, t) acts on the image charges, which were assumed to follow the motion of the real charges above the surface instantaneously. The fluctuation-dissipation theorem, 〈R(T, t₁), R(T, t₂)〉 = 2kTηδ(t₁ - t₂), relates the stochastic force and the friction, and the Langevin equation of motion (27) was used, m∂²x/∂t² = -∂V/∂x - η ∂x/∂t + R(T, t). Although the friction coefficient is a function of the distance d, the hydrodynamic term (28) (η/2)∂(kT/η)/∂x is absent because electron-hole pairs in the metal do not exhibit collective behavior on this time scale.

Resonance frequencies of the three conformations of the dipolar rotor 1 in structure B were evaluated at 10, 100, 200, and 300 K in simulations without applied electric field and image charge friction. The Fourier transform of the orientational angle φ of the rotator shows a peak at the resonance frequency of the undamped rotor. The damping of the rotor was studied in runs in which image charge friction was applied, the metal was kept at 0 K, and the drop of rotor temperature was monitored starting at 300 K. Spontaneous thermal rotation of the dipolar MMP rotor 1 in structure B was simulated for 7.5 ns at 300-600 K. The trajectories were converted into an Arrhenius plot to yield the frequency factor and activation energy for the easiest hop. To obtain the rate of energy absorption, we determined the rate of temperature increase, dT/dt. Image charge friction was turned off, and an alternating electric field E = (E cos ωt, 0, 0) was applied perpendicular to the surface: v = 340 GHz, E = 10⁹ V/m; v = 90 GHz, E = 10⁹ V/m; v = 340 GHz, E = 5 × 10⁹ V/m; v = 90 GHz, E = 5 × 10⁹ V/m.

During simulations of 1 in alternating electric field, the metal was kept at 10, 100, 200, or 300 K. In each run, the field frequency was constant, and its amplitude E was increased in the first half of the simulation and then decreased, at a constant rate. Frequencies were 5-150 GHz, and the simulation lengths were 18-75 ns. The response of the MMP rotor 1 to an alternating electric field also was investigated with most atoms fixed at equilibrium position, and only the central tetrafluorodihydrophenanthrene rotator and the two neighboring phenylene groups were allowed to move. The dynamics of the MMP rotor 3 was studied at 10 K at 5-225 GHz.

The total simulation time was several microseconds. To judge the rotor's propensity for unidirectional rotation, as opposed to random flipping, we defined the average lag a = 1 - 1/v × ∂φ(t)/∂t. It is zero for a rotor unidirectionally synchronous with the electric field, where one cycle of the alternating field causes a 2π turn of the rotor in the favored direction. It equals unity if the rotor has no preferred direction of rotation or does not turn at all. Large fluctuations in a(t) were removed by averaging over time, and a(t) was transformed to a(E). The average lag a can be thought of as the probability that the rotor skips a cycle of the driving electric field, with turns in the wrong direction counted negative.

Results

Free Rotors. The calculated dipole moment of the dipolar rotator is 3.5 debye (BLYP) and 9.6 debye (UFF, much less accurate), and the potential barrier for the internal rotation of 4 is about 3 kcal/mol.

Gold Surface-Mounted Rotors. For each of the three diastereomers of the dipolar rotor 1, the computed energy of structure A is approximately 6 kcal/mol higher than that of B. The MMP conformation has the lowest energy, the PPP conformation is 3-4 kcal/mol higher, and the PMP conformation is about 6 kcal/mol above PPP. The transition barrier for the MMP to MMM conversion is about 14 kcal/mol. The angle of rotation φ is defined as 0° when the fluorine atoms are close to the surface (“rotator pointing in”) and 180° when they are far from it (“rotator pointing out”).

The rotational potentials of the dipolar rotors in attachment A are similar for the three stereoisomers. At rest, the rotator has its dipole approximately parallel to the surface (φ ≈ 90° or 270°). Rotation is blocked by two high barriers: 30-60 kcal/mol at φ ≈ 180° and 70-80 kcal/mol at φ = 0°.

In conformations B, the tentacles do not interfere with rotation. The rotational potentials of 1 in the MMP, PMP, and PPP conformations are qualitatively different (Fig. 3). The PPP potential is quite symmetric with respect to mirror reflection through a plane containing the axle and normal to the surface (sign reversal on φ). It has two major minima at 0° and 180°, with the latter about 2 kcal/mol higher. The potential of the PMP rotor is again nearly symmetric and shows two pairs of minima. One is located at ±45° and the other, approximately 2 kcal/mol higher in energy, at 180°± 45°. The highest barrier (about 3 kcal/mol) is found at 160°. The MMP potential is not symmetric and has two almost degenerate minima at 30° and 210°. At 135° there is a barrier of 5.5 kcal/mol, and at 315° there is a barrier of 8 kcal/mol. At 90° and 260°, there are two shallow local minima that are approximately 3 kcal/mol higher in energy than the two minima at 30° and 210°.

Fig. 3.

Rotational potentials of rotors in conformation B on Au(111) surface.○, 1 MMP; ⋄, 1 PPP; ×, 1 PMP; dotted line, 3 MMP.

Fig. 3 also shows the potential of the dipolar MMP rotor 3 (no tentacles). It has two minima at 30° and 210°, with the latter 3 kcal/mol higher in energy. There are two approximately 7.5 kcal/mol barriers at 160° and 260° and two smaller ones at 90° and 340°.

Rotor Dynamics. Resonance frequencies. The Fourier transforms of φ(t) obtained for 1 at 10 K without external electric field show several prominent peaks. The librational frequencies are 225 GHz (PPP), 326 GHz (PMP), and 340 GHz (MMP). For PPP, noise increases with temperature, but the peaks do not shift. For MMP, low-frequency noise is found in addition to the peaks at 200 and 300 K. For PMP, low-frequency intensity already shows up at 100 K, and at 200 K the peaks disappear.

Energy absorption. The dipolar rotor 1 absorbs energy at least 10 times and often as much as 1,000 times faster than the nonpolar rotor 2. The rates are comparable for the three stereoisomers of 1. For all dipolar rotors, energy absorption is remarkably less efficient at 340 GHz.

Energy dissipation. When friction is turned on and the metal is held at 0 K, the temperature of the rotors drops approximately exponentially with a damping constant of about 50 ± 30 GHz, almost the same for all stereoisomers of the dipolar and nonpolar rotors.

Thermally activated hopping. For the rotational barriers of the dipolar MMP rotor in structure B, an Arrhenius plot of the temperature dependent transition rates yields a frequency factor f = 3.5 × 10¹¹ s^-1 and an activation energy ΔV = 5.4 kcal/mol.

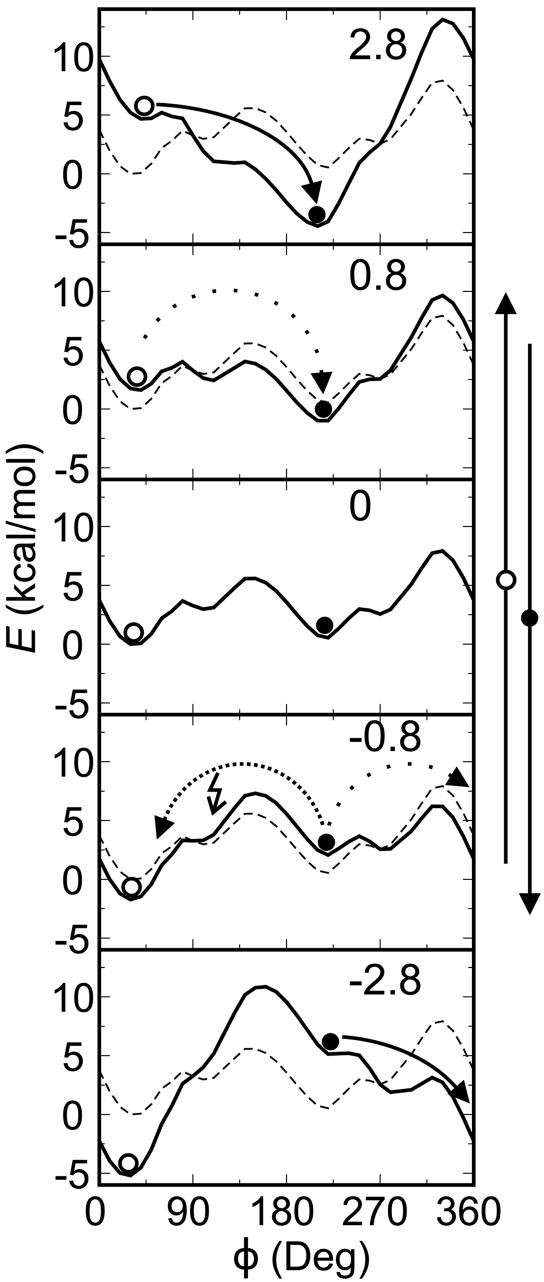
Effect of alternating electric field at low temperature. Fig. 4 illustrates the effect of the electric field on the rotational potential V(φ) of rotor 1. Fig. 5 shows that at 10 K, the three diastereomers of 1 show very different unidirectional response upon the application of an alternating electric field. PPP has no preferred direction of rotation, PMP shows some directional preference, and MMP shows the most.

Fig. 4.

Rotational potentials of 1 in electric fields. Thermal and driven mechanisms of unidirectional rotation are shown (see text). The electric field strength is given in GV/m.

Fig. 5.

Rotational response φ(t) for PPP, PMP, and MMP rotor 1 to a gradually increasing electric field oscillating at ν = 90 GHz (10 K).

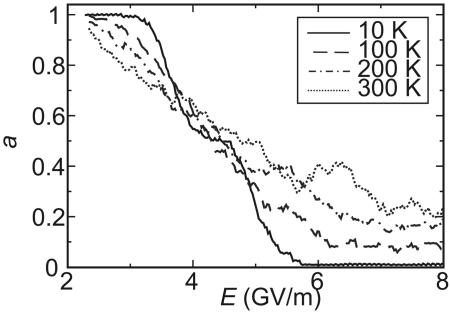
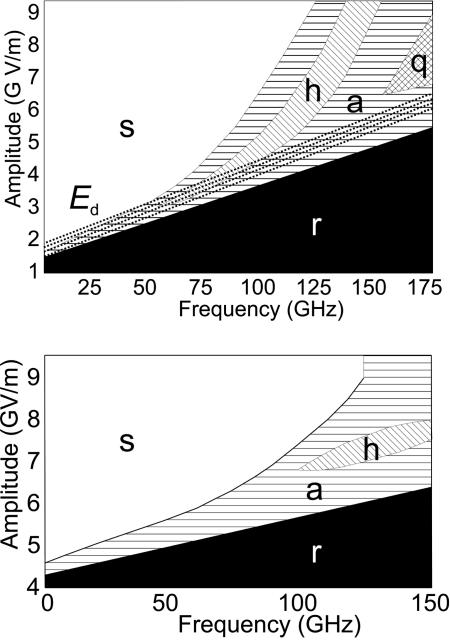
Fig. 6 shows plots of a(E) against time for the MMP rotor 1 at field frequency v = 90 GHz. At 10 K, there is no rotational response below a threshold field amplitude E_bo, and a(E) is close to 1. Above E_bo, the rotor responds with directional motion, and a(E) decreases until at the critical field E_c it is indistinguishable from zero. Both E_bo and E_c increase as v grows. As before (29), we define regimes of rotor motion: in the synchronous regime, a = 0, and every cycle of the electric field causes one full turn of the rotor, always in the same direction (see Movie 1, which is published as supporting information on the PNAS web site). In the random regime, a ≈ 1, and there is no directional response. When E lies between E_c and E_bo, the rotor is in the asynchronous regime, 0 < a < 1. At v < 67.5 GHz, a(E) decreases approximately linearly between E_c and E_bo. At v > 67.5 GHz, however, a distinct range of E exists within the asynchronous regime, where a ≈ 1/2 (Fig. 6). Here, every other field cycle is successful in making the rotor turn, and every other cycle fails. This half-synchronous regime is shown in Movie 2, which is published as supporting information on the PNAS web site (again at 90 GHz). At v > 150 GHz, there appears to be a region of quarter-synchronous regime, where a is approximately 1/4, but we are less certain, because the results are very noisy. Fig. 7 shows the time-dependent potential for two cycles of the electric field and typical trajectories at 9 GHz (synchronous) and 90 GHz (half-synchronous). When both stands including the six attached phenyl rings were frozen, the half-synchronous regime was not observed. At >150 GHz, rotor 3 also exhibits random, asynchronous, and half-synchronous rotation for E less than about 7.5 GV/m, but the transition to synchronous rotation expected at higher electric field strength does not take place. Fig. 8 summarizes the results for the MMP rotors 1 and 3 at 10 K in phase diagrams, where the regimes of rotation are shown as a function of the frequency v and amplitude E.

Fig. 6.

The average lag a(E) at ν = 90 GHz as a function of field strength.

Fig. 7.

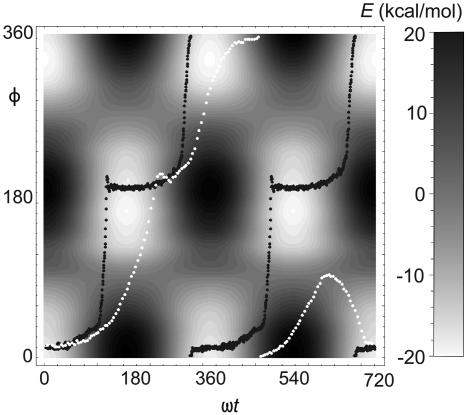
Potential map V(φ, t) and trajectories of synchronous (black points, ν = 9 GHz) and half-synchronous (white points, ν = 90 GHz) motion of surface-mounted 1 in the (φ, ωt) plane (10 K, E = 4.34 GV/m).

Fig. 8.

Phase diagram for the motion of MMP rotors 1 (Upper) and 3 (Lower) at 10 K (s, synchronous; a, asynchronous; h, half-synchronous; q, quarter-synchronous; r, random).

Effect of alternating electric field at elevated temperatures. An increase in temperature has several effects on a(E). Random fluctuations increase, and the half-synchronous regime gradually disappears (Fig. 6). In the range of weak electric fields (thermal regime), unidirectional rotation is facilitated (a is reduced), and for strong electric fields (driven regime), it is inhibited (a is increased). The electric field strength at which the transition from thermal to driven motion occurs is labeled E_d. It is an approximately straight line in Fig. 8, increasing from approximately 2.7 GV/m at v = 25 GHz to approximately 6 GV/m at v = 175 GHz.

Discussion

Force Field. The approximate nature of UFF appears acceptable, because we concentrate on qualitative trends. The clearly exaggerated UFF dipole moment makes it easier for electric field to influence rotor motion, and in reality roughly twice stronger fields would be needed.

Rotational Potentials. In free 4, the benzene ring to which the phenyl model rotator is attached is free to reorient, and for every value of the driving angle β, the biphenyl torsion can assume its optimal angle α. When V(β) is plotted as a function of α(β), the curve closely matches the potential of the torsion in biphenyl. The V(β) plot as a function of β is a nonlinearly scaled plot of biphenyl torsion. There is no doubt that in freely floating molecules 1-3, rotation about the rotor axle is nearly unhindered and fast at room temperature, with about 3 kcal/mol barriers similar to those in biphenyl, in agreement with NMR results (9). The calculated 6.1 kcal/mol barrier to inversion of 9,9,10,10-tetrafluoro-9,10-dihydrophenanthrene also agrees with NMR results for this compound (6.7 kcal/mol) and for 1 (6.3 kcal/mol) (9).

The rotation of 1 and 3, and presumably also 2, is severely impaired in the surface-mounted conformations A because of the steric effects of the tentacles, and in none of the diastereomers can the rotator dipole easily assume an orientation perpendicular to the surface. In contrast, in conformations B the rotator is not hindered, and the barriers to rotation remain low.

The shape of the potential curves (Fig. 3) can be easily understood by adding the interaction of the rotator dipole with its image inside the metal to the biphenyl-like torsional interactions at the two rotator ends. The former is symmetric with respect to the plane σ containing the axle and perpendicular to the surface. In the diastereomeric pairs with equal helicity at the two stands (PPP, PMP) the latter is nearly symmetrical as well, because the torsional barriers at the two ends of the axle add out of phase and are complementary. If the helicity of the two stands differs (MMP), the benzene rings at the two ends of the axle are coplanar and the torsional barriers they produce add in phase. Because these rings are twisted approximately 35° out of the plane of the cyclobutadiene rings, the rotator experiences a potential that is not symmetric relative to the plane σ.

Dynamics of Surface-Mounted Rotors. The validity of the method hinges on the demonstration by Head-Gordon and Tully (30) that Langevin dynamics with memory-less friction is a good approximation for the treatment of effects of the metal on adsorbate motion. We refer to their work (30) for a very detailed derivation based on electronic structure theory. Modeling the surface attachment through bonds to fixed atoms is a crude approximation, but we assume that it is sufficient for this study of the rotational behavior of the central rotator, where both surface attaching CpR₅ systems merely ensure that the rotor stays attached to the gold.

Energy Absorption and Dissipation. The comparison of rotors 1 and 2 exposed to an alternating electric field clearly shows that the dominant mechanism for energy absorption in this frequency range is the induction of rotational/librational motion of the rotator dipole. The energy absorption is most efficient at 90 GHz, because motion in this frequency range is significant at the starting temperature of the simulations, 300 K. Energy dissipation through image charge friction is sufficient to cool the molecule at all but the harshest conditions. This finding justifies the neglect of motion of the gold atoms and therefore of energy dissipation through redistribution of molecular vibrational energy into metal phonons. Its inclusion would lead to a further increase in damping and may modify the details of the phase diagrams in Fig. 8 but is unlikely to change them qualitatively.

Induced Motion. The barriers in all rotational potentials for the surface-mounted rotors in conformation A exceed 30 kcal/mol and prohibit all rotation under realistic conditions. The dipole is locked in one of two minima and points sideways. No strong influence of the electric field on its orientation is expected, as was indeed observed in the scanning tunneling microscope experiments for approximately 2/3 of the rotors (9).

For conformations B, the rotational barriers are low enough to allow rapid thermal transitions among all local minima at room temperature. The activation energy for the lower barrier obtained from molecular dynamics, 5.4 kcal, agrees well with the potential energy barrier of about 5.5 kcal/mol. As expected, the frequency factor f = 3.5 × 10¹¹ s^-1 is higher than that of thermal rotation of a barrier-less rotator assuming equipartition, v_FR = (1/2π)(kT/I)^1/2, which yields 7.5 × 10¹⁰ s^-1 at 300 K. Comparing it with Kramers' rate of thermally activated barrier crossing, r_K = ω_minω_max/2πη e^-ΔE/kT (31), where ω_min/max/=sqrt(|d²V/Idφ²|)isthe angular frequency at the minimum and maximum, yields η ≈ 1.8 THz. This friction constant is much higher than the one we obtained for the temperature decay of the whole molecule, because it includes intramolecular vibrational redistribution. We conclude that the rotational dynamics is overdamped.

An applied electric field of approximately 1 GV/m affects the energies of the minima (Fig. 6). Depending on its polarity, minima at which the dipole is pointing in are stabilized (destabilized), and those at which the dipole is pointing out are destabilized (stabilized). For the MMP rotor, where the two minima are nearly degenerate in the absence of an electric field, a relative population of 99:1 is expected at 25°C in a static electric field of approximately 1 GV/m. Upon reversal of the scanning tunneling microscope bias voltage, the MMP rotator will flip at a temperature-dependent rate, and a change in the local work function was indeed observed on about 1/3 of the dipolar rotors 1 in barrier height imaging experiments at room temperature but not on similar nonpolar rotors (9). The slow blinking observed when the same rotor was found to sometimes reorient upon field alternation, and sometimes not, was assigned to random transformation of individual rotors between conformations of type A and B, respectively.

Unidirectional Rotation. Unidirectional motion in thermal equilibrium would violate the second law of thermodynamics (32). The basic requirement for a potential conducive to unidirectional rotation in an oscillating linear (as opposed to rotating) electric field is the absence of a plane of symmetry σ containing the axis of rotation z and the field direction x. An xy plane of symmetry may be present, and the chirality present in our system is not essential. The forces exerted by the asymmetric potential have to be comparable with the driving electrical force. If the latter is too strong, the effect of the asymmetric potential is negligible, and the rotor will flip randomly in both directions. This behavior is observed in Fig. 8 for rotor 3, whose rotational potential is significantly less asymmetric than that of 1 (Fig. 3) but is still sufficient to allow synchronous unidirectional rotation at lower driving frequencies where weaker fields suffice.

The potential of the PPP rotor 1 is symmetric, and we did not observe a preferred direction of rotation in the simulations (a ≈ 1). The positions of the extrema in the potential of the PMP rotor are symmetric, but the values of the energy do not match exactly. Thus, it is reasonable that the simulations show a slight unidirectional response. Ideal for unidirectional rotation by a linear field is a potential in which barriers have similar height in the absence of electric field and are modulated with inverse phase. We have shown above how the molecular structure forces the MMP potential to meet these requirements. In both the “rotator out” and “rotator in” minima, the dipole axis is tilted approximately 30° from the surface normal, and the application of an alternating electric field modulates their relative energy.

Thermal Unidirectional Rotation. It is easiest to describe the unidirectional response of the MMP rotor in the adiabatic regime, where the modulation of the potential is much slower than the molecular response. At low electric field strength, μE < V_rot, both potential minima are nearly degenerate, and it is equally likely that the rotator points in or out. Through electric field modulation, the position as well as the depth of the minima and height of the barriers oscillate and induce unidirectional rotation by biased hopping from minimum to minimum (Fig. 4). Initially, the dipole is oriented at 30°. In a weak electric field (the three central frames, dotted line), it jumps over the lower barrier at 135° to the minimum at 210°. After the field direction reverses, it again jumps to higher values of φ. The process is repeated, and φ increases continually.

This regime of unidirectional rotation is referred to as thermal, and a two-state kinetic analysis is well known (33-35). Averaging the hopping rates for a half cycle of the electric field to account for its sinusoidal variation yields fexp(-ΔV/kT)[I₀(-2μE)/kT) - L₀(-2μE)/kT)] (I₀ and L₀ are the modified Bessel and Struve functions, respectively) (36). With α_1,2 (β_1,2) denoting average transition rates into the next minimum on the left (right), the rotation rate is 2v[(α₁ - α₂)² - (β₁ - β₂)²]/[Σ (v + Σ)], where Σ = α₁ + α₂ + β₁ + β₂. The kinetic model (34) accounts well for the simulation results when the driving frequency is low and the instantaneous activation energy exceeds kT at all times. At 5 GHz and 300 K, the model predicts the transition from random to synchronous rotation to occur between 0.4 and 0.9 GV/m, whereas in the simulations it takes place between 0.5 and 1.0 GV/m.

Driven Rotation. At an electric field strength of about 1.1 GV/m, the dipole-electric field interaction is strong enough to annihilate the barriers of the intrinsic rotational potential (Fig. 4, top and bottom frames, wide arrows). Instead of oscillating in depth, the minima now actually move along the rotational coordinate with the frequency of the alternating electric field: φ_min(t) ≈ φ_min (0) + ωt. Synchronous unidirectional rotation no longer relies on the availability of thermal energy, which actually can impede it by allowing the rotor to skip to another minimum (arrow to the left in Fig. 4). As temperature increases, such undesirable hops occur more often, and the average lag increases a (Fig. 6). In the absence of electric field, the potential minima are degenerate; therefore, the average torque acting on the rotator during a transition between two minima is 2μE/π. For overdamped driven rotation it follows that η = μE/π²v. We obtained η = 1.5 THz, in reasonable agreement with the friction constant 1.8 THz derived from the Arrhenius plot and Kramers' theory.

Origin of Subharmonic Motion. Subharmonic resonances are well known in the classical dynamics of simple one-dimensional systems, e.g., parametrically driven harmonic oscillators, and in studies of classical chaos (37). However, we believe that subharmonic conformational motion has not been described before in a single-molecule simulation with a standard and realistic force field, and it is of interest to examine its mechanistic origin. Because we observe it both in 1 and in 3, it appears to have some generality. At the same time, we note that it is suppressed when only the rotator in 1 is allowed to move and the rest of the molecule is held rigid, and the phenomenon is clearly sensitive to the details of rotor motion.

From the viewpoint of nonlinear dynamics, the synchronous and half-synchronous regime would be classified as 1:1 and 1:2 resonances (38). We did not proceed farther in this direction and instead offer a simple mechanistic explanation. Fig. 7 shows the potential V(φ, t), where electric field phase is proportional to t. At 9 GHz, rotor motion is nearly adiabatic, and the black trajectory follows the minimum energy path synchronously, with a periodicity of v = 2πω. At 90 GHz, friction is sufficient to make rotor motion nonadiabatic, and the white trajectory deviates from the minimum energy path. It is therefore not constrained to 2πω periodicity, and asynchronous rotation can occur. Both trajectories start in a basin at φ ≈ 30°. In the first half of an electric field cycle, this basin gradually disappears, and another one grows at φ ≈ 210° (cf. Fig. 4). The minimum energy path followed by the 9-GHz trajectory leads to an abrupt hop from the former to the latter basin, but at 90 GHz, almost half a cycle of the electric field elapses before the rotor arrives in the latter basin and meets again with the minimum energy path. In the second half of the cycle, the basin at φ ≈ 210° gradually disappears, and at 9 GHz the rotator performs another abrupt hop to the original basin at φ ≈ 30°, thus completing a successful 360° turn. The 90-GHz trajectory also finishes a successful 360° turn, but it is now delayed so much that it does not arrive in the original basin at φ ≈ 30°. When it finally reaches φ ≈ 30°, it has already lagged too much to join the minimum energy path. During the third half-cycle of the electric field, it encounters the growing barrier at φ ≈ 135°, which repels the rotor back into the original φ ≈ 30° basin during the fourth half-cycle, causing it to skip the second turn. At the end of two field cycles, the 90-GHz rotor again finds itself at the minimum energy path in the original basin at φ ≈ 30°, and the process is ready to resume.

If the electric field strength is increased somewhat, the rotor moves a little faster during the second half cycle, but it will still collide with the barrier at φ ≈ 135° during the third-half cycle and meet the original trajectory during the fourth half-cycle in the basin located at φ ≈ 30°. The rotor will continue to perform half-synchronous motion until the electric field is strong enough to allow it to pass the barrier at φ ≈ 135° in the third half-cycle. At this point, there is a sudden transition from half-synchronous to synchronous motion.

If the strength of the electric field is reduced, the rotor is a little slower and also will converge with the original trajectory during the fourth half-cycle in basin at φ ≈ 30°. When the electric field strength is lowered further, there are two possible limiting behaviors. In the first case, the field drops below E_d, and, in the absence of thermal effects, there will be no rotation. The second possibility is that the rotor will not make the first half-turn in time to pass the barrier at φ ≈ 315°. Then, it will be pushed back into the basin at φ ≈ 210° in the third cycle, and the resulting motion will be quarter-synchronous, a = 0.75. According to this explanation, if V(φ) had two identical barriers and wells, we would observe only quarter-synchronous motion and no half-synchronous motion. Such frequency locking of molecular rotors may have implications for their ultimate use in nanotechnology.

Summary

Molecular dynamics simulations for the three stereoisomers of gold surface-mounted altitudinal rotor 1 and the MMP isomer of rotor 3 with inclusion of electronic friction account for experimental observations in static fields. They predict interesting behavior in high-frequency oscillating fields normal to the metal surface, including synchronous and half-synchronous unidirectional rotation of the MMP isomers, whose rotational potential is asymmetric. They also clearly reveal the two regimes of unidirectional rotation and provide a computational confirmation of qualitative considerations (4). Thermal energy enables unidirectional rotation in the thermal regime but hinders it in the driven regime.

We ascribe the single-molecule parametric oscillator frequency locking in the synchronous, half-synchronous, and quarter-synchronous regimes to an interplay of the time-dependent potential barriers and friction that results from the motion of image charges in the metal substrate. In the presence of more than two dominant rotational barriers, it might be possible to design molecular rotors that lock to other subharmonic frequencies.