Unified description of temperature-dependent hydrogen-bond rearrangements in liquid water

Abstract

The unique chemical and physical properties of liquid water are a direct result of its highly directional hydrogen-bond (HB) network structure and associated dynamics. However, despite intense experimental and theoretical scrutiny spanning more than four decades, a coherent description of this HB network remains elusive. The essential question of whether continuum or multicomponent (“intact,” “broken bond,” etc.) models best describe the HB interactions in liquid water has engendered particularly intense discussion. Most notably, the temperature dependence of water's Raman spectrum has long been considered to be among the strongest evidence for a multicomponent distribution. Using a combined experimental and theoretical approach, we show here that many of the features of the Raman spectrum that are considered to be hallmarks of a multistate system, including the asymmetric band profile, the isosbestic (temperature invariant) point, and van't Hoff behavior, actually result from a continuous distribution. Furthermore, the excellent agreement between our newly remeasured Raman spectra and our model system further supports the locally tetrahedral description of liquid water, which has recently been called into question [Wernet, P., et al. (2004) Science 304, 995-999].

In a continuum model, liquid water comprises a random, three-dimensional network of hydrogen bonds (HBs) encompassing a broad distribution of O-H···O HB angles and distances. Therefore, the concept of a “broken” HB is an arbitrary one. This ambiguity is often evident in molecular dynamics (MD) simulations of water, where, to define an “intact” or “broken” HB, an arbitrary energetic (1-4) or geometric (5-7) definition is used. However, the temperature dependence of the Raman (8) and IR (9, 10) spectra and, more recently, the x-ray absorption spectrum (11, 12) seem to indicate the existence of spectrally distinguishable HB configurations. Such results have typically been interpreted as indicating that liquid water comprises two classes of HB domains: intact (or “ice-like”) and broken. Furthermore, recent ultrafast HB dynamics measurements have attributed distinct relaxation times to specific substructures (13, 14) or have ascribed the slow relaxation component (>1 ps) to HB “breakage” (15). These claims have been supported by molecular dynamics (MD) simulations, which have been interpreted as indicating that the time and temperature dependence of the IR spectrum results from the breaking and reforming of HBs (16, 17). To test this interpretation, we have performed extensive temperature-dependent Raman measurements of HOD in H₂O and in D₂O, as well as Monte Carlo (MC) simulations of H₂O over a similar temperature range.

The Raman OH stretching region (3,200-3800 cm^-1) of liquid water is characterized by a highly asymmetric band structure and an isosbestic point between 3°C and 85°C. Both of these observations have been interpreted as evidencing two distinct types of structures (18). In fact, the existence of an isosbestic point has commonly been considered a fingerprint of two-state behavior (9, 18). Such a point can arise from distinct spectral components corresponding to interconverting chemical species that vary in intensity, but not in shape or position, upon a change in, for example, temperature (19). But, as we will show, simple thermal variations of a single species' lineshape can generate isosbestic points as well.

Methods

Experimental Methods. We have recorded the spontaneous Raman spectrum for 14% (by mole) HOD in H₂O and also in D₂O from 278 to 353 K (Fig. 1). The Raman spectra of the -OH and -OD stretching regions of HOD are considerably less complex than those of either pure water or D₂O because of the reduced intramolecular and intermolecular coupling (20, 21), thus providing a convenient probe of the local HB interactions. The liquid H₂O used in these measurements was deionized and filtered (18.2-MΩ resistivity Milli-Q, Millipore), and the D₂O, which had a stated purity of 99.9%, was used as is. The solutions of HOD in H₂O (or D₂O) were prepared by diluting 7% by mole of H₂O (or D₂O) in D₂O (or H₂O). At these concentrations, the effects of intermolecular coupling of the OD and OH oscillators from HOD in H₂O and D₂O should be minor (21).

Fig. 1.

Comparison of experimentally measured Raman spectra, and calculated electric field distributions, at similar temperatures. (A and B) Raman spectra measured for the -OD stretch of HOD in H₂O (A) and the -OH stretch of HOD in D₂O (B). (C) Distribution function for the electric field E experienced by the proton projected onto the OH covalent bond.

All Raman spectra reported in this work were recorded by using a 500-mm single-grating spectrometer coupled to a liquid N₂-cooled charge-coupled device camera. The spectral resolution was ≈15 cm^-1. It was confirmed that the spectra were not instrument-broadened by comparing the spectral contours recorded at lower resolution to those measured at higher resolution (4 cm^-1). Spectra were typically collected at each temperature for 40 s. The 514.5-nm line of an Ar⁺ ion laser was used as the light source (500-mW power at the sample), and the sample holder was a 20-mm cuvette. Vertically polarized light was separated from the incident laser beam by using a polarizing cube, which was also used to direct the beam into the sample cuvette, and the scattered light was collected at 90° to the incoming beam. The collected light was filtered to remove the Rayleigh-scattered radiation. The collected light (all polarizations) was focused into a fiber optic that is coupled to the spectrometer. It was confirmed that the fiber optic effectively scrambles the polarization, thereby removing any unwanted polarization effects from the grating. Temperature control was accomplished by using a hot plate to slowly warm the initially cold sample, and a calibrated thermocouple was used to monitor the temperature of the sample. Measurements were typically made between 0°C and 80°C in 2°C increments. Temperature fluctuations were <0.4°C during any measurement.

Simulation Methods. We have investigated the temperature dependence (273-373 K) of hydrogen bonding in MC simulations of liquid water by using the SPC/E effective pair potential. Our model system comprised N = 108 periodically replicated, rigid water molecules. Long-range electrostatic contributions to this potential were computed by using the Ewald summation. The Metropolis MC algorithm was used to sample configurations from isothermal-isobaric ensembles at 1 atm of pressure and temperatures ranging from 278 to 373 K in 5-K increments. At each temperature, 10⁵ N moves were performed to equilibrate the system, and data were collected over runs of 10⁶ N MC moves. Errors are reported as twice the standard deviation from four independent runs at each temperature. We have restricted our attention to classical, time-independent averages, for which atomic masses are irrelevant. The results, therefore, apply equally well to HOD in D₂O and DOH in H₂O. Our results also apply to the statistical mechanics of pure H₂O and D₂O, but the connection with vibrational spectroscopy is much looser in these cases. The collective nature of vibrational modes in isotopically pure liquids prohibits a simple description in terms of local order parameters.

Results and Discussion

To explore the molecular significance of the temperature-dependent Raman spectrum, we have calculated the electric field (E) exerted on the proton by all surrounding molecules projected onto the OH covalent bond (Fig. 1C). It has recently been shown that the local electric field is closely related to the IR (22, 23) and Raman (23) spectra of the OH stretch. The strong resemblance of p(E) to the measured Raman spectra (Fig. 1) verifies that E accurately describes the influence of aqueous environments on the vibrational frequency of an OH(OD) oscillator. It further implies that inhomogeneous broadening determines basic features of these lineshapes.

The -OH and -OD Raman spectra, as well as the electric field distributions shown in Fig. 1, exhibit a clear isosbestic point at ω^* ≅ 3,480 cm^-1, ω^* ≅ 2,570 cm^-1, and E^* ≅ -1.5 V/Å, respectively (ω^* denotes the position of the isosbestic point). Although superficially suggestive of two-state behavior, and almost universally interpreted this way, the phenomenon results simply from the local nature of the order parameters probed (OH/OD oscillator frequency and electric field) and the limited temperature range in question (≈0-100°C). In fact, the distribution p(x) of any order parameter x is invariant to a limited change in temperature wherever the derivative

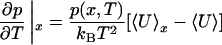vanishes. Here, U is potential energy and 〈...〉 denotes a thermal average. Similarly, 〈...〉_x denotes a thermal average over the restricted set of configurations for which x has a specified value. We have confirmed by simulation of our model system that 〈U〉_E^* differs only slightly from 〈U〉 at the isosbestic point over the entire temperature range examined. This behavior can explain the observed isosbestic points in the Raman and IR spectra of liquid water and very likely underlies the observed isosbestic point in the IR (24) and Raman (25) spectra of liquid methanol as well. In fact, a thermal distribution of harmonic oscillators exhibits an isosbestic point at the expected position. Therefore, the widespread assumption that an isosbestic point unambiguously implies two distinct populations of bonded and nonbonded absorbers is incorrect.

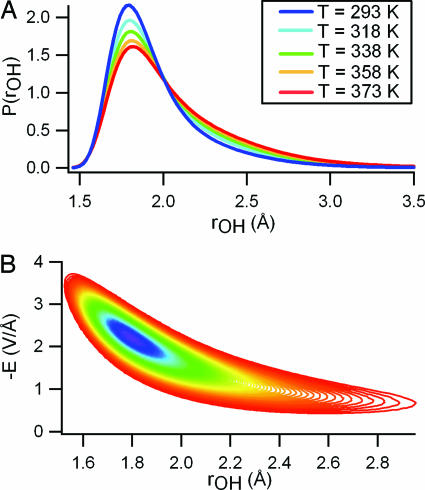
To establish a direct connection between the spectroscopy, the local electric field, and the HB structure, we have calculated the distribution of HB distortions (r_OH). We have defined r_OH as the distance from a hydrogen to the nearest (but not covalently bound) oxygen atom within a cone of width π/3 (Fig. 2A). This distribution provides a one-dimensional order parameter that is sensitive to fluctuations in both HB distance and angle. The calculated distributions of HB interactions p(r_OH) also show a clear isosbestic point, indicating that 〈U〉_r^* - 〈U〉 varies only weakly with temperature. The correlation between E and the HB order parameter r_OH is shown explicitly in their joint probability distribution function (Fig. 2B). The electric field experienced by the proton (E) varies strongly for small distortions (r_OH < 2.2 Å) but exhibits little additional change for larger distortions. Therefore, the distribution of distorted HBs experience only a small range of electric fields, resulting in the observed shoulder in p(E). This argument can be extended to explain the shoulder observed in the measured Raman spectrum, which has typically been assigned to a distinct population of broken HB configurations.

Fig. 2.

Plots of the calculated HB distortions and their correlation with the calculated electric field. (A) Distribution functions for HB distortions (r_OH) at several different temperatures. (B) Contour plots of the joint distribution function of r_OH and E at 298 K. Contour colors mark the decay of the distribution, with violet representing highest probability density and red representing lowest probability density. Points on the outermost contour are 22 times less probable than those on the inner contour. The local electric field varies only weakly as a function of HB distortion for molecules with r_OH > 2.2 Å resulting in the observed shoulder in p(E).

Furthermore, for any given value of r_OH (or E) in the domain of Fig. 2, we have found that the shape of δU(r_OH) = 〈U〉_r - 〈U〉 [or δU(E) equivalently defined] is nearly independent of temperature. δU(r_OH) (Fig. 3) thus acts as an effective energy function for HB distortion. Its single minimum and featureless rise with increasing r_OH strongly support a continuum, rather than two-state, picture of HB fluctuations. The shape and magnitude of δU(r_OH) is largely determined by interactions between the donor molecule and the adjacent molecule that accepts a (perhaps strongly distorted) HB (shown in Fig. 3). HB strain is therefore primarily opposed by forces between this pair. More collective effects are apparent in the energy of large distortions (r_OH > 2.25 Å), which is noticeably lower than the corresponding pair energy. This stabilization arises from interaction of the HB acceptor with other nearby molecules. Overcoordination (five or more neighbors in the first solvation shell) of the HB acceptor is common among structures with r_OH > 2.25 Å. Distorting one HB of an overcoordinated molecule evidently allows compensatory strengthening of others.

Fig. 3.

Effective energy of HB distortion as a function of r_OH (Inset) computed at T = 298 and 373 K. We averaged the total potential energy of our model system, within many small intervals of r_OH, over a trajectory of 10⁶ MC steps per molecule. We have isolated the contribution to this energy from pair interactions between HB donor and acceptor, δU_pair. Averages of δU_pair within small intervals of r_OH are shown for the same two temperatures. All functions have been shifted vertically to have a common minimum energy of zero. Error bars represent twice the standard deviation computed from five independent simulations. δU_r closely follows the pair energy, especially for weak distortions. Deviation of δU_r from δU_pair(r) = 〈U_pair〉 _r - 〈U_pair〉 at large r_OH is accompanied by exceptionally favorable interactions between the HB acceptor and its three (excluding the HB donor) or often more neighbors.

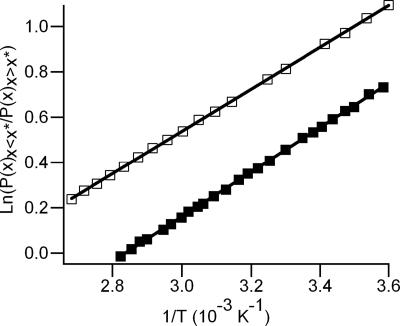
The weak temperature dependence of δU(r_OH) also justifies a van't Hoff analysis of the distributions p(r_OH). Van't Hoff behavior is commonly considered an indicator of a two-state system; however, a continuous system will exhibit very similar behavior as well. A van't Hoff plot can be constructed by bisecting the ensemble at the isosbestic point r^* and plotting the natural logarithm of the ratio of areas above and below the isosbestic point vs. 1/T. The slope of such a plot yields the difference in average energy between the two subensembles: i.e.,

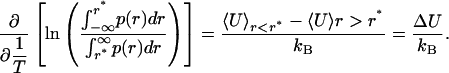This division, however, is arbitrary, because the form of δU(r_OH) does not change in any meaningful way at this apparent isosbestic point. Indeed, bisecting the ensemble at any value of r_OH gives relative populations that vary exponentially with 1/T. Selecting values in the interval 1.9 Å < r_OH < 2.75 Å (the range of distorted species) as the bisection point yields linear van't Hoff plots with slopes in the range of 1.44 ± 0.01 kcal/mol < ΔU < 2.62 ± 0.03 kcal/mol. This energy range simply reflects the scale of variation in δU(r_OH) over the corresponding interval in r_OH. We have also performed an analogous van't Hoff analysis of p(E) and the experimental Raman spectra by bisecting each at the isosbestic point (Fig. 4). Although the isosbestic point is an arbitrary dividing point in terms of H bonding, it represents a mutual point of reference between the electric field distributions and the measured Raman spectra. As with the distribution of HB lengths [p(r_OH)], linear van't Hoff plots are obtained by using any value of ω or E, as is expected for a continuous distribution. When the isosbestic point is used, the resulting van't Hoff slope (ΔU) is 2.0 ± 0.1 kcal/mol from the -OH Raman spectra and 1.84 ± 0.01 kcal/mol from the E distributions. This agreement is rather remarkable, considering the relatively simple nature of the SPC/E potential and that E only approximately reflects the vibrational frequency. A van't Hoff analysis of the -OD Raman spectra yields a slope of 2.2 ± 0.1 kcal/mol, ≈0.2 kcal/mol higher than the corresponding value derived from the -OH Raman spectra. This measured isotope effect is consistent with the fact that the D₂O HB is stronger than that for H₂O, as evidenced by the difference in their enthalpies of vaporization (26). We note that our van't Hoff analysis of the Raman spectra is somewhat different from the more typical method employing Gaussian decomposition (8, 27, 28). Gaussian decomposition inherently assumes distinct populations of absorbers, but, given the results presented here, such an assumption is unjustified. As such, the fact that the -OH and -OD Raman spectra can be accurately fit by two Gaussian components is most likely fortuitous.

Fig. 4.

Van't Hoff plots for the measured -OH Raman spectrum (filled squares) and for the computed local electric filed distributions (open squares). The error bars are approximately the marker size. The solid lines represent the linear fit (R² > 0.999) with a slope of ΔU/R. ΔU, which is the difference in energy between the two H-bonding subdistributions, as explained in the text, is determined to be 2.0 ± 0.1 kcal/mol (Raman) and 1.84 ± 0.01 kcal/mol (electric field). This close agreement between results from experiment and simulations constitutes compelling evidence for a continuous distribution of HB geometries and energies in liquid water.

The numerical results we have presented are not dynamical in nature, but the energy function δU(r_OH), which accounts for the temperature dependence of Raman spectra, does suggest a dynamical scenario for HB distortion. Given the absence of an energy barrier to relaxation, local structures with large values of r_OH are expected to return to lower energy arrangements on the time scale of basic molecular motions (e.g., librations, HB vibrations, etc.). Molecular dynamics simulations and ultrafast two-dimensional infrared spectroscopy indeed show that strained HBs rarely persist for >200 fs (29). In light of this compelling agreement between atomistic computer simulations and experimental Raman and IR spectroscopies of liquid water, previous studies that ascribe slow relaxation (>1 ps) to breakage or distortion of HBs (13) or that depend on a two-state interpretation of isosbestic points (15) should be reconsidered. Furthermore, these results indicate that intermolecular arrangements in liquid water are well represented by the SPC/E potential (i.e., locally tetrahedral), in stark contrast to recent claims that liquid water instead comprises rings and chains (12).

Conclusion

Using temperature-dependent spontaneous Raman spectroscopy in conjunction with MC simulations, we have shown in this report that the distribution of HB geometries and energies in liquid water are continuous. We have presented a microscopic interpretation for many of the experimentally observed features in the Raman spectrum long considered to be strong evidence for a multistate system, including the isosbestic point, asymmetric band profile, and van't Hoff behavior. Furthermore, we have calculated an effective HB energy indicating a single basin of attraction, consistent with recent findings from ultrafast dynamics measurements (29).