Quantitative evolutionary design of nutrient processing: Glucose

Abstract

Quantitative evolutionary design involves the numerical relationships, evolved through natural selection, of biological capacities to each other and to natural loads. Here we study the relation of nutrient-processing capacities of the intestine and of organs beyond it (such as liver and kidneys) to each other and to natural loads of nutrients normally consumed. To control experimentally the rate of nutrient delivery to organs beyond the intestine, we administered nutrients directly into the veins of rats by the method of total parenteral nutrition (TPN). Control rats consuming the TPN solution by mouth ingested glucose at 42 mmol/day and processed it completely, as gauged by negligible appearance of glucose in urine and feces. Experimental rats receiving TPN were able to process infused glucose completely at rates up to 92 mmol/day. At higher infusion rates, they were unable to process further glucose, as gauged by rises in serum and urinary glucose levels and serum osmolality. At the highest infusion rates, they exhibited diuresis, dehydration, and both decreased weight gain and survival. These symptoms closely resemble the human diabetic condition known as nonketotic hypertonicity. Thus, a rat's body has a safety factor of 2.2 (=92/42) for glucose processing: it can process glucose at a rate 2.2 times its voluntary intake. This safety factor represents apparent excess capacity that may have evolved to process other nutrients converted into glucose, to minimize the risk of loads swamping capacities, to handle suddenly increased nutrient requirements, or to effect rapid mobilization of glucose.

A central problem of integrative biology is termed quantitative evolutionary design: what is the quantitative relation between biological capacities and the peak natural loads on them (1–7)? Are capacities approximately equal to peak loads, or do they exceed them by some reserve capacity or safety factor? Examples of such relations include a bone's strength compared with the actual stresses on it, peak milk output of mammary glands compared with pups' milk requirements, and an enzyme's V_max value (maximal reaction rate) compared with actual reaction rates in the body. Do biological elements operating in series (such as muscles and tendons, or enzymes in a reaction chain) have similar capacities?

Of course, the same questions also arise for human-engineered machines and structures, in which the capacities of elements are consciously designed by engineers who know the expected operating load. (For instance, by what factor does the load under which an elevator cable would break exceed the load that the elevator is certified to lift?). Although biological systems differ in that their capacity/load relations evolved through natural selection rather than through conscious design, numerical values of safety factors (capacity/load ratios) nevertheless prove remarkably similar in engineered and biological systems (1, 3, 4).

At first thought, one might predict capacities to have been designed or to have evolved to be closely matched to loads, and series capacities to be closely matched to each other, to avoid the waste of energy and space associated with excess capacities that could never be used. In practice, there are many reasons why this often proves not to be the case: capacities exceed their loads by safety factors typically of 1.2 to 10, and series capacities are not always equal to each other. Understanding the reasons for this variation in safety factors is currently one of the major problems in quantitative evolutionary design.

Biological design questions arise at all levels of organization, from questions of microdesign at the molecular level (such as enzyme reaction chains) to questions of grand design at the level of relations between whole organs. The most extensive studies of grand design are those by Taylor, Weibel, and colleagues (5–7), who compared oxygen-transporting capacities of the main elements in series in the mammalian system for aerobic exercise: lungs, heart, muscle capillaries, and muscle mitochondria. Our paper is instead concerned with grand design of the mammalian system for nutrient processing. Nutrients are processed by several organs in series, being first consumed by mouth, then hydrolyzed and absorbed in the intestine, metabolized in liver and other organs, and finally excreted (in the original form or as metabolites) by the kidneys. Can all of those organs process nutrients at rates exceeding the animal's voluntary intake? Is the intestine's capacity for supplying nutrients to the rest of the body equal to, greater than, or less than the capacity of the liver, kidneys, and other organs to process those nutrients? One might expect the nutrient-processing capacities of these organs to have evolved under severe design constraints, because nutrient processing is essential to survival, the organs involved are among the most energetically costly in the body (8), and the organs show strong up- and down-regulation in response to nutrient availability and demand (9–11).

A practical problem in answering these questions about nutrient processing in series arises from that series layout itself. Normally, an animal consumes nutrients by mouth at a rate that the animal itself chooses, and there are limits to how much one can force-feed an animal to test whether its body can process nutrients at higher rates. For instance, if the intestine were a rate-limiting bottleneck with lower nutrient-processing capacities than those of organs acting later on nutrients, such as liver and kidneys, one would never be able to supply nutrients by mouth at higher rates to those later organs to measure their higher capacities. This potential limitation can be overcome by bypassing the mouth and intestine and introducing nutrients directly into the veins by the method of total parenteral nutrition (TPN), used clinically to nourish patients who for any reason cannot be nourished by mouth. When nutrients are administered intravenously, does the body's capacity to process nutrients reveal itself as exceeding the nutrient load that the animal normally consumes by mouth? We shall discuss the extent to which differences between the routes of nutrient administration might affect the results for reasons other than removing a rate-limiting bottleneck in the intestine. Here we use a rat TPN model (12–14) to administer nutrients intravenously. This paper focuses on glucose processing because carbohydrates are normally the main source of calories to rats (as well as to human patients nourished by TPN), but similar questions also arise for processing of amino acids and of lipids.

Materials and Methods

Surgical and TPN Procedures.

We maintained male Sprague–Dawley rats (initial body mass 200 g) on a 16-h/8-h light/dark cycle in a room maintained at 26°C. Rats were kept in metabolic cages to allow for separation and collection of urine and feces. Catheters were implanted into 80 rats by a modification of Steiger's method (15). Briefly, rats were anesthetized with ketamine (90 mg/kg), xylazine (18 mg/kg), and acepromazine (30 mg/kg) given intramuscularly. After shaving and cleansing the scapular and right thoracic areas with betadine, we made a 2.5-cm dorsal incision between the shoulders and a 2.0-cm ventral midline incision up the neck from the suprasternal notch, and pulled a 40-cm length of 0.025-inch internal diameter silastic catheter under the skin from the dorsal incision through to the ventral side. We dissected free the right external jugular vein to insert the catheter 2.8 cm down the jugular and into the superior vena cava, tied it in place, and flushed it with saline. The catheter's other end was threaded through a flexible spring shield, whose dacron flange was sutured to the suprascapular tissue, and the shield was attached to an infusion swivel, which was connected via silastic tubing to a Harvard syringe pump for continuous infusion. We gave all rats 0.3 mg/kg buprenorphine orally as analgesia for the first 48 h after the surgery.

Control and experimental rats were maintained for a total of 7 days after catheterization. Control rats (n = 15) were catheterized, received saline infusion (0.9% NaCl) without nutrients via the catheter (12 ml/day), and were offered the TPN solution orally in ad libitum quantities. Each liter of TPN contained 262 ml of 70% dextrose, 419 ml of 15% Novamine, 189 ml of 20% Intralipid, and 13.0 ml of Cernevit-12 multivitamins for infusion (all from Baxter Healthcare, Mundelein, IL); 0.57 ml of vitamin K (Phoenix Pharmaceuticals, St. Joseph, MO); 12.2 ml of lypholyte multielectrolyte concentrate, 8.7 ml of sodium phosphate, and 8.7 ml of MTE-6 mixture of trace elements (all from American Pharmaceutical Partners, Los Angeles); 86.9 ml of calcium gluconate (American Reagent Laboratories, Shirley, NY); and 0.24 ml iron dextran (Schein Pharmaceutical, Morristown, NJ). The solution's caloric content was 1.093 kcal/ml, its osmolality was 1,700 mOsmol/kg.

We infused experimental rats with saline (12 ml/day) for the first 2 days after surgery, during which time they were offered the TPN solution orally ad libitum. We then infused them with TPN at 56 ml/day (57 mmol/day glucose) for 2 days, during which time they had no access to oral food. Finally, beginning on the fifth day of the experiment, we infused them with one of six experimental levels of TPN infusion for 3 days (57 mmol/day glucose, n = 15 rats; 85.5 mmol/day glucose, n = 5; 94 mmol/day glucose, n = 9; 105.5 mmol/day glucose, n = 8; 114 mmol/day glucose, n = 18; or 142.5 mmol/day glucose, n = 10), during which time rats continued to have no access to oral food. Thus, control rats received saline infusion for 7 days, whereas experimental rats received saline infusion for 2 days, 57 ml/day TPN infusion for 2 days, and finally the experimental level of infusion for 3 days. We added 60 units per day of heparin to the infusate (saline and TPN) for the duration of the experiment.

All rats had free access to water at all times. We measured water intake, urine production, and (in orally fed rats) oral consumption of TPN solution daily.

Blood, Urine, and Fecal Analyses.

Seven days after implanting the catheters, we anaesthetized the rats with pentobarbital (75 mg/kg) given i.p., exposed their chest cavity, and withdrew blood by cardiac puncture. Serum was separated in a Vacutainer serum separator tube (Becton Dickinson) by centrifuging at 4,000 rpm in an IEC CENTRA-7R (Needham Heights, MA) for 10 min at 4°C, and the serum was frozen at −80°C until analysis. We determined serum glucose by the glucose oxidase method (Sigma kit 115), and serum osmolality with a vapor pressure osmometer (Wescor, Logan, UT).

As will be discussed, we used urinary glucose, serum glucose and osmolality, and survivorship to assess whether glucose processing ability was exceeded. It was not possible to obtain serum samples from individuals that died spontaneously. Although all rats at the four lower experimental infusion rates survived the 3-day treatment, only 4 of 14 rats infused at 114 mmol/day, and 0 of five at 142.5 mmol/day survived for 3 days. Thus, we studied two separate sets of rats receiving the 114 mmol/day treatment, and two sets receiving the 142.5 mmol/day treatment. One set was used to determine 3-day survivorship at that treatment level, and the other set was killed within 1 day to obtain serum for analysis. We used the first set of rats to calculate survival of the 114 and 142.5 mmol/day treatments only for those 14 and 5 individuals, respectively, in that first set. We used the second set of rats to obtain serum samples from enough rats at those two highest infusion rates before the rats died; we catheterized and administered the 142.5 mmol/day treatment to 5 additional rats, which we killed to obtain serum 18 h after the treatment began; and we similarly administered the 114 mmol/day treatment to four additional rats, which we killed 24 h after the treatment began. For reasons to be explained, serum glucose and osmolality values of the four rats surviving the 114 mmol/day treatment rats and killed at 3 days differed (by ANOVA) from values from the four rats killed at 24 h; those two sets of data will be considered separately.

We collected urine and measured its volume daily during the 3 days of treatment infusion (during the last 3 days of saline infusion for the control rats), and determined urine glucose values for the first 24 h of infusion with the experimental load. For the five rats infused with 142.5 mmol/day TPN for only 18 h, we collected urine for that period, then killed the rats and extrapolated urine volumes to a 24 h value. We used data from the first day of experimental treatment for all rats in all comparisons of urine values: i.e., although rats at the four lower infusion rates survived for all 3 days of treatment infusion, we used the urine data only for the first day to permit comparisons with the 114 and 142.5 mmol/day rats, many of which did not survive 3 days. Urine glucose values for day one were similar (by ANOVA) to those for days two and three for the rats at the four lower infusion rates. Thus, for 114 mmol/day treatment rats, we based urine glucose data on 18 rats, because all rats survived for at least 24 h, but we considered serum glucose and osmolality data separately for the four rats that survived to 3 days, and for the four rats killed at 24 h.

In a separate experiment to determine the completeness of glucose absorption, we fed five noncatheterized additional rats the TPN solution orally ad libitum for 5 days, collected their feces, and tested it for the presence of glucose by the glucose oxidase method.

Small Intestinal Glucose Uptake Capacity.

We measured the small intestine's size and glucose uptake rate to calculate its maximal uptake capacity for glucose. We anaesthetized 9 of the 15 control rats with i.p. pentobarbital (75 mg/kg), exteriorized the small intestine, flushed the lumen with saline, measured the small intestine's length, then divided it into three equal-length regions (proximal, mid, and distal) and weighed each region. We measured in vitro glucose uptake rates across the intestinal brush-border membrane of small intestinal segments by the everted sleeve method (16). Briefly, the three intestinal regions were everted and maintained in cold oxygenated Ringer's solution, then four adjacent 1-cm sleeves were cut from each region. We measured uptake by mounting sleeves individually on glass rods and incubating the rods in a modified Ringer's solution containing 50 mM of the transported isomer d-glucose and trace d-[¹⁴C]glucose, plus (as tracer) the nontransported isomer l-[³H]glucose to measure glucose in adherent fluid plus glucose taken up passively. After incubation, we removed tissue sleeves from the rods, weighed them wet in a tared vial, solubilized the sleeves (Solvable, Packard) for 24 h, added scintillation fluid (Ultima Gold, Packard), and counted them by using a dual channel program (Beckman Instruments). We measured two replicate sleeves from each region. The total uptake capacity of the whole length of the small intestine for glucose was obtained by calculating, for each intestinal region, the product of its uptake rate (nmol/min/mg sleeve wet mass) times the region's mass, then summing the products of the three regions.

Statistics.

We used ANOVA to test for treatment effects on urinary glucose, serum glucose, serum osmolality, mean daily water intake, mean daily urine output, and 7-day growth (final mass minus initial mass), and to test for treatment day effects on water consumption and urine production at each treatment level. We used analysis of covariance (ANCOVA) to test for treatment effects on organ mass using final body mass as the covariate. If treatment effects were detected by ANOVA or ANCOVA, we used the Tukey–Kramer honestly significant difference (HSD) test to compare values at different treatments to each other; this test is robust to unequal sample sizes (17, 18). It calculates a least significant difference to determine significance at the P < 0.05 level (18).

Results

Controls.

Control rats receiving saline were fed TPN formula orally ad libitum. During the last 3 days of the experiment, they consumed 5.2 ± 1.4 ml/day of water, 41 ± 2 ml/day of TPN solution, hence 46 ± 2 ml/day of total fluid, and produced 30 ± 3 ml/day of urine. The TPN solution consumed contained 45 ± 2 kcal/day, including 42 ± 2 mmol/day of glucose.

Experimental Treatments.

Survivorship, urinary glucose, and serum glucose and osmolality.

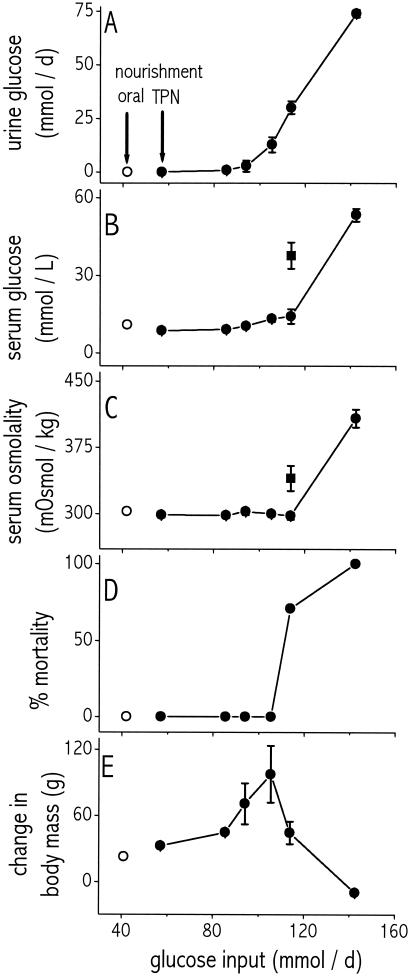
Rats infused with the three lowest glucose loads (57, 85.5, 94 mmol/day) were normal in all respects depicted in Fig. 1, even though all of those loads exceeded by up to 2.2-fold the oral load consumed ad libitum. In particular, there was no mortality during the 3 days of experimental infusion (Fig. 1D). Values of urinary glucose (Figs. 1A and 2B; means 0.036–2.9 mmol/day), serum glucose (Fig. 1B; 8.6–10.4 mmol/liter), and serum osmolality (Fig. 1C: 299–303 mOsmol/kg) were similar among the three loads and similar to values of control rats (0.0056 ± 0.001, 10.8 ± 0.4, and 302 ± 3, respectively; Tukey–Kramer HSD).

Figure 1.

Effect of glucose input load (mmol/day) on urinary glucose output (A), serum glucose concentration (B), serum osmolality (C), mortality (D), and weight gain (change in body mass) (E). ○, Oral nourishment; ●, TPN nourishment at the indicated load for 3 days; ■, TPN-nourished rats at a load of114 mmol/day glucose, killed after 24 h. Values for a load of 142.5 mmol/day in A–C and E refer to rats killed after 18 h. Note that urinary glucose output begins to increase at a load of 94 mmol/day and that serum glucose and osmolality begin to increase, and weight gain begins to decrease, at 114 mmol/day, with a concomitant rise in mortality. n = 4–18 rats per data point. Bars indicate SEM; bars are omitted for SEMs smaller than the size of the graphed symbol.

Rats infused with the next higher load (105.5 mmol/day) also had zero mortality and values normal in all respects, except that urinary glucose was elevated slightly (to 13 ± 3 mmol/day), but significantly (Tukey–Kramer HSD).

At the next higher load of 114 mmol/day, mortality jumped to 71%, with rats dying on days two and three of treatment (Fig. 1D). Those four rats that survived 3 days of infusion had significantly elevated urinary glucose (30 ± 2 mmol/day), but had serum glucose (14.1 ± 2.8 mmol/liter) and serum osmolality (298 ± 4 mOsmol/kg) similar to control rats. However, rats killed after only 24 h of infusion at 114 mmol/day had significantly elevated values not only of urinary glucose (43 ± 8 mmol/day) but also of serum glucose (38 ± 10 mmol/liter) and serum osmolality (340 ± 14 mOsmol/kg). At first, it seems paradoxical that rats at this load had more abnormal values after only 1 day than after 3 days. However, the rats alive at 1 day included some that would have died on day two or three as a result of those abnormal values, whereas the rats alive after 3 days were necessarily individuals that adapted well and did not have abnormal values. In support of this explanation, we note that the coefficient of variation of serum osmolality was higher for the rats killed at 1 day than for the rats that survived to be killed at 3 days (8% vs. 3%, respectively).

Finally, at the highest load of 142.5 mmol/day, all rats died before the end of 1 d. For the four rats intentionally killed at 18 h, urinary glucose (74 ± 2 mmol/day), serum glucose (53 ± 3 mmol/liter), and serum osmolality (408 ± 10 mOsmol/kg) were all far higher than control values.

Weight gain.

All rats that survived for all 3 days of TPN infusion gained weight, as did control rats. Weight gain increased with increasing load up to 105 mmol/liter (gain of 98 ± 26 g, compared with only 23 ± 4 g for control rats), then fell off to 44 ± 10 g for the load of 114 mmol/day. Rats at the highest nutrient load, 142.5 mmol/day, which were killed after 18 h of treatment infusion, actually lost weight despite receiving the most nutrients (Fig. 1E).

Water intake and urine output.

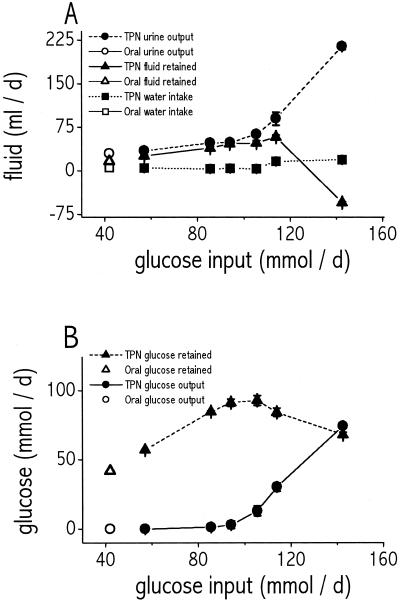
As also true for weight gain (preceding paragraph), we calculated water intake and urine output only for rats that survived for all 3 days of TPN infusion, hence the 142.5 mmol/day load is excluded from this analysis (no rats survived for 3 days). Because treatment day (day 1, 2, or 3) had no effect on either water intake (P = 0.9, ANOVA) or urine production (P = 0.12, ANOVA) at any treatment level, we calculated mean daily rates averaged over all 3 days (Fig. 2A). Water intake did not vary among controls and infusion loads (P = 0.13, ANOVA), but urine output increased with load (P < 0.0001, ANOVA).

Figure 2.

(A) Effect of glucose input load (mmol/day) on urine output (circles), total fluid retained (triangles), and water intake (squares). Filled symbols, TPN-nourished rats. Open symbols, orally nourished rats. Fluid volume retained was calculated as the sum of TPN infused plus water consumed minus urine output, neglecting evaporative water loss. Note that, at the highest infusion rate of 142.5 mmol/day glucose, urine output increases greatly, leading to paradoxical dehydration (negative fluid retained). Values are averages of the three treatment days for all groups except rats of the 142.5 mmol/day treatment group, which were killed after 18 h of infusion; their values were extrapolated to 24 h. Values for the 114 mmol/day treatment group are from the four rats that survived infusion for 3 days. (B) Effect of glucose input load on glucose retained (triangles) and glucose output (circles). Filled symbols, TPN-nourished rats. Open symbols, orally nourished rats. Glucose retained was calculated as glucose input minus urinary glucose output (fecal glucose output was negligible). Note that rats were able to retain a maximum of 92 mmol/day glucose, which suggests a ceiling on glucose processing capacity. n = 4–18 rats per data point. Bars indicate SEM.

Small Intestinal Glucose Uptake Capacity.

Uptake capacity was 26 ± 3 mmol/day (n = 9).

Discussion

We shall discuss five issues: comparison of TPN and oral nutrient delivery; capacities of the TPN and oral routes; interpretation of safety factors; why rats become impaired or die at high TPN rates; and possible limiting roles of TPN nutrients other than glucose.

Comparison of TPN and Oral Nutrient Delivery.

Our TPN infusion was delivered at a constant rate day and night, whereas rats are known to feed orally more at night than by day. Does that difference affect the comparison?

We think not: the difference is minor for three reasons. First, fully 30% of rats' total food intake is during the light phase (19); we observed that our rats consumed oral TPN throughout the day; and food intake in the dark phase has two separate peaks, during the first 3 and last 3 hours of darkness (20). Second, the pyloric sphincter regulates food transit from the stomach to the small intestine, so that food presence and absorption from the small intestine are much steadier throughout the day than is food consumption (21). From measurements of gastric emptying times (22, 23), we calculate that the rats in our study would have required 13 h to empty their stomachs of the food consumed at night even if they had eaten nothing by day; this calculation agrees with observations that food remains in a rat's stomach and small intestine for 12–24 h after food deprivation (refs. 24 and 25, and unpublished data). Finally, mRNA and protein of the intestinal brush-border glucose transporter SGLT1 are present throughout the 24-h cycle (26), permitting rats to continue to transport glucose. Thus, nutrient processing proceeds throughout the day even in orally fed rats.

Capacities of the TPN and Oral Routes.

TPN route.

TPN-nourished rats receiving glucose at up to 94 mmol/day had normal serum glucose and osmolality values and processed and retained virtually all infused glucose, as judged by their low urinary glucose output (Figs. 1A and 2B). Rats infused at 105.5 mmol/day also had normal serum glucose and osmolality, but excreted 12% of the infused glucose into their urine. Thus, actual glucose processing was 91 mmol/day for rats infused at 94 mmol/day (=94 mmol/day intake minus 3 mmol/day urinary output), and was virtually the same (92.5 mmol/day) for rats infused at 105.5 mmol/day (=105.5 mmol/day intake minus 13 mmol/day urinary output).

At the higher infusion rates of 114 or 142.5 mmol/day, rats showed signs of severe impairment: high mortality, elevated serum glucose and osmolality, a paradoxical decrease in glucose processed and retained despite the higher glucose intake (filled triangles in Fig. 2B), paradoxically decreased weight gain despite that higher nutrient intake (Fig. 1E), significantly reduced kidney mass corrected for body mass (only 0.61 ± 0.02 g for 114 mmol/day rats, vs. 0.68 ± 0.02 g for 105.5 mmol/day rats; Tukey–Kramer HSD), and (at 142.5 mmol/day) negative water balance (see filled triangles in Fig. 2A, indicating net dehydration).

Thus, the upper limit to glucose processing by the TPN route is about 92 mmol/day.

Oral route.

The ad libitum oral glucose intake of our rats was 42 mmol/day, a factor of 2.2 smaller than that upper limit to glucose processing by the TPN route. That oral intake of 42 mmol/day was processed virtually completely; glucose loss was only 0.004 ± 0.0006 mmol/day in the urine (n = 15), and only 0.19 ± 0.03 (n = 5) in the feces. However, it cannot be claimed that 42 mmol/day is the maximum rate of glucose processing possible by the oral route; all that we know is that rats chose to consume glucose at that rate.

How can the small intestine's maximal glucose uptake capacity of 26 mmol/day be only 62% of that glucose oral intake of 42 mmol/day, given that the oral intake is processed almost completely? The explanation is that rats also process glucose by fermentation in the cecum (27–29). For instance, in our study those individual rats with larger ceca (corrected for body mass) had less glucose in the feces than did rats with smaller ceca (type I linear regression, P = 0.05, n = 5). Because we measured glucose uptake capacity of the small intestine but not glucose fermentation capacity of the cecum, we do not know the total glucose processing capacity of the entire intestine, other than to say that it evidently exceeds ad libitum oral glucose intake (because oral intake was processed almost completely). Hence, we also cannot compare total intestinal capacity with the capacities of organs acting later on nutrients, such as liver and kidneys.

Interpretation of Safety Factors.

The safety factor, for glucose processing, of the body beyond the intestine is 2.2. That is, the body can actually process double its normal glucose load. Why has the body evolved that apparent excess capacity?

In reality, this a modest safety factor, toward the low end of the biological range; some other biological element have safety factors as high as 7 (3, 4). On reflection, there are many obvious reasons why biological elements have evolved to be “overdesigned.” Four reasons for the existence of reserve capacity for glucose processing include the following.

Our TPN solutions contained substantial concentrations of amino acids and lipids as well as of glucose, and typical oral diets of rats contain fructose as well as glucose. All of those nutrients may to varying degrees become converted into glucose, so that the actual glucose load faced by the body may exceed the glucose load ingested orally or infused by TPN.

The penalty for inadequate glucose-processing capacity is impairment or death, as encountered in our rats infused with the highest glucose loads. High penalties for performance failure are associated with high safety factors in other biological systems and in human-engineered systems, to decrease the risk of failure (3, 4). More specifically, in any real situation the load and capacity are not exactly constant with time and among individuals, but instead there are distributions of both capacity values and load values; a high safety factor reduces the failure zone of overlap between the low tail of the capacity distribution and the high tail of the load distribution (see figure 1 of ref. 4).

Animals may experience suddenly increased food requirements, e.g., if they encounter a cold environment or a situation requiring high physical activity. If glucose-processing capacities are up-regulated slowly or not at all with increasing load, a capacity that would constitute unutilized reserve under normal conditions would then suddenly be required.

Finally, glucose-processing elements may appear overdesigned for steady-state glucose processing because their capacity is required for some other purpose, such as effecting rapid mobilization or metabolism of glucose.

Why Do Rats Become Impaired or Die at High TPN Rates?

At high TPN rates, our rats exhibited six symptoms: high serum glucose (extreme hyperglycemia), high serum osmolality, high urinary glucose excretion (glucosuria), high urine volume (diuresis), negative water balance (dehydration), and high mortality. All six of these features also characterize a clinical condition of diabetic humans known as nonketotic hypertonicity (NKH) (30, 31). The underlying cause of NKH in humans is that diabetes leads to high serum glucose concentrations, exceeding the kidneys' threshold for complete reabsorption of glucose from the glomerular filtrate. That nonreabsorbed glucose remains in the urine, pulling along water and other solutes (especially salt) by the mechanism known as osmotic diuresis, resulting in large volumes of hypotonic urine, dehydration, increasingly hypertonic serum, and ultimately death. Both in humans and in our rats, the rise in serum glucose concentration accounts for only part of the rise in serum osmolality; it accounts for 57–63% of the rise in humans (30, 32, 33) and for 40–70% of the rise in our rats. The remainder of the rise in serum osmolality in humans represents the rise in serum concentrations of ions (especially sodium) and urea; the same solutes probably contribute in rats, along with a rise in amino acid concentrations, because of the amino acid content of the infused TPN. The main difference between human NKH and our rats' condition is that the rise in serum glucose in human NKH is caused by diabetes, but in our rats it is caused by the glucose content of our infused TPN. Another difference is the more rapid onset of symptoms in our rats (within a fraction of 1 day) than in humans (typically over several days), but that difference is perhaps to be expected just because we abruptly began to administer a high glucose load to our rats by TPN.

Future Directions: Limiting Roles of Other TPN Nutrients.

This paper has focused on measurements of glucose processing during TPN infusion, because glucose is the solute accounting for the most calories in our TPN solution. Our solution also contained amino acids and lipids, so one might wonder whether capacity for processing them at high TPN rates becomes exceeded just as we found for glucose. We have made no measurements of lipids, but preliminary measurements suggest that this may indeed be true for amino acids. Urinary excretion of total nitrogen (measured by the total Kjeldahl nitrogen method) and of urea increased with increasing TPN infusion rate. TPN nitrogen retained by the rats increased with infusion rate over our three lowest rates but then decreased at higher rates, much as we observed for glucose retention (Fig. 2B). Hence, rats may also have a ceiling on nitrogen processing, and the exceeding of this ceiling may contribute to their symptoms at high TPN infusion rates. More detailed studies of nitrogen- and lipid-processing capacities in relation to normal loads should be a priority for future research in this area.

Abbreviations

TPN

total parenteral nutrition

HSD

honestly significant difference