Survival dynamics of starving bacteria are determined by ion homeostasis that maintains plasmolysis

Abstract

The ability to survive starvation is an integral part of bacterial fitness and determines composition, turnover and biodiversity in microbial ecosystems. Starving bacteria enter a state known as plasmolysis in which their cytoplasm contracts from the cell wall. Plasmolysis is often thought to be a pathological, passive condition, arising automatically from the lack of ATP. Here we show that contrary to this notion, maintaining plasmolysis is an active, ATP-consuming state that is essential for starvation survival. We show that ion homeostasis to maintain plasmolysis consumes the largest part of the energy budget of starving cells and directly determines death rates in starvation. Our mathematical model accurately predicts death rates for various starvation conditions and perturbations. This enabled the development of an optimized starvation medium that would be ideally suited for preserving and transplanting natural microbial communities by maintaining viability but preventing outgrowth of a subset of the species.

Microorganisms in natural environments, such as water bodies^1–3, soil^4,5, sediments^6–8 and human microbiota^9–12, are frequently starving. It was realized early in the era of microbiology that this phase of the life cycle is central to understanding bacterial fitness^13–15. Although genes and environmental conditions affecting starvation survival have been identified^16–23 and numerous mutations^24–26 and physiological alterations^17,27–29 in response to starvation have been discovered, some of the most fundamental questions remain unanswered. Specifically, what causes bacteria to irreversibly lose their viability and what determines their lifespan during starvation survival?

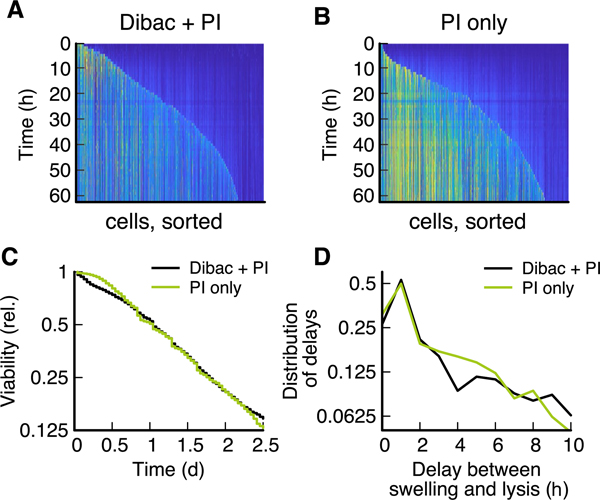
Here we study carbon-starved Escherichia coli K-12 in minimal medium. Within the first 10 days of starvation, viability decreases exponentially to 0.1% (Fig. 1a) before starvation-specialized mutants begin to play a role^15,24. The phenotype of exponential decay was described almost a hundred years ago¹⁴ and is remarkably conserved in natural environments^3,5,7. It can be replicated in controlled laboratory settings^{13,14,28,30–32}, with the decay rate and specific dynamics depending on the organism (Extended Data Fig. 1a). To better understand the dynamics of the cell death process, we imaged individual starving bacteria with live-cell, time-lapse microscopy and tracked viability using a live-dead stain (Fig. 1b). We thereby captured the cell death of thousands of individual bacteria by live-imaging, and a consistent picture of the cell death process emerged. As in previous studies^28,29, we found that within a few hours of nutrient depletion, the cytoplasm of most E. coli cells contracts and detaches from the cell wall at the poles. Figure 1c, has an image at 16 h (see also Fig. 1d and Extended Data Fig. 2c, and see Extended Data Fig. 2a,b for quantification and statistics). This process is called plasmolysis, and the cells remained in this state until shortly before cell death. The first events in the cell death cascade that we identified were the spontaneous depolarization of the cytoplasm, detected using the membrane potential probe DiBac4(3) (Fig. 1c), which coincided with swelling of the cytoplasm (Fig. 1c,e). We quantified the delay between depolarization and swelling for individual cells (Fig. 1f) and found that these events occurred effectively simultaneously (−0.05 ± 0.50 h). Swelling of the cytoplasm led to a breakdown of plasmolysis and, ultimately, stretching of the cell envelope, resulting in a measurable transient increase in cell length (Fig. 1e and Extended Data Fig. 2d). Shortly after, dying bacteria lysed, as reflected in permeabilization, detected by propidium iodide (PI) staining (Fig. 1b and Extended Data Fig. 2e), as well as a sudden loss of a substantial fraction of the cellular biomass, quantified with quantitative phase microscopy (QPM) (Fig. 1g and Extended Data Fig. 2f). We determined the time point of lysis using QPM relative to the time point of depolarization for individual cells (Fig. 1h) and found a time delay of roughly two hours (2.0 ± 1.4 h) between depolarization and lysis, suggesting that lysis, presumably the final irreversible step of cell death, is causally downstream of depolarization and swelling. Indeed, we confirmed that cytoplasmic expansion and subsequent lysis dynamics were neither affected by DiBac4(3) staining (Extended Data Fig. 3) nor could lysed cells recover upon nutrient re-addition. On the other hand, we detected a fraction of depolarized cells that could repolarize and resume growth upon nutrient re-addition (Extended Data Fig. 4), suggesting that before lysis, the cell death process was still reversible.

Fig. 1 |. Survival dynamics of E. coli in carbon starvation.

a, Viability of E. coli K-12 NCM3722 in the N+C− minimal medium shows a roughly exponential decay (batch). Viability is measured in terms of colony-forming units (CFU per ml) (Methods). The line is an exponential fit. Data points are an average of n = 3 replicates and error bars show the standard deviation. b, Tracking viability of bacteria by live-imaging starvation with PI staining. Bacteria exhibit a seemingly random decay in viability, as illustrated by single-cell traces of seven bacteria. c, Live-cell imaging of E. coli during starvation. Plasmolysis, the retraction of the cytoplasmic membrane from the cell envelope, lasted from the first hours of starvation until shortly before death (see the kymograph). The first sign of the cell death process was that the cytoplasm spontaneously depolarized (cyan DiBac4(3) signal turns on at 26 h). This coincided with the beginning of swelling of the cytoplasm. Swelling continued until the bacterium was no longer in plasmolysis and the cell envelope became stretched. Finally, the bacterium lysed (arrow at 26.3 h). For a systematic analysis of many cells, see Extended Data Fig. 2. d, Transmission electron micrographs during exponential growth, 2 h and 48 h in starvation of three representative cells. Note that the inner membrane is closely aligned with the cell envelope during growth but retracts at 2 h in starvation. Excess material is visible in the undulating membrane and in blebs in the periplasm. At 48 h, the excess membrane has disappeared. The near spherical shape of the inner membrane indicates that it is under tension. e, Cell envelope length of single cells, aligned to time point of swelling (grey, with the mean in red). Number of bacteria was 858. f, Delay between depolarization and stretching. Swelling and depolarization closely coincided, t_delay = (−0.05 ± 0.5) h. g, Single-cell biomass, measured with QPM (Methods) aligned to the time point of lysis. Loss of biomass was 28 ± 7%. Number of bacteria was 34. h, Delay between loss of biomass (time point of steepest slope of biomass data) and time point of depolarization, t_delay = (2.0 ± 1.4) h. Number of bacteria was 34. a.u., arbitrary units; IM, inner membrane; P, periplasm; C, cytoplasm; rel., relative.

Plasmolysis requires that the internal concentration of osmolytes reduces below the external concentration to induce water efflux and shrinkage of the cytoplasm. This requires the active export of ions. Without this export, cells would reach thermodynamic equilibrium in which the total concentration of intracellular osmolytes, including both ions and biomolecules like metabolites, proteins, RNA and DNA, would exceed the concentration of ions in the medium, resulting in a build-up of osmotic pressure that is incompatible with plasmolysis. Indeed, we observed that depolarization immediately resulted in cytoplasmic swelling (Fig. 1e), which eventually resulted in lysis (Fig. 1g). This active ion transport continuously dissipates the electrochemical gradient and consumes ATP^33,34 because ions diffuse back into the cell across the plasma membrane down their concentration gradients³⁵. If this hypothesis is correct, ion homeostasis should be an indispensable active process in starving bacteria and a major contributor to maintenance energy cost, which is what we set out to test.

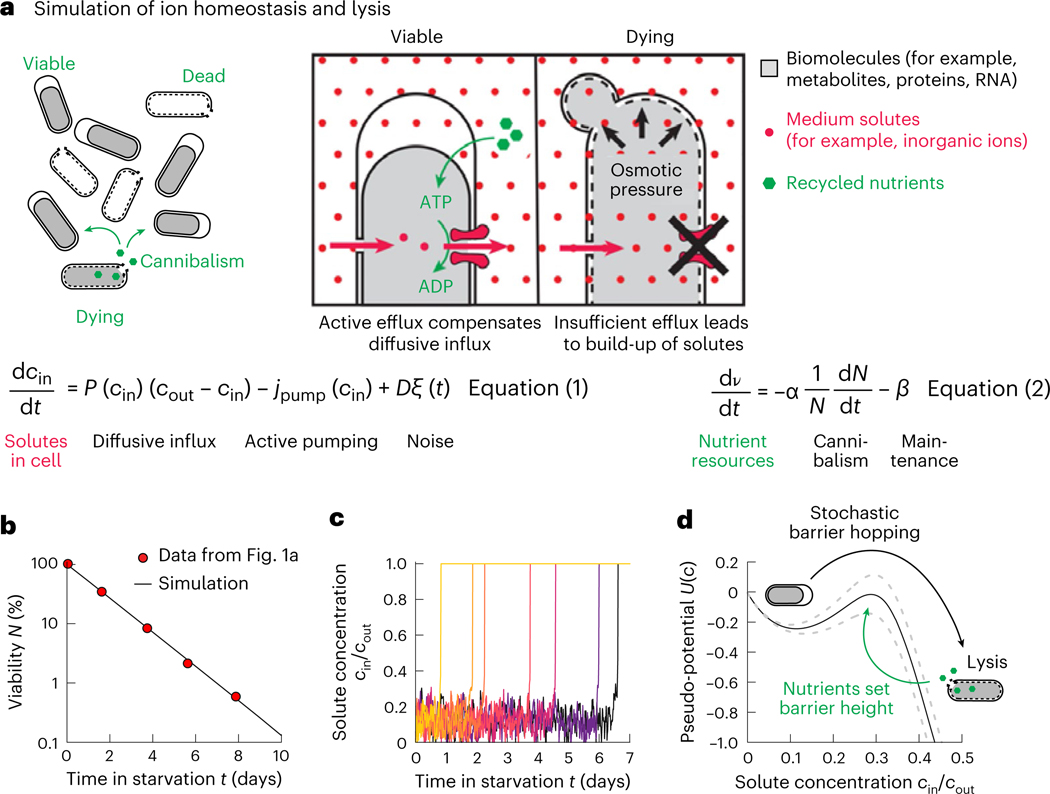
To start, we wanted to know if the hypothesis that ion homeostasis is central to survival is consistent with the seemingly random, and rapid, loss of depolarization. Naively, one may expect that all cells gradually lose their polarization as they deplete their internal resources. It was a priori not clear how a highly stochastic and continuous decay process could emerge from these concepts. Therefore, we formulated a simplified model of ion homeostasis, which was implemented in a computer simulation and reflects the maintenance of concentration gradients and osmoregulation (Fig. 2a):

$$\frac{\text{d}{c}_{\text{in}}}{\text{d}t}=P\left(c_{\text{in}}\right)\left(c_{\text{out}}-c_{\text{in}}\right)-j_{\text{pump}}\left(c_{\text{in}}\right)+D\xi (t).$$ (1)

Fig. 2 |. Simulation of maintenance of ion homeostasis.

a, Nutrients released by lysis are cannibalized by viable bacteria (left) and are used to export ions from the cytoplasm to the medium (right). If sufficient nutrients are present to support this active transport, then the cytoplasm contracts (plasmolysis) until the concentration of solutes from the biomass balances $c_{\text{out}}$. Insufficient pumping leads to a collapse of ion gradients, osmotic water inflow and swelling, resulting in lysis. The dynamics of the internal solute concentration $c_{\text{in}}$ are given by diffusive influx (Fick’s law with permeability $P$, ion gradient $\text{Δ}c=c_{\text{out}}-c_{\text{in}}$), active pumping ($j_{\text{pump}}$, which is a part of the total maintenance $\text{β}$) and normally distributed noise $\xi (t)$. Stretching of the membrane by increased turgor pressure (that is, decreased $\text{Δ}c$) increases $P(\text{Δ}c)$. The level of nutrients in the medium $\nu$ depends on the release of nutrients (recycling yield $\alpha$) and maintenance $\beta$. $N$ is the number of viable bacteria in the culture. See Supplementary Note: ‘Mathematical Model’ for details of the model. b, Simulated starvation of 10⁵ bacteria (black line) compared to experimental data from Fig. 1a. c, Dynamics of single-cell solute concentration for bacteria dying at different time points shows small fluctuations around a low solute concentration, followed by a sudden spontaneous loss of homeostasis (see the experimental data in Fig. 1b). d, The model can be mapped onto a potential $U(c)$ (black line) with $\text{d}c/\text{d}t=-U^{\prime }(c)+\xi (t)$. The height of the barrier self-adjusts. Dashed lines show the effect of a 10% change in death rate on the potential barrier.

The dynamics of the internal solute concentration ${\text{c}}_{\text{in}}$ are given by diffusive influx (Fick’s law with permeability P, ion gradient $\text{Δc}={\text{c}}_{\text{out}}-{\text{c}}_{\text{in}}$), active pumping ($j_{\text{pump}}$, which is a part of the total maintenance $\text{β}$) and normally distributed noise $\text{ξ}(\text{t})$ with diffusion constant D. To build this minimalistic model, we used a coarse-grained approach with a single, effective ion species and considered only diffusion, neglecting effects from membrane potential. However, it would be straightforward to generalize our model to include several ion species and electric terms, as in previous models of ion transport^36–38. In the model, the cell maintains a low cytoplasmic concentration ${\text{c}}_{\text{in}}$ of this ion, thereby reducing osmotic pressure and maintaining plasmolysis. Ions from the medium (Fig. 2a, red dots) diffuse back into the cytoplasm down their concentration gradient and are exported using active transport, which consumes energy (equation (1)).

The energy required for ion transport is, in turn, provided by biomolecules $v$ released from dying cells (with recycling yield $\alpha$) that are cannibalized by surviving cells¹⁵ and used for maintenance (maintenance rate $\beta$), as established by previous observations³⁰ (Fig. 2):

$$\frac{\text{d}v}{\text{d}t}=-\alpha \frac{1}{N}\frac{\text{d}N}{\text{d}t}-\beta .$$ (2)

It has been shown that nutrient recycling during starvation is fast so that few nutrients accumulate in the supernatant, which is why we performed a timescale separation in the model and assumed that the nutrients available to a viable cell $v$ are in a steady state (Methods; the assumption is checked in Extended Data Fig. 5).

Next, we assumed that as the osmotic pressure builds up (reflected in an increasing internal ion concentration $c_{\text{in}}$), the plasma membrane stretches and permeability increases^39–41. We implemented this pressure dependence of permeability implicitly, using a concentration-dependent permeability $P\left(c_{\text{in}}\right)$. Similarly, we assumed that the pumping rate $j_{\text{pump}}\left(c_{\text{in}}\right)$ vanishes at a critical internal ion concentration, reflecting that once the membrane becomes stretched beyond a certain point, the cell lyses and the proton motif force collapses. Fluctuations were introduced through a normally distributed noise term. These could stem from temporal variations in permeability, pumping or nutrient availability. A subtle point is that because E. coli is unable to precisely control the turgor pressure in response to changes in medium salt concentrations^42,43, we assumed in our model that cells indiscriminately export ions, resulting in a contraction of the cytoplasm, rather than exporting just the bare minimum to achieve a pressure balance. This assumption is consistent with the observation that bacteria are in plasmolysis during starvation.

On simulating this model, we indeed found that it is possible to obtain an exponential decay in the viability of the population (Fig. 2b), such that individual bacteria randomly and rapidly lose their ion homeostasis (Fig. 2c). Before death, the bacteria maintain their internal ion concentration low (Fig. 2c), which means that the turgor pressure vanishes and the cytoplasm contracts. This spontaneous death process can be understood as a stochastic escape from a potential well (Fig. 2d), like the classic Kramer’s escape model in physics⁴⁴. The dynamics takes place in an abstract potential well, created by the active salt transport of the cells. Inside the potential well, starving cells have a low internal salt concentration and are in plasmolysis. However, stochastically due to noise in the system, a small number of cells hop over the barrier, which reflects the increasing salt concentrations and the uncontrolled expansion that leads to lysis. The hopping rate depends on the height of the barrier. However, unlike the classic Kramer’s escape model in which the height of the barrier is fixed, the potential barrier is created by nutrients released from dying cells that hopped over the barrier. Hence, the barrier height depends on the rate of cells crossing it. This creates a feedback loop. If too few cells are dying, the barrier height is low and more cells will cross it. This will result in more dying cells, which release more nutrients, which will in turn increase the barrier height. Conversely, if the barrier is too high, few cells will cross it and, therefore, too few nutrients will be released by dying cells, decreasing the barrier height. This feedback leads to a quasi-steady state in which most bacteria are supplied with just enough nutrients to remain in the potential well, but the potential barrier remains low enough to allow cells to escape the well at a low rate and provide nutrients to support surviving cells. Therefore, even small fluctuations in the underlying biological variables, like salt concentrations, ATP levels or membrane permeability, are sufficient to result in a highly stochastic exponential decay in viability (Supplementary Note: ‘Mathematical Model’). This closely resembles our experimental observations, as we found that most starving cells remain in plasmolysis (low internal ion concentration) but that a subset randomly undergoes spontaneous expansion and lysis (with an ion influx and crossing the potential barrier) (Fig. 1b). Thus, this simulation qualitatively captures the observed dynamics.

Crucially, these simulation results are largely independent of microscopic modelling assumptions concerning stretching, pumping or nutrient recycling (Extended Data Fig. 5) because of the self-adjusting barrier height mechanism. Hence, we next sought to derive a coarse-grained formulation of the model to derive quantitatively testable predictions. First, we assumed that the internal ion concentration $c_{\text{in}}$ is in a steady state (most cells in the population are at the bottom of the potential well). In this case, ion efflux from active transport $j_{\text{out}}$ is balanced by passive diffusive influx $j_{\text{in}}$. Fick’s law of diffusion states that the diffusive influx $j_{\text{in}}$ is proportional to the concentration gradient of ions across the membrane, $j_{\text{in}}=P\text{Δ}c$, where $P$ is the permeability of the membrane in plasmolysis and $\text{Δ}c=c_{\text{out}}-c_{\text{in}}$ is the ion gradient. Hence, the energy expenditure of bacteria due to pumping ions, denoted by $\beta$, is given by $\beta =\kappa j_{\text{out}}=\kappa P\text{Δ}c$, where $\kappa$ is the pumping cost. On the other hand, energy for this active transport process comes from nutrients released by dying cells. If the death of a cell yields $\alpha$ nutrients that are divided up equally among all $N$ viable bacteria, and $-\dot{N}$ are dying per unit time, then the rate at which a bacterium is supplied with nutrients is $-\alpha \dot{N}/N=\alpha \gamma$, where $\gamma$ is the death rate. Here we assumed that nutrient liberation, uptake and internal conversion are fast and reach a steady state during the exponential decay phase (Methods and Extended Data Fig. 5 for a detailed discussion). In addition, we assumed that all nutrients are used for maintenance of osmoregulation just as they are supplied, $\alpha \gamma =\beta$. Thus, by combining nutrient recycling and the cost of osmoregulation, we obtained a simple quantitative relation for the death rate as a function of permeability, ion concentration gradient and the recycling yield:

$$\gamma =\frac{\kappa P\text{Δ}c}{\alpha }.$$ (3)

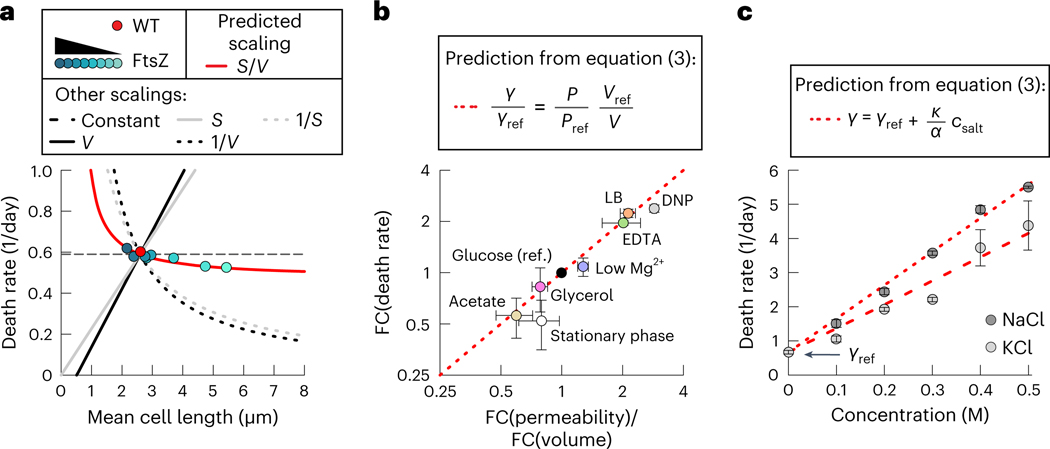
Equation (3) makes a highly non-trivial prediction that the death rate depends on cell shape. The permeability $P$ is proportional to the cell surface area $S$ because diffusion happens across the cell membrane, whereas the recycling yield $\alpha$ is proportional to the cell volume $V$, as shown in ref. 32, because bigger cells liberate more biomass when they die. Thus, according to equation (3), the death rate should scale with the surface-to-volume ratio of bacteria, $\gamma \propto S/V$, if all other factors are constant.

To compare the ion homeostasis model to these alternative mechanisms, we varied the cell length of E. coli using a titratable expression construct of the cell division protein FtsZ (Extended Data Fig. 6). Remarkably, we observed an almost constant death rate, despite a 2.5-fold variation in average length (Fig. 3a). These data are incompatible with several other scalings that might be expected from alternative models (Fig. 3a, black lines). Moreover, FtsZ-deprived cells also typically contain several copies of chromosomal DNA⁴⁵, which suggests that DNA damage is also unlikely to be rate limiting for survival. The slight decrease of death rate in longer cells closely matches the estimated surface-to-volume ratio of rod-shaped bacteria, as predicted by equation (3) (Fig. 3a, red line), but the changes in the surface-to-volume ratio are too small for us to confidently discern $S/V$ scaling from a constant death rate.

Fig. 3 |. Cost of ion homeostasis determines the death rate.

a, Death rate of wild-type (WT) and mutant ptac-ftsZ (37), induced with varying levels of IPTG, resulting in a change in cell length (Extended Data Fig. 6). The death rate is compared to the predicted $S/V$ scaling, and proportional or inverse scaling with either $S$ or $V$. b, Fold change (FC) of death rate, measured in batch cultures plotted versus fold change of mean permeability (Methods) times the inverse fold change of volume, both measured with time-lapse microscopy. The theoretical prediction is the unity line in dashed red. The reference (ref.) condition is growth in the minimal medium with glucose (black). Cultures were supplemented with different carbon substrates during growth (acetate or glycerol), grown to the stationary phase on glucose or cultured in LB. For the low Mg²⁺ case, the Mg²⁺ concentration was changed during starvation from 0.4 to 0.1 mM. For other cells, 1 mM of EDTA was added in starvation or 1 mM of di-nitrophenol (DNP) was added in starvation. Error bars for the death rate show the standard deviation of three biological replicates. The permeability and volume changes were for an average of 2,000 to 20,000 individual bacteria and measured in duplicates. c, Death rate of cultures supplemented with either KCl or NaCl during starvation. Fits are $R^2=0.99$ (NaCl) and $R^2=0.96$ (KCl). Error bars show the standard deviation of three biological replicates.

This scaling is not obvious because there are many plausible alternative mechanisms of cell death that would result in a strong cell size dependence of the death rate. For example, if death were caused by a single, rare catastrophic event, such as damage of the cell membrane or the spontaneous formation of a toxic protein aggregate, then the death rate would increase for larger cells as more potential ‘sites’ for death would be available. Thus, the death rate would be proportional to the surface area $\gamma \propto S$ or the cytoplasmic volume $\gamma \propto V$. On the other hand, if death were caused by a random decay of essential components (for example, ribosomes or DNA damage) in either the cell’s membrane or cytoplasm, a bigger cell would survive longer due to having higher reserves of this essential limiting component and the death rate would decrease with increasing cell size.

Next, we wondered whether differences in death rates that are observed when bacteria are grown in different conditions could be explained by our model. Different growth conditions before starvation are known to affect the maintenance rate for unknown reasons, with faster growth leading to a higher maintenance rate and faster death³². These changes in the death rate are not accounted for by a change in $S/V$ because $S/V$ decreases for faster growth (because cells become bigger), although the death rate increases. Many aspects of bacterial physiology may change with changing growth rates. However, according to our model, changes in the death rate should result from changes in the small number of physiological variables in equation (3). Changes in the proteome allocation of the cell envelope⁴⁶ suggest that permeability could be a key parameter changing between these conditions. To test this hypothesis, we cultured E. coli in different growth media, washed them and resuspended them in a carbon-free medium. From equation (3), the fold change of the death rate should be reflected in the fold changes of permeability and volume, $\text{FC}(\gamma )=\text{FC}(P)\text{F}{\text{C}}^{-1}(V)$, if other parameters like the cost of pumping remain constant. The volume term accounts for the larger number of biomolecules released by bigger cells. Indeed, quantifying the average permeability for these starvation conditions using the slope of PI staining dynamics (Extended Data Fig. 7d) between 0 and 10 h showed that the change in the death rate in slow-growth carbons and rich media could be explained primarily by the effect on permeability and volume (Fig. 3b). This does not mean that complex physiological changes are not occurring between different growth rates but that their effect on the death rate appears to be mediated by their effect on a few physiological variables. To more directly test the causality of the effect of permeability, we permeabilized E. coli with low Mg²⁺, EDTA or di-nitrophenol. As expected, these perturbations resulted in faster death rates (Fig. 3b). Moreover, death rates for all experimental conditions closely followed the model prediction of equation (3) (Fig. 3b, identity line in red).

Finally, if osmoregulation were critical to the cells’ survival, as hypothesized in our model, then the death rate should depend on the medium composition. Equation (1) predicts that increasing the external ion concentration $c_{\text{out}}$ should lead to an increase in ion gradients and an increase in diffusive influx, which needs to be balanced with a higher pumping rate to keep the internal ion concentration low. The resulting higher maintenance cost should lead to a linear increase of the death rate. Indeed, supplementing the medium with either NaCl or KCl led to a linear increase in the death rate, up to a tenfold increase at 0.5 M for both salts (Fig. 3c). The slope of the curve may reflect ion-specific permeability and pumping costs. According to the model, the increase of the death rate should be unique to osmolytes that permeate the membrane. Indeed, adding 0.5 M 3-(N-morpholino)propanesulfonic acid (MOPS), to which the cell is impermeable, did not increase the death rate (Extended Data Fig. 8), demonstrating that the linear increase in Fig. 3c was not simply due to ‘osmotic stress’.

Conversely, we wondered whether it would be possible to reduce the death rate by lowering the salt concentrations in the medium, as predicted by equation (3). Decreasing the concentration of our phosphate-buffered minimal medium (N+C−) decreased the death rate but only by about a third, before increasing again at low osmolarity (Extended Data Fig. 9). At first, this appears to violate our proposed model, as equation (3) predicts a direct proportionality between salt ions and death rate. However, this result can easily be understood within the framework proposed in this work. A minimum level of external osmolytes is crucial to balance the internal osmotic pressure from metabolites, biomolecules and cellular counterions and to prevent cell swelling. Hence, in the absence of salt in the medium, the cell is unable to prevent osmotic swelling and stay in plasmolysis, with detrimental effects on its starvation survival.

We, therefore, reasoned that it should be possible to overcome this limitation of cell survival by removing salt from the medium to minimize the maintenance cost while simultaneously osmotically balancing the turgor pressure. We found that 0.2 M MOPS was sufficient to balance the cytoplasmic pressure and maintain cells in plasmolysis in starvation in a low-salt medium. Remarkably, removing normal medium salts and adding MOPS led to a fourfold decrease in the death rate compared to regular starvation conditions (Fig. 4a). We refer to this starvation-optimized medium as a low-salt, osmo-balanced medium.

Fig. 4 |. Rescued starvation survival in a low-salt, osmo-balanced medium.

a, Starvation survival in either a standard starvation medium (black, data from Fig. 1a) or a low-salt, osmo-balanced medium (green). The death rate decreased 4.0-fold for the latter. n = 3. b, The maintenance rate decreased 10.2-fold in the low-salt, osmo-balanced medium. See Methods and Extended Data Fig. 10 for quantification. P = 0.0001 obtained using a one-tailed t-test. Units are femtomol glucose per viable cell (fmol per CFU). c, Time-lapse images of E. coli in the low-salt, osmo-balanced medium. After depolarization, the cytoplasm does not swell and the bacterium does not lyse. d, Delay in the distribution between depolarization and permeabilization. In the N+C− medium (black), both events occur in rapid succession. In the low-salt, osmo-balanced medium (green), the events are disconnected by 1.5 ± 0.5 days. N+C−, 14,498 bacteria. Low-salt, osmo-balanced, 11,023 bacteria.

We found that the maintenance cost in the low-salt, osmo-balanced medium was more than tenfold lower during starvation than in the regular starvation medium (Fig. 4b, Extended Data Fig. 10 for quantification and refs. 30,32 for the method). This result suggests that E. coli normally spends over 90% of its energy budget on exporting ions. To check the generality of this result, we tested whether this improvement in survival was unique to E. coli. In fact, other bacterial species showed the same improved starvation survival in this low-salt, osmo-balanced medium (Extended Data Fig. 1b,c). Together, the findings in Figs. 4a and 3c demonstrate that starvation survival can be controlled across a more than 40-fold range of death rates, simply by changing the medium salt composition.

To confirm that our low-salt, osmo-balanced medium maintained cells in plasmolysis and prevented cytoplasmic swelling, we performed live-imaging of E. coli. Several days into starvation, bacteria began to depolarize, presumably due to a lack of energy. However, depolarized bacteria remained in plasmolysis and did not swell and lyse (Fig. 4c). Unlike normal starvation conditions, the bacteria permeabilized only several days after the loss of their membrane potential (Fig. 4d).

Together our data show that the cost of ion homeostasis used to maintain plasmolysis determines the dynamics of bacterial starvation survival. Ion homeostasis used to maintain plasmolysis consumes the lion’s share of a starving cell’s energy budget (Fig. 4b). Maintaining plasmolysis is essential for starvation survival (Fig. 1d–g). Because nutrient starvation is a ubiquitous condition for microorganisms in natural environments, the principles underlying starvation survival uncovered in this work could elucidate microbial ecology in many nutrient-poor environments. A better understanding of the physiology of microbial starvation is essential for understanding many ecological processes in natural environments, such as in water bodies^1–3, soil^4,5, sediments^6–8 or even human microbiota^9–12.

Why bacteria need to remain in plasmolysis during starvation remains an open question. Perhaps plasmolysis helps reduce ion influx by reducing the surface area of the cytoplasm and the permeability of the plasma membrane. Another possibility is that vanishing turgor pressure is required during starvation. During plasmolysis, the turgor pressure is zero, as there is no mechanical contact between the cell poles and the cytoplasm, and therefore, the cell envelope is not under stress. Because expansion of the cell envelope may be driven by turgor pressure⁴⁷, we hypothesized that a lack of turgor during starvation may be required to prevent the expansion of the cell envelope during starvation. Starving cells have a limited capacity to synthesize cell wall building blocks to reinforce the cell wall, such that uncontrolled expansion would result in lysis. Indeed, this is precisely the phenotype that we observe for dying cells using time-lapse microscopy (Fig. 1).

Finally, some of the concepts elucidated in this work may be more general and apply to other ageing biological systems. Here, we found that cells must maintain a sufficiently rapid, ATP-consuming process to counteract a simultaneously occurring death-promoting process that does not require ATP. This pattern is probably not unique to E. coli. For example, elegant recent works have shown that yeast at frigid temperatures must produce antioxidants rapidly enough to reduce the level of reactive oxygen species sufficiently to prevent cell death⁴⁸. These examples seem to converge on the idea that a balance between competing processes—viability-sustaining processes that dissipate energy to maintain order and viability-ending processes that increase entropy and push the system towards equilibrium (death)—govern whether and when a cell irreversibly loses its viability.

The idea that the maintenance of order requires constant energy expenditure whereas decay into disorder occurs spontaneously is intuitive and probably applies broadly, including to systems far from thermodynamic equilibrium and even to complex non-thermodynamic systems.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41567-024-02511-2.

Methods

Strains

All strains used in this study were derived from wild-type E. coli K-12 strain NCM3722 (ref. 49). To titrated FtsZ, the construct ptac::FtsZ of strain VIP205 (ref. 50) was transferred to NCM3722 by P1 transduction. The bacteria used for Extended Data Fig. 1 were environmental isolates kindly provided by the laboratory of Roberto Kolter.

Culture medium

In this work we used two distinct culture media. Our standard medium was N−C− minimal medium⁵¹, containing K₂SO₄ (1 g), K₂HPO₄·3H₂O (17.7 g), KH₂PO₄ (4.7 g), MgSO₄·7H₂O (0.1 g) and NaCl (2.5 g) per litre. The medium was supplemented with 20 mM NH₄Cl as a nitrogen source and 0.1% glucose as the sole carbon source, unless indicated otherwise. For carbon or nitrogen starvation, N−C− minimal medium was prepared either without carbon (N+C−) or without nitrogen supplement (N−C+), respectively. The second medium was our osmo-balanced medium, which contains 0.2 M MOPS, titrated to pH 7 with KOH, and 1 mM MgCl₂, 0.1 mM CaCl₂, 0.16 mM K₂SO₄, 0.5 mM K₂HPO₄ and 22 mM NH₄Cl and lacks a carbon source. Cultures starved in the osmo-balanced medium were grown beforehand in N−C− medium supplemented with NH₄Cl and glucose.

Growth protocol

Growth was performed in batch cultures in glass test tubes (Fisher Scientific) with disposable, polypropylene Kim-Kap closures (Kimble Chase) in a water bath shaker kept at 37 °C. Single colonies were picked from a lysogeny broth (LB) agar plate, grown in LB until saturation and used to inoculate overnight cultures in N−C− minimal media supplemented with NH₄Cl and glucose. Dilutions were chosen such that cultures did not saturate overnight to ensure continuous exponential growth. The next day, cultures were diluted into fresh minimal medium and grown for at least five doublings. Starvation was induced by centrifugation (5,000 relative centrifugal force for 3 min), removal of supernatant and resuspension in fresh, carbon-free N−C− minimal medium or osmo-balanced medium. This protocol was chosen to avoid bacteria using waste products such as acetate after glucose was depleted⁵². For nutrient sources without acetate excretion (for example, glycerol), this washing step did not alter the survival kinetics³⁰. To achieve ‘stationary phase’ adaptation, we used the effect of excreted waste products and let E. coli grow on glucose until depletion, followed by washing 12 to 24 h later.

Viability counting

Samples were diluted in fresh N−C− minimal medium without a carbon substrate to an estimated target density of 4,000 CFU per ml using a multi-channel pipette and a 96-well plate. 100 μl of diluted culture were spread onto LB agar using plating beads (Rattler, Zymo Research) and incubated for 24 h. LB agar was supplemented with 25 μg ml⁻¹ of 2,3,5-triphenyltetrazolium chloride to stain colonies red and increase contrast for automated colony counting using an automated CellProfiler pipeline⁵³. Images were taken on a Rebel T3i (Canon) mounted on top of a Lightpad A920 (Artograph).

Live-cell microscopy

To image individual bacteria for 7 days, we designed a ‘no-flow’ chamber that minimizes nutrient contamination and evaporation. The chamber consists of a sandwich of a coverslip (22 × 50 mm, No 1.5, VWR) and a microscope slide (3” × 1” × 1 mm, VistaVision, VWR), with a thin layer of polydimethylsiloxane (PDMS) in between. At the top and bottom, the culture was in contact with inert glass, which prevented evaporation or leakage of nutrients from the plastic. Two holes were laser-cut into the microscope slide (Universal Laser Systems PLS 6.150D) through which the chamber will be filled. The PDMS layer (Sylgard 184, 1:10 ratio, Dow Corning) was spin-coated onto a silicon wafer for 30 s at 500 rpm (Laurell, WS-650MZ-23NPPB), cured at 85 °C for 1 h, peeled off and gently draped over the microscope slide. Then, the incubation chamber was cut out of the PDMS with a laser cutter and unwanted PDMS pieces were removed from the microscope slide with tweezers. The resulting microscope slide with a PDMS chamber was plasma-treated at 50 W for 10 s in O₂ with a duty ratio of 255 (Tergeo Plasma Cleaner, Pie Scientific), and the cover slide was placed on top. The finished chamber was cured overnight at 85 °C.

Cultures taken after exponential growth to optical density (OD) 0.5 were starved according to the above protocol and stained with 5 μg ml⁻¹ DiBac4(3) and 1.25 μg ml⁻¹ PI (Thermo Fisher Scientific) 10 min after entry to starvation. The no-flow chamber was then filled with the stained, starved culture at OD 0.5 through the laser-cut holes, in an identical way as in the batch experiments. The holes were then sealed (AlumaSeal, Sigma-Aldrich), and the chamber was centrifuged with the cover slide side down at 1,200 relative centrifugal force for 2 min to adhere the bacteria to the cover glass. The majority of bacteria stably adhered to the glass surface for 7 days without coating. Apart from the filling and centrifugation period, which were at room temperature, the culture and chamber were kept at 37 °C throughout the process.

Phase contrast and fluorescence microscopy was performed on a Nikon Ti-2 equipped with a ×100 phase contrast immersion oil objective, Hamamatsu Flash 4.0 sCMOS camera, Lumencor Spectra-X light engine and OkoLab cage microscope incubator set to 37 °C. For the time-lapse images, Nikon Elements was used to control illumination times (phase, 200 ms, green 10 ms and red 10 ms) and illumination strength (phase, 100%, green 10% and red 10%). A combination of perfect focus, a z-stack (four steps of 0.4 μm) and a software autofocus (postacquisition) were used to obtain continuous images of bacteria in focus.

The single-cell dry mass was measured using QPM on a Nikon Eclipse Ti with a Nikon, CFI Plan Apo Lambda ×100 objective with 1.5 numerical aperture and ×2 magnifier lens (EX2C extender, Thorlabs) and a commercial phase sensor (SID4bio, Phasics). In the trans-illumination light path, a coloured-glass band-pass filter (FGB39, Thorlabs) was mounted to select the blue light to increase the spatial resolution. This phase sensor enables single-shot acquisition of quantitative phase through quadriwave lateral shearing interferometry⁵⁴ using a two-dimensional diffraction grating (modified Hartmann mask) positioned a short distance from a CCD sensor. A raw image of the quantitative phase, measured as the optical path difference (OPD), was induced by both the sample and the optical system itself. We used the computationally enhanced QPM method as reported previously⁵⁵ to obtain the OPD of the optical system and fit the background fluctuations, which were then subtracted from the raw image to obtain the OPD of the cell. The dry mass $m$ was computed from the cell’s OPD through the relation $m=(1/\alpha )\oint \text{OPD}(x,y)\text{d}x\text{d}y$, where $\alpha =\text{d}n/\text{d}c$ is the average refractive index increment of cellular materials and the integral is over the cell area $S$. We used $\alpha =0.18$ ml g⁻¹ to convert the OPD to dry mass, which is the typical value for most cellular materials⁵⁶.

The time-lapse images were analysed in MATLAB. First, regions of interest with an object in phase contrast resembling a bacterium were identified. Next, for each time point, the correct focal plane was identified, the fluorescence background was subtracted and the regions of interest were cut out and saved separately. Finally, regions of interest were analysed, and the total fluorescence (summation of the values of all pixels) as well as length, width and area of the individual bacteria were recorded. For the QPM analysis, a segmented bacterium was dilated and the total phase shift was integrated to yield the total biomass. This analysis yielded 14,500 single-cell time traces of bacteria starving in the N−C− medium (Fig. 1) and 11,000 in the osmo-balanced medium (Fig. 4).

Scanning electron microscopy protocol

A culture was harvested by filtering 2 ml of exponentially growing or starving bacterial culture at OD 0.5 through a 0.22 μm filter (Durapore 0.22 μM PVDF membrane, GVWP02500, Millipore) held on a vacuum micro-filtration device (25 mm glass filter holder, XX1012502, Millipore). Immediately after this step, the filter was submerged in Karnovsky fixative (15732–10, Electron Microscopy Sciences). Cells were dislodged from the filter by repeated but gentle pipetting with a 1 ml pipette and kept in fixative solution for 1 h at room temperature. After 1 h, 500 μl of fixative containing cells were added to a 12 mm glass coverslip kept on a 35 mm petri plate (glass coverslips were precoated with poly-L-lysine) and centrifuged in a swing bucket centrifuge (Eppendorf) for 10 min at 5,000g. After centrifugation, the glass coverslips with adherent cells were placed in histology tissue fixation and processing cassettes (electron microscopy sciences), and the cassettes were sequentially dipped in a graded series of ethanol (30%, 50%, 75%, 80%, 90%, 95% and 100%). Grades of ethanol were prepared using anhydrous ethanol, 200 proof, obtained from Electron Microscopy Sciences (15058). Cells were kept in each grade of ethanol for 10 min, and the 100% ethanol step was repeated three times with fresh ethanol to ensure perfect dehydration. After this step, the cells were kept submerged in 100% ethanol overnight (at 4 °C) and taken to Harvard’s Center for Nanoscale Systems (CNS) next morning for further processing. Before microscopy, cells were critical point dried in a Tousimis critical point dryer, mounted on a scanning electron microscopy sample holder and coated with heavy metal (gold or palladium) using a sputter coater (Hummer) and imaged by a scanning electron microscope (JEOL 5600 LV). Processing steps at CNS and imaging was aided by the CNS stuff and facility in charge.

Transmission electron microscopy protocol

For the transmission electron microscopy, bacterial cell samples were collected similarly as for the scanning electron microscopy. Briefly, 2 ml of bacterial culture at OD 0.5 was taken, and cells were harvested by filtration. A filter containing harvested cells was immediately dipped in Karnovsky fixative, and cells were dislodged from the filter by gentle pipetting. Cells in fixative were taken to CNS for further processing. At CNS, cells in fixative were centrifuged to obtain a cell pellet, and the pellet was embedded in resin and thin sections were prepared. Cut sections were mounted on an electron microscope grid and imaged using a transmission electron microscope (HT7800, Hitachi).

Quantification of permeability

Live-cell microscopy with PI staining, as described see above, was used to measure single-cell permeability. The fluorescence signal was integrated over the entire area of each cell, as identified by thresholding in phase contrast, to calculate the total PI staining per cell of each cell per time point. The PI staining rate of each cell was fitted as a direct proportionality in the period from 0 to 10 h to calculate the total permeability across the membrane. To calculate the change of permeability compared to the reference condition, we used a no-flow chamber with six parallel channels, which allowed us to measure the permeability of five conditions and the reference condition in the same experiment.

Quantification of single-cell parameters

To quantify plasmolysis, the threshold for segmentation of the bacterium was chosen such that it contained only the cytoplasm (dark area). To quantify the length of the cell envelope, the threshold was increased such that the cell envelope (light grey area) was included in the segmentation. Both thresholding techniques are semi-quantitative, as the exact boundary of the outer and inner membrane cannot be resolved with phase microscopy, but they circumvent the problems generated by potentially toxic membrane stains.

The fluorescence signals from DiBa4(3) and PI were integrated over an entire segmented bacterium and normalized to the cell area to correct for differences in cell size. The time points of depolarization and permeabilization were determined by the first time the signal reached a threshold. For depolarization, the threshold was chosen to be the local minimum of the bimodal histogram of DiBac4(3) signals of all cells throughout 7 days of starvation. For PI, the threshold was chosen manually.

To align single-cell stretching and biomass loss, we searched in the vicinity of the time point of depolarization for the largest increase in length and the largest decrease in biomass, respectively. The time delays between the time point of depolarization and the time points of stretching and biomass loss are reported in Fig. 1.

Cell size

The cell volume was computed as $V=\pi {(w/2)}^2(l-w)+4/3\pi {(w/2)}^3$ where $w$ and $l$ are width and length of each cell, whose shape was considered to be a cylinder (with radius $w/2$ and height equal to $(l-w)$) with two semi-spheres at the ends (with radius $w/2$). The surface area was calculated analogously as $S=4\pi {(w/2)}^2+w/2(l-w)$. Because the cell width changed only marginally in the FtsZ titration, we assumed it to be constant and took the formulas of $S$ and $V$ at wild-type width to plot the length dependence of the surface and volume in Fig. 3.

Extended Data

Extended Data Fig. 1 |. Starvation of other substrates and of other bacterial species.

(A) Six gram-positive and gram-negative bacteria starved in N+C- medium, with previous growth on N + C+ with 0.1% glucose. (B) Starvation of the same bacteria as panel B, but in ‘osmo-balanced’ medium, identical to Fig. 4. (C) Comparison of death rates in N+C- (black) and low-salt, osmo-balanced medium (green). In all bacteria death rate in low-salt, osmo-balanced medium is slower than in N+C-, with the effect size being different for individual bacterial species.

Extended Data Fig. 2 |. Characterization of cellular dynamics during starvation.

(A) Length of the cytoplasm of 25 individual bacteria measured by thresholding in phase contrast (grey, cut off 1 h before lysis) and the average of 14,498 bacteria (red). (B) Histogram of the contraction of the cytoplasm in individual bacteria at 24 h. Note that in the vast majority of bacteria (99.7%), the cytoplasm shrunk. (C) Surface electron micrographs (SEM) of E. coli during growth show homogenous ridges of the cell envelope. In starvation the ridges on the surface are deeper, and a ‘sock-like’ structure is visible where the cytoplasm has contracted. In a dead cell, the surface is smooth, indicating that the surface structure is actively maintained. (D) Stretching of the cell envelope measured by thresholding in phase contrast. Cell envelope stretching is defined as the maximum length of the cell envelope divided by the average length of the cell envelope prior to expansion. (E) Increase of propidium iodide (PI) staining intensity upon lysis. For about 87% of bacteria a clear increase of staining was observed. A smaller subpopulation of 13% showed no discernable increase of biomass, possibly because DNA, the agent being stained by PI, was expelled upon lysis. (F) Loss of biomass distribution, measured as the ratio of the average biomass up to 6 h prior to lysis and the average biomass 9 h after lysis). # of bacteria: 34.

Extended Data Fig. 3 |. Impact of DiBac4(3) staining on lysis dynamics in a side-by-side comparison.

A no-flow chamber with two channels was used, and both channels were filled with the cells from the same culture. (A & B) Fluorescence signal of PI of individual cells over time (pixels along a column) for cultures stained either with PI and DiBac4(3) (4447 cells) or only with PI (5254 cells). Cells are sorted according to their time-point of lysis, defined as the first time-point when PI fluorescence signal crossed a threshold. Because cells stained with both DiBac and PI showed a lower PI fluorescence signal, the threshold used for DiBac4(3) + PI was chosen lower than for PI only. (C) Viability, defined as the fraction of cells that have not yet crossed the threshold defined in PI signal, decreases similarly for both cases. While the overall survival curve is similar between both experiments, there is a slight increase in death in early starvation (0 to 0.5 days) for cultures stained with DiBac4(3). (D) The delay between swelling and lysis was calculated as the time difference between the maximum increase in length prior to the cell crossing the PI threshold. The delay for DiBac4(3) and PI-stained cells is $\tau =(2.4\pm 1.2)$ h and for PI only we obtained $\tau =(2.5\pm 1.2)$ h, obtained by measuring mean and standard deviation in the regime from 0 to 10 h.

Extended Data Fig. 4 |. Recovery after nutrient addition.

E. coli, previously grown on minimal medium supplemented with glucose, were starved by washing and transferred to a chip with attached medium reservoirs. After 14.4 h (red dashed lines in panels A-D) fresh minimal medium with 0.2% glucose was flushed through the chip by exchanging the fluid in the reservoirs. Length, DiBac4(3) and PI fluorescence was recorded throughout starvation and recovery. DiBac4(3) is an indicator of membrane potential, while PI indicates lysis. Only cells that could be tracked for at least 2.5 h after glucose addition are included in the analysis (5256 total). (A, C) Length, normalized to the first 3 hours of starvation of individual cells that were either polarized or depolarized. DiBac4(3) thresholded at 150 A.U. Percentages indicate the fraction of cells of the respective classification that were able to recover within the time course of the experiment. (B, D) DiBac4(3) signal of the cells shown in panels A &C. Note that some bacteria in panel B depolarize after nutrient addition (orange arrows), while in panel D a cell can be seen that repolarizes (purple arrows). (E & F) Dibac4(3) at 14 h plotted against the maximum PI staining prior to 14 h for individual cells that either recovered or did not recover. Cells are only shown if they could be tracked for at least 2.5 h post glucose addition. Red lines indicated thresholds of ‘depolarization’ and ‘lysis’. Numbers indicate the number of cells in each quadrant. The depolarized, but not PI-stained cells in panel E had in common that they depolarized only shortly prior to nutrient supplementation (more than 1 h, less than 2 h), which indicates that depolarization is reversible unless it lasts too long. No PI-stained cell recovered.

Extended Data Fig. 5 |. Simulation with explicit nutrient recycling.

We used the same parameters as in the simulation shown in the main text but implemented nutrient recycling explicitly. Cell death would release nutrients into the medium, from where they are taken up by viable cells in a Michaelis-Menten type manner. (A) Viability in the simulation decreases exponentially. (B) Nutrients resources $\mathit{\nu }$ of an individual cell (blue), with time average (red). Nutrient resources are constant during the simulation. (C) and (D) same as left panels, but with external nutrient supply. Simulation with alternative parameters: (E) Viability, (F) nutrient resources. In this implementation we reduced the Hill coefficient of membrane stretching to 5 and the Km of membrane stretching to 0.4. Death rate is unchanged due to the self-adjusting manner of the system (compare to panels A-D).

Extended Data Fig. 6 |. Titration of cell length with ptac-ftsZ, induced with IPTG during growth.

Dark shades of cyan indicate high expression of ftsZ, while bright shades indicate low expression of ftsZ. (A) Cumulative distribution of cell length for different induction levels (cyan) and wild-type (red). Note that at low induction levels the spread of the distribution increases. (B) Example images of the lowest and highest induction of FtsZ.

Extended Data Fig. 7 |. Propidium iodide and DiBac4(3) staining.

(A) Viability of E. coli after 24 h of starvation in the presence of either DiBac4(3) or Propidium Iodide at the indicated concentrations show no significant decrease in viability compared to an untreated control culture. Error bars show standard deviation of three biological replicates. (B) Propidium iodide staining dynamics of individual viable bacteria stained for 24 h in batch, washed and resuspended in fresh, carbon-free and stain-free medium. (C) Distribution of staining rates (slope of exponential fits to PI fluorescence signal) in carbon-free and stain-free medium. Mean unstaining rate is slow compared to the timescale of the experiment, meaning that staining can be considered irreversible. (D) Example of a PI staining time-trace. Lysis leads to a rapid increase of PI staining. Prior to lysis, we observe a slow increase of permeability. Because PI staining is irreversible, the slope of the absolute fluorescence signal is a measure for the total permeability of a bacterium. (E) Comparison of the permeability (measured between 0 and 10 h after entry to starvation) for a culture permeabilized with 1 mM EDTA compared to control.

Extended Data Fig. 8 |. Effect of MOPS on death rate.

MOPS, balanced with KOH to pH7 was to culture media, such as the base concentration of N-C- medium remained constant. Data points and error bars show mean and standard deviation of three biological repeats. Compare this figure to Fig. 3C, where 0.5 M NaCl or KCl led to a 10-fold increase of death rate.

Extended Data Fig. 9 |. Effect of medium composition on death rate.

All cultures were grown in regular N + C+ medium supplemented with 10 mM glycerol and starved by switching medium. Reference: regular N + C- medium (red) n = 3. Change in medium concentration means that the starvation medium was prepared with increased or decreased concentrations of all N + C- salts (white), n = 1. In all conditions, the concentration of the phosphate buffer was sufficient to balance the pH during starvation, checked with pH strips.

Extended Data Fig. 10 |. Dependence of the maintenance rate on the medium.

(A) Example of a lag time measurement used for quantification of maintenance rate. After 1 day in starvation the culture in minimal medium with glucose as the previous carbon source we readded a small concentration of glucose (40 μM) and measured viability (grey) relative to a control without glucose addition (black). Using the average change in viability ${\mathbf{K}}^{-1}{\sum }_{\mathbf{k}}{\mathbf{N}}_{\mathbf{k}}^{+}/{\mathbf{N}}_{\mathbf{k}}^{-}$ where k are individual data points and $\mathbf{K}$ is the total number of data points per lag time (here: 3) and the death rate $\mathit{\gamma }$, determined using the entire death curve shown in Fig. 4. Note that to achieve the change in viability (here: 47%) by growth, the culture would require addition of at least 500 μM. Concentrations of glucose added in the experiment are below levels for which growth is observed. Details on the maintenance rate protocol can be found in Ref. 5. (B, C) Lag times of three independent experiments, where each culture was split, and varying glucose concentrations were added (symbols correspond to identical experiments). Maintenance rate $\mathit{\beta }$ is extracted as the inverse of the slope. Maintenance rate in N + C- minimal medium is around 10-fold higher than in ‘Osmo-balanced’ minimal medium.

Data availability

All data analysed are available in the supporting information. Raw microscopy data and strains can be shared upon request. Source data are provided with this paper.